
PAŃSTWOWA WYŻSZA SZKOŁA ZAWODOWA W CHEŁMIE
INSTYTUT NAUK TECHNICZNYCH
Laboratorium Mechaniki Płynów
Ćwiczenie 5
Badanie przepływu w warstwie przyściennej.
Opracował: dr inż. Dariusz Mika

1. Wprowadzenie teoretyczne.
POJĘCIE WARSTWY PRZYŚCIENNEJ
Występujące w technice przepływy płynów lepkich są przepływami, w których siły
tarcia są małe w porównaniu z siłami bezwładności. Woda i powietrze - płyny, z którymi
najczęściej spotykamy się w różnych zagadnieniach technicznych - odznaczają się małą
lepkością, a zatem już przy stosunkowo niewielkich prędkościach otrzymujemy podczas ich
przepływów duże wartości liczby Reynoldsa. W równaniach Naviera-Stokesa, w miarę
zwiększania się liczby Reynoldsa, wyrazy zależne od lepkości stają się coraz mniejsze w
porównaniu z wyrazami bezwładnościowymi, a dla liczb Reynoldsa
Re
, wyrazy te
dążą do zera, a równania ruchu nie różnią się już od równań dotyczących płynu doskonałego.
W odróżnieniu od płynu doskonałego (a więc nielepkiego), w którym tylko składowa
normalna prędkości musi znikać na nieprzepuszczalnej ścianie, w płynie lepkim również
składowe styczne prędkości znikają na tego rodzaju ścianie. Warunki te nie zależą od
prędkości płynu w punktach odległych od granicy. Oznacza to, że podczas przepływu płynu
pseudodoskonałego (tzn. z dużą prędkością) siły lepkości są dominujące w pobliżu ściany
sztywnej (lub granicy różnych płynów), chociaż w głównej masie płynu dominują siły
bezwładności. Rozwiązanie tego problemu polega na podzieleniu całego obszaru
poruszającego się płynu na dwa nierówne podobszary (rys. 1.) i prowadzeniu rozważań
osobno dla każdego z nich. Podział ten - zaproponowany przez Prandtla - polega na
wprowadzeniu podobszaru, w którym siły lepkości są całkowicie pomijalne, oraz drugiego, w
którym ich wpływ jest decydujący
.
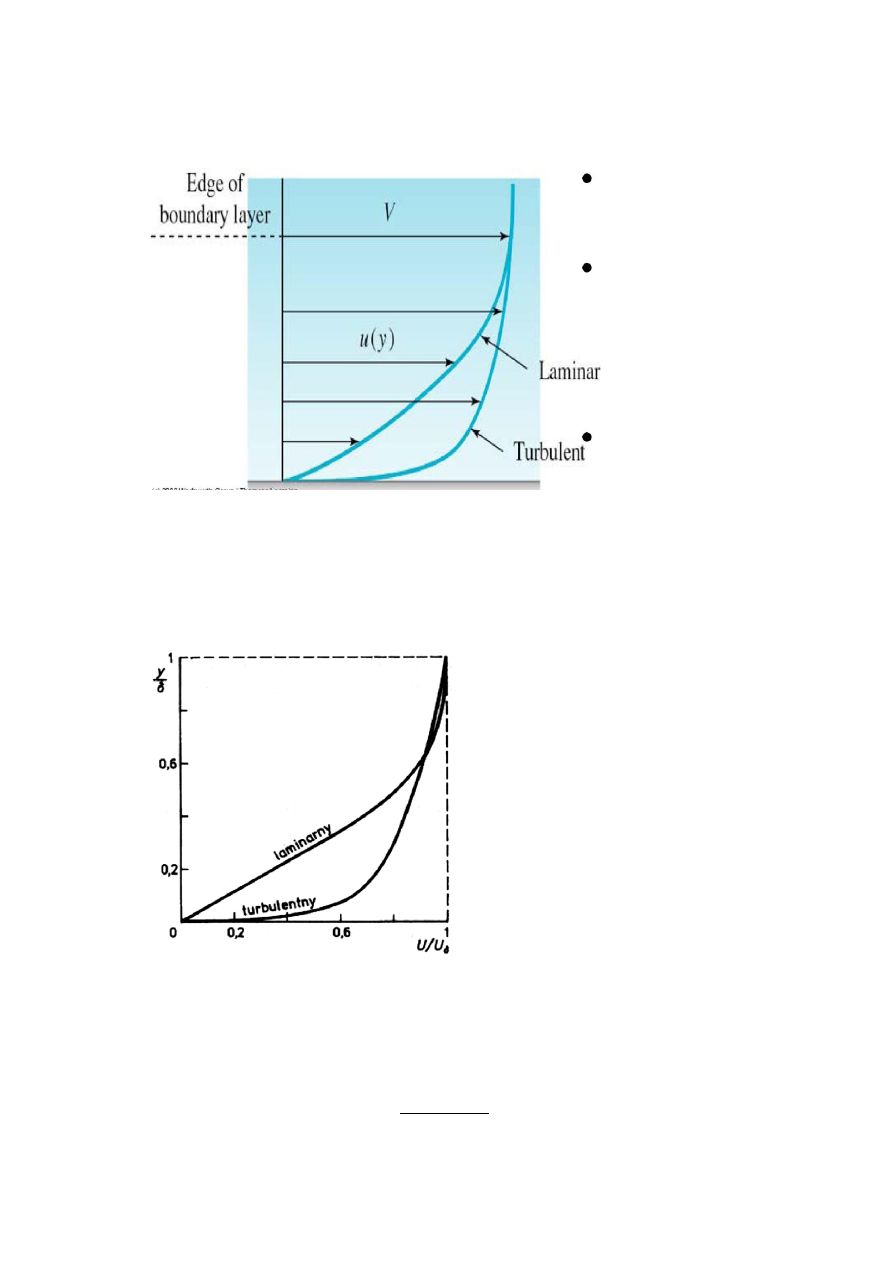
Rys. 1. Obraz warstwy przyściennej.
Warstwę płynu poruszającą się blisko granicy ośrodków (np. ściany) nazywa się
warstwą przyścienną. Przez to pojęcie rozumiemy zarówno warstwę przyścienną tworzącą się
na opływanej nieprzenikliwej powierzchni, jak i warstwę graniczną tworzącą się w
przepływie swobodnym otoczonym przepływem potencjalnym (struga zatopiona, ślad za
opływanym ciałem).
W warstwie przyściennej występują intensywne zmiany prędkości od zera na ścianie do
wartości równej prędkości płynu poza nią. Między warstwą przyścienną a główną masą płynu
nie ma wyraźnego rozgraniczenia, toteż nie można ściśle zdefiniować zasięgu warstwy.

Zwykle przyjmuje się, że warstwa przyścienna sięga do miejsca, w którym prędkość jest o 1%
mniejsza od prędkości przepływu potencjalnego, tj. prędkości, jaka ustaliłaby się w tym
punkcie podczas przepływu płynu doskonałego.
Grubością
warstwy przyściennej nazywa się taką odległość od powierzchni ciała, dla
której zmiana prędkości przepływu w kierunku prostopadłym do powierzchni ściany jest w
przybliżeniu równa zeru. Grubość tej warstwy narasta stopniowo w miarę oddalania się (w
kierunku przepływu) od krawędzi natarcia (miejsca podziału strug opływających ciało) - rys.
1.
Poza warstwą przyścienną leży podobszar, w którym siły masowe (bezwładności)
dominują nad siłami lepkości i w związku z tym płyn uważa się za doskonały. Podczas
rozważania przepływu wokół ścian o kształtach regularnych przyjmuje się, że poza warstwą
przyścienną przepływ kształtuje się tak jak w ruchu potencjalnym.
RÓWNANIA PRZEPŁYWU W LAMINARNEJ WARSTWIE PRZYŚCIENNEJ
W celu wyznaczenia parametrów przepływu w pobliżu ścian należy uwzględnić lepkość
płynu i rozwiązać równanie ruchu w postaci Naviera-Stokesa. Wobec małej grubości warstwy
przyściennej, w porównaniu z długością opływanej ściany (
1
/
l
), równania Naviera-
Stokesa sprowadza się w rozważanym przypadku do uproszczonej postaci, zwanej
równaniami Prandtla.
Zakłada się płaski ustalony przepływ płynu nieściśliwego wokół gładkiej nieruchomej
ściany, opływanej przez płyn z prędkością
V
. Pomija się siły ciężkości, a przepływ poza
warstwą traktuje jako potencjalny.
Rozważmy opływ płaskiej poziomej ściany o skończonej długości l - w kierunku osi x
(rys. 1), będącym kierunkiem przepływu swobodnego - i nieskończonej, w poprzecznym
kierunku z, tzn.
z
>. Wtedy dla x < 0 przepływ nie jest zaburzony obecnością
ściany.
Równania Naviera-Stokesa oraz ciągłości przepływu przybierają postać
2
2
2
2
1
y
v
x
v
x
p
y
v
v
x
v
v
x
x
lepkoć
x
y
x
x
,
2
2
2
2
1
y
v
x
v
y
p
y
v
v
x
v
v
y
y
lepkoć
y
y
y
x
, (1)
0
y
v
x
v
y
x
.
gdyż prędkość nie zmienia się w kierunku osi z.

Ścisłe rozwiązanie tego układu równań różniczkowych jest zagadnieniem b. trudnym.
Wprowadzając jednak pewne założenia oraz oszacowując rząd wielkości poszczególnych
składników równań i odrzucając składniki niższego rzędu, układ równań przyjmuje postać
2
2
1
x
v
x
p
y
v
v
x
v
v
x
lepkoć
x
y
x
x
,
y
p
1
0
, (2)
0
y
v
x
v
y
x
.
Drugie z równań układu (2) umożliwia sformułowanie wniosku, że ciśnienie w warstwie
przyściennej jest stałe wzdłuż normalnej do opływanej powierzchni, ma więc tę samą wartość
na powierzchni, co i na granicy warstwy. Wynika stąd dalszy wniosek, że w podobszarze
warstwy przyściennej ciśnienie jest wyłącznie funkcją zmiennej x, identyczną z funkcją
określającą ciśnienie na powierzchni opływanej płynem doskonałym. Wnioski te,
sformułowane na podstawie rozważań teoretycznych, zostały potwierdzone licznymi
doświadczeniami.
Po uwzględnieniu drugiego równania układu (2) otrzymamy ostatecznie wspomniane
wcześniej równania Prandtla
2
2
1
y
v
x
p
y
v
v
x
v
v
x
lepkoć
x
y
x
x
, (3)
0
y
v
x
v
y
x
.
Równania te, choć wyprowadzono je jako odnoszące się do płaskiej płyty, są słuszne i
w bardziej ogólnych przypadkach dwuwymiarowych przepływów, z tym jednak, że promień
krzywizny ściany w każdym jej punkcie jest wielokrotnie większy od grubości warstwy
przyściennej w tym punkcie.
Z drugiego równania (2) wynika, że ciśnienie nie zmienia się w poprzek warstwy
przyściennej, a zatem, mimo jej istnienia, ciśnienie statyczne można mierzyć bezpośrednio na
opływanej powierzchni.
Metoda rozwiązywania zagadnień przepływów płynów lepkich, z wykorzystaniem
koncepcji warstwy przyściennej i równania Prandtla, polega na:
Wyznaczeniu przepływu płynu nielepkiego wokół ciała, a szczególnie rozkładu
ciśnienia p(x) na ścianie.

Rozwiązaniu równań Prandtla z uwzględnieniem wyznaczonego rozkładu ciś-
nienia i odpowiednich warunków brzegowych.
Taka droga postępowania jest wprawdzie dokładna, ale dość uciążliwa. Nie będzie
zatem przedstawione rozwiązanie układu równań Prandtla, a jedynie zostaną naszkicowane
tylko główne wyniki tego rozwiązania.
Rozwiązanie układu równań (3) umożliwia znalezienie rozkładu prędkości w warstwie
przyściennej, a stąd naprężenia stycznego. W przypadku opływu ściany płaskiej (lub o
niewielkiej krzywiźnie) można pokazać, że naprężenia styczne w warstwie przyściennej
przyjmują postać (sposób wyprowadzenia tej zależności znajduje się w dodatku A do
ćwiczenia). Jest to tzw. zależność całkowa Karmana
0
0
)
(
dy
u
V
u
dx
d
(4)
gdzie u=v
x
- prędkość płyny wzdłuż płyty.
Definiując wielkość Θ, nazywaną liniową miarą zmniejszenia strumienia pędu jako
dy
V
u
V
u
0
1
(5)
zależność całkową Karmana możemy przedstawić w uproszczonej formie
)
(
2
0
V
dx
d
(6)
Grubość laminarnej warstwy przyściennej, obliczona dla bieżącej (lokalnej) liczby
Reynoldsa
x
V
x
Re
(7)
wynosi
x
x
x
Re
5
)
(
(8)
2. Cele ćwiczenia
Celem ćwiczenia jest badanie warstwy przyściennej przy opływie płaskiej płytki,
wyznaczenie rozkładu prędkości w tej warstwie oraz wyznaczenie naprężeń stycznych na
powierzchni płytki.

3. Zadania
a) Wyznaczyć profile prędkości u(y) w funkcji wysokości y w warstwie
przyściennej wzdłuż powierzchni płaskiej płytki , grubość warstwy przyściennej
na każdej stacji pomiaru oraz lokalną liczbę Reynoldsa,
b) Wyznaczyć profile prędkości w bezwymiarowej formie
/
y
versus
V
u /
c) Wyznaczyć naprężenia styczne na powierzchni płytki korzystając z całkowego
wzoru Karmana
4 Przebieg ćwiczenia.
Ćwiczenie przeprowadzane jest z wykorzystaniem tunelu aerodynamicznego
edukacyjnego Aerolab typu otwartego. W komorze testowej tunelu należy umieścić płaską
płytkę wyposażoną w specjalny próbnik (10-kanałowy manometr) tzw. "mouse". Otwarte
końcówki próbnika "mouse" umieszczone są kolejno na 0.018, 0.025, 0.030, 0.040, 0.060,
0.100, 0.120, 0.160, 0.200 cala od powierzchni płyty. Drugie końcówki próbnika należy
podpinać do multi-manometru tunelu. Drugie gałązki manometru są otwarte do atmosfery w
związku z tym manometr mierzy różnicę ciśnienia całkowitego na przekroju pomiarowym i
ciśnienia atmosferycznego. Należy pamiętać o odpowiedniej konwencji znakowej
odczytywania wysokości słupków cieczy w manometrach. Wysokości powyżej przyjętego
poziomu zerowego bierzemy ze znakiem (-) (podciśnienie w stosunku do ciśnienia
atmosferycznego) natomiast wysokości poniżej poziomu zerowego ze znakiem (+)
(nadciśnienie). Aby obliczyć ciśnienie dynamiczne w śladzie aerodynamicznym otrzymane
wyniki pomiaru ciśnienia należy odnieść do ciśnienia statycznego sekcji testowej (ciśnienie
dynamiczne jest różnicą między ciśnieniem całkowitym a ciśnieniem statycznym). Do
otrzymanych wyników należy dodać więc różnicę między ciśnieniem otoczenia a ciśnieniem
statycznym sekcji testowej
st
P
p
p
p
0
1
0
. Różnicę tych ciśnień odczytujemy korzystając
z sondy Prandtla umieszczonej w sekcji testowej tunelu. Otrzymane wyniki będą wówczas
stanowiły ciśnienie dynamiczne p
d3
=Δp+Δp
P0-1=
(p-p
0
)+(p
0
-p
st
)=p-p
st.
. Za pomocą sondy
Prandtla wyznaczamy dodatkowo ciśnienie dynamiczne przepływu niezakłóconego
2
1
2
025
,
0
P
O
H
d
z
g
p
.
Należy ustawić prędkość na wartość 15-20 m/s i przeprowadzić pomiary dla 3 pozycji
zdefiniowanej na prowadnicy próbnika "mouse". Wyniki pomiaru wraz z odległością
otworów pomiarowych sondy od krawędzi płyty należy zapisać w tabelce ćwiczeniowej.
5. Opracowanie wyników pomiaru.
Wyniki pomiarów należy przedstawić w formie wykresu prędkości przepływu u(y)
versus odległość od powierzchni płyty y dla każdej stacji pomiarowej (zadanie a)).
Przykładowy wykres tego rodzaju dla jednej stacji pomiarowej przedstawia rys. 2.
Otrzymane profile prędkości odpowiadające poszczególnym stacjom należy przedstawić w
formie wykresy z rys. 1.
Rys. 2. Przykład rozkładu prędkości w warstwie przyściennej.
Dla każdej stacji pomiarowej należy wyznaczyć grubość warstwy przyściennej oraz
lokalną liczbę Reynoldsa. - wzory (7) i (6).
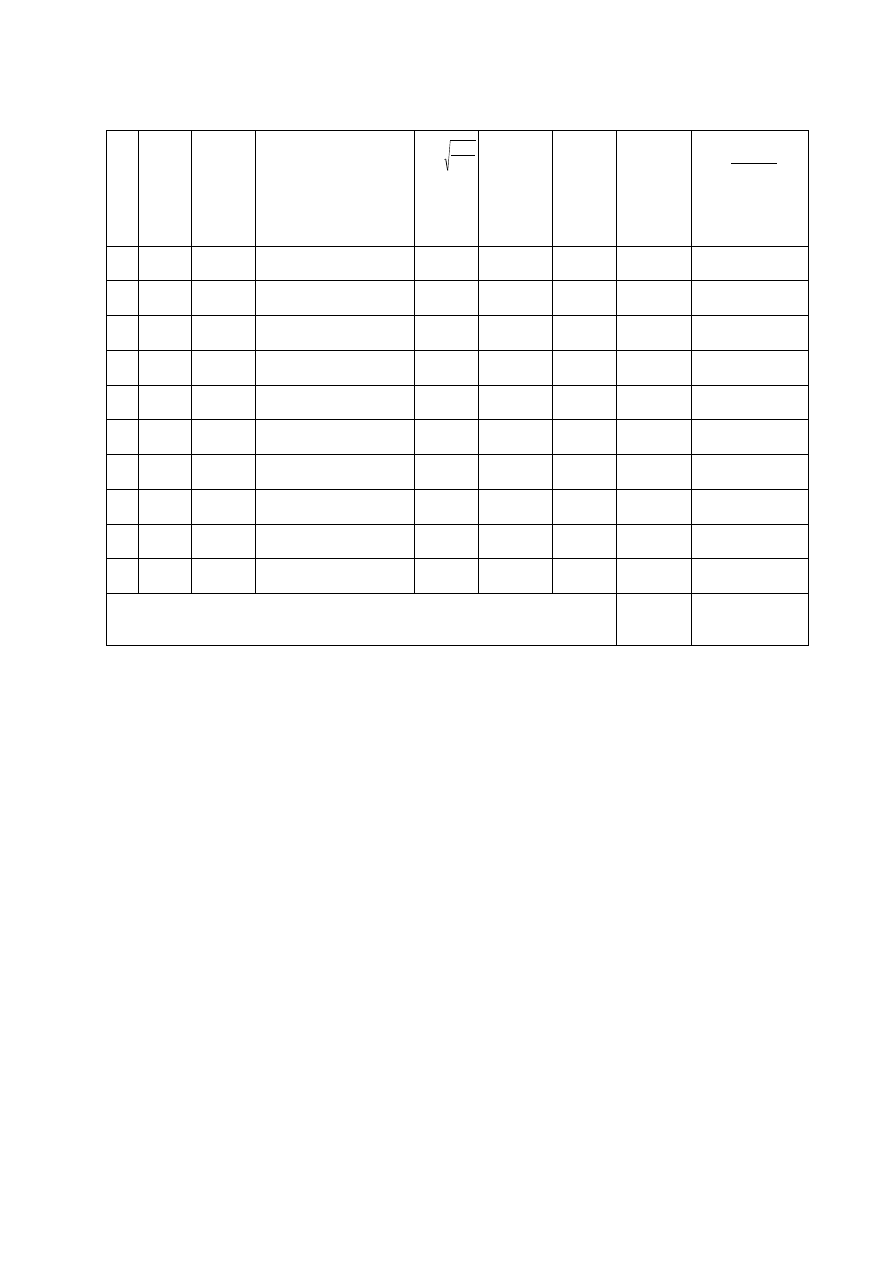
W zadaniu b) należy wyznaczyć
profile prędkości w bezwymiarowej formie
/
y
versus
V
u /
(zadanie b))
. Przykład
tego typu wykresu został przedstawiony
na
rys. 3.
Rys. 3. Przykład profilu prędkości w
warstwie przyściennej przedstawiony w
formie
bezwymiarowej
/
y
versus
V
u /
.
Zadaniu c) polega na wyznaczeniu naprężeń stycznych na powierzchni płytki z
przybliżonego całkowego wzoru Karmana. Wartość pochodnej wyznaczamy w sposób
przybliżony korzystając z ilorazu różnicowego dla dwóch kolejnych stacji pomiarowych.
x
n
n
1
0
(9)
v
x
y

gdzie:
0
)
(
dy
u
V
u
n
- całka występująca we wzorze Karmana wyznaczona dla
n-tej stacji pomiarowej,
x
- odległość pomiędzy dwiema kolejnymi stacjami pomiarowymi .
Wartość całki występującej we wzorze Karmana możemy wyznaczyć stosując np.
metodę trapezów.
1
1
1
0
)
2
(
)
(
n
i
i
i
i
i
y
dy
u
V
u
(10)
gdzie:
)
(
i
i
u
V
u
- iloczyn występujący pod całką we wzorze Karmana;
)
(
1
i
i
i
y
y
y
- różnica odległości między dwoma kolejnymi próbnikami
sondy "mouse".
Obliczenia naprężeń stycznych należy wykonać dla dwóch początkowych i dwóch
końcowych stacji pomiarowych
Literatura
1.
Kabsch K, H. Szewczyk: Mechanika Płynów, Oficyna Wydawnicza Politechniki Wrocławskiej,
Wrocław 2001.
2.
Bukowski J, Kijkowski P.: Kurs mechaniki płynów, PWN, Warszawa 1980.

Zadanie do wykonania:
1. Wyznaczyć profile prędkości u(y) w funkcji wysokości y w warstwie przyściennej
wzdłuż powierzchni płaskiej płytki , grubość warstwy przyściennej na każdej stacji
pomiaru oraz lokalną liczbę Reynoldsa,
2. Wyznaczyć profile prędkości w bezwymiarowej formie
/
y
versus
V
u /
3. Wyznaczyć naprężenia styczne na powierzchni płytki korzystając z całkowego
wzoru Karmana
t
ot
=.......[°C]; p
ot
=...........[Pa]; q=......[Pa];
V
=......[m/s];
.....
pow
[kg/m
3
];
1000
2
O
H
[kg/m
3
];
..........
025
,
0
1
0
0
1
0
P
P
z
g
p
p
p
;
1
0
P
z
-
wysokość słupa cieczy manometru odpowiadająca różnicy ciśnienia
atmosferycznego i ciśnienia statycznego sekcji testowej [cal].
Tabela ćwiczeniowa do zadanie a) i b)
Stacja pomiarowa nr 1. x
1
=.......[mm];
Lp
.
i
y
[m]
z
[cal]
1
0
2
025
,
0
P
O
H
iDyn
p
z
g
p
[pa]
pow
idyn
i
p
u
2
[m/s]
V
u
i
/
)
(
i
i
u
V
u
[m
2
/s
2
]
i
i
i
y
y
y
1
[m]
i
i
i
i
y
)
2
(
1
[m
3
/s
2
]
1
2
Państwowa Wyższa Szkoła Zawodowa w Chełmie
Laboratorium
Mechaniki Płynów
Laboratorium mechaniki płynów, ćwiczenie nr 5
Temat ćwiczenia: „ Badanie przepływu w warstwie przyściennej."
Imię i nazwisko
Grupa
Semestr/rok akademicki
Prowadzący
Data wykonania ćwiczenia/godz.
Ocena

3
4
5
6
7
8
9
10
----------------
9
1
i
i
Stacja pomiarowa nr 2. x
2
=.......[mm];
Lp
.
i
y
[m]
z
[cal]
1
0
2
025
,
0
P
O
H
iDyn
p
z
g
p
[pa]
pow
idyn
i
p
u
2
[m/s]
V
u
i
/
)
(
i
i
u
V
u
[m
2
/s
2
]
i
i
i
y
y
y
1
[m]
i
i
i
i
y
)
2
(
1
[m
3
/s
2
]
1
2
3
4
5
6
7
8
9
10
----------------
9
1
i
i
Stacja pomiarowa nr 3. x
3
=.......[mm];
Lp
.
i
y
[m]
z
[cal]
1
0
2
025
,
0
P
O
H
iDyn
p
z
g
p
[pa]
pow
idyn
i
p
u
2
[m/s]
V
u
i
/
)
(
i
i
u
V
u
[m
2
/s
2
]
i
i
i
y
y
y
1
[m]
i
i
i
i
y
)
2
(
1
[m
3
/s
2
]
1
2
3
4
5
6
7
8
9
10
----------------
9
1
i
i

Dodatek do ćwiczenia A.
Rozważmy układ równań Prandtla opisujący parametry przepływu w warstwie
przyściennej
2
2
1
y
v
x
p
y
v
v
x
v
v
x
lepkosć
x
y
x
x
A1
0
y
v
x
v
y
x
A2
Z równania Bernoulliego dla przepływu niezakłóconego (poza warstwą przyścienną)
mamy
const
V
p
2
2
1
A3
różniczkując to wyrażenie względem współrzędnej x
x
p
x
V
V
1
A4
Z zależności Newtona wiemy, że naprężenia styczne są proporcjonalne do gradientu
prędkości w kierunku prostopadłym do przepływu
dy
dv
x
A5
różniczkując to wyrażenie względem x oraz pamiętając, że
lepkosc
otrzymujemy
2
2
1
y
v
y
x
lepkosc
A6
podstawiając otrzymane wyrażenia do zależności A1 oraz całkując obie strony po
zmiennej y otrzymujemy

0
0
1
h
x
y
x
x
dy
x
V
V
y
v
v
x
v
v
A7
Całkując równanie ciągłości A2 mamy
h
x
y
dy
x
v
v
0
A8
Rozważmy teraz drugi składnik zależności A7. Całkując go przez części otrzymujemy
h
y
x
h
y
x
h
x
y
dy
y
v
v
v
v
dy
y
v
v
0
0
0
A9
Wykorzystując warunki brzegowe:
0
y
x
v
v
dla
0
y
oraz
V
v
x
i
h
x
y
dy
x
v
v
0
dla
h
y
otrzymujemy
h
h
y
x
x
h
x
y
dy
y
v
v
dy
x
v
V
dy
y
v
v
0
0
0
A10
a wykorzystując równanie ciągłości A2 mamy
h
h
x
x
x
h
x
y
dy
x
v
v
dy
x
v
V
dy
y
v
v
0
0
0
A11
Podstawiając to wyrażenie do A7 otrzymujemy
0
0
1
2
h
x
x
x
dy
x
V
V
x
v
V
x
v
v
A12
można zauważyć, że
x
v
x
v
v
x
x
x
2
2
A13
oraz

x
v
V
x
V
v
x
V
v
x
x
x
stąd
x
V
v
x
V
v
x
v
V
x
x
x
A13
podstawiając to do A12 i odpowiednio grupując otrzymujemy
h
h
x
x
x
dy
v
V
dx
dV
dy
v
V
v
x
0
0
0
1
)
(
)
(
A14
Jest ogólna postać zależności Karmana dla przepływu w warstwie przyściennej.
Dla opływu ściany płaskiej zakładamy, że prędkość strumienia niezakłóconego nie
zmienia się
const
V
. Stąd dla takiego przypadku wzór Karmana upraszcza się
h
dy
u
V
u
dx
d
0
0
)
(
A15
gdzie:
x
v
u
Ponieważ dla
y
(dla obszaru poza warstwą przyścienna) wartość całki jest stała
możemy ostatecznie zmienić granicę całkowania
0
0
)
(
dy
u
V
u
dx
d
A15
Powyższą zależność wyprowadzić można również stosując zasadę zachowania
strumienia pędu.
Wyszukiwarka
Podobne podstrony:
Badanie przeplywu w warstwie pr Nieznany
Badanie przepływomierzy masowych i objętościowych powietrza
wzór z rozwiązaniem aerodynamika II warstwa przyścienna
Zastosowanie efektu Dopplera do ultrasonograficznych metod badania przepływu krwi
Badanie przepływu@-5, Technika cieplna
badanie przeplywu cieczy prawo Nieznany (2)
Badania dyfraktometryczne warstw wierzchnich
badanie tranzystora warstwowego
Badania przepływającego płynu BP
19 - Badanie przepływu cieczy, Studia, II rok, Fizyka Eksperymentalna
Badanie przepływomierzy masowych i objętościowych powietrza
Zastosowanie efektu Dopplera w badaniu przeplywu krwi
Lab 2 Knapczyk, Maszyny przeplywowe badanie pompy wirowej
Suszenie konwekcyjne ziarna w nieruchomej warstwie przy stałym kierunku przepływu czynnika suszącego
2.3.1 Używanie warstw do analizy problemów związanych z przepływem informacji, 2.3 Modele działania
OI16 Badanie praw przeplywu pra Nieznany
II16 Badanie praw przeplywu pradu
więcej podobnych podstron