POLITECHNIKA BIAŁOSTOCKA

WYDZIAŁ ELEKTRYCZNY

___________________________________________________________

Laboratorium Miernictwa Elektrycznego

Mostek Thomsona

ć

wiczenie nr 6

Białystok 1998

Ć

wicz. nr 6 Mostek Thomsona

1

1. Wprowadzenie

ostek Thomsona jest układem przeznaczonym do pomiaru szczególnie
małych rezystancji - od ułamków milioma (m

Ω

) do kilku omów (

Ω

).

S

ą

to rezystancje porównywalne z rezystancjami przewodów

ł

ą

cz

ą

cych, których obecno

ś ć

jest nieunikniona w ka

ż

dym układzie pomiarowym.

Dla przykładu rezystancja mierzona w niniejszym

ć

wiczeniu ma warto

ś ć

R

X

≈

1 m

Ω

, tymczasem miedziany przewód ł

ą

cz

ą

cy o długo

ś

ci 0,5 m

i przekroju 1,5 mm

2

ma rezystancj

ę

R

p

≈

6 m

Ω

(rys.1)

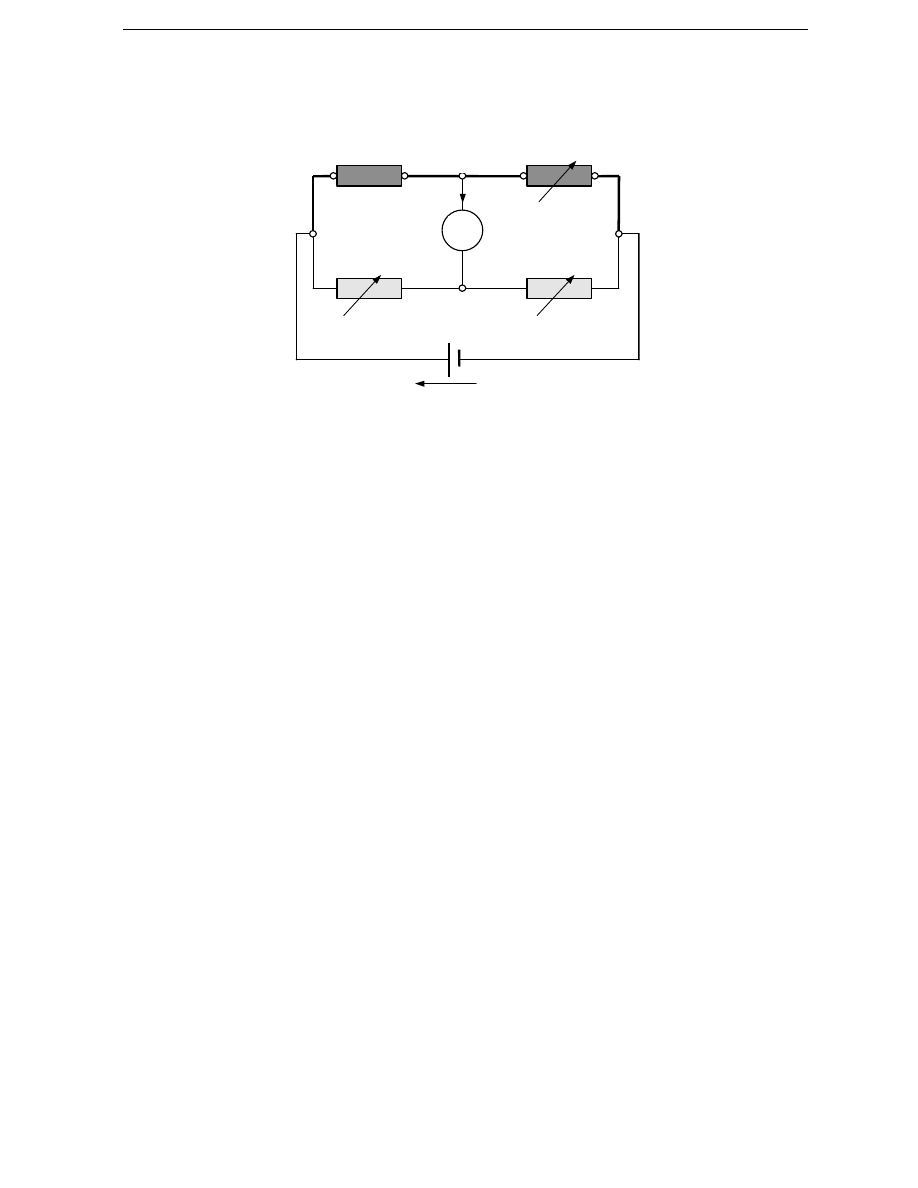
B

A

R

P

R

X

R

P

Rys.1. Rezystancja mierzona R

x

wraz z przewodami ł

ą

cz

ą

cymi.

Próba pomiaru tak małej rezystancji w układzie mostka Wheatstone’a

zako

ń

czyłaby si

ę

wynikiem obarczonym olbrzymim bł

ę

dem.

Na rys.1 przedstawione jest jedno z czterech ramion mostka Wheatstone’a.

Pomijaj

ą

c inne aspekty maj

ą

ce wpływ na bł

ą

d pomiaru, nale

ż

y zauwa

ż

y

ć

,

ż

e w

układzie tego mostka zostałaby zmierzona rezystancja całej gał

ę

zi AB. Jej

warto

ś ć

dla przytoczonych wy

ż

ej warto

ś

ci rezystancji R

X

, R

P

wyniosłaby:

R

AB

= R

x

+ 2R

p

= 13 m

Ω

Wynik pomiaru trzynastokrotnie przewy

ż

szałby wi

ę

c warto

ś ć

rzeczywist

ą

rezystancji R

x

, za

ś

bł

ę

dy pomiaru wyniosłyby odpowiednio:

a) bł

ą

d bezwzgl

ę

dny:

Ω

⋅

=

−

=

∆

m

R

R

R

x

AB

12

b) bł

ą

d wzgl

ę

dny:

δ

R

x

R

R

=

=

∆

100%

1200%

!!!

M

Ć

wicz. nr 6 Mostek Thomsona

2

Zaproponowany w roku 1862 przez fizyka angielskiego Williama

Thomsona (od roku 1892 lorda Kelvina) układ do pomiaru małych rezystancji
wywodzi si

ę

z układu mostka Wheatstone’a, którego schemat ideowy jest

przedstawiony na rys. 2.

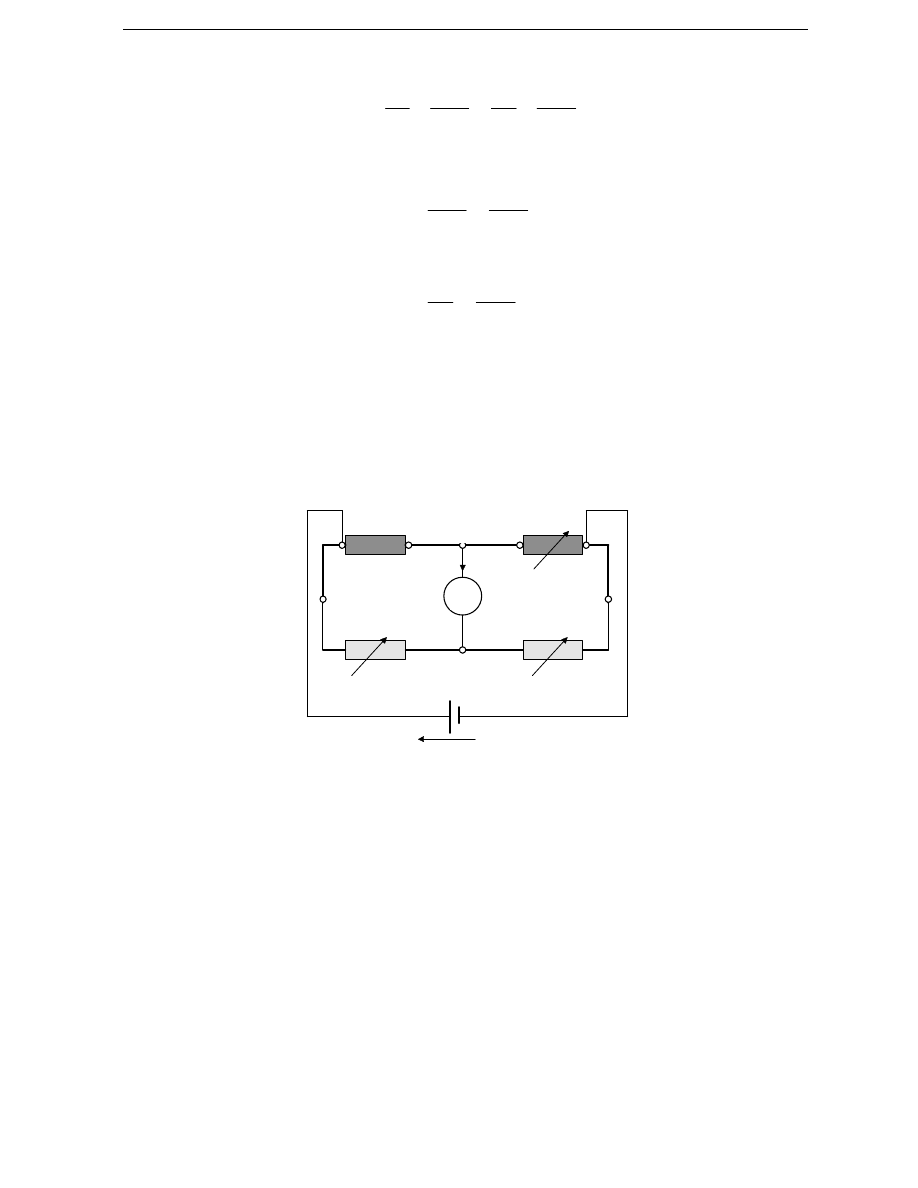
U

Z

I

G

R

4

R

3

R

2

R

1

G

A

G

F

E

D

C

B

Rys. 2. Schemat ideowy mostka Wheatstone’a

z bardzo małymi rezystancjami R

1

, R

2

Na schemacie tym pogrubiono cztery odcinki przewodów ł

ą

cz

ą

cych: AB,

CD, DE, FG. Ich rezystancje s

ą

porównywalne z rezystancjami rezystorów R

1

,

R

2

i odgrywaj

ą

znacz

ą

c

ą

rol

ę

w górnych ramionach mostka. Natomiast

rezystancje R

3

, R

4

maj

ą

warto

ś

ci rz

ę

du co najmniej kilkuset omów (cz

ę

sto kilku

lub kilkunastu kiloomów), wobec czego wpływ przewodów wyst

ę

puj

ą

cych

wokół nich mo

ż

na całkowicie zaniedba

ć

.

Wyja

ś

nijmy jeszcze,

ż

e potrzeba pomiaru bardzo małej rezystancji R

1

,

poci

ą

ga za sob

ą

konieczno

ś ć

wł

ą

czenia do układu jeszcze jednej rezystancji tego

samego rz

ę

du. Z analizy bł

ę

du nieczuło

ś

ci mostka Wheatstone’a wynika,

ż

e

powinna ni

ą

by

ć

rezystancja R

2

. Kwestia ta jest szczegółowo omawiana na

wykładzie dotycz

ą

cym mostka Wheatstone’a.

Pierwszym

krokiem

na

drodze

przekształcania

układu

mostka

Wheatstone’a w układ mostka Thomsona jest przeniesienie odcinków AB oraz
FG przewodów ł

ą

cz

ą

cych do tych gał

ę

zi mostka, w których s

ą

one nieszkodliwe,

a wi

ę

c do gał

ę

zi zawieraj

ą

cych du

ż

e rezystancje R

3

, R

4

. Osi

ą

ga si

ę

to przez

doprowadzenie przewodów biegn

ą

cych od

ź

ródła zasilania bezpo

ś

rednio do

zacisków B i F małych rezystancji R

1

, R

2

. Rezultat takiego zabiegu

przedstawiono na rys. 3.

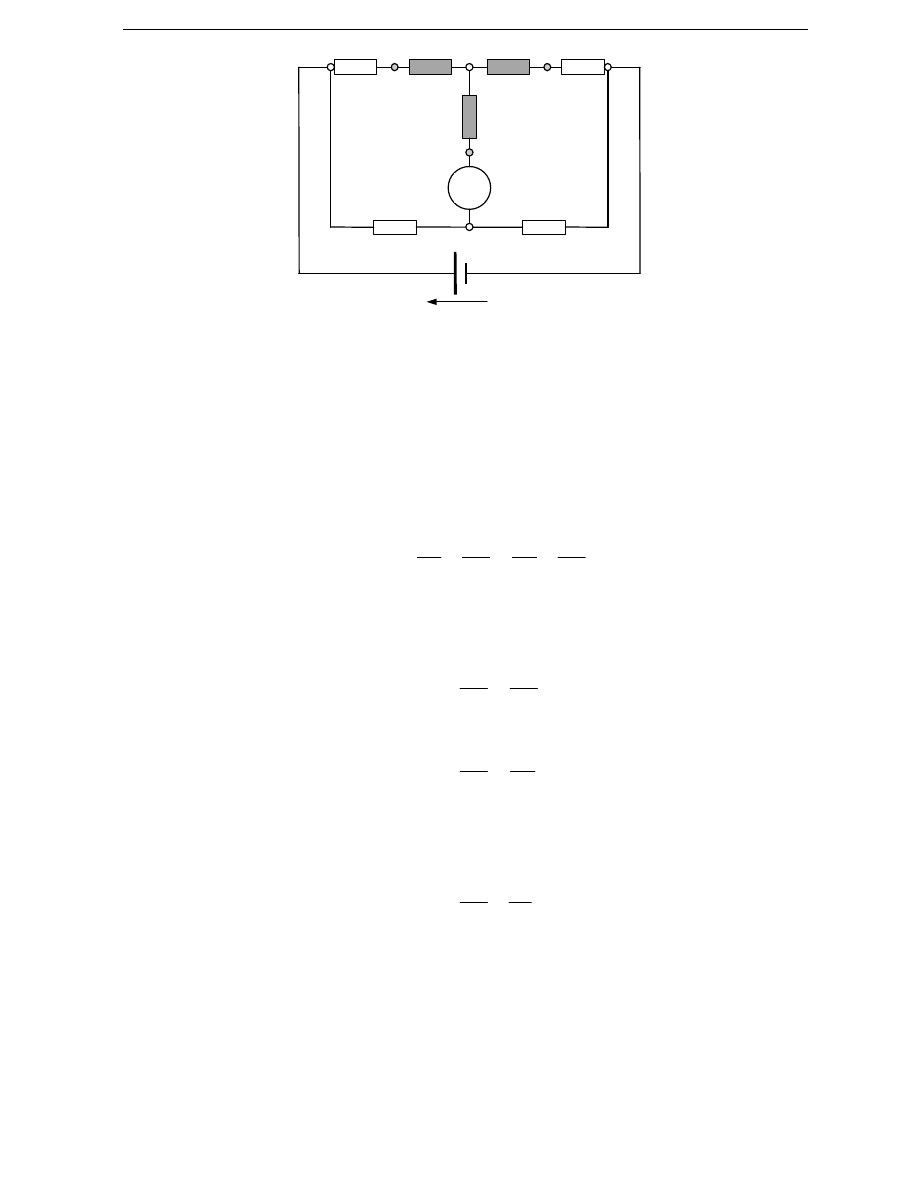
Dla układu mostka Wheatstone’a z rys. 3 napiszemy równanie równowagi,

uwzgl

ę

dniaj

ą

c w nim rezystancje przewodów CD i DE.

(

)

(

)

3

2

4

1

R

R

R

R

R

R

DE

CD

+

=

+

(1)

Ć

wicz. nr 6 Mostek Thomsona

3

Dziel

ą

c obie strony równania (1) przez wyra

ż

enie R

3

R

4

, otrzymuje si

ę

zale

ż

no

ś ć

(2

4

4

2

3

3

1

R

R

R

R

R

R

R

R

DE

CD

+

=

+

(2)

Z zale

ż

no

ś

ci tej wynika,

ż

e gdyby spełniony został warunek (3),

4

3

R

R

R

R

DE

CD

=

(3)

lub, co na jedno wychodzi, warunek (4),

DE

CD

R

R

R

R

=

4

3

(4)

to z równania równowagi (1) znikłyby paso

ż

ytnicze rezystancje R

CD

i R

DE

przewodów CD i DE i równanie to przyj

ę

łoby posta

ć

(5)

3

2

4

1

R

R

R

R

=

(5)

to znaczy zawierałoby jedynie rezystancje rezystorów wyst

ę

puj

ą

cych

w ramionach mostka.

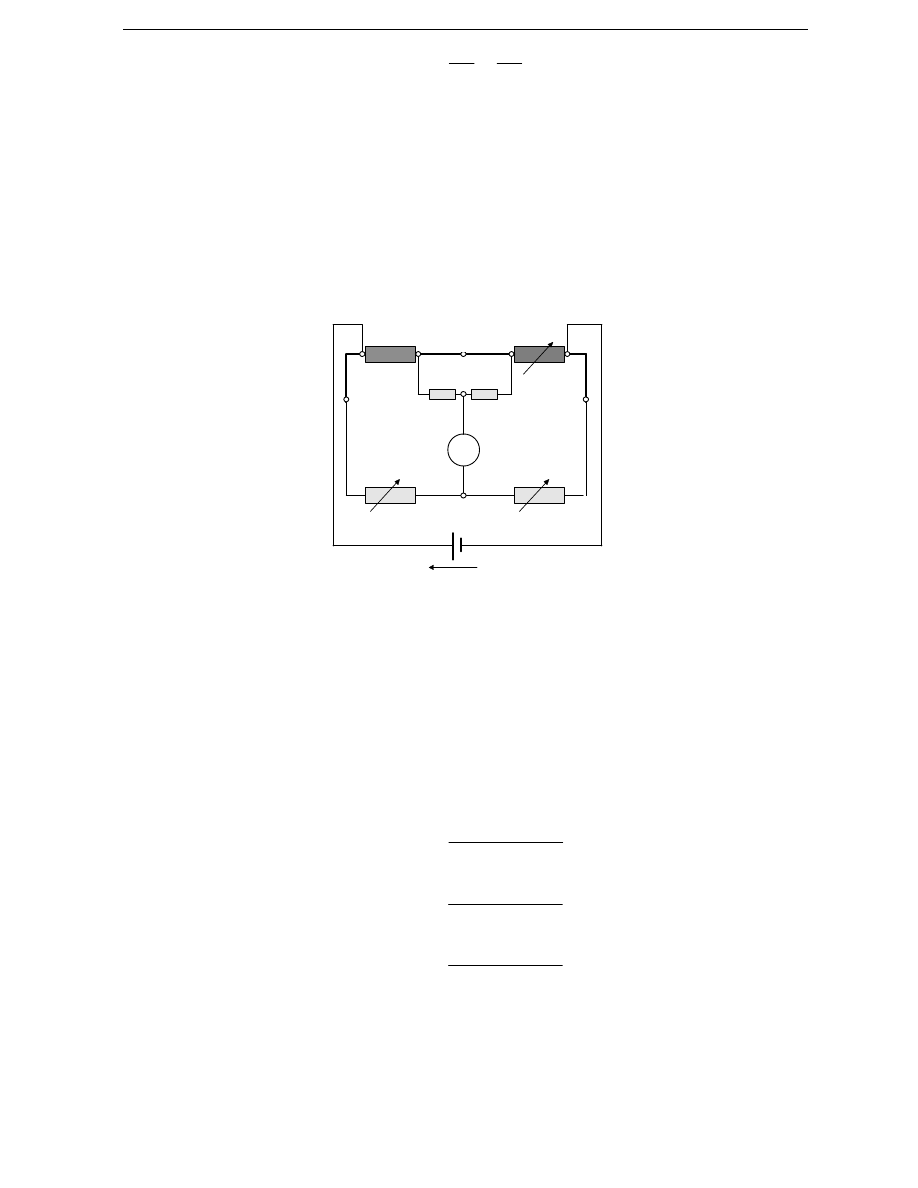
U

Z

I

G

R

4

R

3

R

2

R

1

G

A

G

F

E

D

C

B

Rys. 3. Schemat układu mostka Wheatstone’a po zmianie punktów przył

ą

czenia

przewodów biegn

ą

cych od

ź

ródła zasilania

Z warunku (4) wynika,

ż

e rozwi

ą

zanie problemu le

ż

y w znalezieniu

wła

ś

ciwego poło

ż

enia punktu D, który powinien dzieli

ć

odcinek przewodu CE na

takie dwie cz

ę ś

ci, których rezystancje miałyby si

ę

do siebie jak R

3

do R

4

.

Praktyczna realizacja tej idei byłaby kłopotliwa z uwagi na niewielkie warto

ś

ci

rezystancji, z jakimi ma si

ę

tutaj do czynienia. Zamiast wi

ę

c dzieli

ć

odcinek CE,

dzieli si

ę

spadek napi

ę

cia na nim przy pomocy rezystancyjnego dzielnika

zło

ż

onego z rezystorów R’

3

, R’

4

(rys. 4) spełniaj

ą

cych warunek (6) ,

identyczny z warunkiem (4).

Ć

wicz. nr 6 Mostek Thomsona

4

4

3

'

4

'

3

R

R

R

R

=

(6)

Poprawno

ść

tego rozwi

ą

zania układowego nie jest oczywista i wymaga dowodu,

który podajemy ni

ż

ej.

Układ przedstawiony na rys. 4 jest ju

ż

układem mostka Thomsona,

narysowanym w do

ść

nietypowy sposób, pokazuj

ą

cym jednak charakte-

rystyczne cechy tego mostka, to znaczy sposób prowadzenia przewodów od

ź

ródła zasilania oraz obecno

ść

dzielnika napi

ę

cia R’

3

, R’

4

.

U

Z

I

G

R

4

R’

4

R’

3

R

3

R

2

R

1

A

H

G

F

E

D

C

B

G

Rys.4. Schemat ideowy mostka Thomsona

Chc

ą

c dowie

ść

prawdziwo

ś

ci warunku (6), przekształcimy trójk

ą

t rezystancji

R

CE

, R’

3

, R’

4

(rezystancje przewodów wyst

ę

puj

ą

cych wokół R’

3

, R’

4

s

ą

do

pomini

ę

cia wobec znacznej rezystancji tych ostatnich) w równowa

ż

n

ą

gwiazd

ę

rezystancji R

A

, R

B

, R

C

. Otrzymany w wyniku tego przekształcenia układ,

przedstawiony jest na rys. 5.

Przy czym:

R

R

R

R

R

R

A

CE

CE

=

+

+

'

'

'

3

3

4

(7)

R

R

R

R

R

R

B

CE

CE

=

+

+

'

'

'

4

3

4

(8)

R

R

R

R

R

R

C

CE

=

+

+

'

'

'

'

3

4

3

4

(9)

Ć

wicz. nr 6 Mostek Thomsona

5

G

E

C

H

R

C

U

Z

R

4

R

3

R

B

R

A

R

2

R

1

Rys.5. Równowa

ż

na gwiazda rezystancji R

A

, R

B

, R

C

Dla czteroramiennego mostka z rysunku 5 napiszemy teraz znane równanie
równowagi

(

)

(

)

3

2

4

1

R

R

R

R

R

R

B

A

+

=

+

Dziel

ą

c obie strony tego równania przez wyra

ż

enie

R R

3 4

, otrzymujemy zale

ż

no

ś ć

(10)

4

4

2

3

3

1

R

R

R

R

R

R

R

R

B

A

+

=

+

(10)

Je

ż

eli w równaniu równowagi (10) maj

ą

wyst

ę

powa

ć

tylko rezystancje

4

3

2

1

,

,

,

R

R

R

R

, trzeba aby spełnione była równo

ś ć

:

4

3

R

R

R

R

B

A

=

,

lub, co na jedno wychodzi:

4

3

R

R

R

R

B

A

=

(11)

Podstawiaj

ą

c do (11) zale

ż

no

ś

ci (7), (8), otrzymuje si

ę

po przekształceniach:

R

R

R

R

'

'

3

4

3

4

=

,

czyli warunek (6), co nale

ż

ało wykaza

ć

.

W literaturze spotyka si

ę

najcz

ę ś

ciej schemat ideowy mostka Thomsona

przedstawiony na rys.6, nie ró

ż

ni

ą

cy si

ę

ideowo od mostka z rysunku 4.

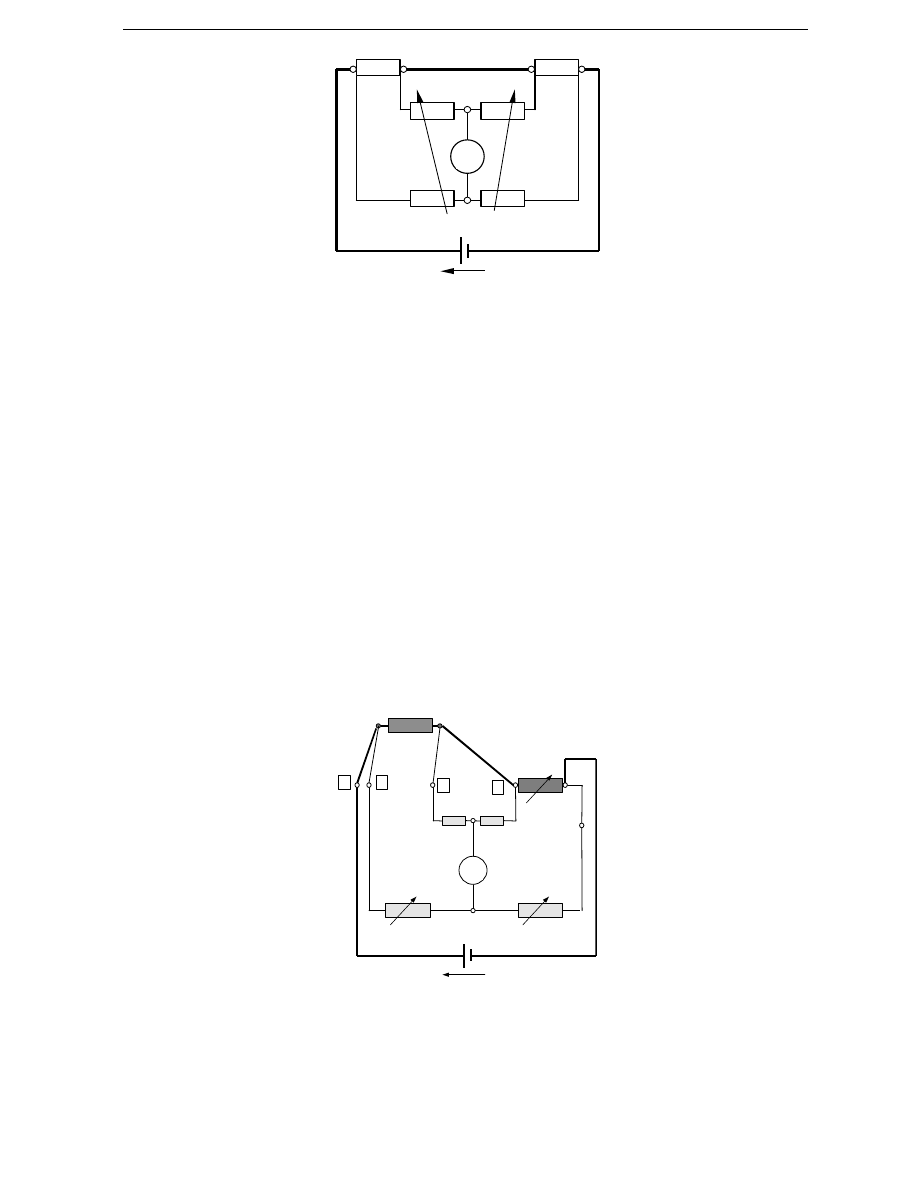
Ć

wicz. nr 6 Mostek Thomsona

6

U

Z

R

4

R

3

R’

3

R

2

R

1

R’

4

G

Rys. 6. „Uporz

ą

dkowany” schemat mostka Thomsona

W mostku z rysunku 6 rezystory R

3

i R’

3

sprz

ę ż

one s

ą

mechanicznie dzi

ę

ki

czemu w ka

ż

dej chwili ich rezystancje s

ą

sobie równe. To samo dotyczy

rezystorów R

4

i R’

4

. Rozwi

ą

zanie takie ułatwia spełnienie warunku (6) podczas

równowa

ż

enia mostka. Równowa

ż

enie odbywa si

ę

przez regulacj

ę

tylko

rezystancji R

3

-R’

3

. Zespół R

4

-R

4

’ słu

ż

y do zmiany zakresu pomiarowego mostka.

Mostek Thomsona ma cztery zaciski wej

ś

ciowe

Pouczaj

ą

ce wydaje si

ę

pokazanie czytelnikowi układu mostka Thomsona

w sposób przedstawiaj

ą

cy wyra

ź

nie cztery zaciski wej

ś

ciowe mostka i nie-

odzowne cztery przewody ł

ą

cz

ą

ce rezystancj

ę

mierzon

ą

R

1

z tym mostkiem.

Przedstawia to rysunek 7.

4

3

2

1

U

Z

R

4

R’

4

R’

3

R

3

R

2

R

1

G

Rys.7. Mostek Thomsona ma cztery zaciski wej

ś

ciowe

Ć

wicz. nr 6 Mostek Thomsona

7

W układzie mostka Thomsona istniej

ą

(zaznaczone na rys.7 grubymi

liniami) gał

ę

zie, w których płynie pr

ą

d o znacznym nat

ę ż

eniu. W mostku

stosowanym w

ć

wiczeniu wynosi ono 20 A. Tak du

ż

y pr

ą

d potrzebny jest do

wywołania na bardzo małych rezystancjach R

1

, R

2

odczuwalnie du

ż

ych spadków

napi

ę ć

zapewniaj

ą

cych dostateczn

ą

czuło

ś ć

układu.

Bł

ą

d podstawowy

Bez dowodu podamy tu wyra

ż

enie na wzgl

ę

dny bł

ą

d graniczny pomiaru

rezystancji mostkiem Thomsona. Dany jest on zale

ż

no

ś

ci

ą

(12).

(

)

δ

δ

δ

δ

δ

δ

δ

δ

R

R

R

R

p

R

R

R

R

R

R

R

1

2

3

4

3

4

3

4

1

2

=

+

+

+

+

+

+

+

'

'

(12)

gdzie:

R

P

- rezystancja przewodu ł

ą

cz

ą

cego rezystancje R

1

i R

2

Je

ż

eli rezystancja

R

P

ma pomijalnie mał

ą

warto

ś ć

(jest ni

ą

np. gruby płaskownik

miedziany), wówczas bł

ą

d wyra

ż

aj

ą

dostatecznie dobrze trzy pierwsze składniki

wyra

ż

enia (12), które staje si

ę

wtedy identyczne z zale

ż

no

ś

ci

ą

wra

ż

aj

ą

c

ą

analogiczny bł

ą

d mostka dotycz

ą

cym mostka Wheatstone’a.

Bł

ą

d nieczuło

ś

ci

Bez dowodu podajemy ni

ż

ej wyra

ż

enie na bł

ą

d nieczuło

ś

ci mostka Thomsona.

(

)

[

]

(

)

[

]

(

)

δ

n

p

p

z

p

I

R R

R

R R

R R

R

R R da

U

R R

R R

R R

R S

=

+

+

⋅

+

+

+

+

+

1

3

4

3

2

3

4

4

2

3

2

4

4

3

(

)

(

)

[

]

(

)

(

)

+

+

+

⋅

+

+

⋅

+

⋅

⋅

+

+

⋅

R

R

R

R R

R

R

R

R

R

da

U

R R

R R

R R

R S

p

G

z

p

I

1

2

3 4

3

4

3

4

2 3

2 4

4

3

2

(13)

gdzie:

U

z

-napi

ę

cie zasilaj

ą

ce

R

G

- rezystancja wewn

ę

trzna galwanometru

R

P

- rezystancja przewodu ł

ą

cz

ą

cego rezystancje R

1

, R

2

S

I

- czuło

ś ć

pr

ą

dowa galwanometru

da - najmniejsze dostrzegalne przemieszczenie wskazówki galwanome

tru (przyjmuje si

ę

umownie da = 0,1 mm)

Ć

wicz. nr 6 Mostek Thomsona

8

2. Przebieg

ć

wiczenia

Na wst

ę

pie nale

ż

y zmierzy

ć

wskazan

ą

przez prowadz

ą

cego rezystancj

ę

R

x

technicznym mostkiem Thomsona typu TMT-2. Jest to niezb

ę

dne do

sprawnego i bezpiecznego przeprowadzenia zasadniczego pomiaru rezystancji
mostkiem laboratoryjnym

Techniczny mostek Thomsona

Techniczny mostek Thomsona u

ż

ywany jest w laboratorium do zgrubnego

pomiaru nieznanej rezystancji R

x

, co pozwala na prawidłowe nastawienie

parametrów mostka laboratoryjnego i przy

ś

pieszenie jego równowa

ż

enia..

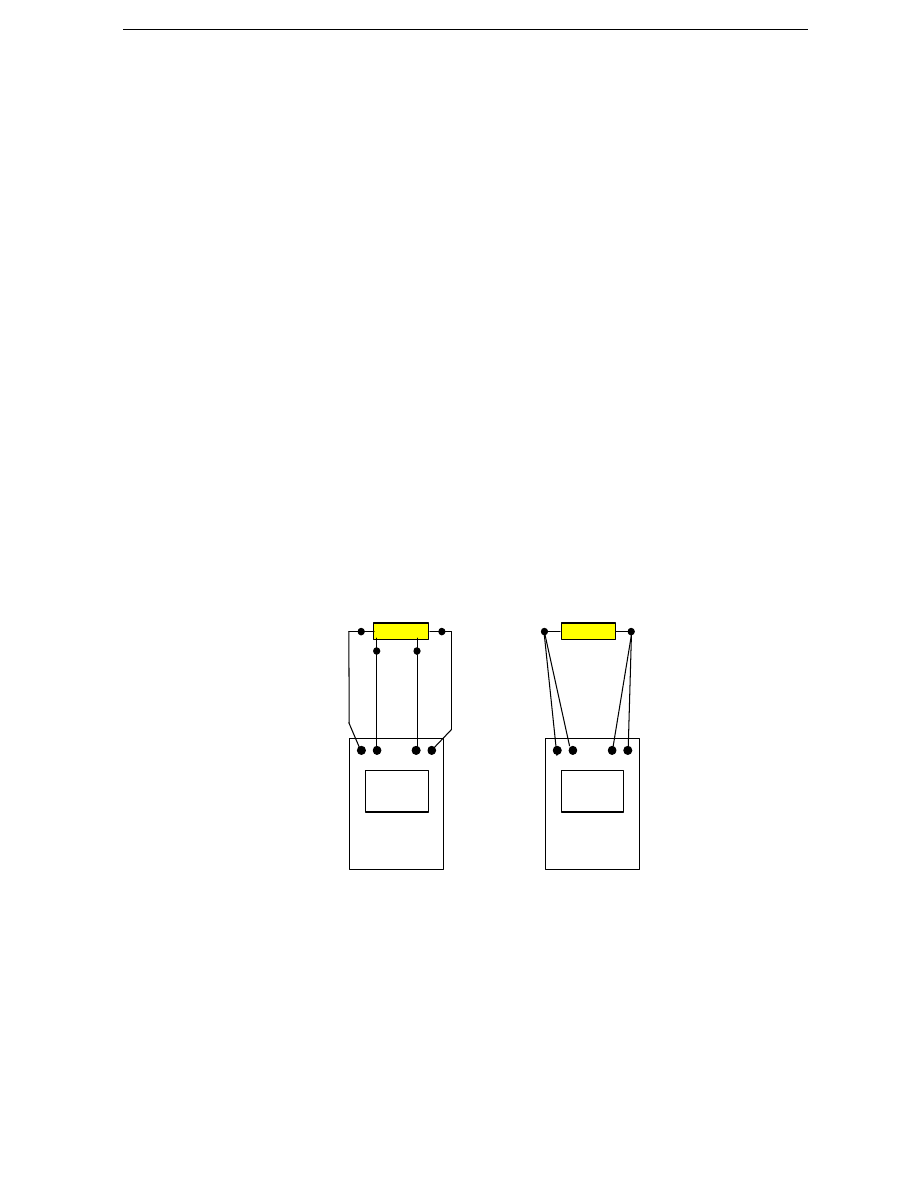
Mostek techniczny ma niewielkie rozmiary i jest łatwy w obsłudze. Na rys.8
przedstawiono sposób przył

ą

czania do mostka rezystancji mierzonej R

X

czterozaciskowej i dwuzaciskowej.

W obydwu przypadkach konieczne jest u

ż

ycie czterech przewodów

ł

ą

cz

ą

cych. Wszystkie „usprawnienia” stosowane niekiedy przez „adeptów”

sztuki mierzenia, a polegaj

ą

ce na zwieraniu par zacisków wej

ś

ciowych i

przył

ą

czaniu rezystancji mierzonej tylko dwoma przewodami, powoduj

ą

powstawanie kilkusetprocentowych bł

ę

dów pomiaru.

T

T

R

x

R

x

R

x

Rys.8. Sposób przył

ą

czania do mostka Thomsona rezystancji mierzonych:

czterozaciskowej i dwuzaciskowej.

Mostek techniczny typu TMT-2 jest zasilany z baterii płaskiej 4,5V ;

przystosowany jest jednak tak

ż

e do zasilania ze

ź

ródła zewn

ę

trznego. Podczas

ć

wiczenia mostek nale

ż

y zasili

ć

z zasilacza stabilizowanego.

Ć

wicz. nr 6 Mostek Thomsona

9

Wynik pomiaru rezystancji mostkiem technicznym:

R

X

= ..................

Ω

Wynik pomiaru, w celu jego weryfikacji, nale

ż

y poda

ć

prowadz

ą

cemu

ć

wiczenie

.

Pomiar rezystancji laboratoryjnym

mostkiem Thomsona

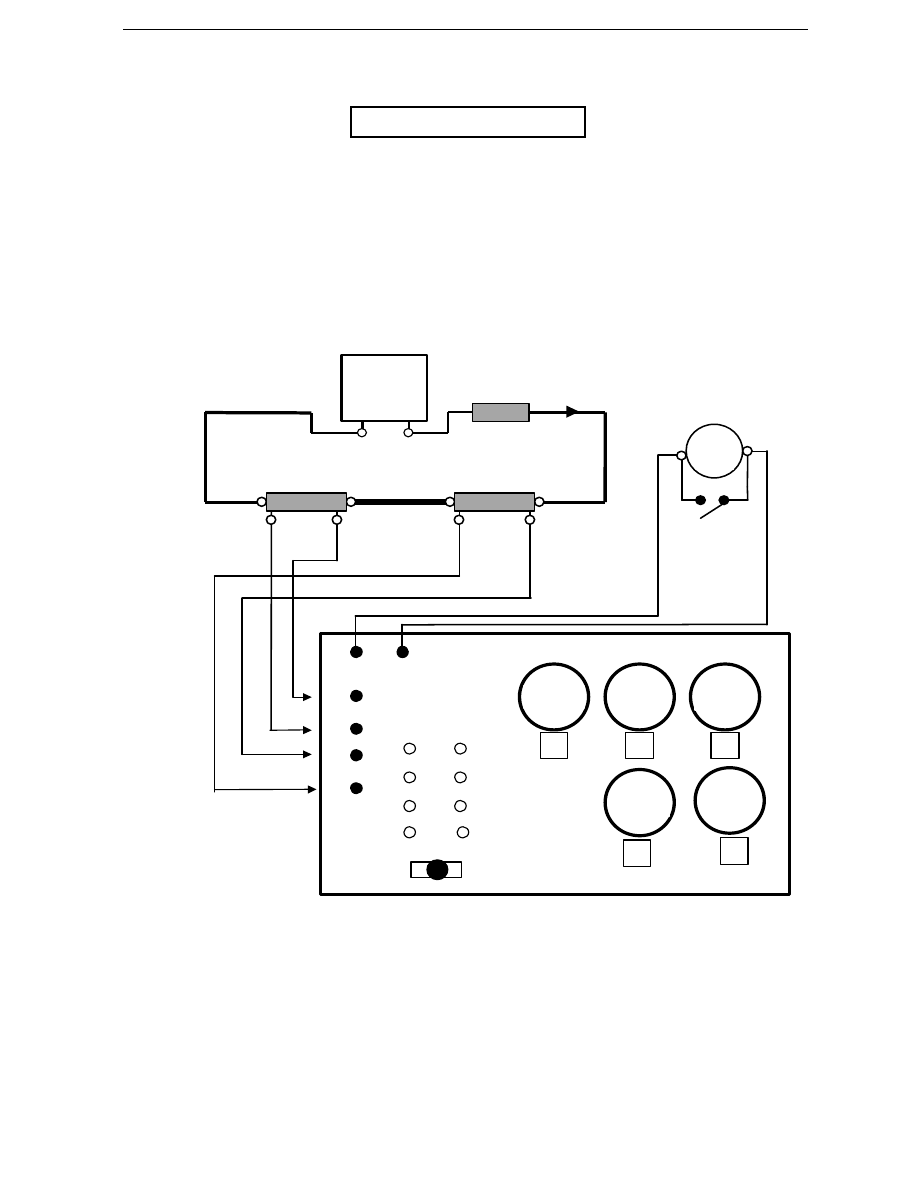
Schemat układu laboratoryjnego mostka Thomsona przedstawiono na

rysunku 9

I

p

R

R

P

R

1

R

2

Z

G

1

10

100

1000

x1000

x10

x100

x0,1

x1

R

=

9

9

9

9

9

G

+

+

N

X

T

0,1G

T

W

G

Z S

Rys.9. Schemat laboratoryjnego układu mostka Thomsona

Ć

wicz. nr 6 Mostek Thomsona

10

Opis elementów mostka

ZS – zasilacz stabilizowany o du

ż

ej wydajno

ś

ci pr

ą

dowej

R – rezystor drutowy o rezystancji 0,6

Ω

R

1

- rezystancja mierzona (bocznik amperomierza magnetoele-

ktrycznego)

R

2

-rezystor wzorcowy (0,001

Ω

)

R

P

- szyna miedziana

G - galwanometr magnetoelektryczny
Z - zwieracz galwanometru
(G - 0,1G) - przeł

ą

cznik (wł

ą

cznik) galwanometru:

•

pozycja „0,1G” oznacza ograniczon

ą

czuło

ś ć

galwanometru

•

pozycja „G” oznacza pełn

ą

czuło

ś ć

galwanometru

•

w pozycji

ś

rodkowej galwanometr jest odł

ą

czony od układu

N, X

T

- pary zacisków, do których doprowadzane s

ą

spadki napi

ę ć

na

rezystorach R

X

i R

W

(miejsce przył

ą

czenia poszczególnych

napi

ę ć

zale

ż

y od warto

ś

ci rezystancji R

W

zmierzonej mostkiem

technicznym - patrz Tablica 1

W - rezystor odpowiadaj

ą

cy rezystorowi R’

4

T - rezystor odpowiadaj

ą

cy rezystorowi R

4

W ka

ż

dej chwili powinno by

ć

W = T

R - pi

ę

ciodekadowy zespół sprz

ę ż

onych mechanicznie rezystorów

R’

3

, R

3

słu

żą

cy do równowa

ż

enia mostka

Zasady zestawiania laboratoryjnego mostka Thomsona

1. Na wst

ę

pie nale

ż

y ustali

ć

miejsca przył

ą

czenia rezystancji R

x

oraz R

w

:

a) gdy R

X

≥≥≥≥

0,001

Ω

Ω

Ω

Ω

nale

ż

y przył

ą

czy

ć

R

X

do zac. X

T

za

ś

R

W

do zac. N

b) gdy R

X

<<<<

0,001

Ω

Ω

Ω

Ω

nale

ż

y przył

ą

czy

ć

R

X

do zac. N za

ś

R

W

do zac. X

T

2. W kolejnym kroku nale

ż

y dokona

ć

wyboru warto

ś

ci rezystancji rezystora

wzorcowego R

w

oraz rezystorów W, T. Wyboru R

W

, W , T dokonuje si

ę

według wskaza

ń

Tablicy 1.

Ć

wicz. nr 6 Mostek Thomsona

11

3. Miejsce przył

ą

czenia rezystora R

X

(zaciski N lub X

T

) decyduje o postaci

równania pomiaru:

dla przypadku a) obowi

ą

zuje zale

ż

no

ś ć

:

R

R

R

T

x

w

=

(13)

dla przypadku b) obowi

ą

zuje zale

ż

no

ś ć

:

R

R

T

R

x

w

=

(14)

Zasady zawarte w punktach 1, 2, 3 ujmuje wyczerpuj

ą

co Tablica 1.

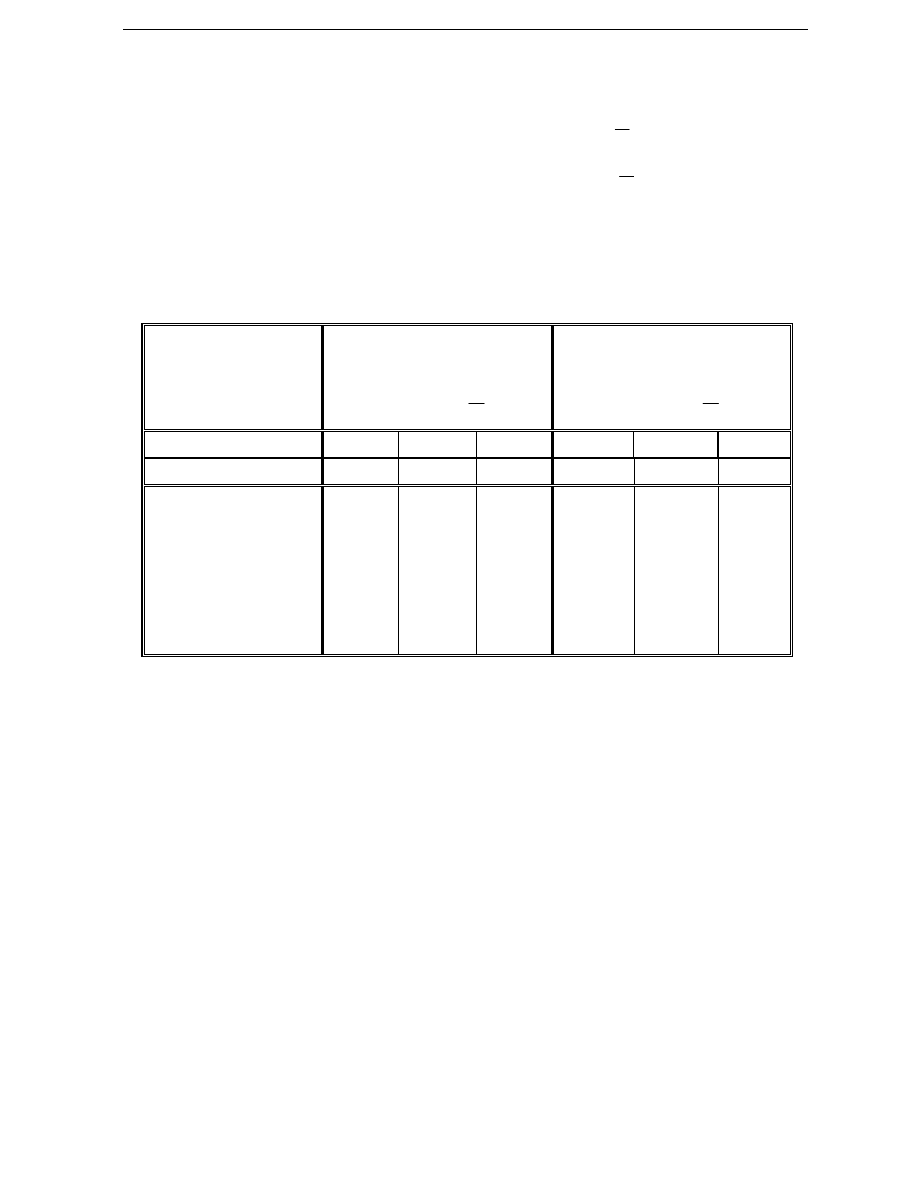
Tablica 1

Przedziały

warto

ś

ci

R

X

R

X

→

X

T

R

W

→

N

R

X

= R

W

R

T

R

X

→

N

R

W

→

X

T

R

X

= R

W

T

R

R

X

R

W

T

W

R

W

T

W

Ω

Ω

Ω

Ω

Ω

Ω

Ω

1-0,1

0,1-0,01

0,01-0,001

0,001-0,0001

0,0001-0,00001

0,00001-0,000001

0,1

0,01

0,001

-
-
-

1000
1000
1000

-
-
-

1000
1000
1000

-
-
-

-
-
-

0,001
0,001
0,001

-
-
-

1000

100

10

-
-
-

1000

100

10

Przebieg pomiarów

Czynno

ś

ci przygotowawcze

Przed zamkni

ę

ciem wył

ą

cznika W (rys.9), nale

ż

y nastawi

ć

okre

ś

lone

parametry mostka tak, aby był on w stanie zbli

ż

onym do stanu równowagi .

Przy

ś

piesza to osi

ą

gni

ę

cie stanu równowagi i zapobiega ewentualnemu

uszkodzeniu czułego galwanometru laboratoryjnego.

Przybli

ż

ony stan równowagi uzyskuje si

ę

, nastawiaj

ą

c odpowiedni

ą

warto

ś ć

pi

ę

ciodekadowego rezystora R, któr

ą

oblicza si

ę

z zale

ż

no

ś

ci (13) lub

(14), podstawiaj

ą

c w niej w miejsce R

X

wynik pomiaru rezystancji mostkiem

Ć

wicz. nr 6 Mostek Thomsona

12

technicznym. Warto

ś

ci rezystorów W, T ustala si

ę

przy pomocy przeł

ą

czników

kołkowych na podstawie Tablicy 1. Jak wiadomo, powinno by

ć

zawsze W = T.

Kolejn

ą

operacj

ą

przygotowawcz

ą

jest wyzerowanie galwanometru. Przy

otwartym wył

ą

czniku W oraz zwieraczu Z nale

ż

y ustawi

ć

ś

wietln

ą

wskazówk

ą

galwanometru na zerowej kresce działowej. W wypadku gdy wyst

ę

puj

ą

trudno

ś

ci

w całkowitym stłumieniu oscylacji wskazówki, przyrz

ą

d uwa

ż

a si

ę

za

wyzerowany, gdy lewa amplituda oscylacji wokół poło

ż

enia zerowego jest równa

amplitudzie prawej. Po wyzerowaniu nie nale

ż

y zmienia

ć

miejsca ustawienia

galwanometru na stole.

Pomiar rezystancji R

x

1. Zamknij wył

ą

cznik W i przy pomocy rezystora R

r

nastaw pr

ą

d pomocniczy I

P

=20 A. Przeł

ą

cznik galwanometru ustaw w pozycji „0,1 G” (ograniczona

czuło

ść

). Reguluj

ą

c rezystancj

ę

pi

ę

ciodekadowego rezystora R, doprowad

ź

wskazanie galwanometru do zera. Ustaw nast

ę

pnie przeł

ą

cznik galwanometru

w poło

ż

enie „G” (pełna czuło

ść

) i w przypadku gdy wskazania galwanometru

oka

ż ą

si

ę

ró

ż

ne od zera, podobnie jak poprzednio zrównowa

ż

mostek.

Warto

ść

rezystancji R, dla której uzyskano zerowe wskazanie galwanometru

zapisz w Tablicy 2. Poszukiwan

ą

warto

ść

R

X

oblicz ze wzoru (13) lub (14).

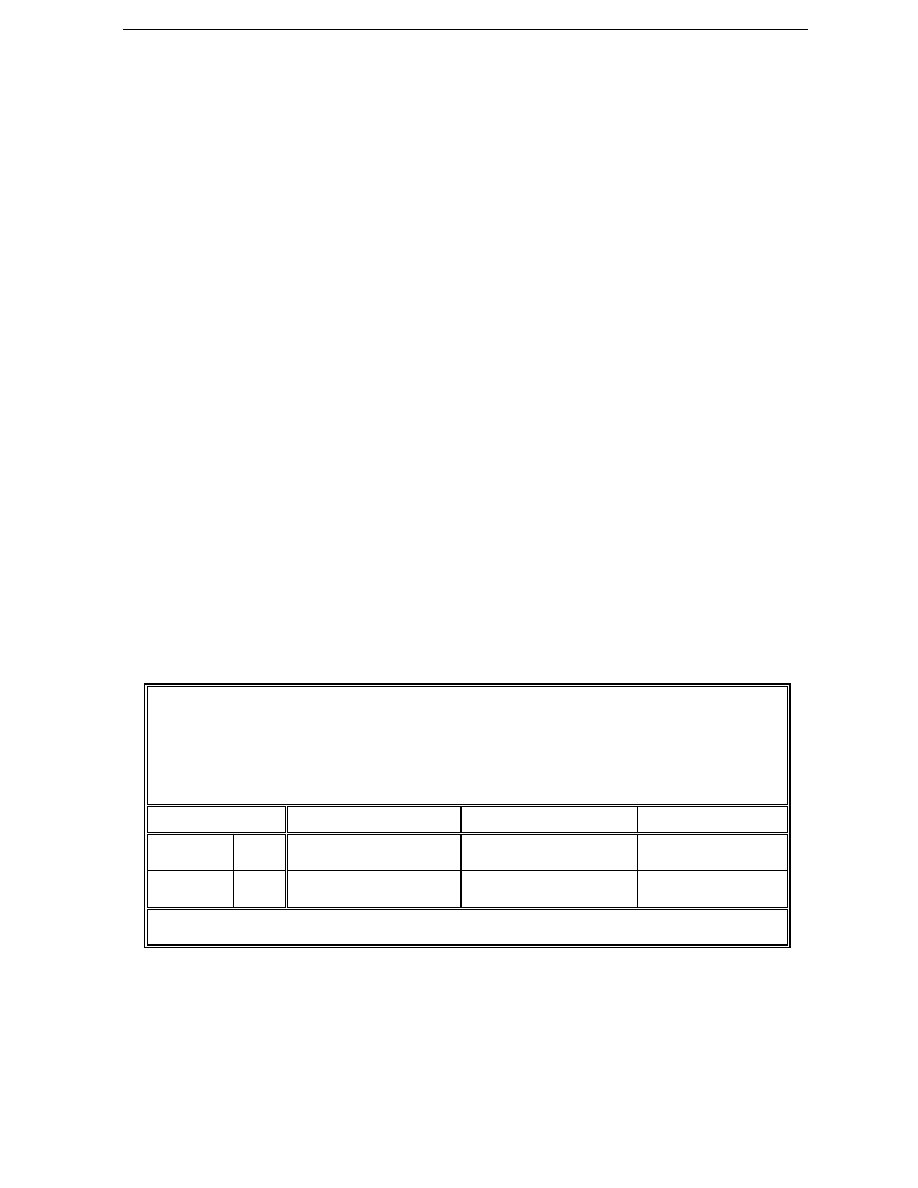
Tablica 2

R

X

= ..........................

Ω

(wynik pomiaru mostkiem technicznym)

R

W

= 0,001

Ω

W = T = ...................

Ω

I

P

= 20 A

Numer pomiaru

1

2

3

R

Ω

R

X

Ω

R

X

Ś

R

= ...................

Ω

Pomiar nale

ż

y powtórzy

ć

trzykrotnie, wskazane jest przy tym, aby za

ka

ż

dym razem dokonywała tego inna osoba z grupy laboratoryjnej. Je

ż

eli

Ć

wicz. nr 6 Mostek Thomsona

13

poszczególne wyniki ró

ż

ni

ą

si

ę

nieznacznie mi

ę

dzy sob

ą

, obliczamy ich

ś

redni

ą

arytmetyczn

ą

.

Wyznaczanie bł

ę

du nieczuło

ś

ci mostka

Definicja bł

ę

du nieczuło

ś

ci

Bezwzgl

ę

dnym bł

ę

dem nieczuło

ś

ci mostka

∆

n

nazywa si

ę

najwi

ę

kszy

przyrost

∆

R

X

rezystancji mierzonej R

X

, nie powoduj

ą

cy jeszcze dostrzegalnego

przemieszczenia wskazówki

ś

wietlnej galwanometru.

W praktyce stosuje si

ę

u

ż

ytkow

ą

definicj

ę

tego bł

ę

du.

Bezwzgl

ę

dnym bł

ę

dem nieczuło

ś

ci mostka

∆

n

nazywa si

ę

przyrost

∆

R

X

rezystancji mierzonej R

X

powoduj

ą

cy najmniejsze dostrzegalne przemieszczenie

wskazówki

ś

wietlnej galwanometru

∆

a. Jego warto

ś ć

przyjmuje si

ę

umownie za

równ

ą

0,1 mm.

Zgodnie z tym ostatnim okre

ś

leniem,

∆

n

=

∆

R

X

(dla

∆

a = 0,1 mm)

(15)

Wzgl

ę

dny bł

ą

d nieczuło

ś

ci natomiast definiuje si

ę

nast

ę

puj

ą

co:

X

n

n

R

∆

=

δ

(16)

Odst

ę

pstwa od definicji

Zgodnie z podan

ą

wy

ż

ej definicj

ą

bł

ę

du nieczuło

ś

ci do

ś

wiadczalne

wyznaczanie bł

ę

du nieczuło

ś

ci wymaga płynnej regulacji rezystancji mierzonej

R

X

. W znakomitej wi

ę

kszo

ś

ci przypadków jest to niemo

ż

liwe, bowiem rezystory

mierzone nie s

ą

na ogół regulowane. Ma to miejsce tak

ż

e w niniejszym

ć

wiczeniu, dlatego definicje (15), (16) stosowane b

ę

d

ą

tutaj w odniesieniu do

rezystancji R słu

żą

cej do równowa

ż

enia mostka.

Poza tym przemieszczanie wskazówki galwanometru o definicyjn

ą

warto

ś ć

∆

a =0,1 mm jest praktycznie niewykonalne, dlatego w

ć

wiczeniu zaleca si

ę

zmian

ę

rezystancji R o tak

ą

warto

ś ć

, która wywoła przemieszczenie wskazówki

o

∆

a = 5 mm, a nast

ę

pnie obliczenie bezwzgl

ę

dnego bł

ę

du nieczuło

ś

ci według

wzoru (17)

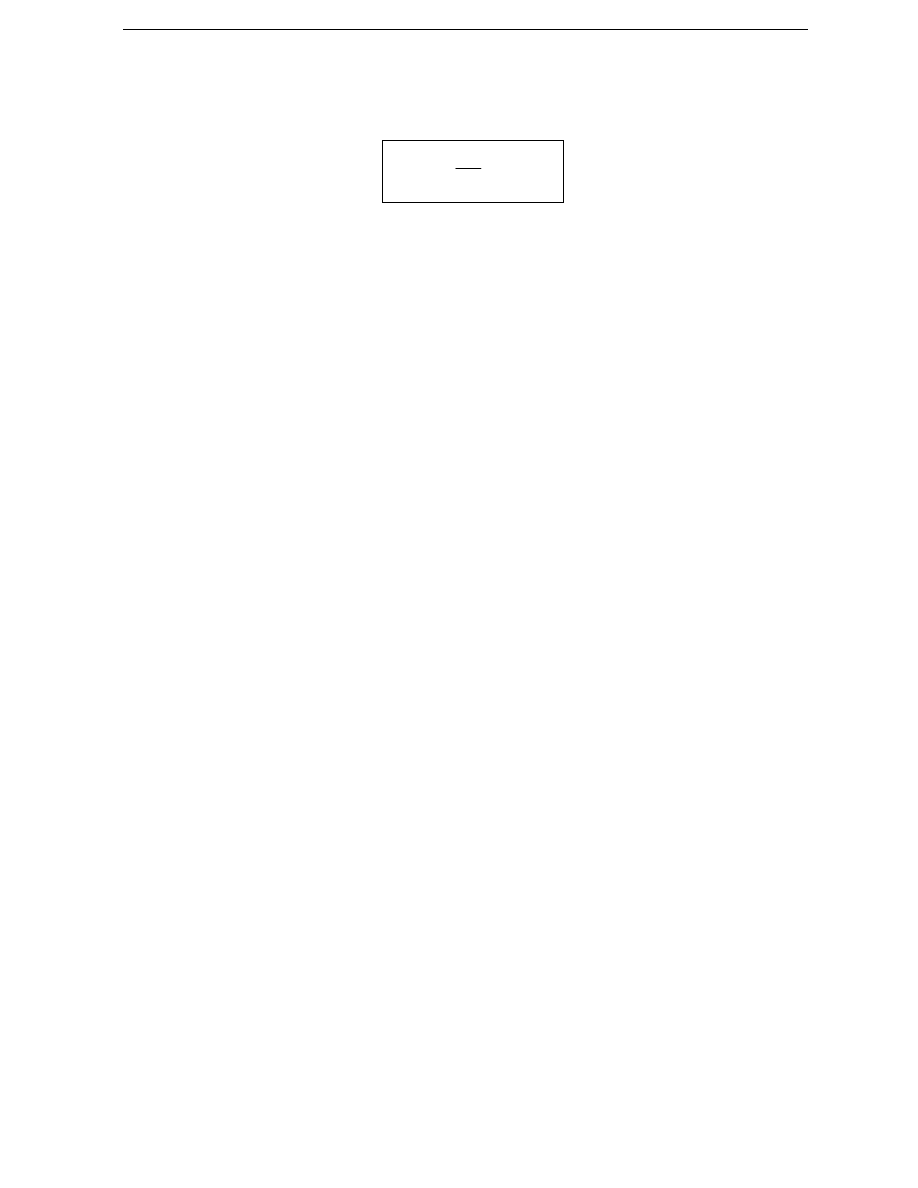
R

R

n

∆

=

∆

=

∆

02

,

0

50

(17)

Ć

wicz. nr 6 Mostek Thomsona

14

który pozwala na drodze teoretycznej ustali

ć

warto

ś ć

∆

R niezb

ę

dn

ą

do

przemieszczenia wskazówki o

∆

a = 0,1 mm.

Bł

ą

d wzgl

ę

dny oblicza si

ę

natomiast według wzoru (18)

%

100

R

n

n

∆

=

δ

(18)

gdzie: R - rezystancja w stanie równowagi mostka.

Przebieg pomiarów

Pomiary bł

ę

du nieczuło

ś

ci odbywaj

ą

si

ę

w układzie przedstawionym na

rysunku 9. według nast

ę

puj

ą

cego porz

ą

dku.

1. Nastaw pr

ą

d pomocniczy I

P

= 20 A

2. Zrównowa

ż

mostek i zanotuj w Tablicy 3 warto

ś ć

rezystancji

R

uzyskan

ą

dla

pr

ą

du galwanometru I

G

=0. Nast

ę

pnie poprzez regulacj

ę

rezystorów R uzyskaj

odchylenie wskazówki galwanometru o

∆

a = 5 mm od poło

ż

enia zerowego w

dowoln

ą

stron

ę

. T

ę

now

ą

warto

ś ć

rezystancji R (

R’

) zanotuj w odpowiedniej

rubryce Tablicy 3. Ze wzorów (17), (18) oblicz bł

ę

dy nieczuło

ś

ci

∆

n

i

δ

n

.

3. Eksperyment powtórz dla ró

ż

nych (wskazanych w Tablicy 3) warto

ś

ci pr

ą

du

pomocniczego I

p

, reguluj

ą

c go przy pomocy rezystora suwakowego R

r

.

Ć

wicz. nr 6 Mostek Thomsona

15

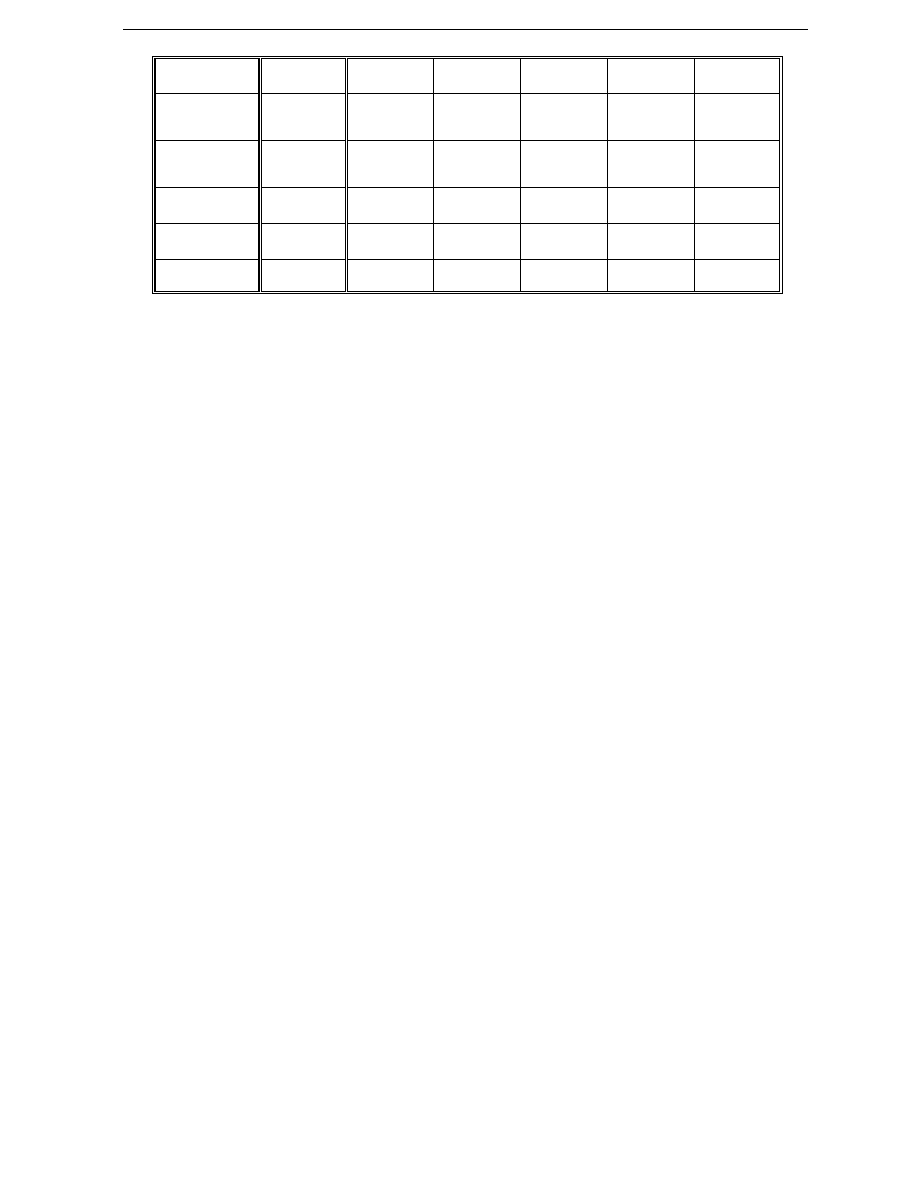
Tablica 3

I

P

A

20

16

12

8

4

R

(I

G

=0)

Ω

Ω

Ω

Ω

R’

(I

G

=5mm)

Ω

Ω

Ω

Ω

∆∆∆∆

R=

||||

R-R’

||||

Ω

Ω

Ω

Ω

∆∆∆∆

n

Ω

Ω

Ω

Ω

δδδδ

n

%

W sprawozdaniu nale

ż

y:

Sporz

ą

dzi

ć

wykres zale

ż

no

ś

ci

( )

δ

n

p

f I

=

Wyja

ś

ni

ć

, dlaczego bł

ą

d nieczuło

ś

ci zale

ż

y od warto

ś

ci pr

ą

du I

P

3. Pytania i zadania kontrolne

1. Dlaczego bardzo małych rezystancji nie mierzy si

ę

mostkiem Wheatstone’a ?

2. Narysuj schemat ideowy mostka Thomsona.
3. Które rezystancje mostka Thomsona maj

ą

b. małe warto

ś

ci, a które du

ż

e?

4. Jaki warunek spełnia

ć

musz

ą

rezystancje R’

3

, R’

4

(rys. 4) ?

5. Napisz warunek równowagi mostka Thomsona (rys. 4).
6. Podaj definicje bezwzgl

ę

dnego i wzgl

ę

dnego bł

ę

du nieczuło

ś

ci.

7. Na czym polegaj

ą

odst

ę

pstwa od definicji bł

ę

dów nieczuło

ś

ci i z czego

wynikaj

ą

?

8. W jaki sposób nale

ż

y przył

ą

czy

ć

dwie ko

ń

cówki przewodu ł

ą

czeniowego

u

ż

ywanego w laboratorium, do technicznego mostka Thomsona o czterech

zaciskach wej

ś

ciowych w celu pomiaru rezystancji tego przewodu?

4. Literatura

1. Lebson S. Podstawy miernictwa elektrycznego WNT, Warszawa 1970
2. Chwaleba A. i inni Metrologia elektryczna WNT, Warszawa 1998
3. Marcyniuk A. i inni Podstawy metrologii elektrycznej WNT, Warszawa 1984