
KONSTRUKCJE STALOWE opr. dr inż. Bernard Kowolik
Materiały pomocnicze do wykonania obliczeń stropu stalowego Strona 1/17
SPIS TREŚCI
I) Obliczenia statyczno-wytrzymałościowe
1. Założenia projektowe ......................................................................................................................................2
2. Opis techniczny................................................................................................................................................5
3. Belka stropowa ................................................................................................................................................5
3.1. Zestawienie obciążeń ................................................................................................................................5
3.2. Przyjęcie przekroju poprzecznego.............................................................................................................5
3.3. Sprawdzenie nośności belki stropowej......................................................................................................5
3.4. Sprawdzenie stanu granicznego użytkowalności (ugięć) ..........................................................................6
3.5. Sprawdzenie warunku nośności w stadium montażu (dla KBI)................................................................6
4. Podciąg .............................................................................................................................................................7
4.1. Zestawienie obciążeń ................................................................................................................................7
4.2. Obliczenie momentów zginających i sił poprzecznych.............................................................................7
4.3. Przyjęcie przekroju....................................................................................................................................7
4.4. Sprawdzenie nośności podciągu (stan krytyczny).....................................................................................8
4.5. Sprawdzenie stanu granicznego użytkowalności (ugięć) .........................................................................9
4.6. Spoiny łączące pasy ze środnikiem...........................................................................................................9
4.7 Połączenie belek stropowych z podciągiem..............................................................................................9
4.8. Sprawdzenie sztywności pośrednich żeberek usztywniających ..............................................................10
4.9. Oparcie podciągu na słupie zewnętrznym...............................................................................................10
4.10. Oparcie podciągu na słupie wewnętrznym............................................................................................11
Słup ....................................................................................................................................................................12
5.1. Zestawienie obciążeń ..............................................................................................................................12
5.2. Określenie długości wyboczeniowych ....................................................................................................12
5.3. WARIANT I - dwuteownik szerokostopowy.........................................................................................12
5.3.1. Przyjęcie przekroju pręta i sprawdzenie nośności..........................................................................12
5.3.2. Głowica słupa..................................................................................................................................12
5.3.3. Nieużebrowana podstawa słupa .....................................................................................................13
5.3.4. Użebrowana podstawa słupa ..........................................................................................................13
5.4. WARIANT II - przekrój złożony (dla KBI)...........................................................................................15
5.4.1. Przyjęcie przekroju poprzecznego słupa i sprawdzenie nośności ..................................................15
5.4.2. Przewiązki .......................................................................................................................................16
5.4.3. Podstawa słupa ...............................................................................................................................16
II) Rysunek konstrukcyjny stropu: belki, podciągu i słupa w skali 1:10

KONSTRUKCJE STALOWE opr. dr inż. Bernard Kowolik
Materiały pomocnicze do wykonania obliczeń stropu stalowego Strona 2/17
Do wykonania obliczeń statyczno-wytrzymałościowych niezbędne jest posiadanie następujących pozycji:
[1] PN-90/B-03200 Konstrukcje stalowe. Obliczenia statyczne i projektowanie.
[2] PN-B-03215:1998 Konstrukcje stalowe. Połączenia z fundamentami. Projektowanie i wykonanie.
[3] PN-82/B-02000
Obciążenia budowli. Zasady ustalania wartości.
[4] PN-82/B-02001
Obciążenia budowli. Obciążenia stałe.
[5] PN-82/B-02003
Obciążenia budowli. Obciążenia zmienne technologiczne. Podstawowe obciążenia
technologiczne i montażowe.
[6] Niewiadomski J. i inni: Obliczanie konstrukcji stalowych wg PN-90/B-03200. PWN, Warszawa 2001 lub
Skrypt P.Śl.
[7] Bogucki W., Żyburtowicz M.: Tablice do projektowania konstrukcji metalowych. Arkady 1996 (lub 1984)
[8] Łubiński M., Filipowicz A., Żółtowski W.: Konstrukcje metalowe - Część l. Arkady 2000.
[10] PN-90/B-03000 Projekty budowlane. Obliczenia statyczne.
Strona tytułowa powinna zawierać temat ćwiczenia projektowego, nazwę biura projektowego (w tym
przypadku Katedry), imię i nazwisko projektanta oraz sprawdzającego (z podpisami) oraz datę wykonania
projektu).
Należy się zapoznać z zasadami wykonywania obliczeń statycznych przedstawionymi w normie [10]
(m.in. odnośnie ramek, numerowania stron, itp.).
Zaleca się pisanie ołówkiem na czystym papierze formatu A4 (pisanie jednostronne). Brudnopisów nie
konsultujemy. Edycja wyników powinna mieć następującą kolejność: wzór – podstawienie liczbowe (bez
jednostek, ale z przelicznikami potęgowymi) – wynik z jednostką. Nie zezwala się na edycję obliczeń w
MathCADzie. Rysunki należy wykonywać w trakcie obliczeń, powinny być staranne, czytelne, z zachowaniem
proporcji. Rysunek konstrukcyjny może być wykonywany techniką komputerową (CAD), ale z zachowaniem
wszystkich zasad wykonywania rysunków budowlanych (wymiarowania, opisów, itp.)
1. Założenia projektowe
Należy wykonać rzut stropu w skali (na A4) z podanymi wymiarami.
Dane h, p
k
, L
stR
, B
stZ
, F należy przyjąć wg tematu konstrukcji żelbetowych.
Rodzaj stali konstrukcyjnej zostanie ustalony przez konsultanta.
Grupy KBI dobierają wymiary stropu samodzielnie (dana jest powierzchnia użytkowa stropu). Pozostałe
gruby mają podane długość i szerokość stropu. Układ elementów konstrukcyjnych zależy od obciążenia i
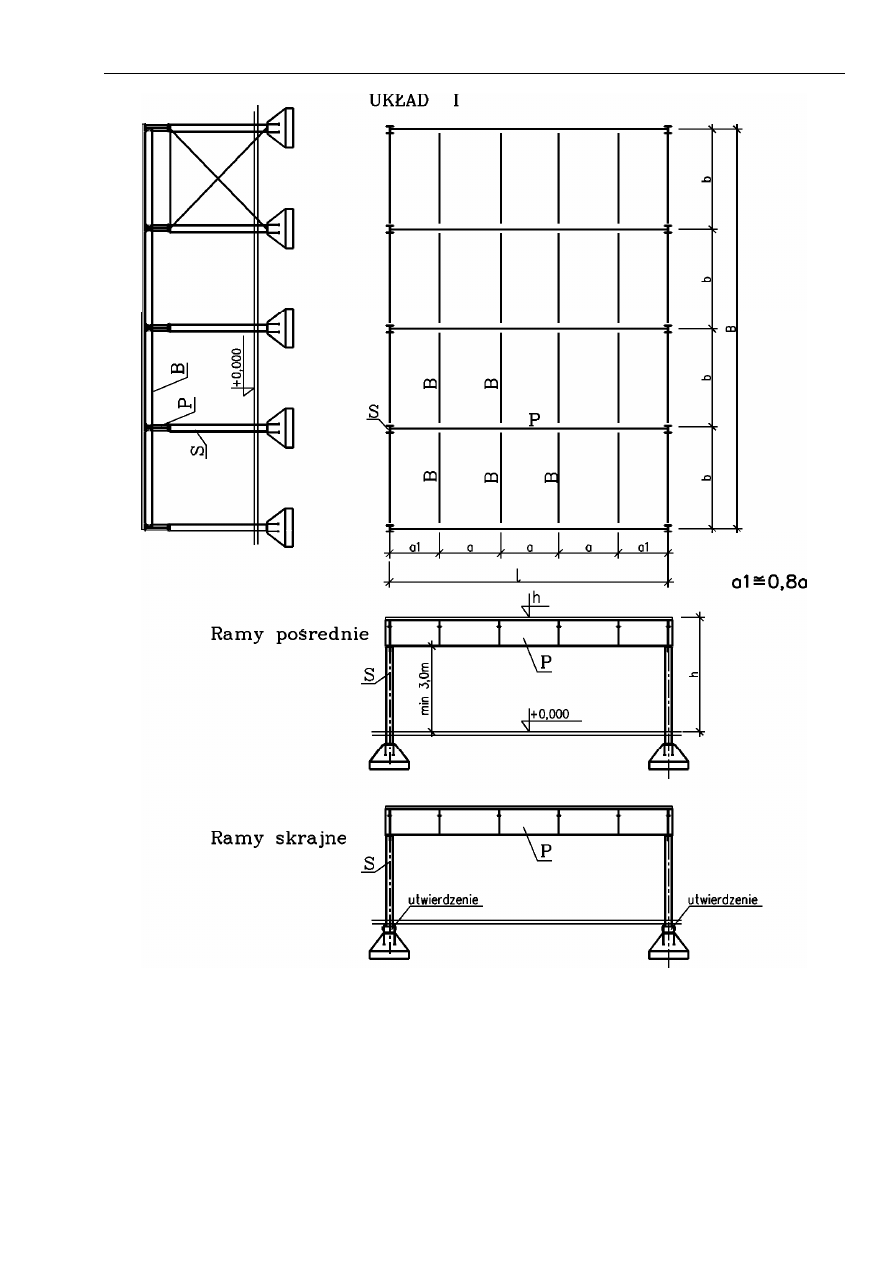
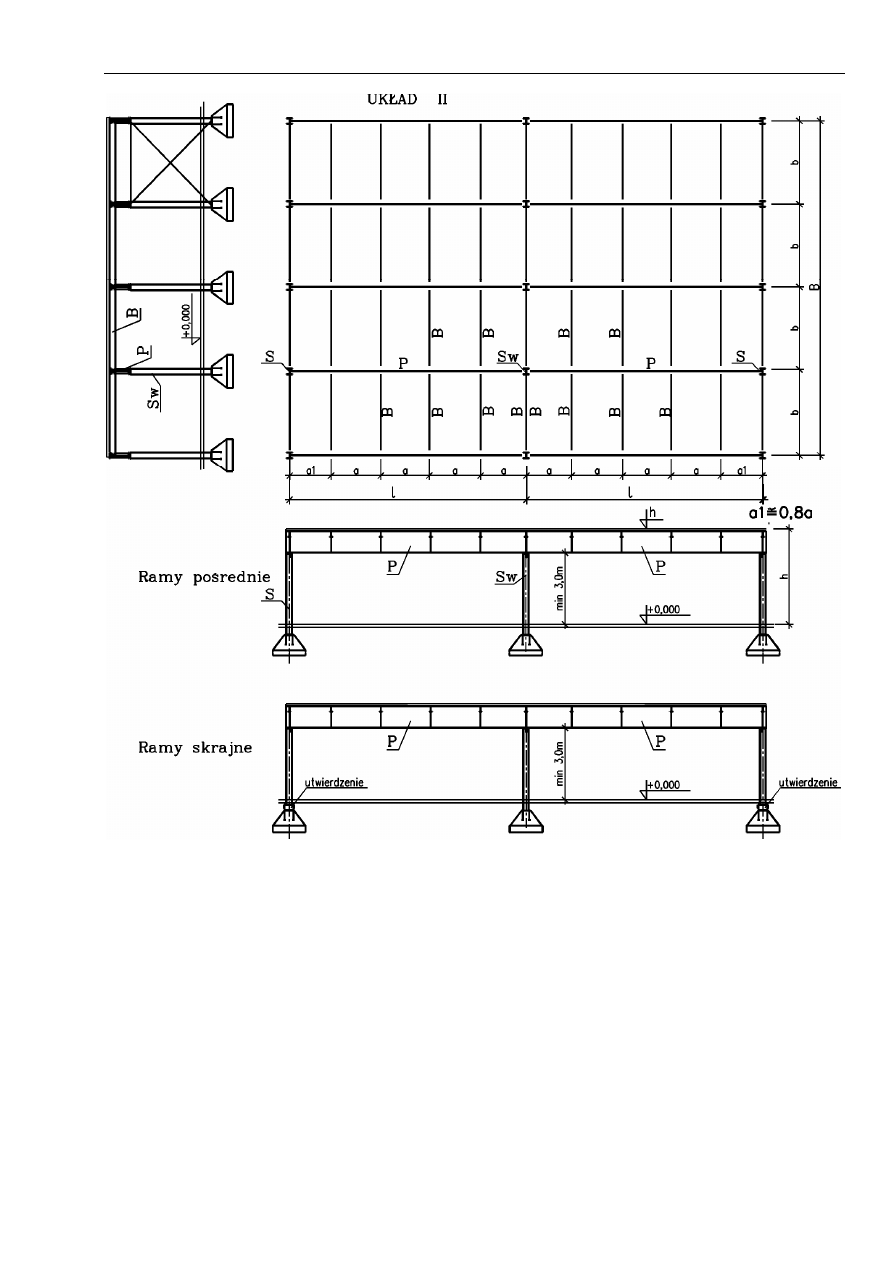
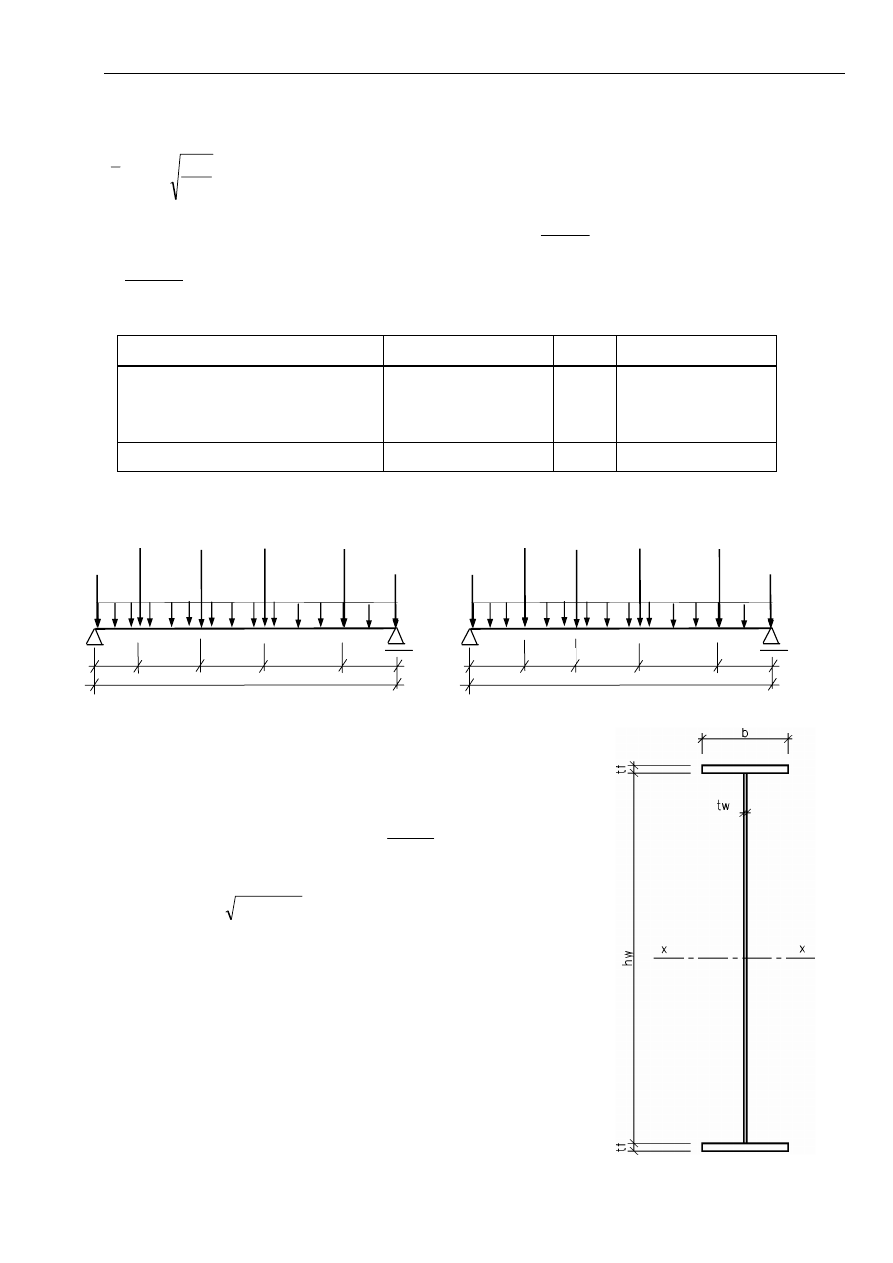
wymiarów stropu. Dwa przykładowe układy pokazano na str.3 i 4, przy tym układ I posiada tylko słupy
zewnętrzne, układ II posiada słupy zewnętrzne i wewnętrzne). Ogólne zasady kształtowania stropu:
- rozstaw belek (żeber):
a = 2,0
÷ 3,0 m;
- rozpiętość belek (odległości pomiędzy podciągami): b = 4,0
÷6,0 m;
- rozpiętość podciągu:
l = 9,0
÷ 16,0 m.
- minimalna wysokość od poziomu posadzki do dolnego pasa podciągu wynosi 3,0 m.
- płytę stropową przyjąć jako żelbetową o grubości 8
÷
10 cm (ewentualnie obliczyć).
Dla wyrównania reakcji z płyty przekazywanych na belki, proponuje się przyjęcie rozstawu skrajnych belek
równych a
1
≅ 0,8 a.
Stateczność konstrukcji jest zapewniona:
- w kierunku podłużnym - przez zabudowanie stężeń (np. typu X)
- w kierunku poprzecznym - przez zaprojektowanie sztywnych ram skrajnych (słupy utwierdzone w
fundamencie, ew. sztywne połączenie podciągu ze słupami) lub poprzez nawiązanie (połączenie) ze
słupem układu poprzecznego hali lub przez zabudowanie stężeń.
KONSTRUKCJE STALOWE opr. dr inż. Bernard Kowolik
Materiały pomocnicze do wykonania obliczeń stropu stalowego Strona 3/17
KONSTRUKCJE STALOWE opr. dr inż. Bernard Kowolik
Materiały pomocnicze do wykonania obliczeń stropu stalowego Strona 4/17
KONSTRUKCJE STALOWE opr. dr inż. Bernard Kowolik
Materiały pomocnicze do wykonania obliczeń stropu stalowego Strona 5/17
2. Opis techniczny
Zostawić stronę pustą. Opis wykonać po skończonych obliczeniach.
3. Belka stropowa
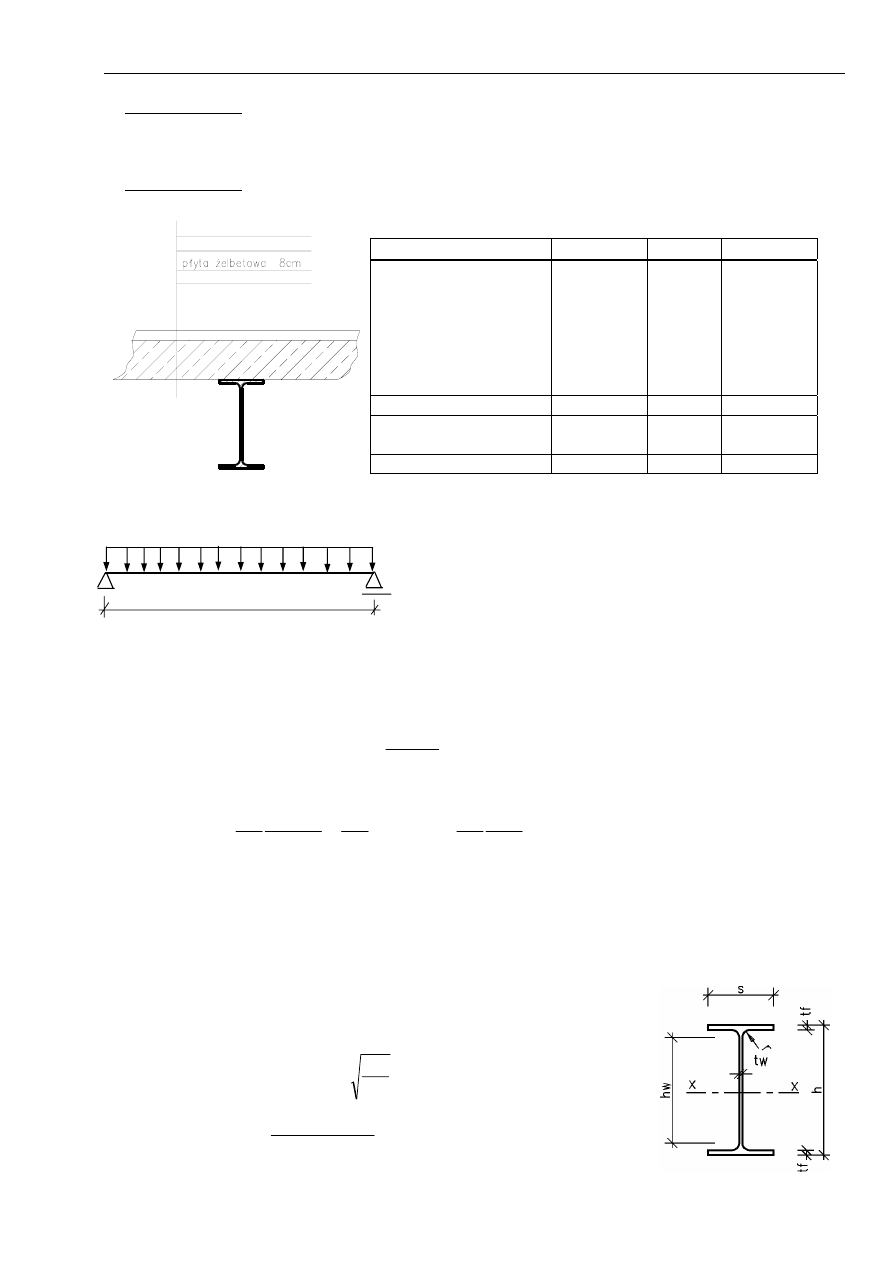
3.1. Zestawienie obciążeń [3,4,5]
3.2. Przyjęcie przekroju poprzecznego
a) Wartości sił wewnętrznych
Wykonać wykresy momentów zginających i sił poprzecznych
R
belki
= ..., V = ...., M
max
= ....
b) Przyjęcie przekroju poprzecznego
wzór (52), wzór (42)
ϕ
L
= 1 (p.4.5.1.c);
α
p
= 1,07 (dla I, IPE),
α
p
= 1,05 (dla HEB, HEA) , (załącznik 4)
f
d
= ... (tabl.2), należy pamiętać, że f
d
zależy od grubości elementu
ze wz. (52) i (42) otrzymuje się
.......
f
M
W
d
L
p
max
potrz
=
ϕ
α
=
z porównania ugięć z dopuszczalnymi
250
E
b
q
384
5
I
250
b
EI
b
q
384
5
u
u
3
k
potrz
x
potrz
x
4
k
gr
⋅
=
⇒
=
=
,
,
max
Należy przyjąć:
- dwuteownik normalny (I) lub równoległościenny (IPE) o W
≥ W
potrz
oraz I
x
≥
I
x,potrz
z „Tablic...”[6]
- dwuteownik szerostopowy HEA o W
≥ W
potrz
oraz I
x
≥
I
x,potrz
z katalogu profili szerokostopowych
Narysować oba przekroje w skali 1:10 z podaniem jego wymiarów i charakterystyki
(I
x
= ..., W
x
=...., A=..., m =.....).
Do dalszych obliczeń należy przyjąć przekrój bardziej ekonomiczny (tzn. o
mniejszym ciężarze)
3.3. Sprawdzenie nośności belki stropowej
a) Klasa przekroju (tabl.6):
d
f
215
=
ε
- dla pasa ściskanego
);
2
.
kl
(
10
);
1
.
kl
(
9
..
t
)
r
2
t
s
(
5
,
0
f
w
ε
ε
<
<
=
−
−
b
q
Warstwa g
k
[kN/m]
γ
f
g [kN/m]
......................................
płyta żelbetowa
25·0,08·a [kN/m
3
·m·m]
....................................
dwuteownik I... (przyjąć
h=(b/24-b/18)
...kG/m = ....kN/m
...
...
...
...
...
...
...
...
...
...
...
...
Razem
g
k
g
Obciążenie użytkowe
p
k
·a
p’
k
...
p’
Suma q
k
= g
k
+p’
k
q = g+p’
KONSTRUKCJE STALOWE opr. dr inż. Bernard Kowolik
Materiały pomocnicze do wykonania obliczeń stropu stalowego Strona 6/17
- dla środnika przy zginaniu (
α=05)
)
2
.
kl
(
78
);
1
.
kl
(
66
....
t
h
w
w
ε
<
ε
<
=
przekrój zalicza się do klasy .... przy zginaniu
b) Sprawdzenie nośności elementu zginanego jednokierunkowo
Nośność przekroju kl.1 i 2 przy zginaniu wz.(42): M
R
=
α
p
⋅W
x
⋅f
d
= ....
Warunek nośności wz.(52):
1
....
M
M
R
L
max
≤
=
ϕ
Ze względów ekonomicznych przekrój powinien być wykorzystany powyżej 80% (jeżeli nie decydują ugięcia).
c) Sprawdzenie nośności elementu ścinanego
ε
<
=
70
....
t
h
w
w
(tabl.10) przekrój jest odporny na utratę stateczności miejscowej przy ścinaniu (
ϕ
pv
= 1);
Nośność przekroju na ścinanie wz.(47) i tabl.10: V
R
= 0,58 A
V
f
d
= ......; przy A
v
= h
⋅t
w
= .......
V =...
≤V
R
=.....
Dla V=...
≤ Vo = 0,6V
R
= ..... nie jest konieczne sprawdzenie warunku (45)
3.4. Sprawdzenie stanu granicznego użytkowalności (ugięć)
(tabl.4)
.......
u
....
u
....
250
b
u
...
EI
b
q
384
5
u
gr
max
gr
x
4
k
max
=
≤
=
=
=
=
=
3.5. Sprawdzenie warunku nośności w stadium montażu (dla studentów KBI)
a) zestawienie obciążeń
b) określenie sił wewnętrznych:
M
mon
= M(g
mon
) + M(P
mon
) = ...... + ........ = ...... kNm
c) moment krytyczny przy zwichrzeniu (porównaj przykład 4.5 w poz. [6])
przepisać wz. Z.1-7 z objaśnieniami oznaczeń
M
cr
= ........................................... (Z1-7)
obliczyć
N
y
= .................. (Z1-4) N
z
= .......................... (Z1-5)
Uwaga: Charakteystki I
w
, I
T
są podane w tablicach [7]
Wspólczynnik A
1
, A
2
, B przyjąć z tablicy Z1-2:
- jak dla obciążenia równomiernie rozłożonego i warunków podparcia P P , jeżeli M(g
mon
)
≥ M(P
mon
)
- jak dla siły skupionej w środku rozpiętości i warunków podparcia P P , jeżeli M(P
mon
) > M(g
mon
)
y
s
= 0, a
o
= h/2, a
s
= y
s
– a
o
= -h/2
Warstwa g
k
[kN/m]
γ
f
g [kN/m]
Płyta żelbetowa
26·0,08·a
ciężar deskowania
(przy
zastosowaniu deskowań
podwieszanych do belek)
g
des
·a
obciążenie montażowe [5]
0,60·a
dwuteownik I (przyjęty w
p.3.2)
...kG/m = ....kN/m
...
...
.....
....
...
...
.....
......
...
...
....
....
Razem
g
k
mon
g
mon
Ciężar montażysty P
k
mon
= 1,0 kN
γ
f
=........ P
mon
= ........kN
b
q
mont
P
mon
KONSTRUKCJE STALOWE opr. dr inż. Bernard Kowolik
Materiały pomocnicze do wykonania obliczeń stropu stalowego Strona 7/17
Policzyć M
cr
= .................. wg wz. Z1-7 wstawiając znak „+“
d) wyznaczenie wspólczynnika zwichrzenia
........
,
=
⇒
=
L
cr
R
L
M
M
15
1
ϕ
λ
(
ϕ
L
odczytać z tabl.11 wg krzywej a
o
)
e) sprawdzenie warunku nośności w stadium montażu:
1
M
M
R
L
mon
≤
= ....
ϕ
4. Podciąg
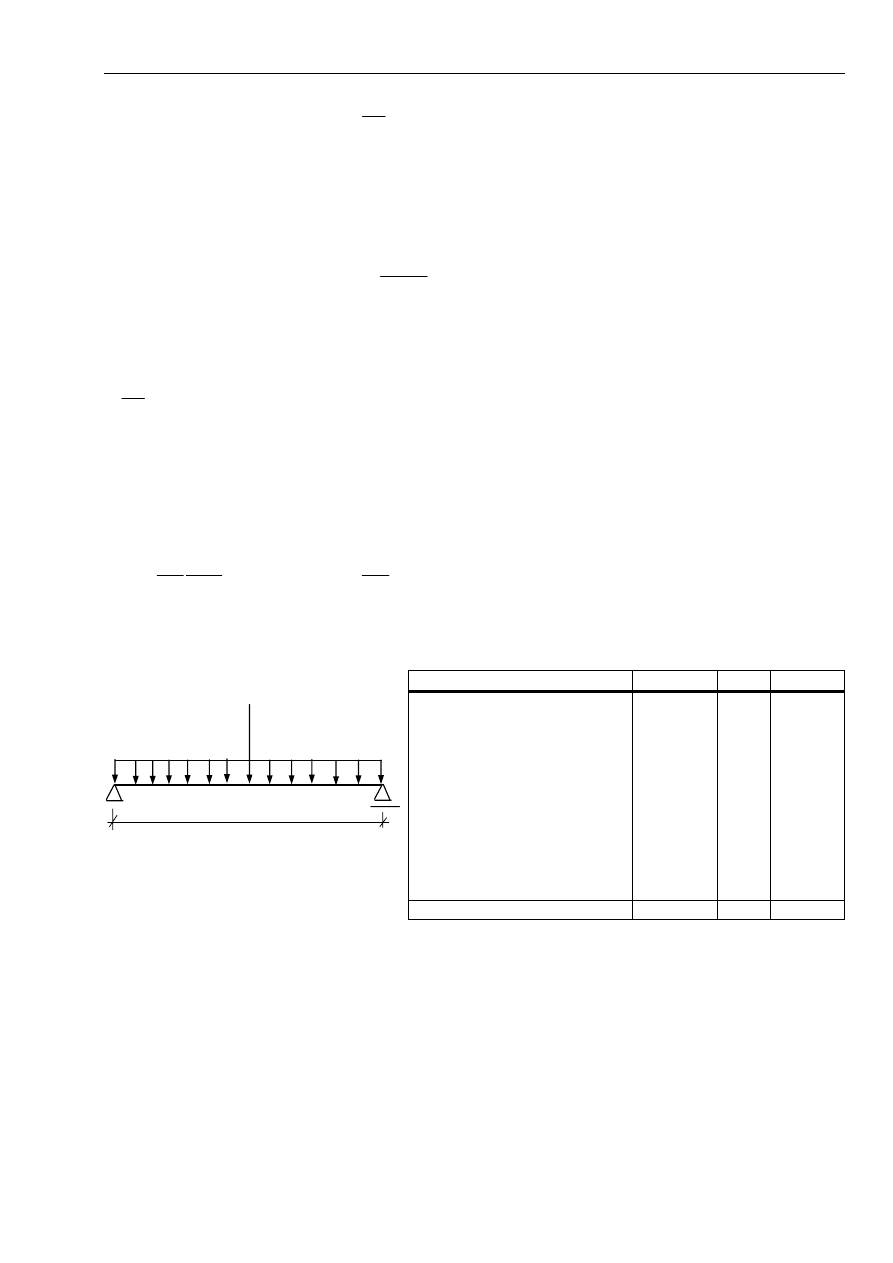
4.1. Zestawienie obciążeń
Obciążenie Charakt.
γ
f
oblicz.
ciężar własny (można przyjąć jak dla
IKS-1200-3)
...kG/m = ....kN/m
g
p
k
[kN/m]
...........
g
p
[kN/m]
Reakcja z belek
F
k
= q
k
·b = .... [kN]
F = 2·R
belki
=.... [kN]
4.2. Obliczenie momentów zginających i sił poprzecznych
- układ I
- układ II
Wykonać wykresy momentu zginającego i sił poprzecznych oraz podać ich wartości w charakterystycznych
punktach (tzn. pod siłami skupionymi)
R
A
= ....., R
B
= ......... V
max
= ...., M
max
=
4.3. Przyjęcie przekroju
ze wz. (52) i (42) otrzymuje się
.......
f
M
W
d
L
max
potrz
=
ψϕ
=
(wstępnie można
przyjąć
ψ
= 0,85
÷
0,95)
........
W
)
2
,
1
0
,
1
(
h
3
potrz
opt
opt
,
w
=
λ
÷
=
λ
opt
= 105
÷
115 dla 18G2A;
λ
opt
= 115
÷
125 dla St4V;
λ
opt
= 125
÷
135 dla St3S
Ze względu na wykorzystanie arkusza blachy zaleca się przyjmować
wysokości h
w
= 710, 850, 960,1100, 1210, 1350 mm. Przy większych
wysokościach zmniejszyć rozpiętość podciągu przez zastosowanie słupa
wewnętrznego.
przyjęto h
w
= .......
t
w
= h
w
/
λ
opt
= .....; lecz t
w
≥ 6 mm
przyjęto t
w
= .......
b = h
w
/5
÷ h
w
/4 = .......; przyjęto b = .......
l
g
p
F
F
F
0,3F
0,3F
a
1
a
1
a
a
a
F
l
g
p
F
F
F
0,5F
0,3F
a
1
a
a
a
a
F

KONSTRUKCJE STALOWE opr. dr inż. Bernard Kowolik
Materiały pomocnicze do wykonania obliczeń stropu stalowego Strona 8/17
.....
6
h
t
W
bh
1
t
2
w
potrz
w
f
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
=
; przyjęto t
f
= .......
policzyć I
x
= ......; W
x
= ....
4.4. Sprawdzenie nośności podciągu (stan krytyczny)
(porównaj przykład 4.3 w podręczniku [6])
a) Sprawdzenie nośności elementu zginanego jednokierunkowo
Klasa przekroju (tabl.6):
- dla pasa ściskanego
);
2
.
kl
(
10
);
1
.
kl
(
9
..
t
)
t
b
(
5
,
0
f
w
ε
<
ε
<
=
−
- dla środnika przy zginaniu (
α = 0.5)
);
4
.
kl
(
105
....
t
h
w
w
ε
>
=
przekrój zalicza się do klasy 4 przy zginaniu
Rozstaw żeberek poprzecznych w belkach o przekroju kl.4 nie powinien być większy niż podwójna wysokość
środnika (p.4.2.6.1c). Jeżeli a>2h
w
należy zastosować żeberka pośrednie i uwzględnić je przy obliczaniu
współczynnika
β.
Rozstawy żeberek:
- gdy nie są konieczne pośrednie a
s
= a (odcinki wewnętrzne) a
1s
= a
1
(odcinki
przypodporowe)
- przy jednym żeberku pośrednim a
s
= 0,5a (odcinki wewnętrzne) a
1s
= 0,5a
1
(odcinki przypodporowe)
Należy sprawdzić, czy a
s
≤
2h
w
i a
1s
≤
2h
w
ze wz. (7)
......
215
f
56
K
t
h
d
w
w
p
=
=
λ
, przy czym dla
β=a
s
/h
w
=... >1 oraz
ν=0 K=K
2
= 0,4+0,6
ν = 0,4 (tabl.8)
z tabl.9 odczytać
ϕ
p
= .....
Dla stanu krytycznego
ψ = ϕ
p
=... wz.(13)
Nośność przekroju kl.4 przy zginaniu wz.(43): M
R
=
ψ⋅W
x
⋅f
d
= ....
Warunek nośności (wz.52):
1
....
M
M
R
L
max
≤
=
ϕ
Należy zaprojektować przekrój ekonomicznie, tak aby wykorzystać nośność powyżej 90%.
b) Sprawdzenie nośności elementu ścinanego
ε
>
=
70
....
t
h
w
w
(tabl.10)
przekrój nie jest odporny na utratę stateczności miejscowej przy ścinaniu
wz. (7)
......
215
f
56
K
t
h
d
v
w
w
p
=
=
λ
, przy czym dla
β= a
1s
/h
w
=... >1 (dla układu I)
β= a
s
/h
w
=... >1 (dla układu II)
K
v
=
β
− /
1
2
65
,
0
=........ (tabl.8)
wz.(17)
1
lecz
/
1
pv
p
pv
≤
ϕ
λ
=
ϕ
Nośność przekroju na ścinanie wz.(16): V
R
= 0,58
ϕ
pv
A
V
f
d
= ......; przy A
v
= h
w
⋅t
w
= .......
V
max
=...
≤V
R
=.....
c) Sprawdzenie nośności elementu zginanego i ścinanego
Dla przekroju belki (x= a
1
, a
1
+a,...), w których V=... >Vo = 0,3 V
R
= ..... konieczne jest sprawdzenie
warunku M
≤ M
R,v
, gdzie M
R,v
należy policzyć ze wz. (46). Dla układu I należy wcześniej policzyć V
R
wg toku
podanego w punkcie b), przy czym uwzględnić
β= a
s
/h
w.
KONSTRUKCJE STALOWE opr. dr inż. Bernard Kowolik
Materiały pomocnicze do wykonania obliczeń stropu stalowego Strona 9/17
d) Obliczenie przekroju w stanie nadkrytycznym – dla chętnych studentów KBI – wykonać wg przykładu 4.5
podręcznika [6]
4.5. Sprawdzenie stanu granicznego użytkowalności (ugięć) (tabl.4)
Ugięcia można policzyć dowolną metodą jako sumę ugięć od obciążenia równomiernie rozłożonego i
skupionego (wartości charakterystyczne), wykorzystując wiedzę nabytą na przedmiocie mechanika
teoretyczna / budowli.
gr
max
gr
F
x
4
k
p
max
u
u
;
....
350
l
u
...
u
EI
l
q
384
5
u
≤
=
=
=
+
=
(u
f
– ug. od obc. skupionych)
4.6. Spoiny łączące pasy ze środnikiem
Przyjąć minimalną grubość spoin z warunku konstrukcyjnego:
⎩
⎨
⎧
=
≤
≤
⎭
⎬
⎫
=
mm
16
t
7
0
a
mm
3
t
2
0
w
nom
f
........
.
.....
.
Przyjęto a =.....mm (dozwolone gr. spoin 3,4,5,6 ..... mm)
Następnie należy sprawdzić warunek (96)
, w którym S – moment statyczny pasa względem osi x-x, V – siła
tnąca w przekroju przypodporowym (V
max
)
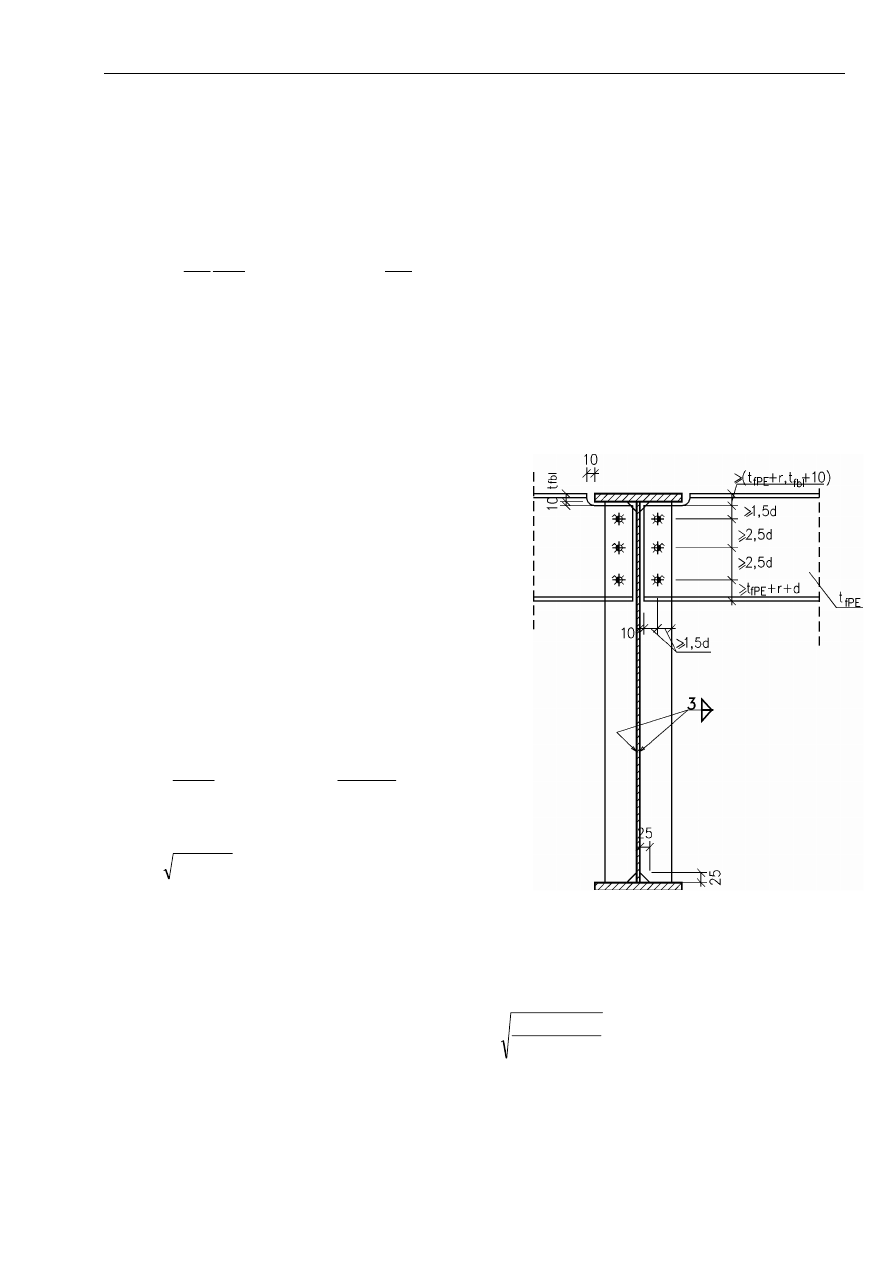
4.7. Połączenie belek stropowych z podciągiem
Należy skonstruować połączenie i wykonać jego obliczenia
na podstawie literatury. Zaleca się wykorzystać rozwiązanie
podane w przykładzie 6.4a [7]„Obliczania konstrukcji
stalowych...” (PWN lub skrypt). Szerokość b
s
żeberka nie
może być mniejsza od 3d+10 mm (d-średnica śruby), zaś
grubość t
s
- od 6mm i od grubości środnika dwuteownika.
- przyjęcie średnicy i klasy śrub (zaleca się stosowanie
śrub M16 i M20 kl. 4.8)
- przyjęcie liczby śrub n > R
belki
/S
Rv
(R
belki
– reakcja z
belki-żebra; S
Rv
wg tabl. Z2-2)
- rozmieszczenie śrub zgodnie z tabl.15 i rys. obok
- określenie nośności S
Rv
i S
Rb
wg tabl.16
- nośność obliczeniowa S
R
= min(S
Rv
i S
Rb
)
- moment w połączeniu M
o
= R
belki
·e
- siły składowe
....
)
(
S
...
max
M
=
⋅
=
=
=
∑
2
i
belki
F
r
r
M
n
R
S
(r
i
– odległość i-tej śruby od ich środka ciężkości)
- sprawdzenie warunku nośności
R
2
M
2
F
S
S
S
S
≤
+
=
W przypadku niespełnienia powyższego warunku należy
zwiększyć liczbę lub średnicę śrub, ewentualnie klasę śrub).
- sprawdzenie warunku 81 w normie [1] – wykonać na podstawie przykładu 6.4a [6].
- sprawdzenie warunku sztywności żeberka (25) w normie [1] I
s
≥ k h
w
t
w
3
,
gdzie k = 1,5(h
w
/a
s
)
2
lecz k
≥ 0,75, I
s
= (b+t
w
)
3
t
s
/12
- spoiny łączące żeberko usztywniające ze środnikiem
ze wz.(94) , przy przyjęciu l
max
= 100a (p.6.3.2.2b)
.....
=
⋅
⋅
=
d
II
belki
potrz
f
100
2
R
a
α
(
α
II
wg tabl.18) , przy tym
grubość spoiny powinna spełniać warunki konstrukcyjne:
⎩
⎨
⎧
=
≤
≤
⎭
⎬
⎫
=
mm
16
t
7
0
a
mm
3
t
2
0
s
nom
w
........
.
.....
.
Przyjęto a = ... mm
KONSTRUKCJE STALOWE opr. dr inż. Bernard Kowolik
Materiały pomocnicze do wykonania obliczeń stropu stalowego Strona 10/17
4.8. Sprawdzenie sztywności pośrednich żeberek usztywniających
Sprawdzają tylko studenci, którzy musieli wg punku obliczeń 4.4 zastosować żeberka pośrednie. Mogą one być
jeno- lub dwustronne. Grubość żeberka nie powinna być mniejsza niż 6 mm a szerokość - niż 60 mm.
Sztywność sprawdzić tak jak podano w p. 4.7.
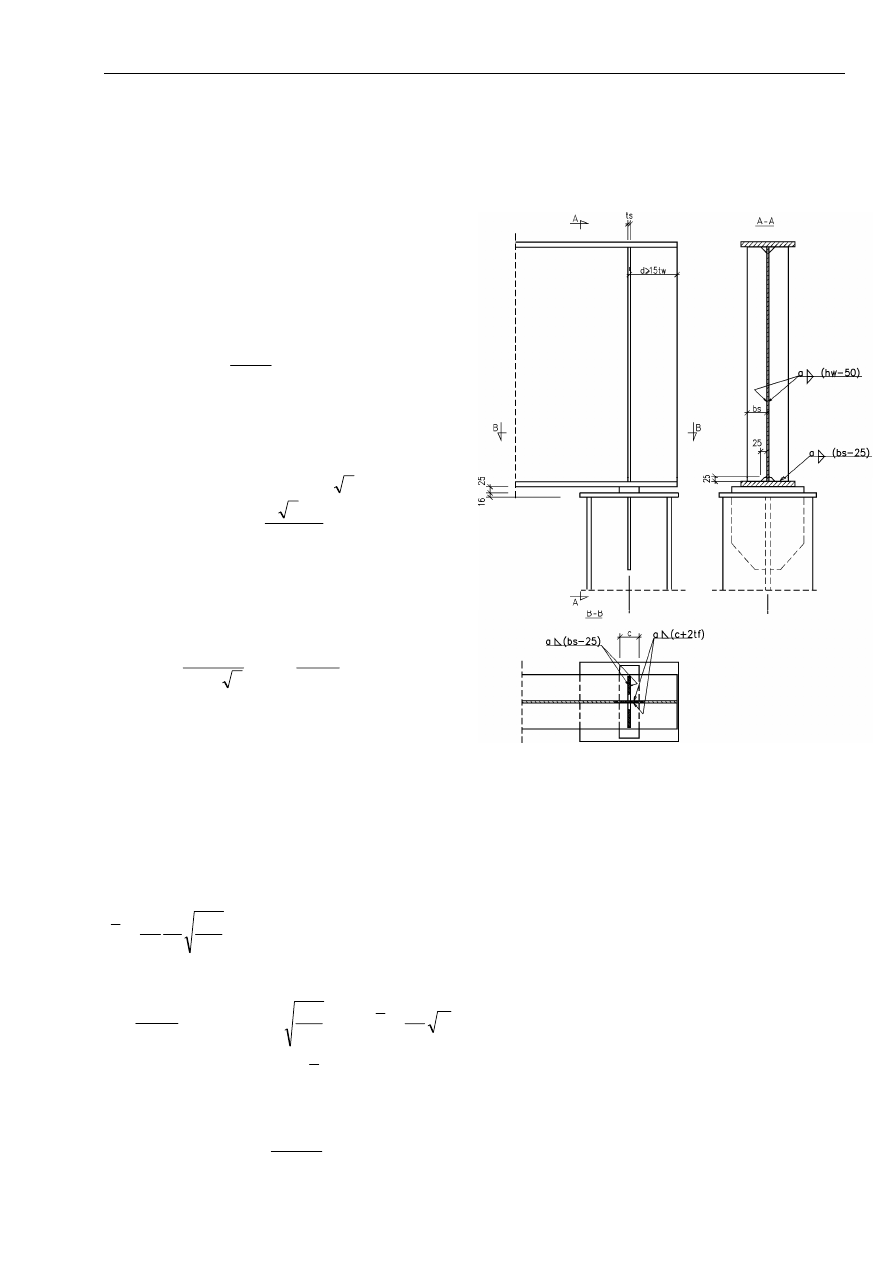
4.9. Oparcie podciągu na słupie zewnętrznym
a) Przyjęcie wymiarów żeberka usztywniającego
- Należy przyjąć płytkę centrującą o szerokości
c = 60
÷
100 mm i grubości 25 mm
- Przyjęto szerokość żeberka b
s
= ......
(można przyjąć b
s
≅ 0,5(b - t
f
) –20 mm)
- Określenie potrzebnej grubości żeberka z warunku
nośności:
........
f
b
2
R
t
d
s
A
potrz
,
s
=
=
(t
s
≥ 6mm)
Przyjęto
s
t = ..... mm
b) Spoiny poziome
Σl = 2(c+2t
f
) + 4(b
s
-25mm) = ......
Ponieważ
τ
II
= 0,
τ
⊥
=
σ
⊥
=
2
/
σ
, to z warunku
(93) obliczamy
d
A
potrz
lf
R
2
a
Σ
χ
=
.
Przyjęto a = .....mm
Należy sprawdzić, czy przyjęta grubość spoiny
spełnia warunki konstrukcyjne.
a
≤
0,7 t
w
.
Sprawdzić warunek (93), gdzie
x
II
A
I
a
2
S
V
,
2
l
a
R
⋅
⋅
=
⋅
=
=
∑
⊥
⊥
τ
τ
σ
, (S – moment
statyczny pasa względem osi x-x, V – siła tnąca w
przekroju przypodporowym (V
max
))
c) Sprawdzenie nośności żeberka usztywniającego
A
s
= 2b
s
t
s
+ 30t
w
t
w
= .......
I
s
≅ t
s
(2b
s
+t
w
)
3
/12 =......... i
s
= .......
klasa przekroju: 0,5 b
s
/t
s
= ........
≤ 14ε
d/t
w
= .... >14
ε - przekrój kl.4
.........
....
.
=
=
⎯
⎯ →
⎯
=
=
p
9
tabl
d
w
215
f
56
K
t
d
ϕ
ψ
λ
(z tabl. 8 jak dla ściskania K = 2,2 +0,8·1,0 = 3,0)
A
s
= 2b
s
t
s
+ 30t
w
t
w
= ..... I
s
≅ t
s
(2b
s
+ t
w
)
3
/12 = ....... i
s
= .............
......;
i
h
8
,
0
s
w
=
=
λ
....
f
215
84
d
p
=
=
λ
;
.....
=
=
ψ
λ
λ
λ
p
;
z tabl.11. wg krzywej "c" dla
....
....
=
ϕ
⇒
=
λ
....
f
A
N
d
s
Rc
=
⋅
⋅
ψ
=
Warunek nośności
0
.
1
...
N
R
Rc
A
<
=
⋅
ϕ
KONSTRUKCJE STALOWE opr. dr inż. Bernard Kowolik
Materiały pomocnicze do wykonania obliczeń stropu stalowego Strona 11/17
d) Spoiny łączące żeberko ze środnikiem podciągu
l
)
mm
25
b
(
4
R
N
s
A
s
Σ
−
=
(jest to część reakcji przekazywana bezpośrednio na żeberko)
ze wz.(94) , przy przyjęciu l
max
= 100a (p.6.3.2.2b)
.....
=
⋅
⋅
=
d
II
s
potrz
f
100
2
N
a
α
grubość spoiny powinna spełniać warunki konstrukcyjne
⎩
⎨
⎧
=
≤
≤
⎭
⎬
⎫
=
mm
16
t
7
0
a
mm
3
t
2
0
nom
........
.
.....
.
min
max
Przyjęto a = .... mm
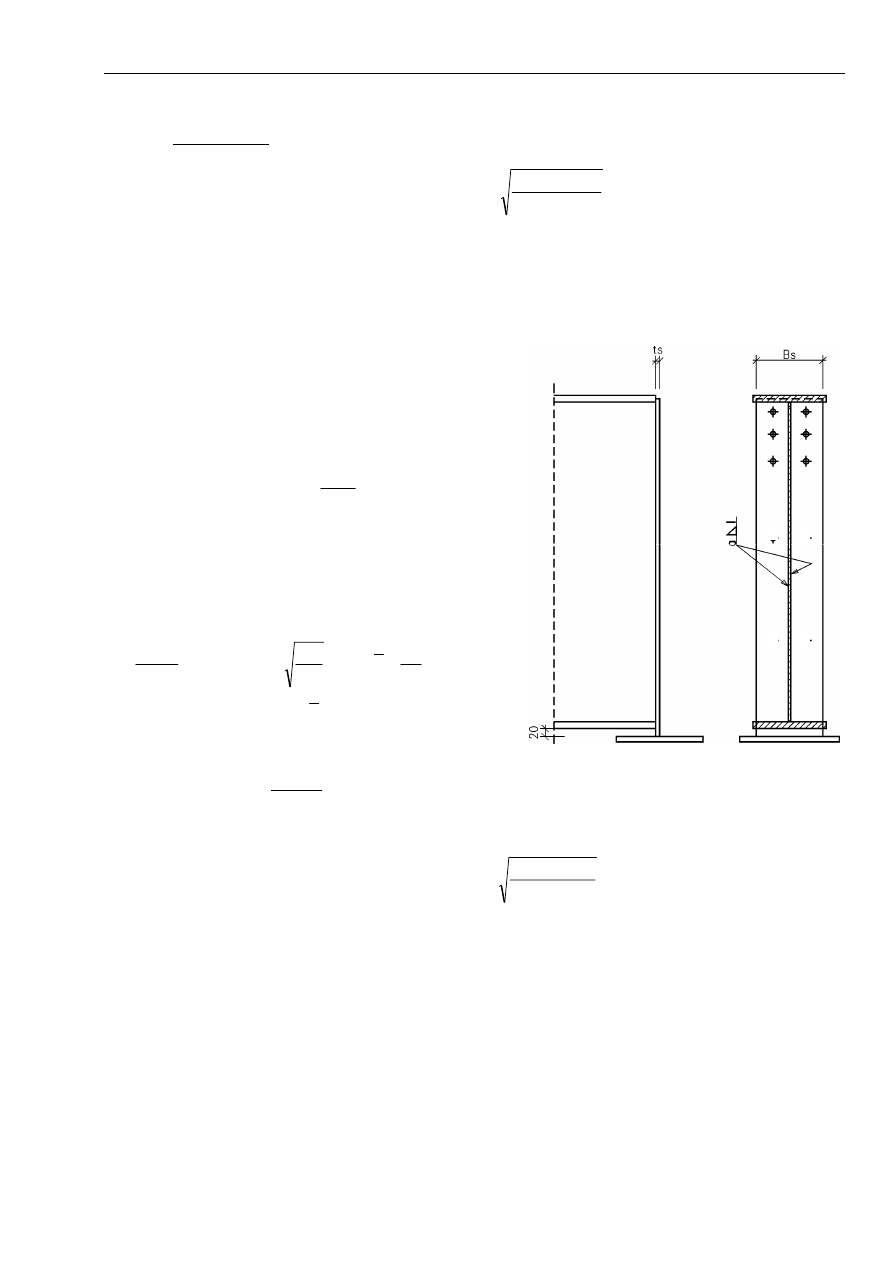
4.10. Oparcie podciągu na słupie wewnętrznym
Punkt ten realizują osoby mające układ II stropu.
a) Przyjęto szerokość żeberka
s
B = ......
(można przyjąć B
s
≅ b - 20 mm)
Określenie potrzebnej grubości żeberka z warunku nośności:
........
f
B
R
t
t
B
A
f
A
N
R
d
s
B
potrz
,
s
s
s
s
d
s
Rc
B
=
=
⇒
⎭
⎬
⎫
⋅
=
=
≤
Przyjęto
s
t = ..
b) Sprawdzenie nośności żeberka
klasa przekroju: 0,5(B
s
-t
w
)/t
s
= ........
≤ 14ε
(przekrój nie jest kl.4)
A
s
= B
s
t
s
+ 15t
w
t
w
= ..... I
s
≅ t
s
B
s
3
/12 = ....... i
s
= .......
......;
i
h
8
,
0
s
w
=
=
λ
....
f
215
84
d
p
=
=
λ
;
.....
p
=
λ
λ
=
λ
;
z tabl.11. wg krzywej "c" dla
....
....
=
ϕ
⇒
=
λ
....
f
A
N
d
s
Rc
=
⋅
⋅
ψ
=
Warunek nośności
0
.
1
...
N
R
Rc
B
<
=
⋅
ϕ
c) Spoiny łączące żeberko ze środnikiem podciągu:
ze wz.(94) , przy przyjęciu l
max
= 100a (p.6.3.2.2b)
.....
f
100
2
R
a
d
II
B
potrz
=
⋅
⋅
=
α
, przy czym grubość spoiny
powinna spełniać warunki konstrukcyjne:
⎩
⎨
⎧
=
≤
≤
⎭
⎬
⎫
=
mm
16
t
7
0
a
mm
3
t
2
0
nom
........
.
.....
.
min
max
Przyjęto a = .... mm
KONSTRUKCJE STALOWE opr. dr inż. Bernard Kowolik
Materiały pomocnicze do wykonania obliczeń stropu stalowego Strona 12/17
hf
h≥
3,0m
5. Słup
Obliczenia wykonać 1x dla słupa zewnętrznego (przy układzie I)
lub wewnętrznego (przy układzie II)
5.1. Zestawienie obciążeń
Reakcja z podciągu (w przypadku słupa zewn.) R
B
= .....
(w przypadku słupa wewnętrznego 2·R
B
= .........)
Ciężar własny słupa (przyjąć np. HEB300) g
⋅H⋅γ
f
= .....
Razem
N = ....
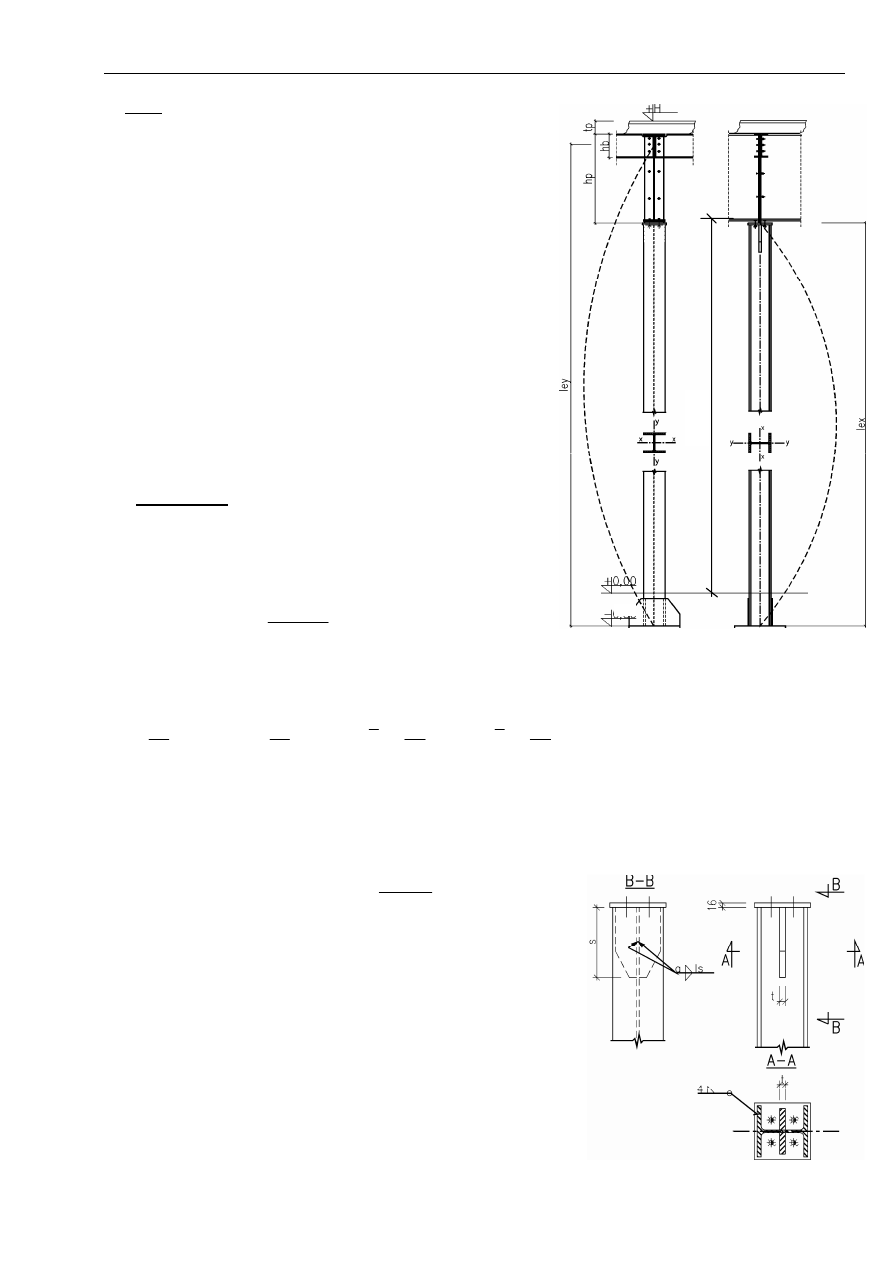
5.2. Określenie długości wyboczeniowych
l
ex
= h – tp - h
p
+ |h
f
| = ...... l
ey
= h – tp – 0,5 h
b
+ |h
f
| = ......
gdzie: h – poziom stropu
t
p
– grubość płyty betonowej z warstwami posadzki
h
b
– wysokość belki (dwuteownika przyjętego w p.3)
h
p
– wysokość żeberka podporowego podciągu
hp = h
w
+ 2t
f
+ 20mm
h
f
- poziom posadowienia (np. h
f
= -0,25 m)
h – wysokość pomieszczenia pod stropem w świetle.
Uwaga: Jeżeli h < 3,0 m należy zmienić poziom posadzki, tak
aby uzyskać h = 3,0 m.
5.3. WARIANT I - dwuteownik szerokostopowy
5.3.1. Przyjęcie przekroju pręta i sprawdzenie nośności
Należy założyć wstępnie:
ϕ
⋅
ψ = 0.5
Potrzebna powierzchnia przekroju z warunku nośności pręta
wz(39) i (34):
.....
=
⋅
⋅
=
d
potrz
f
N
A
ψ
ϕ
Należy przyjąć dwuteownik szerokostopowy HEB.....
Narysować przekrój, sprawdzić jego kl. na ściskanie.
Podać jego wymiary (na rysunku) i parametry przekroju A, i
x
, i
y
......
i
l
......;
i
l
y
ey
y
x
ex
x
=
=
λ
=
=
λ
;
......
........;
p
y
y
p
x
x
=
λ
λ
=
λ
=
λ
λ
=
λ
Współczynniki wyboczeniowe z tabl.11:
ϕ
x
- wg krzywej "b",
ϕ
y
- wg krzywej "c".
ϕ = min(ϕ
x
,
ϕ
y
)
Nośność obliczeniowa (wz.33):
.....
f
A
N
d
Rc
=
⋅
⋅
ψ
=
dla kl. 1,2,3
ψ
= 1
Warunek nośności (wz.39)
0
1
N
N
Rc
.
......
<
=
⋅
ϕ
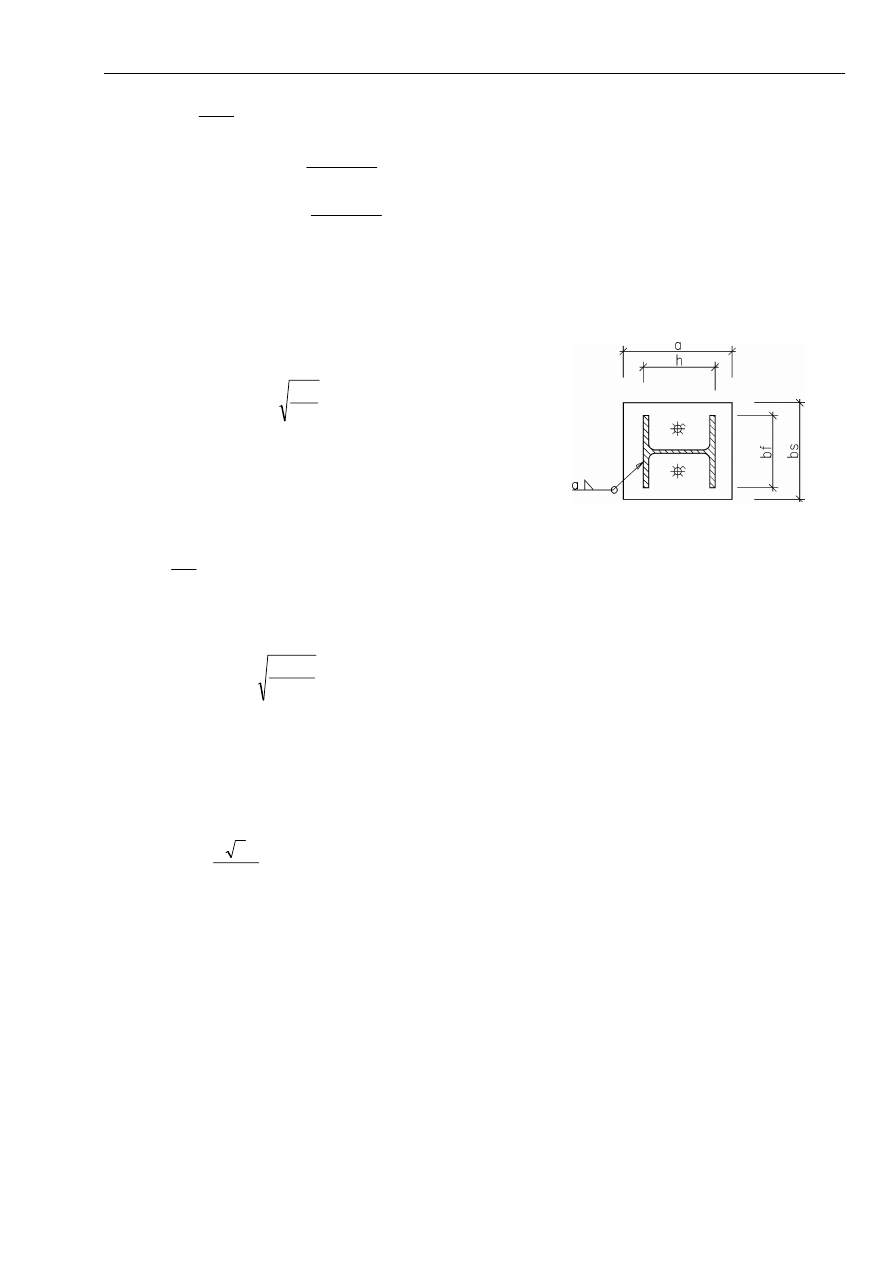
5.3.2. Głowica słupa
Przyjąć grubość żeberka
- dla słupa zewnętrznego t
≥ t
s,potrz
( t
s,potrz
wg p.4.9 obliczeń)
- dla słupa wewnętrznego t
≥ 2·t
s,potrz
( t
s,potrz
wg p.4.10 obliczeń)
Spoiny łączące żeberko ze słupem:
Warunki konstrukcyjne:
⎩
⎨
⎧
=
≤
≤
⎭
⎬
⎫
=
mm
16
t
7
0
a
mm
3
t
2
0
w
nom
.......
.
.......
.
Przyjęto spoinę o grubości a =.....
KONSTRUKCJE STALOWE opr. dr inż. Bernard Kowolik
Materiały pomocnicze do wykonania obliczeń stropu stalowego Strona 13/17
⇒
≤
=
∑
d
II
F
f
al
F
α
τ
- dla słupa zewnętrznego
.......
f
a
4
R
l
d
II
A
s
=
⋅
⋅
≥
α
- dla słupa wewnętrznego
.......
f
a
4
R
2
l
d
II
B
s
=
⋅
⋅
≥
α
Przyjęto długości żeberek l
s
= ....
5.3.3. Nieużebrowana podstawa słupa wg [2]
Przyjęto beton B-..... wg PN-B-0.3264:1999
a) wymiary blachy podstawy
- szerokość
m
h
b
2
h
a
f
+
=
wz.(B.4)
-długość
b
s
= b
f
+ 2t
wz. (B.5)
gdzie h, b
f
- wysokość i szerokość półki dwuteownika
m – współczynnik z tablicy B.1 normy [2]
t – grubość blachy podstawy (wstępnie założyć np. t = 20 mm)
....
f
......
ab
N
b
s
c
=
≤
=
=
σ
gdzie f
b
wg punktu 3.3. normy [2] (można przyjąć f
b
= 0,8f
cd
; f
cd
– wytrzymałość obliczeniowa betonu wg
PN-B-0.3264:2002)
- grubość
d
c
f
mf
h
b
7
,
1
t
σ
=
wz. (B.3)
Należy wstępnie założyć grubość blachy t (np. t =16mm), obliczyć zależności (B.4), (B.5) i (B3). Po wyliczeniu
grubości t wg (B3) należy przeprowadzać obliczenia powtórnie, aż do momentu uzyskania zgodności w
grubościach.
b) Spoiny łączące trzon słupa z blachą podstawy
Ze wz. 93 normy [1] przy
τ
II
= 0 otrzymuje się
...
l
f
N
2
a
d
potrz
=
=
∑
κ
Podać warunki konstrukcyjne (p.6.3.2.2. normy)
Przyjęto a
sp
=......mm
Uwaga. Jeżeli powierzchnia przekroju słupa będzie obrobiona mechanicznie, to można przyjąć, że 75% siły
ściskającej N przekaże się przez docisk, więc w powyższym wzorze można wstawić 0,25xN zamiast N.
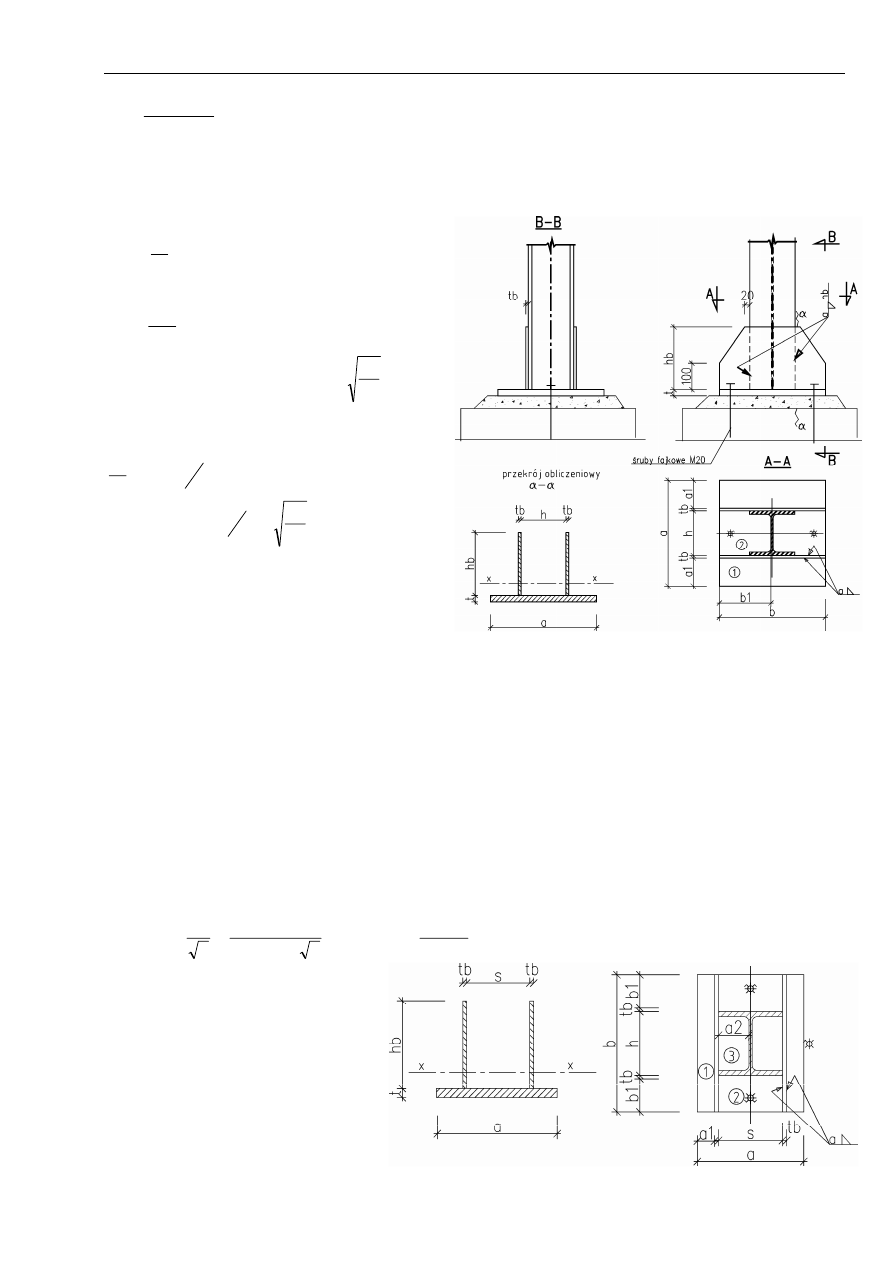
5.3.4. Użebrowana podstawa słupa wg [2]
A) blacha trapezowa równoległa do stopki dwuteownika
Przyjęto beton B-..... wg PN-B-0.3264:1999
a) Spoiny łączące blachę trapezową ze słupem:
Podać warunki konstrukcyjne...............
Przyjęto spoinę o grubości a = ... mm
KONSTRUKCJE STALOWE opr. dr inż. Bernard Kowolik
Materiały pomocnicze do wykonania obliczeń stropu stalowego Strona 14/17
h
h
lecz
......,
f
a
4
N
h
b
d
II
b
≥
=
α
⋅
⋅
=
przyjęto h
b
= ....
Grubość blachy t
b
= .... zaleca się przyjąć tak, aby przekrój
α
-
α
nie był klasy 4
h
b
/t
b
≤ 25ε
b) Blacha podstawy
b
f
N
b
a
≥
⋅
,
należy przyjąć a =..... i b = ....; przy
tym zaleca się, aby a
1
= 3
÷
10 cm, b
1
≥
5,0 cm,
b
c
f
....
b
a
N
≤
=
⋅
=
σ
Płyta 1 – wspornikowa:
......
f
a
73
,
1
t
d
c
1
1
=
⋅
=
σ
Płyta 2 – podparta na 3 krawędziach. Moment
wyznacza się ze wzorów Galerkina
....
h
....
h
b
1
=
⇒
=
ω
współczynnik z tablicy B.2.
[2] 2 wiersz
......
f
h
h
t
d
c
2
=
⋅
⋅
=
σ
ω
Zalecane jest wyrównanie grubości t
1
i t
2
(momentów M
1
i M
2
), co można osiągnąć poprzez
zmiany wymiarów a i b.
t = max (t
1
, t
2
)
c) Sprawdzenie elementu złożonego z blachy poziomej oraz blach trapezowych wykonuje się w przekroju
α-α.
M
α-α
= 0,5
σ
c
a·(0,5b-0,5s)
2
= ........
V
α-α
=
σ
c
a·(0,5b-0,5s) = ........
Dla przekroju
α-α należy wyznaczyć położenie osi obojętnej oraz policzyć charakterystykę geometryczną I
x
i
W
xmin
.
Nośność przekroju: M
R
= W
xmin
f
d
= ............, V
R
= 0,58 2·t
b
·h
b
f
d
=.......
Warunki nośności: M
α-α
≤ M
R;
V
α-α
≤ V
R.
Jeżeli V
α-α
≥ 0,3 V
R
to
należy sprawdzić
warunek: M
α-α
≤ M
R,v,
gdzie
M
R, v
wg wz.(45)
d) Spoiny łączące blachy trapezowe z blachą poziomą
Z warunku konstrukcyjnego należy przyjąć grubość spoiny a
sp
= .................
Σl = 4b – 2s = ........
........
........,
=
=
=
⋅
⋅
=
=
=
−
⊥
⊥
∑
sp
x
II
sp
a
4
I
S
V
2
l
a
N
2
α
α
τ
σ
τ
σ
(S – moment statyczny blachy poziomej
względem osi x-x)
Następnie należy sprawdzić warunek
(93)
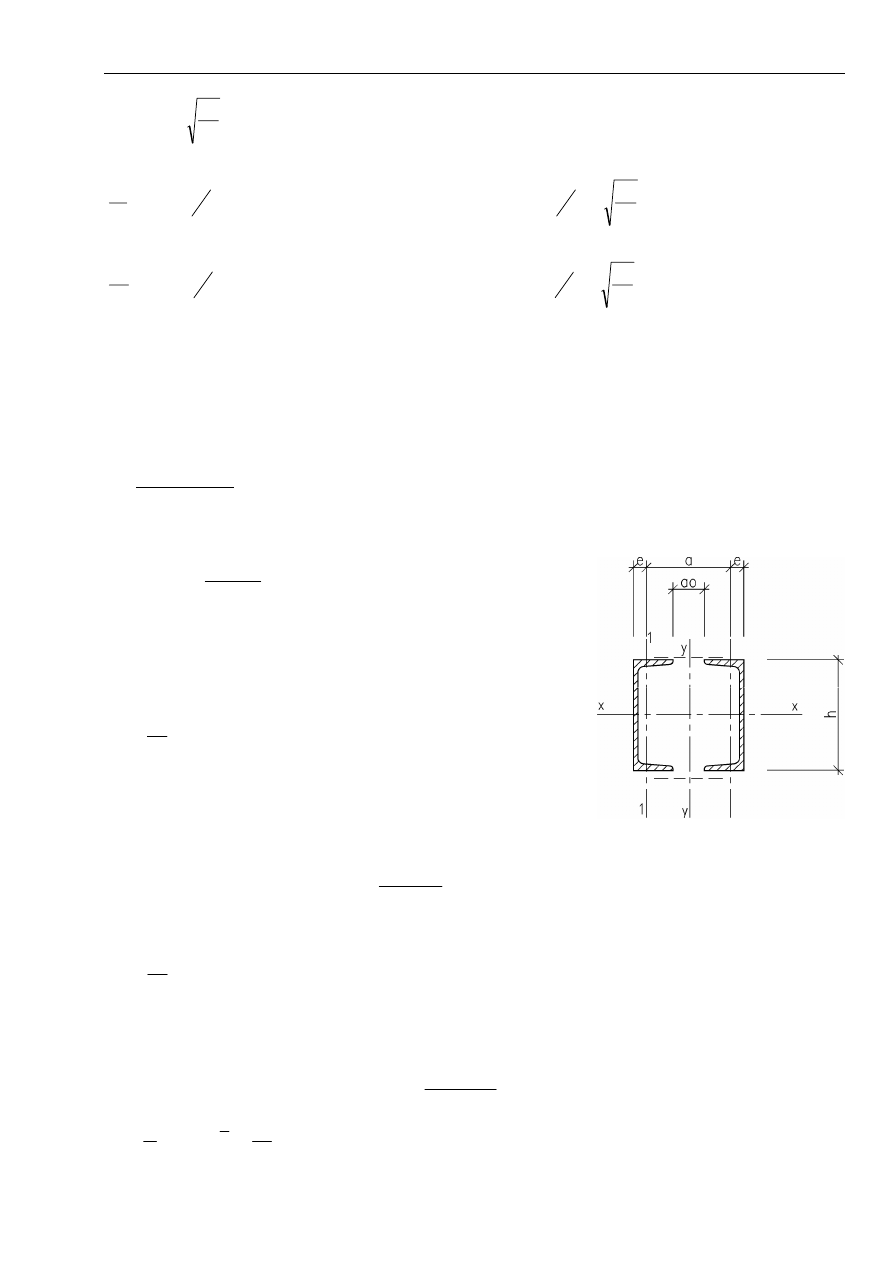
B) blacha trapezowa prostopadła do
stopki dwuteownika
Przeprowadza się jak w punkcie A),
przy tym można wyróżnić 3 płyty.
Płyta 1 – wspornikowa:
KONSTRUKCJE STALOWE opr. dr inż. Bernard Kowolik
Materiały pomocnicze do wykonania obliczeń stropu stalowego Strona 15/17
......
f
a
73
,
1
t
d
c
1
1
=
⋅
=
σ
Płyta 2 – podparta na 3 krawędziach. Moment wyznacza się ze wzorów Galerkina
....
....
=
⇒
=
s
s
b
1
ω
współczynnik z tablicy B.2. [2] 2 wiersz
......
=
⋅
⋅
=
d
c
2
f
s
s
t
σ
ω
Płyta 3 – podparta na 4 krawędziach
....
....
=
⇒
=
h
h
a
2
ω
współczynnik z tablicy B.2. [2] 1 wiersz
......
f
h
h
t
d
c
3
=
⋅
⋅
=
σ
ω
Zalecane jest wyrównanie grubości t
1
i t
2
( momentów M
1
i M
2
), co można osiągnąć poprzez zmiany wymiarów
a i b.
t = max (t
1
, t
2
, t
3
)
Siły wewnętrzne w przekroju
α-α: M
α-α
= 0,5
σ
c
a·b
1
2
= ........
V
α-α
=
σ
c
a·b
1
= ........
Długość spoin poziomych
Σl = 4b – 2h = ........
5.4. WARIANT II - przekrój złożony
(dla KBI)
5.4.1. Przyjęcie przekroju poprzecznego słupa i sprawdzenie nośności
a) Potrzebna powierzchnia przekroju z warunku nośności pręta wz(39) i
(34):
.....
f
N
A
d
potrz
=
⋅
⋅
=
ψ
ϕ
Należy założyć wstępnie:
ϕ
⋅
ψ = 0,8. Przyjąć 2 ceowniki [.... o
rozstawie w świetle ok. a
o
= 8 cm. Podać wymiary (na rysunku) i
parametry przekroju A, i
1
,i
x
, i
y
.
b) Sprawdzenie nośności względem osi materiałowej
.
......;
i
l
x
ex
x
=
=
λ
Współczynnik wyboczeniowy z tabl.11:
ϕ
x
=.......... - wg krzywej "c",
Nośność obliczeniowa (wz.33):
.....
f
A
N
d
Rcx
=
⋅
⋅
=
ψ
dla kl. 1,2,3
ψ
= 1
Warunek nośności (wz.39)
0
.
1
......
N
N
Rcx
x
<
=
⋅
ϕ
b) Sprawdzenie nośności względem osi materiałowej
......;
i
l
y
ey
y
=
=
λ
Przyjęcie przewiązek
Należy przyjąć parzystą liczbę przewiązek. Zaleca się przyjąć wstępnie n = 2 lub 4 przewiązki pośrednie.
Osiowa odległość pomiędzy przewiązkami
......;
1
n
cm
30
l
l
ex
1
=
+
−
=
..........
....
..........
......;
i
l
1
p
v
v
1
1
v
=
→
=
=
=
=
ϕ
λ
λ
λ
λ
(wg krzywej „c”)
KONSTRUKCJE STALOWE opr. dr inż. Bernard Kowolik
Materiały pomocnicze do wykonania obliczeń stropu stalowego Strona 16/17
2
v
2
y
m
2
m
λ
λ
λ
+
=
, gdzie m – liczba gałęzi
..........
....
..........
y
p
m
m
=
→
=
=
ϕ
ψ
λ
λ
λ
(wg krzywej „b”)
gdzie
ψ = min (ϕ
p
;
ϕ
1
), dla kl. 1, 2, 3 przekroju gałęzi
ϕ
p
= 1
Nośność obliczeniowa (wz.33):
.....
f
A
N
d
Rcy
=
⋅
⋅
=
ψ
Warunek nośności (wz.39)
0
.
1
......
N
N
Rcy
y
<
=
⋅
ϕ
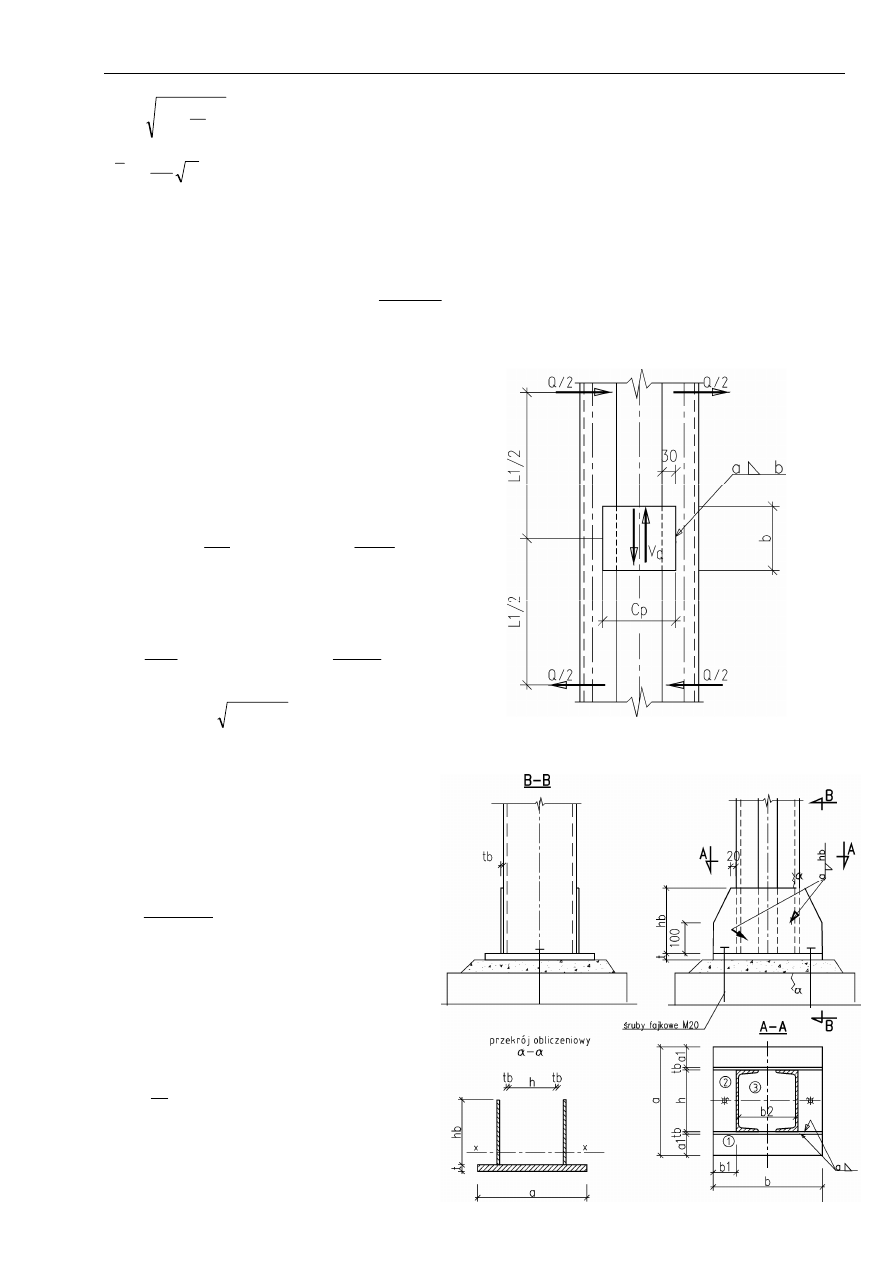
5.4.2. Przewiązki
Przewiązki pośrednie powinny mieć szerokość b
≥
100
mm skrajne co najmniej 1,5 b. Grubość t
≥
6 mm. Zaleca
się, aby nachodziły po 3cm na gałąź.
Przyjęto b = ......, t = ........, c
p
= .............
Wg wz. (62)
Q = 0,012 A f
d
Siła poprzeczna i moment wg wz. (63)
......
M
.....;
Q
=
=
=
=
2
c
V
a
2
Ql
V
p
Q
1
Q
Naprężenia w spoinach:
Podać warunki konstrukcyjne dla spoiny.
Przyjęto spoinę a
sp
= .....mm.
........
;
...
=
⋅
=
=
=
2
sp
Q
M
sp
Q
F
b
a
6
M
ba
V
σ
τ
wg wz. (95)
d
2
M
2
F
f
⊥
≤
=
+
α
σ
τ
........
5.4.3. Podstawa słupa wg [2]
Przyjęto beton B-..... wg PN-B-0.3264:1999
a) Spoiny łączące blachę trapezową ze słupem:
Podać warunki konstrukcyjne...............
Przyjęto spoinę o grubości a = ... mm
mm)
250
1,5b;
(
h
lecz
......,
f
a
4
N
h
b
d
II
b
≥
=
⋅
⋅
=
α
b- wysokość przewiązki
Grubość blachy t
b
= .... zaleca się przyjąć tak,
aby przekrój
α
-
α
nie był klasy 4.
h
b
/t
b
≤ 25ε
b) Blacha podstawy
b
f
N
b
a
≥
⋅
,
należy przyjąć a =..... i b = ....;
przy tym zaleca się, aby a
1
= 3
÷
10 cm,
b
1
≥
6,0 cm,
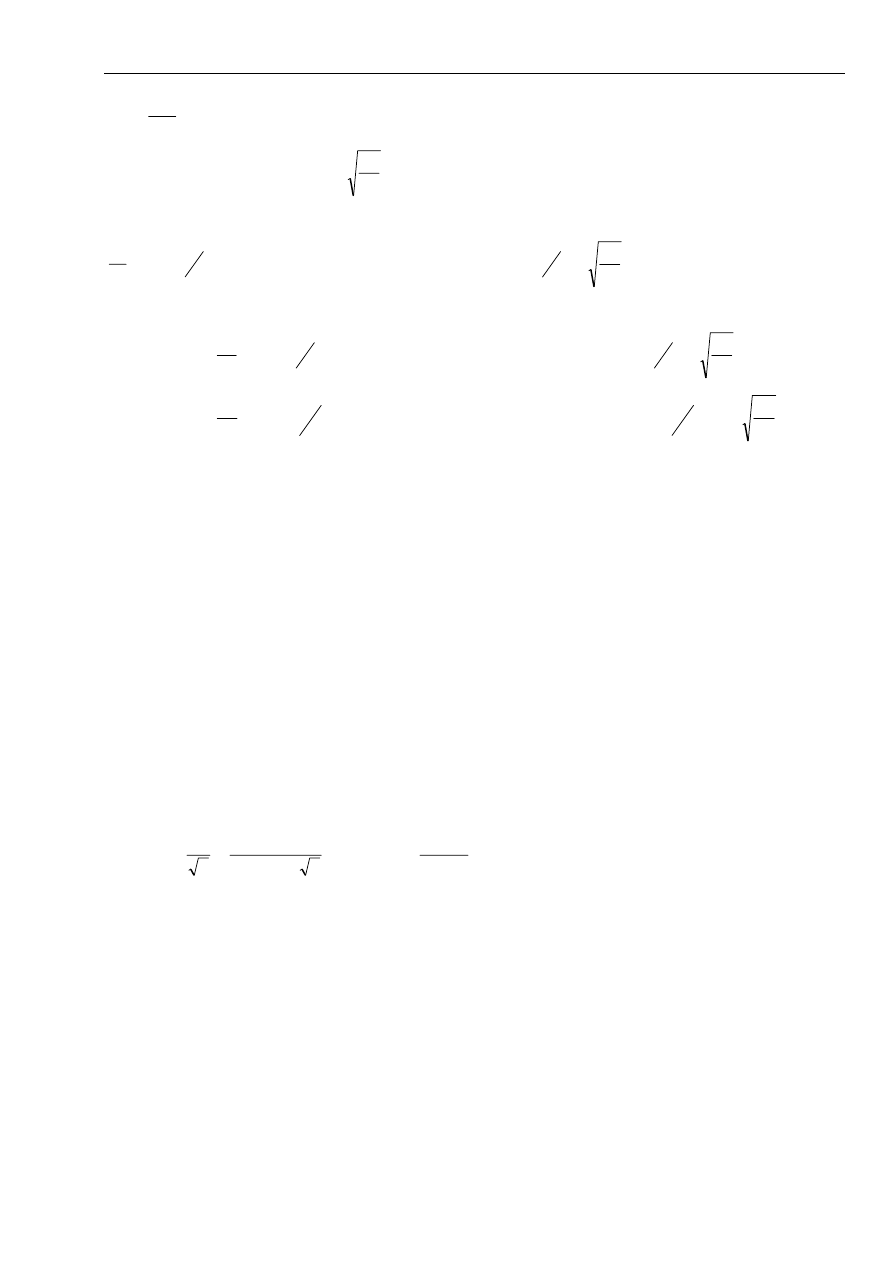
KONSTRUKCJE STALOWE opr. dr inż. Bernard Kowolik
Materiały pomocnicze do wykonania obliczeń stropu stalowego Strona 17/17
b
c
f
....
b
a
N
≤
=
⋅
=
σ
Płyta 1 – wspornikowa:
......
f
a
73
,
1
t
d
c
1
1
=
⋅
=
σ
Płyta 2 – podparta na 3 krawędziach
....
h
....
h
b
1
=
⇒
=
ω
współczynnik z tablicy B.2. [2] 2 wiersz
......
f
h
h
t
d
c
2
=
⋅
⋅
=
σ
ω
Płyta 3 – podparta na 4 krawędziach
- dla b
2
< h
....
h
....
h
b
2
=
⇒
=
ω
współczynnik z tablicy B.2. [2] 1 wiersz
......
f
h
h
t
d
c
3
=
⋅
⋅
=
σ
ω
- dla b
2
>h
....
....
=
⇒
=
2
2
b
b
h
ω
współczynnik z tablicy B.2. [2] 1 wiersz
......
=
⋅
⋅
=
d
c
2
2
3
f
b
b
t
σ
ω
Zalecane jest wyrównanie grubości t
1
i t
2
(momentów M
1
i M
2
), co można osiągnąć poprzez zmiany wymiarów
a i b.
t = max (t
1
, t
2,
, t
3
)
c) Sprawdzenie elementu złożonego z blachy poziomej oraz blach trapezowych wykonuje się w przekroju
α-α.
M
α-α
= 0,5
σ
c
a·b
1
2
= ........
V
α-α
=
σ
c
a·b
1
= ........
Dla przekroju
α-α należy wyznaczyć położenie osi obojętnej oraz policzyć charakterystykę geometryczną I
x
i
W
xmin
.
Nośność przekroju: M
R
= W
xmin
f
d
= ............, V
R
= 0,58 2·t
b
·h
b
f
d
=.......
Warunki nośności: M
α-α
≤ M
R;
V
α-α
≤ V
R.
Jeżeli V
α-α
≥ 0,3 V
R
to
należy sprawdzić
warunek: M
α-α
≤ M
R,v,
gdzie
M
R, v
wg wz.(45)
e) Spoiny łączące blachy trapezowe
Z warunku konstrukcyjnego należy przyjąć grubość spoiny a
sp
= .................
Σl = 2b + 2b
1
........
........,
=
=
=
⋅
⋅
=
=
=
−
⊥
⊥
∑
sp
x
II
sp
a
4
I
S
V
2
l
a
N
2
α
α
τ
σ
τ
σ
(S – moment statyczny blachy poziomej względem
osi x-x)
Następnie należy sprawdzić warunek (93)
Koniec obliczeń
Wyszukiwarka
Podobne podstrony:
agh strop stalowy zakres
PN 90 B 03200 Konstrukcje stalowe obliczenia i projektowanie
PM 90 B 03200 Konstrukcje stalowe Obliczenia statyczne i projektowanie
norma PN 90 B 03200 Konstrukcje stalowe Obliczenia statyczne i projektowanie
BO, STROP KLEINA OBLICZENIA (mk)
PN 90 B 03200 Konstrukcje stalowe Obliczenia statyczne i projektowanie
PN 90 B 03200 Konstrukcje stalowe Obliczenia statyczne i projektowanie(2)
OPIS TECHNICZNY strop stalowy
agh strop stalowy, zakres
Projekt hali stalowej obliczenia
PN 90 B 03200 Konstrukcje stalowe Obliczenia statyczne i projektowanie(2)
agh strop stalowy zakres
Zebranie obciazen z plyty zelbetowej na strop stalowy
Zebranie obciazen z plyty zelbetowej na strop stalowy
więcej podobnych podstron