Miłość, seks i matematyka

Autor: Piotr Wołowik

e-mail:

[e-mail]

Okres długiej zimy przejawia się niskimi temperaturami oraz krótkimi dniami. Krótkie dni wiążą

się z niedoborem światła słonecznego wpływającego na nasze samopoczucie. Stąd nic dziwnego, że
nadchodząca wiosna, budząca do życia przyrodę, przynosi nam także dopływ świeżych sił witalnych i
optymizmu.

Powszechnie panuje przekonanie, że na wiosnę najłatwiej się również zakochać. Jest to dość

łatwe, o ile obiekt naszego zainteresowania również odwzajemnia nasze zainteresowania. Po etapie
zakochania, przychodzi czas na ewolucję naszych uczuć, które mogą przerodzić się w ich stopniowe
wygaśnięcie lub w inne dojrzalsze formy.

Sam proces ewolucji uczuć jest bardzo inspirujący i nieodłącznie związany z procesem życia. Czy

można w ogóle mówić o zrozumieniu uczuć i odkryć choć trochę z ich tajemnicy?

Powszechnie panuje pogląd, że uczucia (i zarazem emocje, które są ich epifenomenami), to taka

strefa życia psychicznego człowieka, gdzie trudno jest cokolwiek przewidzieć ani zrozumieć. Ale czy na
pewno? Wszystkie procesy fizyczne można modelować równaniami matematycznymi. Sama matematyka
jest nauką obiektywną i zamodelowanie przy jej pomocy procesu naszego życia, może być w pełni
bezbłędne. Przy jej pomocy przewidzimy i odkryjemy wzory równań rządzących naszym życiem, ich
pewne nieuniknione następstwa w czasie. Dodatkowo możemy się dowiedzieć jak sobie z nimi
optymalnie poradzić. Czy uda ma się uchwycić relacje mężczyzna – kobieta przy pomocy matematyki,
obdzierając tą tajemniczą strefę do prostego ujęcia pewnych zależności wzorami matematycznymi.

Spróbujmy i zobaczmy jak matematyka i pewne relacje wpływają na nasze preferencje uczuciowe.

Wyposażeni w tą wiedzę i świadomi zależności jakim podlegamy, może postaramy się je jakoś
wykorzystać na naszą korzyść w codziennym życiu.

Wyruszmy więc na krótką wycieczkę i zobaczmy jak matematyka wpływa na nasze życie miłosne,

w kolejnych etapach przez jakie przechodzimy – od tego co nam się podoba u partnera, przez teorię
optymalnego podrywania i równań opisujących ewolucję uczuć, aż do ustalenia matematycznych
kompromisów w małżeństwie.

Faza I – Matematyczne proporcje czyli co nam się podoba

O ile można się spierać nad wartością artystyczną i pięknem określonych dzieł sztuki, to jeżeli

chodzi o współczesne kanony piękna urody męskiej i żeńskiej są one ogólnie stałe. To prawda, każda
kultura ma własny wzorzec piękna, ale pewne cechy są niezmienne od rodzaju rasy ludzkiej. Dominujące
męskie i żeńskie hormony podczas okresu dojrzewania wykształcają inne cechy fizyczne dominujące u
każdej płci. Mężczyźni mają szersze barki i węższe biodra, kobiety odwrotnie. Współczesny wzorzec
piękna dla kobiet, podtrzymywany przede wszystkim przez media lansujące dość nierealistyczny ideał
piękna – to surowy wymiar 90-60-90. Mężczyźni w obecnej erze promowanych wzorców urody, jeszcze
takich zdefiniowanych standardów matematycznych proporcji nie posiadają.

Dlaczego proporcje są tak ważne? Według teorii ewolucyjnych, zarówno mężczyźni, jak i kobiety

wybierają partnerów, którzy umożliwią im powodzenie reprodukcyjne. Kobiety, przy doborze partnera,
chcąc zapewnić sobie sukces reprodukcyjny, kierują się bardziej takimi cechami potencjalnego
kandydata, jak jego pozycja społeczna i materialna. Sama uroda ma w tym wypadku dużo mniejsze
znaczenie, istotny może być tylko wzrost mężczyzny oraz atletyczna budowa ciała. Mężczyźni natomiast
kierują się w doborze partnerki jej atrakcyjnością fizyczną, będącą zgodnie z teoriami ewolucyjnymi
odzwierciedleniem jej powodzenia reprodukcyjnego. Istotnymi dla nich sygnałami zdrowia kobiety są:
gładka, czysta skóra, błyszczące włosy, pełne wargi i owa niska proporcja obwodu talii do obwodu w
biodrach (sygnalizująca łatwość rodzenia dzieci).

Są to sygnały niezależne od społeczności, ale czy można coś powiedzieć o specyficznej urodzie

męskiej lub żeńskiej twarzy? Istnieją pewne niezależne od kultury cechy anatomiczne twarzy decydujące

1

o jej atrakcyjności. Oczywiście sama twarz musi być idealnie symetryczna, dodatkowo posiadać cechy
charakterystyczne dla małych dzieci – a więc duże oczy oraz mały nos.

Problem pojawia się w momencie, gdy ktoś chce sobie poprawić twarz przy pomocy chirurgii

plastycznej. Ma typowe cechy decydujące o urodzie czyli symetryczną twarz, duże oczy, mały nos ale
widzi, że jego twarzy jednak czegoś jeszcze brakuje do ideału. Wie, że mogłoby być lepiej, ale jak ustalić
co wymaga korekty plastycznej? Jak ustalić co powinno być poprawione? Z pomocą przychodzi
matematyka i geometryczna złota proporcja podziału odcinka mająca związek również z liczbami
Fibonacciego. Jest to taki podział odcinka gdzie umiejscowiony na nim punkt powoduje podział w takich
proporcjach, że krótszy odcinek do dłuższego ma się tak jak dłuższy do całego odcinka (który został
podzielony). Często był kiedyś stosowany w konstrukcjach architektonicznych, rzeźbach lub dziełach
malarskich w celu ich estetycznego wyglądu. Proporcje tego typu są powszechne w przyrodzie.
Zainteresowany może się więcej o tym dowiedzieć ze strony:

http://goldennumber.net

.

Z pomocą złotej proporcji podziału można skonstruować idealną maskę charakterystycznych

rysów twarzy, którą może posłużyć się chirurg plastyczny poprawiając nasz wygląd. Maska taka nałożona
na twarz, ukaże jakie punkty należy poddać korekcji aby twarz stała się idealnie proporcjonalna (wg
estetycznego złotego podziału). Oczywiście nie da się zmienić odległości rozstawu oczu – ale istnieją
cechy , które można bez problemu poddać poprawie. Wyjątkowo interesująca jest strona:

http://www.beautyanalysis.com

. Zawiera ona szereg różnych animacji pokazujących użyteczność takiej

maski idealnych proporcji (choć sam sposób jej konstrukcji jest chroniony patentem) oraz prezentację jak
„leżą” na twarzy ludzi uważanych za pięknych (lub w przypadku mężczyzn za wyjątkowo przystojnych,
jak choćby Pierce Brosnan czy Tom Cruise). Możliwe jest także pobranie takiej maski i nałożenie jej w
programie graficznym na swoje zdjęcie twarzy w celu zobaczenia, co u nas przydałoby się oddać w ręce
chirurga plastycznego.

Maska skonstruowana wg proporcji geometrycznego złotego podziału.

2

Rysunki ze strony

http://www.beautyanalysis.com

Kiedy już wiemy czego brakuje nam do doskonałych matematycznych proporcji wyglądu

możemy oddać się w ręce chirurga plastycznego, który usunie nasz mankamenty urody.

Następnym krokiem jest znalezienie odpowiedniego partnera. Zobaczmy użyteczność „królowej

nauk” również w tym zagadnieniu.

Faza II – Jak optymalnie poderwać

Kto oglądał film o genialnym matematyku-nobliście Johnie Nashu pt. „Piękny umysł” z

pewnością pamięta scenę, jak wpadł on na swoją genialną teorię. Kilku mężczyzn w barze chciało
poderwać grupę dziewczyn. W grupie tej wyróżniała się urodą pewna blondynka. Kadr z filmu z
wypowiedzią Johna Nasha olśnionego nagłą ideą swojego odkrycia wygląda następująco:

Nazywamy to lekcją Adama Smitha. Ojca współczesnej ekonomii. We współzawodnictwie,

indywidualne ambicje służą wspólnemu dobru. ... Każdy odpowiada za siebie. I odkładamy na bok
przyjaźnie. ... { Jeżeli nie weźmiesz się za blondynę, nikt się nie zabawi. } ... Adam Smith się mylił. ... Tu
chodzi o blondynkę. Najpierw wszyscy spróbują z nią ... ale dostaną kopa .... później pójdą po koleżanki
... ale też się nie uda, bo nie chcą być tymi drugimi. A co jeżeli nikt nie ruszy na blondynkę? Nikt nie
wejdzie sobie w drogę ... i nie obrazimy pozostałych dziewczyn. I wszyscy wygrywają. To jedyny sposób,
żeby się udało. Adam Smith powiedział, że każdy w grupie ... powinien robić to co dla niego najlepsze.
Tak powiedział ... ale to nie jest pełne. ... trzeba wziąć poprawkę na grupę ... każdy robi to co dla niego i
dla grupy jest najlepsze - równocześnie.

Mamy tutaj do czynienia z tzw. matematyczną teoria gier. Oprócz zastosowania do podrywania

dziewczyn, znajduje szczególne zastosowanie tam, gdzie wymagane jest szukanie kompromisów (w
ekonomii, polityce). Z tej dziedziny przyznano bardzo dużo nagród Nobla, łącznie z tegorocznymi w
ekonomii. Postaram się ją czytelnikom trochę przybliżyć w zagadnieniu jakim ją widział John Nash. Jest
to bardzo skomplikowana dziedzina, ale na nasz użytek dotyczący podrywania, rozważmy hipotetyczną
sytuację grupki ludzi na bezludnej wyspie, która pozwoli nam zrozumieć jej główną ideę. Przykład
(wartości liczbowe i imiona) zaczerpnięty z popularnonaukowej książki „Mathematics and Sex” Clio
Cresswell.

Na samotnej wyspie znalazło się 8 osób. Cztery kobiety (Lisa, Susan, Deborah, Elizabeth) i

czterech mężczyzn (Gerard, Tom, Will, Hugh). Każda z nich ma swoje osobiste preferencje, z którą
osobą chciałaby się związać. Oznacza to liczba w tabelce, tj. numer kandydata na swojej liście
preferencji. Weźmy pierwszy wiersz z tabelki mężczyzn. T preferuje w pierwszej kolejności L, potem S,
potem D i na końcu E. I tak dla każdej osoby. Podobnie z kobietami L preferuje na pierwszym miejscu G,
na drugim T, potem W i na końcu H. Preferencje D i E są takie same. Najbardziej podoba im się kolejno
W, T, G i H.

Przedstawiają to poniższe tabele:

3

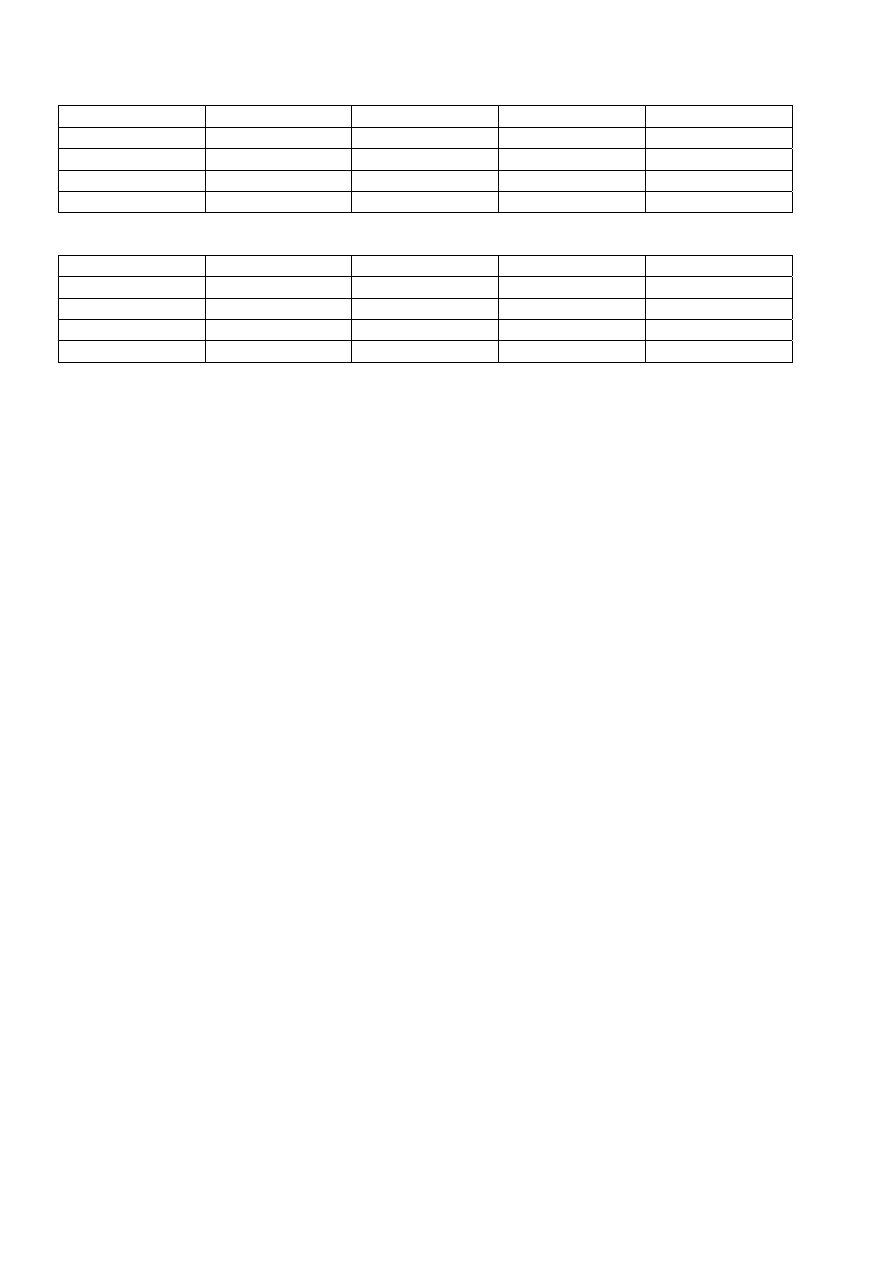
Tabela preferencji mężczyzn

Lisa

Susan

Deborah

Elizabeth

Tom

1 2 3 4

Will

1 2 4 3

Hugh

1 4 2 3

Gerard

3 1 2 4

Tabela preferencji kobiet

Tom

Will

Hugh

Gerard

Lisa

2 3 4 1

Susan

3 1 4 2

Deborah

2 1 4 3

Elizabeth

2 1 4 3

Zobaczmy jak będzie wyglądało naturalne łączenie się w pary. Prawie wszystkim mężczyznom

najbardziej podoba się Lisa, ale może ją dostać tylko jeden z nich. Podobnie wszystkim kobietom
najbardziej podoba się Will, ale jest on tylko jeden i uszczęśliwić może tylko jedną z nich. Hugh z kolei
nie podoba się żadnej z kobiet i może gdyby to nie była samotna wyspa, mógłby zostać starym
kawalerem. Wszyscy mężczyźni nie znają optimum teorii gier Nasha i zaczynają zaloty. T, W i H starają
się o L, G o S. Lisa wybiera Toma, bo jest on najwyżej jej listy preferencji (poza Gerardem który niestety
preferuje Susan i z powodu braku innych zalotników zostaje przez nią zaakceptowany, choć sama Suzan
byłaby szczęśliwa, gdyby mogła się związać z W). W i H których odrzuciła L, biorą się za następne
dziewczyny na ich liście preferencji. W za S, a H za D. S która do tej pory była z G, zostawia go dla W
(jest on wyżej na jej liście preferencji). Natomiast D żeby nie zostać stara panną wybiera H. Jest on
ostatni na jej liście preferencji, ale zawsze lepsze to niż zostać samotną. G rzucony przez S zaczyna zaloty
do drugiej na jego liście preferencji czyli D. D bardziej preferuje G niż Hugh i się z nim wiąże. H znowu
został sam i wziął się za osamotnioną E z którą już pozostał.

Na tym koniec. Układ relacji ustalania partnerów osiągnął stan równowagi. Każdy „odnalazł”

swoją drugą połowę: T związał się L, W z S, G z D, H z E. Można powiedzieć, że każdy jest ogólnie
zadowolony. Proces dział się naturalnie i nie miał nic wspólnego z rozwiązaniem Nasha. Jeżeli nie – to
czy mogłoby być lepiej? Oceńmy zadowolenie grupy z takiego rozwiązania i zobaczymy czy jest to
sytuacja dla nich optymalna. Jak ocenić poziom satysfakcji całej grupy? Dodajmy liczby
charakteryzujące poziom satysfakcji z odpowiednich partnerów z jakimi osoby te się związały. Im
poziom ten jest niższy, tym oczywiście lepiej, bo każdy musiał robić mniej ustępstw zadowalając się
partnerami znajdujących się na dalszych miejscach swojej listy preferencji. Dla mężczyzn poziom
satysfakcji wynosi 8, dla kobiet 10. Przy pomocy teorii gier możemy odkryć ze gdyby L związała się z T,
S z G, D z H oraz E z W, poziom satysfakcji mężczyzn i kobiet byłby większy i wynosił odpowiednio 7 i
9. Satysfakcja ludzi w grupie byłaby większa (T z L taka sama, bo matematyczne optimum znowu łączy
ich w parę) oprócz indywidualnych satysfakcji W i S. Związek tych osób powoduje mniejsza wartość
satysfakcji całej grupy. Gdyby potrafili poświęcić się dla innych, to 6 osób czułoby się w związkach
lepiej kosztem tych dwóch osób. Jest to bardzo ciekawy przykład działania dla dobra wspólnego całej
grupy, kosztem własnych preferencji.

Rozważmy jeszcze raz tą sytuację z uwzględnieniem, że teraz kobiety starają się w swoich

zalotach o mężczyzn. Końcowa sytuacja wygląda następująco: Lisa wiąże się z G, D z T oraz ponownie S
z W i E z H. Oceńmy satysfakcję kobiet i mężczyzn jako całej grupy. Otrzymujemy odpowiednio 8 oraz
11. Co to oznacza? Kobiety, które przejęły inicjatywę w zalotach, jako cała grupa skończyły lepiej –
bardziej zadowolone niż jak by pozostały bierne i pozwoliły aby to mężczyźni się o nie starali. Jest to
bardzo istotny przykład, gdyż mówi coś bardzo istotnego. Każdy kto pierwszy podejmuje inicjatywę
zawsze wychodzi na tym lepiej niż jak przyjmuje postawę bierną. Warto o tym wiedzieć – nie jest to
tylko oczywisty truizm (który każdy z pewnością wie intuicyjnie), ale ma on swoje matematyczne
uzasadnienie

4

Wszystkie powyższe zależności stosowane w dużej skali (większa liczba osób niż nasze

przykładowe 8), mają sens tylko w przypadku, gdy w grupie nie wyróżnia się żadna osoba której
atrakcyjności zaburza możliwość wypracowania odpowiedniego stanu satysfakcji grupy. Jeżeli na
przykład byłby na wyspie jakiś przystojny aktor, swoją obecnością obniżyłby atrakcyjność pozostałych
mężczyzn w kobiecych oczach, a że mogłaby go zdobyć tylko jedna kobieta, poziom zadowolenia
pozostałych kobiet ze swoich partnerów byłby bardzo niski. Dlatego dawanie i kreowanie przez media
pożądanych kobiecych idolów (i odwrotnie, męskich idolek) powoduje osłabienie satysfakcji ze swoich
partnerów. Jakie jest wyjście z tej sytuacji, gdy osoba atrakcyjna negatywnie wpływa na potencjalne
zadowolenie całej grupy? Zachować się zgodnie z kadrem z filmu „Piękny umysł”. W filmie blondynka
wyróżniająca się uroda i podobająca się wszystkim mężczyznom została „matematycznie optymalnie
zignorowana”, co spowodowało, że pozostali mężczyźni zaczęli dobrze się bawić w towarzystwie jej
koleżanek.

Powyższy sposób przedstawienia zagadnienia użyteczności teorii gier w łączeniu ludzi w pary jest

dość przesadzony, ale proszę zobaczyć jego użyteczność w przypadku organizowania przyjęcia. Znając
listy preferencji poszczególnych osób, można wszystkich idealnie połączyć w pary, tak żeby byli
najbardziej zadowoleni jako cała grupa. W końcu o to chodzi dla organizatora, żeby się wszyscy na
przyjęciu dobrze bawili. Oczywiście nie należy wtedy zapraszać wyjątkowo atrakcyjnych osób, żeby
swoją obecnością nie zaburzyły tego stanu.

Tyle na temat łączenia się w pary mówi teoria gier. A co zrobić, gdy nie grozi nam bycie na

samotnej wyspie? Wyposażeni w wiedzę, że inicjatywa w kontaktach męsko-damskich zawsze się opłaca
– jak spróbować najoptymalniej znaleźć swoją drugą połowę?

Gdy już zaczniemy nasz podbój i spotykamy się z kolejnymi partnerkami lub partnerami – i w

każdej lub każdym coś nam nie pasuje, skąd wiadomo, żeby już się jednak zatrzymać i przestać szukać
dalej. Takie poszukiwanie może się ostatecznie skończyć tym, że się całkowicie zestarzejemy i wraz ze
spadkiem naszej atrakcyjności, będziemy także musieli ograniczać nasze wymagania w stosunku do
poszukiwanego partnera. Gdy w odpowiedniej chwili się nie zatrzymamy – efekt może być taki, że
zostanie nam tylko wspomnienie o kimś i żałowanie, że się jednak z nim nie związało na stałe (samemu
już nie można do tej osoby wrócić, bo już pewnie dawno związała się z kimś innym). Jak sobie z tym
problemem poradzić matematycznie?

Załóżmy optymistycznie, że będziemy sprawdzać 100 kandydatów (istotne jest, że do odrzuconej

osoby nie można wrócić). Jedna z matematycznych teorii optymalnego wyboru (jej wyprowadzenie jest
dość trudne) mówi, sprawdź ze zbioru dostępnych kandydatów (kandydatek) 37% jako tzw. „ciąg
testowy” (dokładnie odwrotność liczby e=2,718281... wyrażona w procentach) i wybierz następnie z
pozostałych najlepszą pod twoim ulubionym względem jaką napotkasz. Matematycznie gwarantuje to
prawdopodobieństwo sukcesu wyboru najlepszego kandydata do około 37% w porównaniu do 1%
(1/100) gdybyśmy wybierali losowo.

Tyle mówi teoria. Problem z tym , że z góry nie wiemy ilu kandydatów będziemy mieli do

„sprawdzenia” oraz braku sprecyzowania, co w ogóle oznacza dla nas „ten najlepszy” zanim jeszcze
nikogo nie „sprawdziliśmy” i nie ustaliliśmy swoich standardów. Pomocna może być odpowiednia
modyfikacja tej teorii podana we wspomnianej książce „Mathematics and Sex” zwana regułą „Twelve
bonk rule” (można to dosłownie przetłumaczyć „regułą 12 (seksualnych) zaliczeń”). Mówi ona sprawdź
12 partnerów, a następnie wybierz najlepszego jaki pojawi się kolejny w porównaniu do najlepszego pod
jakimś względem z tych dwunastu testowanych. Da Ci to szanse 75% na odniesienie sukcesu z
właściwym wyborem, względem ustalenia wśród tej dwunastki swojego ulubionego typu.

Faza III - Dynamika miłości

Jeżeli już dwoje osób w jakiś sposób przypadnie sobie do gustu, następuje najciekawsza rzecz

dotycząca ewolucji ich obustronnych uczuć – konkretnie dynamika i wzajemny wpływ ich uczuć na
siebie.

Wszelką dynamikę oddziaływania obiektów można idealnie opisać rachunkiem różniczkowym, za

którego twórcę uważa się Newtona.

5

Oddziaływanie dynamiczne (np. grawitacyjne planet, układów sprężyn, itp.) oraz wszelki ruch

obiektów są zjawiskami fizycznymi do których opisu idealnie nadaje się matematyka, a w szczególności
wspomniany rachunek różniczkowy – perfekcyjnie potrafi uchwycić wszystko, co ulega zmianie w
czasie. Czy przy jego pomocy można także uchwycić dynamikę uczuć relacji mężczyzna – kobieta (jeżeli
potraktujemy ich jako obiekty oddziaływujące na siebie), która również ulega zmianie w czasie?

Sam rachunek różniczkowy zawsze stanowi trudność do zrozumienia szczególnie dla studentów

kierunków nietechnicznych, ponieważ zazwyczaj nie jest należycie tłumaczony (z powodu braku
ciekawych przykładów w życiu). Jest on bardzo ważny, gdyż przy jego pomocy można opisać i
zrozumieć procesy we wszystkich dziedzinach nauki, takich jak również: medycyna, biologia, chemia,
itd.

Z problem tłumaczenia rachunku różniczkowego poradził sobie w genialny sposób jeden z

wykładowców na Harwardzie. Swoim studentom przy jego pomocy opisał miłość Romea i Julii, których
pewne aspekty każdy sam z pewnością po zastanowieniu się odnajdzie w ewolucji uczuć do swojej
wybranki.

Równania te jako układ zależnych od siebie zależności można zapisać:

( )

( )

( )

( )

(

)











×

=

−

×

=

t

R

b

t

J

dt

d

t

J

a

t

R

dt

d

( )

Powyższe równania opisują reakcje uczuciowe jednej z osób na zaloty drugiej. J(t) oznacza

funkcję ewolucji uczuć Julii do Romea, a R(t) odwrotnie. Skomplikowanie wyglądający symbol
pochodnej opisuje zmianę funkcji (jak ona się zmienia), co może być trochę intuicyjnie trudne do
zrozumienia. Pochodna odpowiada w pewnym sensie pamięci funkcji o poprzednich wartościach jakie
ona miała i o ile się w przeciągu danego czasu zmieniła. Jeżeli funkcja zmienia się szybko (gwałtowny
wzrost w krótkim odcinku czasu), to jej pochodna ma duża wartości i odwrotnie.

Powyższy układ równań wyraża następujący proces. Romeo stara się o Julię, im zaczyna w

swoich zalotach bardziej na nią naciskać – tym Julia bardziej się wycofuje (znak ujemny przy pochodnej).
To z kolei powoduje, że Romeo myśli sobie, że już się Julii nie podoba i sam zaczyna się w zalotach
ograniczać. Romeo myśli jak typowy mężczyzna swoimi kategoriami czyli funkcją 1 i tego, że
zainteresowanie musi być wyraźnie odwzajemnione - wydaje mu się, że taka sama relacja rządzi
uczuciem Julii. Julia z kolei podlega funkcji 2, widząc słabnące zainteresowanie swoją osobą i chcąc być
dalej adorowana, zaczyna przejawiać zainteresowanie osobą Romea. Romeo widzi, że Julii na nim
zaczyna zależeć i teraz znowu on przejmuje inicjatywę zaczynając ponownie przejawiać większe
uczuciowe zainteresowanie osobą Julii.

Szybkość i intensywność zmian określają parametry a i b. U niektórych uczucia zalotów mogą być

dość gorące u innych letnie, jakkolwiek idealnie podlegają powyższemu układowi równań.

Jest to bardzo ważny przykład, który z pewnością każdy mężczyzna odnajdzie w swoim życiu w

relacji z kobieta. Staramy się o kobietę i im robimy to bardziej intensywnie, tym ona bardziej się cofa
(można to również wytłumaczyć natręctwem). Myślimy, ze już nasza osoba ją nie interesuje , dajemy
sobie spokój i okazuje się, że ona zaczyna wysyłać sygnały niosące nam treści, że chce być dalej
adorowana. Takie coś jest wyjątkowo nie zrozumiale dla niektórych mężczyzn myślącymi kategoriami
równania 1 i wydającym się, że podobnie jest u kobiet. Często bywa to źródłem nieporozumień, ale jak
ktoś zna te równania, to będzie mu to już łatwiej zrozumieć.

Układ tych równań nie może wyglądać inaczej. Tylko tego typu funkcje zapewnić mogą stabilne

trawie uczuć o charakterze oscylacyjnym, wnosząc do naszego życia uczuciowego nowe treści,
powodując upadki i wzloty emocjonalne dające przede wszystkim możliwości dojrzewania uczuć ku ich
głębszym formom.

Sprawa z takim przedstawieniem ewolucji uczuć jest bardzo ciekawa. Matematyka jest

doskonałym narzędziem do odkrycia zaszyfrowanych przez naturę wzorów rządzących naszym życiem.
Naukowo zajmuje się tym wielu badaczy. Najbardziej znanym z nich jest Włoch Sergio Rinaldi.
Przeanalizował on i przedstawił równaniami matematycznymi ewolucję uczuć renesansowego włoskiego

6

twórcy Franciszka Petrarki. Sam Petrarka nieśmiertelną sławę zyskał głównie dzięki zbiorowi wierszy
lirycznych w języku włoskim Il canzoniere. Zbiór ten, uznany za arcydzieło literatury światowej, składa
się z 366 utworów, głównie sonetów. Pod polskim tytułem bardziej znane są jako „Sonety do Laury”. Są
one owocem wzniosłego uczucia, jakim obdarzył on przypadkowo spotkaną zamężną kobietę. Jego
wielka platoniczna miłość trwała ponad 20 lat. Nie skończyła się nawet wraz ze śmiercią ukochanej.
Stanowiła dla niego źródło natchnienia i udręki zarazem, była szczęściem i przekleństwem.

Naukowiec znalazł zbór równań opisujący wzajemna relacje uczuć Petrarki i Laury, czego

wyrazem są treści wyrażane przez poetę w swoich kolejnych sonetach.

Zasadnicze pytanie co nam daje powyższa analiza? Istotą jej jest znalezienie stabilnego cyklu

uczuć o charakterze oscylacji. Jeżeli znajdzie się odpowiednie współczynniki równań układu dynamiki
uczuć relacji kobieta-mężczyzna – spowoduje to, że „układ uczuć” wejdzie w nieskończony cykl
oscylacji podobny do rezonansu (elektrycznego lub mechanicznego). Zagwarantuje to wieczne trwanie
miłości, która oczywiście będzie przeżywać swoje upadki i wzloty, ale trwać będzie w stabilnym cyklu w
nieskończoność. Nieodpowiednie parametry spowodują, że układ będzie miał tendencję do wygaśnięcia
uczuć, które oznaczać mogą rozstanie się partnerów. Sergio Rinaldi znalazł takie wartości parametrów
równania, które idealnie odzwierciedliły zmiany uczuć Petrarki do Laury, czego dowodem są sonety o
odpowiedniej treści.

Jeżeli znajdziemy równania opisujące nasze uczucia i określimy odpowiednie parametry – dzięki

temu przewidzimy, jak nasze uczucia będą ewoluowały, zrozumiemy, że ich charakter oscylacyjny jest
nieunikniony jeśli relacja ma być autentyczna i trwała. Przewidzimy kiedy w czasie należy się
spodziewać kryzysu objawiającego się wzajemnym spadkiem uczuć oraz kiedy on powinien minąć.

Faza IV - Małżeństwo – funkcja użyteczności

Ostatnim etapem jaki nam pozostaje do matematycznego rozpatrzenia jest małżeństwo. Pojawiają

się pierwsze nieporozumienia i kłótnie. Zobaczmy czy matematyka może nam jakoś pomóc w
rozwiązywaniu konfliktów. Dotyczyć one mogą różnic w sprawie jakości sprzątania określonych miejsc,
jakości potraw, wychowania dzieci, itp. spraw.

Spotkaliśmy się już z teorią gier dotyczącą szukania kompromisów. Zasadniczym problemem jest

jednak przełożenie pewnych nieprecyzyjnych pojęć, jak np. poziom zadowolenia z kompromisu na
wartości liczbowe, które nadają się do odpowiedniej matematycznej obróbki (np. przez teorie gier).

Chcąc jakościowo uchwycić poziom subiektywnego zadowolenia z pewnych spraw w ujęciach

ekonomicznych, politycznych, psychologicznych, socjologicznych, itp. – matematycy wprowadzili
pojęcie tzw. funkcji użyteczności (ang. utility function). Jest to funkcja bezjednostkowa (no chyba, że
jednostkami są jednostki szczęścia). Odzwierciedla nasze wewnętrzne zadowolenie z jakiś faktów.
Mieliśmy już w pewnym sensie z nią do czynienia w przypadku listy preferencji rozbitków na samotnej
wyspie. Inny przykład. W grze w kasynie bardzo bogaty człowiek wzbogacił się o 1000 000 zł. Ponieważ
sam już jest bardzo bogaty, ta kwota dla niego nic nie znaczy w porównaniu dla człowieka biednego,
któremu odmienić potrafi całkowicie życie i zadowolenie z niego. Funkcja użyteczności wpływająca na
zadowolenie z zysku dla biednego i bogatego dotycząca wielkości zarobku jest inna. 1000 000 zł zysku
dla bogacza, w kwestii zadowolenia może odpowiadać 10 zł zysku dla biedaka. Możemy skonstruować
dla obu z nich odpowiednie ciągłe funkcje rozważając wszelkie możliwe zyski jakie mogą im się trafić.

Rozważmy teraz sprawę sprzątania mieszkania w małżeństwie, będącego często przedmiotem

kłótni. Każdy z małżonków posiada określoną własną funkcję użyteczności charakteryzującą jego
subiektywne zadowolenie z posprzątanych miejsc w mieszkaniu.

Ukażmy idee w dość przesadzony sposób aby uchwycić jej znaczenie dla funkcji dyskretnych.

Mąż ma małe wymagania do czystości lustra w łazience, mało z niego korzysta, w ogólnie nie zwraca na
nie uwagi i dla niego jest albo czyste albo brudne (funkcja dwuwartościowa 1 i 0). Poziom czystości
dywanu (jest on dla niego już trochę bardziej istotny niż lustro) ocenia w kategoriach brudny i wymaga
sprzątnięcia (poziom 0), lekko brudny i może jeszcze niech się bardziej zabrudzi zanim warto włożyć
wysiłek i go odkurzyć (poziom 5) oraz czysty i nie trzeba sprzątać poziom 10). Ekran telewizora – często
z niego korzysta i jego czystość od nagromadzonego kurzu jest dość istotna (skala 100-czysty, 50 – da się
oglądać, 0 - brudny), itd. –można ustalić funkcję użyteczności dla pozostałych rzeczy.

7

Dla jego żony czystość tych przedmiotów ma inne znaczenie. Bardziej zadba o czyszczenie lustra

niż ekranu telewizora.

Dla męża ogólny poziom czystości w mieszkaniu jest zadowalający, gdy suma składowych

odpowiednich funkcji użyteczności przekroczy jakiś próg.

Różne przedmioty posiadają inne wagi dla różnych małżonków i tutaj pojawia się główny

problem. Bez ustalenia i poznania funkcji użyteczności (przypisaniu odpowiednich wartości) dla swojego
małżonka – może to być źródłem nieustannych kłótni.

Tak można zrobić dosłownie ze wszystkim. Zdefiniować funkcję użyteczności dla wszystkiego i

kiedy już będą wspólnie ustalone, wiedzieć jak pewne rzeczy wpływają na skałę zadowolenia swojego
małżonka.

Mając ustalone funkcje użyteczności, oraz wzajemne relacje między nimi, można je zastosować

do bardziej skomplikowanych metod matematycznych optymalizacji (teoria gier jest tylko jedną z nich).

8