Sprawozdanie

Temat ćw3: Interpolacja i aproksymacja

Sprawozdanie wykonali:
Marek Niemiec

152139

Michał Wróbel

152180

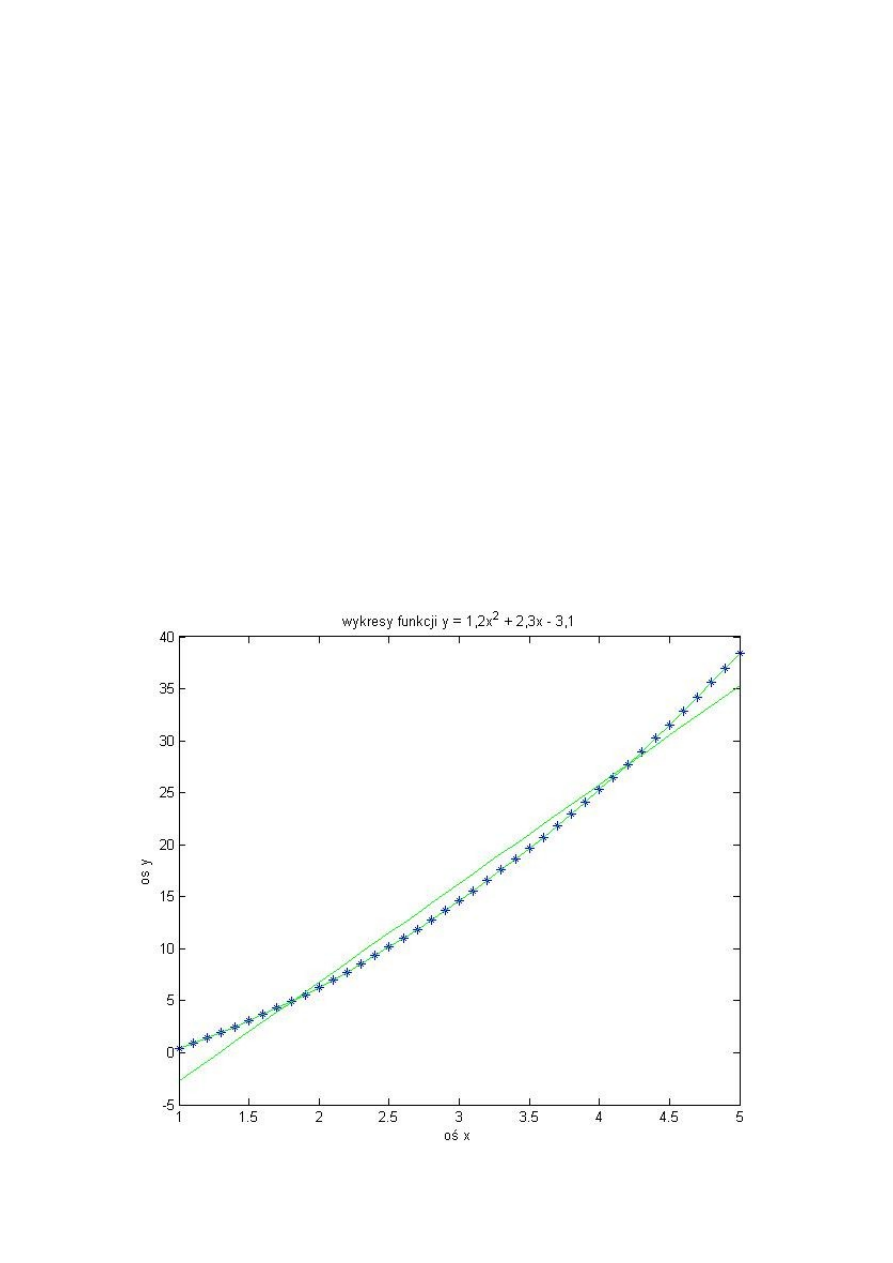
Pierwszą funkcją, która poddaliśmy aproksymacji była funkcja pierwotna

y=1,2 x

2



2,3 x−3,1 . Najpierw wyznaczyliśmy punkty wykresu dla pierwotnej funkcji

(niebieskie gwiazdki). Następnie za pomocą funkcji polyfit i polyval aproksymowaliśmy funkcje
dla węzłów od 1 do 4 (linie zielone).

M-funkcja wygląda następująco:

% funkcja y=1,2x^2 + 2,3x - 3,1

x=1:0.1:5;
y=(x.*x)*1.2 + x.*2.3 -3.1;

% funkcja

plot(x,y,

'b*'

),xlabel(

'os x'

),ylabel(

'os y'

),title(

'wykresy funkcji y = 1,2x^2 +

2,3x - 3,1'

)

hold

on

for

n=1:4

p=polyfit(x,y,n);
yw=polyval(p,x);

plot(x,yw,

'g-'

)

end

Tak wyglądają wykresy przedstawiające powstałe funkcje:

Wykres wyglądająca jak wykres funkcji y=ax+b powstał przez aproksymację danych dla

węzłów n=1. Wykresy powstałe przez aproksymację danych dla węzłów n=2,3,4 pokrywają się z
wykresem funkcji bazowej.

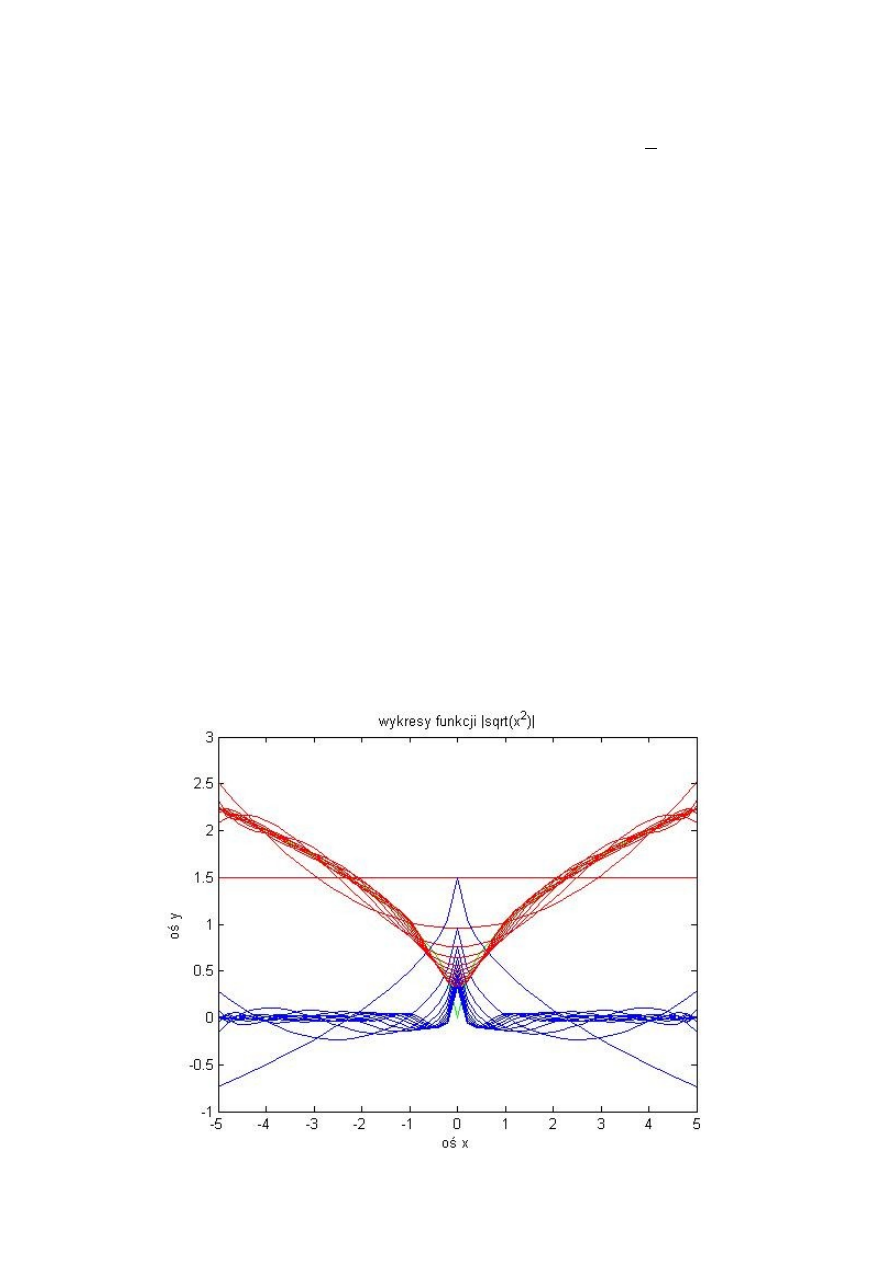
Kolejna funkcją, którą poddaliśmy aproksymacji była funkcja y=

∣



x

∣

. Najpierw zostały

wyznaczone punkty i na ich podstawie został wykreślony wykres funkcji bazowej (zielona linia).
Następnie aproksymowaliśmy funkcję w zakresie węzłów n=1:50 . W przedziale dla n=1:20
uzyskaliśmy następujące funkcje (czerwona linia) oraz błąd wynikający z aproksymacji (niebieska
linia).

M-plik wygląda następująco:

% |sqrt(x^2)| - funkcja modu³ pierwiastek z x

x1=-5:0.2:5;

y1=abs(sqrt(x1.*1));

% wyniki funkcji

plot(x1,y1,

'g-'

),xlabel(

'os x'

),ylabel(

'os y'

),title(

'wykresy funkcji |

sqrt(x^2)|'

)

hold

on

for

n=41:43

pf=polyfit(x1,y1,n);

yz=polyval(pf,x1);
plot(x1,yz,

'r-'

)

% wykres funkcji uzyskanej poleceniem matlaba

blad=yz - y1;
plot(x1,blad,

'b-'

)

% wykres bledu (róznicy jaka powstala miedzy wynikami)

%%%%%%%%

end

figure;
hold

on

for

n=1:4

%wielomian czybyszewa

w_cz=seqcheb(n,2);
w_cz_p=polyval(w_cz,x1);

plot(x1,w_cz_p,

'r--'

)

end

Dla n=1:20 wykresy funkcji aproksymowanej maja postać:

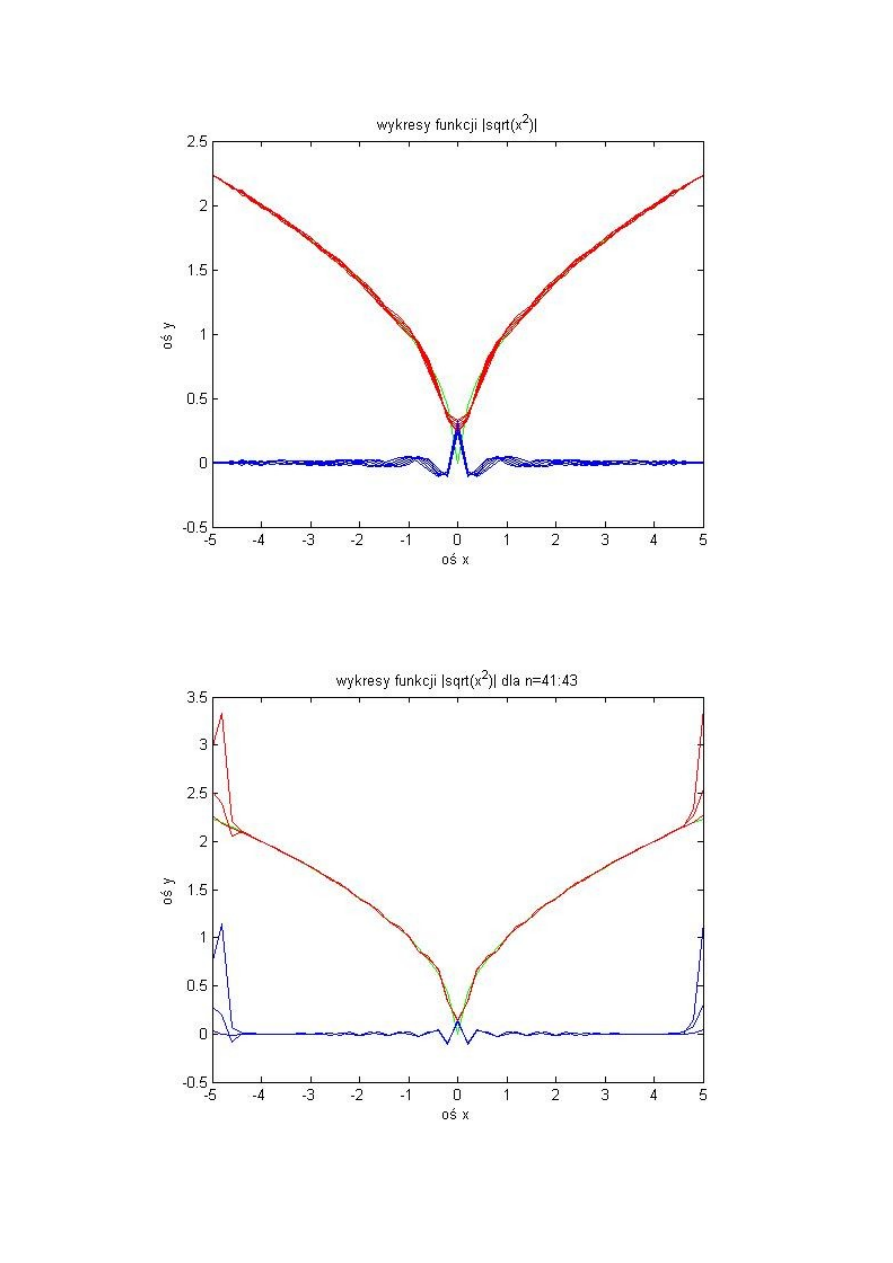
Dla n=20:30 wygląda to tak:

Dla n=30:40 wykresy funkcji zbytnio nie zmieniają kształtu jednak po przekroczeniu

węzłów n=41 po brzegach zaczynają się pojawiać oscylacje co świadczyło by o wystąpieniu
zjawiska Rungego.

Następnym zadaniem było napisanie funkcji aproksymującej zbiór elementów,

wykorzystanie tej funkcji w zadaniach oraz porównanie wyników z funkcjami matlaba polyfit i
polyvil.

Pierwszym zadaniem z tej serii była aproksymacja danych dla funkcji pierwotnej

y=ax

2



bxc . M-plik ma następującą konstrukcje:

% wielomian y=ax^2 + bx +c
% obliczamy a,b,c

fi0=[1 1 1 1];
fi1=[0 1 2 3];

fi2=[0 1 4 9];
format

long

e

;

x=[0 1 2 3];

%dane wejsciowe

y=[1 2 4 8];

%dane wyjsciowe

Fi=[ones(size(x)); x; x.*x]

% funkcja obliczajaca wartosci przy wielomianie

A=Fi * Fi';
A

b=Fi * y';
b

c=inv(A) * b;
c

% funkcja matlaba

axb=polyfit(x,y,2);

axb
y_axb=[axb(1,3)*x.*x + axb(1,2)*x + axb(1,1)]

plot(x,y,

'g'

),xlabel(

'os x'

),ylabel(

'os y'

),title(

'wykresy funkcji y=ax^2 + bx

+ c'

)

hold

on

plot(x,y_axb,

'r--'

)

blad=y_axb - y;
plot(x,blad,

'b'

)

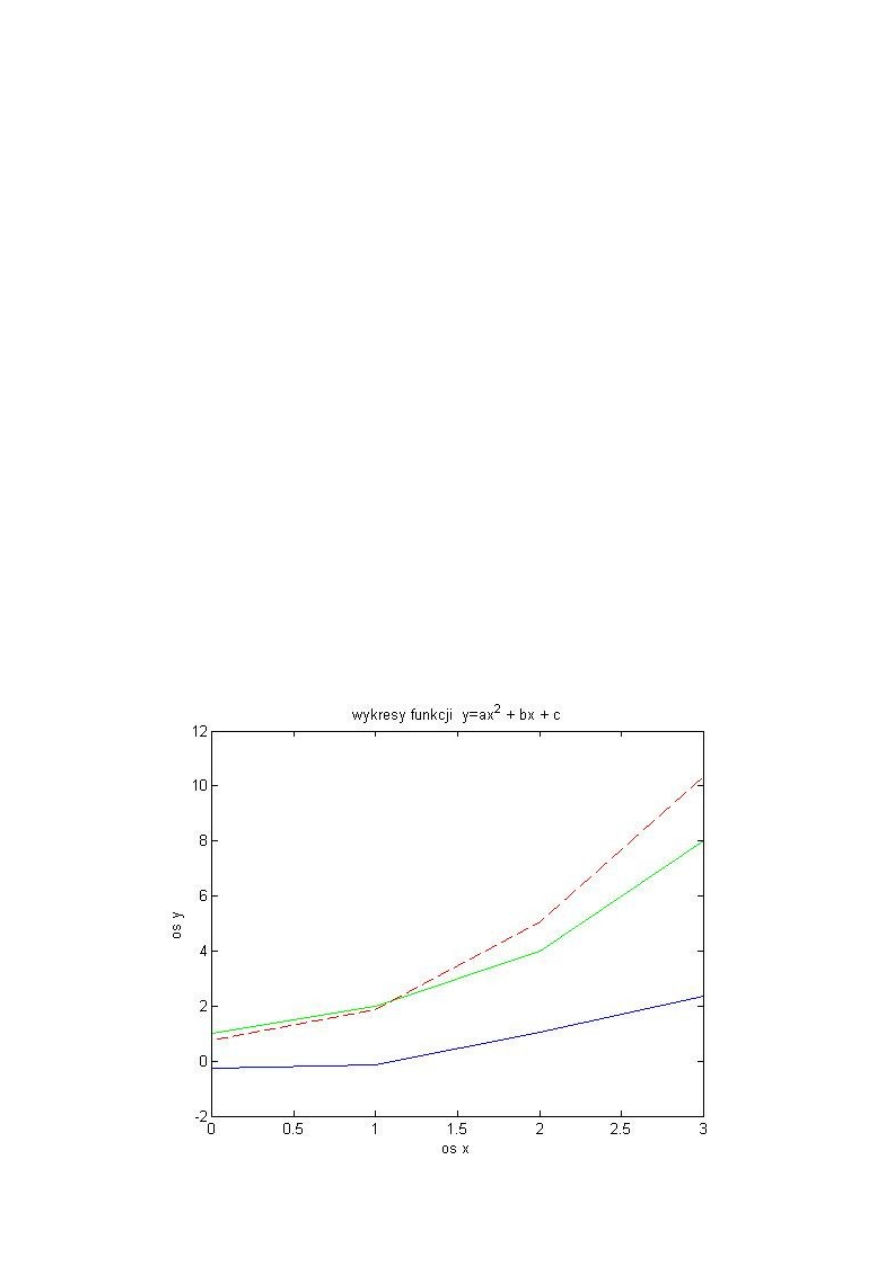
Powstałe wykresy przedstawiają wykres funkcji bazowej (linia zielona), wykres funkcji

powstałej przez aproksymacje (przerywana linia czerwona) oraz wykres błędu (linia niebieska). Jak
widać na krańcach przedziału błędy są duże dla aproksymacji funkcją matlaba dla węzłów n=2.

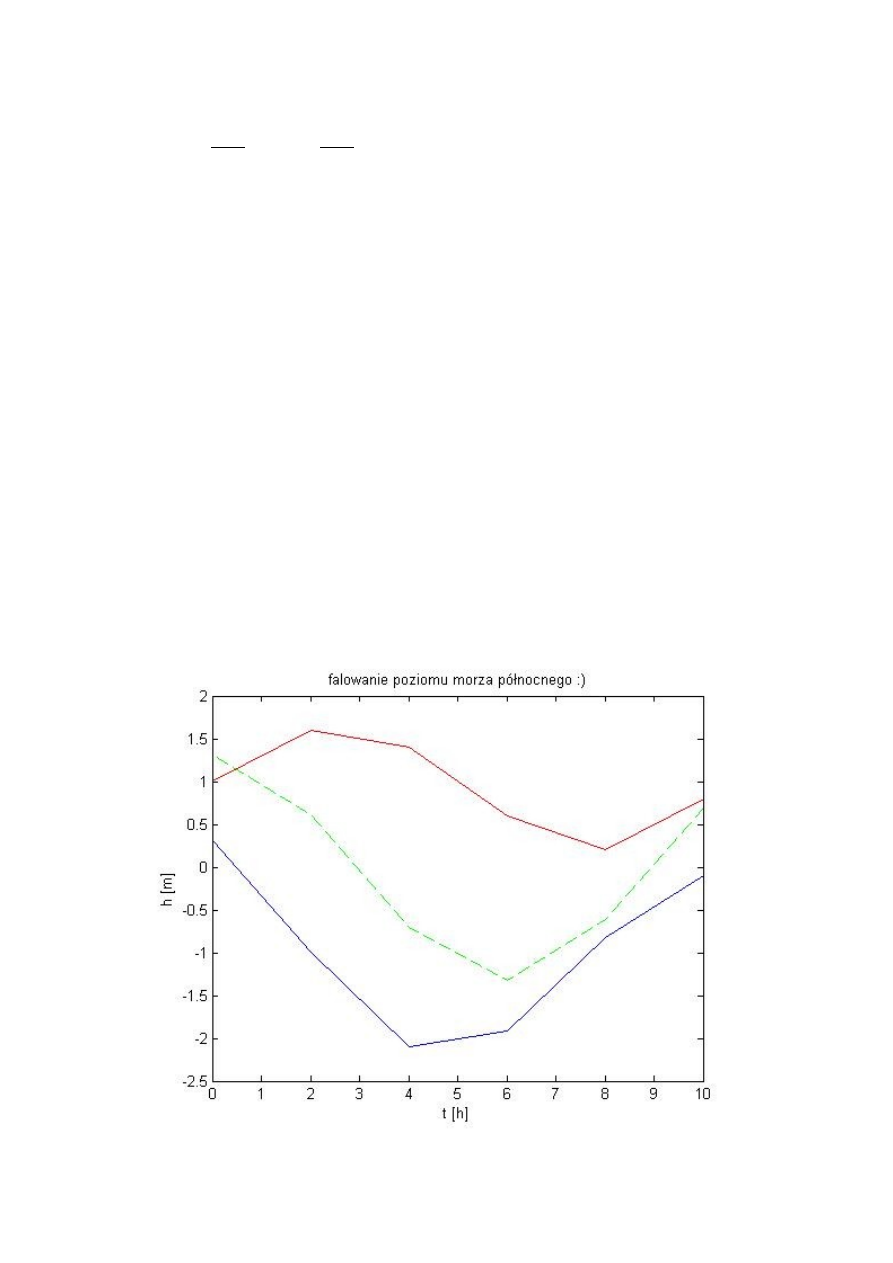
Drugim zadaniem było uzyskać funkcje opisującą zjawisko przypływów w Morzu

Północnym aproksymując serię danych pomiarowych. Funkcja pierwotna miała postać

M =h

0



a1sin

2 t

12



a2cos 

2 t

12



. W zadaniu korzystaliśmy z utworzonego algorytmu i

funkcji Matlaba. M-pik wygląda tak:

% zadanie 1: z poziomem morza pólnocnego
% M(x)=h0 + a1*sin((2*pi*t)/12) + a2*cos((2*pi*t)/12)

t=[0 2 4 6 8 10];
h=[1.0 1.6 1.4 0.6 0.2 0.8];

Mi=[ones(size(t)); sin((2*pi*t)/12); cos((2*pi*t)/12)]
A1=Mi *Mi';

A1
b1=Mi * h';

b1
c1=inv(A) * b;

c1

% funkcja matlaba

figure;
poziom=polyfit(t,h,2);

poziom

% b³¹d

blad2=h_poziom-h
h_poziom=[poziom(1,1) + poziom(1,2)*sin((2*pi*t)/12) +

poziom(1,3)*cos((2*pi*t)/12)];
plot(t,h,

'r'

),title(

'falowanie poziomu morza pólnocnego :)'

),xlabel(

't

[h]'

),ylabel(

'h [m]'

)

hold

on

plot(t,blad2,

'b'

)

plot(t,h_poziom,

'g--'

)

Wykresy przedstawiające wykres funkcji bazowy (linia czerwona), wykres funkcji

uzyskanej poleceniem matlaba (linia przerywana zielona) oraz wykres funkcji błędu (linia
niebieska).

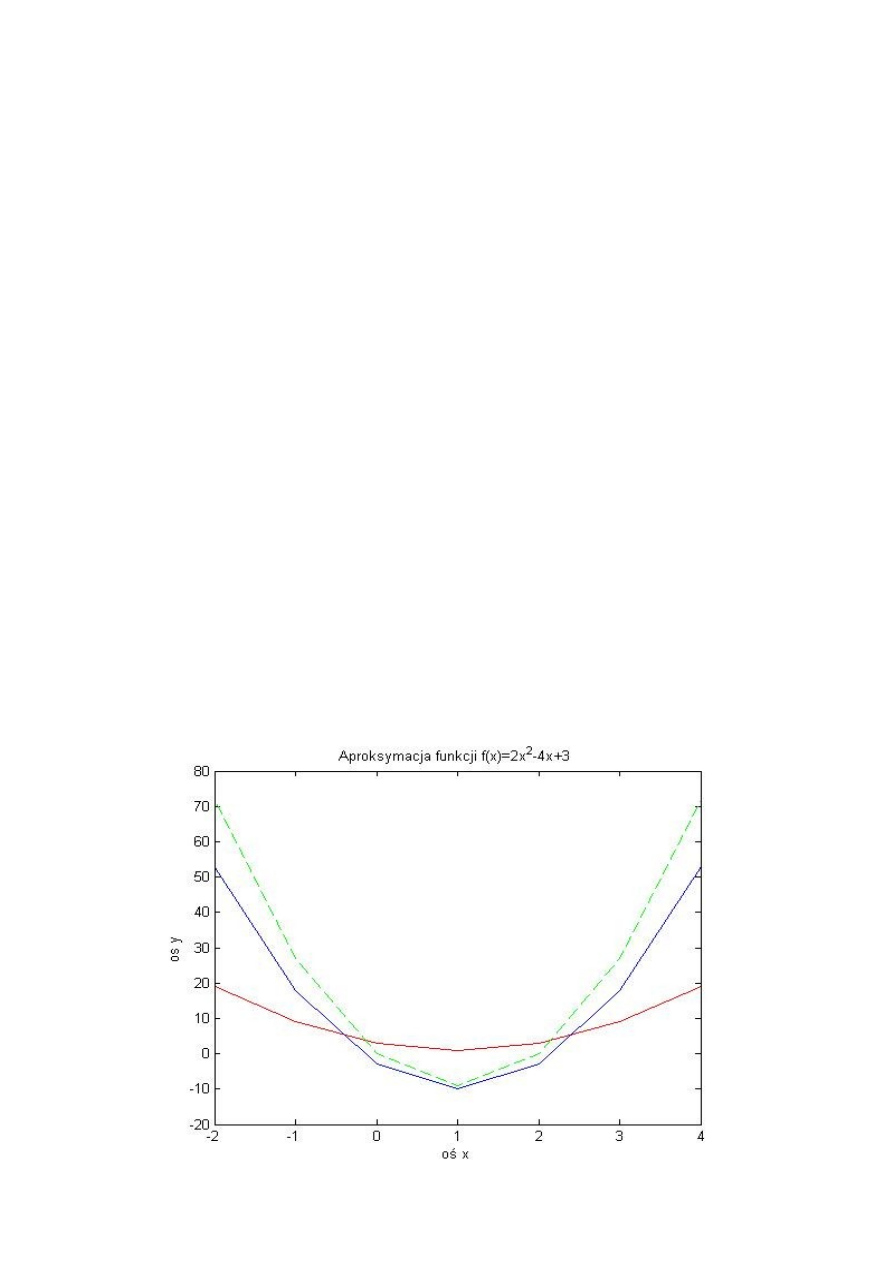
Trzecim zadaniem z tej serii było aproksymacja funkcji kwadratowej dla dwóch funkcji

bazowych, która minimum osiąga w p. W=(1,y) oraz nie przecina osi x. Jako funkcji pierwotnej
użyliśmy funkcji y=2x

2

−

4x3 . Wszystkie obliczenia zostały zrobione w M-pliku.

% zadanie 2: aproksymacja funkcji kwadratowej, która minimum osiaga
% w punkcie o wspólrzedne w=(1,y) oraz funkcja nie przechodzi przez os 'x'

% do zadania zostala przyjeta funkcje f(x)=2x^2 - 4x + 3
% funkcja przybiera postac po przeksztalceniu f(x)=3 + 2(x^2 - 2x)

% oznaczymy sobie funkcje bazowe jako a0 i a1.
% Funkcja przybiera postac f(x)=a0 + a1(x^2 - 2x)

% dane obliczylismy wykorzystujac funkcje kwadratowa

format

long

e

;

xk=[-2 -1 0 1 2 3 4];
yk=[19 9 3 1 3 9 19];

% korzystamy z funkcji napisanej w poprzednim zadaniu a nastepnie
% porównujemy wyniki z funkcja matlaba oraz z przyjetym równaniem

Fk=[ones(size(xk)); xk.*xk - 2*xk];
Fk

A2=Fk *Fk';
A2

b2=Fk * yk';
b2

c2=inv(A2) * b2;
c2

% funkcja matlaba

fun_kw=polyfit(xk,yk,1);

fun_kw
yk_fun_kw=[fun_kw(1,1)+fun_kw(1,2)*(xk.*xk - xk*2)];

blad3=yk_fun_kw - yk;
figure;

plot(xk,yk,

'r'

),xlabel(

'oœ x'

),ylabel(

'os y'

),title(

'Aproksymacja funkcji

f(x)=2x^2-4x+3 '

)

hold

on

plot(xk,yk_fun_kw,

'g--'

)

plot(xk,blad3,

'b'

)

Wykresy przedstawiające wykres funkcji bazowy (linia czerwona), wykres funkcji

uzyskanej poleceniem matlaba (linia przerywana zielona) oraz wykres funkcji błędu (linia
niebieska).

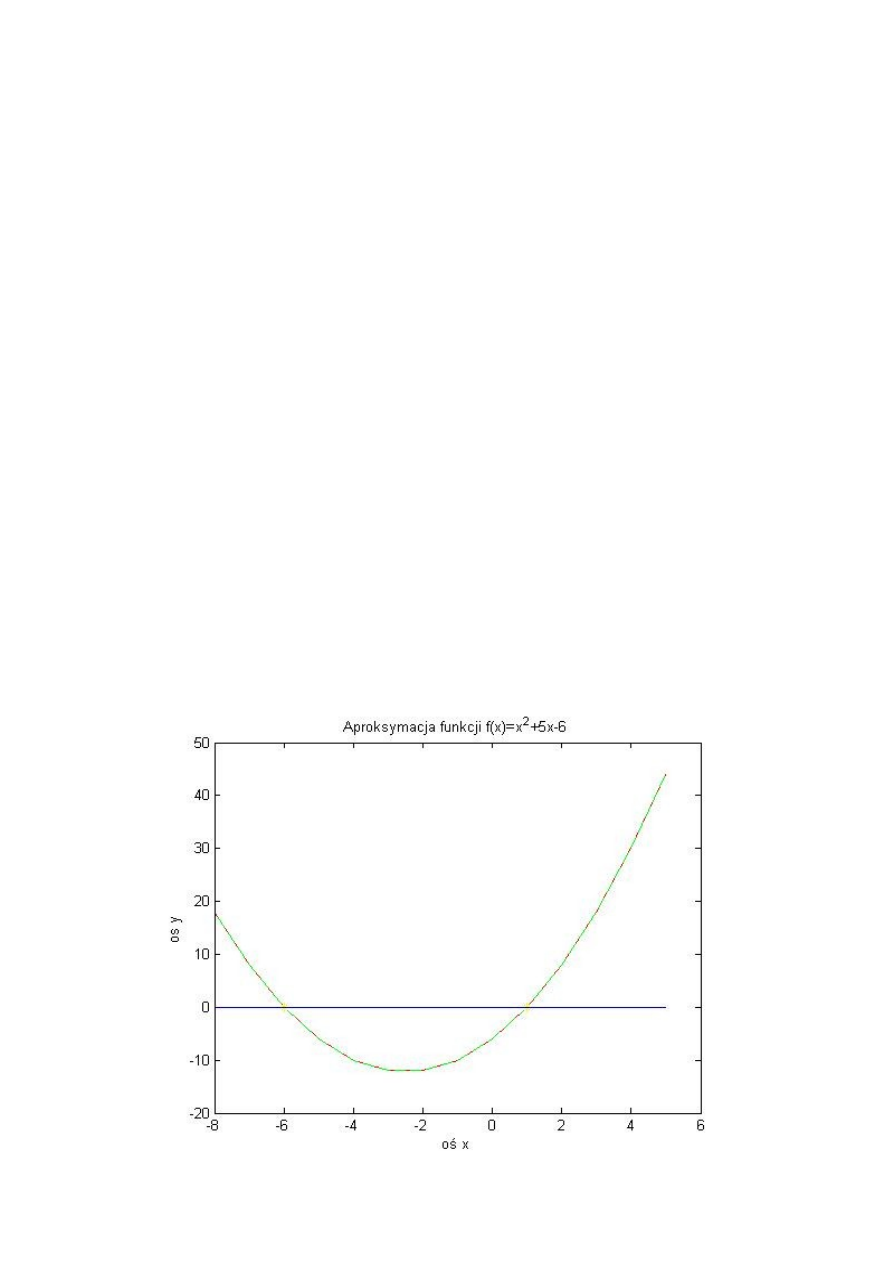
Czwartym zadaniem z było aproksymacja funkcji kwadratowej, która posiada miejsce

zerowe w punkcie z=(1,0). Aproksymacje ma być przeprowadzona dla trzech funkcji bazowych.
Jako funkcji pierwotnej użyliśmy funkcji y=x

2



5x−6 . Wszystkie obliczenia zostały zrobione

w M-pliku.

% zadanie 3: aproksymacja funkcji kwadratowej, która ma miejsce zerowe w
% punkcie p0=(1,0)

% do zadania zosta³a przyjêta funkcja f(x)=x^2 + 5x - 6
% oznaczymy sobie funkcje bazowe (w tym zaaniu wyznaczymy je 3)

% f(x)= a0 + a1x + a2x^2 gdzie a0= -6, a1=5, a2=1

xw=[-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5];

yw=[xw.*xw + 5*xw - 6];

% korzystamy z naszej funkcji :) i liczymy

Fw=[ones(size(xw)); xw; xw.^xw];
Fw

A3=Fw *Fw';
A3

b3=Fw * yw';
b3

c3=inv(A3) * b3;
c3

% funkcja matlaba

fun_kw2=polyfit(xw,yw,2);

fun_kw2
yw_fun_kw2=[fun_kw2(1,3)+fun_kw2(1,2)*xw + fun_kw2(1,1)*(xw.*xw)];

blad4=yw_fun_kw2 - yw;
figure;

plot(xw,yw,

'r'

),xlabel(

'oœ x'

),ylabel(

'os y'

),title(

'Aproksymacja funkcji

f(x)=x^2+5x-6 '

)

hold

on

plot(xw,yw_fun_kw2,

'g--'

)

plot(-6,0,

'y*'

,1,0,

'y*'

)

% miejsca zerowe funkcji pierwotnej

plot(xw,blad,

'b'

)

Wykresy przedstawiające wykres funkcji bazowy (linia czerwona), wykres funkcji

uzyskanej poleceniem matlaba (linia przerywana zielona),wykres funkcji błędu (linia niebieska)
oraz zostały zaznaczone miejsca zerowe jako żółte gwiazdki.

W czwartym zadaniu widać, że wykresy funkcji pierwotnej i funkcji uzyskanej przez

aproksymacje dla trzech funkcji bazowych pokrywają się natomiast wykres błędu jest na poziomie
0. Porównując to do wyników z zadania 3, gdzie przy aproksymacji korzystaliśmy z dwóch funkcji
bazowych wynika, że aby uzyskać maksymalną zgodność funkcji pierwotnej i funkcji
aproksymowanej powinniśmy używać do aproksymacji danych możliwie największą liczbę funkcji
bazowych. Analizując początkowe zadania (funkcje kwadratowe oraz pierwiastek) widać, że
wielomiany należy aproksymować dla liczby węzłów n nie mniejszej od stopnia wielomianu –
widać to na przykładzie aproksymacji dwóch funkcji kwadratowych. Liczby węzłów n nie można
także podnosić do nieskończoności. Aproksymacja funkcji pierwiastka dowodzi, że liczbę węzłów
należy określać w pewnym przedziale – większym od stopnia wielomianu i mniejszym od jego
pewnej wielokrotności, którą najlepiej określić empirycznie.

Porównując metody aproksymacji używane w zadaniach lepszy wynik uzyskiwaliśmy dla

funkcji napisanej w oparciu o aproksymacje średniokwadratową. Funkcje Matlaba polyfit i polyval
dawały wykresy o dużym błędzie niedokładności w stosunku do wykresu funkcji pierwotnej.