Podejście parametryczne i nieparametryczne
w identyfikacji systemów
To pytanie można interpretować na dwa sposoby:
Zagadnienia Hasiewiczowskie i laboratoria Wachela
Zagadnienia Czemplikowskie – identyfikacja systemów dynamicznych
Podczas odpowiedzi skupmy się na Hasiewiczu, ale nie dajcie się zagiąć na Czemplik. Dołączony
jest pdf z jej skondensowanymi slajdami.
W zadaniu identyfikacji parametrycznej przyjmuje się na wstępie pewien model
identyfikowanego systemu. Za pomocą procedury identyfikacyjnej wyznacza się skończoną
liczbę parametrów tego modelu. Jednak zaproponowanie uniwersalnego modelu
matematycznego niektórych nieliniowych zjawisk jest niemożliwe, lub tak kłopotliwe, że
wygodniejszym podejściem jest identyfikacja nieparametryczna tzn. odtwarzanie
identyfikowanej charakterystyki punkt po punkcie na podstawie skończonej liczby pomiarów.
1 Podejście parametryczne
1.1 Zadanie parametryczne
Przykładem identyfikacji parametrycznej jest wykorzystanie zależności między wielkościami
statystycznymi dla danego rozkładu. Przykładowo:
Ponieważ dla rozkładu wykładniczego o gęstości
okazuje się, że wartość oczekiwana jest
równa
, a świetnym estymatorem EX jest średnia arytmetyczna, to obliczywszy średnią z
pomiarów można wyestymować sobie gęstość tego rozkładu, a z niego dystrybuantę itd.
Trzeba jednak a priori mieć pewność co do postaci funkcji gęstości.
1.2 Metoda najmniejszych kwadratów (ang. least squares)
1.2.1 Kroki
Wybór stopnia wielomianu aproksymującego
zapisanie równania całego systemu w postaci Y = Xa
przekształcenie równania do postaci:
X
T
Y = X
T
Xa
a = (X
T
X)
-1
X
T
Y
Podejście parametryczne i nieparametryczne w identyfikacji systemów
2
W zależności od tego, którego stopnia wielomianem będzie przybliżanie, np dla stopnia trzeciego macierz
X jest zbudowana z czterech kolumn:
[x
3
x
2
x
1
x
0
]
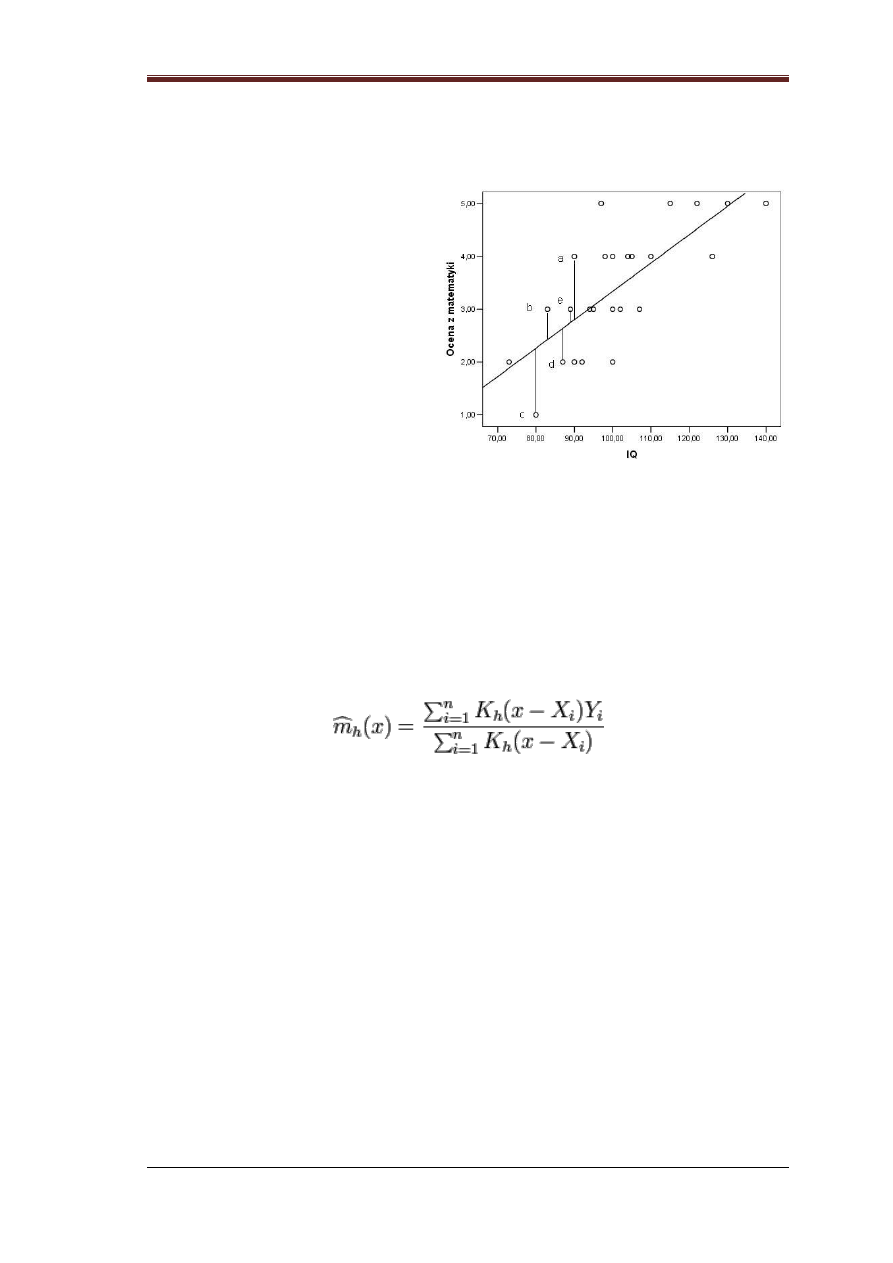
Gdzie te iksy są to pionowe wektory składające się z punktów pomiarowych (same iksy). Czyli np IQ.
[1 1 1 1]
Pierwszy pomiar
[8 4 2 1]
Drugi pomiar
[27 9 3 1]
Trzeci pomiar
Wektor Y to po prostu igrek z pomiarów,
czyli np. ocena z matematyki.
Symbol a oznacza wektor współczynników
wielomianu aproksymującego.
Gdy wymnożymy zgodnie z równaniem to
wyjdzie wektor współczynników. Obok
przykład dla aproksymacji wielomianem
pierwszego rzędu.
Modyfikacje tej metody jawią się jako :
MNK - system Hammersteina
MNK - system Wienera
MNK - liniowy system statyczny
Ich naturalnym środowiskiem występowania jest opracowanie w pdfie Michała Marzyńskiego.
2 Podejście nieparametryczne
2.1 Metoda regresji jądrowej – estymator Nadaraya-Watsona
Funkcję estymuje się w kolejnych punktach zgodnie ze wzorem:
Jest funkcja jądra K(x), którą nakłada się na przebieg z przesunięciem o Xi, gdzie Xi to bieżący
punkt estymowany. Funkcja jądra jest symetryczna całkowalna w całej dziedzinie i całkuje się
do 1. Jak się wymnoży przez cały przebieg tą funkcję jądra to wyjdzie, że największy wpływ
mają próbki w pobliżu Xi zgodnie z wagą jądra. Wtedy trzeba wszystko zsumować i podzielić
(bo funkcja jądra z tych wszystkich punktach nie będzie sumować się do jedynki).
2.2 h - parametr wygładzania
przy h
-> 0 Nh -> ∞
2.3 Podsumowanie metody regresji
Estymator jądrowy regresji charakteryzuje się bardzo duża odpornością na zaszumienie
charakterystyki odniesienia, jednak wymaga wykonania stosunkowo dużej liczby par
obserwacji (punktów z charakterystyki odniesienia).
Wyniki estymacji są w pewien sposób uzależnione od doboru funkcji jądra.
Podejście parametryczne i nieparametryczne w identyfikacji systemów
3
2.4 K-NN – K najbliższych sąsiadów
Metoda dla systemów dyskretnych, w których niekoniecznie pomiar jest zbierany z równym
odstępem czasu. Wartość funkcji w kolejnych punktach jest równa średniej z K najbliższych
sąsiadów. Oznacza to, że trzeba wziąć K punktów, które leżą na osi X najbliżej estymowanego
punktu (najbliżej w dziedzinie czasu) i uśrednić odpowiadające im wartości Y.
Estymator działa jak filtr dolnoprzepustowy, im większe K tym większe tłumienie.
Dość skuteczny i prosty w implementacji.