Akademia Górniczo-Hutnicza

Katedra Robotyki i Mechatroniki

Identyfikacja i analiza sygnałów

Laboratorium 10

Metody nieparametryczne w identyfikacji i analizie

sygnałów

Przetwarzanie sygnałów z zastosowaniem procedur statystycznych

Signal Processing Toolbox zawiera zestaw ważniejszych funkcji do estymacji pewnych
charakterystyk sygnałów losowych. W szczególności są to narzędzia do estymacji funkcji
korelacji i kowariancji ciągu danych oraz funkcje gęstości widmowej mocy sygnałów
dyskretnych.

Korelacja i kowariancja

Funkcje

xcorr

i

xcov

estymują wzajemną korelację i kowariancję ciągów procesów

losowych. Autokorelacja i autokowariancja są traktowane jako specjalne przypadki korelacji i
kowariancji wzajemnej.
Korelacja wzajemna ciągów jest wielkością definiowaną jako:

{

}

)

m

n

(

y

)

n

(

x

E

)

m

(

xy

R

+

⋅

=

( 0 )

gdzie x(n) i y(n) są stacjonarnymi procesami losowymi, -

∞

< n <

∞

oraz E jest operatorem

wartości oczekiwanej. Kowariancja wzajemna jest równa korelacji z usuniętą średnią.













−

+

−

=

)

y

m

)

m

n

(

y

)(

x

m

)

n

(

x

(

E

)

m

(

xy

C

( 1 )

gdzie m

x

i m

y

są wartościami średnimi korelowanych ciągów.

Zwykła estymata bazująca na M próbkach x(n) i y(n) jest deterministyczną korelacją
wzajemną ciągów:











<

−

≥

+

=

∑

−

−

=

0

m

dla

)

m

(

Rˆ

0

m

dla

)

m

n

(

y

)

n

(

x

)

m

(

Rˆ

xy

1

m

M

0

n

xy

( 2 )

Zakłada się, że x(n) i y(n) są indeksowane od 0 do M - 1, a R

xy

(m), od -(M - 1) do M - 1.

Funkcja

xcorr

realizuje powyższy wzór, wykorzystując algorytmy bazujące na FFT dla

danych ciągów wejściowych x(n) i y(n), zawartych w wektorach x i y o długościach M.
Przykładowo:

x=[1 1 1 1 1]';
y=x;

xyc=xcorr(x,y)

•

xyc =

•

1.0000

•

2.0000

•

3.0000

•

4.0000

•

5.0000

•

4.0000

•

3.0000

•

2.0000

•

1.0000

Sekwencja wynikowa ma długość dwa razy większą od długości ciągu wejściowego minus
jeden. Tak więc M-ty element jest korelowany przy zerowej zwłoce. Również zauważamy
znane impulsy trójkątne na wyjściu, będące wynikiem splotu dwóch przebiegów
kwadratowych.

Funkcja

xcov

estymuje kowariancję własną i wzajemną danych wejściowych. Posiada ona te

same opcje i przelicza te same równania, co funkcja korelacji, ale najpierw usuwa wartości
średnie z przebiegów x i y.

Obciążenie i normalizacja
Estymator jest obciążony, jeśli jego wartość oczekiwana nie jest równa wartości wielkości,
którą estymuje. Wartość oczekiwana dla przebiegu funkcji

xcorr

wynosi:

{

}

∑

−

−

=

−

=

+

=

1

m

M

0

n

xy

xy

)

m

(

R

)

m

M

(

)

m

n

(

y

)

n

(

x

E

))

m

(

R

(

E



( 3 )

Funkcja

xcorr

wyznacza estymator nieobciążony, dzieląc sumę (3) przez M

−

m



, jeśli

zadamy parametr

‘unbiased’

po sekwencji elementów wejściowych:

xcorr(x,y,’unbiased’);

Mimo że estymator jest nieobciążony, punkty końcowe (bliskie

−

(M

−

1) i M

−

1 mają

stosunkowo dużą wariancję, ponieważ funkcja

xcorr

wylicza je na podstawie niewielu

punktów danych. Możliwym rozwiązaniem jest dzielenie estymaty przez M, używając w tym
celu parametru

‘biased’

:

xcorr(x,y,’biased’);

W tym schemacie jedynie próbka korelacji przy zerowym opóźnieniu (M-ty element wyjścia)
jest nieobciążona. Ta estymata jest często bardziej pożądana niż nieobciążona, ponieważ
unika ona losowej, dużej wariancji w końcowych punktach korelowanej sekwencji.
Funkcja

xcorr

umożliwia także zastosowanie innego schematu normalizacji:

xcorr(x,y,'coeff');

Polega on na podzieleniu estymaty wyjściowej przez

norm(x)norm(y)

w taki sposób, że

współczynnik korelacji przy zerowym opóźnieniu ma wartość jeden.

Sygnały wielokanałowe
Dla sygnału wielokanałowego funkcje

xcorr

i

xcov

estymują własną i wzajemną korelację i

kowariancję ciągu danych dla wszystkich kanałów jednocześnie. Mając daną macierz

S

o

wymiarach M na N, reprezentującą sygnał N kanałowy (jedna kolumna dla pojedynczego
kanału), funkcja

xcorr(S)

oblicza macierz korelacji własnej i wzajemnej dla sygnałów

zawartych w

S

. Otrzymana macierz wynikowa posiada wymiary (2M

−

1) na N

2

. Przykładowo,

jeśli

S

jest sygnałem trzykanałowym

S=[s1 s2 s3];

to rezultaty działania funkcji

R=xcorr(S)

są podawane następująco:

R=[Rs1s1 Rs1s2 Rs1s3 Rs2s1 Rs2s2 Rs2s3 Rs3s1 Rs3s2 Rs3s3].

W Matlabie dostępne są ponadto dwie funkcje

cov

i

corrcoef

. Stosując te funkcje, można

wyznaczyć estymaty kowariancji oraz znormalizowanej kowariancji pomiędzy różnymi
kanałami przy zerowym przesunięciu. Wyżej wymienione funkcje zestawiają wyniki swego
działania w macierzy kwadratowej.

Gęstość widmowa mocy

Celem analizy widmowej jest wyznaczenie częstotliwościowej zawartości sygnału, procesu
losowego lub układu, bazując na skończonych zbiorach danych. Estymacja widmowej
gęstości mocy jest użyteczna w różnych zastosowaniach, włączając detekcję sygnałów
zakłóconych szumem o szerokim paśmie.
Widmowa gęstość mocy (PSD) stacjonarnego procesu losowego x(n) jest związana z funkcją
korelacji sygnału dyskretnego poprzez dyskretną transformację Fouriera.

∑

∞

− ∞

=

ω

−

=

ω

m

m

j

xx

xx

e

)

m

(

R

)

(

P

( 4 )

Funkcja gęstości widmowej mocy posiada taką własność, że jej całka w danym paśmie
częstotliwości jest równa mocy sygnału x(n) w tym paśmie. PSD jest specjalnym
przypadkiem funkcji wzajemnej gęstości widmowej (CSD), zdefiniowanej pomiędzy dwoma
sygnałami x(n) i y(n) w postaci wzoru:

∑

∞

− ∞

=

ω

−

=

ω

m

m

j

xy

xy

e

)

m

(

R

)

(

P

( 5 )

Tak jak w wypadku funkcji korelacji i kowariancji, polecenia Matlaba estymują PSD i CSD
dla sygnałów o skończonej długości.

Istnieje wiele różnych metod estymacji PSD. Można jednak zgrupować je w dwóch
kategoriach: estymacji parametrycznej i nieparametrycznej. Główną techniką stosowaną w
SPT jest nieparametryczny algorytm, opracowany przez Welcha. W przyborniku
wykorzystano tę metodę w funkcjach

psd

,

csd

,

tfe

, oraz

cohere

. Wśród metod

parametrycznych stosowana jest funkcja

pmem

, dokonująca estymacji widma metodą

„maksymalnej entropii”. Bardziej szczegółowe omówienie funkcji do estymacji PSD,
wykorzystujących algorytmy parametryczne, znajduje się plikach pomocy Matlaba.

Metoda Welcha
Jedną z metod estymacji gęstości widmowej mocy jest wyznaczenie dyskretnej transformaty
Fouriera próbek konkretnej realizacji danego procesu, a następnie obliczenie kwadratu z
wartości bezwzględnej wyniku. Przykładowo, wyznaczono PSD dla 1001-elementowego
sygnału

xn

, składającego się z dwóch sinusoid i szumu.

Fs=1000;
t=0:1/Fs:1;

xn=sin(2*pi*50*t)+2*sin(2*pi*120*t)+...
randn(size(t));

Zgrubny estymator PSD wyznacza się z

xn

stosując instrukcje:

Pxx=abs(fft(xn, 1024)).^2/1001;

Powyższy estymator jest nazywany periodogramem. Skalowanie kwadratu wartości
bezwzględnej z FFT przez kwadrat normy okna danych zastosowanego do sygnału (w tym
wypadku okna prostokątnego o długości 1001), gwarantuje to, że estymator ten jest
asymptotycznie nieobciążony. To znaczy, że jeśli liczba próbek wzrasta, wartość oczekiwana
periodogramu przybliża się do prawdziwej wartości PSD. Problemem przy estymacji PSD
metodą periodogramu jest fakt, że jego wariancja jest duża i nie maleje przy wzrastającej
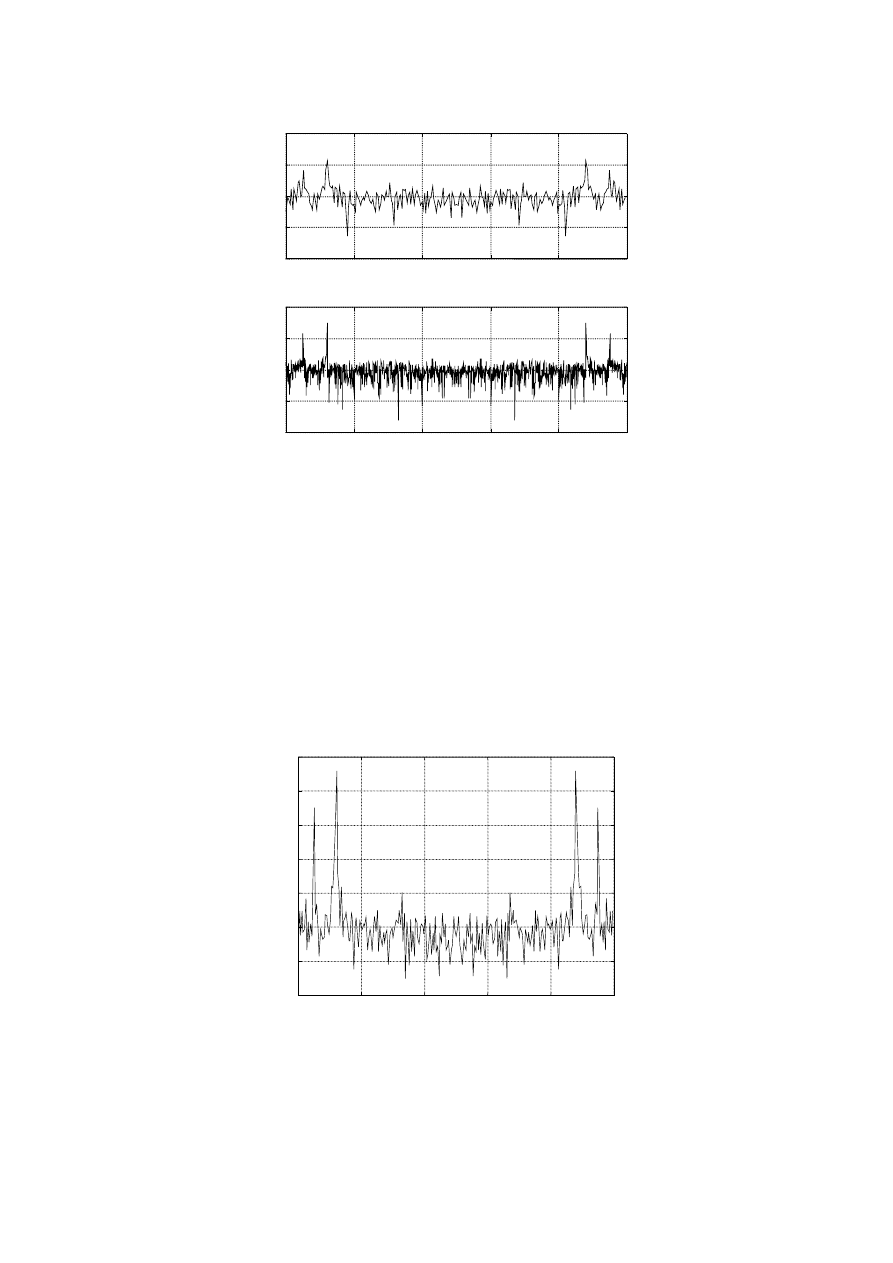
liczbie próbek. Następne dwa przykłady pokazują, że pomimo wzrostu długości
analizowanego wektora, periodogram nie wygładza się.

Pxx_short=abs(fft(xn,256)).^2/256;

subplot(2,1,1)
plot((0:255)/256*Fs,10*log10(Pxx_short),'black')

grid,
title('Periodogram krótkiego sygnału')

xlabel('Częstotliwość w Hz'), ylabel('Widmo mocy (dB)');
subplot(2,1,2),

plot((0:1023)/1024*Fs,10*log10(Pxx),'black')
grid,

text(250,45,'Periodogram dłuższego sygnału')
xlabel('Częstotliwość w Hz'), ylabel('Widmo mocy (dB)');

0

200

400

600

800

1000

-40

-20

0

20

40

Periodogram krótkiego sygnału

Częstotliwość w Hz

W

id

m

o

m

oc

y

(d

B

)

0

200

400

600

800

1000

-40

-20

0

20

40

Periodogram dłuższego sygnału

Częstotliwość w Hz

W

id

m

o

m

oc

y

(d

B

)

Rys. 1 Periodogramy dla sekwencji o różnych długościach

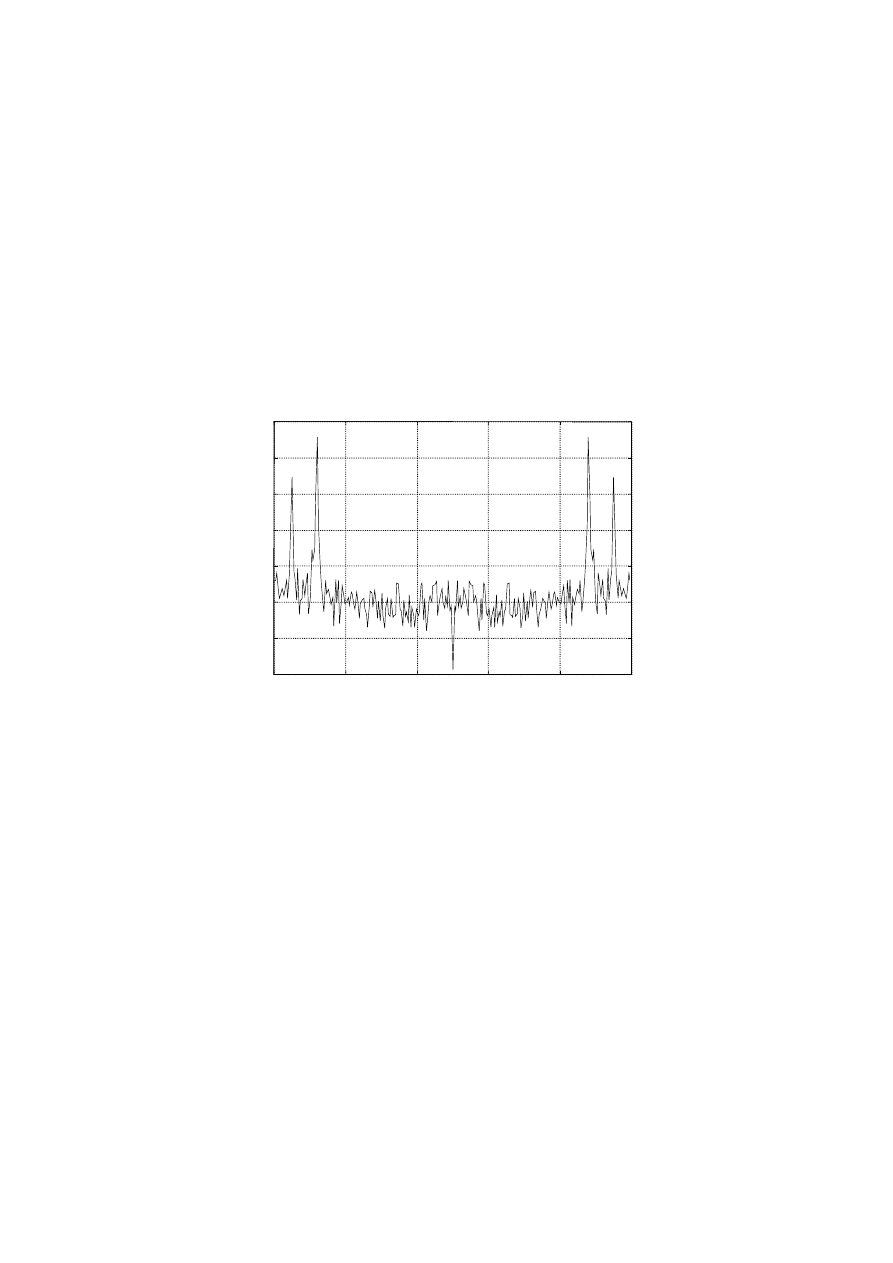
Redukcja wariancji estymatora PSD następuje przez podzielenie sygnału na nie nakładające
się fragmenty oraz uśrednianie ich widm w dziedzinie częstotliwości.

subplot(1,1,1),
Pxx=(abs(fft(xn(1:256))).^2+...

abs(fft(xn(257:512))).^2+...
abs(fft(xn(513:768))).^2)/(256*3);

plot((0:255)/256*Fs,10*log10(Pxx),'black')
grid,

xlabel('Częstotliwość w Hz'), ylabel('Widmo mocy (dB)')
title('Uśredniony periodogram (fragmenty sygnału nie nakładają

się)')

0

200

400

600

800

1000

-10

-5

0

5

10

15

20

25

Częstotliwość w Hz

W

id

m

o

m

oc

y

(d

B

)

Uśredniony periodogram (fragmenty sygnału nie nakładają się)

Rys. 2 Periodogram uśredniony w nie nakładających się przedziałach

Taki uśredniony estymator posiada jedną trzecią wariancji periodogramu o długości 256,
otrzymanego wcześniej. Uśredniając więcej próbek, można otrzymać w rezultacie niższą
wariancję. Długość sygnału ogranicza jednakże liczbę możliwych do utworzenia odcinków

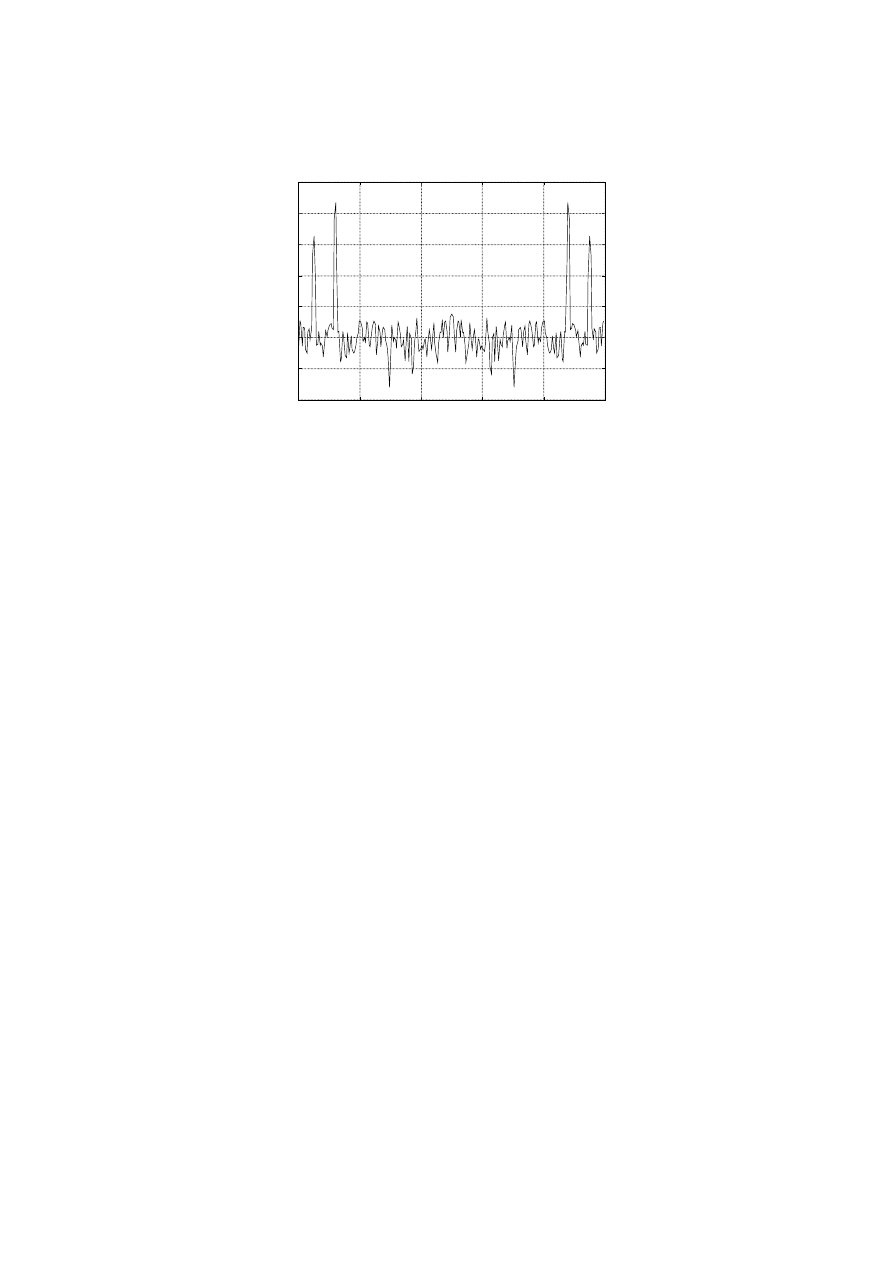
(do 3 sekcji o długości 256 w poprzednim przykładzie). By uzyskać większą ilość sekcji,
dzielimy sygnał na fragmenty nakładające się.

Pxx=(abs(fft(xn(1:256))).^2+...
abs(fft(xn(129:384))).^2+...

abs(fft(xn(257:512))).^2+...
abs(fft(xn(385:640))).^2+...

abs(fft(xn(513:768))).^2+...
abs(fft(xn(641:896))).^2)/(256*6);

plot((0:255)/256*Fs,10*log10(Pxx),'black'),grid,
xlabel('Częstotliwość w Hz'), ylabel('Widmo mocy (dB)')

title('Uśredniony periodogram (próbki nakładają się)')

W tym wypadku odcinki są statystycznie zależne, co z kolei powoduje wzrost wariancji.
Należy więc znaleźć kompromis pomiędzy liczbą fragmentów sygnału i stopniem ich
nakładania.

0

200

400

600

800

1000

-10

-5

0

5

10

15

20

25

Częstotliwość w Hz

W

id

m

o

m

oc

y

(d

B

)

Uśredniony periodogram (próbki nakładają
się)

Rys. 3 Periodogram uśredniony w nakładających się przedziałach

Inną drogą do poprawienia własności statystycznych estymatora periodogramu jest
zastosowanie nieprostokątnego okna czasowego do wygładzenia końców analizowanych
danych. W rezultacie otrzymujemy zmodyfikowany periodogram. Operacja ta redukuje efekt
zależności nakładających się sekcji, ponieważ okno zmniejsza amplitudę do zera przy ich
brzegach. Nieprostokątne okno czasowe zmniejsza poziom bocznych interferencji (lub
„przecieku widma”), równocześnie jednak powodując wzrost szerokości prążków
widmowych. Z odpowiednim oknem czasowym (Hamminga, Hanninga lub Kaisera) oraz 50
procentowym nakładaniem się analizowanych odcinków sygnału uzyskuje się estymator o
znacznie zmniejszonej wariancji.
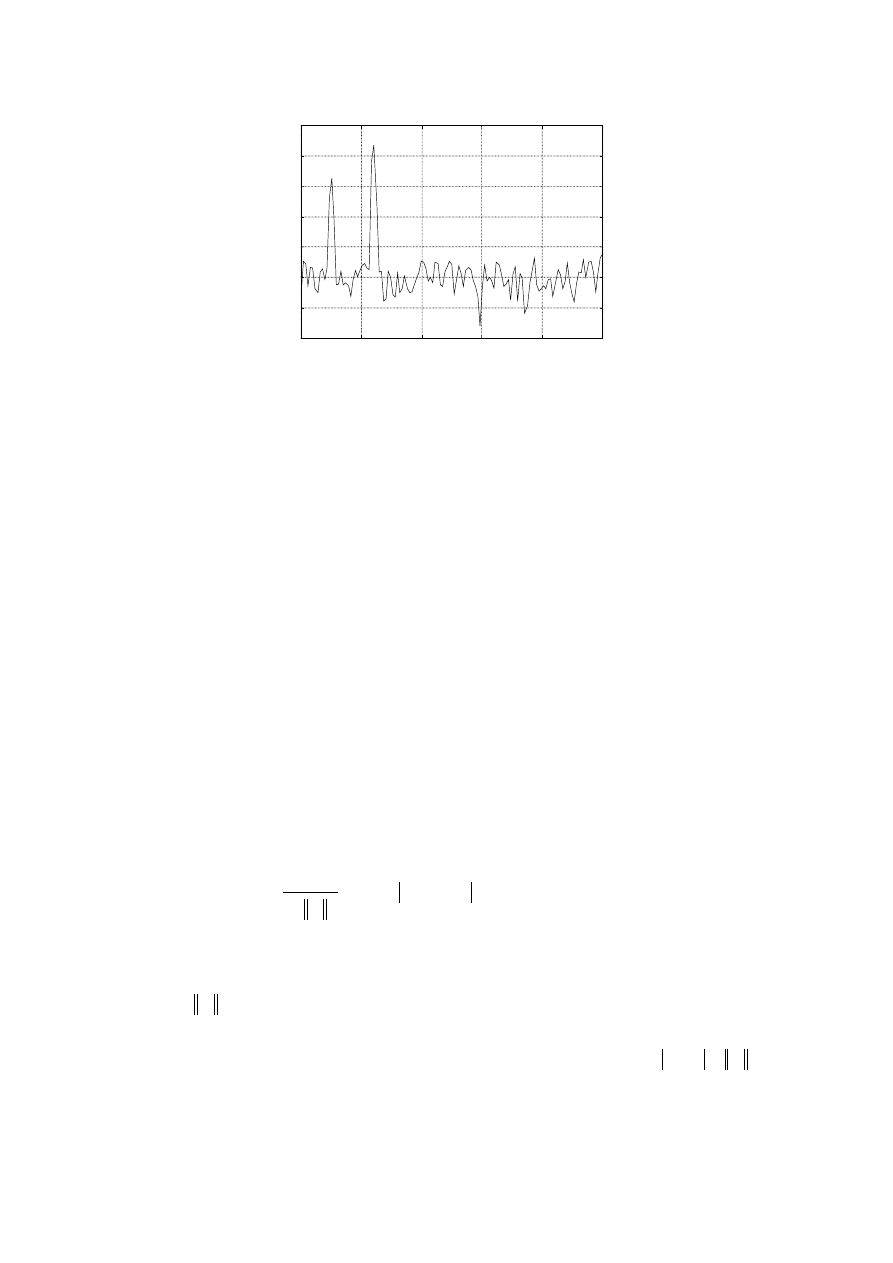
Rezultat zastosowania okna Hanninga do analizowanego sygnału przedstawiono na rys. 4. W
tym celu zrealizowano następujące funkcje:

w=hanning(256)';

Pxx=(abs(fft(w.*xn(1:256))).^2+...
abs(fft(w.*xn(129:384))).^2+...

abs(fft(w.*xn(257:512))).^2+...
abs(fft(w.*xn(385:640))).^2+...

abs(fft(w.*xn(513:768))).^2+...
abs(fft(w.*xn(641:896))).^2)/(norm(w)^2*6);

plot((0:255)/256*Fs,10*log10(Pxx),'black')

grid,
xlabel('Częstotliwość w Hz'), ylabel('Widmo mocy (dB)')

title(‘Periodogram zmodyfikowany oknem Hanninga')

0

200

400

600

800

1000

-10

-5

0

5

10

15

20

25

Częstotliwość w Hz

W

id

m

o

m

oc

y

(d

B

)

Periodogram zmodyfikowany oknem Hanninga

Rys. 4 Periodogram zmodyfikowany oknem Hanninga

Na rysunku 4 można zauważyć, że prążki widma rozszerzyły się, a poziom szumów wydaje
się być mniejszy w porównaniu z poprzednimi wykresami.

Przedstawione tutaj metody: uśredniania oraz zmodyfikowanego periodogramu należą do
metod opartych na algorytmie Welcha. Zawarte w przyborniku SPT funkcje

psd

i

csd

umożliwiają dobór odpowiednich parametrów analizy (długość FFT, rodzaj okna, szerokość
nakładania się próbek) w trakcie obliczeń PSD i CSD dla jednego lub dwóch sygnałów przy
pomocy metody Welcha.

Obliczanie funkcji widmowej gęstości mocy za pomocą procedur SPT
Funkcja

psd

uśrednia i skaluje zmodyfikowany periodogram z realizacji sygnału

pozbawionych trendu. Jako argumenty funkcji należy wyszczególnić parametry, które sterują
wykonaniem algorytmu.
Funkcja

psd

, obliczając estymator PSD dla sekwencji

xn

używa domyślnie okna czasowego

Hanninga oraz FFT o długość 256 próbek. Zadany ciąg jest dzielony na nienakładające się
sekcje oraz jest usuwany trend.

Pxx=psd(xn);

Jeśli oryginalna sekwencja wyrażona jest w woltach V, Pxx posiada jednostkę V

2

.

Poniżej został powtórzony ostatni z podanych przykładów. Do jego realizacji przyjęto 128
jako liczbę nakładających się próbek oraz nie usunięto trendu z sygnału.

nfft=256;

Fs=1000;
window=hanning(256);

noverlap=128;
dflag='none';

Pxx=psd(xn,nfft,Fs,window,noverlap,dflag);

Częstotliwość próbkowania zadawana jako jeden z parametrów, nie odgrywa większej roli w
obliczeniach, pomaga jednak w skalowaniu osi częstotliwości wykresu. Funkcja

psd

bez

żadnych parametrów wyjściowych generuje wykres przedstawiony na rys 5.

psd(xn,nfft,Fs,window,noverlap,dflag);

xlabel('Częstotliwość Hz'),
ylabel('Amplituda widmowa mocy (dB)')

0

100

200

300

400

500

-10

-5

0

5

10

15

20

25

Częstotliwość Hz

A

m

pl

itu

da

w

id

m

o

w

a

m

oc

y

(d

B

)

Rys. 5 Periodogram uzyskany w wyniku działania funkcji

psd

Dostęp do wektora, dla którego obliczana jest PSD, uzyskujemy dodając drugi parametr
wyjściowy. Wektor ten jest użyteczny podczas nieautomatycznego wykonywania wykresu
PSD.

[Pxx,f]=psd(xn, Fs, 256, noverlap, dflag);

plot(f,10*log10(Pxx))

Dla rzeczywistego sygnału

xn

,

psd

oblicza widmowe gęstości mocy jedynie dla

częstotliwości od 0 do częstotliwości Nyquista. We wcześniejszych przykładach, w których
estymator PSD był generowany przy pomocy FFT, zakres częstotliwości zawierał się w
granicach od 0 do częstotliwości próbkowania.

Obciążenie i normalizacja
Analizując przedstawione powyżej wyniki obliczeń funkcji

psd

, można zauważyć kilka

charakterystycznych cech analizowanego sygnału

xn

. Poziom szumów jest mały, oscyluje

wokół zera decybeli (dB) i z założenia jest to biały szum o wariancji 1. Ponadto moc sygnału

xn

jest skoncentrowana w dwóch prążkach o częstotliwościach 50 i 120 Hz. Prążek o

częstotliwości 50 Hz jest 6 dB poniżej prążka o częstotliwości 120 Hz. Na tej podstawie
można stwierdzić, że sinusoida o wyższej częstotliwości posiada dwukrotnie większą
amplitudę (10

6/20

=2.0). Niestety na podstawie rzeczywistej wysokości prążków nie można

wiele powiedzieć o oryginalnej amplitudzie sinusoid bez dokonania dodatkowych analiz.
W celu uzyskania użytecznych informacji o amplitudzie prążków badanych sinusoid, trzeba
zauważyć, że wartość oczekiwana estymatora PSD jest określana wzorem:

{

}

∫

π

π

−

θ

θ

−

ω

θ

π

=

ω

d

)

(

W

)

(

P

w

2

1

)

(

P

E

2

xx

2

xx



( 6 )

Wielkość ta, jest splotem wartości PSD z podniesioną do kwadratu wartością bezwzględną
dyskretnej transformaty Fouriera zastosowanego okna W(

ω

), podzielony przez kwadrat jego

normy. Wielkość skalująca (norma okna) jest sumą kwadratów współczynników funkcji okna:

∑

=

2

2

)

n

(

w

w

( 7 )

Równanie (6) wskazuje na fakt, że jeśli P

xx

(

ω

) posiada prążek o wysokości 1 przy określonej

częstotliwości

ω

0

, to estymator będzie w przybliżeniu przyjmował wartość

2

2

w

/

)

0

(

W

dla

tej częstotliwości. Tak więc, by uzyskać estymator amplitudy oryginalnych prążków, należy
pomnożyć wynik działania funkcji psd przez norm

2

(w)/sum

2

(w), gdzie w jest wektorem okna.

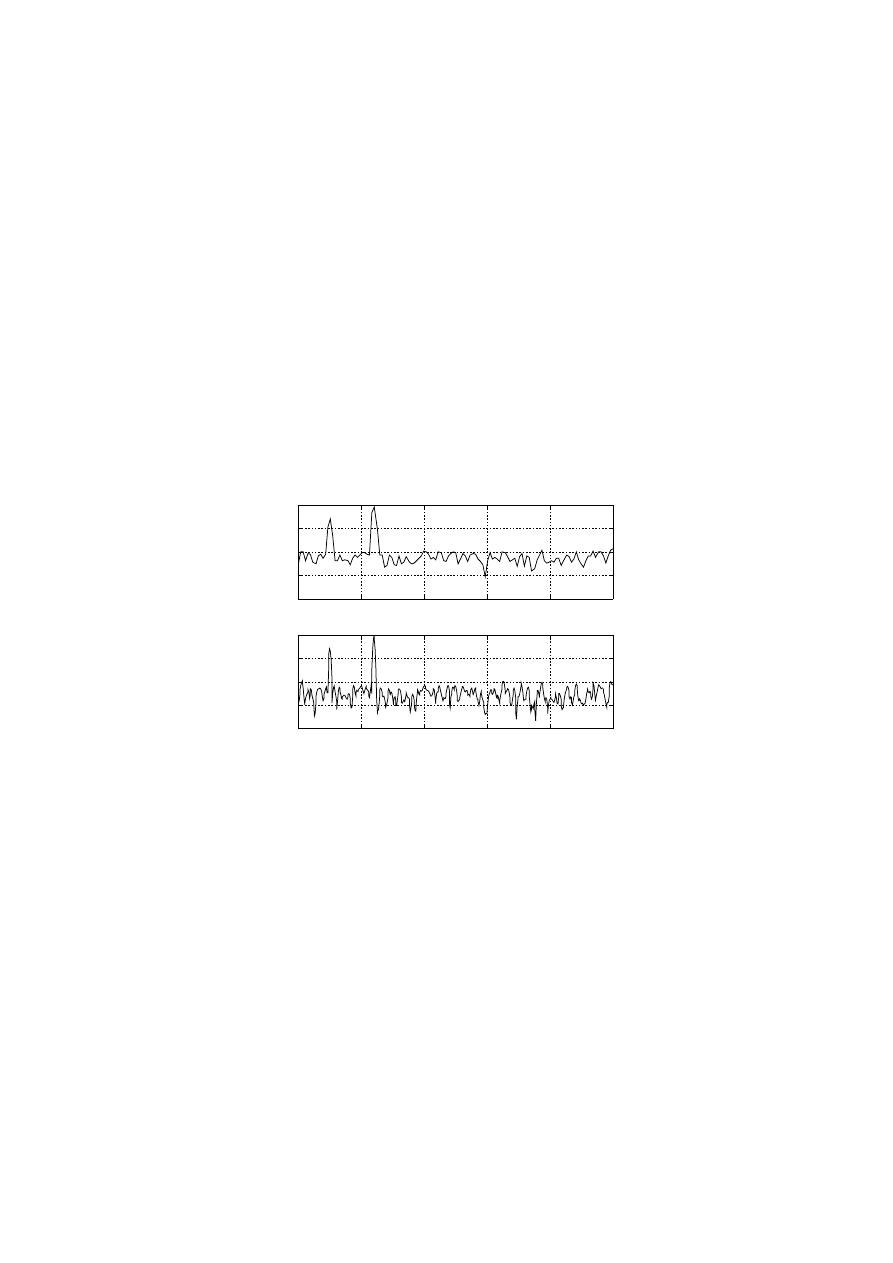
Wynika to z twierdzenia Parsevala iż sum

2

(w)=sum

2

(W). Skalowanie jest niezależne od

długości i kształtu okna. Przykładowo:

w1=hanning(256); w2=hanning(500);
[Pxx1,f1]=psd(xn,256,Fs,w1,128,'none');

[Pxx2,f2]=psd(xn,1024,Fs,w2,250,'none');
subplot(2,1,1), plot(f1,10*log10(Pxx1*norm(w1)^2/sum(w1)^2),...

'black'),grid,
subplot(2,1,2), plot(f2,10*log10(Pxx2*norm(w2)^2/sum(w2)^2),...

'black'),grid

Na obydwu wykresach (rys. 6), które pokazują widma jedynie dla dodatnich częstotliwości
(częstotliwości ujemne są takie same), prążek dla wyższej częstotliwości posiada wartość 0
dB, a dla niższej -6 dB. Amplituda sinusoidy o częstotliwości 120 Hz, 0 dB, odpowiada
kwadratowi amplitudy równemu 1. Wynika to z faktu, iż sinusoida o amplitudzie równej 2
posiada widmo z dwoma eksponencjalnymi składnikami o amplitudzie 1, dla dodatnich i
ujemnych częstotliwości. Podobnie, sinusoida o częstotliwości 50 Hz posiada dwa składniki
częstotliwości, dodatni i ujemny, równe kwadratom amplitudy (1/2)

2

lub 10log10(0.25)= -6

dB.
Należy również zauważyć, że drugi wykres posiada nieznacznie niższy poziom szumu,
będący wynikiem większej długości okna.

0

1 0 0

2 0 0

3 0 0

4 0 0

5 0 0

- 4 0

- 3 0

- 2 0

- 1 0

0

0

1 0 0

2 0 0

3 0 0

4 0 0

5 0 0

- 4 0

- 3 0

- 2 0

- 1 0

0

Rys. 6 Przeskalowane periodogramy

Związek Parsevala
Całka z PSD, obliczona dla całego pasma częstotliwości, jest miarą całkowitej energii
sygnału. Za pomocą obliczenia funkcji

psd

można w przybliżeniu sprawdzić tę zależność

(zgodność obliczeń energii w dziedzinie czasu i częstotliwości) dla danego sygnału:

[Pxx,f]=psd(xn,256,Fs,256,128,'none');
format long

sum(xn.^2)/length(xn)

•

ans =

•

3.60376766505040

sum(Pxx)/length(Pxx)

•

ans =

•

3.68430077838700

Obliczenie procentowej zawartości energii w sygnale w danym paśmie częstotliwości,
wymaga zsumowania estymatora PSD jedynie dla wybranych prążków widma. Tak więc

procentową energię sygnału

xn

w paśmie od 40 do 60 Hz wyznacza się stosując sekwencje

instrukcji Matlaba:

ind=find(f>40&f<60)

•

ind =

•

12

•

13

•

14

•

15

•

16

sum(Pxx(ind))/sum(Pxx)

•

ans =

•

0.13369450463404

Obliczenie funkcji wzajemnej gęstości widmowej
Estymując, przy pomocy metody Welcha, wzajemną gęstość widmową dwóch sygnałów o
równej długości

x

i

y

, funkcja

csd

oblicza periodogram jako iloczyn FFT z

x

oraz wartości

sprzężonej do wyniku FFT z

y

. Przetwarzanie sygnałów przy pomocy funkcji

csd

(a więc:

dzielenie na próbki, usuwanie trendu, stosowanie okien) odbywa się w ten sam sposób, jak dla
funkcji

psd

.

Pxy=csd(x,y,nfft,window,nowerlap,dflag);

Przedziały ufności
Za pomocą funkcji

psd

i

csd

można obliczać przedziały ufności dla estymatorów gęstości

widmowych. Można wprowadzić jako argument wejściowy parametr

p

, który podaje

przedział ufności (w procentach).

[Pxx,Pxxc,f]=psd(x,nfft,Fs,window,noverlap,...

p,dflag);
[Pxy,Pxyc,f]=csd(x,y,nfft,Fs,window,noverlap,...

p,dflag);

Parametr

p

musi być wielkością skalarną zawartą w granicach od 0 do 1.

Funkcje zakładają normalny rozkład periodogramu z nienakładającymi się próbkami. Jeśli te
założenia są spełnione, wtedy

p

⋅

100% jest prawdopodobieństwem, że w przedziale

[Pxx-

Pxxc(:,1), Pxx+Pxxc(:,2)]

zawiera się rzeczywista wartość PSD. Jeśli próbki

nakładają się, przedział ufności nie jest wyznaczony poprawnie, a funkcja wyświetla
ostrzeżenie.

Innym rozwiązaniem jest przyjęcie założenia, że periodogramy posiadają rozkład chi
kwadrat. Jeśli dostępny jest przybornik Statistics Toolbox, można obliczyć poziom ufności

p

⋅

100% dla tak przyjętego rozkładu, stosując następujące funkcje:

k=fix((length(x)-noverlap)/(length(window)-noverlap));

alfa=1-p;
confid=2*k*Pxx*(1./chi2inv([1-alfa/2 alfa/2],2*k));

gdzie

k

jest liczbą sekcji użytych do obliczenia estymatora PSD, zaś

confid

jest

dwukolumnową macierzą, składającą się z górnych i dolnych zakresów ufności. Wówczas
mamy

p

⋅

100%-owe prawdopodobieństwo, że poziom ufności

[Pxx - confid(:,1)

Pxx+confid(:,2)]

zawiera rzeczywistą PSD. Ten poziom ufności jest wiarygodny

jedynie, gdy sekcje nie pokrywają się.

Estymator funkcji przejścia

Jednym z zastosowań metody Welcha jest identyfikacja modeli funkcjonalnych. Jednym z
tego rodzaju modeli jest funkcja przejścia układu. Zakłada się, że badany obiekt H jest
układem liniowym o stałych współczynnikach, oraz x(n) i y(n) są odpowiednio jego wejściem
i wyjściem. Wtedy prawdziwa jest zależność:

)

(

P

)

(

H

)

(

P

xx

xy

ω

ω

=

ω

( 8 )

gdzie H jest widmową funkcją przejścia.
Znając sygnały x(n) i y(n) można zdefiniować estymator funkcji przejścia układu jako:

)

(

Pˆ

)

(

Pˆ

)

(

Hˆ

xx

xy

ω

ω

=

ω

( 9 )

Metoda ta pozwala na estymację zarówno amplitudy jak i fazy sygnału. Funkcja

fte

wykorzystuje metodę Welcha do obliczenia CSD i PSD, a następnie formuje ich iloraz w celu
estymowania funkcji przejścia. Funkcja

tfe

posiada taką samą składnię jak funkcja

csd

.

W poniższym programie przefiltrowano sygnał

xn

przy pomocy filtru FIR, a następnie

wyznaczono charakterystykę amplitudowo-częstotliwościową oraz estymowaną funkcję
przejścia:

h=ones(1,10)/10;

yn=filter(h,1,xn);
[Hest,f]=tfe(xn,yn,256,Fs,256,128,'none');

H=freqz(h,1,f,Fs);
subplot(2,1,1), plot(f,abs(H),'black')

title('Rzeczywista amplituda funkcji przejścia')
xlabel('Częstotliwość w Hz')

subplot(2,1,2), plot(f,abs(Hest),'black')
text(110,1.08,'Estymata amplitudy funkcji przejścia')

xlabel('Częstotliwość w Hz')

Funkcja koherencji

Funkcja koherencji określa związek pomiędzy dwoma sygnałami w dziedzinie częstotliwości.
Kwadrat modułu koherencji pomiędzy sygnałami x(n) i y(n) wyznacza się ze wzoru:

)

(

P

)

(

P

)

(

P

)

(

C

yy

xx

2

xy

xy

ω

ω

ω

=

ω

( 10 )

Iloraz ten jest liczbą rzeczywistą z przedziały [0,1] i jest miarą korelacji pomiędzy sygnałami
x(n) i y(n) dla danej częstotliwości

ω

.

Funkcja

cohere

dla zadanych ciągów próbek

x

i

y

oblicza PSD i CSD, a następnie iloraz

kwadratu wartości bezwzględnej CSD przez iloczyn PSD dla

x

i

y

. Jej parametry i sposób

działania jest podobny do funkcji

csd

i

tfe

.

Funkcję koherencji pomiędzy ciągiem wejściowym

xn

i wyjściowym

yn

filtru rozważanego

w poprzednim rozdziale wyznaczono za pomocą sekwencji instrukcji:

0

100

200

300

400

500

0

0.5

1

Rzeczywista amplituda funkcji przejścia

Częstotliwość w Hz

0

100

200

300

400

500

0

0.5

1

Estymata amplitudy funkcji przejścia

Częstotliwość w Hz

Rys. 7 Charakterystyki amplitudowo-częstotliwościowe zadanej i estymowanej funkcji przejścia filtru

clf,

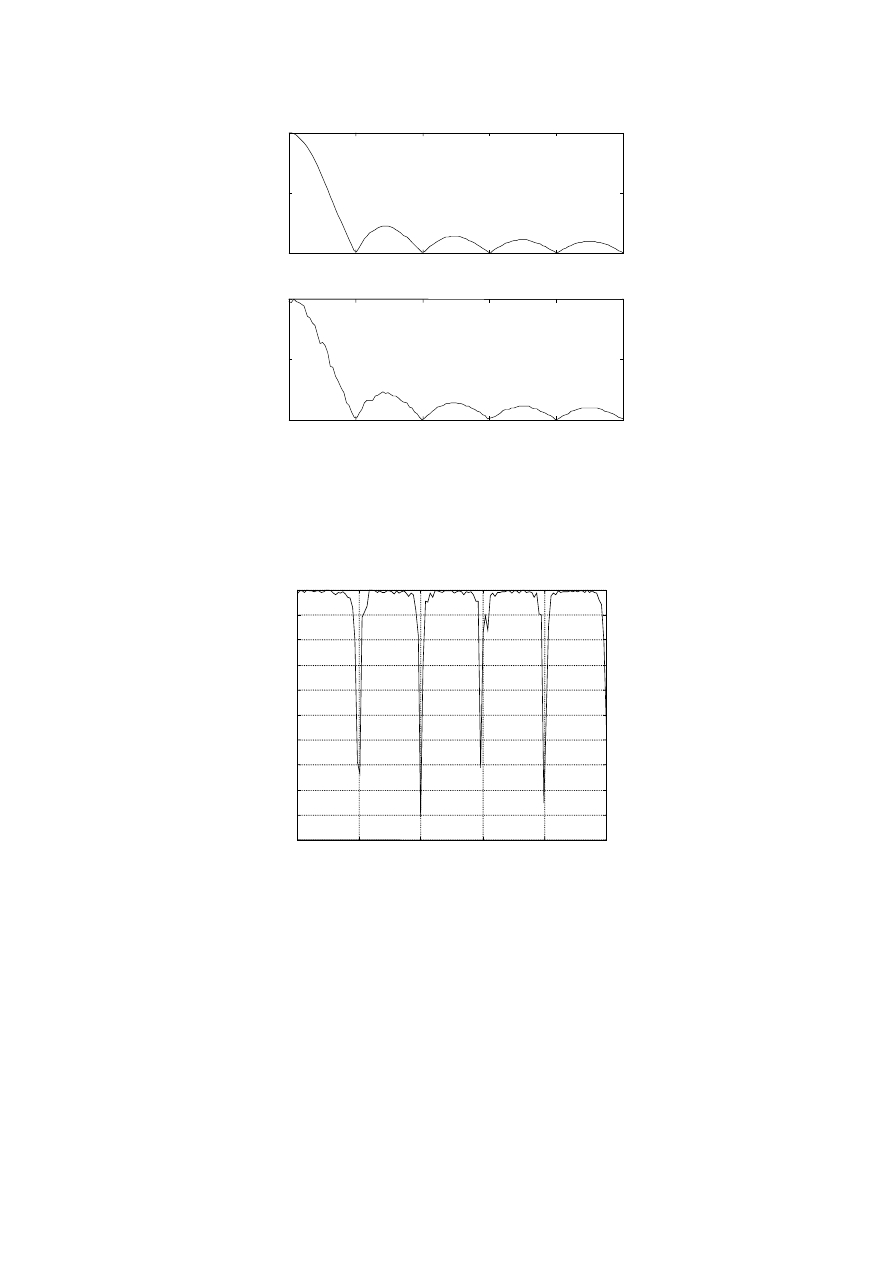
cohere(xn,yn,256,Fs,256,128,'none')
title('Funkcja koherencji')

0

100

200

300

400

500

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

Częstotliwość

E

st

ym

a

to

r

fu

nk

cj

i k

oh

er

en

cj

i

Funkcja koherencji

Rys. 8 Przebieg funkcji koherencji

Dla sygnałów z poprzedniego przykładu koherencja obliczona za pomocą funkcji

cohere

wynosi 1.

Uwaga

W obecnych wersjach toolboxu Signal Processing przepisano funkcje obliczających
estymatory działające w dziedzinie częstotliwości. W chwili obecnej zmiennie mogą być
stosowane funkcje:

–

do obliczania gęstości widmowej mocy:

–

[Pxx,f] = psd(xn,nfft,Fs,window,noverlap,dflag);

–

[Pxx,f] = pwelch(xn,window,noverlap,nfft,Fs);

–

do obliczania wzajemnej gęstości widmowej

–

[Pxx,f] = csd(xn,yn,nfft,Fs,window,noverlap,dflag)

–

[Pxx,f] = cpsd(xn,yn,window,noverlap,nfft,Fs);

–

do obliczania widmowej funkcji przejścia:

–

[Pxx,f] = tfe(xn,yn,nfft,Fs,window,noverlap,dflag)

–

[Pxx,f] = tfestimate(xn,yn,window,noverlap,nfft,Fs);

–

do obliczania funkcji koherencji:

–

[Pxx,f] = cohere(xn,yn,nfft,Fs,window,noverlap,dflag)

–

[Pxx,f] = mscohere(xn,yn,window,noverlap,nfft,Fs);

Zadania do wykonania

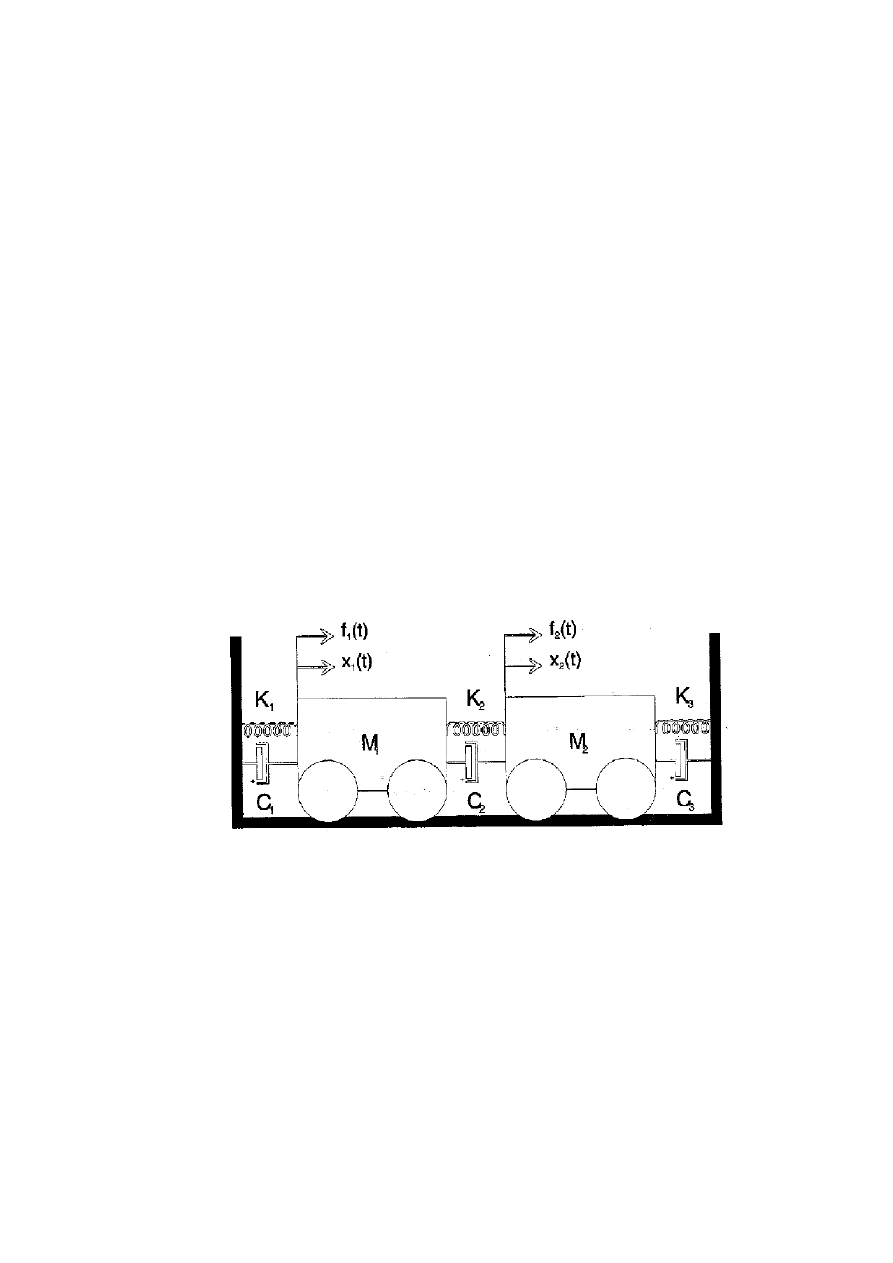
1. Wykonać symulację układu testowanego o dwóch stopniach swobody dla parametrów

ustalonych w trakcie zajęć z modelowania. Zarejestruj sygnały testowe w postaci
przebiegów wymuszających oraz sygnałów odpowiedzi dla poszczególnych stopni
swobody. Sygnały odpowiedzi powinny być w postaci wektorów przemieszczeń,
prędkości i przyspieszeń o odpowiedniej długości.

Dane: M

1

= 10, M

2

= 7, C

1

= 0.7, C

2

= 0.9, C

3

= 0.7, K

1

= 120, K

2

= 200, K

3

= 170

2. Dla zapisanych danych dokonaj wyznaczenia estymatorów gęstości widmowych

mocy, widmowych funkcji przejścia oraz funkcji koherencji. Aby estymatory miały
znaczenie statystyczne konieczna jest praca z przebiegami o odpowiedniej długości.
Wykonaj niezależnego wyznaczenia stosownych estymatorów bazując na sygnale
wymuszającym oraz:

•

sygnałach przyspieszeń

•

sygnałach prędkości

•

sygnałach przemieszczeń.

3. Porównaj wykonując stosowne wykresy wyniki estymacji uzyskane w punkcie 2.

Skomentuj wyniki eksperymentu.

4. Powtórz zadania 2 i 3 dodając do symulacyjnych danych wyjściowych szum o

amplitudach na poziomie 10% i 20% sygnału.