Zjawisko fotoelektryczne

Zjawisko Comptona

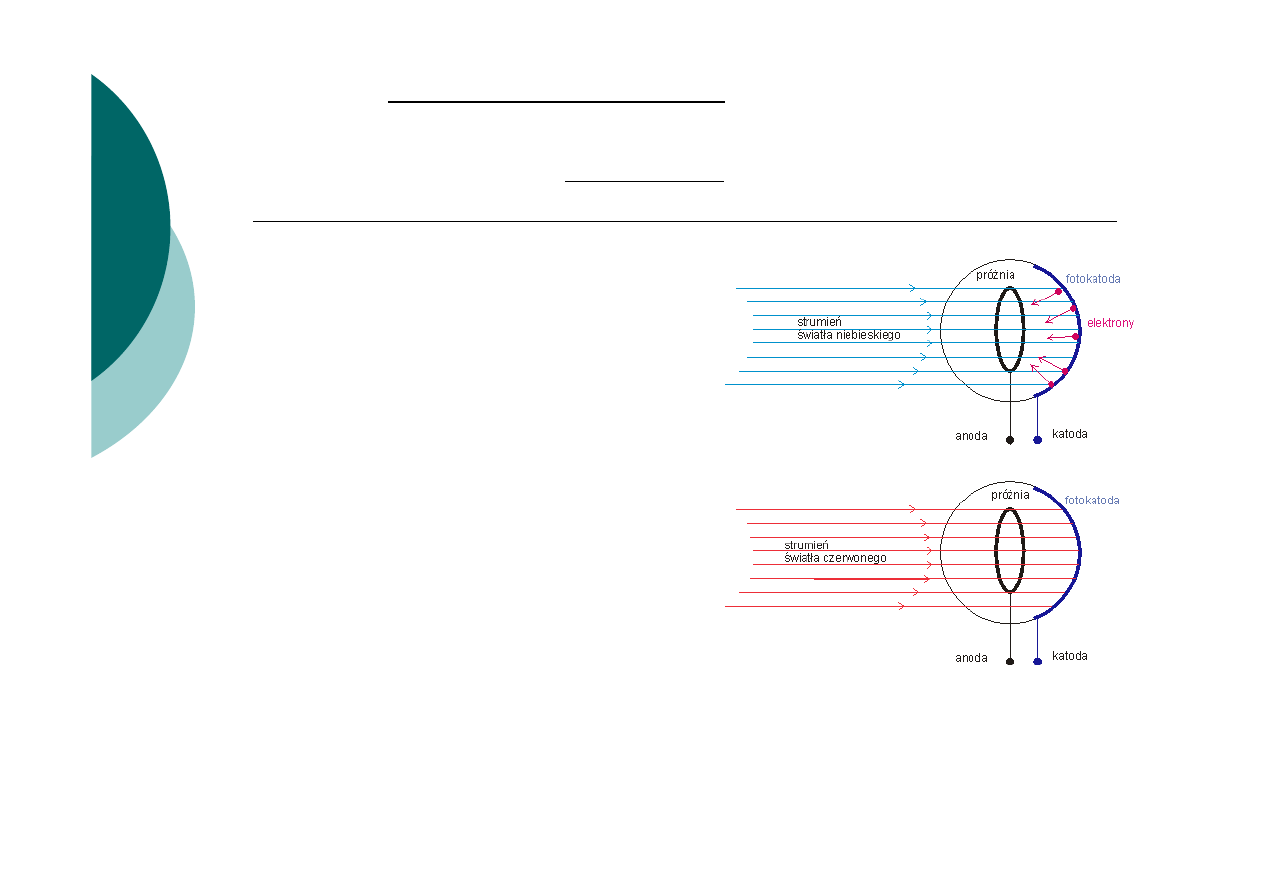
Zjawisko fotoelektryczne polega na emisji elektronów z
powierzchni metalu pod wpływem padającego
promieniowania elektromagnetycznego. Zjawisko to jest
obserwowane dla światła widzialnego np. dla cezu,
natomiast dla wielu innych metali zjawisko to
obserwowane jest w promieniowaniu ultrafioletowym,
rentgenowskim i

γ

.

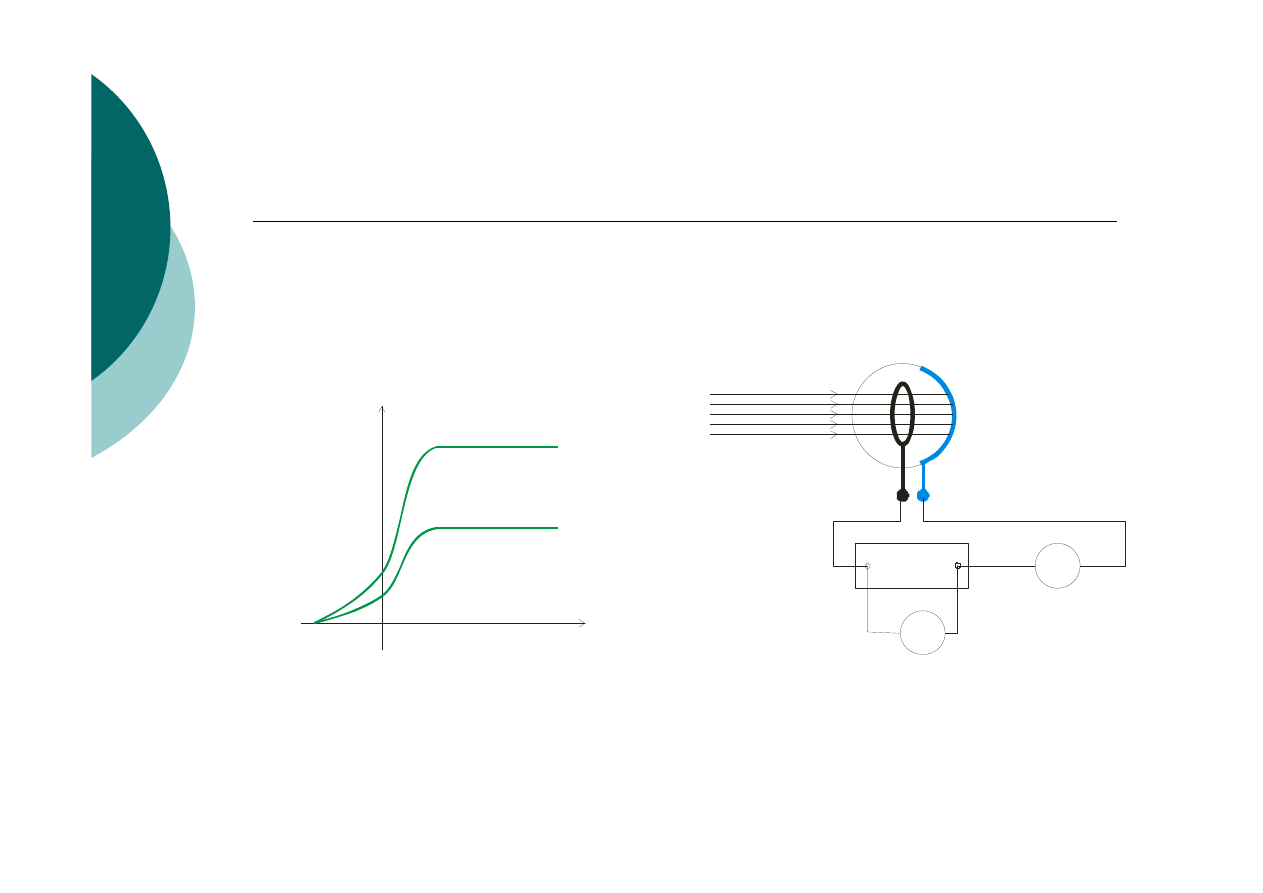
Charakterystyka prądowo – napięciowa Schemat układu do badania
(częstotliwość

ν

= const)

efektu fotoelektrycznego

strumie

ń

ś

wiatła

zasilacz

G

V

I

U

h

U

2

1

Φ > Φ

1

Φ

Istnieje progowa częstotliwość, poniżej której zjawisko
nie występuje.
Energia elektronów nie zależy od natężenia światła.

Klasyczna teoria falowa
nie potrafi tego wytłumaczyć.
Energia niesiona przez fale
jest proporcjonalna do
kwadratu amplitudy i
do kwadratu częstotliwości.
Zatem przy mniejszej
częstotliwości
wystarczyłoby
zwiększyć amplitudę
promieniowania.

Foton

Wyjaśnieniem sprzeczności w tym zjawisku zajął się
Albert Einstein( otrzymał za to nagrodę Nobla).

Światło to zbiór pojedynczych fotonów o energii

Równanie Einsteina:

-energia fotonu

Φ

w

– praca wyjścia elektronu

Energia kinetyczna elektronu

U

H

– napięcie hamowania

h

ν

k

w

h

E

ν

= + Φ

h

ν

2

1

2

k

H

E

mv

eU

=

=

Zjawisko Comptona

Przy przejściu wiązki promieniowania rentgenowskiego
lub gamma o długości fali λ przez absorbent, oprócz
promieniowania o tej samej długości, pojawia się
promieniowanie o długości fali większej λ’> λ
i zależnej od kąta obserwacji.

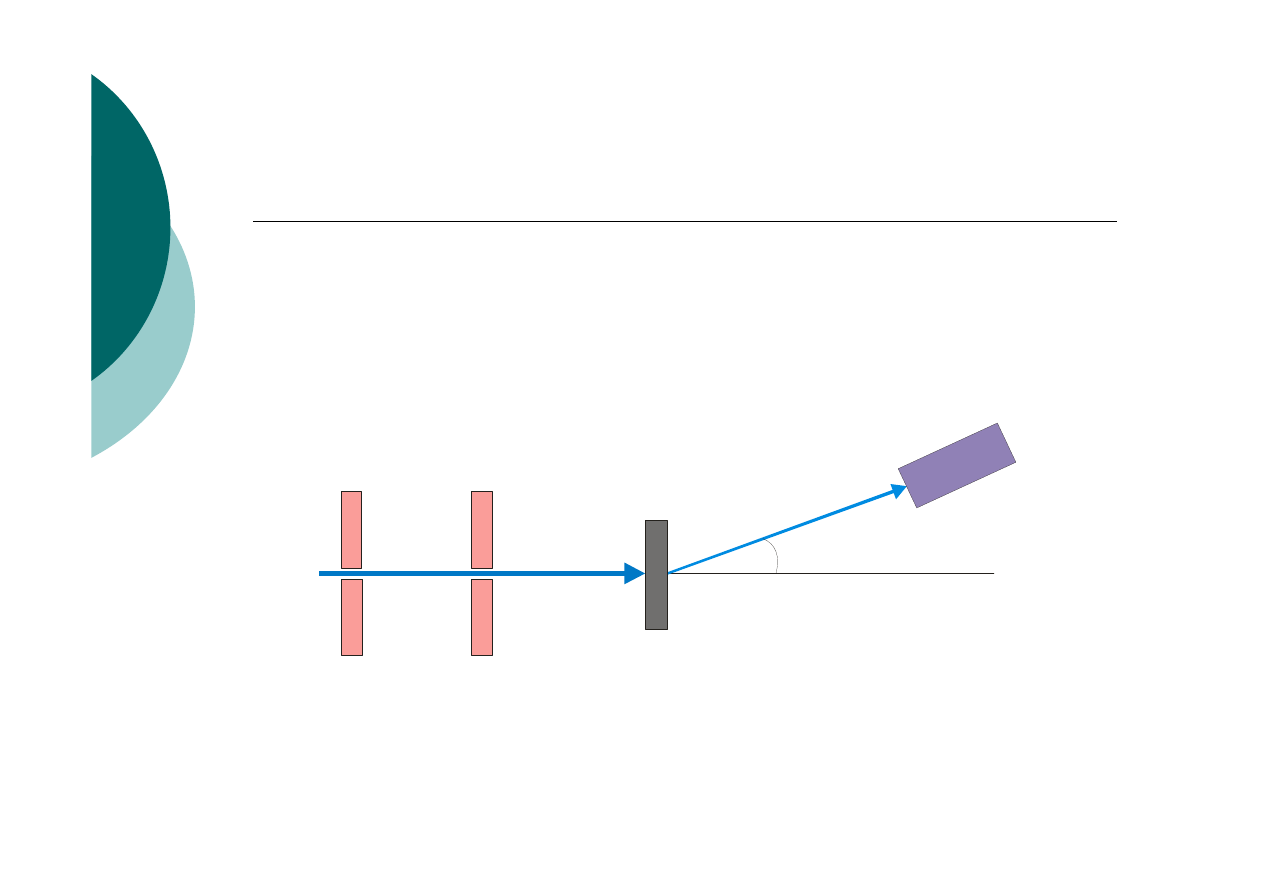
Schemat aparatury Comptona

szczeliny kolimuj

ą

ce

λ

λ

'

θ

tarcza
grafitowa

detektor

promieniowanie rentgenowskie

rozproszone promieniowanie
rentgenowskie

Pojedynczy foton promieniowania rentgenowskiego
mający energię

i pęd

zderza się z elektronem

swobodnym, w efekcie czego wylatuje nowy foton o
mniejszej energii .

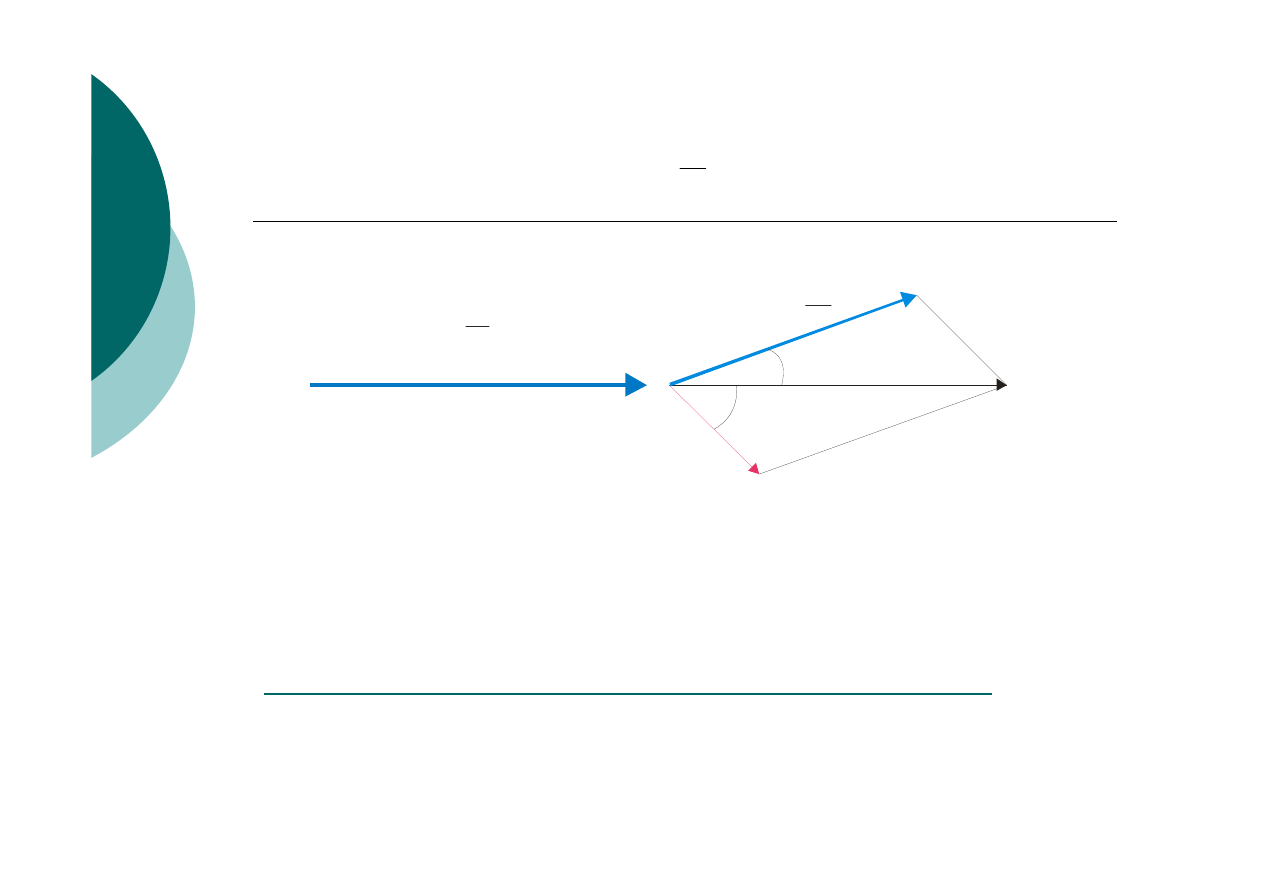
Zasada zachowania pędu w zjawisku Comptona

http://physics.bu.edu/~duffy/semester2/c35_compton.html

h

ν

f

h

p

c

ν

=

'

h

ν

przed zderzeniem

po zderzeniu

f

h

p

c

ν

=

θ

ϕ

e

p

mv

=

'

'

f

h

p

c

ν

=

elektron

foton’

foton

Zasada zachowania energii w postaci relatywistycznej

m

0

– masa spoczynkowa

elektronu

m – masa relatywistyczna

elektronu

Zasada zachowania pędu dla układu foton-elektron

składowe równoległe

składowe prostopadłe

Wzór Comptona

Comptonowska
długość fali elektronu

2

2

0

'

h

m c

h

mc

ν

ν

+

=

+

ν

ν

θ

ϕ

ν

θ

ϕ

=

+

=

−

'

cos

cos

'

0

sin

h

h

p

c

c

h

psin

c

'

(1 cos )

e

λ λ

θ

= + Λ −

12

2,42631 10

e

e

h

m

m c

−

Λ =

=

⋅

Ś

wiatło – korpuskuła czy fala?

Zjawisko

Teoria falowa

Teoria

korpuskularna

Odbicie

TAK

TAK

Załamanie

TAK

TAK

Interferencja

TAK

NIE

Dyfrakcja

TAK

NIE

Polaryzacja

TAK

NIE

Efekt fotoelektryczny

NIE

TAK

Efekt Comptona

NIE

TAK

Promieniowanie rentgenowskie

(X)

Promieniowanie rentgenowskie (X ray)
promieniowanie elektromagnetyczne o krótkiej długości
fali (10

-13

÷

10

-8

) m i energiach 100 eV do 100 keV.

Promieniowanie rentgenowskie o małej energii nazywa
się promieniowaniem miękkim, natomiast o dużej –
twardym.

Własności promieniowania rentgenowskiego

rozchodzi się prostoliniowo.
Wywołuje fluorescencję niektórych substancji
Wywołuje jonizację ośrodka, przez który przechodzi.
Zaczernia klisze fotograficzne.
Potrafi przenikać przez szkło, papier i metale.

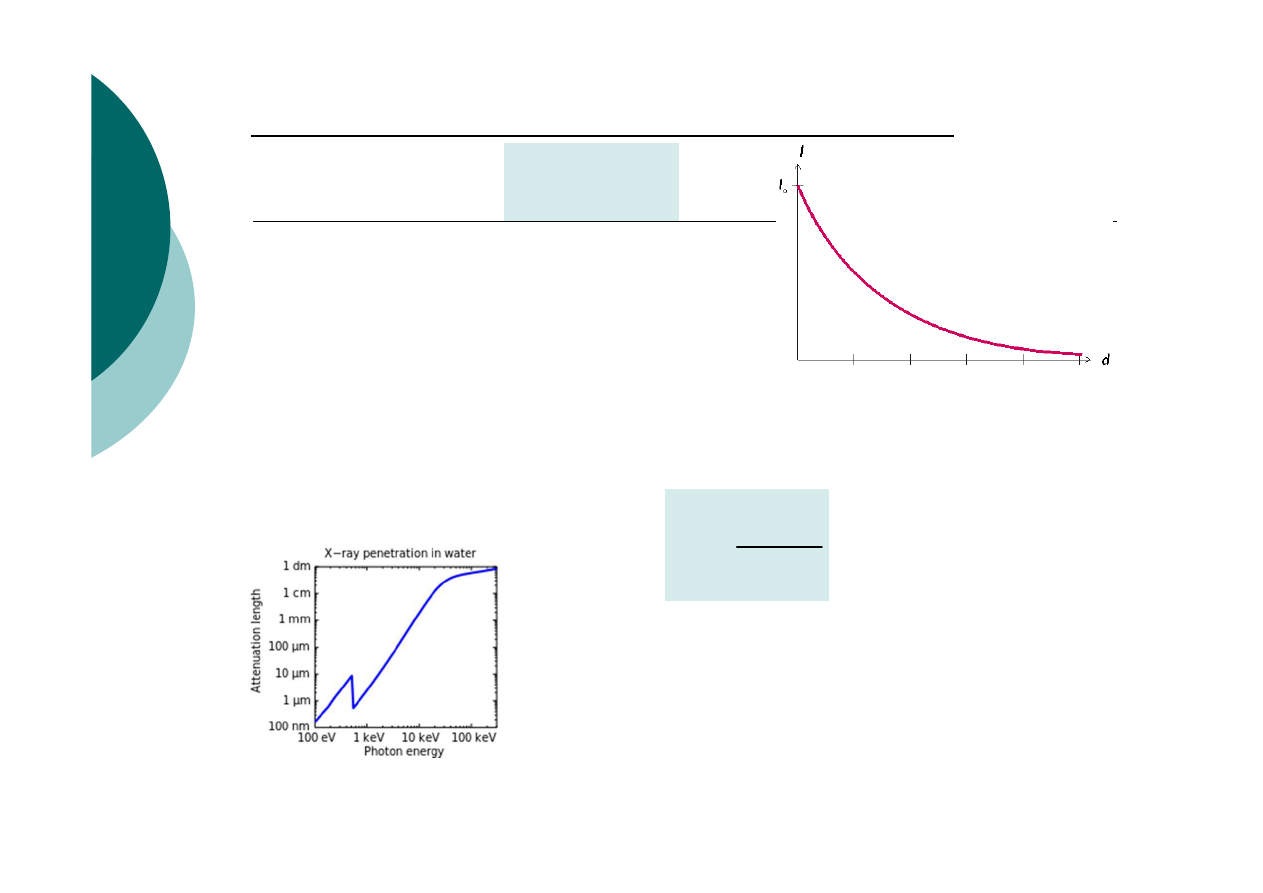
Pochłanianie promieniowania rentgenowskiego

I - natężenie promieniowania
µ – liniowy współczynnik absorpcji
d- grubość warstwy pochłaniającej

Liniowy współczynnik absorpcji zależy od liczby
porządkowej Z pierwiastka w układzie okresowym i od
energii promieni X

Przenikliwość promieniowania X

zależy od energii fotonów

0

d

I

I e

µ

−

=

3

3

(

)

Z

h

µ

ν

∼

h

ν

Zastosowania promieniowania

rentgenowskigo

Radiografia ;rentgenodiagnostyka
Badane ciało jest prześwietlane wiązką promieniowania
rentgenowskiego. Obraz prześwietlenia jest zapisywany
na filmie fotograficznym , lub za pomocą układu
scyntylatorów lub diod półprzewodnikowych.

Na zdjęciach rentgenowskich widać
wyraźnie ślady kości, ze względu
na zawartość nich wapnia Z=20;
tkanki miękkie mają wartość Z
o wiele mniejszą
(H, Z=1; C, Z=6, O, Z=8).

Pierwsze zdjęcie rentgenowskie

wykonane przez Röntgena.

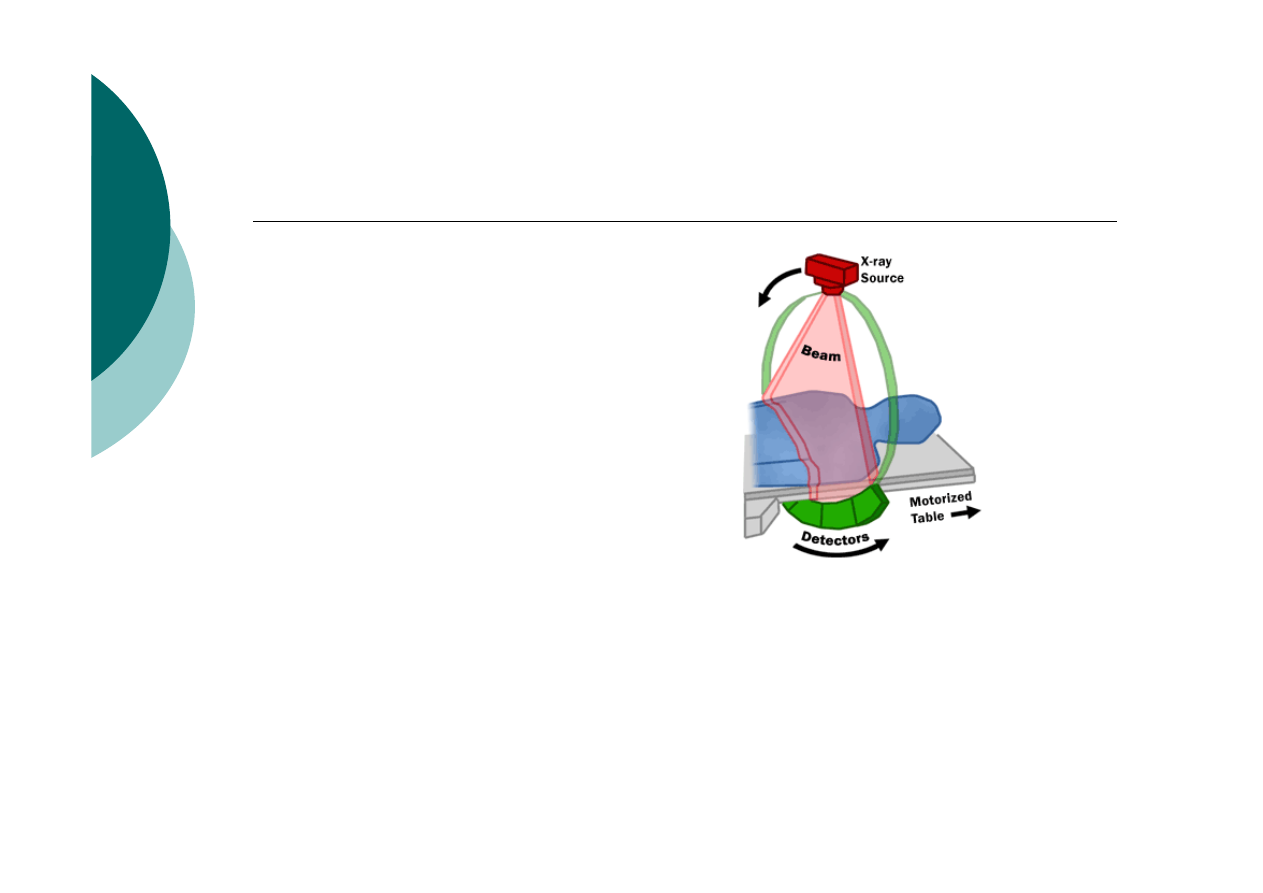
Rentgenowska tomografia komputerowa
Godfrey H. Hounsfield i Allan Cormack otrzymali
Nagrodę Nobla (1979) za wynalezienie i budowę
tomografu komputerowego.

Defektoskopia rentgenowska

Mechanizmy powstawania

promieniowania rentgenowskiego

Promieniowanie rentgenowskie hamowania.
Rozpędzony w lampie rentgenowski elektron uzyskuje
energię kinetyczną, a przy uderzeniu w anodę
gwałtownie hamuje. Część tej energii może zostać
wypromieniowana w postaci pojedynczego kwantu
promieniowania rentgenowskiego. Inna część energii
jest tracona w postaci ciepła wydzielonego w anodzie.
Promieniowanie hamowania ma widmo ciągłe, w
którym występują wszystkie długości fali aż do
λ

min

- krótkofalowa granica promieniowanie hamowania

U – napięcie przyspieszające

min

hc

eU

λ

=

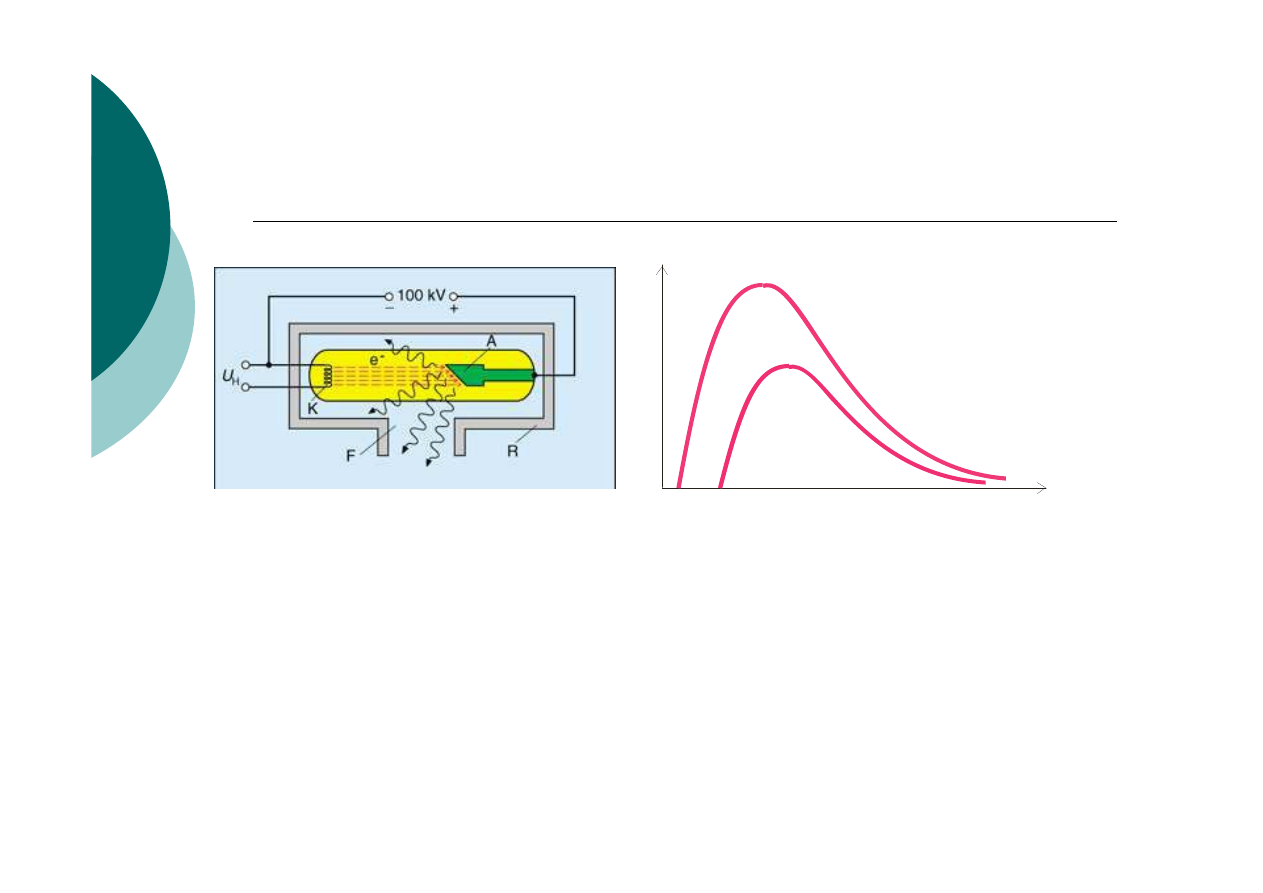
Widmo promieniowania
rentgenowskiego
hamowania dla różnych napięć
przyspieszających

min

λ

min

'

λ

λ

λ

( )

U

U

U’>U

Schemat aparatury
rentgenowskiej

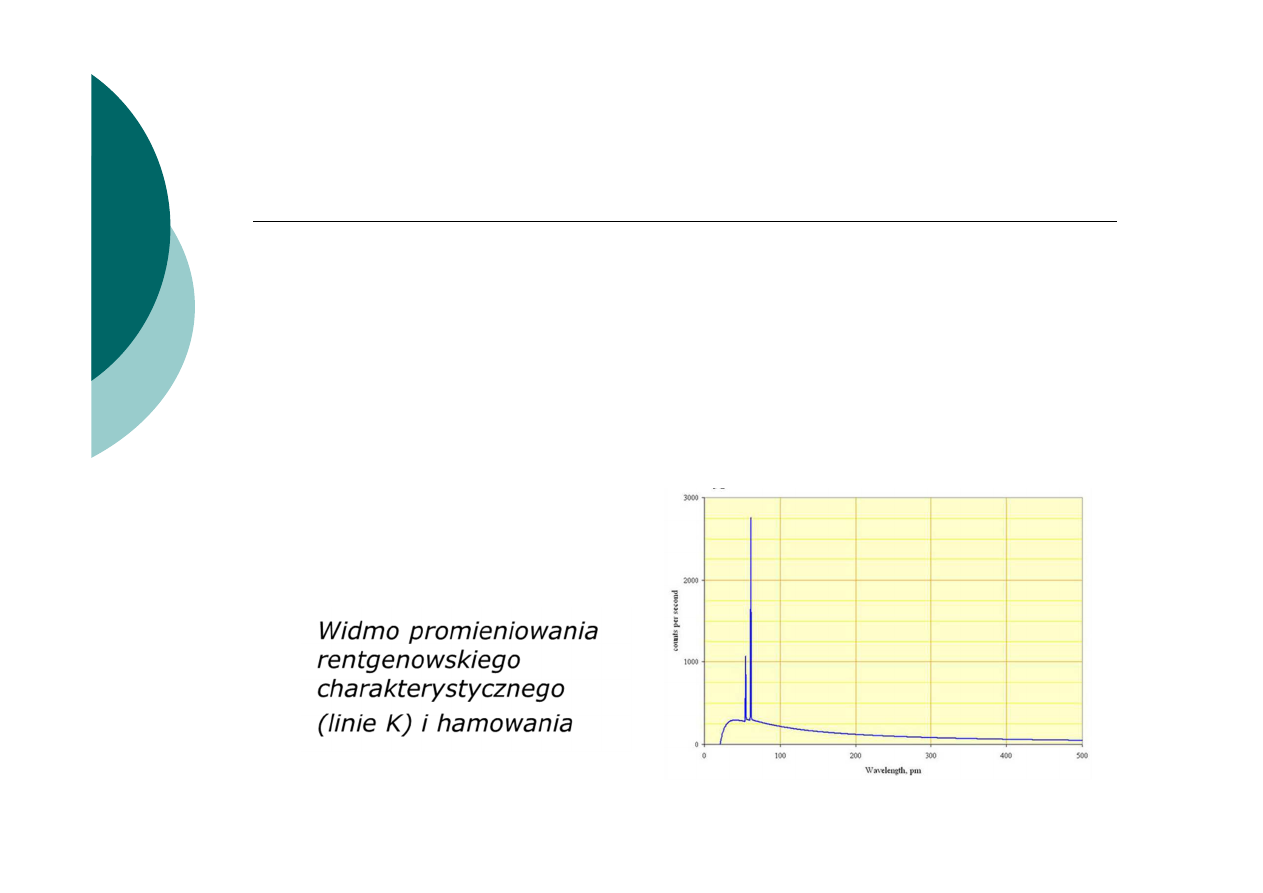
Promieniowanie rentgenowskie
charakterystyczne.

Elektrony o odpowiednio dużej energii przy zderzeniu z
atomami anody mogą wybić elektrony z powłok
znajdujących się blisko jądra – z powłoki K i L.
W ten sposób powstaje luka, którą może zapełnić
elektron z powłok zewnętrznych. Przejście elektronu z
wyższego poziomu energetycznego na niższy daje
emisję fotonu rentgenowskiego

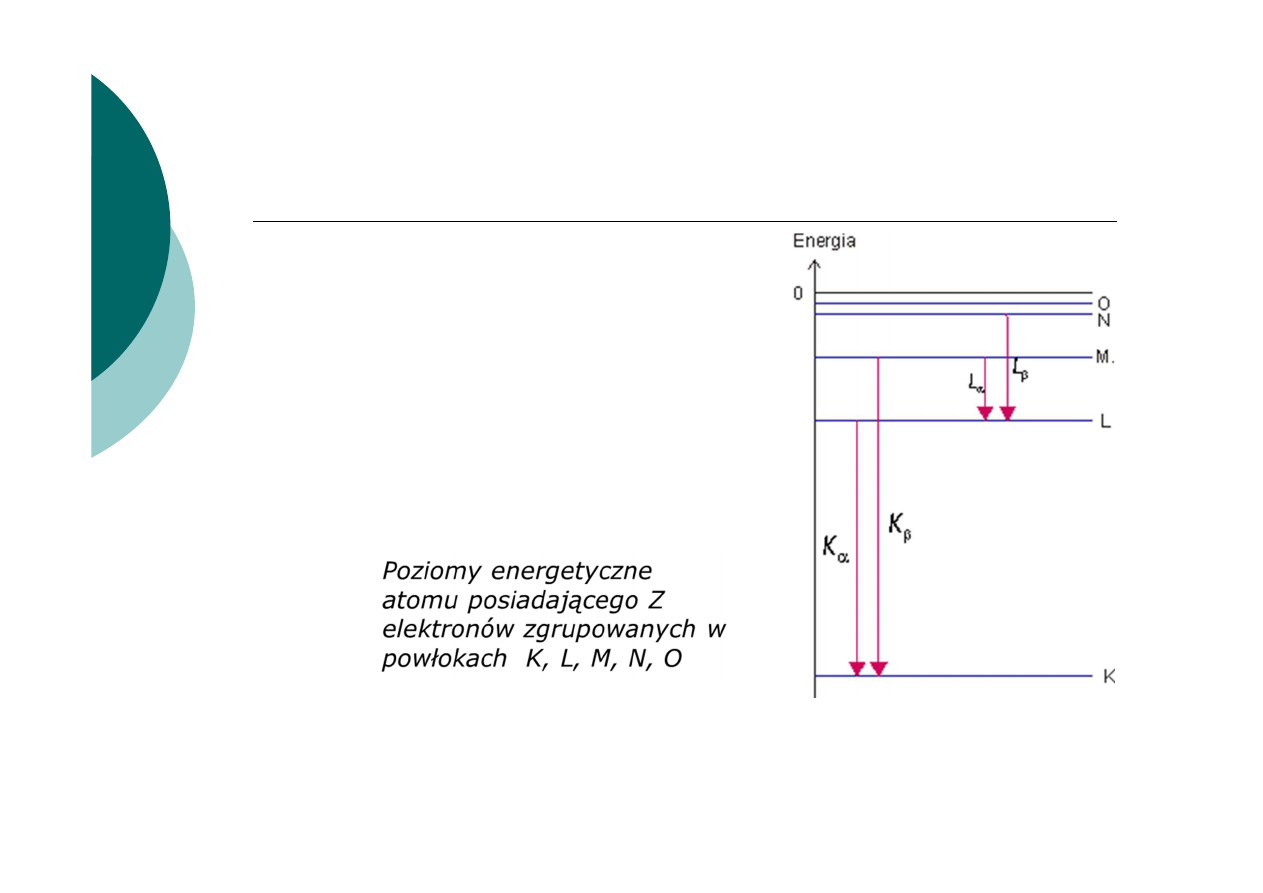
Obserwowane linie widma promieniowania
charakterystycznego grupują się w serie:

Seria K: K

α

przejście L→K

K

β

przejście M→K

Seria L: L

α

przejście M→L

L

β

przejście N→L

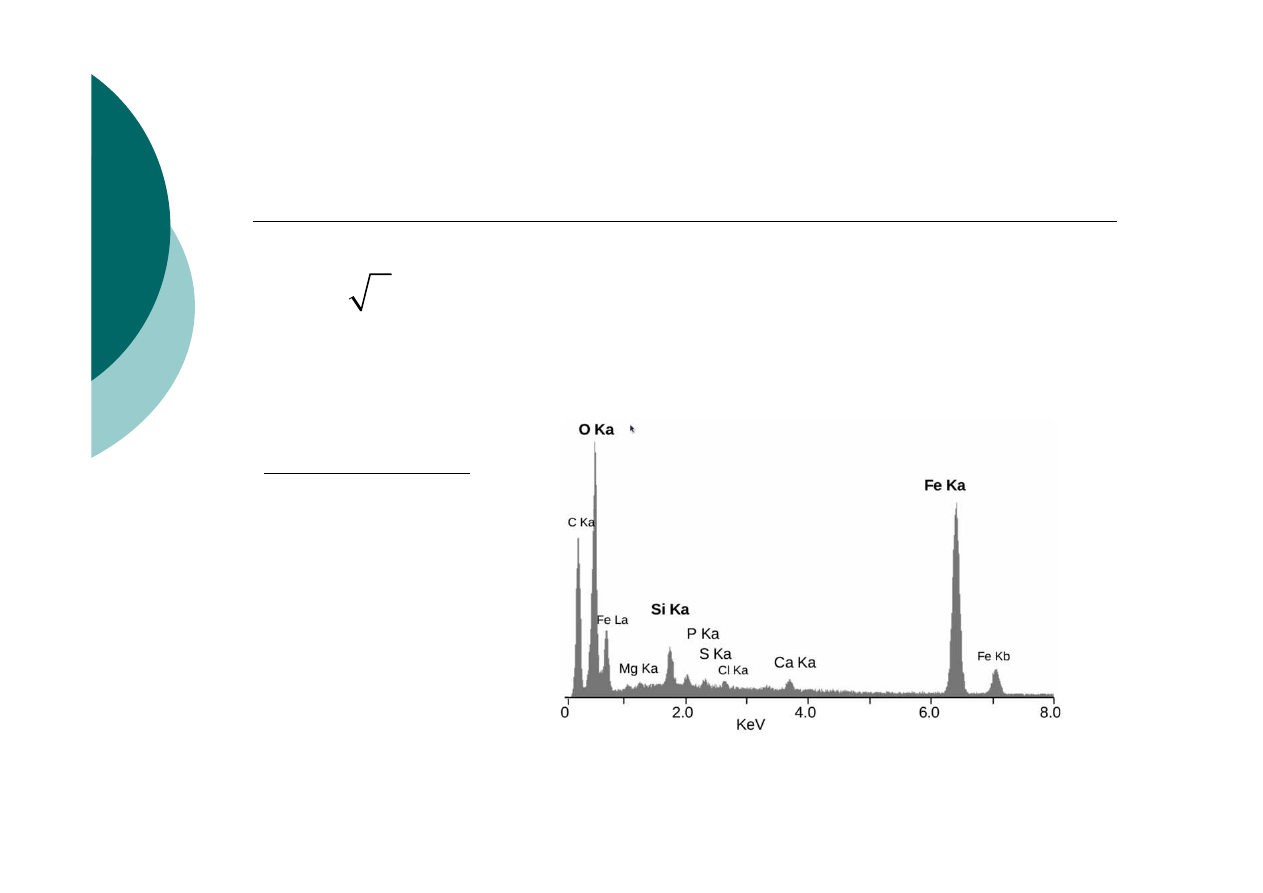
Prawo Moseleya.

Częstotliwość promieniowania charakterystycznego

A, σ – stałe dla danej serii
Z – liczba atomowa

pierwiastka

Zastosowanie
Badanie składu
Pierwiastkowego
substancji

(

)

A Z

ν

σ

=

−

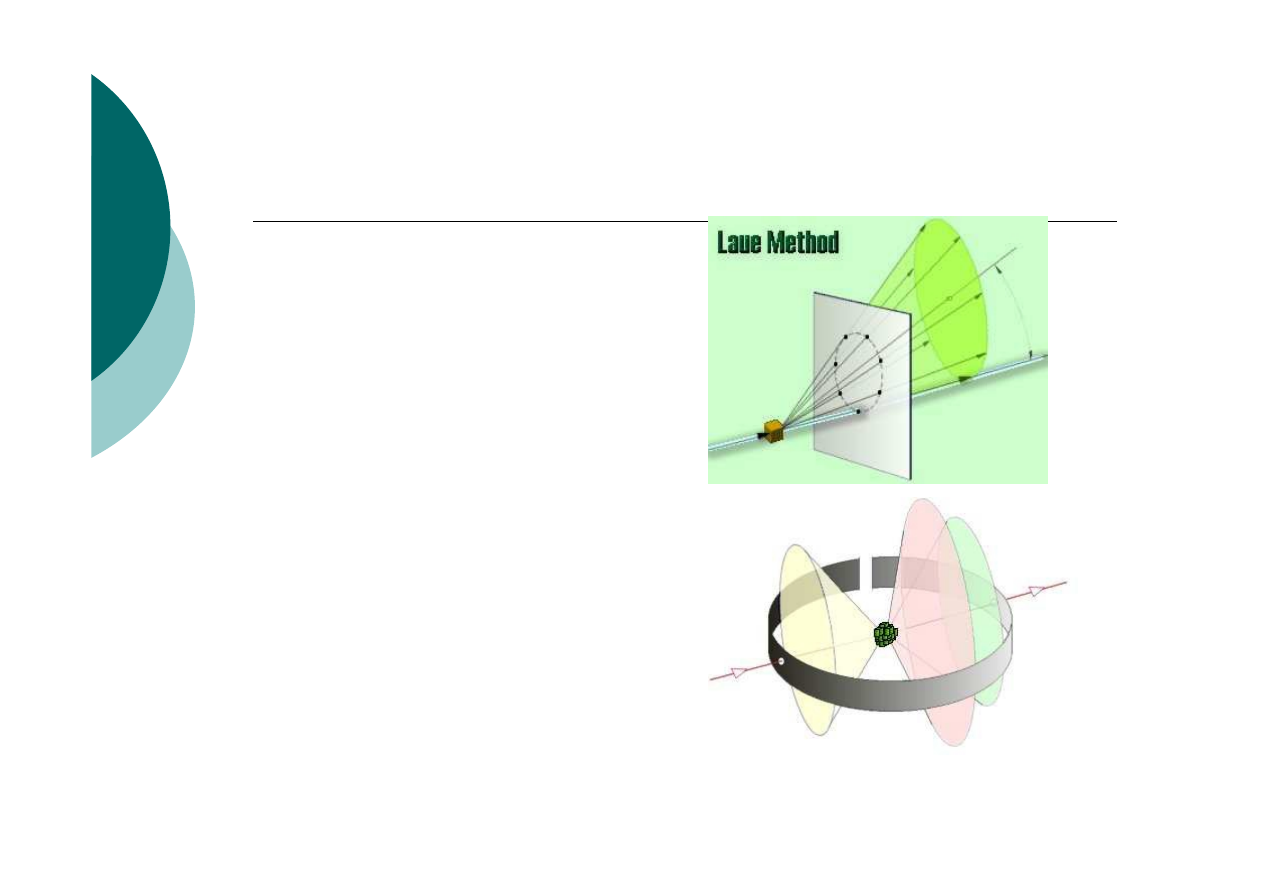
Dyfrakcja promieni rentgenowskich

Krystalografia

Metoda Lauego
(widmo ciągłe X)

Metoda proszkowa
Debyea –Scherrera
(

λ

= const)

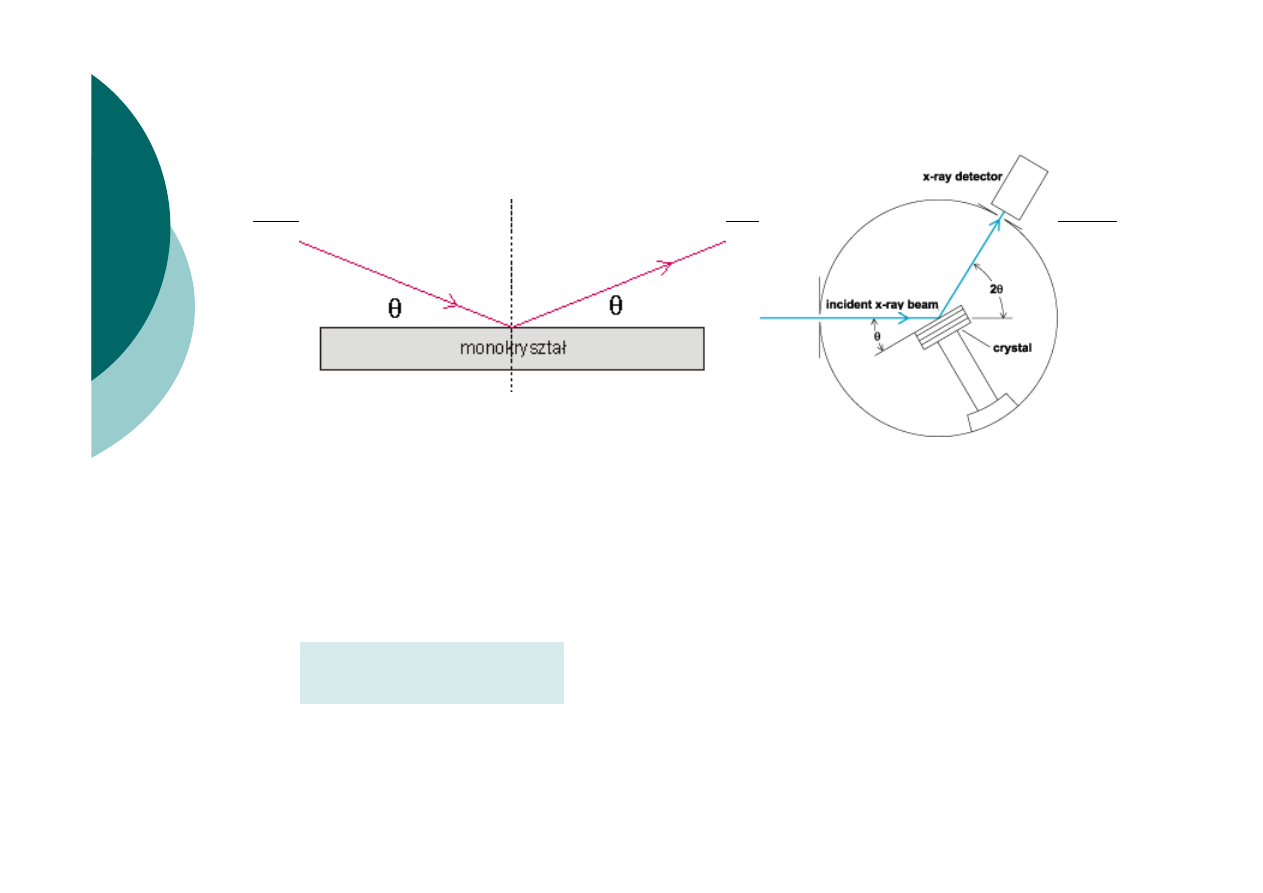
Metoda obracanego kryształu

Selektywne odbicie promieniowania rentgenowskiego
pod kątem odbłysku. (

λ

= const)

Wzór Bragga – Wulfa

m – rząd widma
θ– kąt odbłysku
d- stała sieci (odległość
między płaszczyznami sieci
krystalicznej)

2 sin

m

d

λ

θ

=

Fale materii

Dualizm korpuskularno-falowy

ś

wiatła

Foton – kwant światła
Światło – fala elektromagnetyczna jest skwantowana.
Energia fotonu

Pęd fotonu

- częstotliwość fali elektromagnetycznej

λ

- długość fali

h - stała Plancka

Światło oddziałuje z materią przekazując energię i pęd
w postaci fotonów.
W czasie „biegu” to fala prawdopodobieństwa
Prawdopodobieństwo jest proporcjonalne do kwadratu
amplitudy pola elektrycznego

E

h

ν

=

E

p

c

=

h

p

λ

=

ν

Fale materii

Louis de Broglie wysunął hipotezę, że każdej cząstce
posiadającej pęd można przypisać falę o długości

Pęd cząstki o masie spoczynkowej różnej od zera

Ruch można opisać jako ruch cząsteczki (korpuskuły)

albo przypisać jej długość fali i opisać jako ruch fali de
Broglie’a , fali materii.

h

p

λ

=

=

p

mv

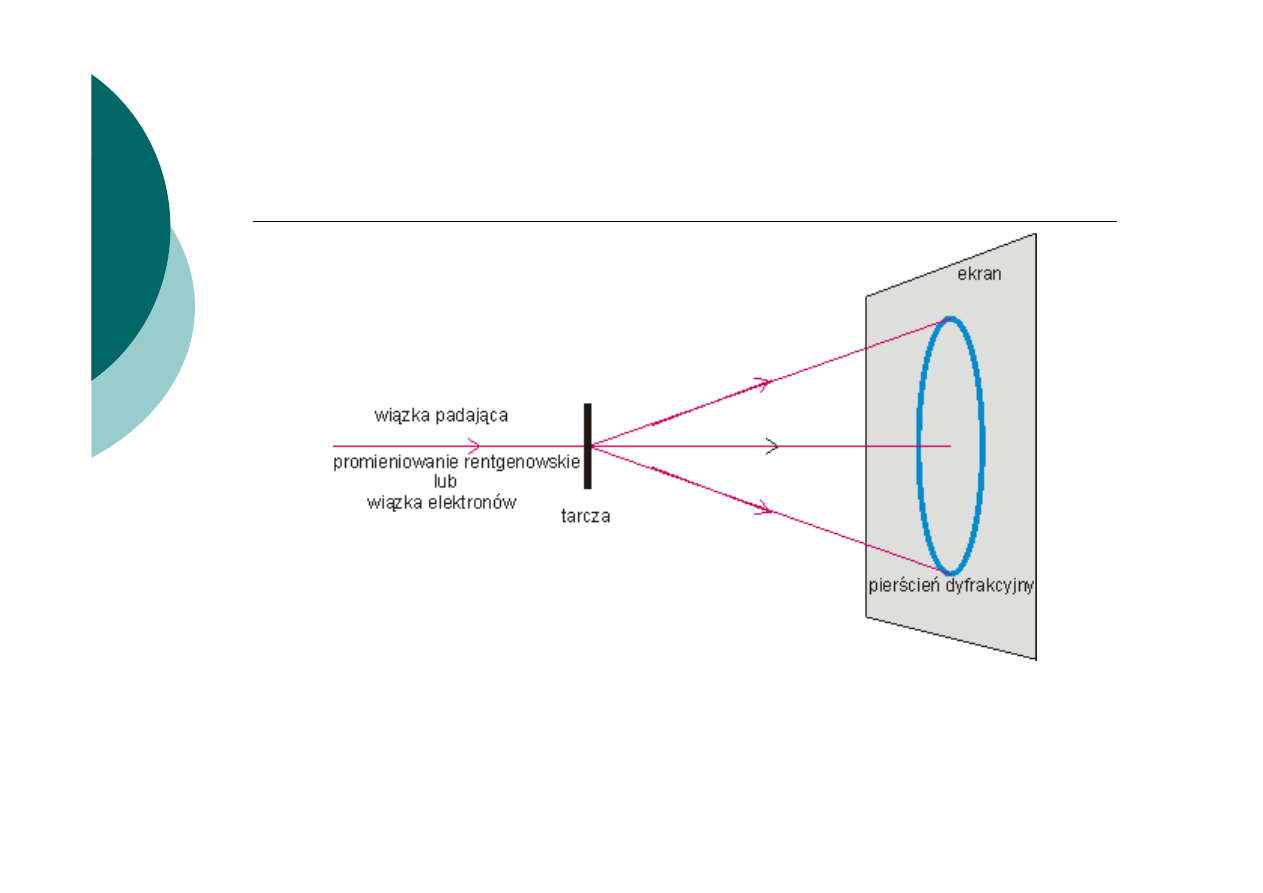
Doświadczalne potwierdzenie istnienia fal materii

Dyfrakcja promieni rentgenowskich i fal materii

Równanie Schrödingera

Funkcja falowa
Fala materii jest opisywana funkcja falową (zespoloną)

- część przestrzenna funkcji falowej
- czynnik zależny od czasu

Ruch jednowymiarowy(przypadek nieralatywistyczny)
Cząstka o masie m porusza się w kierunku x mając
energię potencjalną U(x).
Fala materii spełnia równanie Schrödingera:

( , , , )

( , , )

i t

x y z t

x y z e

ω

ψ

−

Ψ

=

( , , )

x y z

ψ

i t

e

ω

−

[

]

2

2

2

2

8

( )

0

d

m

E U x

dx

h

ψ

π

ψ

+

−

=

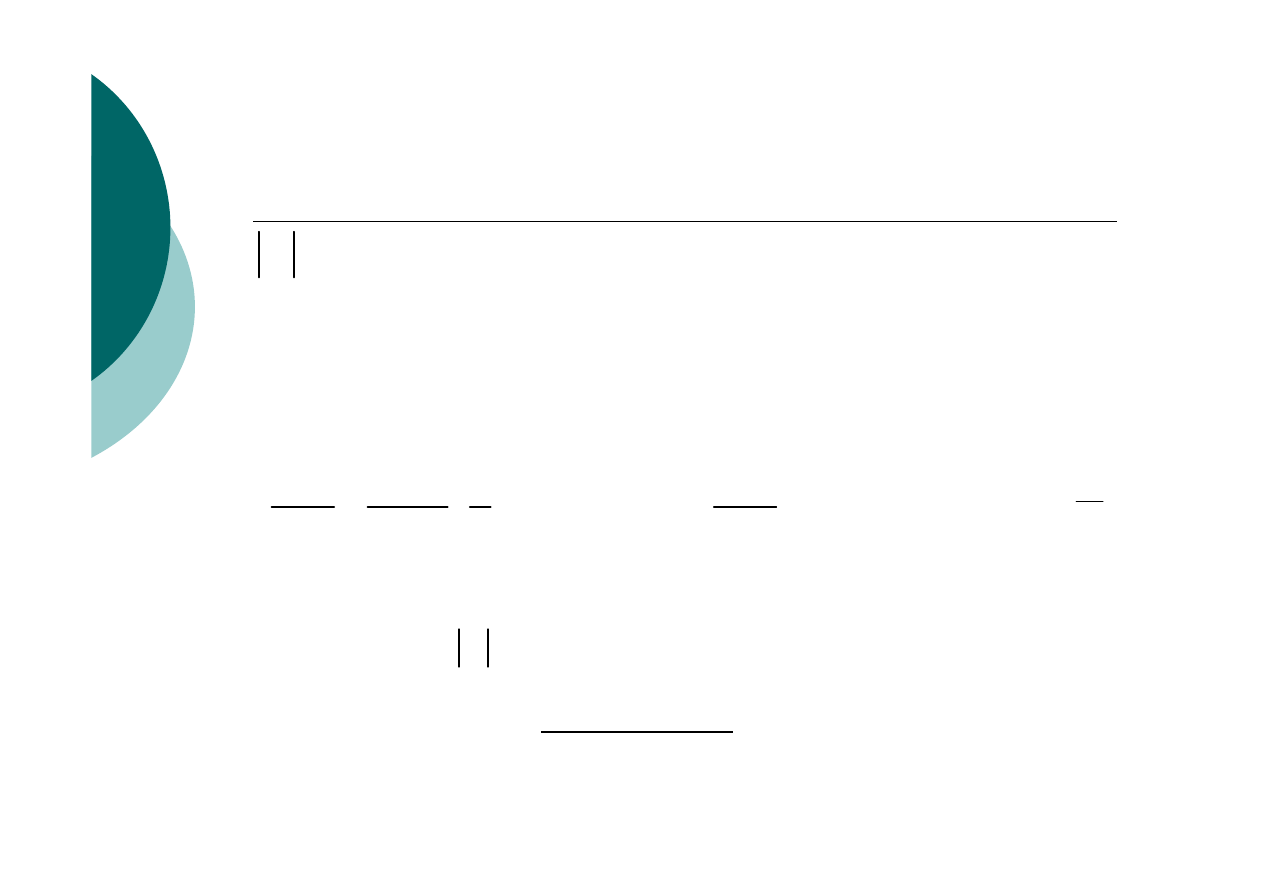
G

ę

sto

ść

prawdopodobie

ń

stwa

prawdopodobieństwo wykrycia cząstki w objętości
dV ( przypadające na jednostkę czasu)

Jeżeli U(x)=0, równanie Schrödingera dla cząstki
swobodnej ma postać:

Dla cząstki poruszającej się w kierunku +x

cząstka może być gdziekolwiek wzdłuż osi x

2

ψ

2

2

2

2

2

8

1

0

2

d

m

mv

dx

h

ψ

π

ψ





+

=









2

2

2

0

d

k

dx

ψ

ψ

+

=

2

p

k

h

π

=

0

( )

ikx

x

e

ψ

ψ

=

2

2

0

const

ψ

ψ

=

=

Zasada nieoznaczono

ś

ci

Heisenberga

Opis mikroświata w mechanice kwantowej jest opisem
falowym. Fali nie można zlokalizować tak, jak można to
uczynić w przypadku cząstki. Z tego opisu falowego
wynikają ograniczenia odnośnie możliwości
jednoczesnego pomiaru dwóch wielkości.
Nieokreśloność położenia cząstki ∆x i pędu ∆p jest
związana następującą zależnością:

Podobna zależność występuje między niepewnością
wyznaczenia energii ∆E i niepewnością wyznaczenia
czasu ∆t:

p

x

∆ ⋅∆ ≥

ℏ

2

h

π

=

ℏ

E

t

∆ ⋅∆ ≥

ℏ

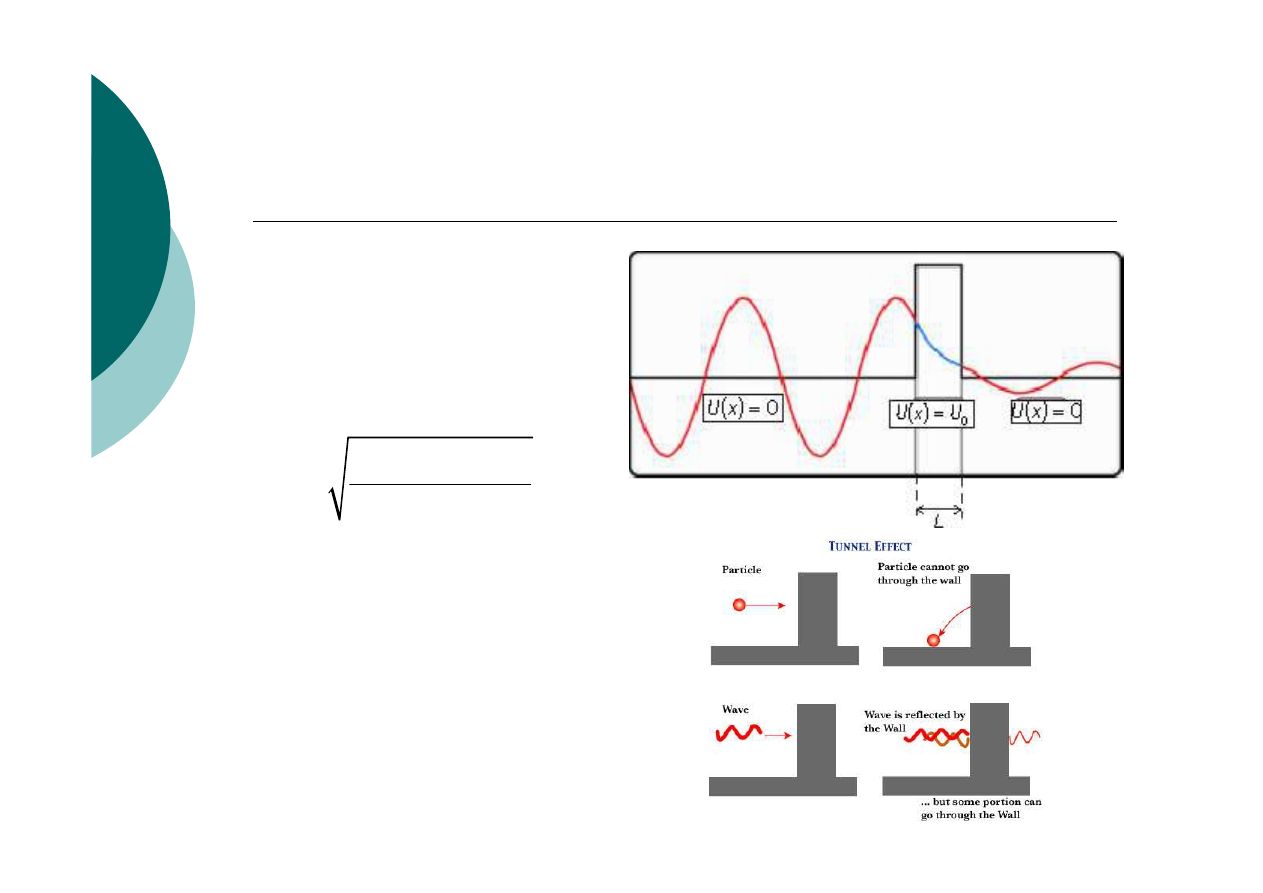
Zjawisko tunelowe

Energia cząstki jest mniejsza od bariery potencjału
o szerokości L
Współczynnik transmisji

Porównanie zjawiska tunelowego

w skali makroskopowej i

mikroskopowej

0

E

U

<

2kL

T

e

−

≈

2

0

2

8

(

)

m U

E

k

h

π

−

=

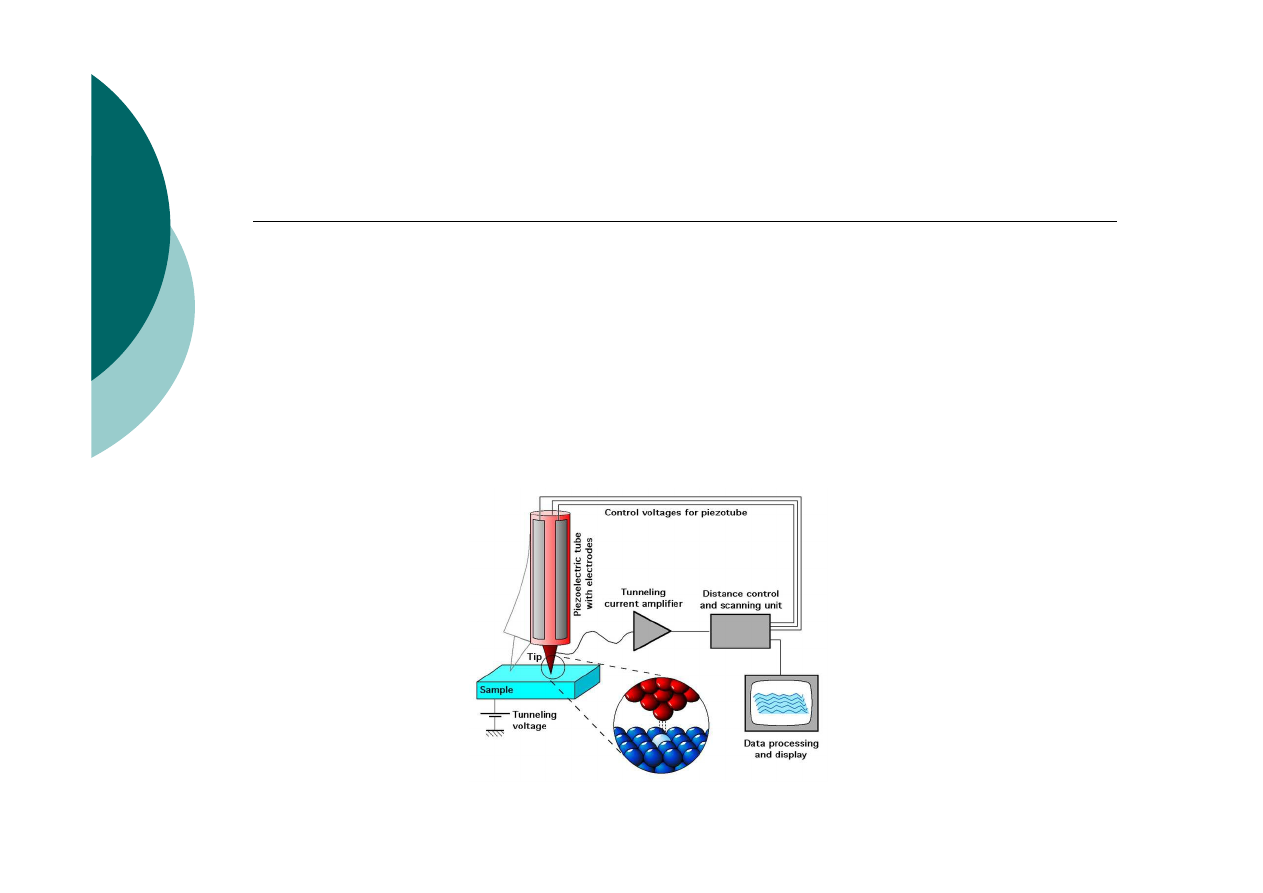
Zastosowanie zjawiska tunelowego

Rozpad promieniotwórczy
Zimna emisja elektronów
Złącze tunelowe (złącze Josephsona)
Dioda tunelowa (Esakiego)
Tranzystor polowy z efektem tunelowym
Skaningowy mikroskop tunelowy