Dualizm

korpuskularno-

falowy

Wykład 5 / semestr II

1

2

Prof. J. Zieliński

 

Terminy zaliczeń poprawkowych w semestrze letnim
2010/11
o 28 marzec

o 18 kwiecień

o 16 maj

o 13 czerwiec

Przypominam, że

Przypominam, że

 na wszystkie kolejne terminy poprawkowe
obowiązują karty zie-lone.

 Do zaliczenia można podejść po zaliczeniu ćwiczeń
rachunko-wych

 zaliczona w terminie zerowym teoria a nie wpisana

zaliczona w terminie zerowym teoria a nie wpisana

do indeksu została skreślona

do indeksu została skreślona

Zaliczenia zaczynają się o
godz. 15
sala 2 bud 5

W tym semestrze

Zaliczenie przedmiotu jest w formie egzaminu

> Aby móc przystąpić do egzaminu trzeba mieć
zaliczone ćwicze-nia i laboratoria. Pozytywne oceny
muszą być wpisane do karty o-cen i do indeksu.

Egzamin składa się z dwóch części:

- Pisemnej student pisze odpowiedź na 3 pytania z
zestawu 4-ech

- Ustnej odpowiedzi uzupełniające na pytania z
zestawu pisemne-go + inne pytania.

16.8. Falowa natura materii

Zjawiska fizyczne i opisujące je prawa przyjęto

dzielić na klasyczne i współczesne.

Fizyka współczesna

opiera się o falową naturę materii i zawiera nową
fundamentalną stałą odkrytą przez Plancka w 1900
r

. Przekonanie wśród fizyków o falowej naturze materii

ugruntowało się w latach dwudziestych XX w.

Zgodnie z takim określeniem fizyki współczesnej,

to wszystko o czym dotychczas mówiliśmy jest fizyką
klasyczną. W tej części poka-żemy, że wszystkie cząstki
elementarne

charakteryzują

się

właściwo-ściami

falowymi, które wpływają na ich zachowanie szczególnie
w niedużych odległościach. Nie wyjaśniając uprzednio
falowych właści-wości materii, niemożliwe byłoby
zrozumienie budowy atomów i mo-lekuł, właściwości
cząstek elementarnych oraz takich działów fizyki jak:
fizyka ciała stałego, fizyka jądrowa, czy też astrofizyka.

Wynikające z falowej natury materii podstawowe

założenia i formalizm matematyczny stanowią przedmiot
badań mechaniki kwantowej.

4

Zdumiewający przewrót w naszych poglądach na

czas i przestrzeń spowodował Einstein. Jednakże
zobaczymy, że falowa natura materii, dualizm
korpuskularno-falowy i ich konsekwencje, okażą się
bardziej

zdumiewające

i

przeczące

zdrowemu

rozsądkowi niż einsteinowski postulat o stałości
prędkości światła we wszystkich inercjalnych układach
odniesienia.

Falowa

natura

materii

jakościowo

przejawia się w tym, że każdą cząstkę cechują
właściwości

falowe i

odwrotnie, dowolna

fala

charakteryzuje się właściwościami cząstek. Jako
pierwszy przykład demonstrujący tę właściwość fal,
rozważymy promieniowanie termiczne.

5

16. 8. 1. Promieniowanie termiczne

 

Jednym z podstawowych zjawisk fizycznych,

którego nie można wyjaśnić na gruncie fizyki klasycznej,
jest

promieniowanie

termiczne

ciał

(zwane

też

promieniowaniem

cieplnym

lub

temperaturowym).

Usunięcie

sprzeczności

między

wynikami

doświadczalnymi a teorią dało początek teorii kwantów.

Promieniowaniem

termicznym

nazywamy

promieniowanie wysyłane przez ciała ogrzane do pewnej
temperatury. Emitowane fale mają długości fal z
szerokiego zakresu widma, ale zwykle główna część
przypada na podczerwień. Promieniowanie termiczne jest
wynikiem

przyśpieszeń

jakich

doznają

ładunki

elektryczne atomów i cząstek. Zatem promieniowanie to
powstaje kosztem ich ruchu cieplnego.

6

Promieniowanie

termiczne

charakteryzujemy

wprowadzając pojęcie zdolności emisyjnej ciała
e(ν,T) zdefiniowanej tak, że e(ν,T)d ν jest energią
promieniowania wysyłanego w jednostce czasu z
jednostki powierzchni o temperaturze T, w postaci
fal elektromagnetycznych o częstościach zawartych
w przedziale od ν do ν + d ν.

Widmo promieniowania termicznego wysyłanego przez
ciało zależy w pewnym stopniu od składu tego ciała.
Wprowadzono pojęcie ciała emitującego promieniowanie
o widmie mającym charakter uniwersalny.

Ciało takie

nazywamy ciałem doskonale czarnym, ponieważ
całkowicie absorbuje promieniowanie termiczne
nań padające

. Przykładem ciała, które ma właściwości

zbliżone do ciała doskonale czarnego, jest sadza. Bardzo
dobrym modelem ciała doskonale czarnego jest
nieprzezroczyste ciało zawierające wnękę z bardzo
małym otworem wejściowym (rys. 10.1). Ponadto
zakładamy, że ścianka wnęki w dużym stopniu absorbuje
padające

promieniowanie.

Powierzchnia

otworu

zachowuje się tak, jak powierzchnia ciała doskonale
czarnego.

7

P r o m ie ń

ś w ie tl n y

P o w ie r z c h n ia

o d u ż e j z d o l n o ś c i

a b s o r p c y jn e j

Wprowadzimy jeszcze pojęcie
zdolności absorpcyjnej, a , i
zdolności

odbicia,

r,

powierzchni charakteryzujące
ciała promieniujące.

Wielkość a wskazującą jaki
ułamek energii padającej na
powierzchnię

zostanie

pochłonięty,

nazywa

się

zdolnością

absorpcyjną

powierzchni,

a

liczbę

r

wskazującą

jaki

ułamek

energii padającej zostanie
odbity,

nazywa

się

zdolnością odbicia

.

Ogólnie biorąc dla dowolnego ciała a i r zależą od
częstości padającego promieniowania i temperatury
powierzchni, tak że a = a(



,T) i r = r(



,T). Między

wielkościami a i r zachodzi związek

   

1





T

,

r

T

,

a





(10.1
)

8

   

1





T

,

r

T

,

a





Dla ciała doskonale czarnego, niezależnie od
częstotliwości promieniowania i temperatury
powierzchni a = 1 i r = 0.

Podstawowym

prawem

odnoszącym

się

do

promieniowania

termicznego

ciał

jest

prawo

Kirchhoffa, które mówi, że

stosunek zdolności

emisyjnej do zdolności absorpcyjnej jest dla
wszystkich powierzchni jednakowy

(10.2)

 

   

T

,

T

,

a

T

,

e











Funkcja ε(ν,T) jest pewną funkcją uniwersalną. Jej sens
fizyczny jest natychmiast jasny, gdy przyjąć a(ν,T) = 1.
Wówczas ε (ν,T) = e(ν,T), tzn., że funkcja ε (ν,T) jest
zdolnością emisyjną ciała doskonale czarnego.

9

Aby uzasadnić prawo Kirchhoffa wyobraźmy sobie

zbiornik (ciało z wnęką) pozostający w temperaturze T.
Jeżeli wyciąć w tym zbiorniku otwór o jednostkowej
powierzchni, to w ciągu jednostki czasu otworem
zbiornika wypromieniuje ilość energii równa ε(ν,T)dν.
Jeżeli otwór nie jest wycięty, to pada na jednostkową
powierzchnię w czasie jednostki czasu taka sama ilość
energii. Część tej energii zostanie zaabsorbowana a(ν,T)
ε(ν,T)dν. W stanie równowagi taką samą ilość energii
ścianka musi wypromieniować. Zatem e(ν,T) = a(ν,T)
ε(ν,T), co jest właśnie prawem Kirchhoffa.

Z powyższego widać jednoznacznie, że zdolność

emisyjną dowolnej powierzchni uzyskujemy mnożąc jej
zdolność absorpcyjną a(ν,T) przez zdolność emisyjną
ciała doskonale czarnego ε(ν,T). Ponieważ zawsze , więc
i e(ν,T) ε(ν,T), tzn. zdolność emisyjna każdej
powierzchni nie jest większa od zdolności emisyjnej
ciała doskonale czarnego.  



10



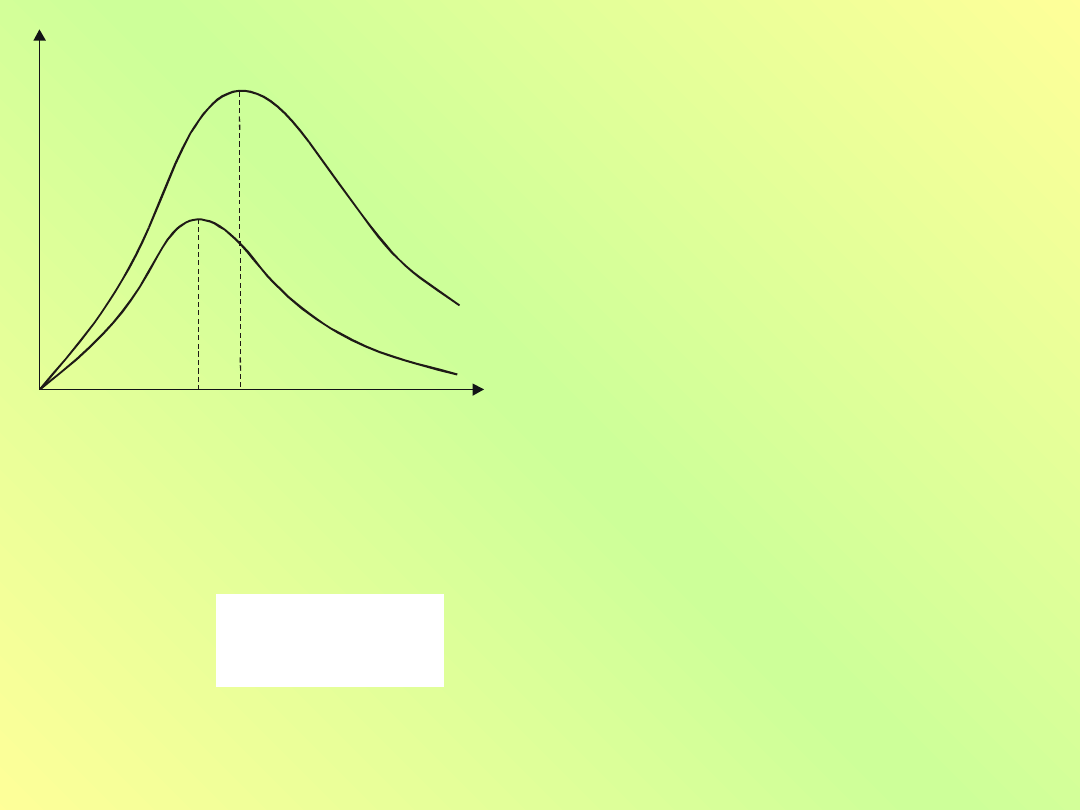
m a x 1



m a x 2



T

1

T > T

2

1



Rys. 10.2. Zależność zdolności
emisyjnej

ciała

doskonale

czarnego od częstotliwości dla
dwóch temperatur T

1

i T

2

.

Pomiary zdolności emisyjnej
ciała doskonale czarnego
doprowadziły do wyników
zaprezentowanych na rys.
10.2, gdzie przedstawiono
ε(ν,T)

jako

funkcję

częstotliwości

dla

dwóch

różnych temperatur T

1

i T

2

(

T

1

< T

2

).

Całkowita energia E

wypromieniowana

przez

jednostkową powierzchnię w
czasie jednostki czasu jest
równa

polu

powierzchni

ograniczonej

każdą

z

krzywych. Energia ta rośnie
z temperaturą według prawa

4

T

E





Wzór powyższy nazywa się prawem Stefana-Boltzmanna, gdyż
był po raz pierwszy wyznaczony przez Stefana, a teoretycznie
wyprowadzony przez Boltzmanna

11

4

T

E





Stała σ jest stałą Stefana-Boltzmanna a
jej wartość wynosi 5,6710

–8

Wm

–2

K

–4

.

Funkcja ε(ν,T) ma maksimum, które zależy od
temperatury. Im wyższa temperatura, tym maksimum
przypada dla wyższej częstotliwości. Między ν

max

a T

zachodzi prosta zależność

(10.4)

Prawo to nazywa się prawem Wiena.

T

const

max







12

Pod koniec XIX w. przeprowadzono bardzo

staranne pomiary promieniowania termicznego ciała
doskonale czarnego. Okazało się jednak, że próby
wyprowadzenia prawa opisującego to widmo oparte na
zasadach fizyki klasycznej, prowadzą do absurdalnych
wyników. Np. Rayleigh i Jeans stosując prawa
klasycznej

elektrodynamiki

dla

promieniowania

zrównoważonego (w którym promieniowanie emitowane
przez

drgające

elektrony

atomowe

stanowiące

oscylatory, jest pochłaniane przez inne atomy) otrzymali
wzór

 

kT

c

T

,

2

2

2









Zauważmy, że z tego wzoru wynika, iż gęstość energii
jest proporcjonalna do

i przy

staje się nieskończona.

Jest to oczywiście sprzeczne z eksperymentem. Jedynie
w zakresie niskich częstotliwości zgodność jest dobra.

2









13

Próbując usunąć rozbieżności między teorią a
doświadczeniem, M. Planck w 1900 r. wysunął hipotezę,

że elektryczny oscylator harmoniczny stanowiący
model elementarnego źródła promienio-wania, w
procesie emisji promieniowania może tracić
energię tylko porcjami, czyli kwantami ΔE, o
wartości proporcjonalnej do częstości ν jego drgań
własnych

. Czyli

(10.6)

gdzie współczynnik proporcjonalności h nosi nazwę
stałej Plancka i wynosi 6,62610

–34

Js.

Wymiarem h jest

działanie = (energia)(czas) = (długość)(pęd) =
(moment pędu).

W związku z tym stałą Plancka nazywa się też
elementarnym kwantem działania.





h

E 

14

Uogólniając swoje rozważania Planck zapostulował, że
energia oscylatora może przyjmować wartości

,

n = 0, 1, 2...

(10.7)

gdzie n jest liczbą kwantową.

Jeżeli teraz przyjąć, że rozkład oscylatorów po

możliwych dyskretnych stanach energii jest określony
rozkładem

Boltzmanna

(patrz

pkt.

15.4)

to

prawdopodobieństwo znajdowania się oscylatorów w
stanie o energii nh



w temperaturze T jest równe ,

gdzie c jest stałym współczynnikiem określonym z
warunku unormowania

Wówczas średnia

energia oscylatora wynosi



nh

E

n







kT

/

nh

exp

c

p

n







1





n

n

p







































0

0

0

n

n

n

n

kT

/

nh

exp

kT

/

nh

exp

nh

nh

p

E









15







































0

0

0

n

n

n

n

kT

/

nh

exp

kT

/

nh

exp

nh

nh

p

E









(10.8)

Średnia energia
oscylatora

Oznaczając

przez x i rozpisując wzór

(10.8) otrzymamy





kT

/

h

exp









...

x

x

x

...

x

x

x

h

E





















3

2

2

1

3

2

1



Zauważmy, że





2

2

1

1

3

2

1

x

...

x

x











natomiast

x

...

x

x

x













1

1

1

3

2

(x <

1)

zatem

16













1

1

1

1

1

2

















kT

/

h

exp

h

x

x

kT

/

h

exp

h

E









Uwzględniając, że w stanie równowagi

termicznej wydatek energii promieniowania
oscylatorów jest całkowicie kompensowany przez
pochłanianie padającego na nie promieniowania,
Planck pokazał, że

 







E

c

T

,

2

2

2







Wobec tego









1

1

2

2

3





kT

/

h

exp

c

h

T

,











(10.9
)

17









1

1

2

2

3





kT

/

h

exp

c

h

T

,











Wzór ten jest słynnym wzorem Plancka na

zdolność emi-syjną ciała doskonale czarnego. Wzór
ten określa rozkład widmowy promieniowania
ciała, który jest w bardzo dobrej zgodności z do-
świadczeniem.

Znając możemy wyliczyć całkowitą energię

emitowaną

w

jednostce

czasu

z

jednostkowej

powierzchni

ciała

doskonale

czarnego

poprzez

scałkowanie wyrażenia .

Otrzymujemy w ten sposób całkowitą zdolność emisyjną
E ciała doskonale czarnego

 

T

,





 

T

,



























0

3

2

0

1

2

kT

/

h

exp

d

c

h

d

T

,

E















18

 



















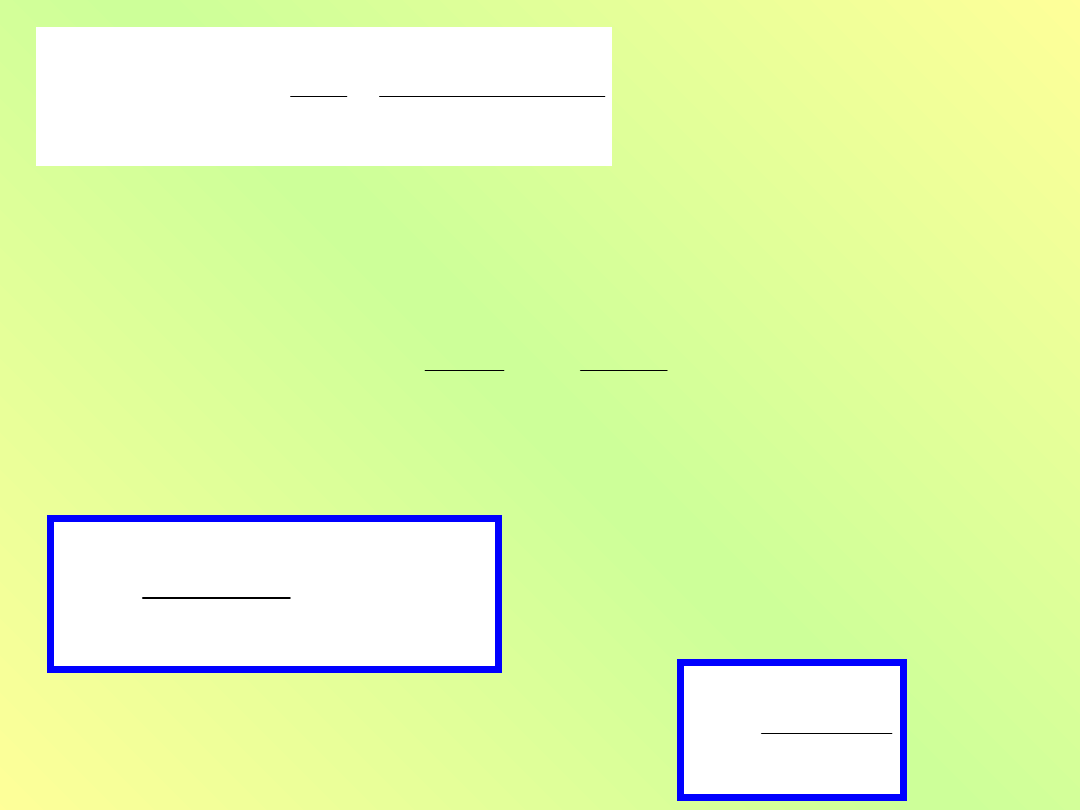
0

3

2

0

1

2

kT

/

h

exp

d

c

h

d

T

,

E















Wprowadzając pomocniczą zmienną

kT

/

h

x













0

3

4

3

2

4

1

2

x

e

dx

x

T

h

c

k

E



otrzyma
my

Występująca tu całka wynosi 



/15. Ostatecznie

więc mamy

4

4

3

2

4

5

15

2

T

T

h

c

k

E









Uzyskaliśmy
teoretycznie wzór
Stefana-Botzmanna,
przy czym stała Stefana-
Botzmanna jest równa

3

2

4

5

15

2

h

c

k







19

Interesujące jest jeszcze zachowanie się funkcji
dla małych częstotliwości. Występującą w mianowniku
funkcję wykładniczą można rozwinąć w szereg,
zostawiając dwa pierwsze wyrazy. Dostajemy wówczas

 

T

,









kT

/

h

kT

/

h

kT

/

h

exp

















1

1

1

Wzór (10.9) dla niskich częstotliwości promieniowania
przybiera więc postać

 

2

2

2









kT

c

T

, 

Jest

to

właśnie

wzór

Reyleigha-

Jeansa.

20

Oznaczając podobnie jak poprzednio

i narzucając warunek istnienia maksimum (d



/dx = 0),

mamy

Pierwiastek tego równania wynosi około 2,822, stąd
wynika

s

–1

K

–1

T.

kT

/

h

x





x

e

x







3

3

10

10

877

5

822

2









,

T

h

k

,

T

h

k

x

max

max



Otrzymaliśmy zatem prawo przesunięć Wiena.

Również to prawo uzyskane z prawa Plancka jest w
bardzo dobrej zgodności z doświadczeniem. Widzimy
więc, że postulat Plancka o tym, że energia nie może
być wypromieniowana w sposób ciągły, doprowadził do
teoretycznego

wyjaśnienia

promieniowania

ciała

doskonale czarnego.

Porcje energii promienistej emitowanej przez

ciało wynoszą hν. Porcje te zostały nazwane
kwantami lub fotonami. Hipoteza Plancka dała
początek fizyce kwantowej, a stała h występuje
obe-cnie we wielu równaniach fizyki atomowej,
jądrowej i ciała stałego.

21

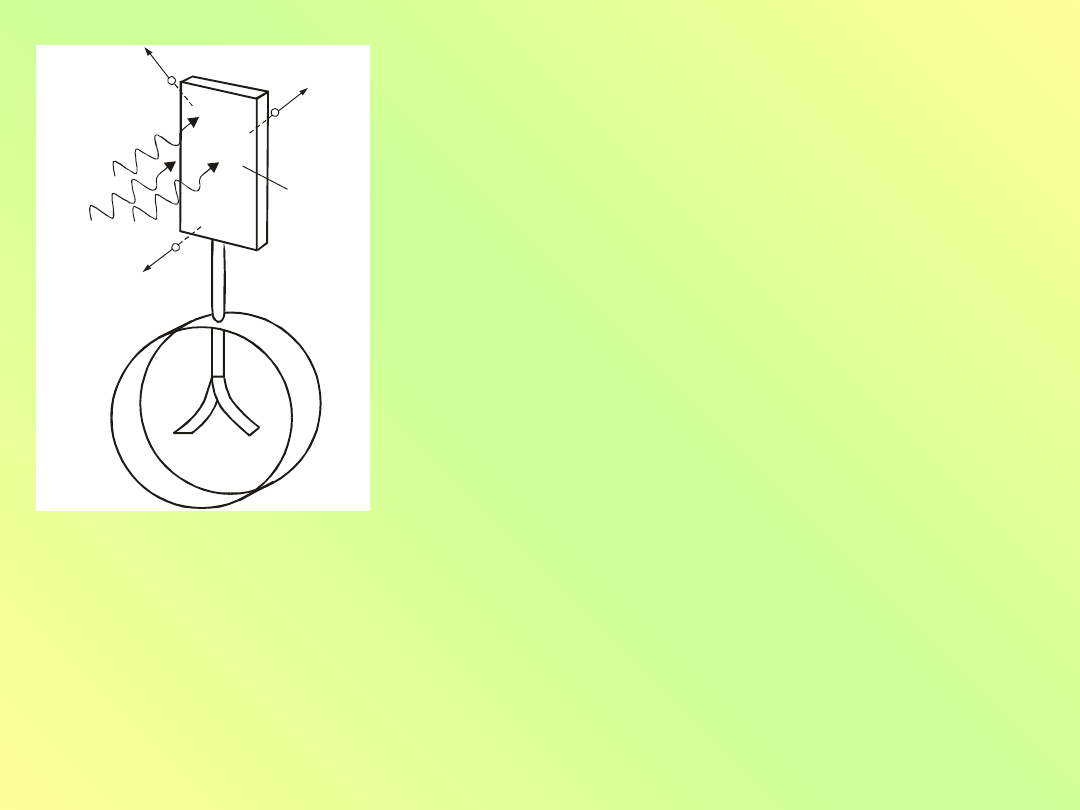
16.9. Fotoefekt

 

W końcu XIX w. odkryto elektron. Wkrótce potem

zauważono,

że

elektrony

uciekają

z

niektórych

powierzchni metalicznych, kiedy na powierzchnię pada
światło

(rys.

10.3).

Od

czasu

eksperymentów

dyfrakcyjnych przeprowadzonych przez Younga na dwóch
szczelinach nie było wątpliwości, że światło jest falą. Taki
pogląd pozwalał wyjaśnić fotoefekt. Amplitudę drgań
swobodnego elektronu w zmiennym polu elektrycznym

zgodnie z wyrażeniem (9.15) zapiszemy w postaci

.

Dlatego można było oczekiwać, że elektron znajdujący się
w pobliżu powierzchni opuści metal gdy amplituda A
przekroczy pewną krytyczną wartość.

t

cos

E

E

o





2



m

/

eE

A

o



22

P ły tk a

m e ta lo w a

Ś w ia tło

e

_

e

_

e

_

+

+

+

+

+

+

Rys. 10.3. Neutralny
elektroskop połączony z
płytką metalową. Przy
oświetleniu płytki przez
światło wybijane są
fotoelektrony i listki
elektroskopu ładowane
są dodatnio

.

Z falowej teorii światła
wynikają następujące wnioski:
elektron nie opuści metalu dopóki
nie przekroczy określonej
wartości krytycznej, energia
emitowanych elektronów wzrasta
proporcjonalnie do , jeżeli
wielkość

(a także natężenie) zachować stałą
a częstotliwość światła zwiększać,
to liczba emitowanych elektronów
powinna zmniejszyć się.

o

E

o

E

2

o

E

23

Jednakże wyniki eksperymentalne obaliły powyższe
przewidywania

:

  progowego natężenia nie zaobserwowano, liczba

uciekających

elektronów

okazała

się

ściśle

proporcjonalna do E

0

2

przy dowolnie małej intensywności

padającego promieniowania,

       energia elektronów okazała się niezależna od

wielkości E

0

,

       zauważono zależność energii elektronów od

częstotliwości; okazało się, że istnieje progowa
częstotliwość ν

0

, powyżej której energia emitowanych

elektronów rośnie liniowo ze wzrostem częstotliwości –
faktycznie energia kinetyczna elektronów zmienia się w
przedziale od zera do maksymalnej wartości K

max

. Na rys.

10.4 pokazano otrzymaną eksperymentalną zależność
K

max

od częstości ν.

24







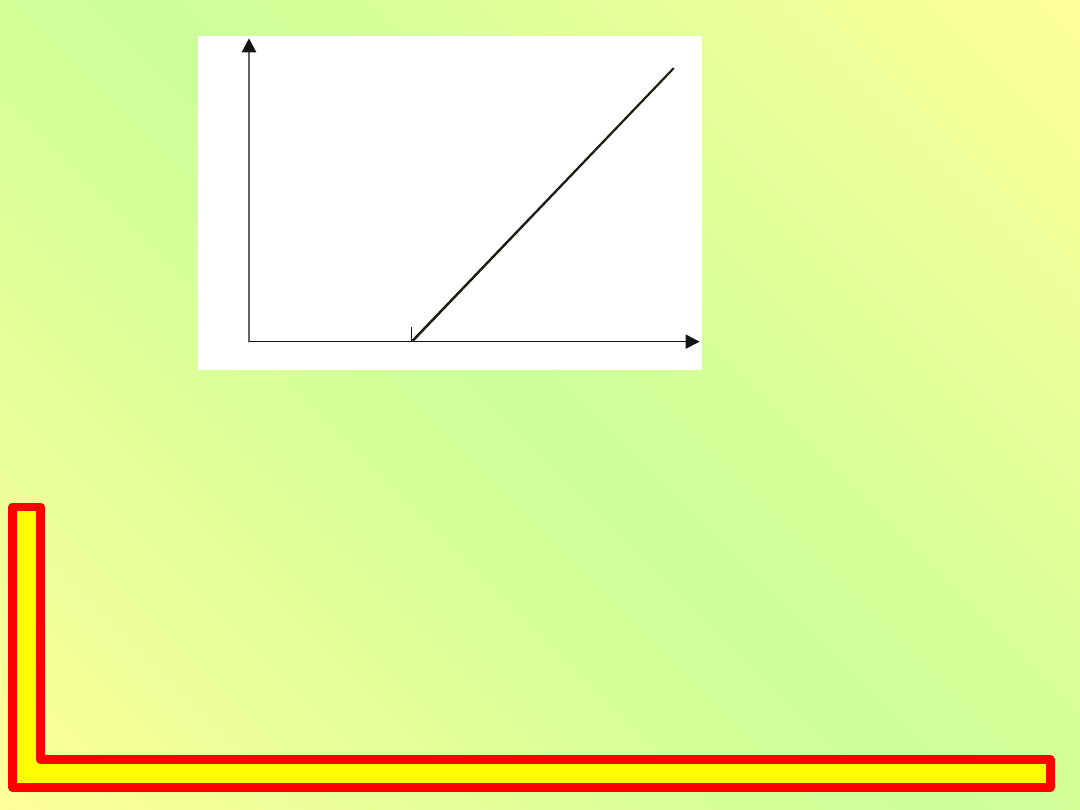
K

m a x

Rys. 10.4. Zależność maksymalnej energii kinetycznej elektronów

wybitych z metalu od częstotliwości światła.

W 1905 r. A. Einstein podał poprawne wyjaśnienie

fotoefektu. Zaproponował śmiałą w tym czasie

ideę, że światło stanowi zbiór kwantów z których

każdy posiada energię hν. Założył również, że te

kwanty światła (obecnie zwane fotonami)

zachowują się podobnie do cząstek materialnych i

że przy zderzeniu foton może być pochłonięty, a

cała jego energia przekazana jest elektronowi.

25

Wówczas nawet Planckowi wydawało się to dziwne.

Jak wobec tego pogodzić prawo interferencji fal z tym, że
jednocześnie światło składa się z cząstek? Przecież np. w
doświadczeniu z dwoma szczelinami cząstka
przechodziłaby bądź przez jedną bądź przez drugą
szczelinę, co wyklucza utworzenie obrazu
interferencyjnego.

Teoria Einsteina wyjaśnia fakty eksperymentalne.
Załóżmy, że aby elektron mógł opuścić metal konieczna
jest strata energii W

0

. Wówczas przy pochłonięciu fotonu

o energii hν, energia elektronu opuszczającego
powierzchnię wynosi hν-W

0

. Jest to możliwa maksymalna

energia kinetyczna

o

max

W

h

K







Powyższy związek jest zgodny z przebiegiem prostej
eksperymentalnej przedstawionej na rys. 10.4. Einstein
przewidział, że nachylenie prostej powinno być
określone stałą Plancka h.

Wielkość W

o

nazywana jest pracą wyjścia i zależy

od rodzaju metalu.

26

Jeżeli elektron jest początkowo w stanie

spoczynku, to przedostając się do metalu przyjmując
energię kinetyczną U

o

. Inaczej mówiąc, układ elektron

w metalu można przedstawić w postaci jamy potencjału
o głębokości U

o

, jak schematycznie pokazano na rys.

10.5. Wewnątrz metalu zewnętrzne elektrony atomu są
swobodne (tj. nie są związane z określonymi atomami),
a ich energia kinetyczna może się zmieniać od zera do
E

F

. Wielkość E

F

nazwana jest energią Fermiego. Jeżeli

elektronowi o energii Fermiego dostarczyć dodatkowo
energii W

o

, to jego energia K= E

F

+ W

0

zaledwie

wystarcza na to ażeby opuścić metal. Innymi słowy,
kiedy elektron opuści metal, jego energia staje się
równa K = 0. Z rys. 10.5 widzimy, że E

F

+ W

0

= U

o

, czyli

W

0

= U

o

- E

F

P o w ie r z c h n ia

h - W



o

h 

W

o

E

E

F

- U

o

0

E n e r g i a

p o te n c ja l n a

Rys. 10.5. Jama potencjału w

której znajdują się elektrony

metalu. Elektron o energii E

F

pochłania foton i przechodzi na

wyższy poziom energetyczny

.

27

W zjawisku fotoefektu po pochłonięciu fotonu o energii
hν, elektron z poziomu o energii E

F

przechodzi na

wyższy poziom energetyczny. Przy tym energia
elektronu na zewnątrz metalu okazuje się równa

hν- W

0

.

Jest to maksymalna możliwa energia, którą może
posiadać wybity elektron K

max

=hν- W

0

. Jeżeli elektron

znajduje się na niższym poziomie (poniżej linii
przerywanej) i pochłania foton o tej energii, to energia
na zewnątrz metalu będzie mniejsza od K

max

.

28

16.10. Efekt Comptona

 

Stosując klasyczną elektrodynamikę wykazaliśmy,

że światło przenoszące energię E posiada pęd p=E/c .
Tak więc kwant świetlny o energii E=hν powinien
charakteryzować się pędem p= hν/c. Jeżeli zamienić ν/c
na 1



, to

(10.11)

Einstein przewidział, że kwanty świetlne (fotony)

będą

zachowywać

się

podobnie

do

cząstek

elementarnych o pędzie p=h/λ .

W przypadku

fotoefektu ten minimalny pęd przekazywany jest całej
próbce metalu i wybitemu z niego elektronowi. Pęd
przyjęty przez metal w takich warunkach jest zbyt mały
i nie można go zmierzyć

,

jednakże przy zderzeniu

fotonu

ze

swobodnym

elektronem

wielkość

przekazywanego pędu można zmierzyć. Proces ten –
rozpraszanie

fotonu

na

elektronie

swobodnym,

nazywany jest efektem Comptona

. Po raz pierwszy

proces ten był eksperymentalnie potwierdzony
przez A. Comptona w 1923 r.



h

p

29

Wyprowadzimy teraz związek

łączący długość fali rozproszonego
fotonu z kątem rozpraszania i
długością

fali

fotonu

przed

zderzeniem. Niech foton o energii pc
i pędzie p zderza się z nieruchomym
elektronem o energii spoczynkowej
mc

2

. Po zderzeniu pęd fotonu będzie

równy p’ i skierowany pod kątem Θ,
jak to pokazano na rys. obok

D o

P o

e

p



'

p

'

e

p

Pęd elektronu odrzutu będzie równy p’

e

, a

całkowita energia relatywistyczna E’

e

. Stosujemy

mechanikę

relatywistyczną,

ponieważ

prędkość

elektronu może osiągnąć prędkości bliskie prędkości
światła. Zgodnie z prawem zachowania energii,
całkowita energia przed zderzeniem równa jest
całkowitej energii po zderzeniu, wobec tego

'

e

E

c

'

p

mc

pc







2

30

czyli

(10.12)

Prawo zachowania pędu daje

Podnosząc obie strony do kwadratu

i odejmując ostatnie równanie od (10.12) mamy









2

2

c

/

E

mc

'

p

p

'

e







'

e

p

'

p

p











2

2

2

2

'

e

p

'

p

'

p

p

p











2

2

2

2

2

2

2

2

2

'

e

'

e

p

c

E

cos

'

pp

mc

'

p

pmc

'

pp

c

m















prawą stronę można zamienić na
m

2

c

2





2

2

2

2

2

2

c

m

pmc

cos

p

mc

p

'

p

c

m













31

stąd znajdujemy

Wykorzystując fakt, że p=h/λ otrzymujemy

czyli

(10.13)

W

eksperymencie

Compton

stosował

promieniowanie rentgenowskie o znanej długości
fali i zauważył, że długość fali fotonów zwiększa się
zgodnie z przewidywaniem według wzoru (10.13).







cos

mc

p

p

'

p







1

1











cos

mc

h

'







1

1

1











cos

mc

h

'







1

Promieniowanie termiczne, fotoefekt, efekt

Comptona i wiele innych eksperymentów z udziałem

światła i atomów potwierdziły, że światło faktycznie

zachowuje się jakby składało się z cząstek o energii

hν i pędzie h/ν .

32

16.11. Dualizm korpuskularno-falowy

Jeżeli byśmy w pierwszych eksperymentach ze

światłem zaobserwowali efekt Comptona i fotoefekt,

to bylibyśmy przekonani o tym, że światło jest
strumieniem fotonów,

które zachowują się jak

wszystkie ”przyzwoite” cząstki.

Przy takim układzie

rzeczy zaobser-wowanie obrazu interferencyjnego od
dwóch szczelin wywołałoby zdumienie.

Faktycznie;

jak

cząstki

mogą

wykazywać

właściwości

klasycznych fal?

Przecież cząstka może przejść tylko

przez jedną lub drugą szczelinę.

Paradoks ten stał się bardziej znaczącym w 1927

r. kiedy to amerykańscy fizycy C. Davisson i L. Germer
odkryli właściwości falowe elektronu. W rzeczywistości
trzy lata wcześniej Louis de Bro-glie w swej
rozprawie doktorskiej założył, że związek (10.11)
słu-szny jest nie tylko dla fotonów, lecz w ogóle dla
wszystkich cząstek. Czyli

i

(10.14)



h

p



h

E 

33

De Broglie założył, że wiązka cząstek

dowolnego

rodzaju

będzie

tworzyć

obraz

interferencyjny

na

odpowiedniej

podwójnej

szczelinie charakterystyczny dla doświadczenia
Younga.

W tych czasach hipoteza de Broglie’a wydawała

się wariacką, bodajże niewłaściwą do ubiegania się o
stopień doktora. Zaledwie po upływie trzech lat nauka
przeżyła wstrząs – eksperyment potwierdził hipotezę.
Wstrząs był spowodowany tym, że wydawało się
niemożliwe aby takie cząstki jak elektrony zachowywały
się jednocześnie jak cząstki i fale.

W przypadku fotonów paradoks można byłoby

usunąć zakładając, że pojedynczy foton przed
przejściem przez dwie szczeliny zdolny jest rozszczepić
się a następnie interferować ze sobą. Jednakże w
przypadku elektronów, w przyrodzie nigdy nie
zaobserwowano

połowy

lub

części

elektronu.

Niezależnie od tego czy detektor znajduje się za
szczeliną A lub B (rys. 10.7) elektron zawsze
wykrywany jest w całości.

34

S tr u m i e ń

e le k tr o n ó w

O d k r y ta ty lk o

s z c z e lin a A

R o z k ła d

e le k tr o n ó w

T y l k o B

T y lk o A

A + B

E k r a n

O d k r y ta ty lk o

s z c z e li n a B

O d k r y te o b i e

s z c z e li n y

B

B

B

A

A

A

Rys. 10.7. Rozkład

intensywności elektronów

zgodnie z fizyką klasyczną

.

r

2

P

2

P

1

r

1

A

B

R o z k ł a d

k la s y c z n y

O b s e r w o w a n y

r o z k ła d

S tr u m ie ń

e l e k tr o n ó w

Rys. 10.8. Rozkład

intensywności

elektronów zgodnie z

teorią kwantową.

35

Z tego punktu widzenia dochodzimy do wniosku, że

pojedynczy elektron może przejść tylko przez jedną z
dwóch szczelin na rys. 10.7 Tak więc rozkład elektronów
na ekranie powinien być sumą rozkładów dla każdej
szczeliny oddzielnie

.

Chociaż logika wywodu wydaje się

być nieskazitelną, rozkład charakterystyczny dla A+B nie
ma miejsca! Zamiast tego obserwujemy klasyczny obraz
interferencyjny dla dwóch szczelin przedstawiony na rys.
10.8

. Nie zachodzi więc zaprzeczenie czystej logiki?

Przecież wszystko to wygląda jakby 100 +100 = 0.
Załóżmy, że w punkcie P

1

na rys. 10.8 znajduje się licznik

Geigera rejestrujący w każdej sekundzie 100 elektronów
kiedy otwarta jest dowolna ze szczelin A lub B. Przy tym,
gdy otwarte są obie szczeliny jednocześnie, licznik
przestaje rejestrować elektrony. Oznacza to, że w punkcie
P

1

przypada minimum interferencyjne . Jeżeli początkowo

otworzyć tylko szczelinę A, a później stopniowo otwierać
szczelinę B, to zgodnie ze zdrowym rozsądkiem możemy
oczekiwać że prędkość zliczeń w miarę odkrywania
szczeliny B będzie stopniowo wzrastać od 100 do 200
zliczeń na sekundę. Zamiast tego obserwujemy
zmniejszanie prędkości zliczeń od 100 do zera.

36

Ponadto, jeżeli licznik Geigera umieścić w punkcie P

2

, to

w miarę otwierania szczeliny B prędkość zliczeń będzie
stopniowo wzrastać od 100 do 400 zliczeń na sekundę,
kiedy druga szczelina jest całkowicie otwarta. Wobec
tego 100 + 100 = 400.

r

2

P

2

P

1

r

1

A

B

R o z k ła d

k la s y c z n y

O b s e r w o w a n y

r o z k ła d

S tr u m ie ń

e le k tr o n ó w

Jedyny sposób wyjaśnienia tych paradoksalnych
wyników polega na stworzeniu nowego formalizmu
matematycznego pozwalającego opi-sać falowe
właściwości cząstek materialnych na poziomie
mikro-świata

,

a

zatem

także

poprawnie

przewidującego

obserwowane

zjawiska

interferencyjne. Formalizm ten musi być wewnętrznie
spójny.

37

16. 12. Funkcja falowa

Formalizm matematyczny za pomocą którego

usuwa się opisane powyżej paradoksy, przypisuje każdej
cząstce materialnej funkcję falową Ψ(x,y,z,t) będącą
funkcją współrzędnych i czasu. Pamiętamy, że natężenie
jest proporcjonalne do kwadratu amplitudy funkcji
falowej. Powróćmy na chwilę do eksperymentu z
elektronami. Elektrony przepuszczane przez szczelinę
padały w określone punkty na ekranie, z tym, że tam
gdzie obserwowaliśmy maksima, elektrony padały
częściej. Okazuje się jednak, że nie możemy z góry
przewidzieć, w którym miejscu dany elektron padnie na
ekran. Znajdując natomiast rozkład natężenia w obrazie
dyfrakcyjnym można określić prawdopodobieństwo, że
elektron padnie w określonym miejscu ekranu. Zatem
kwadrat amplitudy funkcji falowej jest proporcjonalny do
gęstości prawdopodobieństwa znalezienia elektronu w
danym elemencie obszaru. Ponieważ funkcja falowa



jest na ogół funkcją zespoloną, to kwadrat amplitudy tej
funkcji wynosi













2

38













2

gdzie jest funkcją sprzężoną z Ψ . Tak więc
jest proporcjonalne do prawdopodobieństwa
znalezienia elektronu w elemencie objętości dxdydz.
Ponieważ suma prawdopodobieństw znalezienia
elektronu w poszczególnych elementach objętości
rozciągnięta na całą przestrzeń musi być równa jeden,
zatem można tak określić funkcję falową, aby był
spełniony warunek

dxdydz

2







1

2





dV

V



Jest to warunek unormowania funkcji falowej

.

Wówczas jest równe gęstości prawdopodobieństwa
znalezienia elektronu.

Formalnie funkcja falowa Ψ charakteryzuje się
właściwościami klasycznych fal, lecz nie reprezentuje
takich wielkości jak np. wychylenie cząstki z położenia
równowagi.

2



39

Jeżeli zdarzenie może przebiegać w kilku

wzajemnie

wykluczających

się

sposobach

(jak

powiedzmy, przy przechodzeniu cząstek przez jedną ze
szczelin A i B) to funkcja falowa takiego zdarzenia
przedstawia sumę funkcji falowych każdego ze
sposobów

To twierdzenie (zasada superpozycji) jest identyczne z
zasadą dodawania amplitud fal w optyce. W
rozważanym wyżej przykładzie,



1

opisuje falę

przechodzącą przez szczelinę A, a



2

– falę

przechodzącą przez szczelinę B. Na ekranie obie
funkcje falowe pokrywają się i dają klasyczny obraz
interferencyjny z dwóch szczelin, przy czym n-te
maksimum określone jest wyrażeniem

2

1











d

/

n

sin

n







40

Przedstawiony formalizm pociąga za sobą szereg

niepewności

wymagających

dalszej

interpretacji

fizycznej. Przypuśćmy, że mamy tak słaby strumień
elektronów, że wysyłamy pojedyncze elektrony. I w tym
przypadku po dostatecznie długiej ekspozycji otrzymuje
się chara-kterystyczny obraz dyfrakcyjny. A więc falowy
charakter jest cechą pojedynczych cząstek.

Zgodnie z prezentacją falową każdemu elektronowi
odpowiada paczka falowa dzieląc się jednakowo
pomiędzy dwie szczeliny. Jednakże umieszczając za
szczeliną A detektor, zauważymy, że przez szczelinę
nigdy nie przechodzi połówka elektronu. Na tym polega
atomizm (zasada niepodzielności), według którego
intensywność fali za szczeliną A charakteryzuje
prawdopodobieństwo znalezienia całkowitego elektronu
w tym miejscu. Ponadto jeżeli detektor umieścić za
szczeliną A, to obraz interferencyjny wygładza się i
otrzymuje się klasyczny wynik, przekształcając obraz
interferencyjny (rys. 10.8) w klasyczny (rys. 10.7).

41

Wielu fizyków, włączając Einsteina, próbowało
wymyślić takie doświadczenie w rezultacie którego
można

byłoby,

nie

naruszając

obrazu

interferencyjnego, ustalić przez którą szczelinę
przeszła dana cząstka;

jednakże wszystkie te próby

były nieudane

.

Wobec tego co przedstawiają fale odpowiadające
elektronowi? Na to pytanie należy odpowiedzieć tak jak
w przypadku fotonów. Fale elektromagnetyczne
propagują się swobodnie w pustej przestrzeni. W
odróżnieniu od fal mechanicznych w tym przypadku nie
istnieje ośrodek przenoszący drgania. Funkcja falowa



nie stanowi bezpośrednio obserwowanej wielkości i w
tym sensie nie wykonuje ruchu drgającego. Fale
klasyczne i fale odpowiadające cząstkom podlegają
równaniom matematycznym tego samego typu. Lecz w
przypadku klasycznym amplituda fali jest bezpośrednio
obserwowana, a dla funkcji falowej



– nie.

42

16. 13. Dyfrakcja elektronów

Eksperyment z dyfrakcją elektronów na dwóch
szczelinach

jest

bardziej

złożony,

ponieważ

charakterystyczna długość fali elektronów jest dużo
mniejsza od długości fal świetlnych zakresu widzialnego.
Obliczymy długość fali elektronu przyśpieszanego
napięciem V = 1000 V, tzn. o energii kinetycznej K =
1000 eV = 1.610

–16

J. Wówczas

i po podstawieniu danych liczbowych otrzymujemy
410

–11

m. Jest to więc wielkość rzędu promienia atomu.

Ponieważ jest także porównywalne z odległością między
atomami w ciele stałym, nasuwa się wniosek, że wiązka
elektronów

odbijając

się

od

płaszczyzn

krystalograficznych powinna wykazać analogiczne
efekty jak w przypadku promieni rentgenowskich.
Uporządkowany szereg atomów na powierzchni metalu
działa podobnie do szczelin cienkiej siatki dyfrakcyjnej.
Właśnie w powyższy sposób Davisson i Germer badali
rozpraszanie powolnych elektronów na płytce niklowej.

mK

h

p

h

2







43

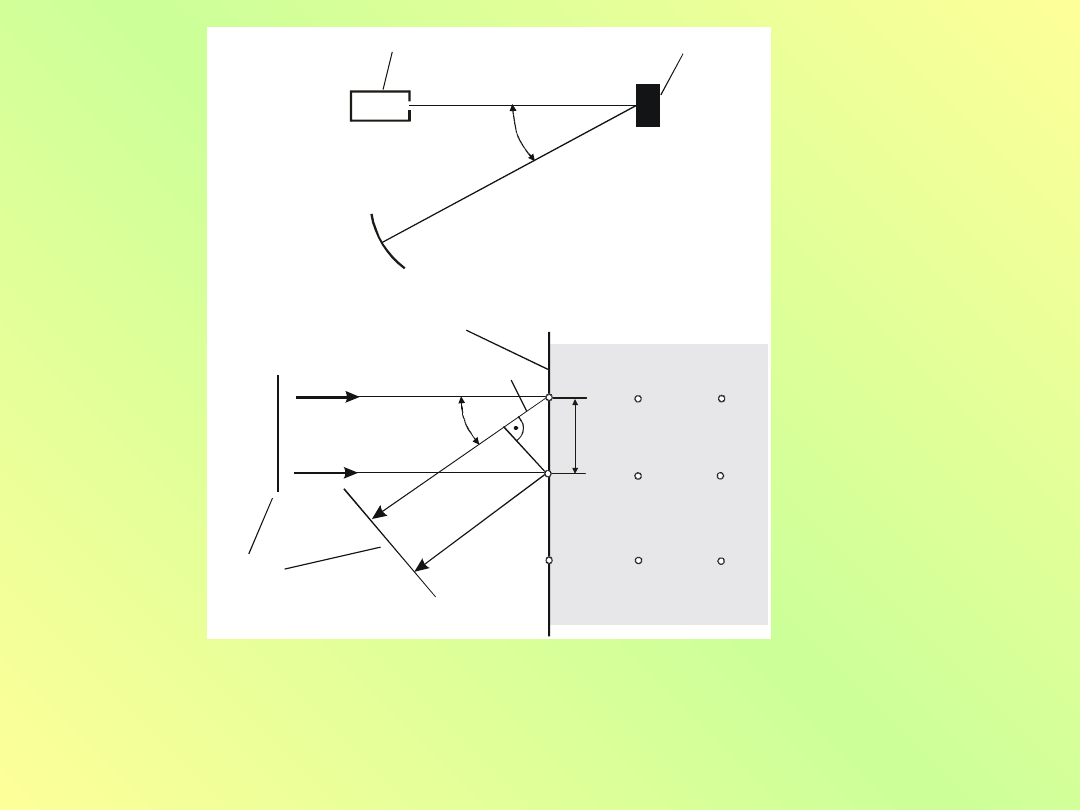
C z o ła

f a l

P o w ie r z c h n ia

k r y s z ta łu

K r y s z ta ł

d

1

1

2

2

D e te k to r

D z ia ło e le k tr o n o w e K r y s z ta ł







 D

Rys. 10.9. (a) Przyrząd do obserwowania dyfrakcji

elektronów od powierzchni kryształu.

(b) Część kryształu silnie powiększona.

44

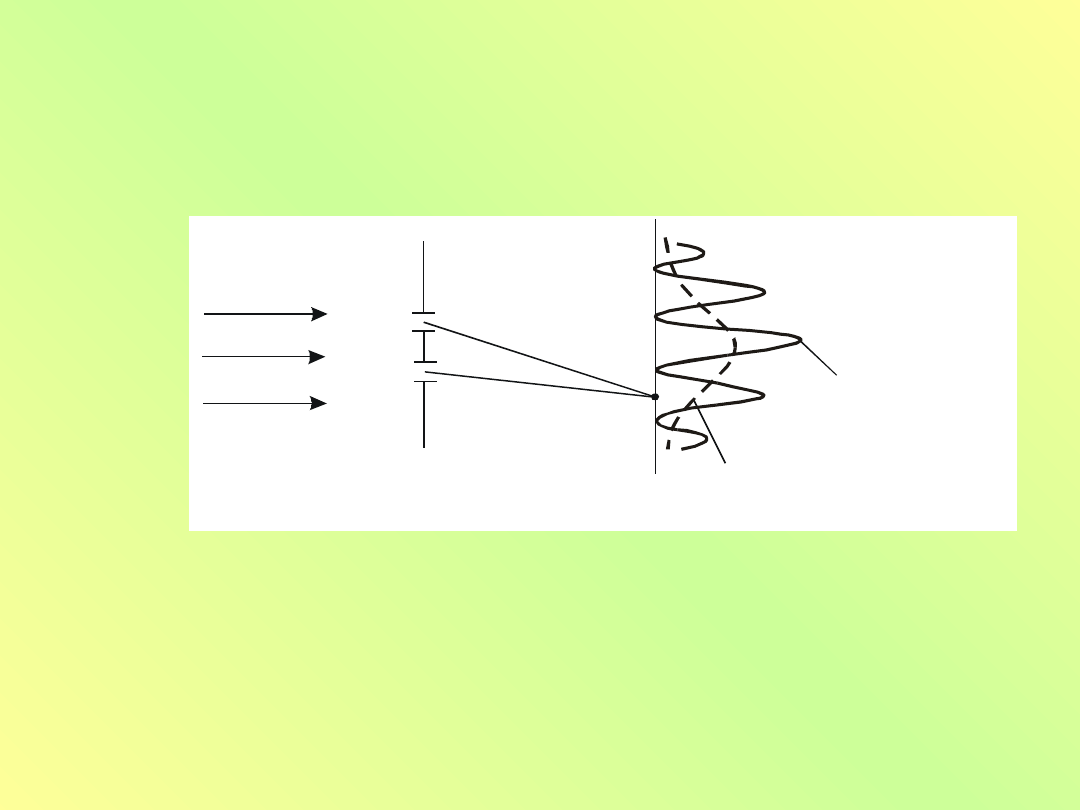
Na rys. 10.9 pokazano schematycznie urządzenie

do obserwacji dyfrakcji elektronów od powierzchni
kryształu. Jako detektor cząstek można stosować ekran
luminescencyjny. Znając wartość kąta Θ przy którym
obserwuje się maksimum intensywności, można
określić stałą Plancka. Jak widać z rys. 10.9b,

w pierwszym maksimum intensywności powinno być
równe długości fali h/p. Wobec tego





sin

d

D 



sin

d

p

h



stąd



sin

pd

h 

45

Należy zauważyć, że w tym eksperymencie, jak i

w kilku innych mających wyjątkowo duże znaczenie dla
rozwoju

fizyki,

wielkiego

odkrycia

dokonano

przypadkowo. Davisson i Germer nie postawili sobie za
cel badanie dyfrakcji elektronów. W 1926 r. Davisson
przedstawił na konferencji w Anglii pewne wyniki badań
rozpraszania elektronów na powierzchni niklu. Uczeni
europejscy zwrócili mu uwagę, że wyniki te można
lepiej

zinterpretować

dyfrakcją

elektronów

niż

klasycznym rozpraszaniem które badał. Po upływie
kilku miesięcy Davisson i Germer otrzymali nowe
wyniki jednoznacznie potwierdzające falową naturę
elektronów, które pozwoliły określić wartość stałej
Plancka z dokładnością do 1%.

Wkrótce po pojawieniu się w 1924 hipotezy de

Broglie'a, angielski fizyk Thompson przystąpił do
systematycznego badania dyfrakcji elektronów na
cienkich foliach metalowych. Jednakże dopiero w 1928 r.
otrzymał

transmisyjne

efekty

dyfrakcyjne

wiązki

elektronów przechodzących przez złotą folię o grubości
10

–5

m.

46

Widzimy, że staranne badania i przemyślane

podejście

okazało

się

mniej

szczęśliwe

od

”przypadkowości” Davissona i Germera. Jednakże
doświadczenie tych dwóch amerykańskich uczonych jest
dobrym przykładem istoty podejścia naukowego. Jeżeli
eksperymentator,

nawet

przypadkowo,

zauważy

niezrozumiały dla niego efekt, to należy dokładnie zbadać
go, dopóki nie osiągnie się pełnej jasności.

Obecnie szczegółowo badane są obrazy dyfrakcyjne

wytwarzane nie tylko przez elektrony, protony, ale
również przez całe atomy. Falowa natura materii jest
wszechstronnie sprawdzona i żadnych odchyleń od
przewidywań

teorii

nie

udało

się

dotychczas

zaobserwować.

47

16.14   Zasada nieoznaczoności

Obserwacje przedmiotów opierają się na

rejestrowaniu

światła

odbitego

przez

te

przedmioty.

Światło w „zderzeniu” z przedmiotem o

dużej masie praktycznie nie zaburza jego ruchu, ale
całkiem inną sytuację mamy w przypadku elektronów

.

Tutaj też spodziewamy się, że zobaczymy elektron gdy
odbijemy od niego światło (tak jak widzimy np. stół
rejestrując światło odbite od niego). W tym jednak
przypadku elektron w zderzeniu z fotonem dozna
odrzutu,

który

całkowicie

zmieni

jego

ruch

(przypomnijmy sobie efekt Comptona). Zmiany tej nie
można uniknąć ani dokładnie ocenić. Gdyby więc
istniały orbity to byłyby one całkowicie niszczone przy
próbie pomiarów mających potwierdzić ich istnienie.
Dlatego wolimy mówić o prawdopodobieństwie niż o
orbitach.

Aby przetestować nasze możliwości pomiarowe
rozważmy wiązkę elektronów padających z prędkością
v

0

na szczelinę o szerokości y, tak jak na rysunku.

48

Jeżeli elektron przechodzi przez
otwór to znamy jego położenie z
dokładnością x.

Elektrony ulegają ugięciu na
szczelinie tak, że na ekranie
obserwujemy obraz dyfrakcyjny.

Oznacza to, że elektrony mają
teraz oprócz prędkości poziomej
także składową w kierunku y (są
odchylone).

Spróbujmy ocenić tę składową pionową prędkości.

Rozpatrzmy np. elektron padający na ekran w miejscu
pierwszego minimum dyfrakcyjnego (punkt a na rysunku
poniżej). Pierwsze minimum jest dane równaniem

ysin



=



a dla małego kąta

y







Aby elektron doleciał do punkt a (1-sze minimum) musi
mieć prędkość pionową v

y

taką, że

0

sin

v

v

y











49

Korzystając z obu powyższych równań otrzymujemy

lub inaczej

v

y

y =



v

0

 

Długość fali wiązki elektronowej jest dana przez h/p

czyli h/mv

0

. Podstawiając to do ostatniego równania

otrzymujemy

co można zapisać

p

y

y  h

 

y

y









0

v

v

0

0

v

v

v

m

h

y

y







50

p

y

y  h

Jeżeli chcemy poprawić pomiar y (zmniejszyć y)

to w wyniku zmniejszenia szerokości szczeliny
otrzymujemy szersze widmo dyfrakcyjne (mocniejsze
ugięcie). Inaczej mówiąc zwiększone zostało p

y

.

Równani to przedstawia ograniczenie nałożone na
dokładność pomiarów przez przyrodę (nie ma nic
wspólnego z wadami aparatury pomiarowej).

Równanie to jest szczególnym przypadkiem ogólnej
zasady podanej przez W. Heisenberga znanej jako

zasada nieoznaczoności

.

W zastosowaniu do pomiaru pędu i położenia głosi ona,
że

h

z

p

h

y

p

h

x

p

z

y

x



















Tak więc żadna składowa ruchu
elektronu nie może być określona
z nieograniczoną dokła-dnością. Ta
sama zasada obowiązuje w odnie-
sieniu do energii i czasu.

51