Akademia Górniczo-Hutnicza

im. Stanisława Staszica

WYDZIAŁ INŻYNIERII MECHANICZNEJ I ROBOTYKI

WYTRZYMAŁOŚĆ MATERIAŁÓW

Projekt nr 1/a

Zestaw nr . . .

Temat:

Obliczyć główne, centralne momenty bezwładności dla
przekroju symetrycznego przedstawionego na rysunku.

Wykonał: Sprawdził:

imię nazwisko ..................................
Rok .... grupa ...... data ...........................
Ocena .........................

1. Dane do obliczeń:

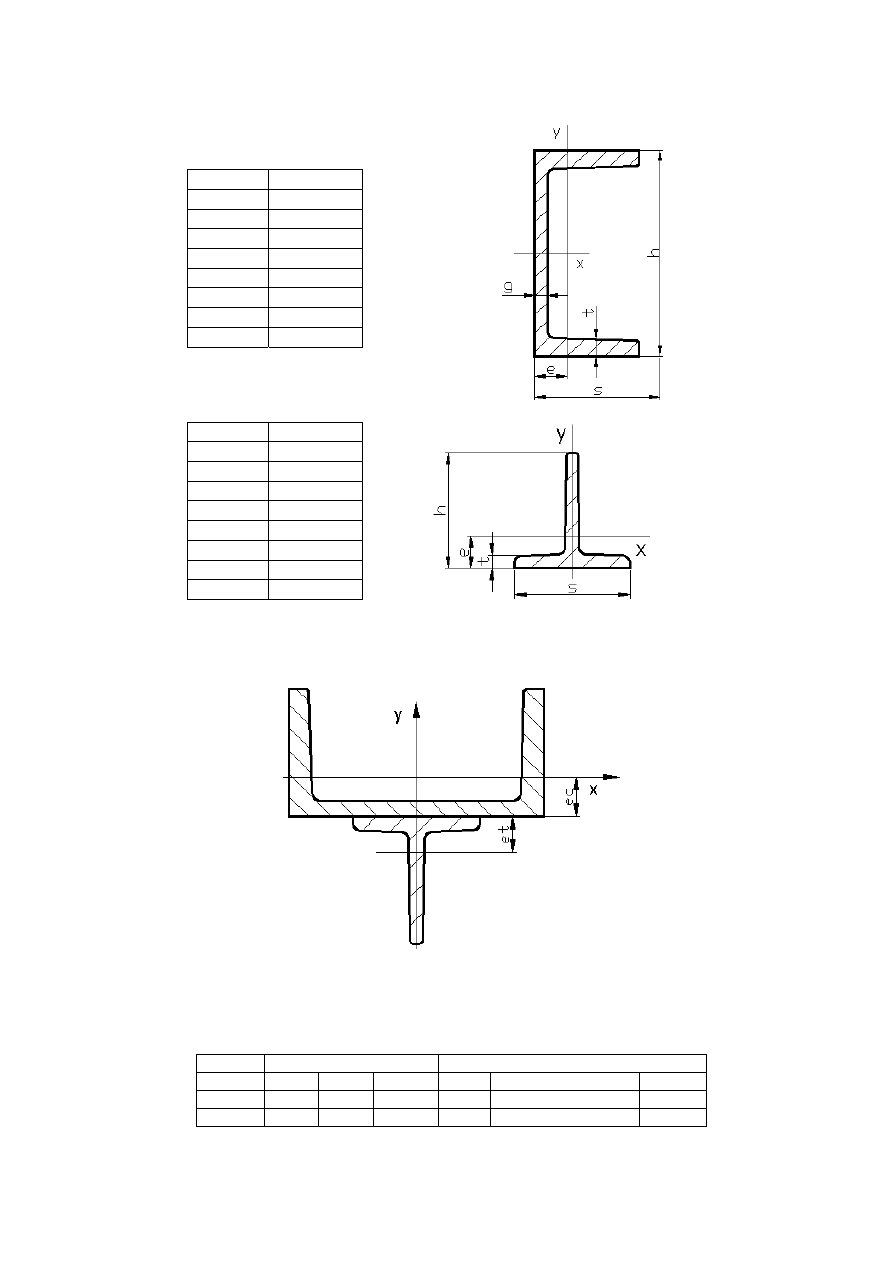
1.1. Charakterystyka geometryczna ceownika C 80

wg. PN-86/H-93403, rys.1.1

symbol wielkość

h 80

mm

s 45

mm

g 6

mm

t 8

mm

A 11

cm

2

Ix 106

cm

4

Iy 19,4

cm

4

e 1,45

cm

rys.1.1 Ceownik

1.2. Charakterystyczna geometryczna teownika T 40x40

wg. PN 91/H-93406, rys.1.2.

symbol wielkość

h 40

mm

s 40

mm

g 5

mm

t 5

mm

A 3,77

cm

2

Ix 5,28

cm

4

Iy 2,58

cm

4

e 1,12

cm

rys.1.2 Teownik

2. Obliczenia środka ciężkości profili względem przyjętych osi x, y:

2.1. Został przyjęty układ współrzędnych 0xy umieszczony w środku ciężkości ceownika, rys.2.

rys.2 Przekrój symetryczny z naniesionymi układami współrzędnymi składowych przekrojów profili
walcowanych i układem 0xy, względem którego obliczany jest środek ciężkości przekroju całkowitego.

2.2. Obliczenia odległości środków ciężkości profili walcowanych od osi x, y, rys.2.

TomaLa

2

profil ceownik

kątownik

symbol xc yc A

c

xt

yt

A

t

wzór

-e

c

- e

c

wartość

0 cm

0 cm

11cm

2

0

cm -1,45-1,12=-2,57cm 3,77cm

2

2.3. Obliczenia środka ciężkości profilu (X

0

Y

0

) względem układu 0xy, rys.2.

cm

X

0

0

=

- ponieważ osi y pokrywa się z osią symetrii przekroju. Środek ciężkości leży na osi y.

cm

A

A

A

y

A

y

A

A

S

S

A

S

Y

t

c

t

t

c

c

t

c

t

x

c

x

x

656

,

0

77

,

3

11

77

,

3

57

,

2

11

0

0

−

=

+

⋅

−

+

⋅

=

+

+

=

+

+

=

=

3. Obliczenia centralnych momentów: bezwładności i dewiacji, tj. obliczanych względem

osi x0, y0 umieszczonych w środku ciężkości profilu.

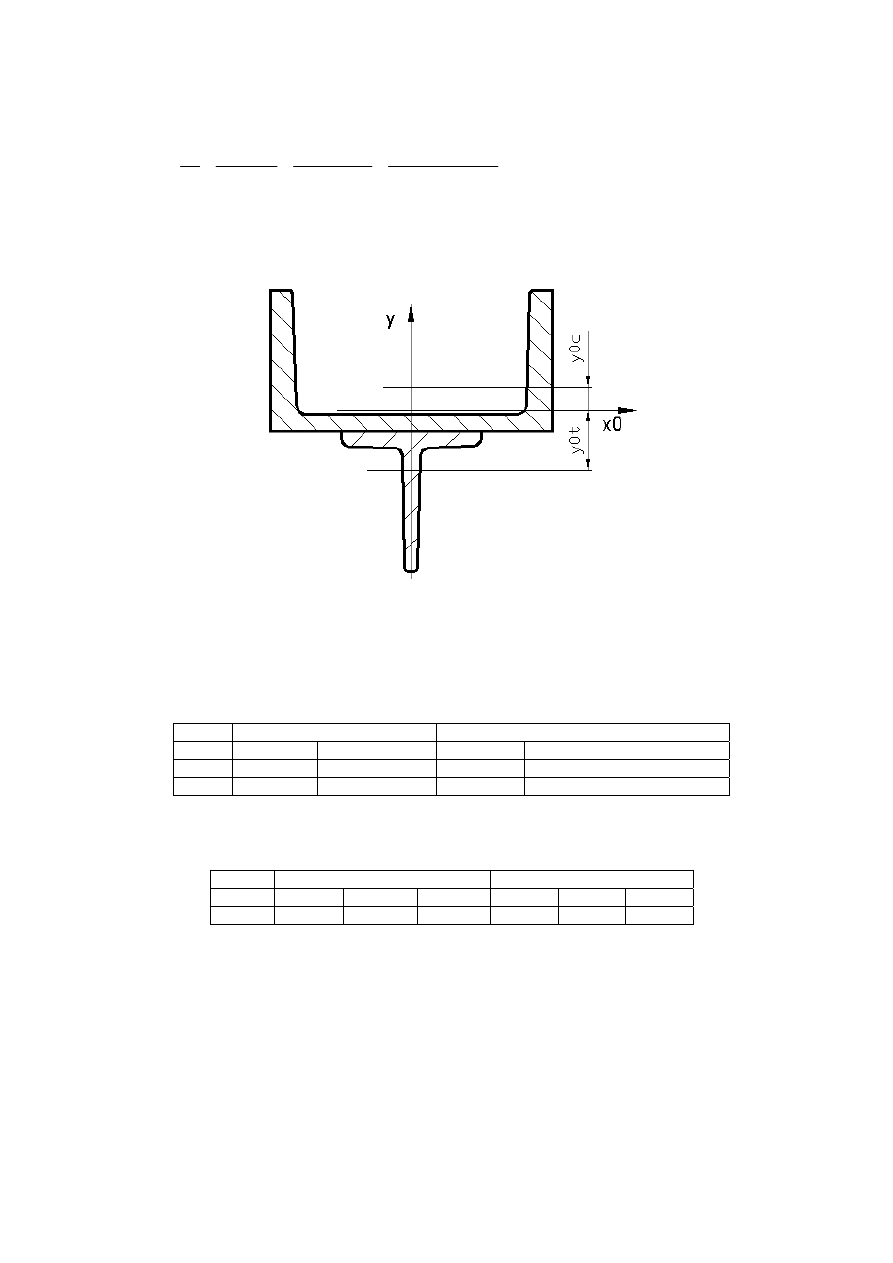
rys.3 Przekrój symetryczny z naniesionymi współrzędnymi układami składowych przekrojów profili
walcowanych i układem 0x0y0 umieszczonym w środku ciężkości przekroju całkowitego.

3.1. Obliczenia odległości środków ciężkości profili walcowanych od osi x0, y0, rys.3.

Uwaga,

zmiany znaków przed wielkościami podanymi w p.2.2 i p.2.3 związane są z tym, że odległości

odczytywane są zgodnie z przesuniętym układem 0x0y0, nie zaś jak poprzednio z osi 0xy.

profil ceownik

teownik

symbol x0c

y0c

x0t

y0t

wzór X

0

-Y

0

X

0

yt-Y

0

wartość

0 cm

0,656cm

0 cm

-2,57+0,656= -1,914cm

3.2. Obliczenia momentów bezwładności względem osi x

0

, y

0

dla całkowitego przekroju

z wykorzystaniem wzoru Steinera, rys.3.

profil ceownik

teownik

symbol A

c

I

xc

I

yc

A

t

I

xt

I

yt

wartość 11cm

2

106cm

4

19,4cm

4

3,77cm

2

5,28cm

4

2,58cm

4

Ponieważ ceownik jest obrócony o kąt 90

o

względem rysunku normowego, oś yc

ceownika

stała się

równoległa do osi xo obliczanego przekroju, tym samym w obliczeniach I

xo

uwzględniane jest I

yc

nie I

xc

.

I

xo

= I

x0c

+I

x0t

= I

yc

+y

0c

2

A

c

+ I

xt

+y

0t

2

A

t

=

19,4cm

4

+ (0,656cm)

2

11cm

2

+ 5,28cm

4

+ (-1,914cm)

2

3,77cm

2

I

xo

=

43,225cm

4

I

yo

= I

y0c

+I

y0t

= I

xc

+ I

yt

=

106cm

4

+ 2,58cm

4

I

yo

=

108,58cm

4

4. Literatura

1. Dyląg Z., Jakubowicz A., Orłoś Z.: Wytrzymałość Materiałów. t I. Wydawnictwo Naukowo-Techniczne,
Warszawa 1997.
2. Siemieniec A, Wolny S.: Wytrzymałość Materiałów. t I. Wydawnictwo AGH, Kraków 1995.

TomaLa

3