Kuźnia Talentów Informatycznych

Zaawansowane algorytmy

Bolesław Kulbabiński, Tomasz Kulczyński, Błaże siński

rof r hab acie ysło

Zeszyt y aktyczny o racowany w ramach ro ektu e ukacy nego

— ona regionalny rogram rozwi ania kom etenc i

uczniów szkół ona gimnaz alnych w zakresie technologii
informacy no komunikacy nych I T

arszawska yższa zkoła Informatyki

ul ewartowskiego

,

arszawa

ro ekt graficzny

Z I I

arszawa

o yright © arszawska yższa zkoła Informatyki
ublikac a nie est rzeznaczona o s rze aży

niwersytet arszawski

< 4 > 

Informatyka + 

St reszczenie

Niniejszy kurs ma na celu pomoc w zgłębianiu najtrudniejszych zagadnień algorytmicznych, które po-
jawiają się na konkursach in ormatycznych.

rzeznaczony jest dla uczniów, którzy opanowali już naj-

ważniejsze podstawowe techniki rozwiązywania problemów in ormatycznych. zczególnie zalecane jest
wcześniejsze zapoznanie się z kursami „ rzegląd podstawowych algorytmów” oraz „ truktury danych
i ich zastosowania” .

urs jest zdecydowanie nastawiony na przygotowanie do konkursów. eden z rozdziałów zawiera

nawet rady co do samej taktyki startowania w zawodach.

pora część kursu zakłada znajomość języka

, nie jest ona jednak wymagana do zrozumienia

większości idei, które staramy się przekazać.

Spis t reści

St reszczenie

4

1

Takt yka

6

.

rzed zawodami . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

.

ybór zadania . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

.

onowne czytanie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

.

estowanie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

.

„ ruty”

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2

St andard Templat e Library

7

.

ontener ector . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

.

teratory . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

.

ary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

.

ontener set . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

.

map . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

.

ortowanie i wyszukiwanie binarne . . . . . . . . . . . . . . . . . . . . . . . . . . . .

.

ermutacje . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3

Haszowanie

13

.

zym jest haszowanie

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

.

ablica haszująca . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

.

aszowanie słów . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

4

Algoryt m

arpa

illera

osenberga

16

.

łownik podsłów bazowych . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

.

orównywanie podsłów . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

.

Najdł uższe powtarzające się podsłowo . . . . . . . . . . . . . . . . . . . . . . . . . .

.

Najdł uższe wspólne podsłowo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

aksymalny przepł yw

1

.

etoda orda- ulkersona . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

.

lgorytm dmondsa- arpa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

.

wierdzenie o maksymalnym przepł ywie i minimalnym przekroju . . . . . . . . . . . .

.

rzekroje w zadaniach . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

> Zaawansowane algorytmy 

< 5 >

6

Skojarzenia

23

6.1

Maksymalne skojarzenia . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

24

6.2

Szybsze rozwiązania . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

25

6.3

Twierdzenie K¨oniga . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

26

7

Przecinanie się obiekt ów geomet rycznych na pł aszczyźnie

28

7.1

rze ię ie dwó

ros y

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2

7.2

rze ię ie dwó

od inków . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2

7.3

rze ię ie ros ej i okręg . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2

7.4

rze ię ie dwó

okręgów . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2

8

Poł ożenie p nkt

wzg ę em obiekt ów pł aszczyzny

2

.1

zględem ros ej . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2

.2

zględem okręg

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

2

.3

zględem wieloką a . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

3

.4

najdowanie najdalszy

nk ów w danym zbiorze . . . . . . . . . . . . . . . . . . .

3

.5

najdowanie najbliższy

nk ów w danym zbiorze . . . . . . . . . . . . . . . . . . .

31

it erat ra

32

< 6 > 

Informatyka + 

1

Takt yka

Jako że kurs jest prowadzony pod kątem rozwiązywania zadań konkursowych, chcielibyśmy przedstawić
kilka naszych przemyśleń co do samego startowania w zawodach informatycznych.

czywiście, nawet najlepsza taktyka nie pomoże, jeśli nie potrafimy zrobić zadań, które są do roz

wiązania.

zęsto jednak, dobre podejście do zawodów może znacznie poprawić nasz wynik.

ozdział będzie składał się ze zbioru dobrych rad dotyczących różnych rodzajów konkursów.

1.1

Przed zawodami

ażnym elementem, o którym często się zapomina, jest przygotowanie jeszcze przed dniem konkursu.
arto spojrzeć na poprzednie edycje, zadania, wyniki.

ostarcza to cennych informacji, czego można

się spodziewać na samych zawodach.

pewnijmy się, że wiemy ile będzie zadań, jak oceniane, jak

jest tworzony ranking.

ie ma czasu, by się nad tym zastanawiać później, podczas trwania rywalizacji.

ardzo ważna jest też ustalenie, czego musimy dokonać, żeby być z siebie zadowolonym.

hcemy

rozwiązać jak najszybciej wszystkie zadania, a może spokojnie i powoli, byle się nie pomylić

może

w ogóle nie chcemy ryzykować i zakładamy od razu, że lepiej zrobić jedno zadanie, ale na pewno dobrze,
niż dwa niepewnie.

a te pytania nie ma uniwersalnej odpowiedzi.

apamiętajmy przede wszystkim

następującą radę

stalmy sobie wyraźne cele jeszcze przed zawodami.

ie dajmy się niczym zaskoczyć.

1.2

W ybór zadania

ierwszy problem, jaki napotykamy po rozpoczęciu zawodów, to dobry wybór zadania, którym się

zajmiemy.

utaj strategia zależy prawdopodobnie od charakteru konkursu. Jeśli są to krótkie zawody,

w których liczy się czas, może opłacać się czytać najpierw zadania o najkrótszej treści i jeśli wydają
się być rozwiązywalne, starać się je zrobić. Jeśli natomiast zawody są dł uższe, a czas nie gra większej
roli, to polecamy na początku przeczytać wszystkie zadania, żeby mieć dobry obraz całości i lepiej
zadecydować, czym się po kolei zająć.

arto wziąć pod uwagę pierwsze wrażenie co do trudności

zadania, jak również własne preferencje tematyczne „ geometria nie” , „ teoria liczb tak sobie” , itp. .

iezależnie od formy konkursu, w zdecydowanej większości przypadków warto przeczytać

wszystkie zadania, ale nie koniecznie na początku zawodów.

luczowym elementem strategii, na którego braku najłatwiej traci się punkty czy pozycję w tego typu

konkursach, jest tzw. „ moment odpuszczenia” .

tóż, jeśli z jakichś powodów nie możemy rozwiązać

zadania, którym się zajmujemy, należy je zostawić i przejść do następnego.

aturalnie nie chodzi

tutaj o poddawanie się przy pierwszej napotkanej trudności.

właśnie dlatego musimy sobie określić,

kiedy decydujemy się na zmianę zadania.

rawdopodobnie będzie to czas w minutach spędzony nad

danym problemem. rzeba przy tym pamiętać, że inaczej traktujemy problemy implementacyjne z nimi
zazwyczaj opłaca się walczyć do końca .

Jeśli nie potrafimy znaleźć dobrego rozwiązania zadania po pewnym, ustalonym z góry czasie,
zostawiamy je i próbujemy rozwiązać następne.

1.3

Ponowne czyt anie

ardzo wiele błędów wynika ze złego zrozumienia treści zadania. Jeśli tylko specyfika zawodów na to

pozwala np. nie są bardzo krótkie , gorąco polecamy następującą metodę

rzeczytajmy cał ą treść zadania jeszcze raz po jego rozwiązaniu.

róbmy to także, jeśli od

dł uższego czasu nie możemy wymyślić dobrego rozwiązania.

o chwili zastanawiania się nad zadaniem obojętne, czy z sukcesem, czy nie możemy nabrać nowego

spojrzenia, albo po prostu lepiej zrozumieć stawiany przed nami problem.

yć może właśnie wtedy

ponowne przeczytanie treści da nam poprawny obraz tego, czego się od nas oczekuje.

> Zaawansowane algorytmy 

< 7 >

1.4

Test owanie

Jak powszechnie wiadomo, tworzenie programów, które będą od razu działał y graniczy z cudem. Bardzo
często popeł niamy błędy, szczególnie w fazie kodowania rozwiązania. Nie powinno nas to zniechęcać,
trzeba tylko umieć sobie z tym problemem radzić.

Jedną z metod est czasem wielokrotne czytanie kodu po ego napisaniu. Niestety, podczas kon

kursu, gdzie esteśmy zdani tylko na siebie, est to zawodna metoda, gdyż ciężko krytycznie spo rzeć
na swo e dzieło i znaleźć w nim usterkę.

użo lepszym sposobem est testowanie programu lub ego fragmentów.

oda my naszemu pro

gramowi konkretne dane i sprawdźmy, czy oblicza poprawny wynik.

arto się przy tym zastanowić

i wybrać dane podchwytliwe czy złośliwe dla naszego algorytmu.

ażne est, aby samemu obliczyć wy

nik, na lepie inną metodą niż ta zaimplementowana w programie i porównać go z wynikiem programu.

robienie kilku testów est na pewnie szą metodą sprawdzenia kodu. Uwaga!

esty dostar

czane wraz z treścią zadania są na bardzo wielu konkursach bardzo proste i nie należy
wnioskować, że program działa ący na nich est poprawny.

1.5

„ Brut y”

Na zawodach w których mamy odpowiednio dużo czasu na takie zabiegi, bardzo dobre efekty przynosi
pisanie „ brutów” — programów, które działa ą szybko tylko dla bardzo mał ych testów, ale są proste
zarówno pod względem same idei rozwiązania, ak i napisanego kodu.

a ąc takiego „ bruta” możemy łatwo sprawdzać nasz program na wielu testach. Nie musimy się

bowiem martwić o liczenie odpowiedzi na kartce, wystarczy spytać „ bruta” o dobrą odpowiedź.

bar

dzo wielu zadaniach możemy wręcz losować testy automatycznie napisać kole ny prosty programik do
takiego losowania i sprawdzać, czy nasze rozwiązanie i „ brut” da ą ednakowe wyniki. Jeśli nie, to

est to sygnał do szukania błędów.

aka metoda szukania błędów przynosi stosunkowo na pewnie sze

rezultaty.

„ Bruta” możemy też wykorzystać w inny sposób. Jeśli nie esteśmy pewni w stu procentach naszego

rozwiązania i nie mamy czasu go uż poprawić, sprawdzić, itp., możemy zastosować metodę łączenia
dwóch programów w eden. o wczytaniu danych nasz nowy program może zadecydować, czy test est
bardzo mał y i w związku z tym bezpiecznie rozwiązywać go „ brutem” , czy też est na tyle duży, że
„ brut” nie da rady i trzeba zaryzykować i posł użyć się niepewnym ale szybszym rozwiązaniem.

akie

wy ście może spowodować przyznanie większe liczby punktów za dane zadanie na konkursach, gdzie
otrzymu e się punkty za każdy poprawnie rozwiązany test.

zadko ednak spowodu e poprawę wyniku

na zawodach, w których trzeba mieć całe zadanie dobrze rozwiązane, aby uzyskać akiekolwiek punkty.

odczas trwania tego kursu będziesz miał okaz ę kilkakrotnie przetestować te rady w praktyce

i wypracować swo ą własną taktykę na startowanie w zawodach.

2

St andard Templat e Library

rawdopodobnie przy te czy inne okaz i spotkałeś się uż z biblioteką

, a pewnie także wykorzysty

wałeś ą w swoich programach.

awiera ona wiele gotowych do użycia implementac i struktur danych

oraz algorytmów.

Niestety ta biblioteka często est nadużywana. Na przykład, ktoś używa multimap tam, gdzie

w zupeł ności starczyłaby zwykła tablica.

latego też biblioteką

za mu emy się szerze dopiero

w kursie dla zaawansowanych, gdy wiecie uż, co można zrobić prostymi metodami.

ntenc ą tego rozdział u est usystematyzowanie wiedzy o te bibliotece i poznanie sposobów do

brego e wykorzystywania w rozwiązaniach zadań algorytmicznych.

kilku mie scach pokażemy też

stosowane przez wielu zawodników sztuczki np. dyrektywy preprocesora , dzięki którym możemy pisać
trochę mnie kodu.

< 8 > 

Informatyka + 

Oczywiście nikt nie powinien się uczyć na pamięć różnych metod z biblioteki STL. Na większości

konkursów np. na Olimpiadzie n ormatyczne dostępna est dla zawodników dokumentac a biblioteki
podobna do te zamieszone na stronie http://www.sgi.com/tech/stl/.

late o też warto się z nią

zapoznać i nauczyć się z nie korzystać.

2.1

K ont ener vect or

rze ląd możliwości biblioteki STL zaczniemy od chyba na bardzie popularne o kontenera vector

który łączy w sobie cechy stosu i tablicy.

oświęcimy mu dość dużo czasu

dyż większość e o cech

odnosi się też do innych kontenerów.

by móc o wykorzystać w pro ramie zwykle piszemy

#include<vector>
using namespace std;

o powodu e dru i wiersz

est to wprowadzenie przestrzeni nazw std „ peł na nazwa” kontenera

vector

to std::vector.

atem aby zaoszczędzić sobie pisania te o std:: przed każdym wystąpie

niem cze oś z przestrzeni nazw biblioteki standardowe polecamy kompilatorowi by robił to za nas.

praktyce zawodowe o pro ramisty nie zawsze est to dobre rozwiązanie natomiast na konkursach

in ormatycznych est bardzo popularne.

ardzo ważną cechą kontenerów z biblioteki STL est to że możemy ich użyć do przechowywania

obiektów dowolne o typu. Stosu e się w tym celu zaawansowany mechanizm ęzyka

akim są sza

blony. Na przykład napisanie vector<int> v; powodu e utworzenie przez kompilator spec alne wers i
kontenera vector przystosowane do przechowywania zmiennych cał kowitoliczbowych. eżeli zdefi
niu emy klasę MojaKlasa to nic nie stoi na przeszkodzie by zadeklarować vector<MojaKlasa> vmk.

ożemy nawet zadeklarować vector<vector<MojaKlasa> > vvmk — est to vector który będzie

przechowywał kontenery vector zmiennych typu MojaKlasa. Uwaga: spac a między dwoma znakami
> >

est istotna — inacze kompilator mylił by e z operatorem przesunięcia bitowe o.
rzy rzy my się teraz kilku ważnie szym metodom o erowanym przez obiekty vector<T> v

• void v.push_ ack a

— dodawanie elementu a na końcu v. est to na tyle często używana

metoda że wiele osób na początku pro ramu używa dyrektywy #de ine

push_ ack

dzięki

które może pisać tylko v.

a

.

• void v.pop_ ack

— usunięcie ostatnie o elementu.

Uwaga:

e wz lędów wyda nościowych metoda ta est typu void czyli nic nie zwraca. eżeli

chcielibyśmy zapamiętać zde mowany element to możemy przed e o zd ęciem skorzystać z me
tody v. ack

która zwróci re erenc ę do ostatnie o elementu.

• v i

to odwołanie do ite o elementu v zupeł nie tak samo ak dla tablicy. Operator ten działa

w czasie stał ym.

etody push_ ack i pop_ ack działa ą w czasie zamortyzowanym stał ym.

arto wiedzieć w aki spo

sób uzysku e się taką wyda ność. Otóż vector pamięta wskaźnik na tablicę elementów odpowiednie o
typu.

oczątkowo est ona mała ma na przykład 5 elementów.

iedy po kilkukrotnym uruchomieniu

push_ ack

braku e w nie mie sca na nowy element wówczas alokowana est nowa dwa razy większa

tablica a zawartość stare est doń kopiowana.

Ćwiczenie 1.

rzucamy do początkowo puste o kontenera vector pewną liczbę elementów.

akłada ąc że est to realizowane tak ak opisano wyże udowodni że dodanie po edyncze o

elementu za mu e zamortyzowany czas stał y.

by prze rzeć wszystkie elementy kontenera vector można napisać pętlę

or

int i

; i <

int

v.si e

; i

...

> Zaawansowane algorytmy 

< 9 >

v.size()

zwraca wynik typu unsigned int dlatego rzutowanie na int jest istotne, jeżeli nie chcemy,

by kompilator męczył nas ostrzeżeniami. Można by też zadeklarować licznik jako zmienną typu unsigned

Powiedzmy jeszcze o ważnej metodzie swap dostępnej dla kontenerów biblioteki

.

ak nie

trudno zgadnąć, zamienia ona ze sobą kontenery przechowywane w dwóch zmiennych. o ciekawe, jest
to wykonywane w czasie stał ym niezależnie od wielkości struktury tak na prawdę podmieniane są tylko
pewne wskaźniki .

ontenerem podobnym do vector, który czasami się przydaje, jest deque — połączenie kolejki

i tablicy.

o operacji wykonywanych na kontenerze vector w czasie zamortyzowanym stał ym dodaje

jeszcze push_front i pop_front, czyli odpowiednio dołożenie i zdjęcie elementu z początku.

iestety

w praktyce ta struktura nie jest tak wydajna jak vector, dlatego też należy jej używać tylko jeżeli jest
to absolutnie konieczne.

2.2

It erat ory

ardzo ważnym i często używanym narzędziem biblioteki

są iteratory. Możemy na nie patrzeć jako

na specjalne wskaźniki, które potrafią przechodzić po elementach kontenerów.

kładnia jest zresztą

taka sama jak w przypadku wskaźników *it oznacza element, na który wskazuje iterator it, ++it
sł uży do zwiększenie iteratora, czyli przejście do kolejnego elementu kontenera, a --it do co ania się

1

.

olejność, w jakiej iterator przegląda elementy kontenera zależy od rodzaju kontenera.

by zadeklarować iterator dla odpowiedniego typu kontenera piszemy kontener::iterator it,

np. vector<int>::iterator it .

achowanie iteratorów dla różnych kontenerów może się mocno

od siebie różnić, stąd konieczność wykorzystania iteratora z odpowiedniej przestrzeni nazw jak np.
vector<int>::

.

Przeglądanie element ów

eżeli chcielibyśmy „ przeiterować” wszystkie elementy kontenera przydadzą się nam unkcje begin()

i end(), które zwracają pierwszy i ostatni iterator w kontenerze. Uwaga:

statni iterator nie wskazuje

na żaden obiekt przechowywany w kontenerze, dlatego nigdy nie należy się odwoł ywać do *(v.end()).

Możemy teraz w inny sposób napisać pętlę przeglądającą elementy v

for (vector<int>::iterator it

v.begin()

it

v.end()

++it)

...

Pętle tego typu wykorzystuje się często, a niestety wymagają one od nas dość dużo pisania.

by

zaoszczędzić sobie czas można próbować napisać makro, które dostając tylko nazwę kontenera i iteratora
tworzyłoby odpowiednią pętlę. Problemem jest to, że na podstawie kontenera zwykle nie można uzyskać
typu potrzebnego iteratora.

a szczęście w kompilatorze gcc, który jest wykorzystywany na większości

zawodów programistycznych, udostępniona jest unkcja __t peof(), dzięki której możemy napisać
następujące makro

define

(i t) for(__t peof((t).begin()) i (t).begin()

i

(t).end()

++i)

Później w programie, jeżeli chcemy pętlę przeglądającą wszystkie elementy kontenera v, wystarczy
napisać

(i v)

.

It erat ory w met odach

teratory są często argumentami i wynikami różnych metod. Przyjrzymy się takiej sytuacji na przykładzie

kontenera ist, czyli listy dwukierunkowej. ej główną przewagą w stosunku do vector czy też deque
jest to, że operacje wstawiania i usuwania pojedynczego elementu ze środka działają w czasie stał ym

do jej elementów nie możemy jednak odwoł ywać się jak do tablicy .

o wstawiania sł uży metoda .insert(it

)

, która umieszcza element o wartości

w liście

przed iteratorem it.

wracana wartość to iterator do właśnie wstawionego elementu.

1

Ist nieją też wersje operatorów ++ oraz -- stawiane za argument em, ale są one mniej wydajne.

< 10 > 

Informatyka + 

W kontenerze list dostępna jest metoda size. Należy jej używać z rozwagą, gdyż nie jest
ustalone, w jakim czasie ona działa. Może się okazać, że obliczenie rozmiaru listy będzie
wymagało przejrzenia wszystkic jej elementów, co będzie bardzo kosztowne.

latego gdzie

tylko można należy raczej używać metody l.empty(), która sprawdza czy lista l jest pusta

zamiast sprawdzać warunek l.size() > 0 .

2.3

Pary

rzy pisaniu programów bardzo często okazuje się, że c cemy przec owywać in ormacje zawarte w kilku

zmiennyc w jednym miejscu. Najbardziej naturalnym rozwiązaniem wydaje się zdefiniowanie klasy,
w której będą ukryte owe zmienne.

zęsto jednak wygodniej jest użyć par.

•

eklaracja pary złożonej ze zmiennyc typów T1 i T2 pair<T1, T2> p.

•

ierwszy i drugi element pary p.first i p.second.

•

tworzenie nowej pary make_pair(a,b)

ary są bardzo wygodnie, między innymi dlatego, że można je ze sobą porównywać za pomocą standar

dowyc operatorów.

perator < wyznacza porządek leksykograficzny na parac

to znaczy, że najpierw

porównujemy pierwsze pozycje z pary. eżeli są różne, to mamy już wyznaczony porządek dwóc par.

eżeli są równe, to porównujmy drugie pozycje par.

ary okazują się na tyle wygodne, że niekiedy używa się ic do przec owywania więcej niż dwóc

zmiennyc . Na przykład 4 obiekty można zgrabnie „ upakować” do pary złożonej z dwóc par.

by sprawniej korzystać z par często stosuje się dyrektywy define. wykle używa się skrótu

MP

zamiast make pair.

wa popularne sposoby skracania first, second to ,

oraz T,

.

2.4

K ont ener set

ontener set sł uży do przec owywania in ormacji o zbiorac uporządkowanyc elementów. lementy

w zbiorze nie mogą się powtarzać, co jest zgodne z matematycznym pojęciem zbioru.

ontener ten jest

zaimplementowany jako drzewo czerwono czarne jedno ze zrównoważonyc drzew poszukiwań .

zięki

temu, poniższe operacje wstawiania, usuwania i szukania elementu mają złożoność logarytmiczną.

• s.insert( )

próbuje wstawić element

do zbioru s.

wraca parę złożoną z iteratora wska

zującego na element równy

oraz wartości logicznej mówiącej, czy mu się udało. Wstawienie

do zbioru nie udaje się, gdy istnieje już w nim element równy .

• s.erase(it)

usuwa element wskazywany przez iterator it.

ardzo ważną cec ą tej unkcji jest

to, że wszystkie iteratory nie wskazujące na usuwany element pozostają poprawne, dalej można
się nimi posł ugiwać.

lement o wartości

można usuwać za pomocą unkcji s.erase( ).

• s.find( )

sł uży do znajdowania elementu w zbiorze, zwraca iterator do elementu o wartości

jeżeli taki iterator nie istnieje to zwraca jedyny iterator, który na nic nie wskazuje, czyli

s.end()

.

eżeli c cemy tylko przekonać się czy dany element występuje w zbiorze możemy sprawdzić

warunek s.co nt( ) > 0.

odobnym kontenerem jest m ltiset, który jednakże pozwala na przec owywanie kilku równyc ele

mentów.

> Zaawansowane algorytmy 

< 11 >

Uporządkowane elementy w zbiorze

Elementy przechowywane w kontenerach set i mutliset są uporządkowane (zwykle zgodnie z porząd-
kiem wyznaczanym przez operator <). Dwa przydatne fakty z tego wynikające:

• s.begin()

to iterator do najmniejszego elementu

•

Przeglądając kolejne elementy za pomocą iteratora (na przykład za pomocą makra FOREACH)

ędziemy widzieli elementy w kolejności niemalejącej (a w z iorze nawet ściśle rosnącej).

Ćwiczenie 2.

algorytmie Dijkstry potrze ny jest kopiec przechowujący dla każdego wierz-

choł ka jego odległość od wierzchoł ka startowego i o sł ugujący następujące operacje:

•

zmień wartość przechowywaną dla pewnego wierzchoł ka (to może wymagać dodania
tego wierzchoł ka jeżeli wcześniej nie yło go w kopcu)

•

znajdź jeden z wierzchoł ków o najmniejszej odległości zwróć tę odległość i usuń go
z kopca.

ak można prosto zrealizować powyższe operacje przy użyciu z ioru z i lioteki

Proponujemy wykorzystać set<pair<int, int> >.

omawianych kontenerach są jeszcze dwie ważne metody:

• s.lower_bound(x)

(ang. dolne ograniczenie) zwraca iterator do pierwszego elementu którego

wartość jest nie mniejsza niż x.

• s.upper_bound(x)

(ang. górne ograniczenie) zwraca iterator do pierwszego elementu którego

wartość jest większa niż x.

o u przypadkach gdy nie istnieje taki element zwracany jest iterator s.end().

Para funkcji o tych samych nazwach wystąpi jeszcze przy omawianiu algorytmów z i lioteki

dlatego do rze jest zrozumieć dlaczego akurat takie są wartości przez nie zwracane. Pomoże w tym
poniższe ćwiczenie:

Ćwiczenie 3.

asz dany multiset<int> ms. apisz pętlę która przechodzi po iteratorach

którym odpowiadają wartości równe 1729.

Defi niowanie wł asnego porządku

zasami chcemy y porządek elementów w z iorze ył inny niż standardowy.

tym celu powinniśmy

zadeklarować specjalną klasę która ędzie miała tylko jedną metodę (a dokładniej operator ()) po-
równującą dwa o iekty określonego typu.

etoda ta musi zachowywać się tak jak < a więc zwracać

wartość true wtedy i tylko wtedy gdy pierwszy argument jest mniejszy od drugiego.

Poniżej prezentujemy przykładową klasę która umożliwia porównywanie elementów typu e tor

względem ich dł ugości:

stru t por_ e

bool operator() ( onst

e tor<int>

a,

onst

e tor<int>

b)

return a.si e() < b.si e()

wróćmy uwagę na jeden z argumentów operatora: onst

e tor<int>

a

.

rgumentem jest refe-

rencja do o iektu a dzięki czemu unikamy kopiowania. o więcej jest ona stała gdyż chcemy upewnić
się że porównywanie dwóch elementów nie zmieni żadnego z nich.

< 12 > 

Informatyka + 

Teraz możemy zadeklarować set złożony z vector<int> uporządkowanych po liczbie elementów:

set<vector<int>, por_vec> zb;

Własną klasę porównującą możemy też wykorzystać, dy chcemy przechowywać w zbiorze elementy,
które nie mają zdefiniowane o operatora <

2.5

map

map<T1, T2>

to słownik przechowujący „ tł umaczenia” obiektów typu T1 na te typu T2

biekty

typu T1 nazywamy kluczami, a typu T2

wartościami W słowniku do jedne o klucza może być

przyporządkowana tylko jedna wartość

rzykładem słownika może być map<string, int> kalendarz przyporządkowujący nazwie mie

siąca je o numer np „ czerwiec”

6

Wy odna składnia pozwala nam korzystać ze słownika jak

z tablicy np : kalendarz["marzec"] = 3;

oza tym map<T1, T2> m przypomina pod wz lędem używania set<pair<T1, T2> > terator

wskazuje na parę klucza i odpowiadającej mu wartości Wstawianie elementu może się odbywać za
pomocą unkcji m insert make_pair t1,t2

lub też za pomocą składni tablicowej

Wyszukiwanie

i usuwanie są analo iczne jak w przypadku zbioru z tą różnicą, że jako ar ument podaje się tylko klucz

eżeli za pomocą składni tablicowej odwołamy się do klucza k, który nie istnieje

w map<T1,T2> to zostanie wstawiona para make pair k, T2
T2

to bezparametrowy konstruktor obiektów T2, który zwykle reprezentuje domyślną war

tość na przykład 0, vector pusty

2.6

Sort owanie i wyszukiwanie binarne

aczynając od sortowania, zajmiemy się teraz ciekawszymi al orytmami dostępnymi w bibliotece T
r umentami unkcji sort p, k są dwa iteratory o dostępie swobodnym np vector<T>

iterator

,

ale też int dzięki czemu możemy stosować tę unkcję do zwykłej tablicy

stawia ona w kolejności

niemalejącej elementy od te o wskazywane o przez p do ostatnie o przed k

atem aby posortować

vector<int> v

należy napisać: sort v begin

, v end

eżeli chcemy sortować elementy, dla których nie ma zdefiniowane o operatora <, lub też chcemy je

ułożyć w innej kolejności to należy dodać unkcję porównującą

oniżej przykład unkcji do porównywa

nia elementów typu vector ze wz lędu na ich dł u ość

wróć uwa ę na jej podobieństwo do operatora

porównujące o wykorzystywane o przez kontener set

bool

por_vec

const vector<int>

a, const vector<int>

b

ret rn a size

< b size

;

by skorzystać z tej unkcji należy podać ją jako trzeci ar ument unkcji sort

ontynuując nasz

przykład, żeby posortować tablicę vector<int> t[1 ] napiszemy sort t,t 1 , por_vec

zasami chcemy, żeby po sortowaniu elementy, które są równe z odnie z obowiązującym

sposobem porównywania, pozostał y wz lędem siebie w niezmienionym porządku

a przy

kład dy w powyższej tablicy t był y dwa kontenery vector: a i b o trzech elementach to
jeżeli początkowo a był przed b, to powinno tak zostać po posortowaniu całej tablicy

or

towanie takie nazywamy stabilnym

est ono zaimplementowane w bibliotece T w unkcji

stable sort

Ćwiczenie 4.

aki będzie wynik sortowania z wykorzystaniem poniższej unkcji porównują

cej
bool por const int

a, const int

b

{ ret rn a >= b; }

zy na pewno jest ona dobrze napisana

> Zaawansowane algorytmy 

< 13 >

W yszukiwanie binarne

W posortowanej tablicy (lub kontenerze vector) możemy oczywiście wyszukiwać binarnie. Do szukania
wartości x w przedziale iteratorów (z dostępem swobodnym) od p do k sł użą unkcje

• binary_search(p, k, x)

— zwraca tylko wartość lo iczną oznaczającą czy x występuje w za

danym przedziale

• lower_bound(p, k, x)

i upper_bound(p, k, x) — podobnie jak w przypadku kontenera

set

zwracają one iterator do pierwsze o elementu odpowiednio nie mniejsze o niż x i większe o

niż x (lub też k jeżeli taki element nie istnieje).

2.7

Permut acje

W rozwiązaniac o dużej złożoności czasowej które sprawdzają wszystkie możliwości zdarza się ko
nieczność enerowania kolejnyc permutacji zbioru.

kazuje się że także do te o istnieje w bibliotece

otowa unkcja bool next_permutation(p, k). Wywołanie jej na przedziale iteratorów o do

stępie swobodnym powoduje zmienienie permutacji tworzonej przez elementy *p *(p+1) . . . *(k-1)
na następną w kolejności leksyko raficznej i zwróceniu true. eżeli taka permutacja nie istnieje (tzn.
aktualna jest największą w kolejności leksyko raficznej) to zwracana jest wartość false a permutacja
jest zmieniana na pierwszą w kolejności leksyko raficznej. ojedyncze wywołanie tej unkcji zajmuje co
najwyżej czas liniowy w stosunku do dł u ości permutowane o przedział u.

oniższy kod powoduje wypisanie wszystkic permutacji zbioru 1, 2, . . . , n

vector<int

v(n)

konstruowany

est vector o n elementach

for (int i

i < n

i++)

v i

i+1

do

for (int i

i < n

i++)

printf(

d

, v i )

printf(

n )

while (next_permutation(v be in(), v end()))

stnieje też unkcja prev permutation która zmienia permutację na poprzednią w porządku

leksyko raficznym.

3

Haszowanie

3.1

Czym jest haszowanie?

aszowaniu można myśleć jak o nadawaniu nowyc nazw obiektom z pewne o ustalone o zbioru.

elem aszowania jest najczęściej zmniejszenie puli możliwyc nazw (uniwersum) do odpowiednio

małe o rozmiaru.

rzykładowo jeśli rozważymy zbiór ludzi mieszkającyc w olsce i będziemy identy

fikować ic po imieniu i nazwisku to możliwyc par < imię nazwisko> może być praktycznie dowolnie
wiele. eśli jednak zec cemy uprościć sobie sytuację i identyfikować ludzi po ic inicjałac to wszyst
kic możliwyc inicjałów jest już tylko 32

2

= 1024 (przy założeniu że al abet liczy 32 litery). nicjał y

są w tym przypadku przykładem hasza (inaczej identyfikat ora lub kodu) czyli właśnie nowej nazwy
obiektu. nnym mniej naturalnym przykładem aszowania może być identyfikowanie ludzi po sumie
kodów

liter w ic imieniu i nazwisku modulo 1000. W tym wypadku możliwyc identyfikatorów

jest tyle co reszt czyli 1000.

iedy zmniejszenie uniwersum nazw może być korzystne Wyobraźmy sobie że c cemy przec o

wywać dla każde o człowieka z pewne o zbioru jakieś dane na przykład datę urodzenia. eśli nawet
przyjmiemy że imiona i nazwiska mają o raniczone dł u ości to wciąż nie będziemy w stanie zaalo
kować osobnej komórki pamięci dla każdej możliwej kombinacji < imię nazwisko> .

dru iej strony

< 14 > 

Informatyka + 

przechowując zbiór ludzi w słowniku będącym drzewem zrównoważonym, skazujemy się na złożoność
co najmniej liniowo-logarytmiczną ze względu na wielkość zbioru

onadto, porównywanie nazwisk może

okazać się bardzo kosztowne w przypadku gdy będą one dł ugie

orzystając z haszowania, moglibyśmy utworzyć tablicę o rozmiarze odpowiadającym rozmiarowi

uniwersum haszy, po czym dla każdego człowieka ze zbioru przechowywać jego dane w tej tablicy pod
indeksem, takim jak hasz z imienia i nazwiska

dczyt i zapis danych mógł by być zrealizowany w czasie

stał ym

czywistym problemem w powyższym rozwiązaniu są tzw kolizje, czyli przypadki, w których dwie,

różnie nazywające się osoby otrzymają takie same hasze

takiej sytuacji nasz algorytm będzie prze-

chowywał dane dwóch różnych osób w tym samym miejscu pamięci, co na pewno doprowadzi do błędu

stnieje wiele różnych metod rozwiązywania problemu kolizji, jedną z nich prezentujemy poniżej

3.2

Tablica haszująca

ablica haszująca rozmiaru M składa się z tablicy początkowo pustych list jednokierunkowych, prze-

chowujących obiekty z U oraz funkcji haszującej h : U → { 0, 1, . . . , M − 1}

unkcja ta, wcześniej

nie ormalnie nazywana „ zmianą nazwy” , generuje dla obiektów ze zbioru U hasze kody będące licz-
bami naturalnymi z przedział u [0, M − 1]

ależy nam na tym, aby hasze należał y właśnie do takiego przedział u gdyż odpowiadają one wtedy

komórkom tablicy

ablica haszująca T udostępnia następujące operacje

void insert(x) {

wstaw obiekt x na początek listy T[h(x)];

}

void delete(x) {

usuń obiekt x z listy T[h(x)];

}

bool

ind(x) {

i (obiekt x

est na liście T[h(x)])

return true;

else

return

alse;

}

zięki temu, że z każdym haszem jest związane nie jedno pole tablicy a lista, kolizje haszy nie powodują

utraty danych

eśli mamy pecha i okaże się, że wszystkie obiekty umieszczone w tablicy mają taki

sam hasz, złożoność powyższych operacji będzie liniowa względem ilości przechowywanych elementów

ednakże przy dobrym wyborze unkcji haszującej oraz założeniu, że liczba elementów w tablicy jest

rzędu O(M ) możemy założyć, że średni czas operacji na tablicy haszującej jest stał y

ozwiązywanie problemu kolizji haszy za pomocą list nosi nazwę met ody ł ańcuchowej

stnieje

wiele innych, bardziej e ektywnych metod radzenia sobie z kolizjami

ożna o nich przeczytać na przy-

kład w

Ćwiczenie 5.

aproponuj prostą unkcję haszującą, przypisującą ciągom znaków liczby cał -

kowite z przedział u [0 . . . 10000]

aimplementuj tablicę haszującą, która wykorzystuje woją

unkcję

orównaj szybkość jej działania na losowych danych testowych z drzewem zrówno-

ważonym np kontenerem set z

> Zaawansowane algorytmy 

< 15 >

3.3

Haszowanie sł ów

Technika haszowania znajduje zastosowanie w wielu algorytmach tekstowych. Ustalmy, dla uproszcze-
nia, że rozważamy słowa złożone z mał ych liter alfabetu angielskiego oraz, że kolejne litery alfabetu
utożsamiamy z kolejnymi liczbami naturalnymi (licząc od zera , to znaczy a

, b

, . . ., z

.

asze dla słów będziemy obliczać w następujący sposób

h(a

0

a

1

. . . a

n

) = (a

0

+ a

1

x + a

2

x

2

+ . . . + a

n

x

n

)

mod p

gdzie p jest dużą liczbą pierwszą a x dowolną ustaloną liczbą cał kowitą większą od rozmiaru alfabetu,
ale mniejszą od p.

artości tej funkcji haszującej możemy łatwo obliczać dla kolejnych, coraz to

dł uższych, sufiksów słowa, stosując zależność

h(a

i

a

i + 1

. . . a

n

) = (a

i

+ x h(a

i + 1

a

i + 2

. . . a

n

))

mod p

W yszukiwanie wzorca w t ekście

astanówmy się jak za pomocą powyższej metody haszowania zrealizować wyszukiwanie wzorca w tek-

ście.

rzyjmijmy następujące oznaczenia

•

m-literowy wzorzec to W = w

1

w

2

. . . w

m

•

n-literowy tekst to T = t

1

t

2

. . . t

n

•

hasz podsłowa t

i

. . . t

i + m − 1

(dł ugości m oznaczmy przez h

i

otrzebujemy szybko obliczyć hasze dla wszystkich m-literowych podsłów tekstu i porównać je z haszem

wzorca.

ając obliczony hasz h

i + 1

dla podsłowa t

i + 1

. . . t

i + m

możemy w czasie stał ym znaleźć hasz

podsłowa zaczynającego się na pozycji t

i

za pomocą łatwego wzoru

h

i

= (t

i

+ x h

i + 1

−

t

i + m

x

m

)

mod p

arto na początku stablicować sobie wartości potęg x modulo p.

ając obliczone wszystkie hasze h

i

porównujemy je kolejno z haszem wzorca h(W ).

eśli dla

pewnego i zachodzi h

i

= h(W ) to na pewno na pozycji i nie ma wystąpienia wzorca W .

eśli

natomiast zachodzi h

i

= h(W ) to z dużym prawdopodobieństwem na pozycji i jest wystąpienie

wzorca W .

czywiście w przypadku jednowymiarowym takie zastosowanie haszowania nie jest zazwyczaj uży-

wane gdyż mamy do dyspozycji szybki i łatwy do zaimplementowania algorytm

. ednakże w przy-

padku dwuwymiarowym haszowanie może okazać się interesującą alternatywą dla dość złożonego al-
gorytmu akera (problem wyszukiwania dwuwymiarowego wzorca w tekście został omówiony w kursie
“ truktury danych i ich zastosowania” .

Ćwiczenie 6.

pracuj szczegół y algorytmu wyszukiwania dwuwymiarowego wzorca w tek-

ście, opartego na haszowaniu słów.

Ćwiczenie 7.

próbuj rozwiązać zadanie Pociągi z

limpiady nformatycznej stosując

haszowanie (zadanie jest dostępne w serwisie

.

< 16 > 

Informatyka + 

4

Algoryt m K arpa-M illera-Rosenberga

Algorytm Karpa-Millera-Rosenberga (w skrócie KMR) jest algorytmem wyszukiwania wzorca w tek-
ście. Dzięki swojej interesującej bu owie znaj uje on także zastosowanie w wielu innyc problemac
tekstowyc . KMR opiera się na utworzeniu la słowa pewnej struktury zwanej sł ownikiem podsł ów
bazowych. truktura ta ma rozmiar Θ(n log n) (g zie n jest ł ugością słowa) i może być zbu owana
w takim samym czasie.

ak zwykle w analizie algorytmów tekstowyc zakła ać bę ziemy że al abet ma stał y rozmiar.

4.1

Sł ownik podsł ów bazowych

Konstrukcja słownika po słów bazowyc polega na obliczeniu aszy la wszystkic po słów wyjścio-
wego słowa o ł ugości 2

p

la p = 0, 1, . . . , log p .

ym razem je nak nie możemy użyć aszowania

takiego jak w roz ziale 3 g yż bę ziemy wymagali o

aszy nieco mocniejszyc własności.

cemy

bowiem nie opuścić o sytuacji w której różne słowa tej samej ł ugości otrzymają te same asze.

rzyjmijmy że bu ujemy strukturę słownika po słów bazowyc

la słowa S = s

0

s

1

. . . s

n − 1

. rzez

i d

p

[t] oznaczmy asz po słowa ł ugości 2

p

zaczynającego się na pozycji t (jeśli takie słowo nie istnieje to

przyjmujemy że i d

p

[t] = ∞ ). ablice i d

p

[] bę ziemy konstruować la kolejnyc p zaczynając o p = 0.

ablica i d

0

[] reprezentuje słowa ł ugości 1 czyli poje yncze litery. Doskonał ym aszem la poje ynczej

litery jest jej pozycja w al abecie (tzn. a

b

etc.). A zatem i d

0

[t] = s

t

.

akie i entyfikatory

speł niają oczywiście założenie unikalności.

astanówmy się teraz jak obliczyć tablicę i d

p+ 1

mając obliczoną tablicę i d

p

. Korzystać bę ziemy

z następującego oczywistego aktu

akt 1.

łowa s[i . . . i + 2

p+ 1

− 1] i s[j . . . j + 2

p+ 1

− 1] są równe wte y i tylko wte y g y są

równe słowa s[i . . . i + 2

p

− 1] i s[j . . . j + 2

p

− 1] oraz są równe słowa s[i + 2

p

. . . i + 2

p+ 1

− 1]

i s[j + 2

p

. . . j + 2

p+ 1

− 1].

nnymi słowy

wa słowa są równe g y ic lewe połowy są równe oraz ic prawe połowy są równe.

lustruje to poniższy rysunek

w

1

w

2

a

1

b

1

a

2

b

2

w

1

= w

2

⇔ a

1

= a

2

∧ b

1

= b

2

a po stawie aktu 1 można zauważyć że obrym aszem i d

p+ 1

[t] jest para (i d

p

[t], i d

p

[t + 2

p

]). My

je nak nie c cemy przec owywać par tylko zamienić je na nowe i entyfikatory w postaci kolejnyc liczb
naturalnyc . Aby to osiągnąć musimy posortować leksykograficznie wszystkie takie pary i entyfikato-
rów a następnie przeglą ając je o najmniejszyc

przy zielać nowe asze w postaci kolejnyc liczb

naturalnyc .

czywiście takie same pary muszą otrzymać ten sam asz.

arto w tym miejscu zaznaczyć że ważne jest aby na każ ym etapie sortować pary i entyfika-

torów w kolejności niemalejącej. ak wkrótce zobaczymy bę zie to miało kluczowe znaczenie przy
porównywaniu leksykograficznym po słów.

auważmy że asze la każ ej

ł ugości słów są liczbami

z prze ział u [0, max(n, |Σ |)] przez co możemy sortowanie par zaimplementować w czasie liniowym np.
używając sortowania kubeł kowego.

to (nieco okrojona) implementacja unkcji build KMR(s) konstruującej słownik po słów bazo-

wyc

la słowa s i zapisującej go w tablicy ids[].

> Zaawansowane algorytmy 

< 17 >

/* Para identyfikatorów, których zbiór będziemy sortowali.

Aby móc zapisać wynikowy hasz musimy pamiętać też indeks
słowa, któremu odpowiada dana para */

struct Pair

int p , p , inde

/* tablica

dwuwymiarowa

identyfikatorów */

ector

ector int

ids

oid build

strin

s

ector int

curr id s.size

ector Pair

pairs

/* hasze słów dłu ości

to kody symboli alfabetu */

for int i

i

s.size

i

curr id i

int

s i

ids.push back curr id

int p

while p

s.size

/* dla kole nych potę

dwó ki p */

curr id.resize s.size

p

pairs.resize s.size

p

for int i

i

s.size

p

i

pairs i .p

ids.back

i

pairs i .p

ids.back

i

p/

pairs i .inde

i

/* posortu

kubełkowo pary identyfikatorów */

bucket sort pairs

/* przydziel nowe identyfikatory */
int new id
for int i

i

pairs.size

i

if i

pairs i

pairs i

new id

curr id pairs i .inde

new id

ids.push back curr id

p *

W powyższym fragmencie kodu pominięty został algorytm sortowania kubeł kowego.

Ćwiczenie 8. Jak zmieni się złożoność funkcji build

gdy zamiast sortowania ku-

beł kowego zastosujemy sortowanie przez scalanie

aimplementuj obie wersje algorytmu

i porównaj czasy ic działania dla dł ugic słów w drugiej wersji możesz wykorzystać funkcję
sort

z

.

< 18 > 

Informatyka + 

4.2

Porównywanie podsł ów

Mając zbudowany słownik podsłów bazowych możemy w czasie stał ym sprawdzić, czy dwa podsłowa są
równe. Oczywiście jest sens sprawdzać równość tylko słów tej samej dł u ości. eśli dł u ość porównywa
nych słów jest potę ą dwójki, sprawdzenie równości sprowadza się do porównania haszy z odpowiedniej
tablicy.

o, jeśli tak nie jest Można skorzystać z prostej obserwacji, podobnej do aktu

Fakt 2.

iech dane będą słowa s

1

i s

2

dł u ości n. iech p będzie największą liczbą cał kowitą,

taką, że 2

p

n. łowa s

1

i s

2

są równe wtedy i tylko wtedy, dy są równe słowa s

1

[0 . . . 2

p

− 1]

i s

2

[0 . . . 2

p

− 1] oraz są równe słowa s

1

[n − 2

p

. . . n − 1] i s

2

[n − 2

p

. . . n − 1].

w

1

w

2

a

1

b

1

a

2

b

2

w

1

= w

2

⇔ a

1

= a

2

∧ b

1

= b

2

orzystając z aktu

wystarczy porównać najdł uższe prefiksy oraz najdł uższe sufiksy, których dł u ości

są potę ami dwójki. eśli założymy, że na początku stablicowaliśmy dla każdej możliwej dł u ości pod
słowa największą potę ę dwójki nie większą niż ta dł u ość, porównywanie podsłów można zrealizować
w czasie stał ym.

eśli przy konstrukcji słownika podsłów bazowych, za każdym razem sortowaliśmy pary identyfi

katorów niemalejąco, to możemy w analo iczny sposób zrealizować w czasie stał ym porównywanie
leksyko raficzne podsłów.

terminach oznaczeń na powyższej ilustracji oznacza to, że wystarczy po

równać leksyko raficznie parę (a

1

, b

1

) z parą (a

2

, b

2

).

o zrobić w przypadku słów różnej dł u ości

ajpierw porównać krótsze słowo z prefiksem dł uższe o o tej samej dł u ości.

przypadku, dy te

okażą się równe, mniejsze leksyko raficzne będzie słowo krótsze.

4.3

Najdł uższe powt arzające się podsł owo

astanówmy się najpierw, jak sprawdzić, czy w słowie istnieją dwa równe podsłowa ustalonej dł u ości.

ażdemu takiemu podsłowu odpowiada para identyfikatorów dwóch krótszych podsłów jak na ilustra

cji do aktu

. Możemy wszystkie takie pary posortować kubeł kowo w czasie liniowym a następnie

sprawdzić czy nie ma dwóch takich samych. eśli dodatkowo, obok pary zapamiętamy indeks w tablicy,
będziemy mo li takie powtarzające się podsłowo łatwo odtworzyć.

eśli w słowie istnieją dwa równe podsłowa dł u ości d, to istnieją również dwa równe podsłowa

każdej dł u ości mniejszej od d są nimi na przykład prefiksy podsłów dł u ości d .

ykorzystując

tę obserwację możemy znaleźć najdł uższe powtarzające się podsłowo w czasie O(n log n) stosując
wyszukiwanie binarne po je o dł u ości.

Ćwiczenie 9.

ak znaleźć najdł uższe podsłowo, które występuje w tekście dokł adnie k

razy

4.4

Najdł uższe wspó ne podsł owo

l orytm znajdowania najdł uższe o wspólne o podsłowa dwóch słów s

1

i s

2

jest analo iczny do al o

rytmu szukające o powtarzające o się podsłowa.

ystarczy zbudować słownik podsłów bazowych dla

słowa s

1

# s

2

dzie „

” jest symbolem nie występującym w al abecie , a następnie znaleźć najdł uższe

powtarzające się podsłowo.

by za warantować, że znalezione podsłowo występuje zarówno w s

1

jak

i w s

2

a nie na przykład dwukrotnie w s

1

musimy przy sortowaniu par identyfikatorów pamiętać

dodatkowo, z które o słowa pochodzi dana para i akceptować tylko powtórzenie pary z różnych słów.

> Zaawansowane algorytmy 

< 19 >

5

M aksymalny przepł yw

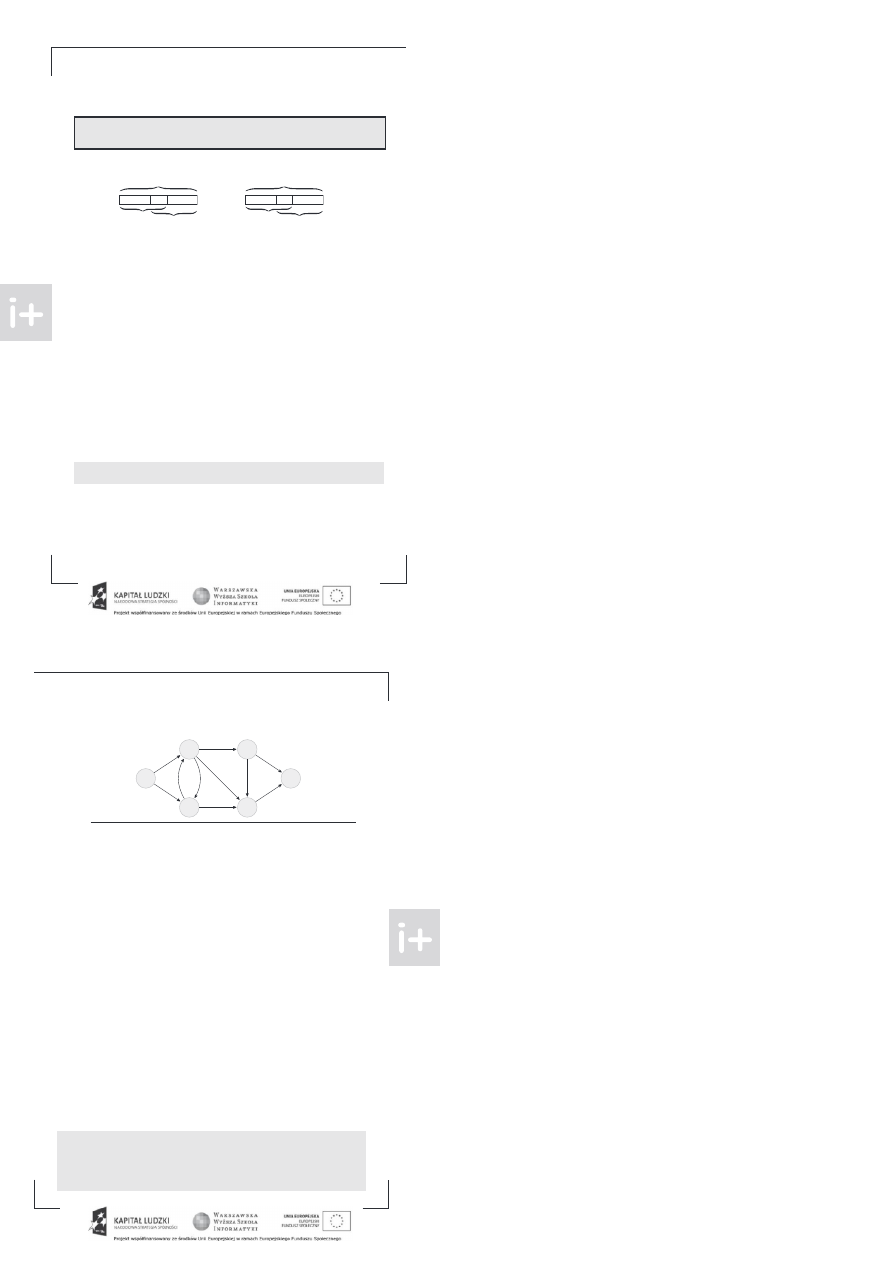
Wyobraźmy sobie, że planujemy sieć rurociągów, która ma za zadanie transportować ropę ze złoża
do rafinerii

amy już mapę z zaznaczonymi rurami, o każdej z nic wiemy, jaka jest jej maksymalna

przepustowość ilość przepł ywającej ropy w jednostce czasu

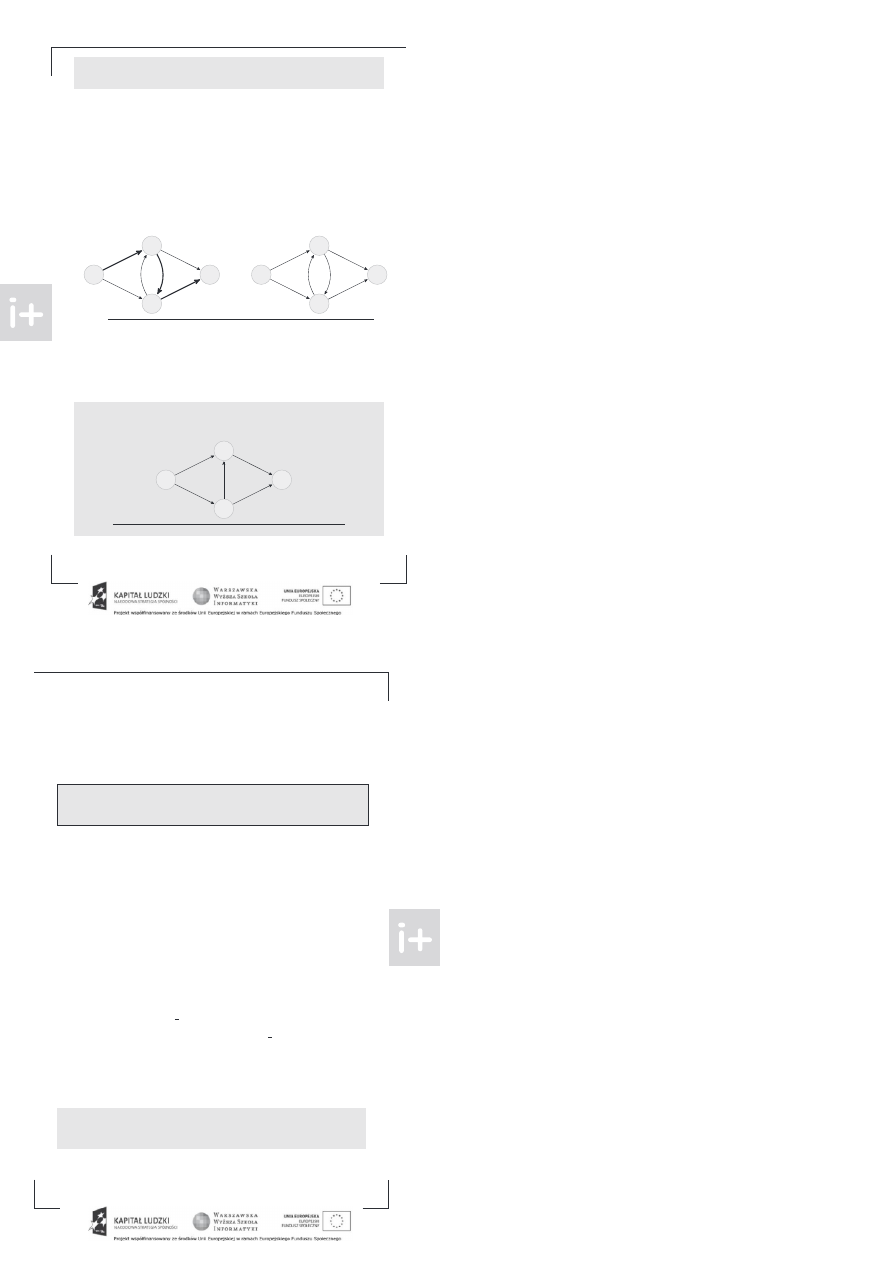
Przykładowa sieć rurociągów z przepust owościami

astanawiamy się teraz, jaka jest przepustowość całej sieci, czyli ile ropy może przez nią przepł ynąć

od złoża oznaczonego numerem 1 do rafinerii numer 6

ozważamy właśnie problem poszukiwania

maksymalnego przepł ywu, który jest tematem tego rozdział u

Formalne ujęcie problemu

amy dany gra skierowany G, z wyróżnionymi dwoma wierzc oł kami źródłem s i ujściem t

ażda

krawędź w grafie ma określoną przepustowość dla krawędzi między wierzc oł kami u i v oznaczamy ją
przez c(u, v) Wymaga to założenia, że między dwoma wierzc oł kami, w jedną stronę, istnieje tylko
jedna krawędź W celu uproszczenia dalszego opisu możemy przyjąć też, że jeżeli w grafie istnieje
krawędź (u, v) to jest także krawędź (v, u)

by dany gra zaczął speł niać to ograniczenie wystarczy

dodać doń krawędzie „ powrotne” z przepustowością równą 0

ra zadany w ten sposób będziemy nazywali siecią, w której będziemy szukali przepł ywu f

est

to unkcja, która dla dwóc wierzc oł ków u i v sieci G mówi nam, ile jednostek przemieszcza się
bezpośrednio między u i v

znacza to, że zawsze f (u, v)

c(u, v) przepł yw przez krawędź między

dwoma wierzc oł kami nie może być większy niż jej przepustowość

stalmy też, że f (u, v) = − f (v, u),

czyli z dodatnim przepł ywem w jedną stronę jest związany ujemny w drugą

rzez przepł yw wc odzący do wierzc oł ka u rozumiemy sumę dodatnic elementów postaci f (v, u),

dla dowolnego wierzc oł ka v

atomiast przepł yw wyc odzący z u to suma dodatnic elementów po

staci f (u, v dla dowolnego wierzc oł ka v

cemy aby przesyłane jednostki nie akumulował y się

w wierzc oł kac , czyli aby dla każdego wierzc oł ka przepł yw wc odzący był równy przepł ywowi wy
c odzącemu

edynie źródło i ujście mogą nie speł niać tego warunku

godnie z nazwą, w źródle

przepł yw wyc odzący może być większy niż przepł yw wc odzący, natomiast w ujściu odwrotnie prze
pł yw wc odzący może być większy od wyc odzącego

ożna udowodnić, że różnica przepł ywu wyc odzącego i wc odzącego do źródła, jest równa róż

nicy przepł ywu wc odzącego i wyc odzącego z ujścia Wielkość tę nazywamy wartością przepł ywu
i oznaczamy W (f ) Maksymalny przepł yw to ten o największej wartości przepł ywu

rawędź (u, v) będziemy nazywali użyteczną, jeżeli f (u, v) < c(u, v)

o krawędzi użytecznej

możemy zawsze przesłać jakiś dodatkowy przepł yw

auważmy, że krawędź (u, v) może być użyteczna,

nawet jeśli ma przepustowość równą 0

zieje się tak gdy przepł yw f (u, v) jest ujemny, czyli gdy z v

do u są przesyłane jakieś jednostki − f (u, v) = f (v, u) > 0

Ćwiczenie 10.

rzy opisie problemu przyjęliśmy założenie, że w grafie nie ma wielokrot

nyc krawędzi między żadną parą wierzc oł ków

ardzo prosto jest zmienić dowolny gra

z przepustowościami do takiej postaci wystarczy krawędzie wielokrotne zastąpić jedną, któ
rej przepustowość będzie sumą przepustowości tamtyc

zy można na podstawie przepł ywu znalezionego w tak zmodyfikowanym grafie skonstruować

przepł yw w oryginalnym grafie

< 20 > 

Informatyka + 

Ćwiczenie 11. Mamy daną sieć w której znajduje się kilka źródeł i kilka ujść. Jak należy
zmienić tę sieć, aby miała po jednym źródle i ujś iu, ale przepł ywy w zmodyfikowanej sie i
dał y się łatwo przełożyć na te w ory inalnej.

5.1

M et oda Forda-Fulkersona

Metoda orda ulkersona jest podstawą wielu al orytmów rozwiązują y

problem maksymalne o prze

pł ywu. ole a ona na konstruowaniu kolejny

przepł ywów aż do osią nię ia przepł ywu maksymalne o.

a zynamy od puste o przepł ywu f (u, v) = 0 dla dowolny

par wierz oł ków .

astępnie szu

kamy ścieżki powiększającej, zyli ś ieżki od źródła do ujś ia złożonej tylko z użyte zny

krawędzi.

Jeżeli takiej ś ieżki nie ma, to mamy już maksymalny przepł yw. Jeżeli zaś znaleźliśmy ś ieżkę złożoną
z wierz oł ków s = v

1

, v

2

, . . . , v

n

= t, to możemy powiększyć przepł yw.

a każdej z krawędzi od v

i

do v

i + 1

możemy przesłać o najwyżej c(v

i

, v

i + 1

) − f (v

i

, v

i + 1

), zatem możemy powiększyć przepł yw

na każdej krawędzi ze ś ieżki o najmniejszą z ty

wartoś i.

la krawędzi (u, v) wielkość c(u, v)− f (u, v)

nazywa się niekiedy przepustowością residualną.

a poniższym przykładzie zostało zilustrowana jedna aza metody orda ulkersona. a tym i na na

stępny

obrazka

etykietki nad krawędzią od u do v będą posta i f (u, v)/ c(u, v).

by nie kompli

kować niepotrzebnie dia ramu zęść krawędzi o zerowej przepustowoś i zostanie pominięta.

s

t

s

t

Wyszukanie ścieżki powiększającej i poprawienie przepł ywu

ietrudno uwierzyć w to, że metoda ta zwró i poprawną odpowiedź.

ormalnie dowiedziemy te o

tro ę później, w twierdzeniu o maksymalnym przepł ywie i minimalnym przekroju.

sza ujmy teraz zas działania metody orda ulkersona.

ażdą azę znalezienie ś ieżki powięk

szają ej i poprawienie przepł ywu można zrealizować za pomo ą pojedyn ze o przeszukiwania ra u

wszerz lub w łąb .

każdej azie zwiększamy przepł yw o o najmniej 1, zatem maksymalna li zba

az jest równa wartoś i maksymalne o przepł ywu. Jeżeli li zbę krawędzi ra u ozna zymy przez m, to

omawiana metoda działa w zasie O(W (f

m ax

) m).

Ćwiczenie 12.

poniższym rafie znajdź maksymalny przepł yw.

ałóżmy, że znajdujemy o wykorzystują metodę orda ulkersona. Jaka jest minimalna

i maksymalna możliwa li zba az, które wykonujemy

s

t

10

9

10

9

10

9

10

9

Graf z podanymi przepust owościami krawędzi

> Zaawansowane algorytmy 

< 21 >

5.2

Algoryt m Edmondsa-K arpa

Ostatnie ćwiczenie pokazuje, że metoda Forda-Fulkersona może działać wolno nawet dla bardzo ma-
ł ych grafów, gdyż liczba faz może okazać się bardzo duża

by poprawić tę sytuację w algorytmie

dmondsa- arpa który jest ukonkretnieniem tej metody poszukujemy zawsze możliwe najkrótszej

tzn o najmniejszej liczbie krawędzi ścieżki powiększającej

ożemy tego prosto dokonać za pomocą

przeszukiwania wszerz Okazuje się, że po dodaniu tego ograniczenia uzyskujemy algorytm wydajny nie-
zależnie od wielkości maksymalnego przepł ywu liczba faz w sieci o n wierzchoł kach i m krawędziach
wynosi co najwyżej nm

by udowodnić powyższe ograniczenie skorzystamy z następującego lematu

Lemat .
Odległością wierzchoł ków nazwiemy dł ugość najkrótszej ścieżki między nimi złożonej tylko
z krawędzi użytecznych

kolejnych iteracjach algorytmu

dmondsa- arpa odległość do-

wolnego wierzchoł ka od źródła nie maleje

owód tego lematu jest trochę techniczny, nie będziemy go tu przedstawiać

ainteresowanych odsyłam

do „

prowadzenia do algorytmów”

rzystąpmy teraz do dowodu oszacowania

każdej ścieżce powiększającej istnieją dwa kolejne wierzchoł ki v

i

i v

i + 1

, dla których przepustowość

residualna c(v

i

, v

i + 1

) − f (v

i

, v

i + 1

) jest najmniejsza na tej ścieżce Oznacza to, że po powiększeniu

przepł ywu wzdł uż tej ścieżki nowy przepł yw między v

i

i v

i + 1

wyniesie f (v

i

, v

i + 1

) + (c(v

i

, v

i + 1

) −

f (v

i

, v

i + 1

)) = c(v

i

, v

i + 1

), a więc krawędź od v

i

do v

i + 1

przestanie być użyteczna

edyną sytuacją,

po której znowu stanie się użyteczna, jest przesłanie przepł ywu od v

i + 1

do v

i

eźmy teraz dowolną krawędź od u do v i obliczmy ile razy w czasie wykonania algorytmu

dmondsa- arpa może być ona krawędzią o najmniejszej przepustowości residualnej na ścieżce po-

większającej

rzez d oznaczmy odległość u od źródła tuż przed jakaś fazą algorytmu, w której usta-

lona krawędź będzie tą o najmniejszej przepustowości residualnej

onieważ ścieżka powiększająca jest

najkrótszą w grafie użytecznych krawędzi, to odległość v od źródła wynosi d+ 1

godnie z tym, co po-

wiedzieliśmy wcześniej, po tej fazie krawędź (u, v) przestanie być użyteczna Oznacza to, że nie będzie
też w żadnej ścieżce powiększającej, dopóki nie prześlemy przepł ywu z v do u

takim zaś momencie

odległość od źródła do v wyniesie co najmniej d + 1 bo odległości nie maleją, zgodnie z lematem ,
a v będzie na najkrótszej ścieżce ze źródła do u, zatem odległość u wyniesie nie mniej niż d + 2

odsumowując powyższy wywód pomiędzy dwoma fazami, w których ustalona krawędź od u do

v będzie tą o najmniejszej przepustowości residualnej, odległość od źródła do u musi się zwiększyć co
najmniej o 2

ako, że największa możliwa odległość to n, każda krawędź może być tą o najmniejszej

przepustowości residualnej co najwyżej

n
2

razy

szystkich krawędzi jest m, a w każdej fazie musi być jakaś krawędź o najmniejszej przepustowości

residualnej, zatem rzeczywiście wszystkich faz będzie nie więcej niż

n
2

m, czyli O(nm)

owyższe ograniczenie na liczbę faz pozwala podać oszacowanie złożoności algorytmu dmondsa-

arpa wynosi ono O(nm

2

) co najwyżej nm faz, każdą wykonujemy w czasie m

stnieją szybsze

sposoby wyszukiwania maksymalnego przepł ywu, oparte o metodę Forda-Fulkersona algorytm

inica

oraz algorytm

alhotry,

umara i

aheshwariego

ą one jednak dość skomplikowane, także w imple-

mentacji

ainteresowani mogą o nich poczytać w książkach „ ombinatoryka dla programistów”

oraz „ lgorytmy optymalizacji dyskretnej”

Ćwiczenie 13.

aimplementuj algorytm dmondsa- arpa

Wskazówka:

łożoność algorytmu powoduje, że zwykle dane nie są zbyt duże i można so-

bie pozwolić na posł użenie się reprezentacją grafu w postaci macierzy sąsiedztwa, a także
trzymanie aktualnych wartości przepł ywu w tablicy kwadratowej

< 22 > 

Informatyka + 

5.3

T wierdzenie o maksymalnym przepł ywie i minimalnym przekroju

Podział wierzchoł ków sieci G o źródle s i ujściu t na dwa zbiory S i T takie, że s ∈ S a t ∈ T nazywamy
przekrojem grafu G.

ówczas przepustowością przekroju nazywamy sumę wszystkich rze ustowości

krawędzi (u, v), które rowadzą z S do T czyli u ∈ S i t ∈ T .

znaczamy ją rzez c(S, T ).

atomiast

sumę rze ł ywów rzez krawędzie rowadzące z S do T nazywamy przepł ywem netto rzez rzekrój
i oznaczamy f (S, T).

ietrudno zauważyć, że rze ł yw netto rzez rzekrój jest nie większy niż jego

rze ustowość f (S, T)

c(S, T ).

o więcej, rze ł yw netto rzez dowolny rzekrój jest równy wartości rze ł ywu. Gdy rzekrój składa

się z dwóch zbiorów, w którym jednym jest tylko źródło, a w drugim wszystkie ozostałe wierzchoł ki
to o rostu definicja rze ł ywu netto i wartości rze ł ywu okrywają się.

by udowodnić ten fakt

dla dowolnego odział u wystarczy zauważyć, że rzekroje S i T oraz S ∪ { x} i T \ { x} mają taką
samą wartość rze ł ywu netto o ile x = t . est tak gdyż różnica tych dwóch rze ł ywów netto
f (S, T ) − f (S ∪ { x} , T \ { x} ) równa jest sumie elementów ostaci f (s

1

, x) dla s

1

∈ S odjąć suma

f (x, t

1

) dla t

1

∈ T .

związku z tym, że − f (x, t

1

) = f (t

1

, x) otrzymujemy, że szukana różnica to

o rostu suma f (y, x) dla wszystkich wierzchoł ków y, czyli różnica wchodzącego i wychodzącego z x
rze ł ywu. a zaś wartość jest równa 0.

formuł ujmy teraz i udowodnimy bardzo ważne twierdzenie

T wierdzenie o maksymalnym przepł ywie i minimalnym przekroju.

danej sieci G jest określony rze ł yw f .

ówczas nastę ujące warunki są równoważne

.

rze ł yw jest maksymalny

. nie istnieje ścieżka owiększająca

. istnieje rzekrój, którego rze ustowość jest równa wielkości rze ł ywu

owód składa się z trzech im likacji

1 ⇒ 2 dowód nie w rost jest trywialny. eżeli istniałaby ścieżka owiększająca to moglibyśmy

wzdł uż niej zwiększyć rze ł yw f co oznacza, że nie był on maksymalny.

rzeczność.

2 ⇒ 3

iech S będzie zbiorem tych wierzchoł ków, które można odwiedzić ze źródła idąc tylko

o użytecznych krawędziach, a T

ozostał ym zbiorem wierzchoł ków. Ponieważ nie ma ścieżki owięk

szającej, to źródło t ∈ T, a zatem S i T jest

ewnym rzekrojem grafu.

godnie z definicją, między S i T nie istnieje żadna użyteczna krawędź, a zatem dla dowolnych

s

1

∈ S, t

1

∈ T

ołączonych krawędzią mamy f (s

1

, t

1

) = c(s

1

, t

1

). Gdy zsumujemy te równości dla

wszystkich możliwych s

1

i t

1

o lewej stronie otrzymamy rze ł yw netto rzez rzekrój S i T a więc

W (f ) zgodnie ze wcześniejszym s ostrzeżeniem , a o rawej rze ustowość rzekroju.

3 ⇒ 1

la dowolnego rzekroju S i T mamy, że f (S, T )

c(S, T ), czyli rze ustowość dowolnego

rzekroju stanowi górne ograniczenie na wielkość rze ł ywu rzez ten rzekrój a zatem też na wielkość
rze ł ywu w sieci . eżeli zatem istnieje rzekrój, dla którego mamy równość między rze ł ywem netto,

a rzekrojem to tym samym nas rze ł yw osiąga największą możliwą wartość.

łaśnie zakończyliśmy dowód twierdzenia. Przy okazji okazaliśmy też formalnie o rawność me

tody orda ulkersona dla sieci o cał kowitoliczbowych rze ustowościach algorytm kończymy, gdy nie
ma już żadnej ścieżki owiększającej, wtedy też uzyskany rze ł yw jest maksymalny. Gdy rze usto
wości są cał kowitoliczbowe, w każdej fazie zwiększamy wartość rze ł ywu o co najmniej 1.

atem

metoda orda ulkersona zawsze się zakończy wykonamy tylko skończenie wiele faz, gdyż skończona
jest wielkość minimalnego rzekroju, który ogranicza z góry wielkość rze ł ywu.

Ćwiczenie 14.

iemy już, że wielkość maksymalnego rze ł ywu jest równa minimalnej

rze ustowości rzekroju. ak możemy wykorzystać metodę orda ulkersona do znalezienia
rzekroju, który ma minimalną rze ustowość

Notatk  

< 23 >

5.4

Przekroje w zadaniach

Okazuje się, że udowodnione właśnie twierdzenie ma znaczenie nie tylko teoretyczne. Na konkursach
zdarzają się trudne zadania, których rozwiązanie polega właśnie na wskazaniu minimalnego przekroju.

rzyjrzyjmy się następującemu przykładowi

pewnym regionie mieszkają dwa wrogo nastawione do sie ie plemiona

r uzanie i

a

nanici.

regionie tym znajduje się wiele wiosek, każda z nich jest zamieszkana przez

mieszkańców jednego plemienia. O ecnie planowane jest zasiedlenie kilku kolejnych wio
sek.

iesz, które wioski są zamieszkane przez r uzan, które przez ananitów, a które czekają

na zasiedlenie.

ając dany gra opisujący drogi między wioskami wskaż takie zasiedlenie,

które zminimalizuje licz ę dróg łączących wioski zamieszkane przez różne plemiona.

dy z góry wiemy, w jaki sposó należy rozwiązać zadanie, nie wydaje się ono ardzo trudne. Należy

z udować sieć, gdzie źródłami ędą wioski zamieszkane przez r uzan, a ujściami te ananickie.

Sieć reprezent ująca wioski oraz poprawne rozwiązanie

(pogrubione są krawędzie liczone w przepustowości przekroju)

ażdy przekrój S i T w takim grafie ędzie stanowił w istocie podział wiosek na ar uzańskie i ananic

kie oczywiście wszystkie źródła ędą w S, a wszystkie ujścia w T .

rzepustowością przekroju ędzie

licz a dróg łączących wioski zamieszkałe przez

r uzan i

ananitów. icz a takich dróg ma yć jak

najmniejsza, zatem poszukiwany podział jest wyznaczany przez minimalny przekrój.

6

Skojarzenia

Skojarzeniem w grafie nazywamy taki podz iór jego krawędzi, że żadne dwie nie stykają się w wierz
choł ku. nnymi słowy z żadnego wierzchoł ka nie wychodzą dwie krawędzie ze skojarzenia.

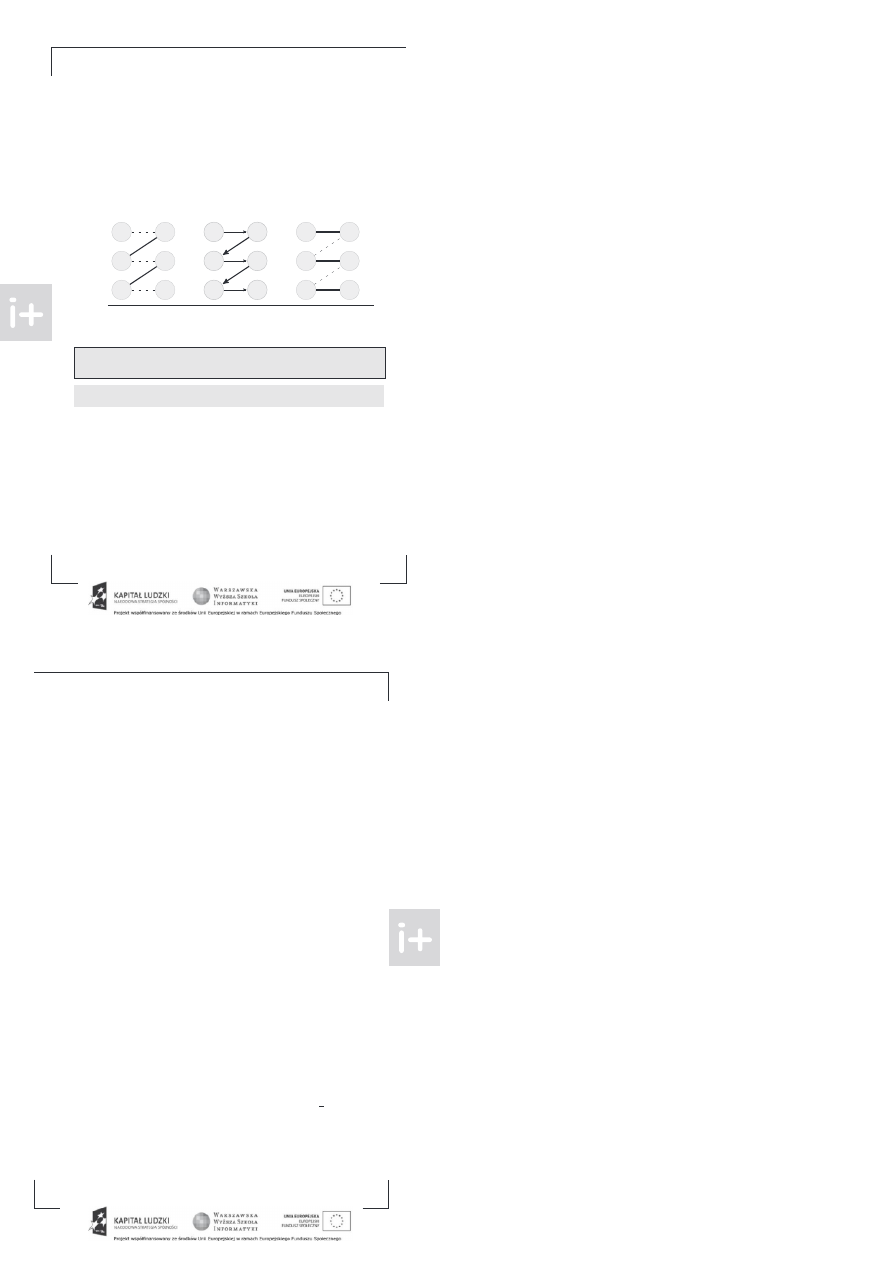
Skojarzenia w grafie i grafie dwudzielnym

ra G nazywamy dwudzielnym, gdy jego wierzchoł ki można podzielić na dwa z iory X i Y w taki

sposó , że nie ma krawędzi pomiędzy wierzchoł kami z jednego z ioru a więc każda krawędź jest po
staci (x, y)gdzie x ∈ X oraz y ∈ Y .

mówmy się na potrze y tego rozdział u, że z iory X i Y zawsze

ędą oznaczał y opisany wyżej podział wierzchoł ków gra u G.

ramach zajęć ędziemy się zajmować wyłącznie skojarzeniami w gra ach dwudzielnych.

ają

one następującą naturalną interpretację

< 24 > 

Informatyka + 

X i Y to zbiory mężczyzn i kobiet. Krawędziami łączymy osoby, które są sobą zaintereso-
wane w sensie matrymonialnym. Oczywiście nie możemy żądać, by jakikolwiek mężczyzna
był zainteresowany tylko jedną kobietą, lub też jakaś kobieta tylko jednym mężczyzną

rzez

skojarzenie rozumiemy wskazanie tyc

ar, które zostaną mał żeństwami tu już obowiązuje

mono amia

Krawędzie które należą do skojarzenia nazywamy skojarzonymi, ozostałe zaś wolnymi. odobnie wolne
będą te wierzc oł ki, które nie są incydentne z żadną krawędzią skojarzenia.

6.1

M aksymalne skojarzenia

ak więc znaleźć maksymalne tj. o największej liczbie krawędzi skojarzenie w rafie dwudzielnym

odobnie jak w rzy adku maksymalne o rze ł ywu będziemy starali się w kolejnyc krokac zwiększać

skojarzenie do óki będzie to możliwe.

rzez ścieżkę powiększającą będziemy teraz rozumieli ścieżkę omiędzy dwoma wierzc oł kami wol-

nymi, której krawędzie będą na rzemian wolne i zajęte.

nalezienie w rafie takiej ścieżki oznacza,

że możemy owiększyć skojarzenie

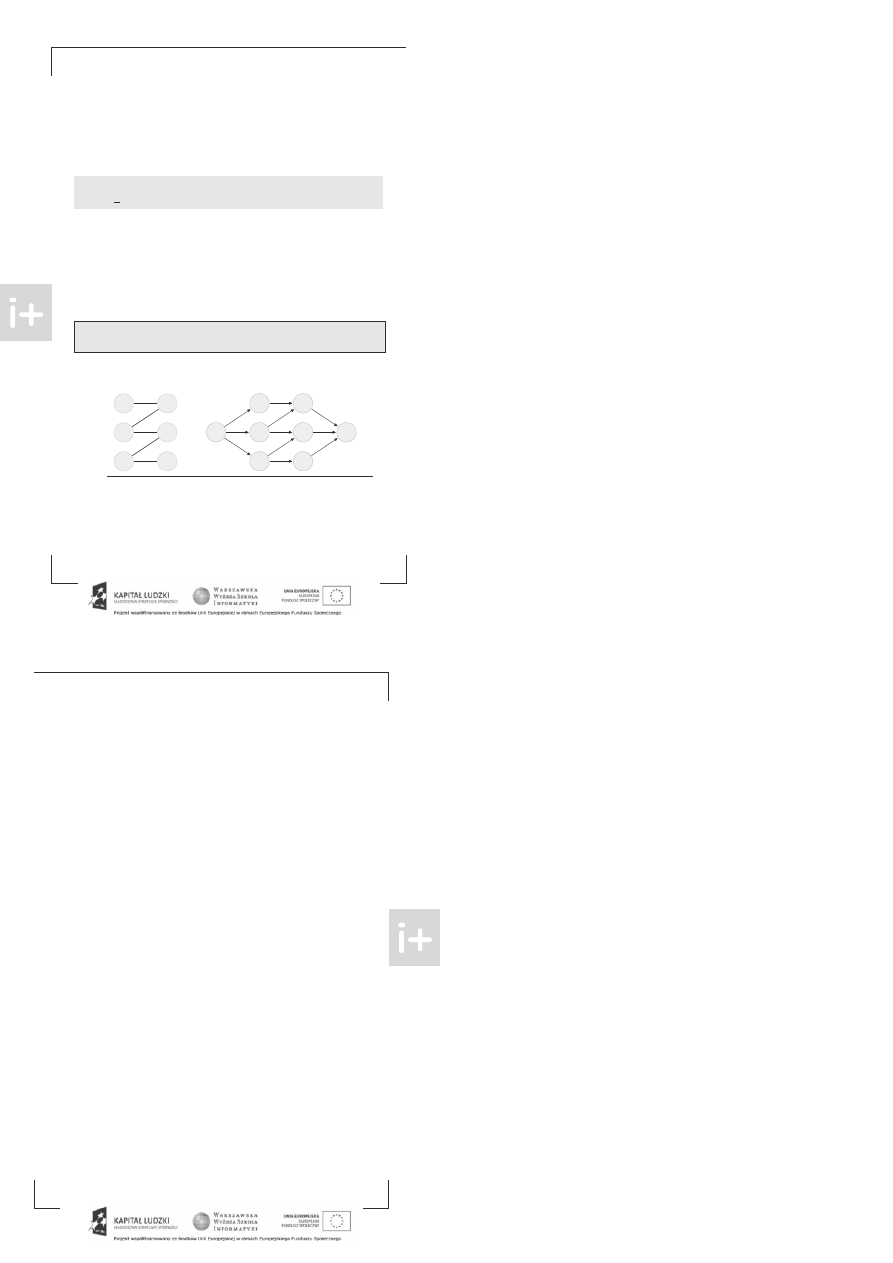
Znalezienie ścieżki powiększającej i zwiększanie skojarzenia

Otrzymaliśmy zatem bardzo rosty al orytm w każdej azie szukamy ścieżki owiększającej. eżeli ona
istnieje, to zwiększamy skojarzenie. eżeli nie, to kończymy.

by udowodnić, że al orytm jest

o rawny otrzebny jest nam nastę ujący akt

T wierdzenie Berge’a.

rafie nie ma ścieżki

owiększającej wtedy i tylko wtedy, dy uzyskane skojarzenie jest

maksymalne.

Ćwiczenie 15.

dowodnij

owyższe twierdzenie.

ożesz o raniczyć się tylko do ra ów

dwudzielnyc , c oć twierdzenie jest rawdziwe dla dowolnyc .

aka jest złożoność za ro onowane o al orytmu dla ra u o n wierzc oł kac i m krawędziac

ta-

kim rzy adku wielkość skojarzenia jest na ewno nie większa niż n.

każdej azie, o znalezieniu

nowej ścieżki

owiększającej wielkość skojarzenia zwiększa się o 1, zatem będzie co najwyżej n az.

o więcej, do znalezienia jednej ścieżki wystarczy rzeszukiwanie ra u w łąb, które zajmuje czas

liniowy wz lędem liczby krawędzi. odsumowując złożoność czasowa te o al orytmu to O(nm).

rzyjrzymy się teraz bardzo rostej im lementacji te o al orytmu dla ra u dwudzielne o G.

zbio-

rac X i Y wierzc oł ki są w onumerowane od 0 do nx − 1 i od 0 do ny − 1 od owiednio.

im lementacji korzystamy z nastę ującyc

lobalnyc zmiennyc

•

Krawędzie ra u incydentne z wierzc oł kiem i -tym z X

rzec owywane są w i -tym wektorze

tablicy vector<int> gr[N].

•

i -tej komórce tablic int skojx[N], skojy[N] rzec owujemy numer wierzc oł ka aktualnie

skojarzone o z i -tym z od owiednie o zbioru X lub Y .

artość − 1 oznacza wierzc ołek wolny.

•

o wykonywania al orytmu

będziemy wykorzystywali tablicę bool odw[N].

> Zaawansowane algorytmy 

< 25 >

Potrzebujemy funkcji, która będzie próbowała znaleźć ścieżkę powiększającą z dane o wierzc oł ka,
a jeżeli się uda to uaktualni skojarzenia

to ona

bool skojarz (int a)
{

if (odw[a])

return false;

odw[a] = true;
FOREACH (it

r[a])

if (skoj [ it] ==

skojarz (skoj [ it]))

sąsiad

it aktualne o wierz

ołka jest woln

lub też

ożna

znaleźć ś ieżkę

owiększają ą za z nają ą się od wierz

ołka

z któr

it jest skojarzon

{

skoj [a] =

it;

skoj [ it] = a;
return true;

return false;

astępnie wystarczy uruc omić tę procedurę dla kolejnyc wierzc oł ków ze zbioru X

int w n =

;

for (int i =

; i

n ; i

)

{

for (int j =

; j

n ; j

)

odw[j] = false;

if (skojarz(i))

w n

;

by się przekonać o poprawności te o rozwiązania, trzeba zauważyć dwa fakty Po pierwsze, jeżeli

istnieje ścieżka powiększająca z dane o wierzc oł ka a tablica odw jest cała ustawiona na false , to
funkcja skojarz na pewno ją znajdzie Po dru ie, dy wierzc ołek raz stanie się skojarzony, to nie
zmieni te o żadne wywołanie funkcji skojarz c oć oczywiście może się zmienić wierzc ołek, z którym
jest skojarzony

atem rzeczywiście możemy próbować znajdować ścieżki powiększające w dowolnej

kolejności, na przykład od zaczynającyc się w 0 do zaczynającyc się w nx − 1

wielu książkac problem maksymalne o skojarzenia w rafie dwudzielnym podaje się jako szcze

ólny przypadek problemu maksymalne o przepł ywu

utaj przedstawiliśmy jednak bezpośrednie roz

wiązanie, by podkreślić je o niezwykłą prostotę

6.2

Szybsze rozwiązania

zy istnieje szybszy sposób znajdowania skojarzenia w rafie dwudzielnym

dpowiedź jest twierdząca

— al orytm

opcrofta arpa rozwiązuje ten problem i działa ze złożonością O(m

√

n)

est to jednak

dość złożony al orytm, dlate o nie będziemy o tutaj omawiać

ainteresowanyc ponownie odsyłamy

do znakomitej książki

itolda ipskie o

Przedstawimy natomiast lekko zmodyfikowaną wersję poprzednie o al orytmu

prawdzie je o

złożoność to nadal O(nm), ale w praktyce działa bardzo szybko, często porównywalnie do al orytmu

opcrofta arpa

Pomysł jest bardzo prosty zamiast za każdym razem czyścić tablicę odwiedzonyc wierzc oł ków

odw

spróbujmy w każdej fazie znajdować od razu kilka rozłącznyc ścieżek powiększającyc

mplementacja wykorzystuje zdefiniowaną wcześniej funkcję skojarz i jest bardzo prosta

< 26 > 

Informatyka + 

int wyn = 0;
bool zmiana;
do {

zmiana = false;

for (int i = 0; i < nx; i++)

odw[i] = false;

for (int i = 0; i < nx; i++)

if (skojx[i]==-1

skojarz(i)){

zmiana = tr e;
wyn ++;

w ile(zmiana);

Ćwiczenie 16. Udowodnij, że jeżeli wielkość maksymalnego skojarzenia w grafie jest równa
M , to w pierwszym obrocie pętli do w ile algorytm znajdzie skojarzenie o liczności co
najmniej

M

2

.

Niestety nie istnieje formalny dowód tego, że algorytm ten wykon je małą liczbę faz — istnieją złośliwe
przypadki, w któryc może on działać nieefektywnie.

praktyce sprawdza się jednak bardzo dobrze. by

c ronić się przed owymi złośliwymi przypadkami można próbować na początk w losowej kolejności

po stawiać wierzc oł ki w listac sąsiedztwa.

6.3

T wierdzenie K ¨oniga

Niekiedy wykorzyst je się maksymalne skojarzenie do obliczania innyc wartości dla graf .

tym

rozdziale zajmiemy się twierdzeni

¨oniga, które jest przykładem takiej syt acji.

aczniemy od definicji pokryciem wierzchoł kowym graf G nazywamy taki podzbiór P jego wierz

c oł ków, że każda krawędź z G jest incydentna z wierzc oł kiem z P .

kaz je się, że zac odzi

T wierdzenie K ¨oniga.

grafie dw dzielnym liczności maksymalnego skojarzenia i minimalnego pokrycia wierzc oł

kowego są sobie równe.

owód tego fakt będzie przeprowadzony na podstawie twierdzenia o maksymalnym przepł ywie i mi

nimalnym przekroj .

by z niego skorzystać m simy jednak mieć sieć zamiast graf

dw dzielnego.

stnieje prosty sposób zyskania odpowiedniej sieci.

s

t

∞

∞

∞

∞

∞

1

1

1

1

1

1

Graf dwudzielny i odpowiadająca jemu sieć

any jest graf dw dzielny D , o dwóc zbiorac wierzc oł ków X i Y

między którymi przebiegają

wszystkie krawędzie graf .

odajemy do niego dwa wierzc oł ki źródło s i jście t. Źródło łączymy

z wierzc oł kami zbior X za pomocą krawędzi o przep stowości 1, podobnie wierzc oł ki zbior Y łą
czymy z jściem.

końc wszystkie krawędzie graf D zamieniamy na skierowane krawędzie od wierz

c oł ków z X do tyc z Y , nadajemy im też bardzo d żą przep stowość — na przykład większą niż
liczba wszystkic wierzc oł ków D .

by speł nić zadane przez nas wcześniej wymagania dotyczące sieci, należy jeszcze dodać dla każdej

krawędzi w sieci krawędź powrotną o przep stowości 0. Uzyskaną w ten sposób sieć oznaczmy przez G.

> Zaawansowane algorytmy 

< 27 >

Pokażemy teraz, że maksymalne skojarzenie w grafie D jest równe maksymalnemu przepł ywowi

w sieci G. Wynika to z tego, że dowolne skojarzenie w D wyznacza przepł yw w G i odwrotnie:

•

Każda krawędź (x, y) w pewnym skojarzeniu w grafie D wyznacza nam ścieżkę s → x →
y → t w G, po której możemy przesłać jedną jednostkę przepł ywu. Krawędzie ze skojarzenia
nie są incydentne ze so ą, a więc uzyskane ścieżki nie mają punktów wspólnyc

poza źródłem

i ujściem .

znacza to, że możemy puścić przepł yw przez wszystkie ścieżki naraz, uzyskując

przepł yw o wartości równej wielkości skojarzenia w D .

•

ając dany przepł yw w sieci G wy ierzmy te krawędzie ze z ioru X do Y , które mają niezerowy

przepł yw mają one zawsze przepł yw równy 1 . auważmy, że co najwyżej jedna wy rana krawędź
może yć incydentna z pewnym wierzc oł kiem x ∈ X

gdy y incydentnyc krawędzi

yło

więcej to przepł yw przec odzący przez x ył y nie mniejszy niż 2, a tymczasem krawędź (s, x)
o przepustowości 1 to jedna krawędź o niezerowej przepustowości wc odząca do x. Podo nie
dowiedziemy, że co najwyżej jedna wy rana krawędź jest incydenta z dowolnym wierzc oł kiem
z Y .

znacza to, że odpowiedniki wy ranyc przez nas krawędzi stanowią skojarzenie w D

o liczności równej wartości rozważanego przepł ywu w G.

Pokażemy teraz równość licze ności minimalnego pokrycia wierzc oł kowego w D i przepustowości
minimalnego przekroju w G. Podo nie jak przed c wilą pokażemy pewnego rodzaju odpowiedniość
między tymi o iektami:

•

amy dany gra D z pokryciem złożonym z wierzc oł ków z ioru P . Wskażemy teraz taki podział

wierzc oł ków sieci G na z iory S i T, że wyznaczany przez nie przekrój ędzie miał przepustowość
równą |P |.

o z ioru S należeć ędzie źródło s, z iór X \ P incydentne z s, ale nie wy rane

do pokrycia oraz z iór Y ∩ P wierzc oł ki incydentne z t, które został y wy rane do pokrycia .
Pozostałe wierzc oł ki wpadają do T .

Policzymy teraz przepustowość tego przekroju, czyli sumę przepustowości krawędzi prowadzącyc
ze z ioru S do T . Po pierwsze zauważmy, że do tej sumy nie zostanie nigdy wliczona przepu
stowość krawędzi (x, y) dla x ∈ X i y ∈ Y .

ożna y ją wliczyć tylko wtedy, gdy x ∈ S czyli

x /∈ P oraz y ∈ T czyli y /∈ P , a zatem istniała y krawędź, której o a wierzc oł ki nie ył y y
w pokryciu P , co stoi w sprzeczności z definicją pokrycia.

atem krawędzie liczone do przepustowości przekroju ędą postaci (s, a) dla a ∈ X ∩ P ⊂ T

oraz (b, t) dla b ∈ Y ∩ P ⊂ S. Widać wyraźnie, że jest ic dokładnie |P |, a każda z nic ma
przepustowość 1, zatem wskazany przekrój rzeczywiście ma przepustowość |P |.

•

eraz mając dany przekrój (S, T) w sieci G z udujemy pokrycie gra u D . ozpatrujemy wszystkie

krawędzie prowadzące z S do T .

la każdej krawędzi postaci (s, x), gdzie x ∈ X ∩ T dodajemy

wierzc ołek x do pokrycia. Podo nie dla krawędzi (y, t), gdzie y ∈ Y ∩ S dodajemy wierzc ołek
y.

atomiast dla każdej krawędzi (x, y), gdzie x ∈ X ∩ S i y ∈ Y ∩ T dodajemy zarówno x jak

i y.

ietrudno zauważyć, że tak wskazany z iór rzeczywiście jest pokryciem: weźmy dowolną krawędź

(x, y) w D , która wyznacza ścieżkę s → x → y → t w sieci G. Ścieżka ta zaczyna się w z iorze
S, a kończy w T , więc któraś z krawędzi (s, x), (x, y), (y, t)

ędzie „ graniczna” między tymi

z iorami, a zatem x, lu y, lu nawet o a wierzc oł ki zostaną dodane do pokrycia.

zięki temu

krawędź (x, y) gra u D

ędzie incydentna z którymś wierzc oł kiem pokrycia.

auważmy teraz, że wprawdzie liczność pokrycia może się różnić od przepustowości przekroju,

ale tylko w przypadku gdy do przekroju wliczymy krawędź prowadzącą z X do Y . Każda taka
krawędź ma przepustowość większą niż |X ∪Y |, więc przepustowość takiego przekroju jest z pew
nością większa niż przepustowość przekroju ({ s} , X ∪ Y ∪ { t} ). Wynika z tego, że jeżeli intere
sują nas minimalne przekroje a ostatecznie pokrycia to nie musimy się zajmować przekrojami,
do któryc wliczają się krawędzie prowadzące z X do Y .

dowodniliśmy właśnie, że liczność minimalnego pokrycia w grafie D jest równa wielkości minimalnego

przekroju w sieci G. Przed c wilą uzyskaliśmy też równość maksymalnego przepł ywu w G i maksy
malnego skojarzenia w D .

wierdzenie o maksymalnym przepł ywie i minimalnym przekroju mówi nam

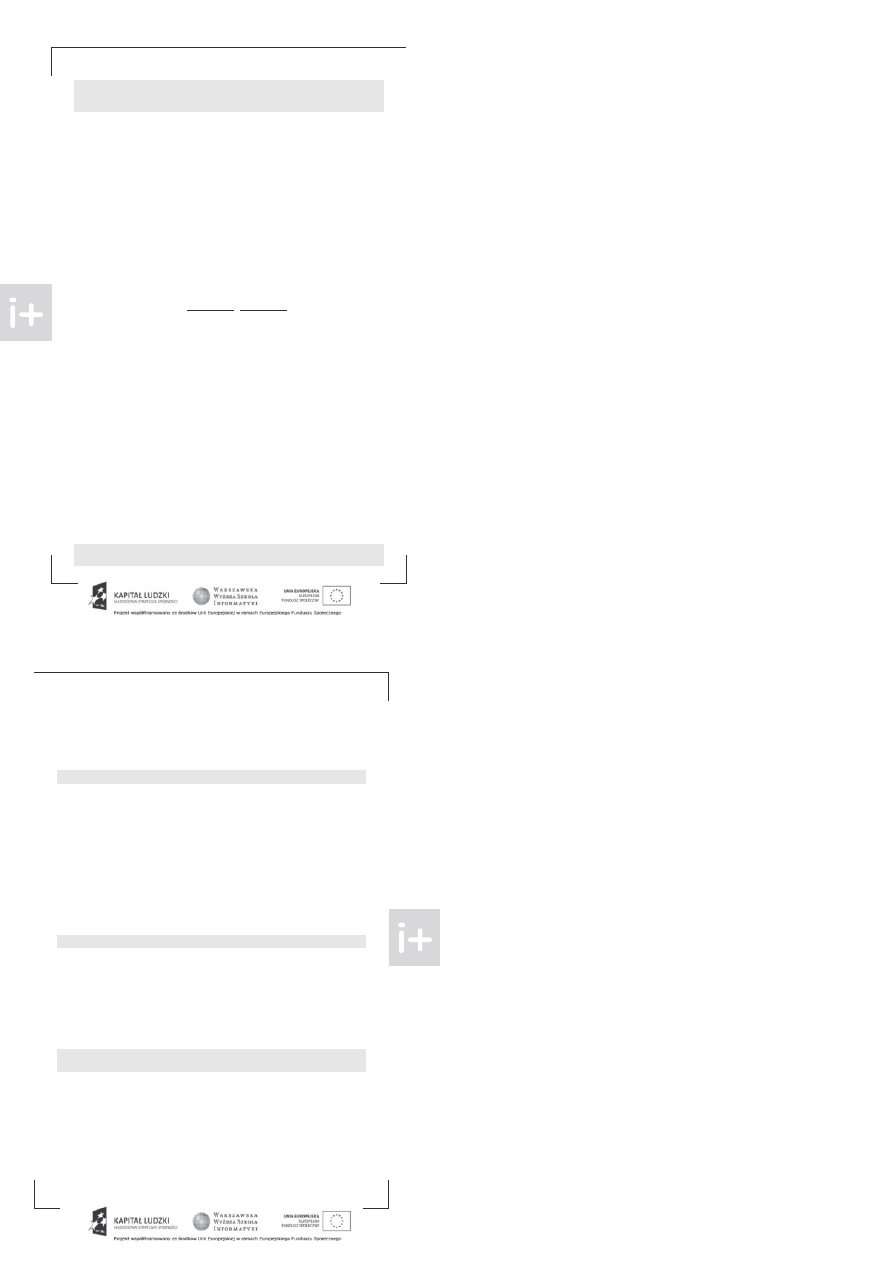
< 28 > 

Informatyka + 

o równości tych dwóch wartości w dowolnej sieci. Zaaplikowanie tego twierdzenia do sieci G kończy
dowód twierdzenia K¨oniga.

Ćwiczenie 17. Wykorzystując twierdzenie K¨oniga, rozwiąż następujące zadanie

a y punkty na płaszczyźnie. le

ini alnie trze a poprowadzić prostych pionowych lu

pozio ych, że y każdy punkt leżał na którejś z nich

7

Przecinanie się obiekt ów geomet rycznych na pł aszczyźnie

iezależnie, jaki

pro le e

geo etryczny

się zaj uje y,

ając pewne o iekty na płaszczyźnie,

ogą nas interesować pewne szczególne punkty.

aturalnie, podstawowy

rodzaje

punktów szcze

gólnych są przecięcia o iektów, tzn.

iejsca gdzie co naj niej dwa o iekty się spotykają. Zaj ij y się

więc sposo a i znajdowania takich punktów.

7.1

Przecięcie dwóch prost ych

roste to najpopularniejsze i najprostsze z o iektów, których przecięcie oże nasinteresować. rzecięcie

dwóch prostych sprowadza się do rozwiązania układu dwóch równań, złożonego z równań opisujących
te proste. eśli przyj ie y, że proste to A

1

x + B

1

y + C

1

= 0 oraz A

2

x + B

2

y + C

2

= 0, to

•

jeśli A

1

B

2

= A

2

B

1

oraz A

1

C

2

= A

2

C

1

, to te dwie proste są jednakowe, a więc ich przecięcie

jest i

równe

•

jeśli A

1

B

2

= A

2

B

1

ale A

1

C

2

= A

2

C

1

, to te dwie proste są równoległe, ale się nie pokrywają

i w taki

wypadku nie

a punktów wspólnych

•

jeśli A

1

B

2

= A

2

B

1

, to jest dokładnie jeden punkt przecięcia i jest ni

C

1

B

2

−

C

2

B

1

A

1

B

2

−

A

2

B

1

,

C

1

A

2

−

C

2

A

1

B

1

A

2

−

B

2

A

1

.

7.2

Przecięcie dwóch odcinków

dcinek jest rag ente

prostej ograniczony

z o u stron, naturalny

więc po ysłe

na znalezienie

przecięcia dwóch odcinków jest przecięcie dwóch prostych, które te odcinki zawierają.

ie jest to

jednakże peł ne rozwiązanie.

oże się owie

zdarzyć, że odcinki nie przecinają się w ogóle, a ich

proste — tak.

iech jeden z odcinków

a końce (x

1

, y

1

) i (x

2

, y

2

), a drugi (p

1

, q

1

) i (p

2

, q

2

). W taki

razie, ich

proste są opisane równania i A

1

x + B

1

y + C

1

= 0 oraz A

2

x + B

2

y + C

2

= 0, gdzie

A

1

= y

1

−

y

2

A

2

= q

1

−

q

2

B

1

= x

2

−

x

1

B

2

= p

2

−

p

1

C

1

= x

1

y

2

−

x

2

y

1

C

2

= p

1

q

2

−

p

2

q

1

ostępuje y teraz tak, jak yś y przecinali te dwie proste, przy czy

•

gdy są tą sa ą prostą, to ich przecięcie jest puste, jedny

punkte

lu odcinkie

a y to

sprawdzić przyporządkowuje y punkto

współ rzędne na tej prostej tak, że odcinki

ają końce

a

1

a

2

oraz b

1

b

2

, odpowiednio, a następnie rozpatruje y odcinek

[max(a

1

, b

1

), min(a

2

, b

2

)].

•

gdy są równoległe ale różne, to odcinki się nie przecinają

•

gdy nie są równoległe, to proste przecinają się w jedny

punkcie a odcinki al o przecinają się

w ty

właśnie punkcie, al o wcale — a y to sprawdzić, pyta y czy tenże punkt należy do każdego

z odcinków.

Ćwiczenie 18.

ak za ienić współ rzędne punktu płaszczyzny (x

1

, y

1

) leżącego na prostej

Ax + B y + C = 0 na jedną współ rzędną opisującą położenie na tej prostej

> Zaawansowane algorytmy 

< 29 >

7.3

Przecięcie prost ej i okręgu

Tym razem załóżmy, że prosta ma równanie y = px + q, a okrąg: (x − a)

2

+ (y − b)

2

= r

2

. Wtedy

mamy:

(x − a)

2

+ (px + q − b)

2

= r

2

x

2

(1 + p

2

) + x(2pq − 2pb − 2a) + a

2

+ (q − b)

2

−

r

2

= 0

Takie równanie kwadratowe umiemy już rozwiązać. Mamy ∆ = 4r

2

(1+ p

2

)− 4(ap+ q− b)

2

, i w zależnoś i

od tego, zy ∆ jest ujemna, równa zero zy dodatnia, mamy zero, jeden lu dwa punkty prze ię ia.

Ćwiczenie 19.

o należy zro ić, gdy prosta jest pionowa o równaniu x = c

7.4

Przecięcie dwóch okręgów

kład równań kwadratowy

może nie yć prosty do rozwiązania. W przypadku układu

(x − a

1

)

2

+ (y − b

1

)

2

= r

2
1

(x − a

2

)

2

+ (y − b

2

)

2

= r

2
2

jest o tyle łatwiej, że po odję iu ty

równań stronami otrzymujemy

(2a

1

−

2a

2

)x + (2b

1

−

2b

2

)y + (a

2
2

−

a

2
1

+ b

2
2

−

b

2
1

+ r

2
1

−

r

2
2

) = 0

o jest równaniem prostej, do której ędą należał y wszystkie punkty prze ię ia. Wystar zy wię prze iąć

tę właśnie prostą z dowolnym z ty

dwó

okręgów i otrzymane punkty

ędą właśnie punktami

prze ię ia okręgów.

edyna wątpliwość nastaje, gdy a

1

= a

2

oraz b

1

= b

2

,

o wtedy otrzymane

równanie nie opisuje prostej.

Ćwiczenie 20.

zym jest prze ię ie okręgów w takim wypadku

8

Poł ożenie punkt u wzg ęde

o iekt ów pł szcz zn

8.1

zg ęde

prost ej

Tym razem nie

prosta ędzie opisana przez dwa różne jej punkty, (x

1

, y

1

) i (x

2

, y

2

). unkt (p, q) leży

po którejś ze stron tej prostej, w zależnoś i od znaku ilo zynu wektorowego wektorów o po zątka
w (x

1

, y

1

) i koń a

w (x

2

, y

2

) i (p, q). W sz zególnoś i, gdy ilo zyn ten jest zerem, punkt leży

na prostej.

Ćwiczenie 21. Mają daną prostą o równaniu Ax + B y + C = 0 oraz dwa punkty (p

1

, q

1

)

i (p

2

, q

2

), sprawdź zy leżą one po dwó

różny

strona

tej prostej.

8.2

zg ęde

okręgu

unkt (x

1

, y

1

) leży względem okręgu o promieniu r i środku w (a, b):

•

wewnątrz okręgu, gdy (x

1

−

a)

2

+ (y

1

−

b)

2

< r

2

•

na okręgu, gdy (x

1

−

a)

2

+ (y

1

−

b)

2

= r

2

•

na zewnątrz okręgu, gdy (x

1

−

a)

2

+ (y

1

−

b)

2

> r

2

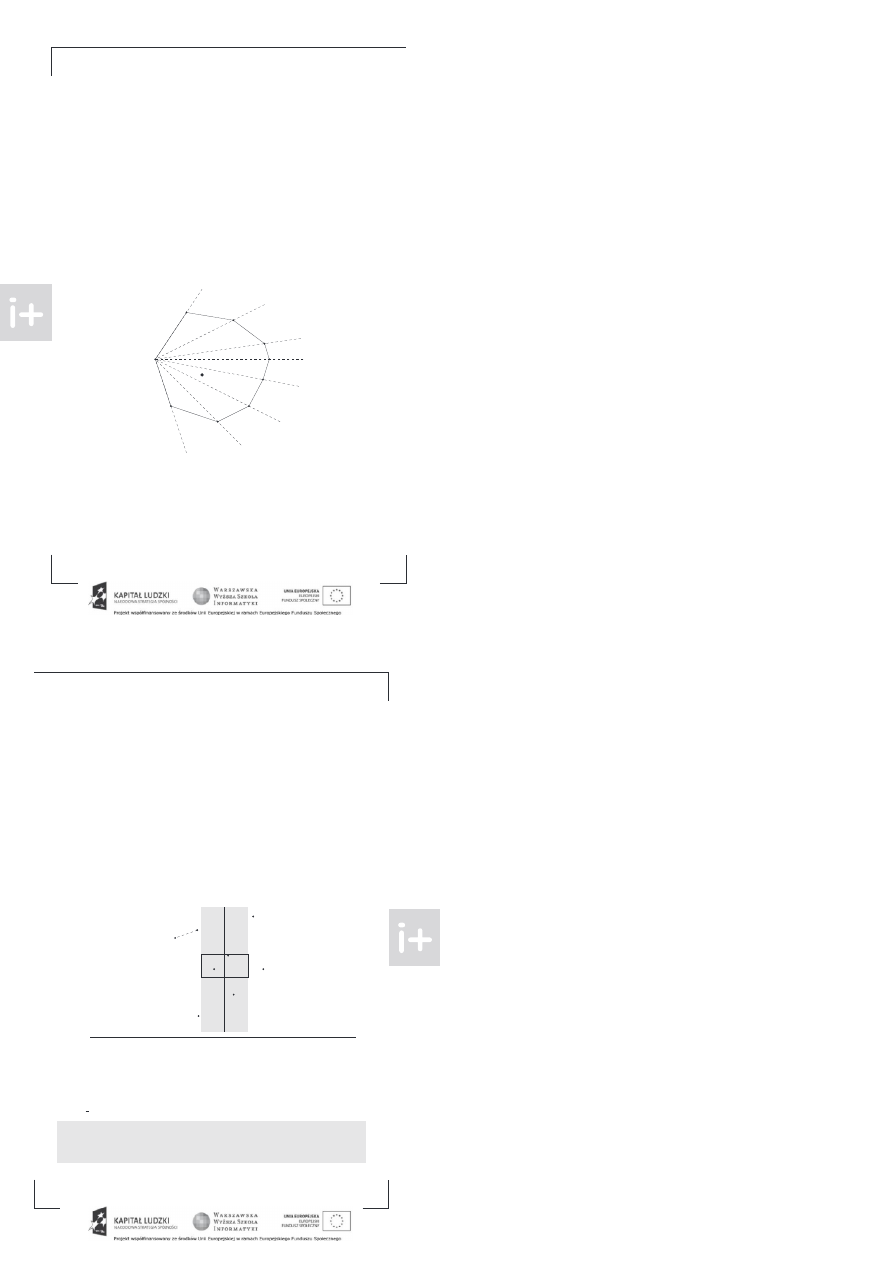
< 30 > 

Informatyka + 

8.3

W zględem wielokąt a

Najpopularniejszą metodą sprawdzania, czy punkt leży wewnątrz wielokąta jest wzięcie pół prostej
o początku w tym punkcie. Jeśli pół prosta ta przecina wielokąt parzystą liczbę razy, to punkt leży
na zewnątrz, a jeśli nieparzystą — wewnątrz.

ile sama metoda jest prosta, należy uważać przy jej

implementacji.

roblemów nastręczają przede wszystkim wierzc oł ki wielokąta leżące na naszej pół

prostej. Najlepiej więc wybrać taką pół prostą, żeby po prostu wierzc oł ków wielokąta na niej nie było.

o więcej, pół prostą można traktować jako odcinek, które o dru i koniec jest po prostu bardzo daleko.
rzykładowo, jeśli interesuje nas punkt (x, y) to często dobrym pomysłem jest wziąć za „ pół prostą”

odcinek [(x, y), (x + 1, y + M )].

la odpowiednio duże o M , taki odcinek przecina tyle samo, co

pół prosta o zawierająca, a także nie zawiera żadnyc wierzc oł ków wielokąta.

akie sprawdzenie wyma a liniowej wz lędem ilości boków wielokąta liczby operacji.

W zględem wielokąt a wypukł ego

Naturalnie, skoro potrafimy rozwiązać ten problem dla dowolne o wielokąta, potrafimy także zrobić
to dla wielokąta wypukłe o.

tym szcze ólnym przypadku możliwe jest jednak znacznie e ektyw

niejsze rozwiązanie. Niec będzie wyróżniony jeden z wierzc oł ków wielokąta, A, a pozostałe ułożone
w kolejności z odnej z ruc em wskazówek ze ara.

oprowadźmy z A wszystkie przekątne, tak aby

podzielić wielokąt na trójkąty.

auważmy, że możemy wyszukać binarnie, pomiędzy którymi dwoma

prostymi zawierającymi przekątne znajduje się interesujący nas punkt, używając iloczynu wektoro
we o do sprawdzenia po której stronie pewnej przekątnej się on znajduje. Na koniec trzeba już tylko
sprawdzić, czy zawiera się w pewnym trójkącie co można zrobić w czasie stał ym c oćby metodą
z pół prostą i obliczeniem parzystości liczby przecięć .

ałość działa w czasie O(log n), dzie n jest ilością boków wielokąta, przy założeniu, że wierzc oł ki

wielokąta podane są po kolei.

8.4

Znajdowanie najdalszych punkt ów w danym zbio ze

amy dany zbiór n punktów na płaszczyźnie i c cemy znaleźć takie dwa z nic , żeby odle łość pomiędzy

nimi była jak największa.

auważmy najpierw, że oba te punkty będą należał y do wypukłej otoczki całe o zbioru.

dyby

bowiem któryś koniec nie należał do otoczki, mo libyśmy o zamienić na pewien punkt otoczki tak,
żeby nadal odle łość była maksymalna albo wręcz większa, co znaczyłoby, że dotąd nie mieliśmy
dobre o rozwiązania .

> Zaawansowane algorytmy 

< 31 >

Zacznijmy więc od znalezienia wypukłej otoczki dla tego zbioru. Następnie, ustalmy punkt a, jeden

z wierzchoł ków otoczki, i poszukajmy dla niego najdalszego wierzchoł ka, b. Będziemy teraz przesuwać
wskaźnik a zgodnie z ruchem wskazówek zegara na kolejne wierzchoł ki otoczki.

skaźnik b aktualnie

najdalszy punkt od a także będzie się przesuwał i także zgodnie z ruchem wskazówek zegara, a kiedy a
zatoczy pełen obrót po otoczce

b uczyni to samo, co oznacza że łączny czas takiego przeszukiwania

będzie liniowy. Zauważmy, że w każdym momencie, aby znaleźć dla danego a optymalne b, przesuwamy
b tak dł ugo zgodnie z ruchem wskazówek zegara, jak dł ugo powiększa to odległość. aka metoda działa
tylko dlatego, że otoczka jest wielokątem wypukł ym.

ałe rozwiązanie działa w czasie O(n log n), który jest potrzebny na znalezienie otoczki wypukłej.

8.5

Znajdowanie najbliższych punkt ów w danym zbiorze

ym razem w danym zbiorze n punktów chcemy znaleźć takie dwa, które leżą najbliżej siebie. roblem

znajdowania najbliższych punktów wydaje się podobny do poprzedniego, jednak jego rozwiązanie jest
zupeł nie inne.

żyjemy metody „ dziel i zwyciężaj” .

eźmy taką pionową prostą na płaszczyźnie, która dzieli nasz

zbiór na pół , tzn. połowa punktów leży po lewej, a połowa po prawej stronie blisko połowa, gdyby było
ich nieparzyście wiele .

unkty które leżą dokładnie na prostej przydzielamy do stron wedle uznania.

ozwiązujemy każdy z dwóch mniejszych podproblemów niezależnie, a następnie przyjmujemy δ jako

mniejszy z dwóch uzyskanych wyników.

ynikiem dla całego zbioru jest albo δ, albo też jakaś mniejsza liczba, jeśli istnieją punkt z lewego

i punkt z prawego zbioru, które leżą od siebie w odległości mniejszej niż δ. Zauważmy ponadto, że takie
punkty muszą leżeć w pionowym pasie szerokości 2δ którego środkiem jest wybrana wcześniej prosta.

δ

δ

δ

δ

Blisko położone punkty z różnych st ron prostej

o więcej, takie dwa punkty muszą leżeć w pewnym prostokącie

wycinku tegoż pasa o wysoko

ści δ.

takim prostokącie może być jednak co najwyżej

punktów, w każdym z kwadratów po ,

gdyż jak wiemy, wyniki dla lewej i prawej części zbioru osobno są równe co najmniej δ. tąd, wystarczy
posortować po współ rzędnej y punkty leżące w pasie szerokości 2δ wokół naszej prostej, a następnie
sprawdzić odległości z każdego z nich do siedmiu kolejnych.

ten sposób uzyskamy wynik dla całego

zbioru.

idzimy, że naiwna implementacja działa w czasie O(n log

2

n) jest to rozwiązanie równości

T (n) = 2T (

n
2

) + O(n log n) .

Ćwiczenie 22.

ak zaimplementować powyższe rozwiązanie aby działało w czasie

O(n log n)
Podpowiedź głównym kosztem każdej azy jest sortowanie punktów pasa po współ rzędnej
y. próbuj wyeliminować ten składnik sortując punkty tylko raz na początku.

< 32 > 

Informatyka + 

Lit erat ura

1. Banachowski L., Diks K., Rytter W., Algorytmy i struktury danych, WNT, Warszawa 2003

2. Cormen T.H., Leiserson C. ., Ri est R.L., tein C., Wprowadzenie do algorytmów, WNT,

Warszawa 200

3. Diks K.,

a inowski

., Rytter W. Wa eń T., Algorytmy i struktury danych,

http://wazniak.mimuw.edu.pl/index.php?title=Algorytmy_i_struktury_danych

.

raham R.L., Kn th D. ., atashnik

., Matematyka konkretna,

WN, Warszawa 2002

. Li ski W., Kombinatoryka dla programistów, WNT, Warszawa 200

. Młodzieżowa Akademia Informatyczna, http://main.edu.pl/

. Standard emplate ibrary rogrammer’s uide, http://www.sgi.com/tech/stl/

.

ysło

. ., Deo N., Kowa ik . , Algorytmy optymalizac i dyskretne ,

WN, Warszawa 1