Â

WIAT

N

AUKI

Styczeƒ 1997 81

W

roku 46 p.n.e. kalendarz
rzymski przesta∏ przystawaç
do pór roku. Korzystajàc z ra-

dy aleksandryjskiego astronoma Sosige-
nesa, Juliusz Cezar wprowadzi∏ dodat-
kowy dzieƒ w co czwartym lub inaczej
„przest´pnym” roku, tak by Êrednia d∏u-
goÊç roku wynosi∏a 365 i

1

/

4

dnia. Z po-

wodu z∏ego zrozumienia tej zasady ka-
p∏ani liczyli ostatni czwarty rok jednego
cyklu jako pierwszy rok cyklu nast´p-
nego. Tak wi´c co trzeci rok stawa∏ si´
rokiem przest´pnym. Tego b∏´du nie
udawa∏o si´ usunàç przez 50 lat.

My nie musimy pope∏niaç podobnych

pomy∏ek. Prawie 10 lat temu Nachum
Dershowitz i Edward M. Reingold
z University of Illinois zdecydowali si´
opracowaç kalendarz dla edytora GNU
Emacs pracujàcego w systemie UNIX.
W wyniku tego projektu powsta∏ pro-
gram komputerowy zamieniajàcy daty
w jednym systemie kalendarzowym na
inny. Uwzgl´dniono 14 kalendarzy: gre-
goriaƒski, juliaƒski, koptyjski, etiopski,
muzu∏maƒski, perski, hebrajski, Majów,
bahajski, chiƒski, starohinduski oraz
wspó∏czesny hinduski, a tak˝e kalen-
darz z czasów rewolucji francuskiej i ten
opracowany przez Mi´dzynarodowà
Organizacj´ Normalizacyjnà (ISO).

Kalendarze sà odmienne w ró˝nych

kulturach, gdy˝ wszystkie próbujà do-
konaç niemo˝liwego: wymierzyç to,
co niewymierne. Nasze jednostki czasu
sà oparte na trzech cyklach astrono-
micznych – dniu, miesiàcu i roku. Âred-
ni 24-godzinny dzieƒ s∏oneczny odmie-
rza czas pomi´dzy kolejnymi poja-
wieniami si´ S∏oƒca nad g∏owà. Okres
pomi´dzy kolejnymi pe∏niami Ksi´-
˝yca jest Êrednim miesiàcem ksi´˝y-
cowym, który trwa 29.530588853 dnia.
Czas potrzebny, by S∏oƒce powróci∏o
na swoje miejsce w pozornej w´drów-
ce po niebie, to Êredni tropikalny rok,
który liczy 365.242199 dnia. Gdyby mie-
siàc ksi´˝ycowy by∏ równy 29.5 dnia,
a rok s∏oneczny 365.25 dnia, to Ksi´˝yc
powtarza∏by swoje ruchy dok∏adnie co
59 dni (2

3

29.5), a S∏oƒce co 1461 dni

(4

3

365.25). Co 86 199 dni (59

3

1461)

uk∏ad Ziemia–Ksi´˝yc–S∏oƒce powra-
ca∏by do dok∏adnie tych samych wzgl´-
dnych po∏o˝eƒ. Kalendarz majàcy
86 199-dniowy cykl by∏by zawsze

precyzyjny (gdy zaniedbamy powol-
ne zmiany spowodowane tarciem
p∏ywów).

Na nieszcz´Êcie dla ludzi tworzàcych

kalendarze stosunki pomi´dzy dniami,
miesiàcami i latami uk∏adajà si´ jak licz-
by niewymierne: nie mo˝na ich przed-
stawiç w postaci u∏amków (korzystajàc
ze wzgl´dnie ma∏ych liczb). Tak wi´c cy-
kle ksi´˝ycowe i s∏oneczne nigdy nie wra-
cajà do identycznie tego samego stanu.

W wi´kszoÊci kultur obowiàzuje ka-

lendarz s∏oneczny, ale sà wówczas k∏o-
poty z miesiàcami; decydujàc si´ na-
tomiast na kalendarz ksi´˝ycowy,
mo˝na nie przejmowaç si´ problemami
zwiàzanymi z porami roku. Bez wzgl´-
du na wybór podstawy kalendarza trze-
ba znaleêç praktyczny sposób na korek-
t´ ma∏ych, kumulujàcych si´ b∏´dów.
Stàd te˝ te komplikujàce ˝ycie przest´p-
ne lata, miesiàce o zmieniajàcej si´ licz-
bie dni i tym podobne rzeczy. ˚eby
uprzytomniç sobie, jak bardzo mo˝e to
byç skomplikowane, wystarczy zajrzeç
do Calendrical Calculations Reingolda
(Cambridge University Press, 1996)

lub obejrzeç t´ ksià˝k´ w Internecie
(http://emr.cs.uiuc.edu/home/rein-
gold/calendar-book/index.html).

Najprostszy system kalendarzowy b´-

dzie numerowa∏ kolejne dni, wybiera-
jàc jakàÊ „epok´” lub dzieƒ poczàtko-
wy. Astronomowie u˝ywajà dnia
juliaƒskiego (z kalendarza Juliusza Ce-
zara), ale Dershowitz i Reingold wolà
swój wynalazek – „ustalonà dat´”, czy-
li rata die, co oznaczajà w skrócie R.D.

Tak wi´c pierwszym dniem systemu
R.D. jest 1 stycznia pierwszego roku ka-
lendarza gregoriaƒskiego, tzn. kalenda-
rza u˝ywanego obecnie. W rzeczywi-
stoÊci nie by∏o ˝adnego pierwszego roku
w kalendarzu gregoriaƒskim, poniewa˝
zosta∏ on wprowadzony w roku 1582
przez papie˝a Grzegorza XIII i ekstra-
polowany w przesz∏oÊç. „Pierwszym”
dniem by∏ poniedzia∏ek, co pozwala
nam przyjàç za zerowy dzieƒ poprze-
dzajàcà niedziel´ i liczyç dni tygodnia
od 0 do 6. W Calendrical Calculations u˝y-
wa si´ wartoÊci R.D. jako wspólnego
punktu odniesienia dla wszystkich sys-
temów kalendarzowych.

REKREACJE MATEMATYCZNE

Ian Stewart

Przewodnik po komputerowym kalendarzu

BEZCHM

URNIE

RÓWNO

N

O

C

W

IOSENNA

PRZEBU

D

Z

ENIE

OWADÓW

DESZCZ

E

POCZÑ

T

E

K

W

IO

S

N

Y

WIELK

IE

ZIMNO

MA¸E

ZI

MN

O

PRZES

ILENIE

ZIMOWE

DU˚Y

ÂN

IEG

NIEWI

EL

KI

ÂNIE

G

POCZÑ

T

E

K

Z

IM

Y

PRZYMR

OZKI

ZIMNA

R

O

SA

RÓWNO

N

O

C

J

E

S

IENNA

BIA¸A

R

O

SA

KONI

EC

UPA¸Ó

W

POCZÑ

T

E

K

J

ESIEN

I

DU˚Y

U

P

A¸

NIEWI

EL

KI

UPA¸

PRZES

ILENIE

LETNIE

ZBO˚E

SI¢ K¸O

SI

ZIARNO

DO

JRZ

EWA

POCZÑ

T

E

K

LAT

A

ZBO˚E

W

Z

RAST

A

D

¸

U

G

OÂ

å S¸O

N

E

C

Z

N

A

360°

30°

60°

90°

120°

150°

180°

210°

240°

270°

300°

330°

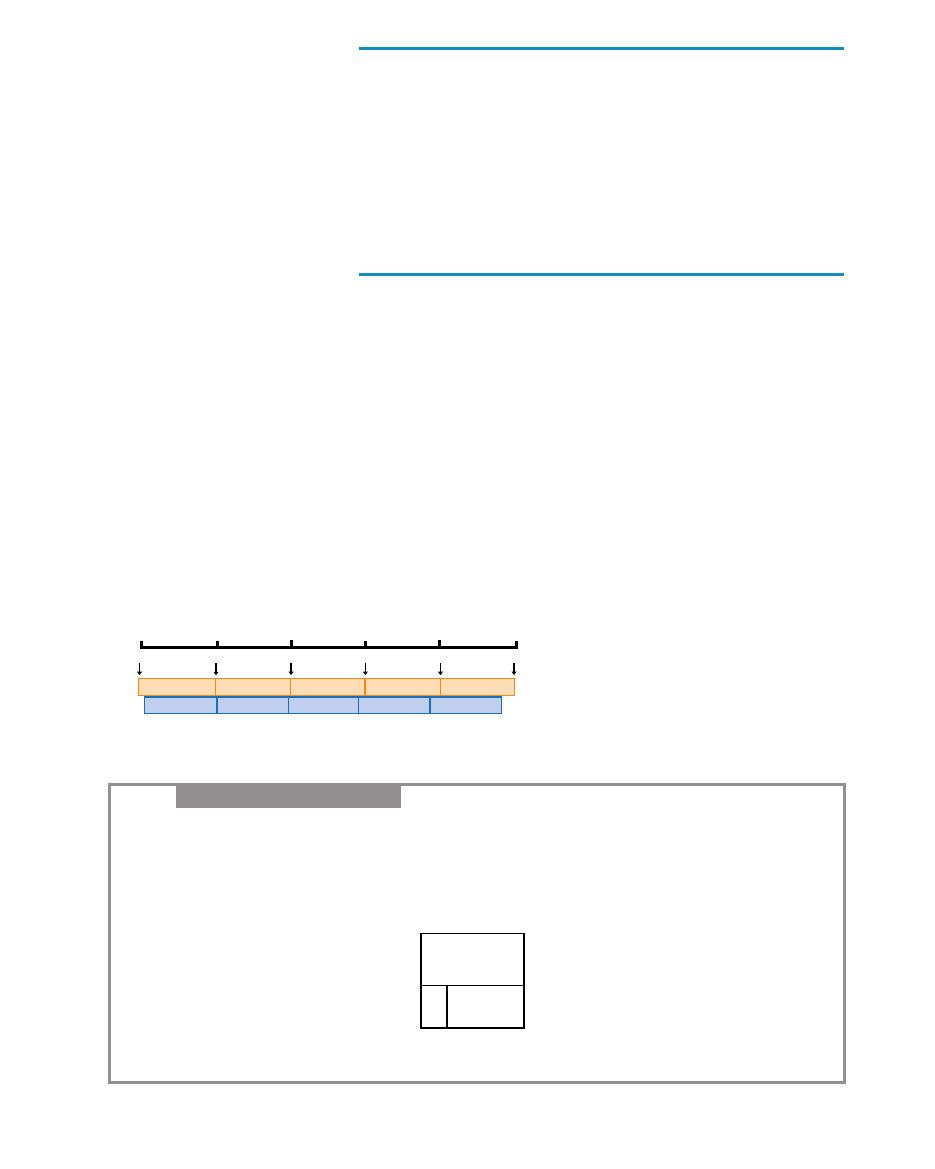
CHI¡SKI KALENDARZ sk∏ada si´ z lat s∏onecznych podzielonych na 24 okresy.

82 Â

WIAT

N

AUKI

Styczeƒ 1997

Poni˝ej, ˝eby zaprezentowaç proble-

my matematyczne spotykane w tego ro-
dzaju rozwa˝aniach, przedstawiam na
rozgrzewk´ dwa zadania.

1. W którym dniu tygodnia przypa-

da poczàtek roku 1 000 000 R. D.?

2. Ile Êrednich tropikalnych lat up∏y-

nie pomi´dzy dniem zerowym i pierw-
szym dniem 1 000 000 R.D.?

Aby odpowiedzieç na pierwsze py-

tanie, zauwa˝my, ˝e dni tygodnia two-
rzà powtarzajàcy si´ cykl o d∏ugoÊci 7.
Dowolny zatem R. D. b´dàcy wielokrot-
noÊcià 7 musi byç niedzielà, a ten, dla
którego reszta z dzielenia przez 7 wy-
nosi 1, musi byç poniedzia∏kiem itd. Mó-
wimy, ˝e numerem dnia jest liczba R.D.
modulo 7. Ogólnie x modulo 7 oznacza
reszt´ z dzielenia x przez 7. Poniewa˝
1 000 000 = 7 x 142857 + 1, resztà z dzie-
lenia 1 000 000 przez 7 jest 1. Tak wi´c
pierwszy dzieƒ 1 000 000 R.D. wypada
w poniedzia∏ek.

By uzyskaç odpowiedê na drugie

pytanie, podzielmy 1 000 000 przez
365.242189, a otrzymany 2737.9093. Z roz-
wiàzania wynika, ˝e w ciàgu 1 000 000
R.D. pojawi si´ 2737 pe∏nych (Êrednich
tropikalnych) lat po 0 R.D. Liczb´ 2737
otrzymaliÊmy, opuszczajàc wszystko po
przecinku. Matematycznie ta operacja od-
powiada funkcji schodkowej „cz´Êç ca∏ko-
wita” [x], co oznacza najwi´kszà liczb´
ca∏kowità mniejszà lub równà x.

Teraz zastanówmy si´ nad zamianà

daty gregoriaƒskiej takiej jak 25 grud-
nia 1996 roku na odpowiadajàcà jej war-
toÊç R.D. Przypomnijmy sobie zasad´
papie˝a Grzegorza polegajàcà na doda-
niu dodatkowego 29 dnia w lutym
w ka˝dym roku b´dàcym wielokrotno-
Êcià 4 z wyjàtkiem lat, które sà wielo-
krotnoÊcià liczby 100 (ale jednoczeÊnie
lata b´dàce wielokrotnoÊcià 400 sà lata-
mi przest´pnymi). Dershowitz i Rein-
gold pokazujà, ˝e ta zasada prowadzi
do przepisu podanego w ramce powy-
˝ej. Tak wi´c dla miesiàca M = 12, dnia
D = 25 oraz roku R = 1996 otrzymuje-
my (a) = 728 175, (b) = 498 – 19 + 4 = 483,
(c) = 336, (d) = –1 oraz (e) = 25. WartoÊç
R.D. jest równa 728 175 + 483 + 336 – 1

+ 25 = 729 018. A zatem numer dnia ty-
godnia wynosi 729 018 modulo 7 = 3,
czyli dzieƒ Bo˝ego Narodzenia 1996 ro-
ku wypada w Êrod´.

Calendrical Calculations z ∏atwoÊcià ra-

dzi sobie z bardzo skomplikowanymi
sprawami – sprawdêmy to na przyk∏a-
dzie wspó∏czesnego kalendarza perskie-
go. Kalendarz ten zosta∏ wprowadzony
w roku 1925, ale jego dzieƒ poczàtkowy
to 19 marca 622 roku – dzieƒ równono-
cy wiosennej, poczàtek ery w kalendarzu
muzu∏maƒskim. Rok dzieli si´ na 12 mie-
si´cy. Pierwszych szeÊç ma po 31 dni, na-
st´pne pi´ç 30 dni, ostatni, esfand, zazwy-
czaj 29 dni, a w latach przest´pnych 30.
Obliczane sà one w sposób skompliko-
wany, w 2820-letnim cyklu jest ich 683.

2820 lat zosta∏o podzielonych na

21 podcykli trwajàcych 128 lat i nast´-
pujàcym po nich cyklu 132-letnim. Ka˝-
dy 128-letni podcykl jest podzielony na
podpodcykle liczàce 29, 33, 33 oraz
33 lata, podczas gdy podcykl 132-letni
dzieli si´ odpowiednio na podpodcy-
kle 29, 33, 33 oraz 37 lat. Na koniec
w ka˝dym podpodcyklu 5, 9, 13 itd. rok
co cztery lata jest przest´pny. Kalen-

darz perski po cyklu 2820-letnim jest

R

ekreacje matematyczne” w sierpniu ub. r. poÊwi´ci∏em spo-
pularyzowanej przez Richarda Padovana „liczbie plastycz-

nej” i stowarzyszonemu ciàgowi „liczb Perrina”. Padovan przy-
pomnia∏, ˝e liczba plastyczna zosta∏a wynaleziona przez
francuskiego studenta architektury Gérarda Cordonniera w ro-
ku 1924 oraz holenderskiego architekta, benedyk-
tyna Hansa van der Laana w roku 1928. Potwier-
dzi∏ te˝ moje domys∏y, ˝e jego rodzina pochodzi z
Padwy.

Ervin Wilson z Los Angeles odkry∏, ˝e ciàg Pa-

dovana (tak chyba powinien si´ on nazywaç) jest
ÊciÊle zwiàzany z gamà muzycznà s’lendro, na
której oparta jest muzyka mieszkaƒców wysp Ba-
li i Jawa. Ta gama oraz inna, zwana pélog, mo˝e
byç otrzymana w sposób elegancki z trójkàta Pas-
cala za pomocà schematów powiàzanych z cià-

giem Padovana. John H. Bonnett, Jr., z Livingston (New Jersey)
przes∏a∏ mi wiele informacji, z których przytocz´ tylko jednà:
jeÊli kwadrat podzielimy na trzy podobne prostokàty (tego sa-
mego kszta∏tu, lecz innej wielkoÊci) jak na rysunku, to stosunek
dwóch wielkoÊci na pionowej kraw´dzi jest liczbà plastycznà.

Jeffrey Shallit z University of Waterloo przypomnia∏, ˝e w roku

1982 znalaz∏ dwie „pseudopierwsze liczby Perrina”, tj. liczby n nie

b´dàce pierwszymi dzielàce liczb´ Perrina A(n).
Sà to n = 271 441 = 521

2

oraz n = 904 631 = 7 x 13

x 9941. (Pierwsza z nich zosta∏a opublikowana
przez Williama W. Adamsa i Daniela Shanksa tak-
˝e w roku 1982.) Obliczenia Stevena Arno, o których
wspomina∏em, dotyczà specjalnej klasy pseudo-
pierwszych liczb Perrina, a nie ich wszystkich. John
P. Robertson z Berwyn (Pensylwania) napisa∏, ˝e
nie znalaz∏ ˝adnych innych pseudopierwszych liczb
Perrina mniejszych ni˝ 2 900 000. Mo˝e ktoÊ z Czy-
telników znajdzie dalsze przyk∏ady?

SPRZ¢˚ENIE ZWROTNE

˚

eby znaleêç wartoÊç R.D. miesiàca M,
dnia D i roku R

z kalendarza grego-

riaƒskiego, wylicz:

(a) 365(R–1)
(b)[(R–1)/4]–[(R–1)/100] + [(R–1)/400]
(c) [(367M–362)/12]
(d) 0, jeÊli M ≤ 2; –1, jeÊli M > 2 oraz R

jest rokiem przest´pnym, a w ka˝dym in-
nym przypadku –2

(e) D;
nast´pnie je dodaj.
Obliczenia te majà nast´pujàcà interpre-

tacj´: (a) jest liczbà dni w latach poprzedza-
jàcych bez dni dodanych w latach przest´p-
nych; (b) jest liczbà dni dodanych w latach
przest´pnych poprzedzajàcych (jeden dzieƒ
co cztery lata z pomini´ciem co setnego ro-
ku, ale co 400 lat dodajemy jeden dzieƒ);
(c) jest sprytnym wzorem na obliczenie dni
w miesiàcach poprzedzajàcych w danym
roku opartym na zasadzie, ˝e luty ma 30
dni, co oczywiÊcie nie jest prawdà, stàd te˝
poprawka (d); w kroku (e) D równa si´
naturalnie liczbie dni danego miesiàca.

x

y

Liczba plastyczna
to stosunek x do y

KOZIORO˚EC

WODNIK

RYBY

BARAN

BYK

BLIèNI¢TA

270°

300°

330°

360°

30°

60°

D¸UGOÂå

S¸ONECZNA

MIESIÑCE

S¸ONECZNE

MIESIÑCE

KSI¢˚YCOWE

10

11

12

1

2

11

PRZEST¢PNY 12

12

1

2

NOWY ROK S¸ONECZNY

STAROHINDUSKI KALENDARZ KSI¢˚YCOWO-S¸ONECZNY zawiera nak∏adajàce si´

miesiàce s∏oneczne i ksi´˝ycowe, z czego wynikajà miesiàce przest´pne.

Rata Die

JENNIFER CHRISTIANSEN

Â

WIAT

N

AUKI

Styczeƒ 1997 83

obarczony b∏´dem wynoszàcym 1.7
min. Tak wi´c pomyliç si´ o ca∏y dzieƒ
wzgl´dem prawdziwych cykli astro-
nomicznych mo˝na by dopiero po up∏y-
wie 2.39 mln lat.

Stary ksi´˝ycowo-s∏oneczny ka-

lendarz hinduski jest zupe∏nie inny.
Podstawà w nim jest cykl trwajàcy
1 577 917 500 dni. „Rokiem” (dok∏ad-
niej: aryjskim rokiem gwiezdnym) jest

1

/

4 320 000

cz´Êç tej liczby, co wynosi

365.258 dnia. Ka˝dy s∏oneczny miesiàc
jest dwunastà cz´Êcià roku, a ka˝dy mie-
siàc ksi´˝ycowy

1

/

53 433 336

cz´Êcià

1 577 917 500-dniowego cyklu, co wy-
nosi 29.531 dnia. Istotà pomys∏u jest to,
˝e oba typy miesi´cy biegnà jednocze-
Ênie. Co pewien czas miesiàc ksi´˝yco-
wy ca∏kowicie zawiera si´ w miesiàcu
s∏onecznym. W takim przypadku ten
miesiàc ksi´˝ycowy uwa˝any jest za
miesiàc przest´pny; bezpoÊrednio po
nim umieszcza si´ dodatkowy miesiàc
ksi´˝ycowy.

W odró˝nieniu od innych kalendarzy

chiƒski jest oparty na konkretnych zjawi-

skach astronomicznych, a nie na regu-
∏ach. W Calendrical Calculations zamiesz-
czono jego najnowszà wersj´ pochodzà-
ca z 1645 roku. Miesiàce sà ksi´˝ycowe
i zaczynajà si´ od nowiu, a lata liczà 12
lub 13 miesi´cy. Jednak˝e uk∏ad miesi´-
cy zale˝y od wchodzenia S∏oƒca w znaki
zodiaku. Rok s∏oneczny dzieli si´ na 12
wi´kszych okresów s∏onecznych zwa-
nych zhongqi i 12 mniejszych zwanych jie-
qi. Ka˝dy z nich odpowiada 15-stopnio-
wemu odcinkowi s∏onecznej d∏ugoÊci, te
wi´ksze odpowiadajà poczàtkowym
o wielokrotnoÊci 30°, a mniejsze punk-
tom pomi´dzy wi´kszymi.

Z zasady najkrótszy dzieƒ roku, zi-

mowe przesilenie, zawsze przypada na
jedenasty miesiàc roku. Miesiàce roku
liczàcego tylko 12 pe∏nych miesi´cy ksi´-
˝ycowych sà zawsze numerowane
w nast´pujàcej kolejnoÊci: 12, 1, 2, 3, 4, 5,
6, 7, 8, 9, 10, 11. Gdy rok ma ich 13, to
jedna z liczb jest powtórzona jako ozna-
czenie miesiàca przest´pnego – pierw-
szego, który nie zawiera wi´kszej cz´-
Êci s∏onecznej. (Poniewa˝ miesi´cy

ksi´˝ycowych jest 13, a wi´kszych ob-
szarów s∏onecznych 12, przynajmniej je-
den miesiàc ksi´˝ycowy nie zawiera
wi´kszej cz´Êci s∏onecznej).

JeÊli kalendarze doby obecnej sà tak

skomplikowane, to jakie mamy widoki
na przysz∏oÊç? Wszystkie ró˝norodne
cykle astronomiczne powoli zmieniajà
swojà d∏ugoÊç z powodu p∏ywowych
si∏ grawitacyjnych. Co wi´cej, mamy ca-
∏y szereg precesji zrównania dnia z no-
cà, które w pewien sposób wià˝à si´
znów z epokami lodowymi, tak wi´c
przysz∏y kalendarz musi byç powiàza-
ny z klimatem.

Powinien on ∏atwo przystosowywaç

si´ do zachodzàcych zmian, a nie opie-
raç na ustalonych wczeÊniej zasadach,
poniewa˝ astronomowie odkryli nie-
dawno, ˝e ruch Uk∏adu S∏onecznego jest
chaotyczny. Nowy Rok A.D. 10 000 000
byç mo˝e wypadnie 1 stycznia, ale nikt
nie potrafi przewidzieç, ile dni up∏ynie
od dziÊ do tego czasu.

T∏umaczyli

Zdzis∏aw Pogoda i Robert Wolak

FUNDACJA NA RZECZ NAUKI POLSKIEJ

■

Konkursy na subwencjonowanie zakupów aparatury badawczej w roku 1997
Rozwój wielu dyscyplin naukowych wymaga dost´pu do nowoczesnej, bardzo wyspecjalizowanej aparatury ba-

dawczej, na której zakup cz´sto nie mogà sobie pozwoliç nawet najlepsze zespo∏y naukowe. Pragnàc przyjÊç im
z pomocà, Fundacja co roku subwencjonuje zakupy unikalnej aparatury badawczej dla dwu wybranych dziedzin
nauki, og∏aszajàc dla ka˝dej z nich konkurs wniosków, dost´pny dla wszystkich zainteresowanych.

Wybierane sà takie obszary badaƒ, które dotyczà rozwiàzywania problemów podstawowych, szczególnie wa˝-

nych z punktu widzenia mo˝liwych zastosowaƒ praktycznych.

W roku 1997 b´dà to: fotochemia szybkich reakcji (konkurs FASTKIN) oraz metody rekultywacji gleby (konkurs

REGLE).

■

Konkurs FASTKIN (fotochemia szybkich reakcji)
Celem konkursu jest wsparcie badaƒ z obszaru fotochemii zwiàzków nieorganicznych i organicznych pro-

wadzàcych do g∏´bszego zrozumienia szybkich reakcji chemicznych oraz skuteczniejszego ich wykorzystania
w praktyce.

Otrzymywanie nowych substancji chemicznych lub te˝ mo˝liwoÊç ∏atwiejszej syntezy zwiàzków ju˝ znanych, to

jedno z wyzwaƒ wspó∏czesnej chemii. Wa˝nà drog´ w tym kierunku otwiera fotochemia. Oddzia∏ywanie kwantów
promieniowania, cz´sto monochromatycznego, z materià pozwala realizowaç reakcje chemiczne, które bez udzia-
∏u promieniowania nie zachodzà. Poznanie mechanizmów tych reakcji, zachodzàcych jedynie w stanie wzbudzo-
nym, oraz badanie ich kinetyki otwiera mo˝liwoÊci praktycznego wykorzystania tych procesów w katalizie, bioche-
mii oraz technologii polimerów i zwiàzków makromolekularnych.

Termin sk∏adania wniosków up∏ywa 31 stycznia.

■

Konkurs REGLE (metody rekultywacji gleby)
Ten konkurs ma na celu wsparcie aparaturowe poszukiwaƒ naukowych prowadzàcych do powstania skutecznych

metod przywracajàcych glebie jej u˝ytkowà wartoÊç.

Potrzeba rekultywacji gleby zniszczonej w wyniku przemys∏owej dzia∏alnoÊci cz∏owieka oraz u˝ytkowania do ce-

lów wojskowych sta∏a si´ istotnym problemem spo∏ecznym i gospodarczym, którego ostroÊç i ekologiczne konse-
kwencje ujawni∏y si´ w pe∏ni w ostatnich latach. W zwiàzku z ró˝norodnoÊcià powsta∏ych zniszczeƒ konieczne jest
zarówno prowadzenie precyzyjnej ich diagnostyki, jak i poszukiwanie w∏aÊciwych metod rekultywacji. Badania z ta-
kich dziedzin, jak agrofizyka czy agrobiologia, powinny doprowadziç do opracowania odpowiednio ró˝norodnych,
fizyko-chemicznych i biologicznych technologii rekultywacyjnych.

Termin sk∏adania wniosków up∏ywa 31 marca.

Adres Fundacji: ul. Gra˝yny 11, 02-548 Warszawa, tel./fax: 45-40-54, 45-40-55 (e-mail: [e-mail]).

Informacje o programie Fundacji dost´pne sà w Internecie: http://sunsite.icm.edu.pl/science/fnp