Praca klasowa- figury geometryczne  

 

 

Imię i nazwisko……………………………. 

 

 

 

Grupa A 

1.  Czy boki trójkąta mogą mieć podane poniżej długości? 

a)  2 cm, 3 cm, 7 cm  

 …… 

b)  4 cm, 0,5 dm, 0,08 m  

 …… 

 

2.  Czy kąty trójkąta mogą mieć podane miary? 

a)  20

°, 7°, 163°  …… 

b)  13

°8’, 93°16’, 74°36’  …… 

 

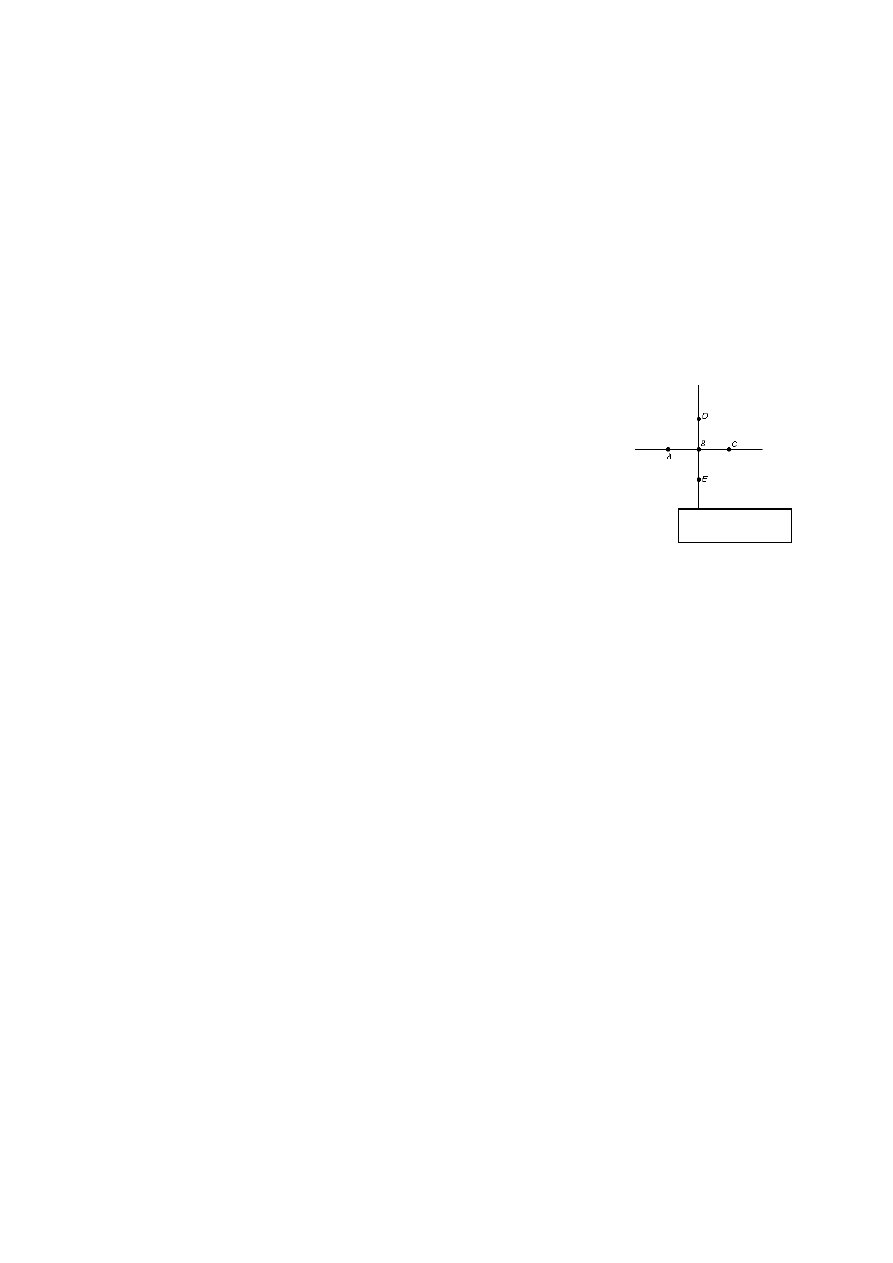
3.  Na podstawie rysunku 1 wypisz :  

 
a)  dwie pary odcinków prostopadłych: …………………………….. 

b)  dwie pary odcinków równoległych:…………………………….. 

 

4.  Które ze zdań jest prawdziwe? 

a)  Jeśli wszystkie boki czworokąta są równe, to także wszystkie jego kąty są równe. 
b)  Jeśli wszystkie kąty czworokąta są równe, to także wszystkie jego boki są równe. 
c)  Jeśli wszystkie boki trójkąta są równe, to także wszystkie jego kąty są równe. 
d)  Jeśli dwa kąty czworokąta są równe, to także dwa jego boki są równe. 

 

5.  W  trójkącie  ABC  kąt  ACB  ma  miarę  52

°,  a  kąt  ABC 48°.  Z  wierzchołka  C  poprowadzono 

wysokość CD. Oblicz miary kątów trójkąta ADC. 
 
 
 
 
 
 

6.  Oblicz pole czworokąta o wierzchołkach: 

a)  A = (-3,-2), B = (2, -2), C = (2,4), D = (-3, 4). 
b)  E = (-1,-4), F = (3, -4), G = (5, 0), H = (-4, 0). 
 
 
 
 

 

Rysunek 1 

7.  Zamień podane jednostki : 

a)  6 km

2

 = ……………………………..m

2

 

b)  32 cm

2

 = ……………………………m

2

 

c)  0,02 km

2

 = ………………………….ha 

d)  470 m

2

 = …………………………….a 

 

8.  Narysuj kąt ostry 

  i kąt rozwarty  . Skonstruuj kąt o mierze      . 

 

 

 

 

 

 

9.  Działka pani Ewy ma kształt trapezu prostokątnego. Podstawy tego trapezu mają długość 8m 

i 10  m,  a  prostopadłe  ramię  ma  długość  30  dm.  Pani  Ewa  80%  powierzchni  działki  obsiała 
burakami.  Ile  opakowań  nasion  buraków  kupiono,  jeżeli  jedno  opakowanie  wystarcza  na 
obsianie 2 m

2

 powierzchni? 

 

 

 

 

 

 

10.  (zadanie  dodatkowe)      Dany  jest  trapez  ABCD,  w  którym  AB 

     .  Na  podstawie  AB 

zaznaczono punkty E i F takie, że EC 

    i FD     . Wykaż, że czworokąty AECD i FBCD 

mają równe pola. 

 

 

 

 

 

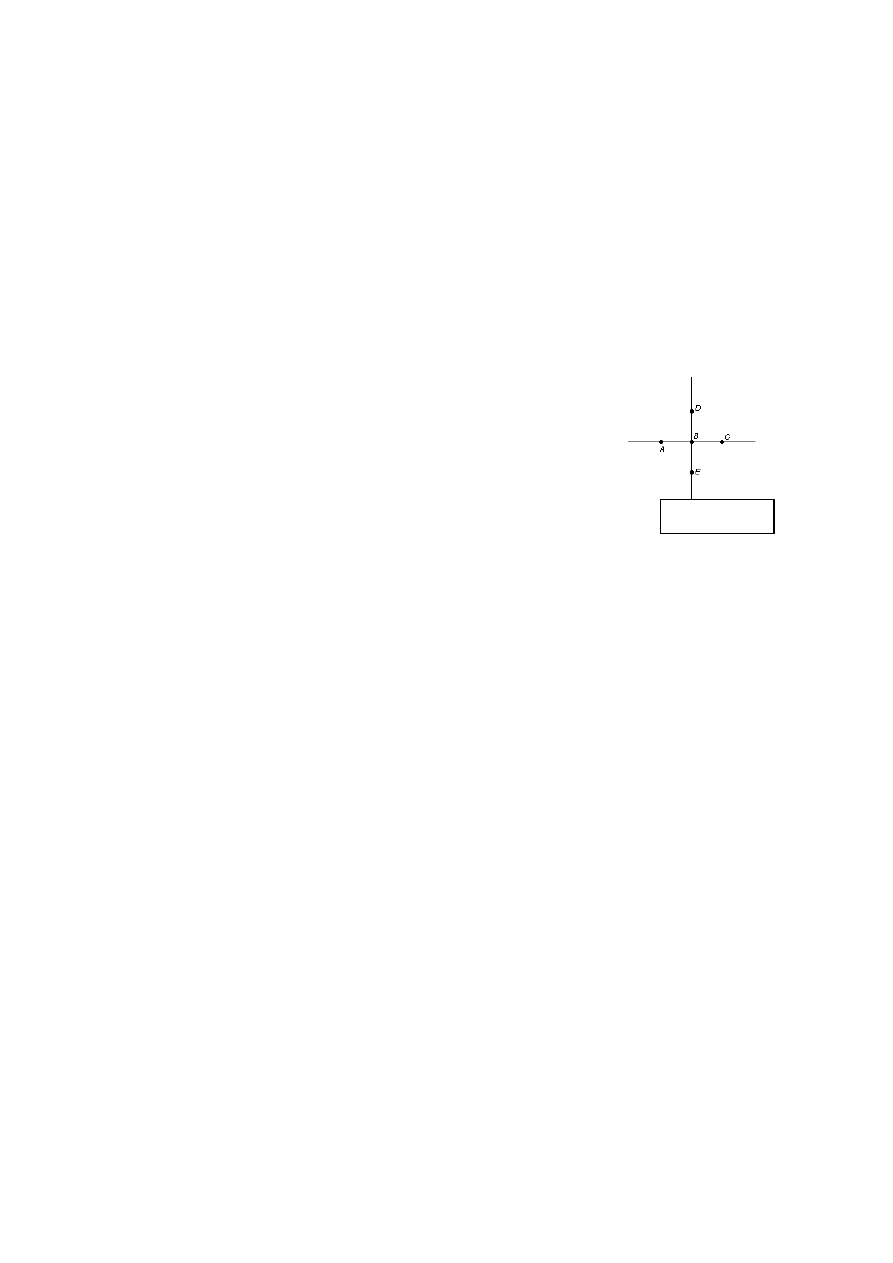
Praca klasowa- figury geometryczne  

 

 

Imię i nazwisko……………………………. 

 

 

 

Grupa B 

1.  Czy boki trójkąta mogą mieć podane poniżej długości? 

c)  3 cm, 4 cm, 7 cm  

 …… 

d)  4 cm, 0,5 dm, 0,07 m  

 …… 

 

2.  Czy kąty trójkąta mogą mieć podane miary? 

c)  28

°, 60°, 92°  …… 

d)  21

°13’, 83°16’, 75°31’  …… 

 

3.  Na podstawie rysunku 1 wypisz :  

 
c)  Dwie pary odcinków równoległych: …………………………….. 

d)  Dwie pary odcinków prostopadłych:…………………………….. 

 

4.  Które ze zdań jest fałszywe? 

a)  Jeśli wszystkie boki trójkąta są równe, to także wszystkie jego kąty są równe. 
b)  Jeśli wszystkie kąty trójkąta są równe, to także wszystkie jego boki SA równe. 
c)  Jeśli wszystkie boki czworokąta SA równe, to także wszystkie jego kąty są równe. 
d)  Jeśli wszystkie kąty czworokąta są proste, to czworokąt ten jest prostokatem. 

 

5.  W  trójkącie  ABC  kąt  ACB  ma  miarę  62

°,  a  kąt  ABC 38°.  Z  wierzchołka  C  poprowadzono 

wysokość CD. Oblicz miary kątów trójkąta ADC. 

 

 

 

6.  Oblicz pole czworokąta o wierzchołkach: 

a)  A = (3,2), B = (-2, 2), C = (-2,-4), D = (3, -4). 
b)  E = (-5,-1), F = (-5, 3), G = (0, 5), H = (0, -4). 

 

 

 

Rysunek 1 

7.  Zamień podane jednostki : 

a)  3 km

2

 = …………………………..m

2

 

b)  61 cm

2

 = ………………………….m

2

 

c)  0,004 km

2

 = ……………………….ha 

d)  70 m

2

 = …………………………….a 

 

8.  Narysuj kąt ostry 

  i kąt rozwarty  . Skonstruuj kąt o mierze      . 

 

 

 

 

 

 

9.  Działka pana Jurka ma kształt trapezu prostokątnego. Podstawy tego trapezu mają długość 8m 

i  30  dm,  a  prostopadłe  ramię  ma  długość  4  m.  Pan  Jurek  70%  powierzchni  działki  obsiał 
trawą.  Ile  opakowań  nasion  trawy  kupiono,  jeżeli  jedno  opakowanie  wystarcza  na  obsianie 
3 m

2

 powierzchni? 

 

 

 

 

 

 

 

10.  (zadanie  dodatkowe)      Dany  jest  trapez  ABCD,  w  którym  AB 

     .  Na  podstawie  AB 

zaznaczono punkty E i F takie, że EC 

    i FD     . Wykaż, że czworokąty AECD i FBCD 

mają równe pola.