BLACK

MG1S3 str. 6

FIGURY GEOMETRYCZNE

NUMER ZADANIA W GRUPIE

WIADOMOŚCI I UMIEJĘTNOŚCI SPRAWDZANE W ZADANIU

POZIOM

A

A

B

B

WYMAGAŃ

1

2

1

2

Znajomość własności wielokątów.

K

2

1

2

1

Znajomość własności rombu.

K

3

4

3

4

Umiejętność wskazywania trójkątów przystających.

K

4

3

4

3

Umiejętność obliczania kątów w trójkącie.

P

5

5

5

5

Umiejętność konstruowania trójkąta o danych bokach i kącie zawartym
między nimi.

R

6

7

6

6

Umiejętność obliczania miar kątów wewnętrznych w trójkącie.

P

7

6

8

7

Umiejętność obliczania pól wielokątów w układzie współrzędnych.

P

8

9

7

9

Umiejętność obliczania obwodów i pól wielokątów.

R

9

8

10

8

Wykorzystanie umiejętności obliczania obwodów i pól wielokątów w za-
daniach tekstowych.

R

10

10

9

10

Umiejętność rozwiązywania zadań tekstowych związanych z oblicza-
niem pól wielokątów. Umiejętność zamiany jednostek długości i pola.

D

11

11

11

11

Umiejętność obliczania pól wielokątów w sytuacji nietypowej.

W

BLACK

MG1S3 str. 14

FIGURY GEOMETRYCZNE

GRUPA A

1.

Które ze zdań jest prawdziwe?

A. Jeśli wszystkie boki czworokąta są równe, to także wszystkie jego kąty są równe.
B. Jeśli wszystkie kąty czworokąta są równe, to także wszystkie jego boki są równe.
C. Jeśli wszystkie boki trójkąta są równe, to także wszystkie jego kąty są równe.
D. Jeśli dwa kąty czworokąta są równe, to także dwa jego boki są równe.

2.

Krótsza przekątna rombu dzieli go na dwa trójkąty:

A. prostokątne

B. równoramienne

C. równoboczne

D. o kątach 50◦, 50◦, 80◦

3.

Dany jest okrąg, w którym cięciwy AB i CD mają taką samą długość. Punkt O oznacza środek tego

okręgu. Trójkąty OAB i OCD są:
A. przystające
B. równoboczne

C. różnoboczne
D. prostokątne

4.

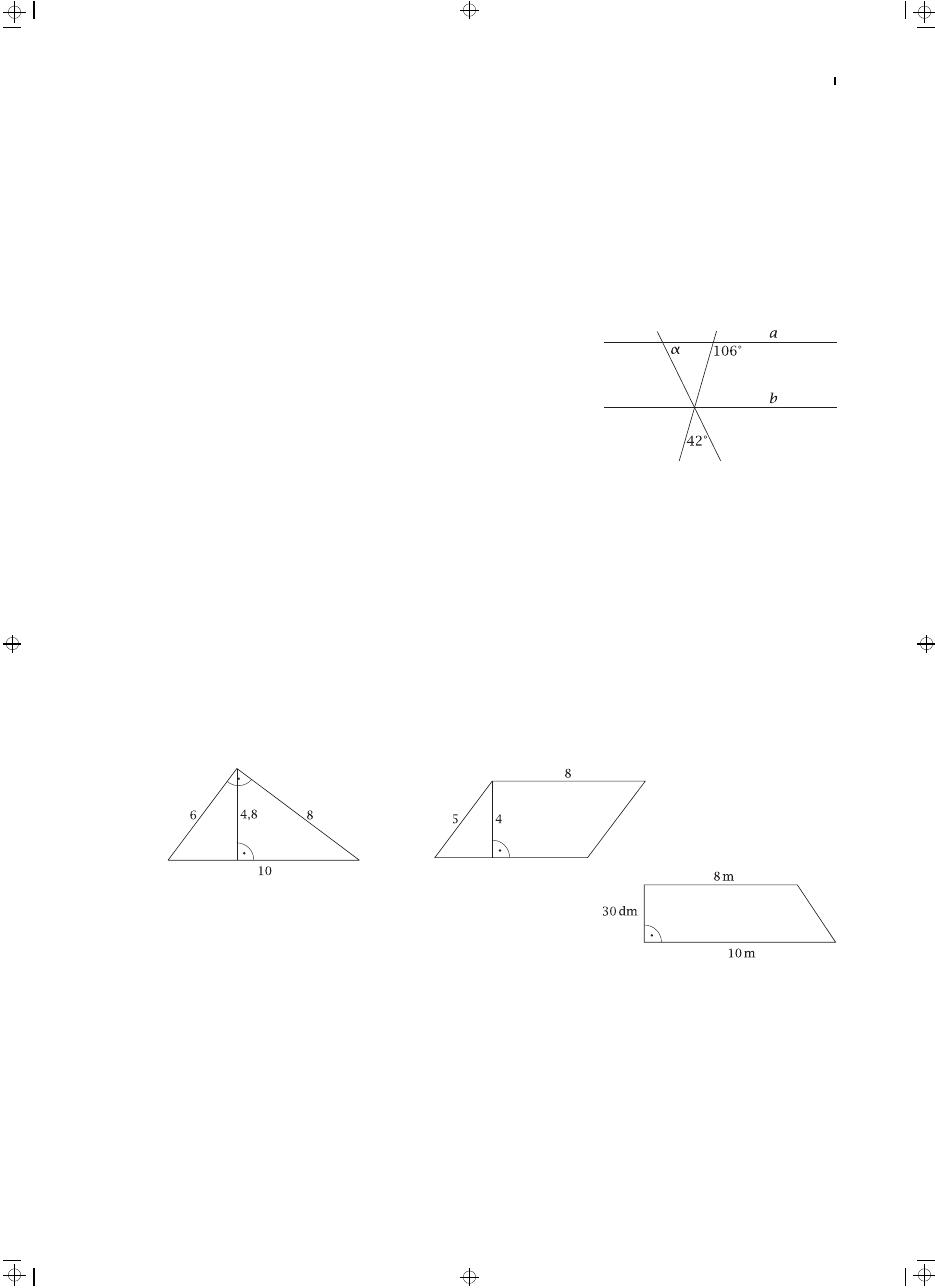
Proste a i b na rysunku obok są równoległe. Kąt α ma miarę:

A. 53◦

B. 90◦

C. 32◦

D. 64◦

5.

Narysuj kąt ostry α oraz odcinki a i b. Skonstruuj trójkąt

o bokach a i b i kącie α zawartym między nimi.

6.

W trójkącie ABC kąt ACB ma miarę 52◦, a kąt ABC — 48◦. Z wierzchołka C poprowadzono wysokość

CD. Oblicz miary kątów trójkąta ADC.

7.

Oblicz pole czworokąta o wierzchołkach A = (−3, −2), B = (2, −2), C = (2, 4) i D = (−3, 4).

8.

Oblicz pola i obwody narysowanych wielokątów.

a) równoległobok

b) trójkąt

9.

Jeden metr kwadratowy pewnej wykładziny kosztuje 27 zł.

Szerokość tej wykładziny wynosi 2,5 m. Czy 100 zł wystarczy na
zakupienie 1,5 metra bieżącego tej wykładziny?

10.

Całą powierzchnię działki w kształcie trapezu o wymiarach

przedstawionych na rysunku obsiano burakami. Ile opakowań na-
sion buraków kupiono, jeżeli jedno opakowanie wystarcza na obsia-
nie 2 m

2

powierzchni?

*11.

Dany jest trapez ABCD, w którym AB CD. Wykaż, że trójkąty ABC i ABD mają równe pola.

BLACK

MG1S3 str. 15

FIGURY GEOMETRYCZNE

GRUPA A

1.

Krótsza przekątna rombu dzieli go na dwa trójkąty:

A. równoboczne

B. prostokątne

C. równoramienne

D. o kątach 50◦, 50◦, 80◦

2.

Które ze zdań jest prawdziwe?

A. Jeśli wszystkie boki trójkąta są równe, to także wszystkie jego kąty są równe.
B. Jeśli wszystkie kąty czworokąta są równe, to także wszystkie jego boki są równe.
C. Jeśli wszystkie boki czworokąta są równe, to także wszystkie jego kąty są równe.
D. Jeśli dwa kąty czworokąta są równe, to także dwa jego boki są równe.

3.

Proste a i b na rysunku obok są równoległe. Kąt α ma miarę:

A. 32◦

B. 64◦

C. 53◦

D. 90◦

4.

Dany jest okrąg, w którym cięciwy AB i CD mają taką samą

długość. Punkt O oznacza środek tego okręgu. Trójkąty OAB
i OCD są:
A. równoboczne
B. przystające

C. prostokątne
D. różnoboczne

5.

Narysuj kąt rozwarty α oraz odcinki a i b. Skonstruuj trójkąt o bokach a i b i kącie α zawartym między

nimi.

6.

Oblicz pole czworokąta o wierzchołkach A = (−3, −2), B = (2, −2), C = (2, 4) i D = (−3, 4).

7.

W trójkącie ABC kąt ACB ma miarę 52◦, a kąt ABC — 48◦. Z wierzchołka C poprowadzono wysokość

CD. Oblicz miary kątów trójkąta ADC.

8.

Jeden metr kwadratowy pewnej wykładziny kosztuje 27 zł. Szerokość tej wykładziny wynosi 2,5 m. Czy

100 zł wystarczy na zakupienie 1,5 metra bieżącego tej wykładziny?

9.

Oblicz pola i obwody narysowanych wielokątów.

a) trójkąt

b) równoległobok

10.

Całą powierzchnię działki w kształcie trapezu o wymiarach

przedstawionych na rysunku obsiano burakami. Ile opakowań na-
sion buraków kupiono, jeżeli jedno opakowanie wystarcza na obsia-
nie 2 m

2

powierzchni?

*11.

Dany jest trapez ABCD, w którym AB CD. Wykaż, że trójkąty ABC i ABD mają równe pola.

BLACK

MG1S3 str. 16

FIGURY GEOMETRYCZNE

GRUPA B

1.

Które ze zdań jest fałszywe?

A. Jeśli wszystkie boki trójkąta są równe, to także wszystkie jego kąty są równe.
B. Jeśli wszystkie kąty trójkąta są równe, to także wszystkie jego boki są równe.
C. Jeśli wszystkie boki czworokąta są równe, to także wszystkie jego kąty są równe.
D. Jeśli wszystkie kąty czworokąta są proste, to czworokąt ten jest prostokątem.

2.

Dłuższa przekątna rombu dzieli go na dwa trójkąty:

A. prostokątne

B. równoboczne

C. równoramienne

D. o kątach 30◦, 30◦, 120◦

3.

W czworokątcie ABCD |AB| = |DC| i |BC| = |AD|. Trójkąty ACD i ABC są:

A. prostokątne
B. równoramienne

C. przystające
D. równoboczne

4.

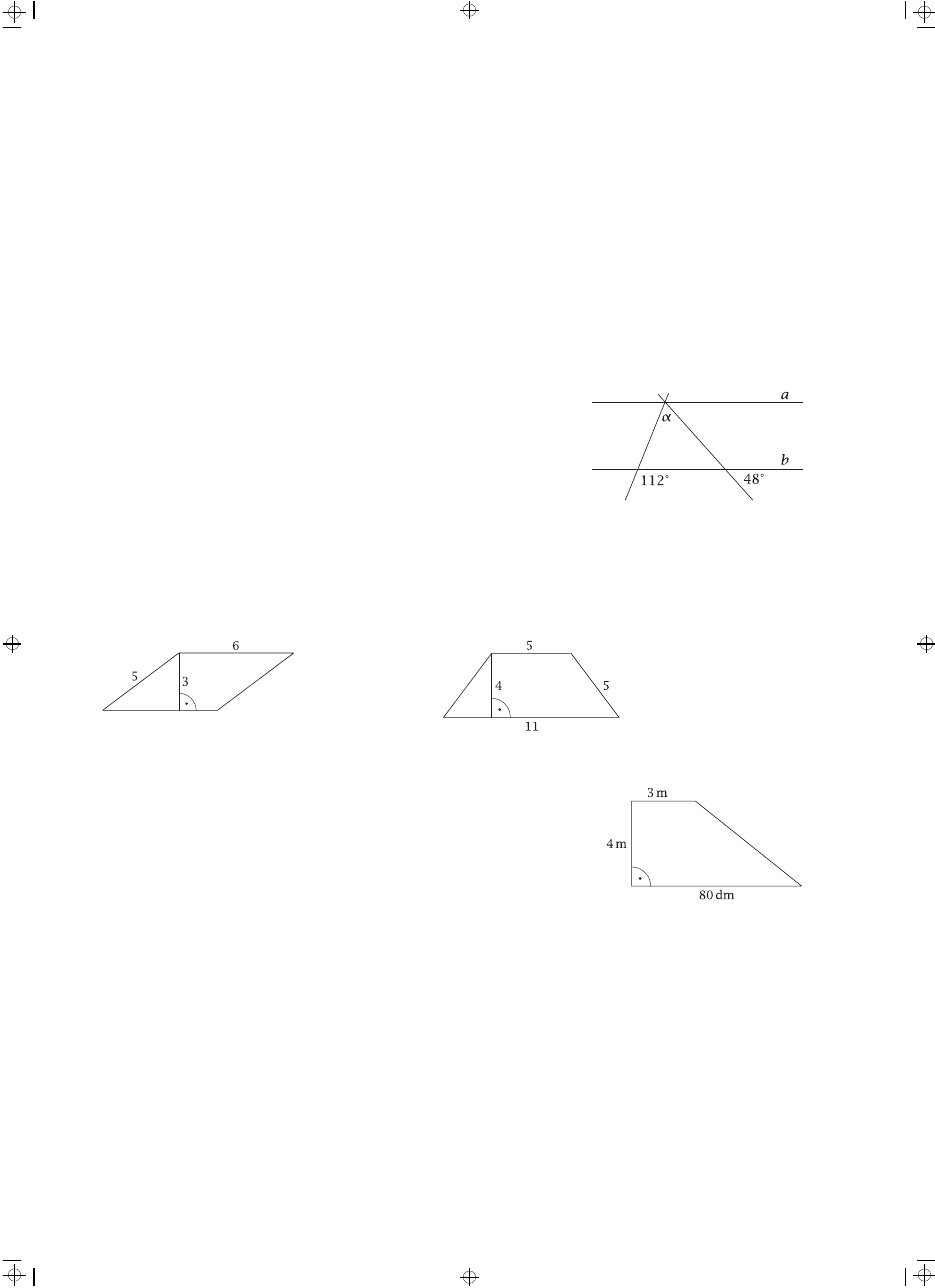
Proste a i b na rysunku są równoległe. Kąt α ma miarę:

A. 56◦

B. 64◦

C. 90◦

D. 20◦

5.

Narysuj kąt rozwarty α oraz odcinki a i b. Skonstruuj trójkąt

o bokach a i b i kącie α zawartym między nimi.

6.

W trójkącie ABC kąt ACB ma miarę 64◦, a kąt BAC — 36◦. Z wierzchołka C poprowadzono wysokość

CD. Oblicz miary kątów trójkąta BCD.

7.

Oblicz pola i obwody narysowanych wielokątów.

a) równoległobok

b) trapez równoramienny

8.

Oblicz pole czworokąta o wierzchołkach A = (−5, −1), B = (1, −1), C = (1, 5) i D = (−5, 5).

9.

Całą powierzchnię działki w kształcie trapezu o wymiarach przedsta-

wionych na rysunku obsiano trawą. Ile opakowań nasion trawy kupiono,
jeżeli jedno opakowanie wystarcza na obsianie 3 m

2

powierzchni?

10.

Jeden metr kwadratowy pewnej wykładziny kosztuje 35 zł. Szero-

kość tej wykładziny wynosi 1,5 m. Czy 200 zł wystarczy na zakupienie
2,5 metra bieżącego tej wykładziny?

*11.

Dany jest trapez ABCD, w którym AB CD. Na podstawie AB zaznaczono punkty E i F takie, że

EC AD i FD BC. Wykaż, że czworokąty AECD i FBCD mają równe pola.

BLACK

MG1S3 str. 17

FIGURY GEOMETRYCZNE

GRUPA B

1.

Dłuższa przekątna rombu dzieli go na dwa trójkąty:

A. o kątach 30◦, 30◦, 120◦

B. równoboczne

C. prostokątne

D. równoramienne

2.

Które ze zdań jest fałszywe?

A. Jeśli wszystkie kąty czworokąta są proste, to czworokąt ten jest prostokątem.
B. Jeśli wszystkie kąty trójkąta są równe, to także wszystkie jego boki są równe.
C. Jeśli wszystkie boki czworokąta są równe, to także wszystkie jego kąty są równe.
D. Jeśli wszystkie boki trójkąta są równe, to także wszystkie jego kąty są równe.

3.

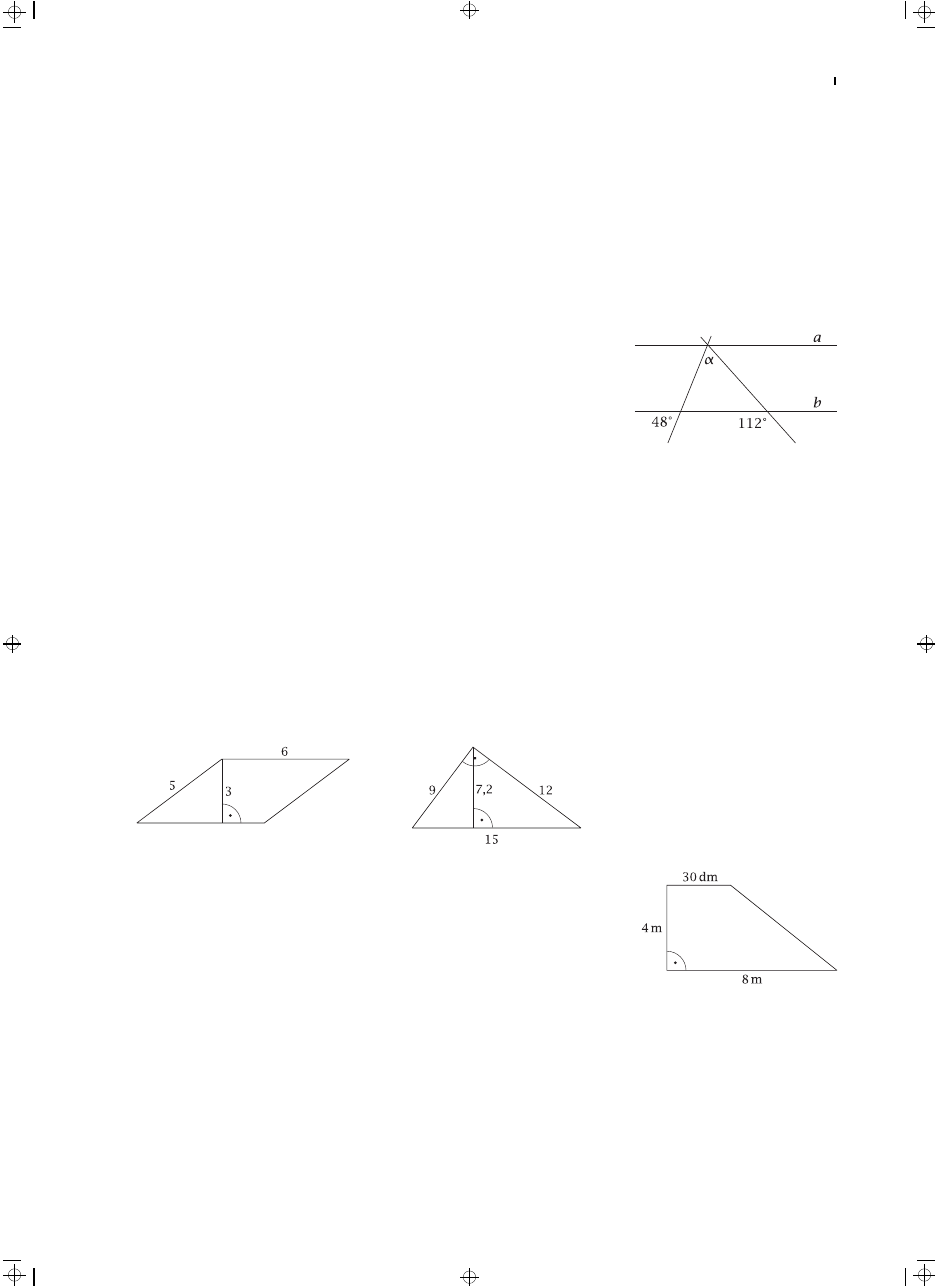
Proste a i b na rysunku są równoległe. Kąt α ma miarę:

A. 90◦

B. 20◦

C. 64◦

D. 56◦

4.

W czworokącie ABCD |AB| = |DC| i |BC| = |AD|. Trójkąty ACD

i ABC są:
A. prostokątne
B. równoramienne

C. przystające
D. równoboczne

5.

Narysuj kąt ostry α oraz odcinki a i b. Skonstruuj trójkąt o bokach a i b i kącie α zawartym między

nimi.

6.

W trójkącie ABC kąt ACB ma miarę 64◦, a kąt ABC — 36◦. Z wierzchołka C poprowadzono wysokość

CD. Oblicz miary kątów trójkąta BDC.

7.

Oblicz pole czworokąta o wierzchołkach A = (−5, −1), B = (1, −1), C = (1, 5) i D = (−5, 5).

8.

Jeden metr kwadratowy pewnej wykładziny kosztuje 35 zł. Szerokość tej wykładziny wynosi 1,5 m. Czy

200 zł wystarczy na zakupienie 2,5 metra bieżącego tej wykładziny?

9.

Oblicz pola i obwody narysowanych wielokątów.

a) równoległobok

b) trójkąt

10.

Całą powierzchnię działki w kształcie trapezu o wymiarach

przedstawionych na rysunku obsiano trawą. Ile opakowań nasion
trawy kupiono, jeżeli jedno opakowanie wystarcza na obsianie 3 m

2

powierzchni?

*11.

Dany jest trapez ABCD, w którym AB CD. Na podstawie AB

zaznaczono punkty E i F takie, że EC AD i FD BC. Wykaż, że
czworokąty AECD i FBCD mają równe pola.

BLACK

MG1S3 str. 33

FIGURY GEOMETRYCZNE

Grupa A:

1.

C

2.

B

3.

A

4.

D

6.

10◦, 80◦, 90◦.

7.

P = 30.

8.

a) P=32, obwód=26, b) P=24,

obwód=24.

9.

Nie.

10.

14 opakowań.

Grupa A :

1.

C

2.

A

3.

B

4.

B

6.

P = 30.

7.

10◦, 80◦, 90◦.

8.

Nie.

9.

a) P=24, obwód=24,

b) P=32, obwód=26.

10.

14 opakowań.

Grupa B:

1.

C

2.

C

3.

C

4.

B

6.

10◦, 80◦, 90◦.

7.

a) P=18, obwód=22, b) P=32, obwód=26.

8.

P = 36.

9.

8 opakowań.

10.

Tak.

Grupa B :

1.

D

2.

C

3.

C

4.

C

6.

10◦,

80◦,

90◦.

7.

P = 36.

8.

Tak.

9.

a) P=18,

obwód=22, b) P=54, obwód=36.

10.

8 opakowań.