Jeden z kątów w trójkącie równoramiennym ma miarę
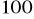
, Oblicz miary pozostałych kątów trójkąta.Jeden z kątów w trójkącie równoramiennym ma miarę
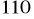
, Oblicz miary pozostałych kątów trójkąta.Oblicz miary kątów trójkąta, którego jeden kąt ma miarę
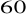
, a różnica dwu pozostałych wynosi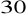
.Oblicz miary kątów równoległoboku, w którym jeden z dwóch kątów sąsiednich jest dwa razy większy od drugiego.
W trapezie prostokątnym miary kątów przeciwległych różnią się o
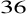
. Wyznacz miary kątów tego trapezu.W prostokącie przekątna tworzy z bokiem kąt o mierze
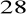
. Oblicz miary kątów między przekątnym tego prostokąta.Wykaż, że połowa sumy długości dwóch boków trójkąta jest większa od długości środkowej trzeciego boku.
Wykaż, że suma odległości punktu wewnętrznego trójkąta od wierzchołków trójkąta jest większa od połowy obwodu.
Litery
,
,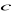
,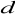
,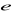
oznaczają długości boków (zobacz rysunek). Czy podane równość wynikają z twierdzenia Pitagorasa? Zaznacz właściwe odpowiedzi.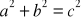
tak nie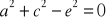
tak nie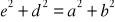
tak nie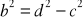
tak nie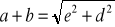
tak nie
Litery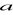
,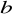
,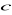
,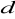
,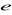
oznaczają długości boków (zobacz rysunek). Czy podane równość wynikają z twierdzenia Pitagorasa? Zaznacz właściwe odpowiedzi.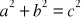
tak nie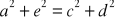
tak nie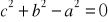
tak nie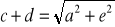
tak nie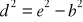
tak nieW trójkącie równoramiennym, różnica długości podstawy i ramienia jest równa 6 cm. Oblicz długość podstawy i ramienia trójkąta, jeśli jego obwód jest równy 36 cm.
Oblicz pole trójkąta, którego dwa boki mają długości 12 cm i 15 cm, a wysokość opuszczona na krótszy bok dzieli go na połowy.
Oblicz długości boków równoległoboku
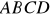
, w którym
stanowi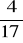
obwodu wiedząc, że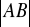
=12 m.W równoległoboku o obwodzie 5 m krótszy bok ma długość 1 dm. Oblicz długość drugiego boku równoległoboku.
W równoległoboku o obwodzie 6 m krótszy bok ma długość 2 dm. Oblicz długość drugiego boku równoległoboku.
Długości boków prostokąta różnią się o 3 cm. Znajdź długości boków tego prostokąta wiedząc, że przekątna prostokąta ma 15 cm długości.
Wysokość trapezu wynosi 8 cm i jest o 2 cm krótsza od jednej z podstaw. Druga podstawa jest 2 razy dłuższa od wysokości. Oblicz pole trapezu.
Wysokość trapezu wynosi 5 cm i jest o 1 cm krótsza od jednej z podstaw. Druga podstawa jest 2 razy dłuższa od wysokości. Oblicz pole trapezu.
W trapezie równoramiennym wysokość opuszczona z wierzchołka kąta rozwartego dzieli większą podstawę na odcinki o długości 4 cm i 14 cm. Obwód trapezu jest równy 38 cm. Oblicz pole trapezu.
Stosunek długości podstaw trapezu prostokątnego równa się liczbie
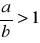
. Przekątne trapezu są prostopadłe. Oblicz stosunek długości przekątnych trapezu.Długości przekątnych rombu są równe 7,2 cm i 4,5 cm. Oblicz wysokość tego rombu.
Długości przekątnych rombu są równe 7,2 cm i 4,5 cm. Oblicz pole i wysokość rombu.Obwód rombu wynosi 40 cm, a długość jego krótszej przekątnej 12 cm. Oblicz pole rombu oraz jego wysokość.
Oblicz pole i obwód zakreślonej figury mając dane
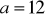
cm.Oblicz pole koła, jeśli jego obwód jest równy
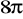
cm.
Oblicz pole i obwód zakreślonej figury mając dane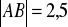
cm,
Skonstruuj:wysokość opuszczoną z wierzchołka A,
dwusieczną kąta przy wierzchołku A,
środkową poprowadzoną z wierzchołka A.
Skonstruuj prostą styczną do okręgu w punkcie X (punkt O jest środkiem okręgu).
a
e
b
d
c
e
d
c
b
a
B
A
D
C
a
a
A
B
C
O
X
Wyszukiwarka
Podobne podstrony:
Figury i przekształcenia, Zbiór zadań, Klasa 2
Wielokąty i figury podobne, Zbiór zadań, Klasa 2
Zdania i zbiory, Zbiór zadań, Klasa 1
Równania i nierówności, Zbiór zadań, Klasa 1
Funkcje wykładnicze i logarytmy, Zbiór zadań, Klasa 2
Liczby i działania, Zbiór zadań, Klasa 1
Trygonometria, Zbiór zadań, Klasa 2
Wielomiany, Zbiór zadań, Klasa 2
zbiór zadań klasa 4 chomikuj
figury geometryczne praca klasowa klasa 7 rok 2017
więcej podobnych podstron