Oblicz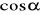
i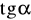
, gdzie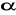
jest miarą kąta ostrego w trójkącie ABC.
Oblicz
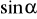
i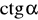
, gdzie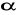
jest miarą kąta ostrego w trójkącie ABC.
Oblicz
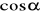
i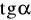
, gdzie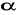
jest miarą kąta ostrego w trójkącie ABC.
Wyznacz długości boków
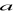
i
.
Wyznacz długości boków i miary kątów w trójkącie prostokątnym
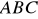
(kąt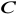
jest prosty), mając dane: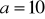
cm,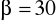
,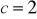
cm,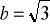
cm,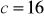
cm,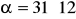
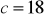
cm,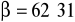
.Rozwiąż trójkąt mając dane
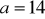
cm,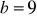
cm,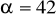
,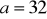
cm,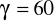
,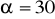
,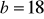
dm,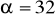
,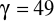
.Rozwiąż trójkąt mając dane
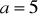
cm,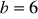
cm,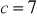
cm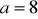
cm,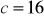
cm,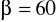
.Oblicz miarę łukową kątów:
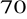
,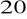
,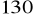
.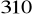
,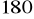
,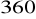
,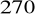
,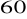
,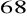
,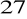
Wyraź w radianach kąty o miarach:
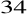
,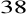
,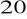
,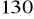
,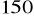
,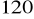
,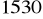
,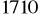
.Jaką miarę stopniową ma kąt
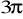
rad,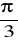
rad,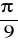
rad,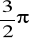
rad,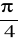
rad,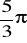
rad,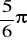
rad,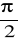
rad?
Oblicz miarę stopniową kątów:
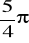
,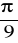
,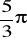
.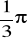
,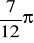
,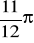
,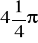
,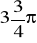
.
Wyznacz miarę łukową kątów wewnętrznych następujących wielokątów foremnych: trójkąta, kwadratu, pięciokąta, sześciokąta.Cztery punkty należące do okręgu dzielą ten okrąg na cztery kolejne łuki o stosunku długości 1:1:4:9. Oblicz miary kątów wewnętrznych czworokąta, którego wierzchołkami są wymienione punkty.
Oblicz
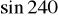
, cos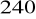
,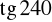
i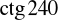
(możesz skorzystać z rysunku zamieszczonego obok).
Oblicz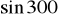
,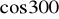
,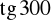
i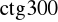
(możesz skorzystać z rysunku zamieszczonego obok).Korzystając ze wzorów redukcyjnych, oblicz
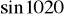
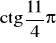
.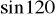
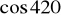
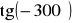
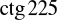
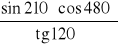
Oblicz stosując wzory redukcyjne:
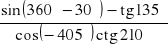
.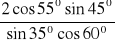
;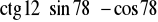
Oblicz (bez użycia tablic) wartość wyrażenia:
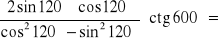
.Oblicz
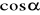
i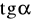
kąta, gdzie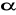
jest kątem, którego drugie ramię przechodzi przez punkt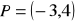
.Oblicz
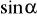
i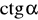
kąta, którego drugie ramię przechodzi przez punkt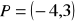
.Oblicz
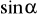
i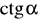
kąta, gdzie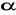
jest kątem, którego drugie ramię przechodzi przez punkt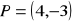
.Oblicz
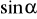
i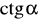
, gdzie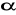
jest kątem, którego drugie ramię przechodzi przez punkt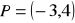
.Oblicz
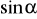
i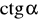
kąta, gdzie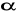
jest kątem, którego drugie ramię przechodzi przez punkt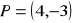
.Oblicz wartości funkcji trygonometrycznych kąta, którego jedno ramię pokrywa się z dodatnią półosią osi
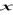
, a na drugim ramieniu leży punkt o współrzędnych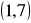
,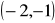
,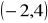
,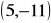
.Naszkicuj wykres funkcji
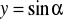
dla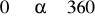
. Określ zbiór wartości. Dla jakich argumentów funkcja przyjmuje wartości ujemne?Korzystając z wykresu funkcji
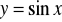
, wskaż wszystkie te liczby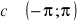
takie, że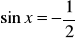
.Korzystając z wykresu
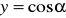
wskaż wszystkie wartości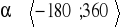
takie, że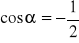
.Naszkicuj wykres funkcji
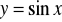
,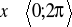
,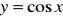
,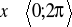
,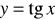
,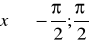
,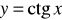
,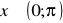
oraz podaj:
dziedzinę,
przedziały, w których funkcja rośnie,
przedziały, w których funkcja maleje,
przedziały, w których funkcja przyjmuje wartości dodatnie,
przedziały, w których funkcja przyjmuje wartości ujemne.
Korzystając z wykresu funkcji
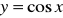
, wskaż wszystkie liczby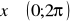
takie, że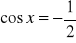
.W oparciu o wykresy odpowiednich funkcji, w przedziale
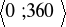
znajdź wszystkie kąty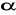
, dla których: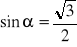
.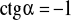
.Naszkicuj wykres funkcji
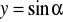
dla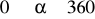
, a następnie korzystając z tego wykresu, określ:Dla jakich argumentów spełniających warunek
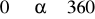
funkcja jest malejąca i jednocześnie przyjmuje wartości ujemne?Która z liczb:
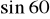
,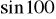
,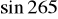
jest mniejsza od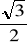
? Rozwiąż: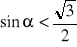
,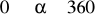
.Naszkicuj wykres funkcji
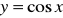
dla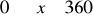
, a następnie korzystając z wykresu, określ:Dla jakich argumentów spełniających warunek
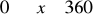
funkcja jest malejąca i jednocześnie przyjmuje wartości ujemne?Która z liczb:
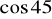
,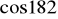
,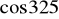
jest mniejsza od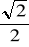
?Rozwiąż:
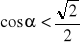
,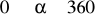
.Narysuj w przedziale
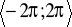
wykres funkcji: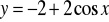
. Wyznacz: zbiór wartości, miejsca zerowe i przedziały, w których funkcja rośnie.Naszkicuj wykres funkcji
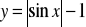
. Na podstawie wykresu omów własności.Udowodnij tożsamość
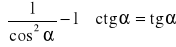
,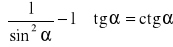
,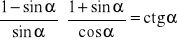
,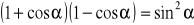
,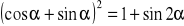
,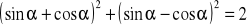
,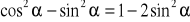
,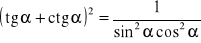
,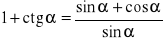
,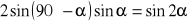
.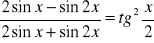
.Wiedząc, że
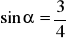
,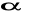
II ćw. wyznacz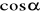
,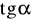
.Oblicz
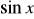
, gdy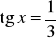
,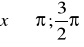
.Oblicz wartości pozostałych funkcji trygonometrycznych wiedząc, że
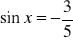
i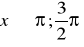
,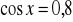
i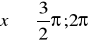
.Oblicz pozostałe wartości funkcji trygonometrycznych, czyli
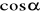
,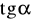
,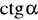
wiedząc, że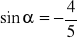
i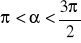
. Która to ćwiartka?Oblicz pozostałe wartości funkcji trygonometrycznych, czyli
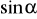
,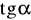
,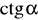
wiedząc, że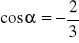
i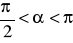
. Która to ćwiartka?Oblicz pozostałe wartości funkcji trygonometrycznych, czyli
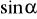
,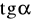
,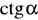
wiedząc, że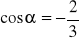
i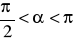
. Która to ćwiartka?Podaj jakie związki zachodzą między funkcjami trygonometrycznymi tego samego kąta.
Oblicz wartości pozostałych funkcji trygonometrycznych kąta
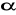
mając dane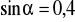
i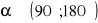
.Wyznacz wartości pozostałych funkcji trygonometrycznych kąta ostrego
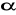
, jeśli: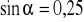
;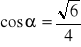
.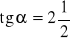
Wiedząc, że:
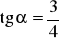
, oblicz wartość wyrażenia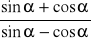
.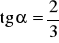
, oblicz wartość wyrażenia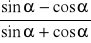
.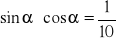
, oblicz wartość wyrażenia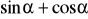
.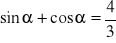
, oblicz wartość wyrażenia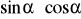
.Oblicz
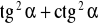
, jeśli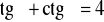
i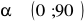
.Rozwiąż:
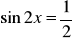
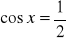
;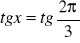
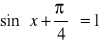
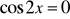
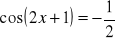
.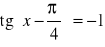
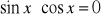
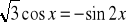
.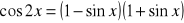
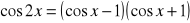
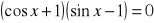
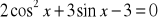
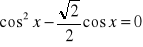
.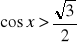
,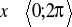
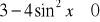
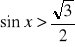
,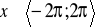
.Rozwiąż graficznie nierówność
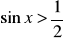
,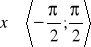
,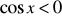
,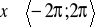
,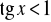
,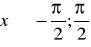
.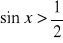
dla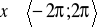
;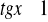
dla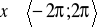
.Wykaż, że dla każdej liczby rzeczywistej
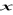
spełniony jest warunek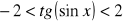
.Rozwiąż

mając dane: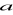
= 32 cm,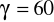
,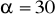
. Oblicz pole tego
.Oblicz pole trapezu równoramiennego, którego podstawy mają długości 14 cm i 8 cm, a kąt rozwarty ma miarę
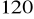
.Oblicz pole trapezu równoramiennego, którego podstawy mają długość 24 cm i 12 cm, a kąt rozwarty ma miarę
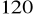
.Oblicz pole i obwód trapezu równoramiennego, którego krótsza podstawa ma długość 3, wysokość jest równa 4, a kąt ostry ma miarę 30°.
Oblicz pole równoległoboku, którego dwa sąsiednie boki mają długość 3 cm i 4 cm oraz tworzą kąt o mierze
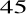
.Oblicz długość krótszej przekątnej równoległoboku
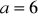
cm,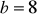
cm, i mierze kąta ostrego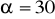
.Dłuższa przekątna rombu ma długość 20 cm. Wiedząc, że miara kąta rozwartego rombu ma
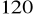
oblicz długość boku rombu.
Oblicz pole trójkąta równoramiennego ABC.Oblicz pole koła opisanego na trójkącie prostokątnym, którego jedna z przyprostokątnych ma długość
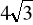
, a kąt ostry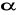
leżący przy tej przyprostokątnej ma miarę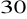
.Oblicz pole koła opisanego na trójkącie prostokątnym, którego jedna z przyprostokątnych ma długość
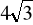
, a kąt ostry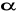
leżący naprzeciw tej przyprostokątnej ma miarę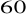
.
Znajdź wartości pozostałych funkcji trygonometrycznych, jeżeli ![]()
i ![]()
.
x
y
![]()
![]()
![]()
4
x
![]()
y
a
![]()
cm
b
A
C
B
![]()
![]()
![]()
A
C
B
![]()
![]()
![]()
C
4
A
B
A
C
![]()
![]()
![]()
B
![]()
C
![]()
4
![]()
A
B
Wyszukiwarka
Podobne podstrony:
Zdania i zbiory, Zbiór zadań, Klasa 1
Równania i nierówności, Zbiór zadań, Klasa 1
Funkcje wykładnicze i logarytmy, Zbiór zadań, Klasa 2
Liczby i działania, Zbiór zadań, Klasa 1
Figury i przekształcenia, Zbiór zadań, Klasa 2
Wielomiany, Zbiór zadań, Klasa 2
Figury geometryczne, Zbiór zadań, Klasa 1
Wielokąty i figury podobne, Zbiór zadań, Klasa 2
zbiór zadań klasa 4 chomikuj
więcej podobnych podstron