Dane są punkty:
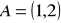
,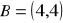
.Wyznacz współrzędne takiego punktu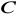
, aby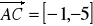
i oblicz współrzędne wektora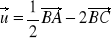
.Dane są współrzędne punktów
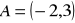
,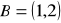
,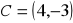
. Oblicz współrzędne wektorów i ich długości.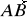
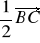
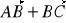
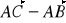
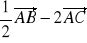
.Oblicz iloczyn skalarny wektorów
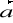
i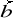
, jeśli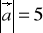
,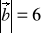
,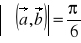
.Dla jakich wartości parametru
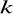
wektory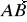
i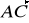
są prostopadłe, jeżeli: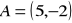
,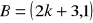
,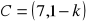
.Mając dane współrzędne punktów

,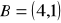
,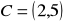
oraz współrzędne wektora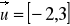
, wyznacz współrzędne obrazów punktów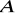
,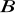
,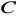
w translacji o wektor
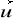
(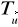
)w symetrii osiowej względem osi OX (
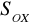
)w symetrii osiowej względem osi OY (
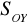
)
w symetrii środkowej względem punktu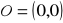
(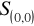
).Korzystając z rysunku, uzupełnij zdania.
Odcinek
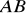
ma długość ……….Jakie współrzędne ma punkt
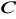
, jeśli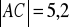
? ……………Pole trójkąta
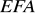
jest równe ……….Środek odcinka
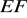
ma współrzędne ………….
Korzystając z rysunku, uzupełnij zdania.
Odcinek
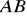
ma długość ……….Jakie współrzędne ma punkt
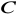
, jeśli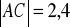
? ……………Pole trójkąta
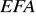
jest równe ……….Środek odcinka
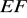
ma współrzędne ………….Napisz równanie prostej
prostopadłej do osi OX, przechodzącej przez punkt
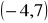
,mającej współczynnik kierunkowy
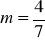
, przechodzącej przez punkt o współrzędnych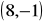
,równoległej do osi OX, przechodzącej przez punkt
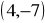
.Znajdź równanie prostej przechodzącej przez punkty
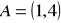
,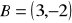
.Napisz równanie prostej przechodzącej przez dwa punkty
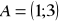
i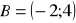
. Oblicz długość odcinka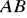
. Zapisz równanie prostej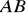
w postaci kierunkowej oraz w postaci ogólnej.Dane są punkty
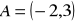
i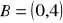
. Napisz równania prostej AB:w postaci kierunkowej.
w postaci ogólnej.
Oblicz długość odcinka AB.
Wyznacz równanie prostej równoległej do prostej
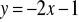
i przechodzącej przez punkt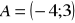
.Wyznacz równanie prostej prostopadłej do prostej
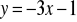
i przechodzącej przez punkt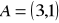
.Znajdź równanie prostej, której wykres jest prostopadły do prostej
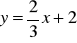
i przechodzi przez punkt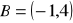
.Znajdź równanie prostej prostopadłej do prostej
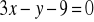
i przechodzącej przez punkt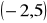
.Napisz równanie prostej
prostopadłej
równoległej
do prostej ![]()
i przechodzącej przez punkt ![]()
.
Napisz równanie prostej
równoległej
prostopadłej
do prostej ![]()
i przechodzącej przez punkt ![]()
.
Wyznacz współrzędne punktu przecięcia się prostych:
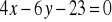
i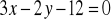
.Napisz równanie prostej, do której należy punkt
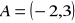
oraz punkt przecięcia prostych o równaniach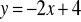
i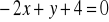
.Boki trójkąta zawierają się w prostych o równaniach:
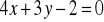
,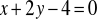
,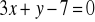
. Oblicz współrzędne wierzchołków trójkąta.Dla jakich wartości parametru
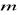
punkt przecięcia prostych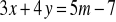
i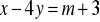
należy do pierwszej ćwiartki układu współrzędnych.Znajdź środek odcinka
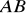
, gdzie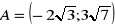
, a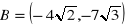
.Znajdź środek odcinka
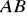
, gdzie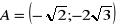
, a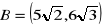
.Znajdź równanie symetralnej odcinka o końcach:
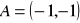
i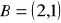
.Znajdź równanie symetralnej odcinka AB, gdzie
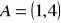
,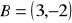
.Znajdź odległość punktu
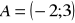
od prostej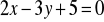
.Znajdź odległość punktu
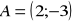
od prostej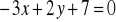
.Dany jest trójkąt ABC, gdzie
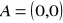
,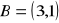
,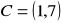
. Wykaż, że ten trójkąt jest prostokątny.Zbadaj, czy trójkąt, którego wierzchołkami są współrzędne:
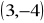
,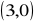
,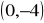
,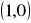
,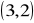
,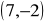
,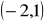
,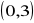
,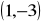
jest prostokątny.
Dane są współrzędne wierzchołków
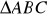
: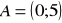
,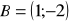
,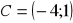
.Napisz równania prostych zawierających boki trójkąta.
Sprawdź, czy
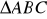
jest prostokątny.Napisz równanie:
środkowej trójkąta poprowadzonej z punktu
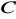
.wysokość trójkąta
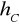
poprowadzonej z punktu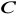
.symetralnej boku
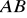
.Oblicz długość wysokości
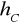
(czyli odległość punktu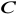
od prostej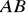
).Na rysunku umieść: środkową, wysokość
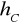
i symetralną boku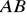
.
Dane są współrzędne wierzchołków ![]()
: ![]()
, ![]()
, ![]()
.
Napisz równania prostych zawierających boki trójkąta.
Oblicz długość boku BC.
Sprawdź, czy trójkąt jest prostokątny.
Napisz równanie:
środkowej trójkąta poprowadzonej z punktu C.
wysokość trójkąta
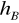
poprowadzonej z punktu B.symetralnej boku AB.
Oblicz długość wysokości ![]()
(czyli odległość punktu B od prostej AC).
Napisz równanie prostej równoległej do prostej AB przechodzącej przez punkt C.
Na rysunku poprowadź: środkową, wysokość i symetralną (z punktu d).
Dane są współrzędne wierzchołków trójkąta ABC: ![]()
, ![]()
, ![]()
.
Napisz równania prostych zawierających boki trójkąta.
Oblicz długość boku BC
Sprawdź, czy trójkąt ABC jest prostokątny.
Napisz równania:
Środkowej trójkąta poprowadzonej z punktu C.
Wysokości trójkąta poprowadzonej z wierzchołka C -
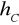
.Symetralnej boku CB.
Oblicz długość wysokości ![]()
.
Napisz równanie prostej równoległej do prostej AB przechodzącej przez punkt C.
Na rysunku poprowadź: środkową, wysokość i symetralną (z punktu d).
Punkty: ![]()
, ![]()
, ![]()
są wierzchołkami trójkąta.
Napisz równanie prostej zawierającą wysokość wychodząca z wierzchołka B.
Napisz równanie środkowej wychodzącej z wierzchołka A.
Napisz równanie symetralnej boku BC.
Oblicz długość obwodu tego trójkąta.
Oblicz długość wysokości wychodzącej z wierzchołka B (punkt a) zadania).
Napisz równanie prostej równoległej do proste BC i przechodzącej przez wierzchołek A.
Dany jest trójkąt o wierzchołkach ![]()
, ![]()
, ![]()
. Napisz:
równanie symetralnej boku
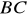
,równanie prostej zawierającej wysokość
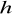
, opuszczoną z wierzchołka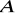
,równanie prostej zawierającej środkową boku
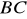
.Oblicz długość wysokości prowadzonej z wierzchołka
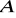
oraz obwód trójkąta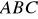
.
W trapezie o podstawach AB i CD dane są punkty ![]()
, ![]()
, ![]()
. Oblicz długość przekątnej AC. Wyznacz równanie prostej AB.
Wyznacz równania wszystkich osi symetrii kwadratu ABCD, gdzie ![]()
, ![]()
, ![]()
, ![]()
.
Dane są współrzędne trzech wierzchołków kwadratu ABCD: ![]()
, ![]()
, ![]()
. Obliczyć współrzędne wierzchołka D. Obliczyć pole tego kwadratu.
W kwadracie ABCD wierzchołek A ma współrzędne ![]()
. Wiedząc, że jedna z przekątnych kwadratu zawiera się w prostej o równaniu ![]()
oblicz pole kwadratu.
Punkty ![]()
, ![]()
, ![]()
są kolejnymi wierzchołkami równoległoboku. Wyznacz współrzędne wierzchołka D.
Punkty ![]()
, ![]()
, ![]()
, ![]()
są wierzchołkami czworokąta ABCD. Oblicz pole tego czworokąta.
Sprawdź, czy para liczb ![]()
należy do zbioru rozwiązań nierówności ![]()
.
Sprawdź, czy para liczb ![]()
należy do zbioru rozwiązań nierówności: ![]()
.
Przedstaw ilustrację graficzną zbioru rozwiązań układu: 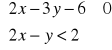
.
Przedstaw ilustrację graficzną zbioru rozwiązań układu: 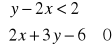
.
Zaznacz część płaszczyzny, którą opisują nierówności: 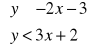
.
Zaznacz część płaszczyzny, którą opisują nierówności: 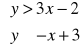
.
Rozwiąż układ nierówności: 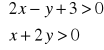
.
Zaznacz w układzie współrzędnych zbiór punktów, których odcięta spełnia warunek ![]()
.
Dane są zbiory: ![]()
, ![]()
, ![]()
. Naszkicuj ilustrację graficzną zbioru ![]()
na płaszczyźnie w prostokątnym układzie współrzędnych.
Zaznacz na płaszczyźnie zbiory
Dany jest trójkąt ![]()
o wierzchołkach ![]()
, ![]()
, ![]()
. Opisz trójkąt ![]()
za pomocą nierówności. Oblicz jego pole i obwód.
Dany jest trójkąt ![]()
o wierzchołkach ![]()
, ![]()
, ![]()
. Opisz trójkąt ![]()
za pomocą nierówności. Oblicz jego pole i obwód.
Dany jest trójkąt ABC o wierzchołkach: ![]()
, ![]()
, ![]()
.
Opisz trójkąt ABC za pomocą układu nierówności.
Oblicz pole trójkąta ABC.
Oblicz obwód trójkąta ABC.
Wyznacz równanie wysokości padającej z wierzchołka C.
Podaj współrzędne środka i długość promienia okręgów o równaniu:
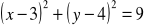
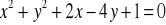
Oblicz pole i obwód jednego z nich.
Naszkicuj okrąg o równaniu
Podaj definicję okręgu. Jakie znasz równania okręgu. Określ położenie punktu ![]()
względem okręgu ![]()
.
Napisz równanie okręgu o środku w punkcie ![]()
przechodzącego przez punkt ![]()
.
Oblicz odległość między środkami okręgów o równaniach: ![]()
, ![]()
.
Określ położenie okręgów ![]()
i ![]()
, jeśli:
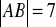
,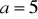
,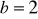
,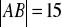
,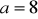
,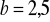
.
Naszkicuj okręgi o równaniach ![]()
i ![]()
. Określ ich wzajemne położenie.
Rozwiąż graficznie układ równań 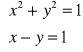
.
Podaj interpretacje geometryczną układu równań: 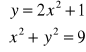
. Ile rozwiązań ma ten układ?
Dla jakich wartości prosta ![]()
jest styczna z okręgiem ![]()
?
![]()
![]()
1
1
F
E
C
B
A
![]()
![]()
1
1
F
E
C
B
A
Wyszukiwarka
Podobne podstrony:
Figury geometryczne, Zbiór zadań, Klasa 1
Wielokąty i figury podobne, Zbiór zadań, Klasa 2
Zdania i zbiory, Zbiór zadań, Klasa 1
Równania i nierówności, Zbiór zadań, Klasa 1
Funkcje wykładnicze i logarytmy, Zbiór zadań, Klasa 2
Liczby i działania, Zbiór zadań, Klasa 1
Trygonometria, Zbiór zadań, Klasa 2
Wielomiany, Zbiór zadań, Klasa 2
zbiór zadań klasa 4 chomikuj
więcej podobnych podstron