
Andrzej Kmieć
Procesy cieplne i aparaty
Oficyna Wydawnicza Politechniki Wrocławskiej
Wrocław 2005

Spis treści
1. Zasady wymiany ciepła.......................
2.3.1. Współczynnik przewodzenia ciepła ciał stałych metalicznych..................................
2.3.2. Współczynnik przewodzenia ciepła w ciałach niemetalicznych................................
2.3.3. Współczynnik przewodzenia ciepła cieczy...........................
2.4.2. Rozkład temperatury w ściance płaskiej..........................
4. Przenikanie ciep ła.............................................................
5.3. Ekonomiczna grubość warstwy izolacji......................
6.3.1. Wprowadzenie..............................................
6.3.2.1. Rozwiązanie analityczne równania różniczkowego przewodzenia ciepła

4
6 3 .2 .2 . Omówienie rozwiązania równania różniczkowego przewodzenia ciepła
w nieskończonej płycie płaskiej...............................................................
6.3.2.3. Analiza nieustalonego przewodzenia ciepła podczas chłodzenia płyty...
65
6.3.3. Chłodzenie lub ogrzewanie cylindra nieskończonego..................................
6.3.5. Chłodzenie lub ogrzewanie ciał o niedużych wymiarach.............................
6.3.6. Rozwiązanie równania Fouriera dla ustalonego przewodzenia ciepła w ścianie
6.3.7. Rozwiązania równania Fouriera dla charakterystycznych przypadków nieusta
Przykład 1.......................
7.2.1. Różniczkowe równanie ruchu ciepła - równanie energii.............................
7.2.2. Równanie energii laminamej warstwy granicznej.........................................
7.2.3. Równanie całkowe energii laminamej warstwy granicznej.................
7.2.4. Rozwiązanie równania energii laminamej warstwy granicznej na płycie płaskiej.
7.2.5. Rozwiązanie równania energii turbulentnej warstwy granicznej na płycie
7.3.1. Wyprowadzenie modułów podobieństwa z równania energii....................................
7.4.2. Wnikanie ciepła podczas przepływu wokół różnorodnych elementów....................
ciepła podczas wymuszonego przepływu laminamego...........................
ciepła w obszarze przejściowym.................................................................
ciepła podczas przepływu swobodnego w warunkach konwekcji naturalnej
ciepła podczas grawitacyjnego spływu cieczy po ścianie.......................
ciepła podczas skraplania pary nasyconej.................................................
7.9.3. Wpływ prędkości i kierunku ruchu pary na wnikanie ciepła podczas kondensacji
7.9.4. Wpływ obecności gazów obojętnych w parze na współczynnik wnikania ciepła...
141
7.9.5. Wnikanie ciepła podczas kondensacji wewnątrz poziomych rur i wężownic
8.4.3. Założenie minimalnej całkowitej powierzchni wymiany ciepła i jednakowych

5
10.4.1. Wymiana ciepła między dwoma równoległymi płytami...........................................
10.4.2. Wymiana ciepła od powierzchni A j zamkniętej przez powierzchnię A2................
10.4.3. Wymiana ciepła między dwoma powierzchniami dowolnie ustawionymi.............
11.8. Obliczanie wymienników dla wybranych przypadków nieustalonej wymiany ciepła
11.8.1. Ogrzewanie (chłodzenie) cieczy przez ścianę zbiornika w stałej temperaturze
11.8.1.1.Chłodzenie cieczy w zbiorniku na wolnym powietrzu..................................
11.8.1.2. Ogrzewanie zbiornika z cieczą za pomocą pary nasyconej.....................
11.8.2. Ogrzewanie (oziębianie) cieczy medium grzejnym (chłodzącym) w zmiennej
11.8.3. Ogrzewanie (oziębianie) cieczy za pomocą zewnętrznego wymiennika ciepła

Przedmowa
Podręcznik zawiera materiał wykładany przez autora na kierunku inżynieria che
miczna i procesowa. Jest on adresowany zarówno do studentów, doktorantów jak
i pracowników wyższych uczelni zainteresowanych zagadnieniami transportu ciepła.
Przedstawiono w nim podstawy teoretyczne ruchu ciepła oraz metody obliczania wy
mienników cieplnych z uwzględnieniem zarówno klasycznych ujęć teoretycznych,
takich jak teoria Nusselta zastosowana do opisu wnikania ciepła podczas skraplania
pary nasyconej, jak i obliczeniowej mechaniki płynów (CFD).
Podręcznik składa się z jedenastu rozdziałów o różnorodnym znaczeniu, i zakre
sie. Zrozumienie podstawowych praw i metod obliczeniowych powinny ułatwić liczne
zamieszczone w nim rysunki.
Autor serdecznie dziękuje swoim współpracownikom: mgr inż. Leokadii Lesz
czyńskiej, mgr inż. Agnieszce Pleśniarskiej, mgr inż. Sebastianowi Englartowi oraz
dr. inż. Romanowi Szafranowi za staranne wykonanie rysunków.
Książkę poświęcam Świętej Pamięci moich Rodziców.
Wrocław, październik 2004
Andrzej Kmieć

1. Zasady wymiany ciepła
1.1. Wstęp
W termodynamice działanie otoczenia na układ jest nazywane pracą, jeżeli wynik
tego działania można sprowadzić do zmiany położenia ciężaru znajdującego się poza
układem względem jakiegoś poziomu odniesienia. Działania otoczenia na układ za
mknięty, które nie mogą być zaliczone do jakiegoś rodzaju prac, są nazywane ze
wnętrznym ciepłem układu, a sposób, w jaki ciepło jest przekazywane - wymianą
ciepła, przepływem ciepła lub przenoszeniem ciepła [1]. W układach otwartych ener
gia jest przekazywana również przez granice układu wraz z przepływającą substancją
w postaci energii kinetycznej, potencjalnej lub entalpii, zwanej często w technice
energią cieplną. Praca lub energia dyssypowana wewnątrz układu jest nazywana cie
płem dyssypacji pracy i występuje w postaci tzw. wewnętrznych źródeł ciepła, wyni
kających z rozpraszania energii mechanicznej (ciepło tarcia), elektrycznej (ciepło
Joule’a) lub z zachodzących reakcji chemicznych. Energia jest skalarną wielkością
fizyczną, która spełnia zasadę zachowania zgodnie z 1 zasadą termodynamiki.
1.2. Pole temperatury
Zgodnie z 11 zasadą termodynamiki przenoszenie energii cieplnej w dowolnym
ciele lub między różnymi ciałami zachodzi zawsze od punktu o wyższej temperaturze
do punktu o niższej temperaturze.
Przestrzeń materialną w ciele stałym, cieczy lub gazie, w której każdemu punkto
wi przyporządkujemy temperaturę, nazywamy polem temperaturowym. Pole tempera
turowe jest również skalarne [2]. Jego punkty o tej samej temperaturze wyznaczają
powierzchnie izotermiczne. Gdy temperatura w dowolnym punkcie pola zależy tylko
od położenia tego punktu, nazywamy je ustalonym (stacjonarnym) polem temperatu
rowym, co wyraża się równaniem:

10
T = T ( x , y , z )
( 1. 1)
Jeżeli tem peratura w dow olnym punkcie p o la zależy rów nież od czasu, to pole ta
kie nazyw am y nieustalonym (lub niestacjonarnym ) polem tem peraturow ym , określo
nym rów naniem
K ształt i ułożenie pow ierzchni izoterm icznych w tym przypadku je s t zależne od czasu.
K ażdem u punktow i p o la tem peraturow ego je s t przyporządkow any w ektor, zw any
gradientem tem peratury:
gdzie n je s t n o rm alną w danym punkcie p o la do pow ierzchni izoterm icznej. G radient
tem peratury tw orzy pole w ektorow e (rys. 1.1). K ierunek gradientu je s t w yznaczony
przez n orm aln ą n, a jej zw rot je s t skierow any ku pow ierzchniom izoterm icznym
o wyższej tem peraturze. W ustalonym polu tem peraturow ym gradient zależy tylko od
położenia rozw ażanego punktu w przestrzeni, nie zależy zaś od czasu. W n ieu stalo
nym polu tem peraturow ym gradient je s t fu n k c ją n ie tylko położenia, ale i czasu.
Jeżeli w określonym czasie A r je s t przekazane ciepło A Q, to średni strum ień cie
p ła Q w yraża się wzorem
Jako chw ilow y strum ień ciepła Q definiuje się granicę, do jakiej dąży stosunek
przekazyw anego ciepła A Q do przedziału czasu Ar, jeże li A r dąży do zera:
T ~ T ( x , y , z , r )
( 1.2 )
(1.3)
Rys. 1.1. Schemat pola temperaturowego:
a) przekrój powierzchni ograniczającej pole
temperaturowe, b) przekrój powierzchni izotermicznych
* -»0
A r
d r
(1.5)

11
w w arunkach ustalonych zaś
Q
( 1.6)
K ierunek przepływ u ciepła, a ściślej strum ienia ciepła, je s t w yznaczony przez
kierunek gradientu tem peratury. Poniew aż ciepło je s t zaw sze przekazyw ane od punktu
o tem peraturze wyższej do punktu o tem peraturze niższej, więc zw rot w ektora stru
m ienia ciepła je s t zaw sze przeciw ny niż zw rot gradientu tem peratury.
Stosunek strum ienia ciepła Q do pow ierzchni A, przez k tó rą ten strum ień prze
pływ a, je s t nazyw any gęstością strum ienia ciepła, zdefiniow aną rów naniem
Q
A
(1.7)
L okalną gęstością strum ienia ciepła q nazyw am y granicę stosunku części AQ do
w ycinka pow ierzchni AA, gdy AA dąży do zera (rys. 1.2)
lim —
Ar->0 AA
dQ
dA
lub w zapisie w ektorow ym
dQ = ędA
( 1.8)
(1.9)
Rys. 1.2. Schemat strumienia ciepła przekazywanego
przez pow ierzchnię; A Ó - część strumienia ciepła
przekazywana przez w ycinek pow ierzchni AA
W ektory gęstości strum ieni ciepła są położone n a pow ierzchniach prostopadłych
do pow ierzchni izoterm icznych. Są to pow ierzchnie adiabatyczne. N a pow ierzchni
zew nętrznej ciała z reguły podaje się składow e gęstości strum ienia ciep ła w kierunku
prostopadłym do pow ierzchni ciała.

12
1.3. Rodzaje wymiany ciepła
Wymiana ciepła jest realizowana na trzy sposoby, różne pod względem fizycznym [2]:
• przewodzenie (kondukcję),
• konwekcję (unoszenie),
• promieniowanie (radiacyjną wymianę ciepła).
Przewodzenie ciepła polega na przekazywaniu energii wewnętrznej między styka
jącymi się elementami ciała lub różnych ciał. W ciałach stałych jest przenoszona
energia drgań atomów w sieci krystalicznej i ruchu swobodnych elektronów, a w pły
nach - energia kinetyczna atomów i cząsteczek. Przekazywanie ciepła wyłącznie
przez przewodzenie zachodzi jedynie w ciałach stałych nieprzenikliwych dla promie
niowania oraz w płynach, gdy nie występuje przemieszczanie się makroskopowych
elementów płynów.
Konwekcja polega na przenoszeniu energii cieplnej z makroskopowymi elemen
tami płynu różniącymi się temperaturą. Może ona zachodzić w przestrzeni nieograni
czonej, np. podczas opływania cząstki ciała stałego lub w przestrzeni ograniczonej,
np. w zbiorniku lub wewnątrz rury wymiennika ciepła. Rozróżniamy konwekcję swo
bodną, czyli naturalną, zachodzącą z udziałem sił masowych działających na elementy
płynu różniące się temperaturą, a tym samym gęstością, oraz konwekcję wymuszoną
przez maszynę albo urządzenie, np. pompę, wentylator, dmuchawę lub mieszadło.
Promieniowanie cieplne, zwane też termicznym, jest przekazywaniem ciepła za
pośrednictwem fal elektromagnetycznych albo fotonów. Energia wewnętrzna ciała
o temperaturze wyższej od temperatury zera bezwzględnego jest emitowana w postaci
fal promieniowania elektromagnetycznego, obejmujących cały zakres długości fal od
zera do nieskończoności lub tylko niektóre długości fal.
Energia radiacyjna promieniowania może być pochłonięta częściowo lub całko
wicie po napotkaniu innych ciał lub innej części ciała wysyłającego promieniowanie.
Promieniowanie, w odróżnieniu od przewodzenia lub konwekcji, może zachodzić
również w próżni.
W niektórych procesach przewodzenie ciepła oraz konwekcyjna i radiacyjna wy
miana ciepła występują jednocześnie, np. w procesach suszenia. W urządzeniach ta
kich jak aparaty służące do wymiany ciepła, zwane wymiennikami ciepła, zachodzi
natomiast połączone przekazywanie ciepła, tzw. przejmowanie lub przenikanie ciepła.
Przejmowanie ciepła, inaczej wnikanie ciepła, polega na łącznym przekazywaniu
ciepła od ściany do płynu przez konwekcję oraz promieniowanie [2]. Przenikanie
ciepła natomiast jest przekazywaniem ciepła między dwoma płynami rozgraniczonymi
stałą przegrodą - płytą lub ścianką rury. Następuje tutaj kolejno wnikanie ciepła od
gorącego płynu do pierwszej ściany, następnie przewodzenie przez przegrodę i wni
kanie ciepła od drugiej ściany tej przegrody do płynu ogrzewanego.

2. Przewodzenie ciepła
2.1. Wstęp
Mechanizm przewodzenia ciepła jest bardzo złożony i w wielu przypadkach nie
został całkowicie poznany. Zależy on przede wszystkim od stanu skupienia ciała,
w którym ciepło jest przewodzone. W przypadku gazów i cieczy ten rodzaj transportu
ciepła polega na przenoszeniu energii kinetycznej od cząsteczek o większej energii do
cząsteczek o mniejszej energii w wyniku kolejnych zderzeń. Zarówno w przypadku
gazów, jak i cieczy transport ciepła powoduje również przemieszczanie się elementów
płynu, co wywołuje sprzężony, konwekcyjny ruch ciepła. Mechanizm przewodzenia
ciepła w ciałach stałych zależy od rodzaju ciała. W przypadku ciał stałych nieprzeźro
czystych przewodzenie jest wyłącznym sposobem transportu ciepła, podczas gdy
w przeźroczystym ciele stałym, takim jak np. w szkło, pewna ilość energii może być
przenoszona również przez promieniowanie. Przyjmuje się, że przewodzenie ciepła
w ciałach stałych jest związane z ruchem fal wywołanych drganiami sieci krystalicz
nej (Ą) oraz ruchem swobodnych elektronów (Xe). Składowe te są addytywne, wobec
czego sumaryczny współczynnik przewodzenia ciepła jest równy ich sumie [3]:
X ^ X ,+ X e
(2.1)
W pierwszym przybliżeniu składowa Xe jest odwrotnie proporcjonalna do elek
trycznej oporności właściwej pe. Dla czystych metali, o małej oporności właściwej,
składowa przewodnictwa cieplnego wynikająca z ruchu elektronów jest podstawową
wielkością. Udział przewodnictwa sieciowego w stopach może być znaczny, a w cia
łach stałych będących złymi przewodnikami prądu elektrycznego (ciałach niemeta
licznych) przewodzenie ciepła jest związane głównie ze składową sieciową X/.
Model fizyczny przewodzenia ciepła w ciałach stałych jest określony na ogół
przez prawo Fouriera, wiążące gęstość strumienia ciepła z gradientem temperatury,
a tylko niekiedy konieczne jest uwzględnienie relaksacji gęstości strumienia ciepła
związanej z przyjęciem skończonej prędkości rozchodzenia się ciepła. Niezbędne jest
podanie równania bilansu energii i rodzaju warunków jednoznaczności jego rozwią

14
zania. W założeniach bilansu energii m usim y określić, czy rozpatruje się ustalone, czy
nieustalone przew odzenie ciepła oraz jeg o w ielow ym iarow ość. D alsze założenia do
ty czą stałości w łaściw ości term ofizycznych oraz braku lub obecności w ew nętrznych
źródeł ciepła.
2.2. Prawo Fouriera sformułowane dla przewodzenia ciepła
O pis m atem atyczny zjaw iska przew odzenia ciepła obejm uje sform ułow anie p ra
w a przew odzenia ciepła, rów n ania różniczkow ego bilansu energii oraz w arunków
jednoznaczności jeg o rozw iązania.
Przew odzenie ciepła p rzebiega n a ogól zgodnie z praw em Fouriera: gęstość prze
w odzonego strum ienia ciepła je s t w prost prop orcjo nalna do gradientu tem peratury
gdzie: V - w ektor zw any n ab la lub operatorem Plam iltona, dT/dn - po cho dn a tem p e
ratury w kierunku prostopadłym do pow ierzchni izoterm icznej, X - w spółczynnik
przew odzenia ciepła (przew odność cieplna) w yrażany w W /(m-K). Z nak m inus w yni
ka z tego, że ciepło je s t przew odzone od tem peratury wyższej do niższej (rys. 2.1).
q ~ -Z g ra d T - - X V T
(
2
.
2
)
lub w postaci skalarnej
d T
(2.3)
1
1
T
T
x
Rys. 2.1. Zależność znaku gęstości strumienia ciepła od gradientu tem peratury
G radient tem peratury je s t w ektorem [1], który m ożna wyrazić:
• w układzie w spółrzędnych prostokątnych (kartezjańskich) (rys. 2.1)
( 2 .4 )

15
» w układzie w spółrzędnych w alcow ych (cylindrycznych)
p . 5 )
'
dr
0 r dr
' dz
• w układzie w spółrzędnych kulistych (sferycznych)
a r
i a r
i a r
0
h ~ T 7
^2'6^
dr
r d&
r d ę
1 są składow ym i w ektora jednostkow ego.
D la jednokierunkow ego przew o dzenia ciepła, np. w kierunku osi.r, strum ień cie
p ła w yraża się w najczęściej spotykanej, szczególnej postaci praw a Fouriera:
Q =
(2-7)
a x
R ów nania (2.2)—(2.6) obow iązują zarów no dla ustalonego, ja k i nieustalonego prze
w odzenia ciepła. Jeżeli m am y do czynienia z ustalonym przew odzeniem , to rozkład
tem peratury (rys. 2.1) nie zm ienia się w czasie, a strum ień ciepła m a w artość stalą. W
przypadku nieustalonego przew odzenia ciepła są one fu n k cją czasu.
2.3. Przewodność cieplna i współczynnik przewodzenia ciepła
Przew odność cieplna różnych substancji je s t zd olnością do w yrów nyw ania ener
gii w ew nętrznej. Jej m iarą je s t w spółczynnik przew odzenia ciep ła A, którego w artość
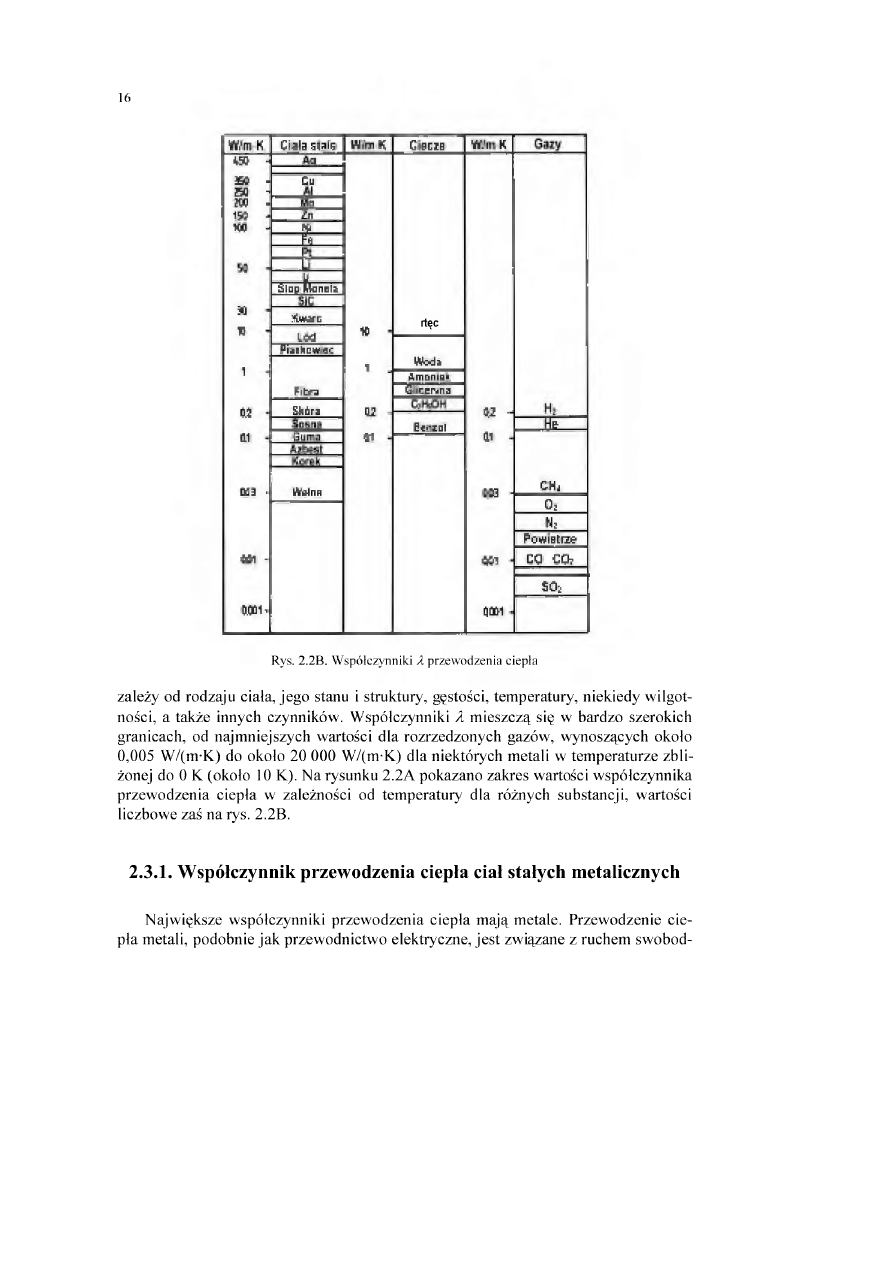
Rys. 2.2A . Zakres wartości w spółczynnika przewodzenia ciepła dla różnych substancji
16
W/m K
Data s:nif
W.mH
C ecie
V
h
'.
ii
K
*M ł.
Łi
BO
no
1»
iw
m
V
1
Cu
L
4
Sine frtancli
'.•íwvc
LWI
a ¡u: kc we.:
Fibra
U
m
KJ .
tu -
Uft-
Ekćn
AWna
W
1
02
01
rtęć
Wodi
Amriniat
~Z rcfjnj
De.i^l
V -i
m
:■?]
W
dan
E
l
CH
j
Oj
N,
Powietrze
CO CO?
soT~
Rys. 2.2B. W spółczynniki X przewodzenia ciepła
zależy od rodzaju ciała, jeg o stanu i struktury, gęstości, tem peratury, niekiedy w ilgot
ności, a także innych czynników . W spółczynniki X m ieszczą się w bardzo szerokich
granicach, od najm niejszych w artości dla rozrzedzonych gazów, w ynoszących około
0,005 W /(m-K) do około 20 000 W /(m-K) dla niektórych m etali w tem peraturze zbli
żonej do 0 K (około 10 K). N a rysunku 2.2A pokazano zakres wartości w spółczynnika
przew odzenia ciepła w zależności od tem peratury dla różnych substancji, w artości
liczbow e zaś n a rys. 2.2B.
2.3.1. Współczynnik przewodzenia ciepła ciał stałych metalicznych
N ajw iększe w spółczynniki p rzew odzenia ciepła m ają m etale. Przew odzenie cie
p ła m etali, podobnie ja k przew odnictw o elektryczne, je s t zw iązane z ruchem sw obod

17
nych elektronów wewnątrz metalu. Zależność między elektronowym przewodnictwem
cieplnym Xe a przewodnictwem elektrycznym oe opisuje prawo
Wiedemanna-Franza-
Lorenzaz 1872 r. [2]
gdzie L - liczba Lorenza, <re - przewodność elektryczna.
Z rozważań ruchu elektronów według statystyki Fermiego-Diraca otrzymano
równanie opisujące liczbę Lorenza:
i = 3( —) =24,5-l(T9,
(V/K)2
(2.9)
gdzie B - liczba Boltzmanna, z - ładunek elektronu.
Z najnowszych badań wynika jednak, że wartości doświadczalne liczby Lorenza
różnią się nieco od wartości teoretycznych obliczonych z równania (2.9) (por. tabe
la 2.1).
Tabela 2.1. Wartości liczby Lorenza
dla metali w temperaturze 0 i 100 °C
Metal
Liczba Lorenza
0°C
100°C
Aluminium
21,2
22,3
Bizmut
33,1
28,9
Kadm
24,2
24,3
Miedź
22,3
23,3
Złoto
23,5
24,0
Iryd
24,9
24,9
Żelazo
24,9
25,6
Ołów
24,7
25,6
Molibden
26,1
27,9
Nikiel
17,7
22,8
Pallad
25,9
27,4
Platyna
25,1
26,0
Ren
25,7
25,7
Srebro
23,1
23,7
Cyna
25,2
24,9
Wolfram
30,4
32,0
Cynk
23,1
23,3
Przewodność cieplna ciał krystalicznych, w tym metali, na ogół maleje ze wzrostem
temperatury (rys. 2.3), ale np. współczynniki przewodzenia ciepła platyny, boru czy rtęci
zwiększają się ze wzrostem temperatury. Ciała krystaliczne wykazują też anizotropowość

18
przewodności cieplnej. Wartości współczynników przewodzenia ciepła zależą też od czy
stości chemicznej metalu; dla czystej miedzi np. X = 386 W/(m-K), a dla miedzi zanie
czyszczonej śladową ilością arsenu - około 120 W/(m-K). Także przewodnictwo cieplne
stopów metali jest gorsze niż ich czystych składników (rys. 2.2B).
Rys. 2.3. Zależność w spółczynnika przewodzenia ciepła metali od tem peratury
2.3.2. Współczynnik przewodzenia ciepła w ciałach niemetalicznych
D użą grupę cial niem etalicznych stanow ią dielektryki. C iała te odznaczają się m a
łą p rzew odnością elektryczną oraz cieplną. Przew odzenie ciepła odbyw a się w nich za
pośrednictw em drgań sieci (fononów ). O drębną grupę stano w ią m ateriały budow lane,
izolacyjne i ognioodporne ceram iczne, których w spółczynniki przew odzenia ciepła są
w przybliżeniu m niejsze od 0,15 W /(m -K) (rys. 2.4), nazyw ane m ateriałam i izolacyj
nym i [2]. N a ogól są to m ateriały porow ate, w łókniste lub ziarniste, w których pory są
w ypełnione pow ietrzem lub gazem o znacznie m niejszym w spółczynniku przew odze
n ia ciepła.
W spółczynnik przew odzenia ciepła takich m ateriałów je s t w ielkością um owną,
ujm ującą oprócz przew odzenia ciepła przez strukturę ciała stałego rów nież przew o
dzenie ciepła i konw ekcję w gazie zaw artym w ew nątrz porów , a niekiedy i udział
prom ieniow ania m iędzy ściankam i porów . Gazy o najm niejszych w spółczynnikach
19
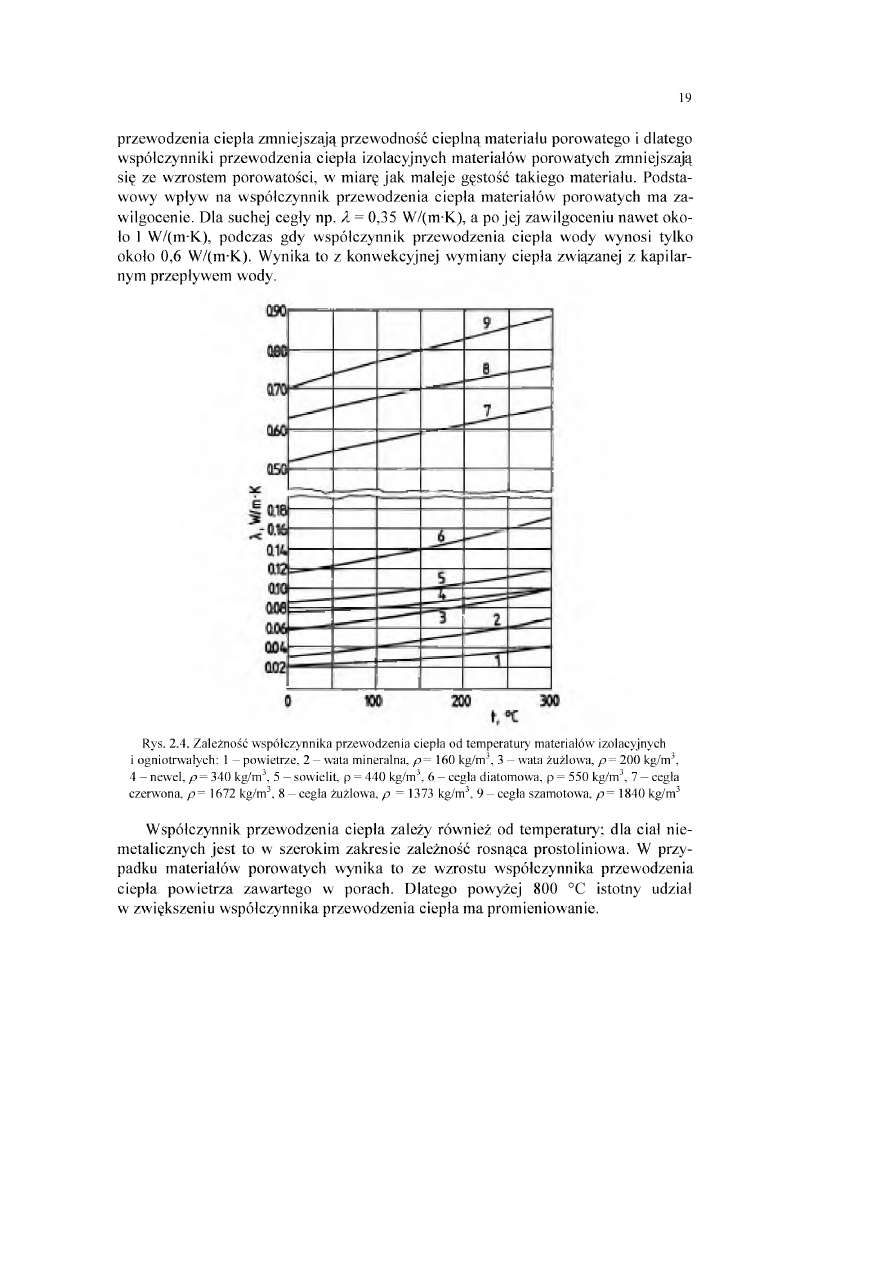
przew odzenia ciepła zm niejszają przew odność cieplną m ateriału porow atego i dlatego
w spółczynniki przew odzenia ciepła izolacyjnych m ateriałów porow atych zm niejszają
się ze w zrostem porow atości, w m iarę ja k m aleje gęstość takiego m ateriału. Podsta
w owy w pływ n a w spółczynnik p rzew odzenia ciep ła m ateriałów porow atych m a za
w ilgocenie. D la suchej cegły np. X = 0,35 W /(m-K), a po jej zaw ilgoceniu n aw et oko
ło 1 W /(m-K), podczas gdy w spółczynnik p rzew odzenia ciepła wody w ynosi tylko
około 0,6 W /(m-K). W ynika to z konw ekcyjnej w ym iany ciepła związanej z kapilar
nym przepływ em wody.
Rys. 2.4. Zależność w spółczynnika przewodzenia ciepła od temperatury m ateriałów izolacyjnych
i ogniotrwałych: 1 - powietrze, 2 - wata mineralna, p = 160 kg/m3, 3 - wata żużlowa, p = 200 kg/m3,
4 - newel, p = 340 kg/m3, 5 - sowielit, p = 440 kg/m3, 6 - cegła diatomowa, p = 550 kg/m3, 7 - cegła
czerwona, p = 1672 kg/m3, 8 - c e g ł a żużlowa, p = 1373 kg/m3, 9 - c e g ł a szamotowa, p = 1840 kg/m3
W spółczynnik przew odzenia ciepła zależy rów nież od tem peratury; d la cial n ie
m etalicznych je s t to w szerokim zakresie zależność rosn ąca prostoliniow a. W przy
padku m ateriałów porow atych w ynika to ze w zrostu w spółczynnika p rzew odzenia
ciepła pow ietrza zaw artego w porach. D latego powyżej 800 °C istotny udział
w zw iększeniu w spółczynnika p rzew odzenia ciepła m a prom ieniow anie.
20
2.3.3. Współczynnik przewodzenia ciepła cieczy
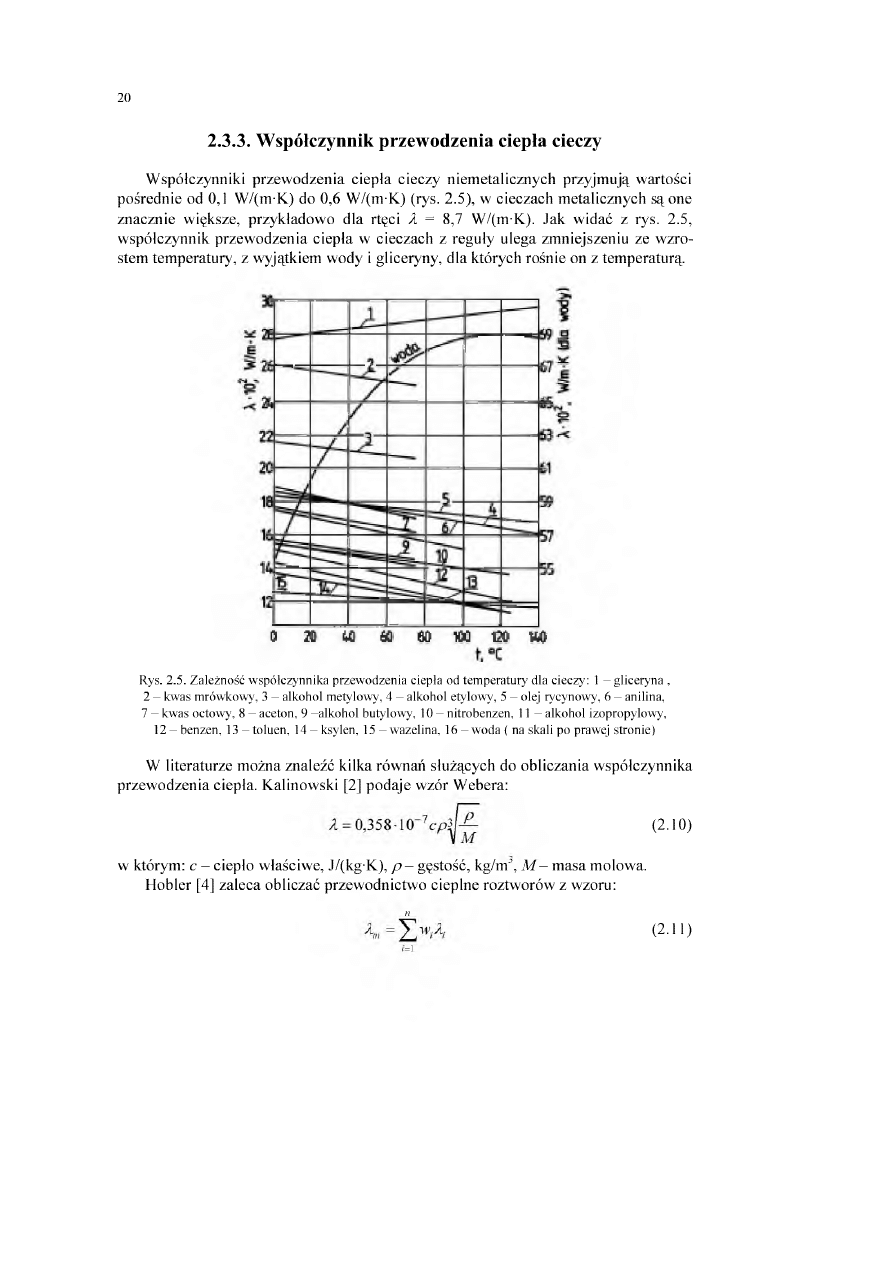
W spółczynniki przew odzenia ciepła cieczy niem etalicznych przyjm ują w artości
pośrednie od 0,1 W /(m-K) do 0,6 W /(m-K) (rys. 2.5), w cieczach m etalicznych są one
znacznie większe, przykładow o dla rtęci X = 8,7 W /(m-K). Jak w idać z rys. 2.5,
w spółczynnik przew odzenia ciepła w cieczach z reguły ulega zm niejszeniu ze w zro
stem tem peratury, z wyjątkiem wody i gliceryny, dla których rośnie on z tem peraturą.
Rys. 2.5. Zależność w spółczynnika przewodzenia ciepła od tem peratury dla cieczy: 1 - gliceryna ,
2 - kwas mrówkowy, 3 - alkohol metylowy, 4 - alkohol etylowy, 5 - olej rycynowy, 6 - anilina,
7 - kwas octowy, 8 - aceton, 9 -alk o h o l butylowy, 10 - nitrobenzen, 11 - alkohol izopropylowy,
12 - benzen, 13 - toluen, 14 - ksylen, 15 - wazelina, 16 - woda ( na skali po prawej stronie)
W literaturze m ożna znaleźć kilka rów nań służących do obliczania w spółczynnika
przew odzenia ciepła. K alinow ski [2] podaje w zór W ebera:
w którym : c - ciepło w łaściw e, J/(kg-K), p — gęstość, kg/nr1, M - m asa m olow a.
H obler [4] zaleca obliczać przew odnictw o cieplne roztw orów z wzoru:
0
20
W
M
60
KM
1»
U0
(2 . 10)
n
(2 . 11)
i=\
21
w którym w, - udział m asow y składników w roztw orze, A, - w spółczynniki przew o
dzenia ciepła dla czystych składników roztw oru.
2.3.4. Współczynnik przewodzenia ciepła gazów
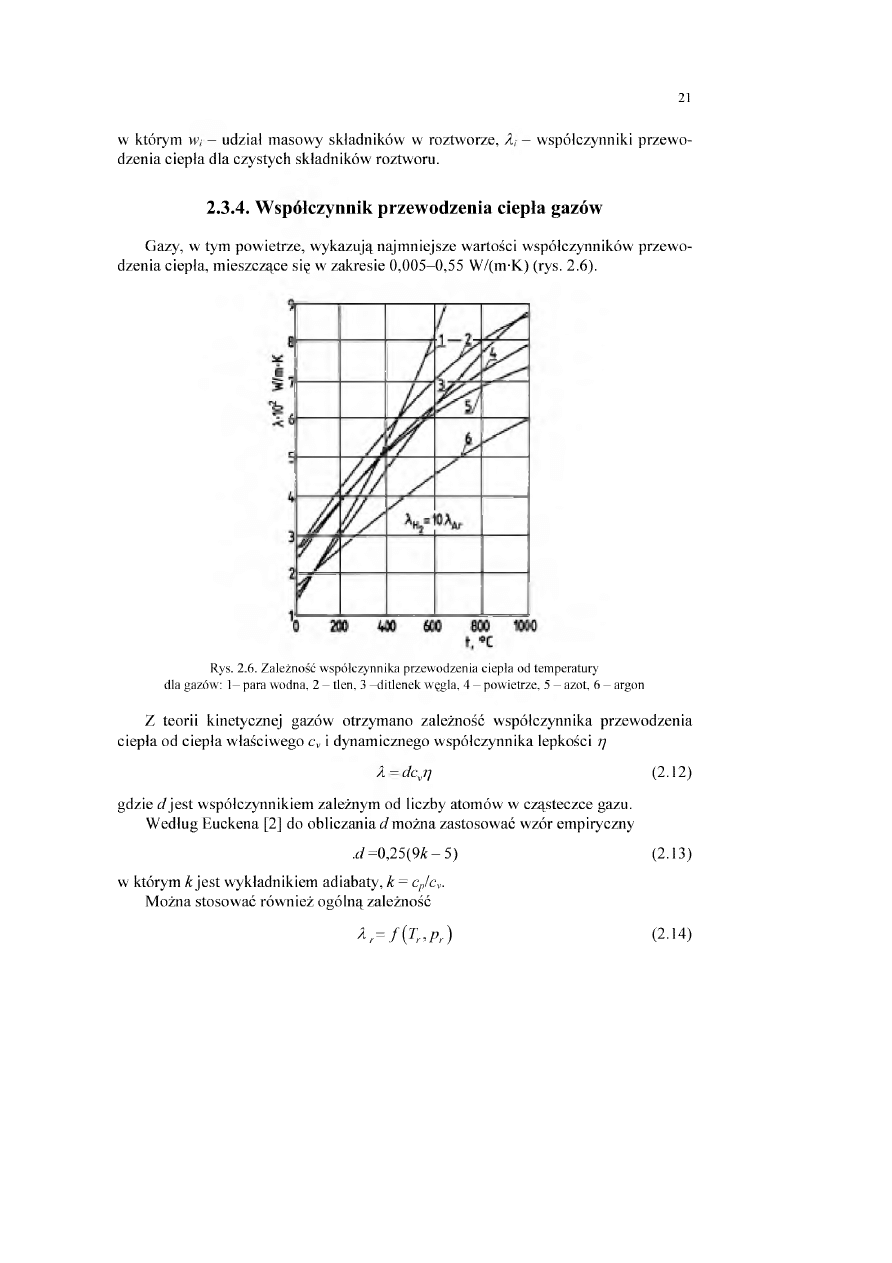
Gazy, w tym pow ietrze, w ykazują najm niejsze w artości w spółczynników przew o
dzenia ciepła, m ieszczące się w zakresie 0 ,00 5-0,5 5 W /(m -K) (rys. 2.6).
Rys. 2.6. Zależność w spółczynnika przewodzenia ciepła od tem peratury
dla gazów: 1 - para wodna, 2 - tlen, 3 -d itle n e k węgla, 4 - powietrze, 5 - azot, 6 - argon
Z teorii kinetycznej gazów otrzym ano zależność w spółczynnika przew odzenia
ciepła od ciepła w łaściw ego c v i dynam icznego w spółczynnika lepkości ?]
A ~ d c vtj
(2.12)
gdzie c/jest w spółczynnikiem zależnym od liczby atom ów w cząsteczce gazu.
W edług E uckena [2] do obliczania d m ożna zastosow ać w zór em piryczny
.c/= 0 ,2 5 ( 9 * - 5 )
(2.13)
w którym k je s t w ykładnikiem adiabaty, k = cp/cv.
M ożna stosow ać rów nież o góln ą zależność
* r = f { T r , P r )
( 2 - 14)
22
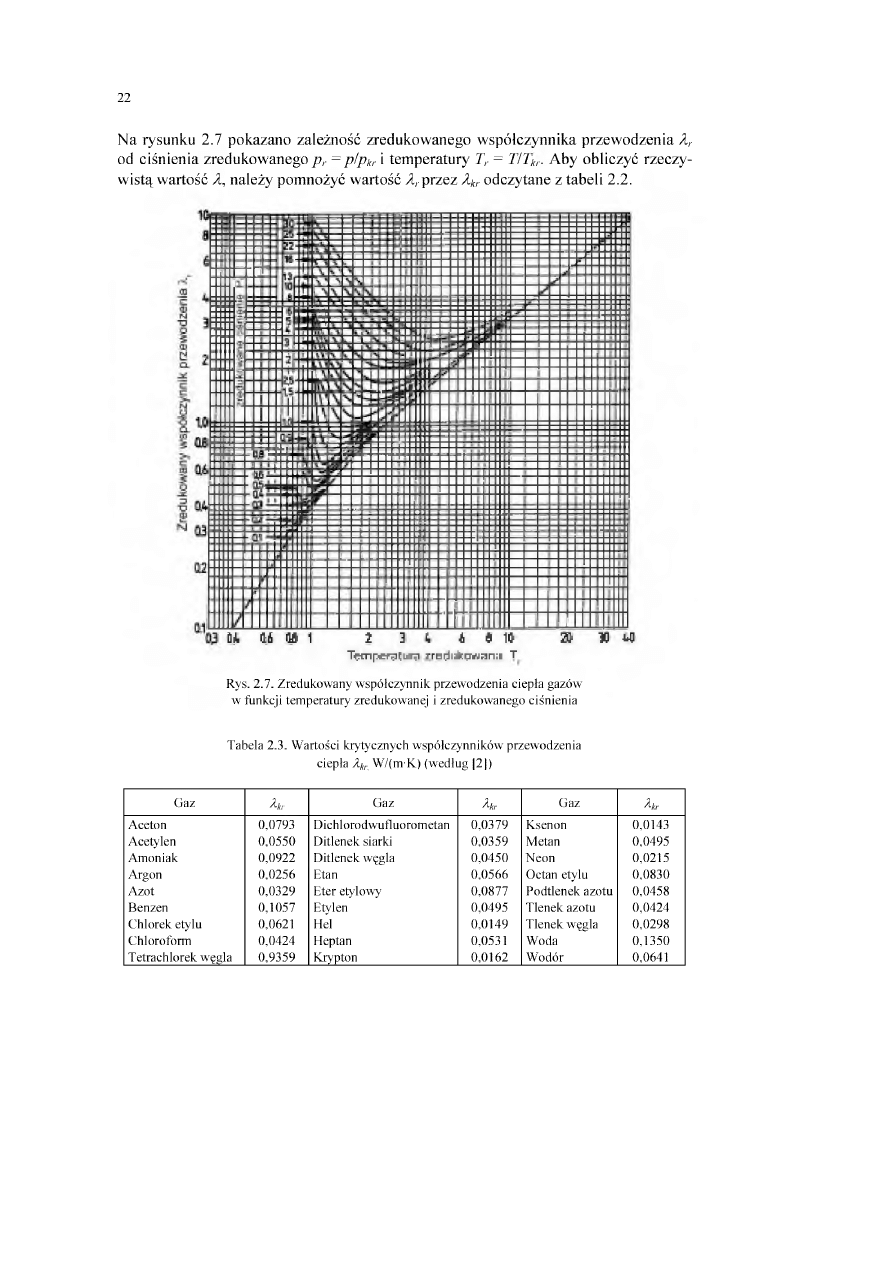
N a rysunku 2.7 pokazano zależność zredukow anego w spółczynnika przew odzenia Ar
od ciśnienia zredukow anego p r = p/ptr i tem peratury Tr = 777*,-. A by obliczyć rzeczy
w istą w artość A, należy pom nożyć w artość A,-przez Akr odczytane z tabeli 2.2.
flłl 1A flfl 1
2
l i ,
« 4 1»
20
3 0 4 ^
T łf r n p m r itL iiT i r r n r l i * r i w a n ; s T
Rys. 2.7. Zredukow any w spółczynnik przewodzenia ciepła gazów
w funkcji tem peratury zredukowanej i zredukow anego ciśnienia
Tabela 2.3. W artości krytycznych współczynników przewodzenia
ciepła Akr W/(m-K) (w edług |2 |)
Gaz
Akr
Gaz
Akr
Gaz
Akr
Aceton
0,0793
Dichlorodwufluorom etan
0,0379
Ksenon
0,0143
Acetylen
0,0550
D itlenek siarki
0,0359
Metan
0,0495
Am oniak
0,0922
D itlenek węgla
0,0450
Neon
0,0215
Argon
0,0256
Etan
0,0566
Octan etylu
0,0830
A zot
0,0329
Eter etylowy
0,0877
Podtlenek azotu
0,0458
Benzen
0,1057
Etylen
0,0495
Tlenek azotu
0,0424
C hlorek etylu
0,0621
Hel
0,0149
Tlenek węgla
0,0298
Chloroform
0,0424
Heptan
0,0531
Woda
0,1350
Tetrachlorek węgla
0,9359
Krypton
0,0162
W odór
0,0641
23
N ajdokładniejsze w artości w spółczynników p rzew odzenia ciepła m ożna jed n ak
otrzym ać z pom iarów dośw iadczalnych albo z tabel lub w ykresów opartych n a bezpo
średnich pom iarach.
2.4.
Ustalony ruch ciepła
przez przewodzenie w ścianie płaskiej
W najprostszym przypadku, tj. dla ściany płaskiej, jej pow ierzchnia przekroju p o
przecznego je s t stała A = const. Jeżeli m aterial, z którego je s t w ykonana ta ścianka,
je s t jednorodny, a całkow ita różnica tem peratury niew ielka, to w spółczynnik przew o
dzenia m a w artość stalą X = const. W tym przypadku rów nanie F ouriera (2.7)
Q = - * A
dT_
dx
(2.15)
m ożna scalkow ać w granicach (rys. 2.8) od x = 0 do x = s i od T = T\ do T = T2. Po
rozdzieleniu zm iennych
>'
' 2
Q ^ = -XA p r
(2.16)
i scałkow aniu otrzym ujem y
Q
s
= - A Ą T 2 - T x)
Q -
(2 .17a)
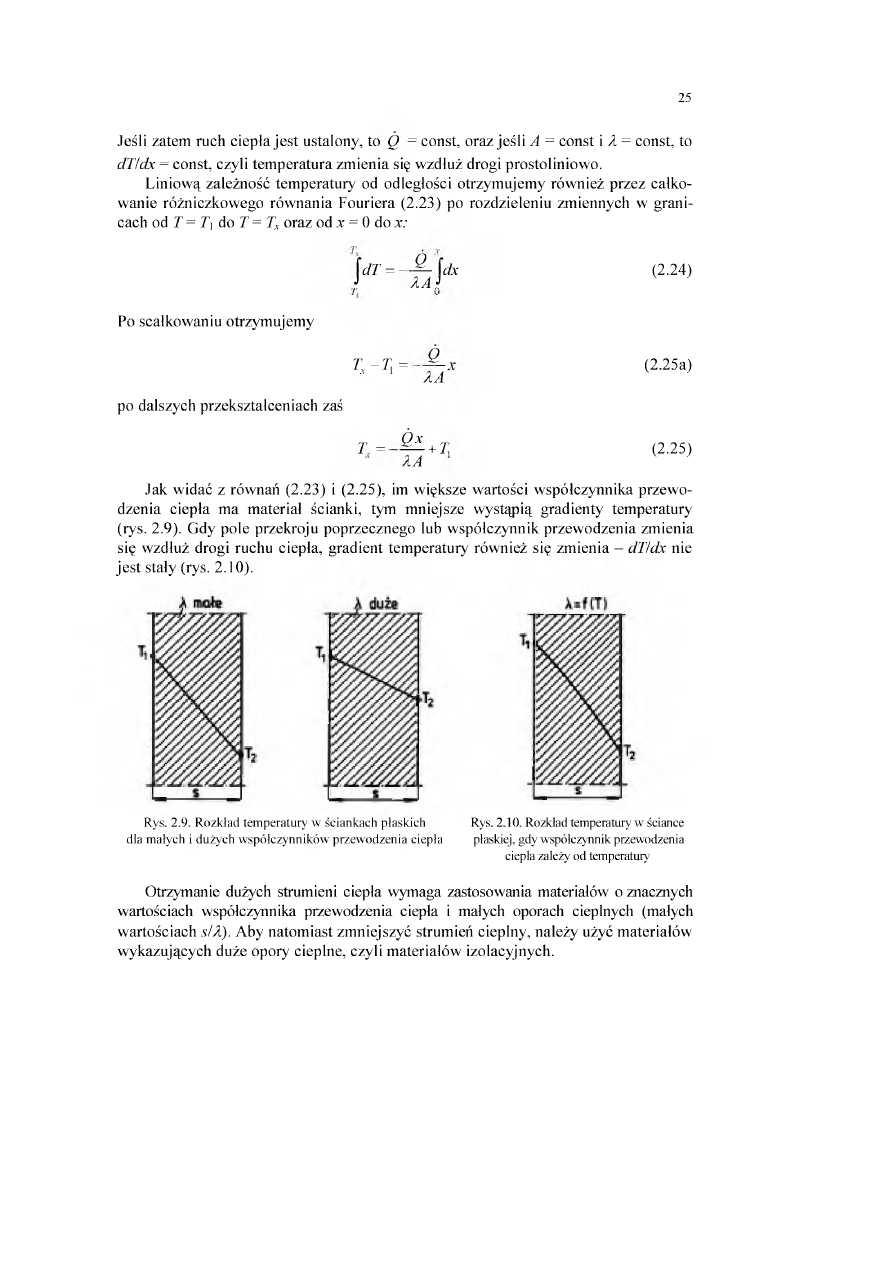
Rys. 2.8. Rozkład tem peratury w ściance płaskiej
Po podzieleniu przez ,v oraz w prow adzeniu znaku m inus do w yrażenia w naw iasie
otrzym ujem y w zór n a strum ień ciepła przew odzonego p rzez jedn ow arstw o w ą ścianę
płaską:
Q = - Ą
t
, -
t
2) = -
a m
s
s
( 2 . 1 7b)

24
Współczynnik przewodzenia ciepła X określa energię cieplną w dżulach, która w ciągu
sekundy przepływa ze ściany o powierzchni 1 tir do ściany przeciwległej, gdy AT= 1 K.
2.4.1. Definicja oporu cieplnego
Ze względu na podobieństwo przepływu strumienia ciepła do przepływu prądu
elektrycznego, do analizy przekazywania ciepła wprowadzono pojęcie oporu cieplne
go [5]. Wykorzystujemy tutaj analogię między równaniami opisującymi ruch ciepła
a równaniem wyrażającym prawo Ohma podczas przepływu prądu elektrycznego
A U = IR
(2.18)
Przyjmujemy, że wartości spadku napięcia AU odpowiada w ruchu ciepła różnica
temperatury AT, natężenie prądu / jest wielkością analogiczną do strumienia cieplne
go (). a oporowi elektrycznemu R przypisujemy opory cieplne R,. wynikające z rów
nań ruchu ciepła. Na tej podstawie równanie Fouriera
dla ustalonego przewodzenia
ciepła (2.17) wyrazimy w następujący sposób:
•
AT
Q = ~
(2-19)
R
a
i otrzymamy wzór na opór cieplny przewodzenia ciepła:
AT
* , = - = -
(2.20)
'¡¿
a
Na tej podstawie otrzymujemy równania oporów cieplnych dla poszczególnych przy
padków ruchu ciepła. Opór cieplny przewodzenia ciepła w ściance płaskiej określa
równanie:
AT
s
R, ——
(2. 21)
Q XA
V
’
strumień cieplny zaś możemy opisać równaniem:
T - T
0
=
(
2
.
22
)
R
a
2.4.2. Rozkład temperatury w ściance płaskiej
Różniczkowe równanie Fouriera (2.7) przekształcamy do postaci:
— = —
(2. 23)
dx
XA
25
Jeśli zatem ruch ciepła je s t ustalony, to Q = const, oraz jeśli A = const i A = const, to
dT/dx = const, czyli tem peratura zm ienia się w zdłuż drogi prostoliniow o.
L inio w ą zależność tem peratury od odległości otrzym ujem y rów nież przez całko
w anie różniczkow ego rów nania F ouriera (2.23) po rozdzieleniu zm iennych w grani
cach od T = T] do T = Tx oraz od x = 0 do x:
\dT = --Q -
J
A A ?
dx
(2.24)
Po scalkow aniu otrzym ujem y
Tx - T y = -
Q_
A A
po dalszych przekształceniach zaś
T. =•
Q x
A A
+ T,
(2.25a)
(2.25)
Jak w idać z rów nań (2.23) i (2.25), im większe w artości w spółczynnika przew o
dzenia ciepła m a m ateria! ścianki, tym m niejsze w ystąpią gradienty tem peratury
(rys. 2.9). Gdy pole przekroju poprzecznego lub w spółczynnik przew odzenia zm ienia
się w zdłuż drogi ruchu ciepła, gradient tem peratury rów nież się zm ienia - dT/dx nie
je s t stały (rys. 2.10).
Rys. 2.9. Rozkład tem peratury w ściankach płaskich
dla małych i dużych współczynników przewodzenia ciepła
Rys. 2.10. Rozkład temperatury w ściance
płaskiej, gdy współczynnik przewodzenia
ciepła zależy od temperatury
Otrzymanie dużych strumieni ciepła wym aga zastosowania m ateriałów o znacznych
wartościach współczynnika przewodzenia ciepła i małych oporach cieplnych (małych
w artościach s/A). A by natom iast zm niejszyć strum ień cieplny, należy użyć m ateriałów
w ykazujących duże opory cieplne, czyli m ateriałów izolacyjnych.

26
2.5. Ustalone przewodzenie ciepła
w wielowarstwowej ścianie płaskiej
Przyjm ijmy, że ściana plaska składa się z n nałożonych n a siebie warstw, z których
każda charakteryzuje się grubością ,V; i współczynnikiem przew odzenia ciepła X-,. Ścianę
tak ą m ożem y rozw ażać jako n pow ierzchni jednow arstw ow ych (por. rys. 2.11, przykład
przegrody trójw arstw ow ej). Otrzymam y w ów czas/; rów nań strum ienia ciepła:
• dla w arstw y 1
Q = k A( T ,-T 2) - T' - T'-
R
v.l
1 dla w arstw y 2
1 dla //-tej w arstw y
R
-12
Q = ^ A ^ T a+J) = ^ - j ^ -
Rys. 2.11. Rozkład temperatury w trójwarstwowej ściance płaskiej
Po pom nożeniu rów nań ((2.26)—(2.28)) przez R , otrzym ujem y
Q Ą = t , - t 2
QR2 = i 2
1
Q K
=T„
(2.26)
(2.27)
(2.28)
(2.29)
(2.30)
(2.31)
27
Po zsumowaniu tych równań stronami otrzymujemy
< 2 K , + ^ 2 +
+ R,„)=T1 -T„+l
(2.32)
Po wprowadzeniu oporu zastępczego jako sumy oporów łączonych szeregowo:
i=n
i=n
^ = Ż * * = Ż T 7
(2-33)
i=l
i=l AiA
otrzymujemy wzór do obliczania strumienia ciepła przewodzonego przez płaską prze
grodę «-warstwową
T - T
Rx
Równanie to jest identyczne z równaniem (2.22), ale opór Rx jest tutaj oporem
sumarycznym.
2.6.
Ustalone przewodzenie ciepła
w jednowarstwowej ścianie rurowej
Przyjmijmy, że ściana rurowa jest wykonana z materiału o współczynniku prze
wodzenia ciepła X niezależnym od temperatury i czasu. Rozmiary rury (rys. 2.12) są
określone przez jej średnicę wewnętrzną d\ i zewnętrzną d2 oraz długość L.
JkT
Rys. 2.12. Rozkład temperatury w ściance rurowej
Dla ustalonego przewodzenia ciepła przez ściankę rury zapiszemy równanie
Fouriera (2.7) w postaci różniczkowej

28
Q = - X A ^ ~
(2.35)
dr
w którym zmiennymi są pole powierzchni A = A(r), temperatura T (temperatura we
wnętrznej ściany rury wynosi 7), zewnętrznej zaś T2) oraz droga, którą stanowi pro
mień r, zmieniający się w granicach od d\/2 do d2l2.
Pole powierzchni możemy zapisać jako funkcję zmiennej niezależnej r.
A = 2nrl.
(2.36)
Po podstawieniu do równania (2.35) otrzymujemy równanie
J J T
Ó — 2/.nl.r—
(2.37)
dr
które ma dwie zmienne, zależną T i niezależną r.
Po rozdzieleniu zmiennych równanie to przyjmuje postać:
•
dr
Q - = -2A.nLdT
(2.38)
r
Całkujemy je w granicach od r\ = d-^/2 do r2 = d/2 oraz od T\ do 7:
dn
r
Q \ — = ^2M L JdT
(2.39)
ĄI2 r
7;
i otrzymujemy równanie:
/
ln
ln— I
(2.40)
\
2
2
2AnL
które po prostym przekształceniu przyjmuje postać:
Ó
d
T ^ T ,
——ln—-
(2.41)
1 2A.nL
d{
Logarytmiczne równanie (2.41) określa rozkład temperatury w ściance rury pod
czas ustalonego przewodzenia ciepła od temperatury 7) do temperatury T2
(rys.
(2.12)).
Aby obliczyć strumień ciepła, równanie różniczkowe (2.38) całkujemy w grani
cach od r\ = d\/2 do r2 = d2
J2, gdy temperatura zmienia się od 7) do T2:
d , / 2
7’,
dr
Q J — = - 2AnL JdT
(2.42)
dt/2 r
1\
Po scałkowaniu otrzymujemy wyrażenie

29
Ś l n ^ - = -2 A tó (r2 -7 ;)
(2.43)
Po uporządkowaniu otrzymujemy wzór określający strumień ciepła:
Z - T ,
Q^2X%L 1 ±2
ln —
(2.44)
Po pomnożeniu licznika i mianownika przez wyrażenie 2s = di_- i/iotrzymujemy
d-y d^
ln —
v
y
f t - r 2) =
AZ.
l n ^
Z/,
i y
(2.45)
^2
4
l n ^
v
4 y
A
(T^ T 2) ^ - A m( T ^ T 2)
gdzie:
U = n d -
obwód rury, m,
A = ndL
- powierzchnia rury, m \
Po uwzględnieniu oporu cieplnego przewodzenia ciepła przez ścianę rurową
R*r =
ln —
d]
2A
otrzymujemy równanie
a
T T] T7
Q - %L -
-
R
(2.46)
(2.47)
-Ar
Równania (2.43)-(2.47) pozwalają obliczać strumień cieplny, gdy dysponujemy
podstawowymi danymi dotyczącymi oporu cieplnego przewodzenia ciepła i wartości
temperatury na ściance rurowej.
2.7. Ustalone przewodzenie ciepła
w wielowarstwowej ścianie rurowej
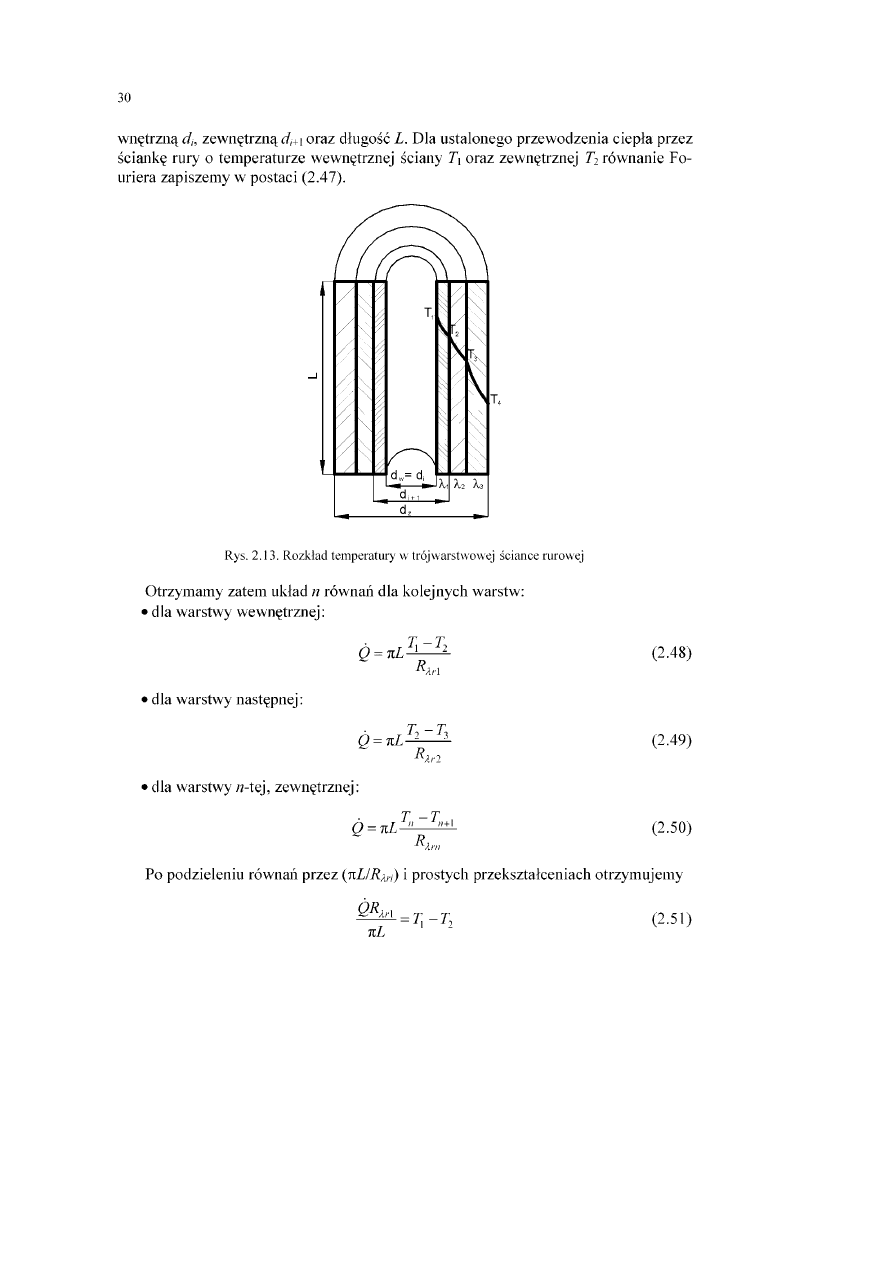
Przyjmijmy, że trójwarstwowa ściana rurowa jest wykonana z materiałów
o współczynnikach przewodzenia ciepła A], A
2
, A
3
niezależnych od temperatury i cza
su. Rozmiary każdej ścianki rurowej (rys. 2.13) są określone przez jej średnicę we
30
wnętrzną dh zewnętrzną dn , oraz długość L. Dla ustalonego przewodzenia ciepła przez
ściankę rury o temperaturze wewnętrznej ściany Jj oraz zewnętrznej 73 równanie Fo
uriera zapiszemy w postaci (2.47).
Rys. 2.13. Rozkład temperatury w trój warstwowej ściance rurowej
Otrzymamy zatem układ n równań dla kolejnych warstw:
• dla warstwy wewnętrznej:
Ó =
(2.48)
dla warstwy następnej:
Q = % L ? ± - i
(2.49)
R-Arl
dla warstwy «-tej, zewnętrznej:
Q = n L Tf1 Tn+l
(2.50)
^Arn
Po podzieleniu równań przez (nL/RM) i prostych przekształceniach otrzymujemy
= T \- T 2
(2.51)
O^Arl
%L

31
- 7\ - 7\
(2.52)
7
iL
^ y - = Tn ~Tn+]
(2.53)
%L
Po dodaniu stronami i wyciągnięciu wyrazu Q /(t
i
L) przed nawias otrzymujemy
+ ^Ar2 + R-Am
^
(2-54)
7iL
Przyjmijmy, że suma oporów RM jest oporem wypadkowym wielowarstwowej
ściany rurowej o warstwach łączonych szeregowo
^ = £ ^ = £ ¿ 1 " ^
(2-55)
/=]
"7
w‘/
Z równania (2.54) otrzymamy wówczas wyrażenie na strumień ciepła przewodzonego
przez rurową ścianę wielowarstwową:
Ó - n l . '1' - '1'"-'
(2.56)
Rj,r
Równanie to jest identyczne w budowie z równaniem dla pojedynczej ściany ru
rowej (2.47), ale tutaj opór R* jest oporem sumarycznym.

3. Wnikanie ciepła
Podczas burzliwego przepływu płynu wzdłuż przegrody płaskiej lub o dowolnej
krzywiźnie rozkład prędkości w kierunku prostopadłym do przegrody jest liniowy,
a na jej powierzchni prędkość jest równa zeru. Zgodnie z hipotezą Prandtla (1904 r.)
w pobliżu przegrody istnieje tzw. warstewka graniczna; elementy płynu (gazu lub
cieczy) przepływają w niej ruchem uwarstwionym, w warstwach równoległych do
kierunku przepływu [ 1 ].
Rys. 3.1. Rozwinięcie warstwy granicznej: 1 - warstwa laminama,
2 - obszar przejściowy, 3 - warstwa turbulentna, 4 - podwarstwa laminarna
5 - podwarstwa buforowa
Na rysunku 3.1 pokazano laminamą warstewkę graniczną (1), obszar przejścio
wy (2), turbulentną warstwę (3) oraz tzw. podwarstwę laminamą (4). Grubość laminar-
nej warstewki granicznej jest bardzo mała, ok. KT6 m, i na ogół nie jest ona wyznaczana
doświadczalnie. Istotne jest jednak to, że w warstewce tej ruch ciepła od przegrody lub
w kierunku przeciwnym zachodzi przez przewodzenie. Wytwarza się przy tym tzw.
termiczna warstwa przyścienna, poza którą temperatura płynu nie zmienia się w kierun
ku prostopadłym do rozpatrywanej powierzchni. Grubość warstewki granicznej zależy
przede wszystkim od kształtu powierzchni opływanej (płyta lub ściana rury, powierzch
nia cząstki kulistej albo inna bryła), lecz także od takich właściwości płynu, jak lepkość
i gęstości oraz od prędkości liniowej przepływu strumienia.
W większej odległości od ściany elementy płynu przemieszczają się również
w kierunku poprzecznym i przejmowanie ciepła wiąże się z konwekcją, czyli ruchem
makroskopowych części płynu różniących się temperaturą. Przenoszenie energii
cieplnej od przegrody do rdzenia strumienia płynu lub w przeciwnym kierunku obej
muje zarówno przewodzenie w warstwie granicznej, zwanej warstwą przyścienną lub

34
warstwą Prandtla, jak i konwekcję w rdzeniu płynu. Ten łączny ruch ciepła jest nazy
wany wnikaniem ciepła (Hobler [4]), a niekiedy przejmowaniem ciepła (Wiśniewski,
Wiśniewski [1], Kalinowski [2]).
Podstawowe równanie ruchu ciepła między powierzchnią przegrody a płynem
znajdującym się z nią w kontakcie ma następującą postać:
Q = aA A T
(3.1)
gdzie: Q - strumień ciepła, J/s, a - współczynnik wnikania ciepła od rdzenia płynu
do powierzchni przegrody lub od przegrody do płynu, W/(m2-K), A - powierzchnia
przegrody w kontakcie z płynem, m2, AT - różnica temperatury w rdzeniu płynu i na
powierzchni przegrody, K. Równanie to nazwano równaniem Newtona.
Współczynnik wnikania ciepła a wyraża ilość ciepła w dżulach, która jest wymienia
na w jednostce czasu (r = 1 s) na jednostkowej powierzchni (A = 1 m2), gdy A T= 1 K.
Wnikanie ciepła w układzie powierzchnia przegrody-płyn może zachodzić na trzy
różne sposoby:
• w zakresie przepływu uwarstwionego - przez przewodzenie,
• w zakresie przepływu burzliwego - przez przewodzenie w warstwie przyściennej
i konwekcę do rdzenia płynu,
• gdy istotny jest również udział promieniowania, całkowity współczynnik wnika
nia ciepła ac obejmuje w zależności od charakteru przepływu płynu albo X!s i tzw.
zastępczy współczynnik wnikania ciepła przez promieniowanie ar albo konwekcyjny
współczynnik wnikania ciepła a i zastępczy współczynnik wnikania ciepła ar. Za
stępczy współczynnik wnikania ciepła ar określa ilość ciepła, jaka jest wymieniana
między powierzchnią przegrody i rdzeniem płynu przez promieniowanie dla r = 1 s,
A = lm2, AT= 1 K.
Współczynnik wnikania ciepła jest funkcją ciśnienia, a także wielu zmiennych za
leżnych od temperatury, takich jak współczynnik przewodzenia ciepła, gęstość, lep
kość oraz ciepło właściwe. Zależy on również od prędkości i charakteru przepływu
płynu oraz od kształtu rozpatrywanej powierzchni wymiany ciepła. Na wartości
współczynników wnikania ciepła wpływają również zmiany stanu skupienia - zjawi
ska towarzyszące wrzeniu cieczy lub skraplaniu pary oraz sposób przejmowania cie
pła, w zależności od tego, czy ruch ciepła jest ustalony, czy nieustalony. Wnikanie
ciepła jest zatem skomplikowanym zjawiskiem związanym bezpośrednio z mechaniką
płynów. Siłą napędową ruchu ciepła jest różnica temperatury AT odpowiadająca gra
dientowi temperatury na drodze przepływu ciepła.
Współczynnik wnikania ciepła może się zmieniać w czasie i wzdłuż opływanej
powierzchni, może się też zmieniać temperatura płynu i powierzchni. Sposoby uśred
niania współczynnika wnikania ciepła i temperatury płynu są umowne. Po uśrednieniu
temperatury płynu i temperatury ścianki wzdłuż powierzchni [1]

35
A
A t
do uśrednienia współczynnika wnikania ciepła wzdłuż powierzchni można wykorzy
stać strumienie ciepła obliczone na dwa sposoby i otrzymać równanie
J'a(Tf - T s)dA
J
Tf ~ Ts
Gdy zmiany temperatury płynu i powierzchni ścianki wzdłuż drogi przepływu nie
są znane, znana jest natomiast temperatura na wlocie (1) i na wylocie (2) z kanału
przepływowego, stosujemy inne podejście. Strumień ciepła przejmowany przez po
wierzchnię ścianki jest równy zmniejszeniu entalpii płynu o strumieniu masy m :
a(Tf - Ts)dA = - mcpd(Tf - Ts)
(3.5)
Po rozdzieleniu zmiennych całkuje się to równanie w granicach:
dla pola po
wierzchni wymiany ciepła
od 0 do A oraz dla różnicy temperatury (7) - T,)i w prze
kroju wlotowym oraz (7 ) - Ts)2 w przekroju wylotowym kanału. Po wprowadzeniu
średniego współczynnika wnikania ciepła i scałkowaniu otrzymujemy
J a d A - a A - m c n ln— --------
(3.6)
1
P
(Tf - T s)2
Po dalszych przekształceniach (podzielenie obu stron równania przez logarytm
stosunku różnic temperatury na końcach wymiennika i pomnożeniu przez te różnice)
otrzymujemy wzór do obliczania strumienia ciepła:
Q = ™ r [ ( T , - T\ - ( Tf - T’ \ ] = s ^ T/
= s a a t -
< 3 j)
W obliczeniach należy zastosować średnią logarytmiczną różnicę temperatury
płynu i powierzchni ścianki na wlocie i wylocie z kanału przepływowego

36
(3.8)
W zależności od kierunku strumienia ciepła temperatura płynu zmienia się w mia
rę oddalania się od powierzchni ciała stałego. Cząstki płynu stykające się z po
wierzchnią ciała stałego przyjmują jego temperaturę i na powierzchni ciała stałego
wytwarza się tzw. termiczna warstwa przyścienna, poza którą temperatura płynu nie
zmienia się w kierunku prostopadłym do rozpatrywanej powierzchni. Często do okre
ślania współczynnika wnikania ciepła stosuje się średnią arytmetyczną temperatury
płynu i temperatury powierzchni ciała stałego.
Podczas przepływu laminamego przez kanał lub rurę temperatura płynu zmienia
się w całym poprzecznym przekroju kanału i do obliczeń stosuje się wówczas średnią
temperaturę płynu określoną na podstawie obliczonej na dwa sposoby entalpii płynu:
Zaniedbując zmiany właściwości płynu, równanie to można zapisać w postaci:
gdzie V jest objętościowym strumieniem płynu.
Podejście analityczne, prowadzące do wyznaczenia współczynników wnikania
ciepła dla każdego przypadku [5-9], obejmuje poszukiwanie rozkładu temperatury
wpłynie opływającym ciało stałe w celu wyznaczenia gradientu temperatury przy
powierzchni^r/ds)». Współczynnik wnikania ciepła odpowiada stosunkowi gęstości
strumienia cieplnego do różnicy temperatury powierzchni i temperatury płynu (Kem-
błowski, Strumiłło i in.[5]):
Wyznaczanie współczynnika a metodą analityczną jest tak skomplikowane, że
wykonano je w nielicznych przypadkach (rozwiązanie Pohlhausena).
— A
(3.9)
A
(3.10)
A
a -
(3.11)

4. Przenikanie ciepła
Przenikanie ciepła jest przekazywaniem ciepła między dwoma płynami rozgrani
czonymi stałą przegrodą - płytą lub ścianką rury. Zachodzi tutaj kolejno wnikanie
ciepła od gorącego płynu do pierwszej ściany, następnie przewodzenie ciepła przez
przegrodę i wnikanie ciepła od drugiej ściany tej przegrody do płynu ogrzewanego.
Przyjmijmy, że ciepło wnika od czynnika A do ścianki płaskiej, następnie zacho
dzi przewodzenie przez ściankę, po czym następuje wnikanie od ścianki do czynni
ka B. Na rysunku 4.1 rozkład temperatury w mediach A i B zilustrowano zgodnie
z teorią termicznej warstwy granicznej. Dla ustalonego ruchu ciepła na wszystkich
etapach ruchu ciepła mamy ten sam strumień ciepła
A
s
Rys. 4.1. Rozkład temperatury podczas
przenikania ciepła przez ściankę płaską
(4.1)
skąd otrzymujemy po przekształceniach

38
a tA
AA
A
Po zsumowaniu spadków temperatury otrzymujemy
O
7> 1 - 7> 2 = 7
r \
1 ^
1
5
1
+ — + —
yO,
A
a 2 j
(4.5)
a stąd strumień cieplny jest opisany równaniem
Q = - ---------- r A(Tn - T f l )=kAAT
(4.6)
s
— + — + —
a,
A a
przy czym
k = -j---------- p
W/(m • K)
(4.7)
— + — + —
źl
a 2
Wielkość k nazywamy współczynnikiem przenikania ciepła. Równanie (4.6) opi
sujące strumień cieplny jest nazywane równaniem Pecleta dla ściany płaskiej,
a współczynnik przenikania ciepła k współczynnikiem Pecleta.
Ruch ciepła między ścianką a otoczeniem może się odbywać przez wnikanie bądź
promieniowanie (por. rozdz. 3). Aby uwzględnić promieniowanie ciepła, wprowadza
się zazwyczaj zastępczy współczynnik ruchu ciepła przez promieniowanie ar [5], któ
ry definiujemy równaniem
& -2 = < * A (T * -T f )
(4.8)
stąd otrzymujemy
“ - = 7 7 r b r \
(4-9)
Po podstawieniu równania na strumień ciepła przekazanego przez promieniowanie

39
Q,.2 =C
o
Ą 0 1.
otrzymujemy ostateczną postać wyrażenia
/ T.,
V10 0 y
Ts 2
\ 100 j
a r
r
(
t
.
v
(
T,->
Y
c 0< zv
2
-
l i o o j
ą l O O j _
T,y-Tf
(4.10)
(4.11)
Sumarycznie ruch ciepła przez wnikanie i promieniowanie opisujemy równaniem
Q = {ak + ar) Ą A T
(4.12)
gdzie «i jest współczynnikiem wnikania ciepła, ar zaś - zastępczym współczynnikiem
ruchu ciepła przez promieniowanie.
4.1. Opory cieplne wnikania i przenikania ciepła
Rozważmy dla przykładu przypadek wnikania ciepła przy gorącej płycie schła
dzanej powietrzem. Strumień ciepła można łatwo obliczyć z równania Newtona:
Q = a xĄ {Tx- T , x) = a 2Ą { T s2- T 2)
(4.13)
które inaczej możemy zapisać:
(4.14)
Rt
R2
W równaniu tym Rt oznacza opór cieplny wnikania po wewnętrznej stronie ściany, R2
zaś opór cieplny wnikania po jej zewnętrznej stronie.
Wykorzystujemy tutaj podobieństwo między równaniami opisującymi ruch ciepła
a równaniem wyrażającym prawo Ohma dla przepływu prądu elektrycznego
/ = —
(4.15)
R
Spadkowi napięcia AU odpowiada w ruchu ciepła różnica temperatury AT, natężenie
prądu / jest wielkością analogiczną do strumienia cieplnego Q, a oporowi elektrycz
nemu R przypisujemy odpowiednie wielkości oporów cieplnych Rh wynikające z od
powiednich równań ruchu ciepła.
Opory cieplne dla wnikania ciepła zapiszemy zatem wzorami

40
oraz
* , = — r
(4-16)
a, A,
R>=— r
i4-17)
a 1A1
Po zastosowaniu równań (4.16) i (4.17) do poszczególnych przypadków ruchu
ciepła otrzymujemy równania definiujące opory cieplne:
• opór cieplny przewodzenia dla ścianki płaskiej
AT
s
r x = - x - = t ~ a
(4 ' 18)
Q
¿ 4
1 opór cieplny wnikania
1 opór cieplny promieniowania
R a - —
(4.19)
a A
^ = — 7
(4-20)
a rA
• opór złożonego ruchu ciepła z wnikania i promieniowania
* “ « = 7 —
' - T l
( 4 2 l )
(«, + a r )A
Po przekształceniu otrzymujemy
’
= ( ą + a r) A = - U - J -
(4-22)
Ra+r
y
7
Ra
R,
Zależność ta, opisująca związek oporów cieplnych wnikania i promieniowania,
odpowiada zależności obowiązującej w obliczaniu oporów elektrycznych łączonych
równolegle.
• Opór cieplny przenikania opisuje równanie
r
‘ =T
a
(423)
Po podstawieniu wyrażenia na współczynnik przenikania ciepła otrzymujemy
R k - R a i + R , + R ai
( 4 -2 4 )

41
Gdy ruch ciepła między ścianką a otoczeniem odbywa się przez wnikanie i pro
mieniowanie, równanie to zapiszemy w postaci:
Rk ^ R u + R; + Ru
(4.25)
Opór cieplny przenikania jest zatem równy sumie oporów wnikania i przewodze
nia ciepła.
4.2. Przenikanie ciepła przez wielowarstwową ścianę płaską
Rozważmy przypadek przenikania ciepła przez ścianę domu do powietrza atmos
ferycznego na zewnątrz domu. Ruch ciepła od rdzenia strumienia ciepłego powietrza
w pomieszczeniu do wewnętrznej powierzchni ściany domu zachodzi przez wnikanie
przy konwekcji naturalnej, po czym następuje przewodzenie w warstwie przez ścianę
domu oraz przewodzenie ciepła w kolejnych warstwach izolacji, po czym wnikanie do
powietrza w powietrzu na zewnątrz domu przy konwekcji naturalnej. Temperatura
ciepłego powietrza wynosi Tu współczynnik wnikania ciepła a.\, temperatura powie
trza atmosferycznego T2, współczynnik wnikania zaś a2. Rozkład temperatury dla
ustalonego ruchu ciepła przez taką ścianę pokazano na rys. 4.2. Temperaturę na kolej
nych ścianach oznaczono symbolami Tsi.
Rys. 4.2. Rozkład temperatury podczas przenikania ciepła
przez trójwarstwową ściankę płaską
Zanalizujmy przenikanie ciepła jako proces złożony z następujących oddzielnych
etapów: wnikania ciepła wewnątrz pomieszczenia od powietrza o temperaturze T\ do
ściany o temperaturze Tsh przewodzenia ciepła przez kolejne trzy warstwy, a następ
nie wnikanie ciepła do powietrza atmosferycznego o temperaturze T2. Otrzymamy
układ trzech równań:

42
Q = a A(T - Tsl)
(4.26)
Q = T
1
- T
( ” + 1 )
(4 27)
R
a
W naszym przykładzie n = 3:
Q = «
2
a (T
s ( n + 1 )
- T
2
)
(4.28)
Jeżeli układ równań przekształcimy w ten sposób, że po lewej stronie będą tylko
różnice temperatury, a następnie dodamy stronami, to otrzymamy:
T - T
2
= Q ' 1
D
1
'
■
+ R
j
+
a 1 A
a 2 A
(4.29)
W nawiasie mamy sumę trzech wyrazów, z których Rx jest oporem cieplnym przewo
dzenia przez ścianę wielowarstwową. Podobnie pozostałe wyrazy nazywamy oporami
cieplnymi wnikania Rai i R^, a całe wyrażenie w nawiasie jest oporem sumarycznym,
e
Rk = Ra
1
+ Rj + Ra
2
(4.30)
Po wprowadzeniu tego wyrażenia do wzoru (4.29) i przekształceniu otrzymujemy
równanie na strumień cieplny, zwane równaniem Pecleta
q
=
(4.31)
Rk
Równanie to można też zapisać w podstawowej postaci:
Q = kA(T - T
2
)
(4.32)
gdzie k jest współczynnikiem przenikania ciepła dla wielowarstwowej ściany płaskiej,
zwanym również współczynnikiem Pecleta. Współczynnik ten oblicza się ze wzoru
kA = — =------------ 1------------
(4.33)
Rk
1
^ s,
1
k
—
+
X
“ ^ + —
a A “ 1 Aj A a 2 A
4.3. Przenikanie ciepła przez przegrodę rurową
Rozważmy przenikanie ciepła podczas przepływu gorącej wody wewnątrz rury.
Ruch ciepła od rdzenia strumienia gorącej wody do wewnętrznej powierzchni rury za-
enie w
rstwach izolacji,

43
wreszcie przez wnikanie do powietrza w hali fabrycznej przy konwekcji naturalnej.
Temperatura gorącej wody wynosi 7j, a współczynnik wnikania ciepła etą, temperatu
ra powietrza T2, współczynnik wnikania zaś a2.
Rys. 4.3. Rozkład temperatury podczas przenikania ciepła
przez trój warstwową ścian kę rurową
Rozkład temperatury dla ustalonego ruchu ciepła przez taką ścianę rurową poka
zano na rys. 4.3. Temperaturę na kolejnych ścianach rurowych oznaczono symbolami
T&. Zanalizujmy przenikanie ciepła jako proces złożony z oddzielnych etapów: wni
kania ciepła wewnątrz rury, przewodzenia ciepła przez kolejne warstwy, a następnie
wnikanie ciepła. Otrzymamy układ trzech równań:
(> = « ,4 ( 7 ;
) = a ]%dwL(T] - T s])
(4.34)
Q ^ n L Tsi ~ Ts(n+r>
(4.35)
R j . r
Q - a 2Az (4(«+i) - T 2) = a 2ndzL(Ts{n+1) - T 2)
(4.36)
Podobnie jak poprzednio po przekształceniu tego układu otrzymujemy:
— - — = 7 j - r ęl
(4.37)
a x ndw L
Ą -R xr =TsX- T s^
(4.38)
%L

44
Q
= Ts(B+1) - T2
(4.39)
a
2ndzL
Po dodaniu stronami i wyciągnięciu przed nawias wyrazu Q /(nL) otrzymujemy
Q ( ~ V +
+ —^ - ) = T - T
2
(4.40)
%L
a
1 aw
a
2 d
z
W nawiasie poza oporem przewodzenia ciepła R& mamy opory wnikania opisane
wzorami
Rarr
1
= ~ ^ ~
(4.41)
a dw
Rar
2
=
a2 dz
(4.42)
Przyjąwszy, że suma tych trzech oporów jest oporem przenikania ciepła przez ścianę
ru
Rkr = Rar1 ± RXr ± Rar2 .
(4.43)
zwany równa
niem Pecleta dla tej przegrody
Q = ^L TTR T^
(4.44)
Rkr
a
współczynnikiem Pecleta dla przegrody rurowej lub liniowym współczynnikiem prze
nikania ciepła [2]
k = - L = -------------- L
(4 4 5 )
Rkr
ln di±L
1
dt
1
—
± X —
± —
a 1dw
i=1 2^i
a 2 dz
otrzymujemy następującą postać równania Pecleta
Q = k r L T - T2)
(4.46)
Wyprowadzone równanie stanowi wzór na strumień ciepła przenikający przez
zwany równaniem Pecleta dla tej przegrody.
45
4.4. Analiza oporu cieplnego pierścieniowej warstwy izolacji
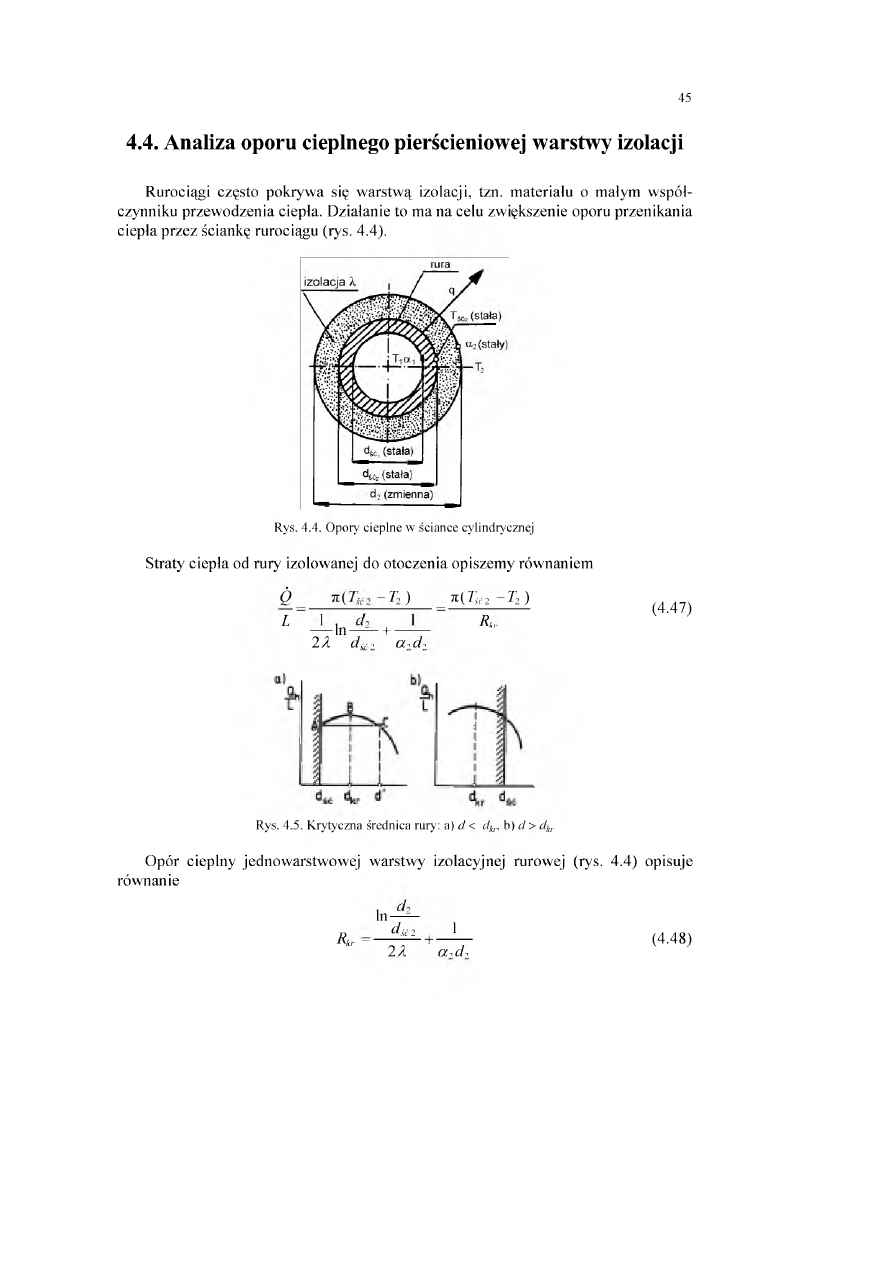
R urociągi często pokryw a się w arstw ą izolacji, tzn. m ateriału o m ałym w spół
czynniku przew odzenia ciepła. D ziałanie to m a n a celu zw iększenie oporu przenikania
ciepła p rzez ściankę rurociągu (rys. 4.4).
Rys. 4.4. Opory cieplne w ściance cylindrycznej
Straty ciepła od rury izolow anej do otoczenia opiszem y rów naniem
^T 2 )
7t( I\r2 ^T2 )
Q.
L
— In
+ ------
2Á.
c/,-.-.-.
a^d^
Rt,
(4.47)
Rys. 4.5. Krytyczna średnica rury: a) d < dkr, b) d > dkl.
O pór cieplny jednow arstw ow ej w arstw y izolacyjnej rurow ej (rys. 4.4) opisuje
rów nanie
ln-
Rkr — '
dść 2
1
2A
a^d^
( 4 .4 8 )

46
Zależy on od średnicy zewnętrznej warstwy izolacji d2. jeśli przyjmiemy stałe warto
ści różnicy temperatury, średnicy wewnętrznej rury d\, współczynników wnikania
ciepła
«1
i a2 oraz współczynnika przewodzenia ciepła X. Ze zwiększeniem zewnętrz
nej średnicy przegrody izolacyjnej d2 rośnie wyraz środkowy równania (4.48), maleje
zaś wartość ostatniego wyrazu. Dla określonej różnicy temperatury strumień ciepła
będzie maksymalny, gdy uzyskamy minimalny opór cieplny. W celu określenia warto
ści średnicy di, dla jakiej wystąpi minimalny opór cieplny, należy rozwiązać równanie
uzyskane po zróżniczkowaniu funkcji Rkr względem d2 i przyrównaniu pochodnej do
zera:
Jest to wzór określający tzw. średnicę krytyczną warstwy izolacyjnej.
Współczynnik wnikania ciepła a2 jest całkowitym współczynnikiem wnikania,
obejmującym zarówno konwekcyjny współczynnik wnikania ciepła a, jak i współ
czynnik wnikania ciepła równoważny promieniowaniu ar.
Aby stwierdzić, czy funkcja opisująca opór cieplny (równanie (4.48)) ma mini
mum czy maksimum, należy zbadać jej drugą pochodną
Druga pochodna funkcji opisującej opór cieplny jest zawsze dodatnia, bo współ
czynnik X jest dodatni. Wynika stąd, że dla średnicy krytycznej określonej równaniem
(4.51) straty ciepła są maksymalne. Ponieważ średnica krytyczna zależy jedynie od
wartości współczynników a2 i X, więc w przypadku małej wartości średnicy rury lub
drutu (rys. 4.5a) jest ona mniejsza od wartości krytycznej. Wówczas pokrywanie
przewodu izolacją powoduje zwiększenie strat ciepła aż do osiągnięcia przez ze
d { R k r )
Q
d ( d 2)
Po wykonaniu tego działania:
d ( R,-,)
1 1
(4.49)
(4.50)
i rozwiązaniu równania ze względu na di otrzymujemy
(4.51)
d 2 ( Rkr)
2
(4.52)
d (d 2 f
2 Xd2'
Po podstawieniu wzoru (4.51) za d2 otrzymujemy
d 1 (Rkr)
a 2
l a l
al
(4.53)
d ( d 2 f
8A3
8A3
8A3

47
wnętrzną średnicę warstwy di średnicy krytycznej
c
/
a
, - .
Dalszy wzrost grubości izolacji
spowoduje zmniejszanie strat ciepła, ale aż do punktu C (rys.4.5a) są one wieksze niż
straty ciepła dla rury bez izolacji. Dopiero po nałożeniu na rurę izolacji o grubości
{ d - dni)/2 i osiągnięciu przez średnicę zewnętrzną izolacji wartości większych od d ,
straty ciepła będą mniejsze niż dla rury nieizolowanej.
W przypadku rur o dużej średnicy (rys 4.5b), dla których średnica zewnętrzna dm
jest większa od średnicy krytycznej dtr, zwiększenie grubości izolacji zawsze
powoduje zmniejszenie strat ciepła. Dzieje się tak z reguły w sieciach cieplnych.
Nakładanie warstwy izolacyjnej obniża straty ciepła, a więc i obniża koszty jed
nostkowe ciepła, jednakże powoduje to zwiększenie kosztów inwestycyjnych. Wy
znaczenie ekonomicznej grubości warstwy izolacji wymaga rozważenia rodzaju izola
cji w zależności od temperatury powierzchni ściany izolowanej jak i sumarycznych
kosztów związanych z zastosowaniem danej izolacji. Ekonomiczną grubość izolacji se
należy wyznaczyć w ten sposób, aby uzyskać minimum sumarycznych kosztów ciepła
i kosztów inwestycyjnych. Zagadnienia te są przedmiotem rozważań w następnych
rozdziałach (rozdz. 5).

5. Izolacja cieplna
5.1. Rodzaje izolacji cieplnej
Zmniejszenie strat ciepła od aparatury do otoczenia możemy uzyskać przez zastoso
wanie warstwy materiału o małym współczynniku przewodzenia ciepła. Są to materiały
stałe, których współczynniki przewodzenia ciepła są mniejsze od 0,15
W/(m-K)
(por.
rozdz. 2.3.2), na ogół porowate, włókniste lub ziarniste, których pory są wypełnione po
wietrzem lub gazem o współczynniku przewodzenia ciepła znacznie mniejszym niż dla
ciała stałego. Efektywne współczynniki przewodzenia ciepła takich materiałów są więc
dostatecznie małe, co zapewnia ich przydatność do wykonania warstwy izolacyjnej.
5.2. Charakterystyka materiałów izolacyjnych
Rodzaj materiału izolacyjnego jest uwarunkowany najczęściej temperaturą izolowanej
powierzchni aparatu. W zakresie niskiej temperatury, tj. równej lub mniejszej od tempera
tury powietrza atmosferycznego, stosuje się masę korkową, wytwarzaną przez zmieszanie
zmielonego korka z odpowiednim lepiszczem. Może ona być użyta w postaci odpowiednio
wyprofilowanych kształtek lub w postaci granulatu. Powszechnie stosowanym materiałem
izolacyjnym jest również wata szklana. W praktyce przemysłowej używa się również weł
ny, filcu itp. Górną granicą stosowania tych materiałów jest temperatura zwęglenia, z regu
ły około 100 °C [3]. W zakresie wyższej temperatury poza watą szklaną używa się wełny
żużlowej, okrzemek, masy magnezjowej, azbestu oraz ich mieszanek. Dopuszczalna tem
peratura dla tych materiałów wynosi 600 °C. Izolację odporną na wysoką temperaturę (od
600 do 800 °C) wykonuje się z wypalonej okrzemki, względnie może być tutaj wykorzy
stany żużel wielkopiecowy.
Do podstawowych warunków prawidłowego funkcjonowania izolacji należą: ści
słe dopasowanie warstwy izolacji do ściany aparatu oraz szczelność przed wpływem
atmosfery, zwłaszcza zawilgocenia. W przypadku izolacji pracującej w niskiej tempe

50
raturze temperatura zewnętrznej powierzchni warstwy powinna być wyższa od tempe
ratury punktu rosy powietrza atmosferycznego, aby uniknąć wykraplania się pary
wodnej.
5.3. Ekonomiczna grubość warstwy izolacji
Nałożenie warstwy izolacyjnej zmniejsza straty ciepła, a więc i obniża koszty
jednostkowe ciepła, jednak powoduje zwiększenie kosztów inwestycyjnych. Ekono
miczną grubość izolacji se należy tak wyznaczyć, aby uzyskać minimum sumarycz
nych kosztów ruchowych (tj. ciepła) i kosztów inwestycyjnych. Koszty inwestycyjne
zależą od ceny izolacji, kosztów robocizny na jej ułożenie oraz czasu ich eksploatacji.
Zarówno koszty ruchowe Kr, jak i koszty inwestycyjne K na ogół są liczone w odnie
sieniu do jednego metra bieżącego rurociągu. Roczne koszty inwestycyjne oblicza się
z równania
K, ^ — AV
(5.1)
Te
w którym: ze - czas eksploatacji w latach, A - cena 1 m3 izolacji wraz z ułożeniem na
powierzchni, V - objętość izolacji odniesiona do jednego metra bieżącego rurociągu.
Objętość izolacji może być obliczona z zależności
K
V = —
(^i + 2s2) ^ d 2
= 7t(i22 + ^ li2)
(5-2)
4
Koszty ruchowe, tj. koszty ciepła, można obliczać wg zależności
Kr =CQ'r
(5.3)
gdzie C - cena jednostkowa energii cieplnej, zł/J, r - czas pracy rurociągu w ciągu
roku, s/rok, ()' - straty ciepła, W/m.
Straty ciepła Qr można obliczać na podstawie szczegółowych analiz lub z rów
nania
Q' = bck'(Tw - T z )
(5.4)
w którym
k ' — %kr
(5.5)
W równaniach tych b oznacza bezwymiarowy współczynnik uwzględniający wpływ
różnicy temperatury płynu i otoczenia, c - bezwymiarowy współczynnik uwzględnia
jący wpływ prędkości wiatru, k' - współczynnik przenikania ciepła odniesiony do
51
jed n eg o m etra bieżącego rurociągu. D ane te m ożna odczytać z tabeli 29 w m onografii
H oblera [4],
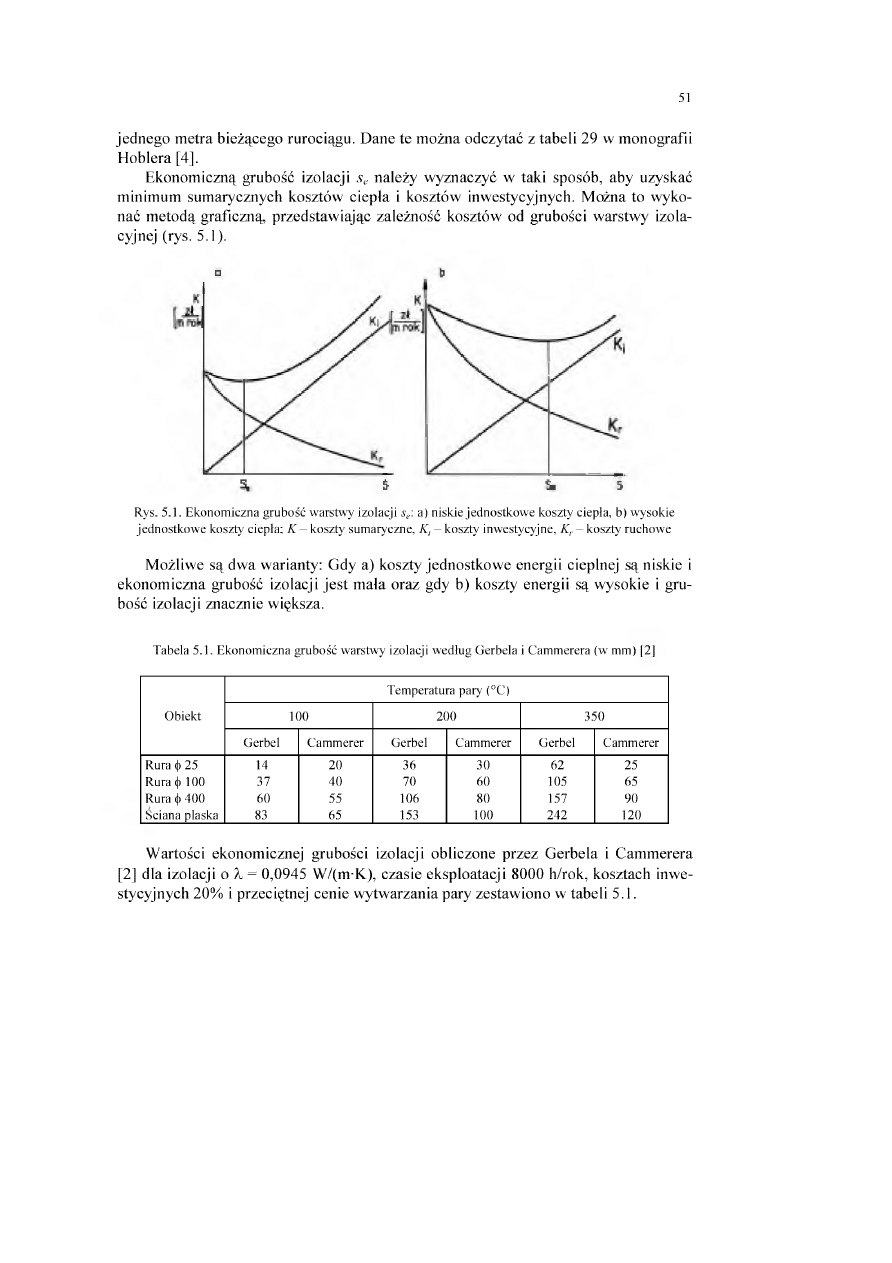
E konom iczną grubość izolacji sc należy w yznaczyć w taki sposób, aby uzyskać
m inim um sum arycznych kosztów ciepła i kosztów inw estycyjnych. M ożna to w yko
nać m eto d ą graficzną, przedstaw iając zależność kosztów od grubości w arstw y izola
cyjnej (rys. 5.1).
a
5
i,
&
Si
£
Rys. 5.1. Ekonomiczna grubość warstwy izolacji sy: a) niskie jednostkow e koszty ciepła, b) wysokie
jednostkow e koszty ciepła; A' - koszty sumaryczne, A, - koszty inwestycyjne, Kr - koszty ruchowe
M ożliw e są dw a w arianty; Gdy a) koszty jedn ostk ow e energii cieplnej są niskie i
ekonom iczna grubość izolacji je s t m ala oraz gdy b) koszty energii są w ysokie i gru
bość izolacji znacznie większa.
Tabela 5.1. Ekonomiczna grubość warstwy izolacji według Gerbela i Cammerera (w mm) |2 |
Obiekt
Temperatura pary (°C)
100
200
350
Gerbel
Camm erer
Gerbel
Cammerer
Gerbel
Cammerer
Rura <|) 25
14
20
36
30
62
25
Rura <|) 100
37
40
70
60
105
65
Rura <|) 400
60
55
106
80
157
90
Ściana plaska
83
65
153
100
242
120
W artości ekonom icznej grubości izolacji obliczone przez G erbela i C am m erera
[2] dla izolacji o X = 0,0945 W /(m-K), czasie eksploatacji 8000 h/rok, kosztach inw e
stycyjnych 20% i przeciętnej cenie w ytw arzania pary zestaw iono w tabeli 5.1.

6.
Przewodzenie ciepła
w warunkach nieustalonych
Zagadnienie przewodzenia ciepła w warunkach nieustalonych ma duże znaczenie
praktyczne w wielu procesach przemysłowych, takich jak np. ogrzewanie lub chło
dzenie materiałów, obróbka cieplna metali, procesy dochodzenia do równowagi ter
micznej aparatów i instalacji. Inną grupę takich procesów stanowią procesy ogrzewa
nia i chłodzenia materiałów w różnego rodzaju aparatach, np. w rekuperatorach,
suszarkach, adsorberach lub reaktorach.
W tych trzech ostatnich urządzeniach, ruch ciepła jest sprzężony z transportem
masy wewnątrz materiału, a niekiedy i z reakcją chemiczną.
6.1. Różniczkowe równanie przewodzenia ciepła
W wielu procesach temperatura ciała zmienia się w czasie i w przestrzeni. Do
rozważań przyjmuje się ograniczone odcinki czasu oraz elementarną objętość ciała.
Otrzymana w ten sposób zależność jest ogólnym równaniem różniczkowym procesu.
W celu wyprowadzenia równania różniczkowego przewodzenia ciepła należy
przyjąć następujące założenia:
• ciało jest homogeniczne,
• parametry fizyczne ciała są stałe,
• odkształcenie rozpatrywanej objętości ciała spowodowane przez zmiany tempe
ratury jest bardzo znikome,
• makroskopowe cząstki ciała są nieruchome,
• wewnętrzne źródła ciepła są rozmieszczone w ciele równomiernie.
Przyjmijmy do analizy prostopadłościan, którego krawędzie są skierowane
równolegle do osi układu współrzędnych i mają długości dx, dy, dz (rys. 6.1).
Temperatura rozpatrywanego prostopadłościanu w danej chwili wynosi T i może
zmieniać się w czasie.

54
y
dx
i
t
i (rJtd
±\
x
Rys. 6.1. Nieustalone przewodzenie ciepła w elemencie w kształcie prostopadłościanu
W celu otrzymania równania przewodzenia ciepła należy ułożyć bilans energe
tyczny prostopadłościanu [5]. Oznaczmy przez dQx, dQy, dQz ilość ciepła dostarczoną
do płaszczyzn prostopadłościanu odległych o x, y i z od osi współrzędnych w czasie
dr w kierunku osi 0x, Oy i Oz (rys.6.1). Ilość ciepła odprowadzoną z powierzchni pro
stopadłościanu odległych od osi układu o x + dx, y + dy oraz z + dz w tym samym
czasie i w tych samych kierunkach oznaczymy przez dQx dx, dQy dy, dQz dz- Ilość cie
pła, jakie dopływa do powierzchni dydz w kierunku osi 0x w czasie dr jest określona
równaniem
Przez powierzchnię odległą od osi y i długości x + dx odpływa w tym samym kie
runku w czasie d r ilość ciepła
Różnica między ilością ciepła dopływającego i odpływającego z prostopadłościa
nu w kierunku osi x w czasie d r jest określona równaniem
Podobnie można wyprowadzić równanie opisujące różnice między ilością ciepła
doprowadzanego i odprowadzanego z prostopadłościanu w pozostałych kierunkach
dOy\ i dQz[.
Sumaryczną ilość ciepła dostarczoną do prostopadłościanu przez przewodzenie
opisuje równanie
dQx - qx dydzd z
(6 .1)
(
6
.
2
)
dOx\ = d(Qx - dQx+dx = qx dydzd r
(6.3)

55
dQi “ (W.i +dQy] + d(J i -■
dqx
dqy dqz
dx
dy
dz
dxdydzdr
(6.4)
Oznaczmy przez dQ2 ilość ciepła wytworzonego wewnątrz tego elementu w cza
sie dr przez wewnętrzne źródło ciepła. Przyjmując za wydajność wewnętrznych źró
deł ciepła qv (W/m3), otrzymamy równanie:
dQ2 ~ q vdVdr
(6.5)
Następnie przyjmiemy, że zmianę energii wewnętrznej ciała o objętości dV w czasie
i/ropisuje równanie
dT
d Q ^ c pp — dVdr
dr
(
6
.
6
)
Korzystając z prawa zachowania energii, według którego ilość energii dostarczona
do elementarnej objętości przez przewodzenie z zewnątrz i z wewnętrznych źródeł cie
pła w czasie dr jest równa zmianie energii wewnętrznej materiału - zgodnie z 1 zasadą
termodynamiki otrzymujemy:
dQt +dQ2 - d Q
(6.7)
Po podstawieniu odpowiednich równań i po przekształceniach otrzymujemy koń
cową postać równania różniczkowego przewodzenia ciepła
ST
dr
zapisywaną również w postaci
cPP
ST
dr
Sqx
dqy
dqz
dx
dy
dz
cpp ^ - divq +q,
cPP
(
6
.
8
)
(6.9)
Wektor gęstości strumienia cieplnego q jest normalny do powierzchni izotermicznej
i jest dodatni w kierunku malejących temperatur. Tak więc wektory q i gradT mają ten
sam kierunek i przeciwny zwrot.
W prostokątnym układzie współrzędnych wektor q ma trzy składowe: qA. q,. qr,
które możemy zapisać za pomocą następujących równań:
. ST
ST
.S T
q x = - x — ,
ą y = - x — ,
ą z = - x —
(X
dy
dz
Po podstawieniu równania (6.10) do równania (6.8) otrzymujemy
ST
Sr
c Pp-~
A K ®
dx v dx
d
ST
X
Sy^ dy
. A K ®
d z \ dz
(6 . 10)
(6.11)

56
Jest to ogólne równanie przewodzenia ciepła w ciele izotropowym z uwzględnie
niem wewnętrznych źródeł ciepła. Równanie to jest nieliniowe, ponieważ współczyn
nik przewodzenia ciepła X jest funkcją temperatury i jego rozwiązanie jest kłopotliwe.
Po przyjęciu stałej wartości współczynnika przewodzenia ciepła równanie (6.11)
można zapisać w następującej postaci:
gdzie V2T - operator Laplace’a. Operator ten we współrzędnych kartezjańskich zapi
sujemy w postaci
Równania (6.12) w uproszczonej postaci są znane w literaturze jako równanie
Fouriera (bez wewnętrznych źródeł ciepła)
równanie Laplace’a (w warunkach ustalonych i bez wewnętrznych źródeł ciepła)
Wyrażenie X!{cpp) o wymiarze (m2/s) jest oznaczane symbolem a i nazywane dy-
fuzyjnością cieplną. Parametr ten, określany również jako współczynnik przewodze
nia temperatury, jest miarą bezwładności cieplnej ciała przewodzącego ciepło. Metale
mają np. duże wartości współczynnika a i temperatura wewnątrz nich szybko się wy
równuje.
Różniczkowe równanie przewodzenia ciepła (6.12) jest zapisywane we współ
rzędnych walcowych lub sferycznych w odniesieniu do ciał o kształcie walcowym lub
kulistym. Operator Laplace’a zapisujemy odpowiednio do przyjętego układu współ
rzędnych:
• dla współrzędnych walcowych (jc = rcosę, y = rsmę, z = z)
£ 1 = ^ _ V 2T + —
(6. 12)
c p p
c p p
V T =
s
2
t
s
2
t
s
2
t
(6.13)
+
+
dx
(Y '
d z 2
(6.14)
równanie Poissona (w warunkach ustalonych)
V2T + — = 0
X
(6.15)
v
2
t
=
o
(6.16)
(6.17)
gdzie r jest promieniem, ę -kątem biegunowym,

57
• dla współrzędnych sferycznych:
V2T=-
ST
2 ST
1
5
(1 —
cos2 0 )
5 2T
(6.18)
ST
1
x
+
S(cos6>) r 2 (1 -c o s 2 0 ) dy/2
gdzie 0 je st odległością biegunową, y/zaś azymutem.
6.2. Warunki jednoznaczności przewodzenia ciepła
Ogólne równanie różniczkowe przewodzenia ciepła opisuje wszystkie możliwe
procesy. Aby podać pełny opis matematyczny określonego procesu, konieczne jest
określenie dodatkowych warunków, tzw. warunków jednoznaczność i. Należą do nich:
1. Warunki geometryczne, charakteryzujące kształt i wymiary ciała, w którym za
chodzi proces przewodzenia ciepła.
2. Warunki fizyczne, tzn. właściwości fizyczne ciała, takie jak przewodnictwo
cieplne, ciepło właściwe, gęstość. Warunki te mogą być wyrażone przez przyjęcie
rozkładu wewnętrznych źródeł ciepła i ich wydajności.
3. Warunki czasowe, które opisują rozkład temperatury w ciele w początkowym
momencie. W ogólnym przypadku dla r = 0
Gdy rozkład temperatury w początkowym momencie jest równomierny, dla r = 0
mamy:
4.
Warunki brzegowe opisujące współdziałanie rozpatrywanego ciała z otocze
niem. Dzielą się one na cztery rodzaje:
• Warunki brzegowe pierwszego rodzaju (Dirichleta): rozkład temperatury na po
wierzchni ciała dla każdego momentu
gdzie: Ts - temperatura powierzchni, x , y , z - współrzędne; w szczególnym przypadku,
gdy temperatura powierzchni pozostaje stała podczas całego procesu ruchu ciepła,
równanie (6.21) upraszcza się do postaci
T = f ( x , y , z )
(6.19)
r = r 0 = const
(
6
.
20
)
Ts = f ( x , y , z , r )
(6.21)
Ts - const
(6.22)

58
• Warunki brzegowe drugiego rodzaju
(Neumanna);
gęstość strumienia cieplnego
w każdym punkcie powierzchni ciała i dla dowolnego czasu jest znana
w szczególnym przypadku gęstość strumienia cieplnego na powierzchni może być
stała w czasie i wówczas
• Warunki brzegowe trzeciego rodzaju (Fouriera); znana jest temperatura otaczają
cego ośrodka oraz zależność, która opisuje wymianę ciepła między ciałem przewo
dzącym ciepło a tym ośrodkiem; wymiana ciepła odbywa się najczęściej na zasadzie
wnikania, promieniowania lub na oba sposoby; proces taki opisuje równanie Newto
na, zgodnie z którym ilość ciepła usunięta z jednostkowej powierzchni ciała w jed
nostkowym czasie jest proporcjonalna do różnicy między temperaturą powierzchni
ciała Ts i temperaturą otoczenia 7)
Ponieważ ta sama ilość ciepła jest przekazywana przez przewodzenie na granicy
ciała, więc zachodzi równość
gdzie: n - normalna do powierzchni ciała, indeks s wskazuje, że temperatura i gra
dient temperatury odnoszą się do powierzchni.
Warunek brzegowy trzeciego rodzaju można zapisać w postaci
• Warunki brzegowe czwartego rodzaju; wymiana ciepła z otoczeniem zachodzi
przez przewodzenie w warunkach doskonałego kontaktu ciał; strumienie cieplne na
powierzchni odgraniczającej ciało i otoczenie są więc jednakowe
(6.23)
qs - q0 =const
(6.24)
q = a(Ts —Tf )
(6.25)
(6.26)
(6.27)
(6.28)
Ogólne równanie różniczkowe wraz z warunkami jednoznaczności daje pełny
opis matematyczny określonego przypadku przewodzenia ciepła. Rozwiązanie takiego
równania można uzyskać analitycznie lub numerycznie.

59
6.3. Analiza przewodzenia ciepła
w warunkach nieustalonych
6.3.1. Wprowadzenie
Przewodzenie ciepła w warunkach nieustalonych należy analizować w odniesie
niu do danego zagadnienia. Uwzględnia się kształt ciała i przyjmuje określone warun
ki brzegowe (por. rozdz. (6.2)).
Po przyjęciu stałej wartości współczynnika przewodzenia ciepła X w razie braku
wewnętrznych źródeł ciepła równanie różniczkowe przewodzenia ciepła we współ
rzędnych kartezjańskich przyjmuje postać
dT
— - a
dr
f d 2 T
ć)~T
yd x 2
d y 2
d z 2 j
(6.29)
Jest to równanie różniczkowe o pochodnych cząstkowych. Do jego rozwiązania
konieczne jest podanie warunków jednoznaczności, charakterystycznych dla rozpa
trywanego przypadku.
6.3.2. Chłodzenie lub ogrzewanie płyty płaskiej
Aby był spełniony warunek, że przewodzenie ciepła zależy tylko od jednej zmien
nej przestrzennej, należy dobrać odpowiednią konfigurację geometryczną. Roz
patrujemy więc przewodzenie w płycie płaskiej, mającej skończoną grubość w kie
runku jednej osi, np.
jc
, rozciągającej się do nieskończoności w dwóch pozostałych
kierunkach. Efekty brzegowe mogą być wówczas pominięte.
Tó
28
Rys. 6.2. Warunki temperaturowe dla nieskończenie długiej płyty płaskiej

60
Przyjmujemy też, że grubość rozpatrywanej chłodzonej płyty wynosi 2 8 (rys. 6.2).
W początkowym momencie r = 0 rozkład temperatury w płycie równomierny, a więc
T = T0 = const. Temperatura otoczenia wynosi Tf. Ciepło jest usuwane z obu po
wierzchni płyty, a współczynniki wnikania ciepła po każdej stronie płyty są jednako
we i stałe w całym procesie.
Wprowadźmy pojęcie nadmiaru temperatury 3, zdefiniowanego jako różnica tem
peratury ciała i temperatury otoczenia
3= T - Tf
Dla jednokierunkowego ruchu ciepła w kierunku osi 0x równanie (6.29) można
sprowadzić do postaci
5 9
^ 9
— = a — —
(6.30)
d r
ek
Warunki początkowe dla r= 0:
3 = T 0- T f = 3 0
(6.31)
Warunki brzegowe zaś dla przypadku przedstawionego na rys. 6.2 mogą być zapi
sane następująco:
• w osi płyty, gdy x = 0
— 1
= 0
(6.32a)
5 x ) x=o
1 na powierzchni płyty, gdy x = 8
^ f ]
=— 9 ^
(6.32b)
5 x ) x=g
X
Równanie różniczkowe (6.30) rozwiązuje się metodą Fouriera. Najpierw poszuku
jemy rozwiązań szczególnych danego równania w postaci iloczynu funkcji, z których
każda zależy od jednej zmiennej, a następnie na podstawie danych warunków brzego
wych określa się wartości stałych występujących w rozwiązaniach szczególnych. Uzy
skane rozwiązanie ma postać albo szeregu utworzonego ze znalezionych rozwiązań
szczególnych, albo całki niewłaściwej o nieustalonych granicach całkowania.
6.3.2.1. Rozwiązanie analityczne równania różniczkowego przewodzenia ciepła
Rozpatrywany problem jest sformułowany przez równanie różniczkowe (6.30),
warunki początkowe (6.31) i warunki brzegowe (6.32a i b). Poszukiwane rozwiązanie
ma postać iloczynu dwóch funkcji, z których jedna jest funkcją czasu r, druga zaś
odległości x
3 - 3(r,x) - ę{r)i//{x)
(6.33)

61
Po podstawieniu funkcji (6.33) do równania (6.30) otrzymujemy nową postać
równania różniczkowego
— — y/{x) - a----- — ę{r)
(6.34)
dr
dx
1
Po rozdzieleniu zmiennych otrzymujemy równanie
(635,
<p{r)
y/(x)
w którym lewa strona jest funkcją czasu, prawa zaś funkcją odległości
jc
.
Ponieważ równanie (6.35) musi być spełnione dla dowolnych wartości
jc
i
r ,
obie
jego strony musza być równe tej samej stałej, którą zapiszemy jako -k 2:
( 6 3 6 )
a <p(T)
w
( *)
Kolejne równania różniczkowe przyjmą wówczas postać:
ę \ v )
+ ak
2
~ 0
(6.37)
+ k
2
^ 0
(6.38)
ę>(r)
¥ " { x )
y/{x)
Stałą k wyznacza się z warunków brzegowych, znak minus natomiast musi być przyję
ty dla procesów ruchu ciepła zmierzających do równowagi cieplnej.
Rozwiązaniem równania (6.37) jest funkcja <p(r) - Qe~ak T, rozwiązaniem
równania (6.38) natomiast jest funkcja typu y/{x) = C
2
sm{kx) + C
3
cos(kx).
Po podstawieniu funkcji <p(r) i y/{x) do równania wyjściowego (6.33) otrzymu
jemy nowe równanie
& - [C2 sin(&r) + C3 cosifaiOjCie^ r
(6.39)
Równanie (6.39) spełnia równanie (6.30) dla każdej wartości stałych Ci, C2, C
3
i k. Stałe te należy wyznaczyć z warunków początkowych i brzegowych.
Rozważmy warunek brzegowy (6.32a): dla v = 0, (d3/dx)x = o= 0. Po zróżniczko
waniu równania (6.39) otrzymamy
,
—
-C }erak zk\CiCO${fa')-C
3
sin(fcc)l n =0
ÄA=o
lub
C2 cos(0) = C3sin(0),
C2 = 0

62
Oznacza to, że rozwiązanie yĄx) = C
2
sin(
0
) musi być odrzucone ze względu na
niespełnienie warunków brzegowych.
Mając na uwadze, że C
2
= 0 oraz oznaczając C
1
C
3
= A, równanie (6.39) możemy
przekształcić do postaci
3 ^ A e ~ ak
2
l cos(kx)
(6.40)
Rozpatrzmy następnie warunek brzegowy (6.32b):
f)
Jx=s
V 4-
Jx=s
Po obliczeniu pochodnej {d&ldx) z równania (6.40) i podstawieniu do wyrażenia
na warunek brzegowy otrzymujemy
k. tc ,,k': sin{ k S ) ^ - A Q - ak2z cos(M )
(6.41)
X
a stąd
kfi
ctg ( k S ) = —
(6.4 la)
ao
~ T
Po wprowadzeniu liczby Biota
B i = —
(6.42)
X
oraz wyrażenia kS= /¿równanie (6.4la) uprości się do postaci
ctgfi = —
(6.43)
Bi
Dla każdej wartości liczby Biota istnieje nieskończenie wiele rozwiązań. Po pod
stawieniu ctgfi = y] oraz fjJBi = y
2
otrzymamy wartości pierwiastków równania (6.43)
(rys. 6.3). Jak wynika z wykresu 6.3, istnieje nieskończona liczba rozwiązań dla /jn,
a każda kolejna wartość jest większa od poprzedniej
M \ < M 2 < M 3 < • • • • < Mn
Każdej wartości liczby Biota odpowiadają określone pierwiastki równania (6.43).
Dla Bi =
00
linia y
2
= fjJBi pokrywa się z osią/i, w związku z czym pierwiastki są miej
scami zerowymi funkcji ctgfi
n
3
5
71
= ~ ,
Bi = ~ x ,
••••
i«« = ( 2 « - l ) -

63
Dla Bi = O (prostay
2
= fjJBi pokrywa się z o siąj) pierwiastki równania (6.43) są
następujące: a = 0, a = n, a =
/jn = { n - 1 )n, gdzie n = 1, 2, 3,... . Dla innych
wartości liczby Biota wartości a są pośrednie. Dla każdego pierwiastka
j u j ,
a
,
A
> . . . ,
A ,
otrzymujemy odpowiednią postać funkcji (6.40)
&\ - Ą cos|
/
ą
— |exp
v
(6.44)
/
Z zależności tej wynika, że funkcje Ą, A, .$*
3
, ..., i9„ są liniowo niezależne
i rozwiązanie ogólne równania pierwotnego należy przedstawić w postaci szeregu
nieskończonego
& = ^ 4 , cos( a - |je x p ^ A 7 p -
(6.45)
Stałe Aj, A2, ..., A„ wyznaczamy z warunku początkowego (6.31); dla r = 0, 3 = $j,
więc
= F (x ) = ^
4
j cos( Aj —
(6.46)
Stalą A„ wyznaczamy jako całkę:
4, =■
A
j
J ( A
j
+ s i n A
j
c o s
A
j
)
J
F (x )c o s| A
j
^ 1 ^
(6.47)
An jest zatem funkcją wyłącznie pierwiastków równania (6.43) i początkowego roz
kładu temperatury F(x).

64
Po podstawieniu wyrażenia na stałą A„ (6.47) do równania (6.45) otrzymamy osta
teczną postać funkcji określającej pole temperatury w chłodzonej płycie jednorodnej:
n
Mn
8
( j u n + s i n / ^ C O S JUn )
f
7
ar
- J e x p ^ Ar -
J F ( x ) c o s ^ „ ^jdx
(6.48)
xcos| jun —
|exp|
-jun
^
Jeżeli w początkowym momencie procesu ( r = 0) profil temperatury w płycie jest
płaski (jak na rys. 6.2), tzn. T
0
- T f = 3 = const, to całka w równaniu (6.47) jest równa
(Ą18//jn)s'm/jn i równanie (6.47) przyjmuje postać
^ = ^
I s r n j ^
(6 49)
Mn + sm M„c°$M„
Po podstawieniu tego równania do równania (6.48) otrzymamy inną postać funk
cji opisującej pole temperatury w chłodzonej (lub ogrzewanej) płycie
& = J
3o2sm/j„
^ l e x p f -pin
(6.50)
^ /i„ + s m /i„ c o s /i„
V.
S )
\
8
~ )
Równanie to wygodniej jest analizować w postaci bezwymiarowej. Po wprowa
dzeniu zmiennych bezwymiarowych: temperatury bezwymiarowej Y = 3/Ą, współ
rzędnej bezwymiarowej X = x
!8
oraz bezwymiarowej liczby Fouriera Fo = az/S
2
otrzymamy ostateczną, bezwymiarową postać równania
r = V
2 Sm
cos(/i„X)exp(^/i„2Fo)
(6.51)
^ Mn + sm Mn
C O S
Mn
6.3.2.2. Omówienie rozwiązania równania różniczkowego
przewodzenia ciepła w nieskończonej płycie płaskiej
Ponieważ szereg opisany równaniem (6.51) jest szybko zbieżny dla liczby Fourie
ra Fo > 0,3, więc równanie to z dostateczną dokładnością możemy przybliżyć za po
mocą pierwszego wyrazu szeregu (« = 1), uzyskując uproszczoną postać równania
bezwym ¡arowego
Y - £>! cos(//lX )e x p (-//l2Fo)
(6.52)
gdzie
A =
.
M\ + sm M\ cosM\
2 ^ ,
( ^
3)

65
Ponieważ wielkości ¡
ą
zależą od liczby bezwymiarowej Biota, więc I)¡ jest rów
nież funkcją liczby Biota i jej wartości mogą być stabelaryzowane.
Rozpatrując graniczne przypadki w osi płyty, gdy X = x/d = 0 oraz cos(/ąO) = 1
i na powierzchni płyty, gdy X = x/d= 1 oraz cos(/ą 1) = cos/ą, oraz oznaczając iloczyn
Z)]cos(0) w osi płyty jako funkcję N(Bi), otrzymamy
Yx=(j - N(Bi)exp(-/u
2
Fó)
(6.54)
Jeżeli natomiast przyjmiemy, że na powierzchni płyty iloczyn A cos(/ą) jest funkcją
P( Bi), to otrzymamy
Yx=x=P(Bi)exp(-n?Fo)
(6.55)
Z równań tych wynika, że temperatura bezwymiarowa Y jest funkcją dwu liczb bez
wymiarowych: liczby Biota i liczby Fouriera. Po zlogarytmowaniu równań (6.54)
i (6.55) otrzymamy
\nY
x=0
= \ n N ( B i ) - f i \2Fo
(6.56)
ln Yx=l = ln P(Bi) - /a2Fo
(6.57)
Logarytm naturalny temperatury bezwymiarowej jest zatem liniową funkcją czasu.
Daje to możliwość rozwiązania równań (6.54) i (6.55) metodą graficzną.
6.3.2.3. Analiza nieustalonego przewodzenia ciepła podczas chłodzenia płyty
Na podstawie wyprowadzonych równań (6.56) i (6.57) można obliczyć tempera
turę na płaszczyźnie symetrii płyty i na jej powierzchni, co pokazano na rys. 6.4 i 6.5.
Wykresy te ilustrują zależność bezwymiarowej temperatury Y= ( T - T,)/(T„ - Tf) od
liczby Fouriera Fo = ar/d'' oraz liczby Biota Bi = ad/Z. Wszystkie te wielkości sta
nowią moduły podobieństwa.
Z rozwiązania równania różniczkowego przewodzenia ciepła wynika, że rozkład
temperatury w płycie chłodzonej opisuje krzywa symetryczna z maksimum w osi płyty,
tzn. dla X = 0 (rys. 6.6). Kolejnej wartości czasu odpowiada kolejna krzywa malejąca
w kierunku powierzchni płyty. Przedłużenia stycznych do krzywych rozkładu tempera
tury w płycie w punkcie X = ± 1 przechodzą przez dwa punkty biegunowe A i-A , znaj
dujące się w odległości ±X
0
od powierzchni płyty; można wykazać, że X
0
= ± 1 [5].
Graficzną postać ogólnego rozwiązania różniczkowego równania przewodzenia
ciepła w nieskończonej płycie płaskiej pokazano na rys. 6.7. Wykres ten ilustruje
zależność bezwymiarowej temperatury Y = (T - I))/(!], - Tf) od liczby Fouriera
Fo = ar/d2, odwrotności liczby Biota MBi = X/(ad) = m oraz liczby podobieństwa
geometrycznego n = x/d. Wszystkie te wielkości są modułami podobieństwa.
66
Rys. 6.4. Zależność graficzna Yv=0= f l(Bi, Fo) dla nieskończonej płyty
Rys.
6 .5.
Zależność graficzna
fy = i
=f>(Bi, Fo) dla nieskończonej płyty
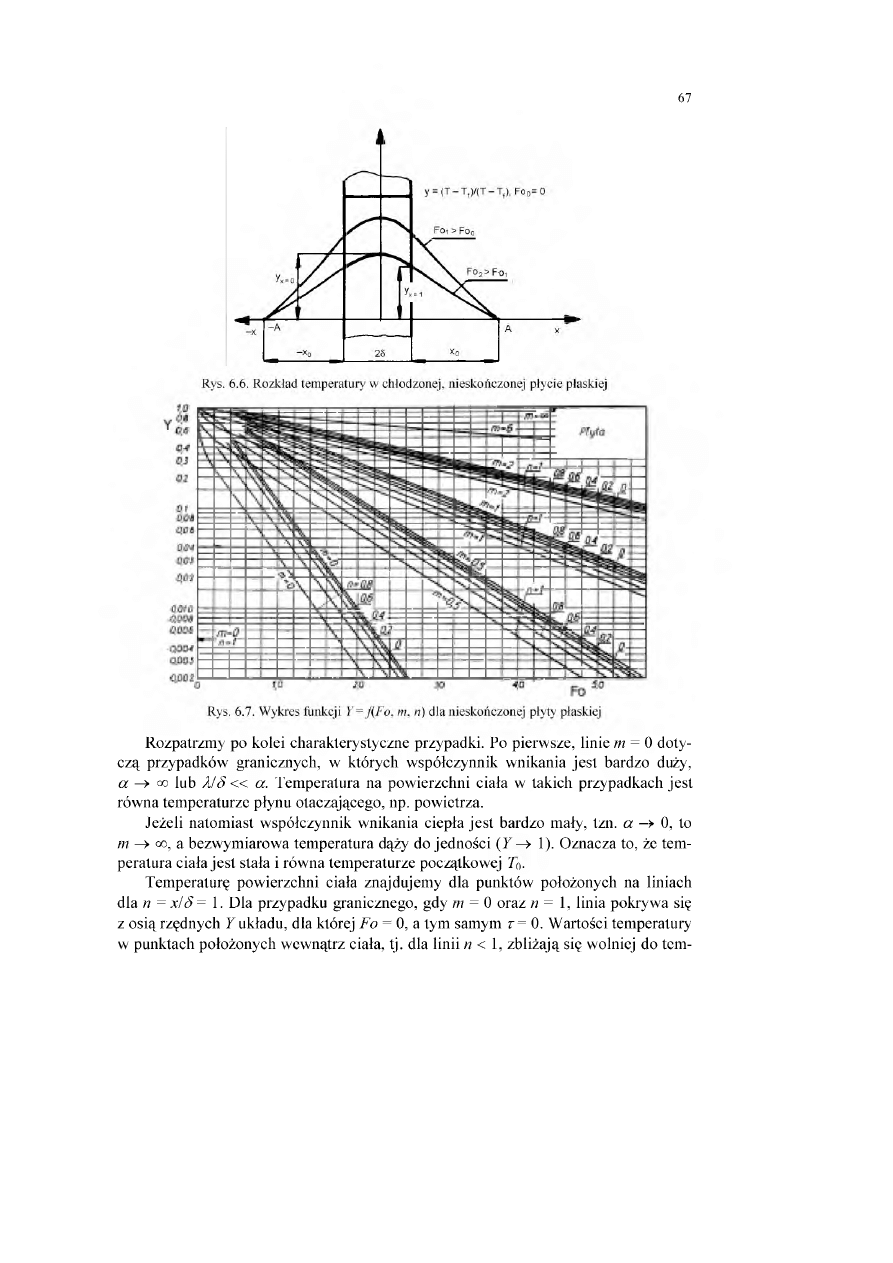
67
Rozpatrzmy po kolei charakterystyczne przypadki. Po pierwsze, linie m = 0 doty
czą przypadków granicznych, w których współczynnik wnikania jest bardzo duży,
ol
—> oo lub X15 « a. Temperatura na powierzchni ciała w takich przypadkach jest
równa temperaturze płynu otaczającego, np. powietrza.
Jeżeli natomiast współczynnik wnikania ciepła jest bardzo mały, tzn. a -» O, to
m —>
oo,
a bezwymiarowa temperatura dąży do jedności (7 —> 1). Oznacza to, że tem
peratura ciała jest stała i równa temperaturze początkowej 70.
Temperaturę powierzchni ciała znajdujemy dla punktów położonych na liniach
dla n = x/S= 1. Dla przypadku granicznego, gdy m = O oraz n = 1, linia pokrywa się
z osią rzędnych 7 układu, dla której Fo = O, a tym samym r= 0. Wartości temperatury
w punktach położonych wewnątrz ciała, tj. dla linii n < 1, zbliżają się wolniej do tern-

68
peratury medium otaczającego i stąd linie dla m = 0 i n < 1 są już nachylone pod pew
nym kątem, co odpowiada liczbom Fouriera większym od zera (a stąd dla r > 0 ).
Temperaturę na płaszczyźnie symetrii płyty (n = 0) w warunkach bardzo dobrej
konwekcji (m = 0) można opisać przybliżonym równaniem:
Ypl =i,273e-2-303 - ^ -
(6.58)
P
0,933
W zakresie niewielkich liczb Fouriera trudno jest odczytać z wykresu na rys. 6.7
dokładną wartość temperatury bezwymiarowej Y; należy się wówczas posłużyć od
powiednimi tabelami (por. np. tabele 33-35 w monografii łłoblera [4]), lub równanie
rozwiązać analitycznie.
6.3.3. Chłodzenie lub ogrzewanie cylindra nieskończonego
W odniesieniu do cylindra (walca) można przyjąć następujące założenia:
• cylinder o promieniu R oddaje ciepło do otoczenia,
• współczynnik wnikania ciepła jest stały dla całej powierzchni,
• temperatura otoczenia jest stała,
• temperatura we wszystkich punktach cylindra jest jednakowa w początkowym
momencie.
Dla stałych warunków brzegowych można wyeliminować zmienną z, sprowadza
jąc zagadnienie do dwuosiowego przewodzenia. Po przekształceniu równania (6.29)
do współrzędnych walcowych z zastosowaniem równań:
x = rcosę
(6.59)
oraz
y = rsm ę
(6.60)
otrzymujemy równanie o prostszej postaci
93
— - a
Sr
f 9r3
1 9 3 ^
dr
1
r dr
(6.61)
Warunki brzegowe i początkowe są następujące:
• dla r= 0 oraz 0 < r < R
3 = 3, = ’/i, ’/'/ = const
(6.62)
• d la r = 0 i r> 0
'd&'
1
r=0
,
=0
(6.63)
dr
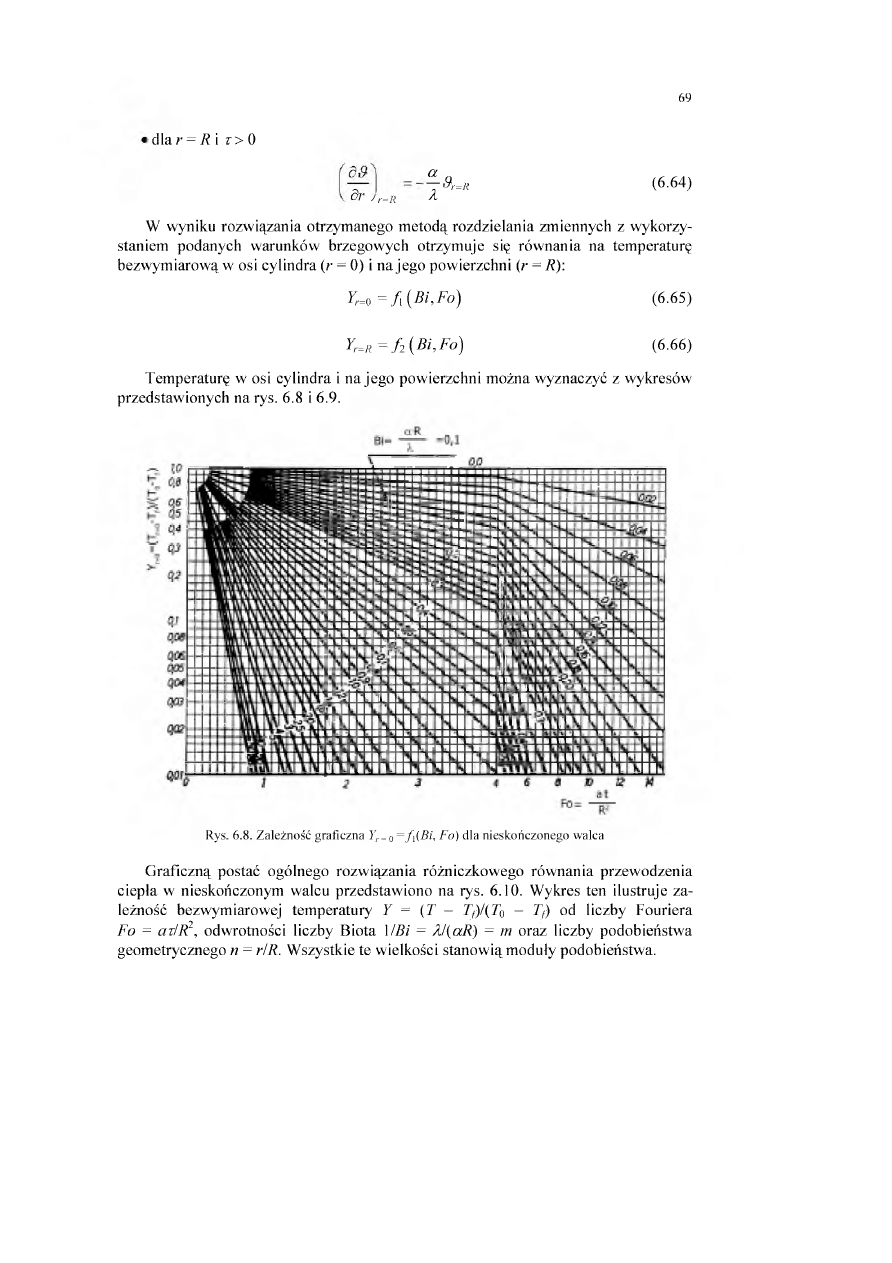
69
1
dla r = R i r > O
5/* / r=fi
a
T
■9,v=yi
(6.64)
W w yniku rozw iązania otrzym anego m eto d ą rozdzielania zm iennych z w ykorzy
staniem podanych w arunków brzegow ych otrzym uje się ró w n an ia n a tem peraturę
bezw ym iarow ą w osi cylindra {r = 0) i n a jeg o pow ierzchni (r = R ):
Yr=0 = f ( B i , F o )
(6.65)
Yr=R = f Ą B i , F o )
(
6
.
66
)
T em peraturę w osi cylindra i n a jeg o pow ierzchni m ożna w yznaczyć z w ykresów
przedstaw ionych n a rys. 6.8 i 6.9.
Rys. 6.8. Zależność graficzna }). = 0 = f\(B i, Fo) dla nieskończonego walca
G raficzną postać ogólnego rozw iązania różniczkow ego rów nan ia przew odzenia
ciepła w nieskończonym walcu przedstaw iono n a rys. 6.10. W ykres ten ilustruje za
leżność bezw ym iarow ej tem peratury Y = ( T - Tf)/(T0 - Tt) od liczby F ouriera
Fo = ar/ R2, odw rotności liczby B iota \!Bi = X!{aR) = m oraz liczby podobieństw a
geom etrycznego n = r/R. W szystkie te w ielkości stano w ią m oduły podobieństw a.
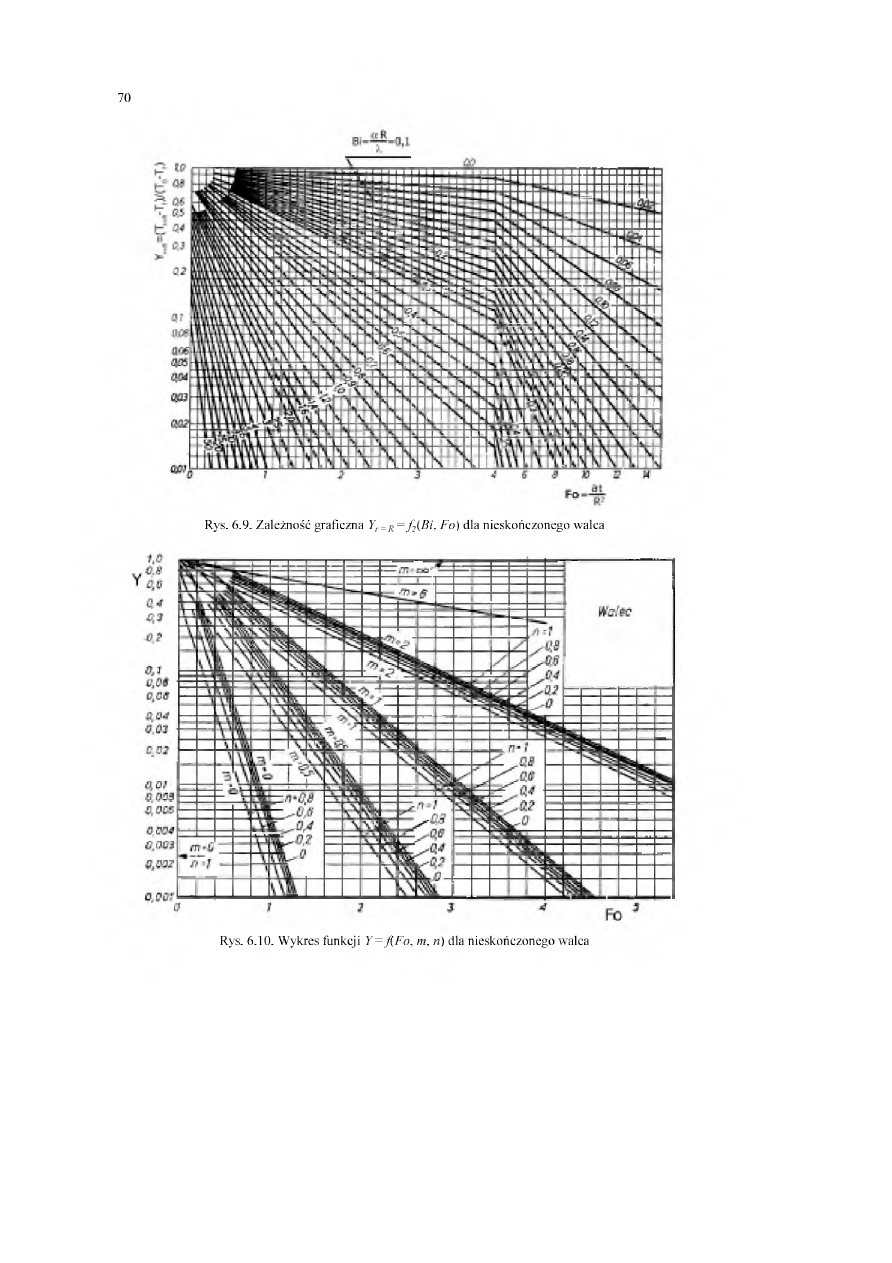
70
Rys. 6.9. Zależność graficzna Yr = R =fo(Bi, Fo) dla nieskończonego walca
Rys. 6.10. W ykres funkcji Y = f ( F o , m, n) dla nieskończonego walca

71
Temperaturę na osi symetrii walca (« = 0) w warunkach bardzo dobrej konwekcji
(.m = 0) można opisać przybliżonym równaniem
Yw ~ l,602e-2,303 —
(6. 67)
0,398
W zakresie niewielkich liczb Fouriera trudno jest odczytać z wykresu (rys. 6.10)
dokładną wartość temperatury bezwymiarowej Y; należy się posłużyć odpowiednimi
tabelami (np. tabele 33-35 w monografii łłoblera [4]).
6.3.4. Chłodzenie lub ogrzewanie kuli
Zanalizujmy chłodzenie kuli o promieniu i? umieszczonej w ośrodku o stałej tem
peraturze. Wartość współczynnika wnikania ciepła od powierzchni kuli do otoczenia
jest również stała. W początkowym momencie temperatura kuli w dowolnym punkcie
wynosi T0.
Załóżmy, że nadmiar temperatury 3 = T - Tf. Równanie różniczkowe przewodze
nia ciepła w kuli przekształcone do współrzędnych sferycznych przyjmie następującą
postać:
d3
— - a
Sr
i d13 2 d 3 ^
d r
r dr j
(
6
.
68
)
Warunki początkowe dla r = 0 są następujące:
• dla 0 < r < R
3 = 3*= T * -T f
(6.69)
warunki brzegowe zaś
• dla r = R (powierzchnia kuli)
l a 3
(6.70)
1 dla r = 0 (środek kuli)
d r )r = R
U
J r=R
^
= 0
(6.71)
dr
J r
= 0
Z rozwiązania równania (6.68) metodą rozdzielenia zmiennych z uwzględnieniem
warunków początkowych i brzegowych otrzymuje się zależności funkcyjne od liczb
bezwym ¡arowych:
• dla środka kuli (r/R = 0)

Yr=0 = Fo (Bi, Fo)
(6.72)
• dla powierzchni kuli (r/R = 1)
Yr=R = Fp (Bi, Fo)
(6.73)
oraz w dowolnym punkcie kuli
Yr = F (Bi, Fo, r / R )
(6.74)
Temperaturę w środku kuli i na jej powierzchni można wyznaczyć z wykresów przed
stawionych na rys. 6.11 i rys. 6.12.
72
Rys. 6.11. Zależność graficzna
Yr
= 0 =
f 1(Bi
,
Fo)
dla kuli
Fo
Rys. 6.12. Zależność graficzna
Yr=R
=
f 2(Bi, Fo)
dla kuli
Graficzną postać ogólnego rozwiązania różniczkowego równania przewodzenia
u-
struje zależność bezwymiarowej temperatury Y = (T - Tf)/(T
0
- Tf) od liczby Fouriera
Fo = at/R2, odwrotności liczby Biota m = 1/Bi = X/(aR) oraz liczby podobieństwa
geometrycznego n = r/R. Wszystkie te wielkości stanowią moduły podobieństwa.
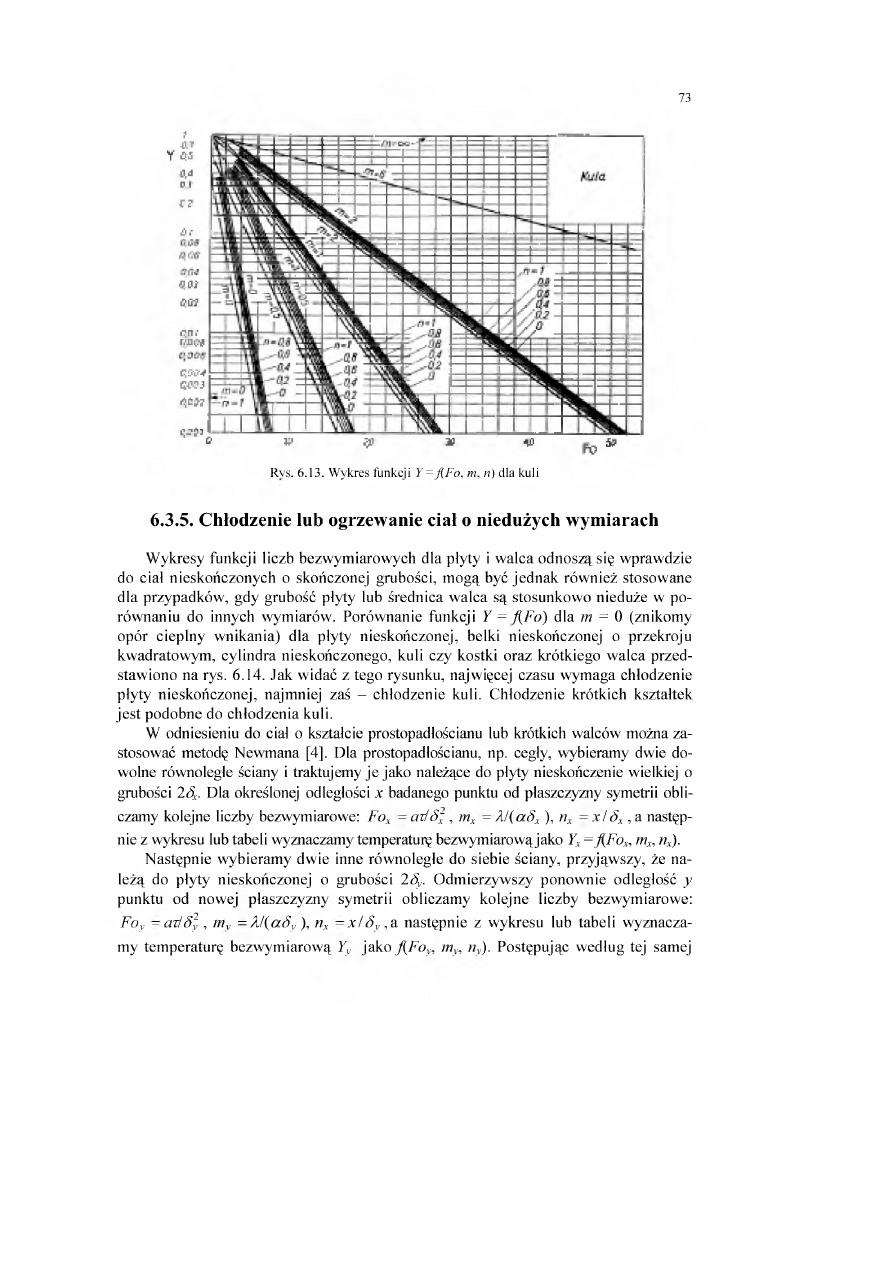
73
i
■cu
Y í J
ax
V I
i
?
¿>
. ■
■
qoí
ÍQ?
r;n.-
r.'-ni/J
GSM
GÍVJ
víffT
ĘJJ]
p
w
ÍÜ
»
^
ho 47
Rvs. 6.13. Wykres funkcji
Y=j[Fo, m, n)
dla kuli
6.3.5. Chłodzenie lub ogrzewanie ciał o niedużych wymiarach
W ykresy funkcji liczb bezw ym iarow ych dla płyty i w alca odnoszą się w praw dzie
do cial nieskończonych o skończonej grubości, m o g ą być je d n a k rów nież stosow ane
dla przypadków , gdy grubość płyty lub średnica w alca są stosunkow o nieduże w p o
rów naniu do innych w ym iarów . Porów nanie funkcji
Y = j { F o )
dla
m
= O (znikom y
opór cieplny w nikania) dla płyty nieskończonej, belki nieskończonej o przekroju
kw adratow ym , cylindra nieskończonego, kuli czy kostki oraz krótkiego w alca przed
staw iono n a rys. 6.14. Jak w idać z tego rysunku, najw ięcej czasu w ym aga chłodzenie
płyty nieskończonej, najm niej zaś - chłodzenie kuli. C hłodzenie krótkich kształtek
je s t podobne do chłodzenia kuli.
W odniesieniu do cial o kształcie prostopadłościanu lub krótkich walców m ożna za
stosować metodę Newm ana [4]. Dla prostopadłościanu, np. cegły, wybieramy dwie do
wolne równolegle ściany i traktujemy je jako należące do płyty nieskończenie wielkiej o
grubości
2SX.
Dla określonej odległości
x
badanego punktu od płaszczyzny symetrii obli
czamy kolejne liczby bezwymiarowe:
F o x - ar!8 ;
,
m x - A /( a S x
),
nx - x / S x
, a następ
nie z wykresu lub tabeli wyznaczamy temperaturę bezwym iarową jako
Yx = j{F ox, mx, nx).
N astępnie w ybieram y dw ie inne rów nolegle do siebie ściany, przyjąw szy, że n a
leżą do płyty nieskończonej o grubości 2
Sv.
O dm ierzyw szy ponow nie odległość
y
punktu od now ej płaszczyzny sym etrii obliczam y kolejne liczby bezw ym iarow e:
F o v - a r ! d l
,
m v ~ A / ( a S v
),
n x - x / S Y
, a następnie z wykresu lub tabeli w yznacza
m y tem peraturę bezw ym iarow ą
Yv
jak o
j{ F o v, m v, n v).
Postępując w edług tej samej
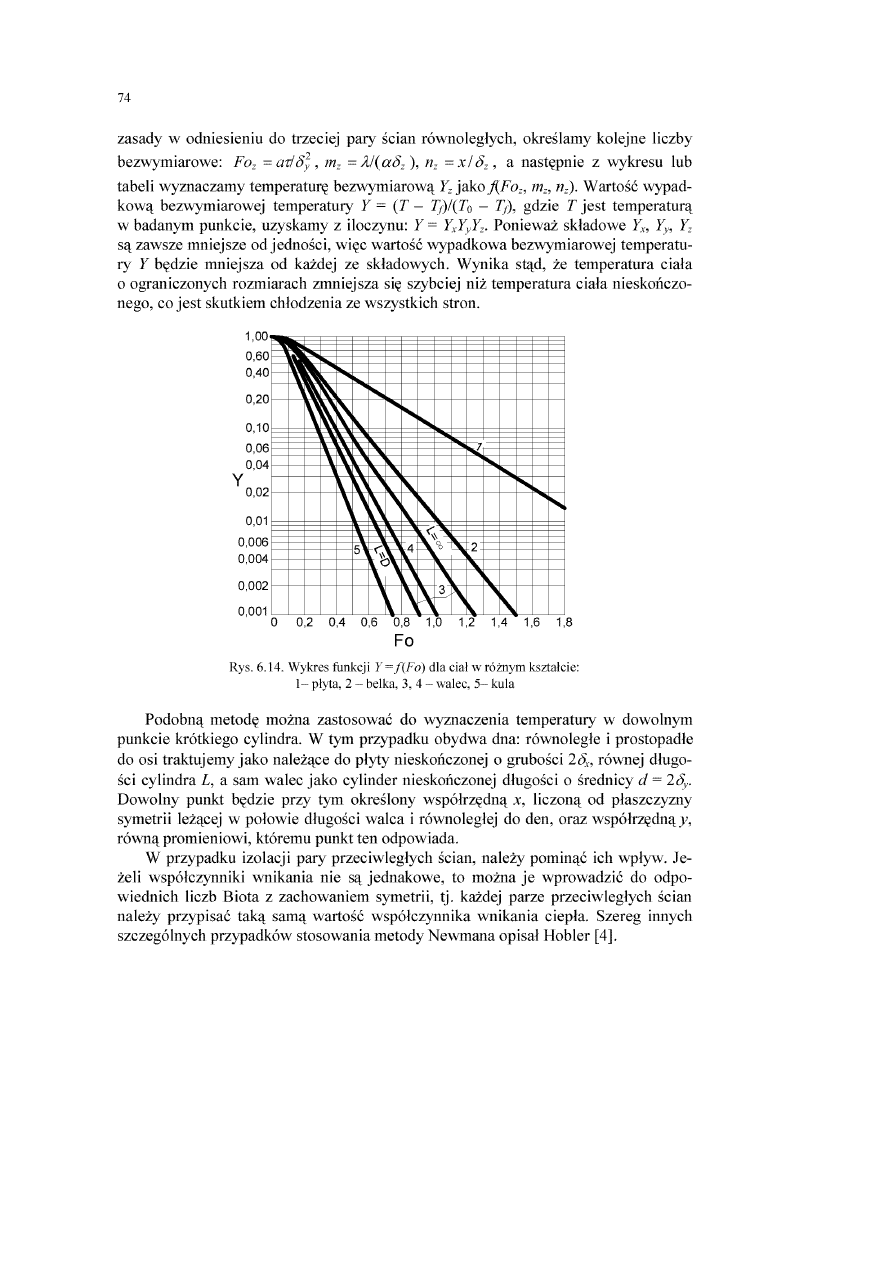
74
zasady w odniesieniu do trzeciej pary ścian równoległych, określamy kolejne liczby
bezwymiarowe: Foz -a rfS y , mz - Xl(a
8
z ), n: - x / S z , a następnie z wykresu lub
tabeli wyznaczamy temperaturę bezwymiarową Yz jako j{Foz, mz, nz). Wartość wypad
kową bezwymiarowej temperatury Y = (T - T,)/(T„ - T,). gdzie T jest temperaturą
w badanym punkcie, uzyskamy z iloczynu: Y= YxYyYz. Ponieważ składowe Yx, Yy, Yz
są zawsze mniejsze od jedności, więc wartość wypadkowa bezwymiarowej temperatu
ry Y będzie mniejsza od każdej ze składowych. Wynika stąd, że temperatura ciała
o ograniczonych rozmiarach zmniejsza się szybciej niż temperatura ciała nieskończo
nego, co jest skutkiem chłodzenia ze wszystkich stron.
Y
1
,
0 0
*
0
,
6 0
:
0
,
4 0
:
0
,
2 0
0
,
1 0
:
0
,
0 6
:
0
,
0 4
:
f
0
,
0 2
-
0,01
:
0,006
:
0,004
:
0,002
0,001
I
s
--- —— — — --- — — — — — --- — — —
\v P W —— — — --- --- — ------ — --- --- --- ---
k\
w
k\
1
3
s
Y W
V
s
S
s
1
.
% ik V \
\
r \
3
--- ------ V l \ \ | V — --- — — —3sZ— --- ---------
\
r
r \
V
3
s
r
s
\
N
\ \
>
s V
V
V
— ------ — —V 5
V
>
N t— --- — — — —
--- ------ — — 5^ r~\
% -
\
2
--- --- --- --- —
\
r v
k
_
\
\
V \
k \
>
\
\ N
73
;
i
\
\
\
0
0,2
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8
Fo
Rys. 6.14. Wykres funkcji
Y=f(Fo)
dla ciał w różnym kształcie:
1 - płyta, 2 - belka, 3 , 4 - walec, 5 - kula
Podobną metodę można zastosować do wyznaczenia temperatury w dowolnym
punkcie krótkiego cylindra. W tym przypadku obydwa dna: równoległe i prostopadłe
do osi traktujemy jako należące do płyty nieskończonej o grubości 28X, równej długo
ści cylindra L, a sam walec jako cylinder nieskończonej długości o średnicy d = 25y.
Dowolny punkt będzie przy tym określony współrzędną jc, liczoną od płaszczyzny
symetrii leżącej w połowie długości walca i równoległej do den, oraz współrzędną^,
równą promieniowi, któremu punkt ten odpowiada.
W przypadku izolacji pary przeciwległych ścian, należy pominąć ich wpływ. Je
żeli współczynniki wnikania nie są jednakowe, to można je wprowadzić do odpo
wiednich liczb Biota z zachowaniem symetrii, tj. każdej parze przeciwległych ścian
należy przypisać taką samą wartość współczynnika wnikania ciepła. Szereg innych
szczególnych przypadków stosowania metody Newmana opisał Hobler [4].

75
6.3.6.
Rozwiązanie równania Fouriera
dla ustalonego przewodzenia ciepła w ścianie płaskiej
Z agadnienie ustalonego przew odzenia ciepła w ścianie płaskiej stanow i p od sta
w owy przykład ruchu ciepła [3, 4, 6]. Z analizujm y przypadek, gdy ściankę o pływ ają
dw a płyny różniące się tem p eratu rą (rys. 6.15).
T ransport ciepła przebiega:
• przez konw ekcję od strum ienia płynu gorącego o tem peraturze Tf] do p ow ierzch
ni ścianki o tem peraturze Ts],
• przez przew odzenie w ew nątrz ścianki,
• przez konw ekcję od pow ierzchni ścianki o tem peraturze Ts2 do strum ienia płynu
zim nego o tem peraturze Tf2,
Rozkład tem peratury w ściance m ożem y określić, rozw iązując rów nanie różnicz
kow e F ouriera z zastosow aniem odpow iednich w arunków granicznych.
W przypadku ustalonego przew odzenia w kierunku osi x rów nanie to przyjm uje
postać rów nania L ap lace’a
I“ - *
Rys. 6.15. W arunki tem peraturow e dla ściany płaskiej
(6.75)
R ów nanie to całkujem y dw ukrotnie
(6.76)

76
\ ^ H
x
= \ Q
c
I
x
(6.77)
J dx
J
otrzymując rozwiązanie w końcowej postaci
T (
x ) = C {x + C 2
(6.78)
Stałe całkowania Ci i C
2
wyznaczamy z warunków granicznych (rys. 6.15). Po
podstawieniu dla a- = 0, T{0) = Ts] otrzymujemy
Ti, =C 2
(6.79)
Podobnie dla a- = s, T(s) = T
s2
ptrzymamy
T
s2
- Q s + C
2
- Q s + Ts]
(6.80)
Po przekształceniu wyznaczymy stałą Ci:
C,
(6.81)
s
Po wprowadzeniu wyrażeń (6.79) na stałą C
2
oraz (6.81) na stałą Ci otrzymujemy
końcową postać równania
T ( x ) - —^ — —^-x + Ts]
(6.82)
s
Temperatura zmienia się zatem liniowo z odległością
jc
. Z równania (6.82) otrzymu
jemy definicję gradientu temperatury w postaci pochodnej
Ł Z k z Z k
(6.83)
dx
s
Na tej podstawie możemy określić gęstość strumienia ciepła:
q = - l ^ - = - { T s, - T s2)
(6.84)
dx
s
oraz strumień przewodzonego ciepła
Q = - X A ^ =— {T
s
, - T s2)
(6.85)
dx
s
Powierzchnia ściany płaskiej A jest stała i prostopadła do kierunku ruchu ciepła.

77
6.3.7. Rozwiązania równania Fouriera dla charakterystycznych
przypadków nieustalonego przewodzenia ciepła
W wielu przypadkach ścisłe całkowanie różniczkowego równania Fouriera daje
bardzo skomplikowane zależności funkcyjne, które jednak można wyrazić jako zależ
ności od liczb Biota i Fouriera. Poniżej podano kilka przykładów przybliżonych roz
wiązań [3].
Płyta o dużej powierzchni i temperaturze początkowej
T0
znajduje się w ośrodku
o temperaturze
Tf.
Przyjęcie, że płyta ma dużą powierzchnię umożliwia pominięcie
wpływu zaburzeń w polu temperaturowym płyty, jakie występują w pobliżu krawędzi.
Przyjmuje się na ogół, że stosunek powierzchni bocznych Ab do powierzchni A jest
bardzo mały (około 1%).
Jeżeli współczynnik przewodzenia ciepła płyty jest duży (A,—*
q o ),
a temperatura
ośrodka jest wyższa od temperatury początkowej płyty (7)>
T0),
to różniczkową ilość
ciepła wnikającą do płyty opisuje równanie:
Przykład 1
dQ = aA(Tf - T )d r
(
6
.
86
)
gdzie
T
jest temperaturą płyty w danym momencie.
Temperatura płyty wzrośnie zgodnie z następującym równaniem
(10 = mcp dT
Z porównania równań (6.86) i (6.87) wynika:
(6.87)
a A^Tf - T ^ d r - m c pdT
(
6
.
88
)
Po podstawieniu
m - V p
(6.89)
otrzymujemy
aA(Tf - T ) d r - VpcpdT
(6.90)
W równaniu tym rozdzielamy zmienne
a A
dT
d r ~ --------
pcP V
Tf - T
(6.91)
i całkujemy w granicach od ro do r oraz od
Ta
do
Tr.
Otrzymujemy

78
a A ,
,
,
Tf - T r
p c p V
( r - r 0 ) = - l n
( 6 .9 2 )
rO
Jeżeli uw zględnim y, że VIA = s, gdzie s je s t grubością płyty ogrzew anej je d n o
stronnie, p o ło w ą zaś grubości płyty ogrzew anej dw ustronnie, a tem peraturę n a p o
czątku procesu oznaczym y p rzez T0, to po przekształceniach otrzym am y następ ującą
zależność
In Y - ln
Tf - T
Tf ^ T
0
a
pep '
(6.93)
Otrzymujemy zależność wykładniczą dla bezwymiarowej temperatury Y = (Tf— T)/(Tf - T0)
Y ~ e pCp S
(6.94)
Rys. 6.16. Rozkład tem peratury w płycie o nieskończenie
dużym współczynniku przew odzenia ciepła
Rozkład tem peratury w om aw ianym przypadku pokazano n a rys. 6.16. Jak w idać,
gdy X =
oo,
m ożna zaniedbać spadek tem peratury w płycie.
Przykład 2
Podobnie ja k uprzednio przyjm ujem y, że w spółczynnik przew odzenia je s t bardzo
duży, ale m a skończoną w artość i spadek tem peratury w płycie m ożna zaniedbać.
R ów nanie (6.94) m ożna zastosow ać jed y n ie z pew nym przybliżeniem
Y = e
p c ,,s
(6.95)

79
Licznik i mianownik wykładnika prawej strony mnożymy przez As
a s X
t
Y = e Xpc”ł
Po wprowadzeniu definicji liczb bezwymiarowych Bi i Fo otrzymujemy
Dla r = 0, Fo = 0 oraz 7 = 1 , tym samym T= T„. Dla r=
qo,
F
o
= oo, 1
samym T=Tf.
(6.96)
(6.97)
= 0, a tym

7. Ruch ciepła przez konwekcję
7.1. Wprowadzenie
W rozdziałach 3 i 4 omówiono konwekcyjny ruch ciepła. Wprowadzono podsta
wowe pojęcia dotyczące mechanizmu wnikania i przenikania ciepła oraz definicję
współczynnika wnikania ciepła opartą na prawie Newtona. Wnikanie ciepła jest uwa
runkowane występowaniem laminamej warstewki granicznej w pobliżu ściany omy
wanej przez płyn. Zjawisko to obejmuje zarówno przewodzenie ciepła w warstewce
granicznej płynu, jak i transport energii wewnątrz strumienia płynu w wyniku kontak
tu elementów płynu o większej energii (tzw. gorących elementów płynu) z obszarem
0 mniejszej energii, tj. obszarem zimnym. Wyróżniamy konwekcję wymuszoną, jeżeli
ruch płynu odbywa się pod działaniem sił zewnętrznych w postaci różnicy ciśnienia
wytworzonej np. za pomocą pompy czy wentylatora. Jeśli natomiast ruch płynu jest
spowodowany tylko różnicą gęstości, np. w wyniku różnicy temperatury, to transport
ciepła w tych warunkach jest określany jako konwekcja naturalna (swobodna). Poda
no też podstawowe definicje współczynnika wnikania ciepła i omówiono sposoby
jego wyznaczania. Wyróżniono metodę doświadczalną i metodę analityczną określa
nia tego współczynnika.
Analityczne wyznaczanie współczynnika wnikania ciepła a wymaga opisu trój
wymiarowego ruchu płynu, tzn. określenia trzech składowych prędkości, temperatury
1 ciśnienia płynu oraz jego gęstości jako funkcji położenia i czasu. Do wyznaczenia
tych sześciu niewiadomych konieczne jest sformułowanie sześciu równań. Dwa pod
stawowe równania różniczkowe stanowią prawa zachowania masy i energii. Kolejne
trzy równania można otrzymać z prawa ruchu Newtona w kierunku każdej współrzęd
nej. Są to równania Naviera-Stokesa. Równanie stanu płynu daje ostatnie równanie.
Rozwiązanie wymaga jednoczesnego rozwiązania wszystkich równań, co może oka
zać się niemożliwe. Dla uproszczenia ruch płynu będzie rozpatrywany jedynie w dwu
kierunkach, co umożliwia wyeliminowanie jednej zmiennej niezależnej i jednej nie
wiadomej. Można też założyć, że płyn jest nieściśliwy, tzn. jego gęstość jest stała, co
pozwala wyeliminować kolejną niewiadomą i do opisu przepływu niezbędne są tylko
cztery równania.

82
7.2. Podstawy teorii wnikania ciepła
7.2.1. Różniczkowe równanie ruchu ciepła - równanie energii
Rozpatrzymy proces wnikania ciepła od ścianki do płynu przepływającego
wzdłuż ściany (rys. 7.1). W wyniku wytworzenia się laminarnej warstewki granicznej
krzywe rozkładu prędkości płynu i temperatury w zależności od odległości od ściany
przyjmują kształt paraboli, spłaszczonej w większej od niej odległości (w strefie poza
warstwą graniczną).
Rys. 7.1. Rozkład prędkości i temperatury
w ogrzewanym płynie opływającym ścianę płaską
Ponieważ proces wnikania ciepła obejmuje również jego przewodzenie w cien
kiej, laminarnej warstwie granicznej, więc można dla niej zastosować równanie
Fouriera
q - - X
f d T \
dy
(7.1)
gdzie y jest normalną do powierzchni ciała.
Gdy zmiany temperatury zachodzą tylko w kierunku współrzędnej prostopadłej
do powierzchni ciała, jak na rys.7.1, normalna jest współrzędnąy.
Zgodnie z prawem Newtona natomiast dla wnikania ciepła obowiązuje równanie
(7.2)
Po przyrównaniu równań Fouriera i Newtona otrzymujemy definicję współczynnika
wnikania ciepła:
X
f d T \
a ■
T s - T f
dy
(7.3)
Zastosowanie tego wyrażenia wymaga znalezienia pochodnej temperatury wzglę
dem odległości od ściany w pobliżu powierzchni ciała. Tym samym należy wyznaczyć
temperaturę płynu T w każdym punkcie pola przepływu. Należy więc sformułować

83
dla przepływu dwukierunkowego płynu nieściśliwego czwarte równanie podstawowe
poza równaniem ciągłości i równaniem Naviera-Stokesa. Jest to tzw. równanie ener
gii, niekiedy nazywane równaniem Fouriera-Kirchhoffa. Aby je wyprowadzić, przyj
mujemy następujące założenia:
Płyn jest nieściśliwy i jednorodny, nie występują wewnętrzne źródła ciepła, cie
pło wydzielane w płynie w wyniku tarcia może być zaniedbane, a całe ciepło dostar
czone do rozpatrywanego elementu płynu jest zużytkowane na zmianę entalpii.
Rozpatrzymy elementarny prostopadłościan o wymiarach dx, dy, dz. Założymy, że
płyn w tym elemencie ma stałe parametry X, cp i p (rys. 7.2). W celu określenia bilan
su różniczkowej ilości ciepła oddawanej przez ten element należy zdefiniować po
szczególne jego składowe dla trzech kierunków jc, y, z. Ilość ciepła dostarczona do
elementarnego prostopadłościanu wzdłuż osi
jc
w jednostkowym czasie dt wynosi
Różnica między ilością ciepła dopływającego i odpływającego w kierunku
jc
wynosi
Rys. 7.2. Nieustalony ruch ciepła
w elemencie w kształcie prostopadłościanu
dQx - qxdydzdt [J]
ilość ciepła zaś opuszczającego ten element w tym samym kierunku
(7.4)
[J]
(7.5)
dx
dx
Podobnie dla pozostałych kierunkowy i z otrzymujemy
dQx i =dQx - dQx+dx = - ^ - d x d y d z d t = - ^ - d V d t
(7.6)
dQy1 = dQy - dQy+dy = - % - dVdt
dy
(7.7)
dQz\ ~dQz - dQz+dz = - % dVdt
(7.8)

84
Po zsumowaniu równań (7.6)-(7.8) otrzymujemy wyrażenie na całkowitą ilość
ciepła dostarczoną do elementu płynu:
dQ = dQx, +dO,t + </£>., = - i ^ L + ^ L + ^
ox
oy
oz
Zgodnie z założeniem ciepło to jest zużywane na zmianę entalpii
dVdt
(7.9)
Po przyrównaniu ostatnich dwóch równań otrzymujemy następujące równanie
pcP
d_T_
dt
\
dx
dy
dz
lub
dT
pcp — = -d i\i/
dt
(7.10)
(7.11)
(7.12)
Należy teraz rozważyć składowe gęstości strumienia ciepła qx, q.. qz. Jeżeli założymy,
że ciepło jest przenoszone w płynie zarówno przez przewodzenie, jak i konwekcję
otrzymujemy następujące wyrażenie dla kierunku jc
q.x
</•,;• 4" qx„
(2-13)
Zgodnie z prawem Fouriera gęstość przewodzonego strumienia ciepła opisuje równanie
dT
q xx
2
dx
W • m
(7.14)
Przyjmiemy, że gęstość strumienia masy na jednostkę powierzchni normalnej do kie
runku przepływu dla kierunku
jc
wynosi pwx. Otrzymamy wyrażenie na składową gę
stości konwekcyjnego strumienia ciepła:
qxa = pcpwxT,
W • nT2
(7.15)
Po zsumowaniu otrzymujemy składową gęstości strumienia ciepła w kierunku w
T
,dT
qx =pcpwxT - A —
dx
Postępując podobnie dla kierunkowy i z otrzymujemy
dT
qy =pc pwyT - X-
dy
(7.16)
(7.17)
oraz

85
qz - pcpwzT - X
dT_
dz
(7.18)
Po zróżniczkowaniu ostatnich trzech równań otrzymujemy pochodne gęstości
strumienia ciepła:
1
dla kierunku jc
1 dla kierunkuj
1 dla kierunku z
dx
%■
dy
%
dz
8
T ^ dwx
: P c p \ W x ~ r + T ~ a
d x
d x
a
d2T
d x2
-pcP
dT m dwv
- + T-
dy
dy
-A
d2T
dy
dT
dwz
a
d2T
dz
2
(7.19)
(7.20)
(7.21)
Po podstawieniu pochodnych (7.19)-(7.21) do równania (7.11) otrzymujemy
dT
.
dt
f d2T drT d
2
T '
s dx
(";)•
( rh
PCPT
dz
~pcP Wr
dT_
dx
■
+ ir,
dT_
dy
■
+ w.
dT_
dz
r cmx
dwy
dw>, ^
+ — — + — -
dx
dy
dz
(7.22)
Jest to ogólna postać równania energii. Przyjmując, że dla cieczy nieściśliwych
dwx
dwy
dw
dx
r r
dz
■
=
0
(7.23)
otrzymujemy po przekształceniach następującą postać równania
dT_
dt
-+WX
dT_
dx
■ + Wy
dT_
dy
■ + w.
dT
A
dz
cpp
d T d T d T
— r H— r H— ~
dx
dy
dz
(7.24)
Jest to równanie energii, zwane równaniem Fouriera-Kirchhoffa, opisujące rozkład
temperatury w przepływającym płynie nieściśliwym.
Wielomian po lewej strony równania (7.24) jest różniczką zupełną temperatury po
czasie. Jeżeli T = f(x ,y, z, t), to
DT
dT d T d x dT dy
8
T dz
Dt
dt dx dt
dy dt
dz dt
(7.25)
gdzie pochodne chddt, dy/dt, i dz/dt stanowią składowe prędkości wx, wy i wz.
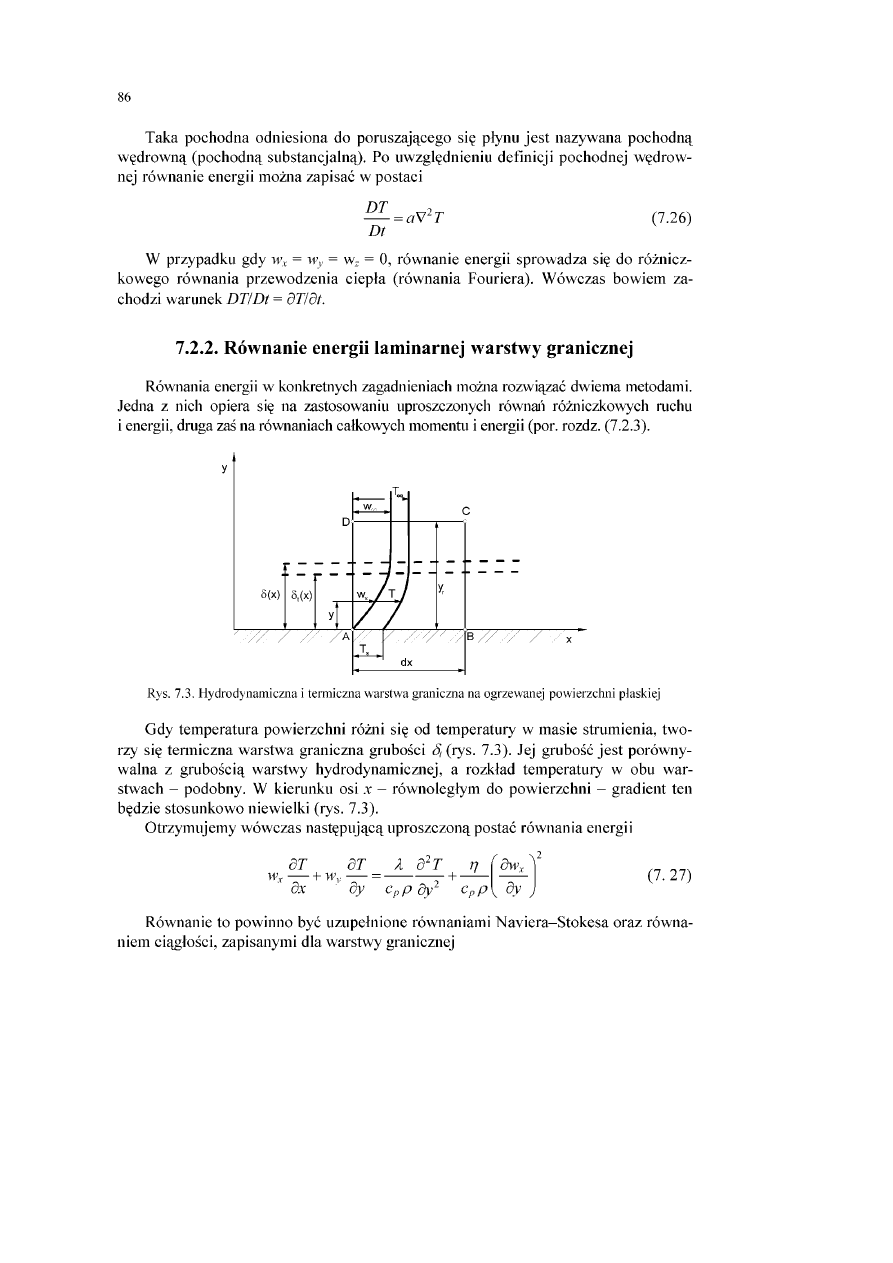
86
Taka pochodna odniesiona do poruszającego się płynu jest nazywana pochodną
wędrowną (pochodną substancjalną). Po uwzględnieniu definicji pochodnej wędrow
nej równanie energii można zapisać w postaci
DT
= aV2T
(7.26)
Dt
W przypadku gdy wx = wy = w- = 0, równanie energii sprowadza się do różnicz
kowego równania przewodzenia ciepła (równania Fouriera). Wówczas bowiem za
chodzi warunek DT/Dt = dT/dt.
7.2.2. Równanie energii laminarnej warstwy granicznej
Równania energii w konkretnych zagadnieniach można rozwiązać dwiema metodami.
Jedna z nich opiera się na zastosowaniu uproszczonych równań różniczkowych ruchu
i energii, druga zaś na równaniach całkowych momentu i energii (por. rozdz. (7.2.3).
Rys. 7.3. H ydrodynamiczna i term iczna warstwa graniczna na ogrzewanej powierzchni płaskiej
Gdy temperatura powierzchni różni się od temperatury w masie strumienia, two
rzy się termiczna warstwa graniczna grubości
8
t (rys. 7.3). Jej grubość jest porówny
walna z grubością warstwy hydrodynamicznej, a rozkład temperatury w obu war
stwach - podobny. W kierunku osi x - równoległym do powierzchni - gradient ten
będzie stosunkowo niewielki (rys. 7.3).
Otrzymujemy wówczas następującą uproszczoną postać równania energii
dT_
dx
dT
X d2T
rj
+ •
'd W r '2
dy
cpp dy
2
cpp
dy
(7. 27)
Równanie to powinno być uzupełnione równaniami Naviera-Stokesa oraz równa
niem ciągłości, zapisanymi dla warstwy granicznej

87
<V,
w.
■ + Wy ■
<v.
dp
d
2
wx
■
+ v-
dx
dy
dx
Qy~
dwx , Qwy
dx
dy
■
=
0
(7.28)
(7.29)
7.2.3. Równanie całkowe energii laminarnej warstwy granicznej
Dla laminarnej warstwy granicznej bilans energii możemy również przedstawić
w postaci całkowej. Analizy zagadnienia dokonujemy na przykładzie bilansu energii
dla elementarnej długości dx termicznej warstwy granicznej.
Na rysunku 7.3 pokazano przepływ płynu wzdłuż ogrzewanej powierzchni o stałej
temperaturze Tw. Rozważamy objętość kontrolną ograniczoną punktami ABCD o jed
nakowym wymiarze b w kierunku prostopadłym do płaszczyzny rysunku. Przyjmuje
my, że energia doprowadzana przez konwekcję oraz ciepło przenoszone przez po
wierzchnię o temperaturze Tw są równe energii odprowadzonej przez konwekcję.
Energia doprowadzona przez przekrój AD wynosi
, p b j wxTdy
(7.30)
Energię odprowadzoną przez przekrój CD opisuje wyrażenie
cppb
V 0
j r
^
yr
j w xTdy + — cpp b j w xTdy
v
dx
(7.31)
Gęstość strumienia płynu w przekroju CD wynosi
cnTx
d_
dx
j
dx
(7.32)
Energię dostarczoną do objętości kontrolnej z tym strumieniem wyrazimy za po
mocą równania:
d_
dx
Ar
j
dx
(7.33)
zmianę gęstości strumienia ciepła na drodze dx powierzchni AB zaś
(
d q w - - / J
h
I
x
f d T '
u
( 7 .3 4 )

88
Po podstawieniu równań (7.30)- (7.34) do równania bilansu energetycznego
otrzymamy
d x - Abdx
cppb \w xTdy+ CpT^pb— f wxdy
o
" H o
y'
d f
y'
= cpp b f w xTdy + — cpp b j wxTdy
(7.35)
dx
Biorąc pod uwagę, że dlay >
8
, temperatura jest wyrównana i równa Tx, za górną
granicę całkowania można przyjąć grubość termicznej warstwy granicznej:
Ą-
f
(Tx -T )w xdy--
d x J
A r d T '
r d T '
o
C p p ^ d y )
Równanie to można również zapisać w postaci
v
Jw
(7.36)
d_
dx
Ut
j
(Tx - T)wxdy -■
cPP
(7.37)
Otrzymane całkowe równanie energii można również zastosować dla burzliwej
warstwy granicznej po wprowadzeniu odpowiedniej gęstości strumienia cieplnego [5].
7.2.4.
Rozwiązanie równania energii
laminarnej warstwy granicznej na płycie płaskiej
Zagadnienia ruchu ciepła z zastosowaniem teorii warstwy granicznej Prandtla
można rozwiązywać dwiema metodami [5]. Pierwsza opiera się na wykorzystaniu
uproszczonych równań różniczkowych ruchu ciepła i energii, druga zaś, mniej do
kładna, ale również często przydatna, na równaniach całkowych momentu i energii.
Równanie energii w warstwie granicznej rozwiązał Pohlhausen w 1921 r. Wyzna
czył on profile prędkości i rozkład temperatury w warstwie granicznej oraz współ
czynniki wnikania ciepła na płycie. Korzystając z rozwiązania równań ruchu płynu
otrzymanego wcześniej przez Blasiusa, Pohlhausen opisał profil prędkości w war
stwie granicznej następującym wielomianem
wx
Wg
'■Cło "ł" &}
+
Cł-y
fzY
UJ
+
Cł
3
(7.38)
w którym stałe określił w ten sposób, aby były spełnione warunki brzegowe
wt (y = 0) = 0
(7.39)

89
przy ścianie oraz na granicy warstwy
w.t {y = 3) = ws
a także
t y )y-s
(7.40)
(7.41)
oraz warunek przyścienny z równania pędu (Naviera-Stokesa)
= 0
f
^
O W,
dy
(7.42)
7
y= S
Z analizy warunków brzegowych wynika, że stałe wynoszą: a
0
= a
2
= 0, u\ = 3/2,
a3 = -1/2 i równanie (7.38) przyjmuje postać
wx
3 y 1
we
2 5 2
(7.43)
Grubość warstwy granicznej opisano zależnością
z
V/2
vx
\ W s )
- 4,64-
1/2
(7.44)
Podobnym wielomianem Pohlhausen opisał profil bezwymiarowej temperatury
V _ T - T S
y
Y
—--------------—
b g
+
b ]
--------H
b 2
T„ - T s
Sr
'
f y
^ 2
ySr j
+ bg
f y ^
ySr j
z zastosowaniem warunków brzegowych przy ścianie
Y y = g
= 0
(7.45)
(7.46)
r d
2
Y '
' <>" Jy=0
= 0
oraz następujących warunków brzegowych na granicy warstwy
Y ( y = Sr ) = \
r d Y _ "
ty jy .
= 0
(7.47)
(7.48)
(7.49)
y=ST
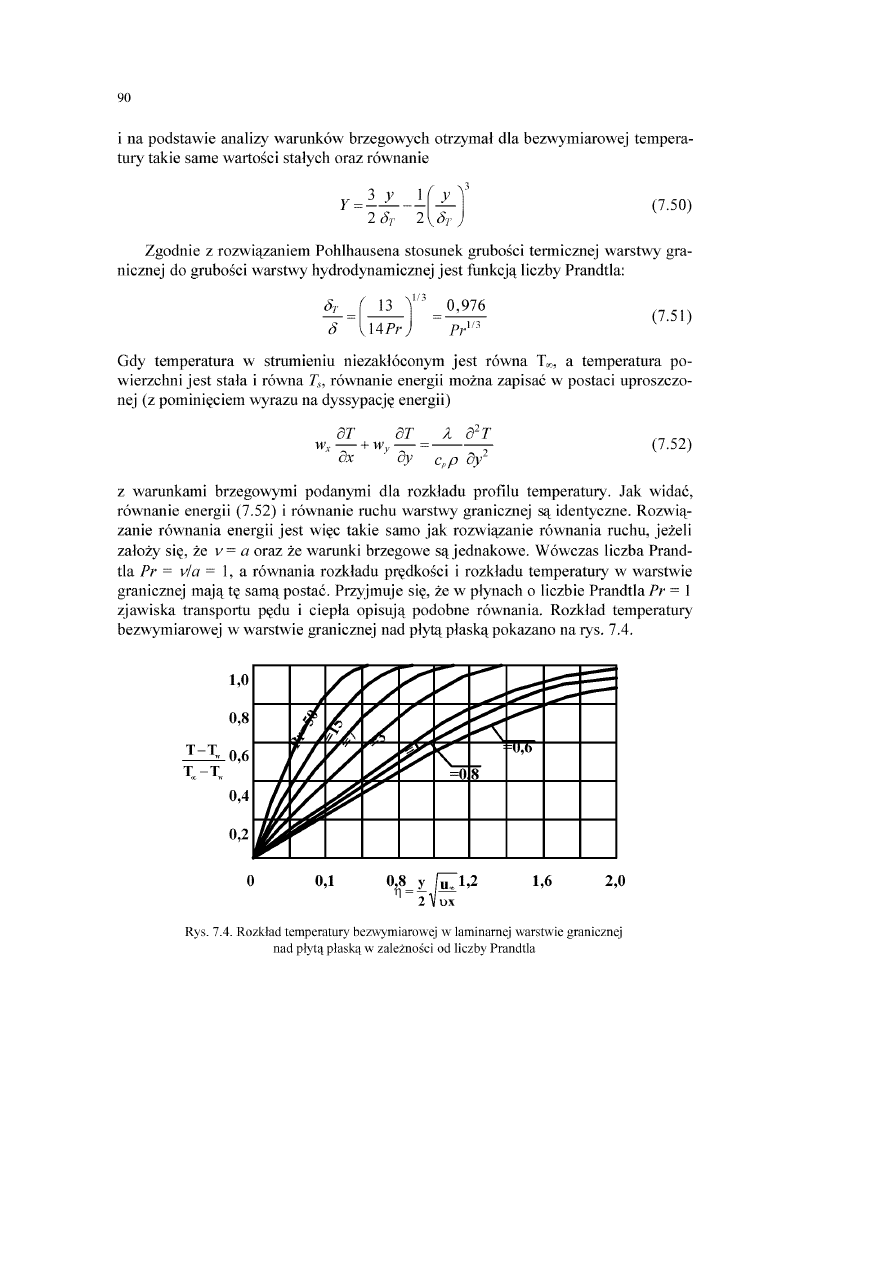
90
i na podstawie analizy warunków brzegowych otrzymał dla bezwymiarowej tempera
tury takie same wartości stałych oraz równanie
2 S r
2
ySr J
(7.50)
Zgodnie z rozwiązaniem Pohlhausena stosunek grubości termicznej warstwy gra
nicznej do grubości warstwy hydrodynamicznej jest funkcją liczby Prandtla:
Sr_
S
13
n
1/ 3
14 p r
0,976
(7.51)
Gdy temperatura w strumieniu niezakłóconym jest równa T„, a temperatura po
wierzchni jest stała i równa Ts, równanie energii można zapisać w postaci uproszczo
nej (z pominięciem wyrazu na dyssypację energii)
Wr
dT_
dx
■ + Wy
dT
A d~T
dy
cp p dy
2
(7.52)
z warunkami brzegowymi podanymi dla rozkładu profilu temperatury. Jak widać,
równanie energii (7.52) i równanie ruchu warstwy granicznej są identyczne. Rozwią
zanie równania energii jest więc takie samo jak rozwiązanie równania ruchu, jeżeli
założy się, że v= a oraz że warunki brzegowe są jednakowe. Wówczas liczba Prand
tla Pr = v!a= 1, a równania rozkładu prędkości i rozkładu temperatury w warstwie
granicznej mają tę samą postać. Przyjmuje się, że w płynach o liczbie Prandtla Pr = 1
zjawiska transportu pędu i ciepła opisują podobne równania. Rozkład temperatury
bezwymiarowej w warstwie granicznej nad płytą płaską pokazano na rys. 7.4.
Rys. 7.4. Rozkład tem peratury bezwymiarowej w laminarnej warstwie granicznej
nad płytą płaską w zależności od liczby Prandtla
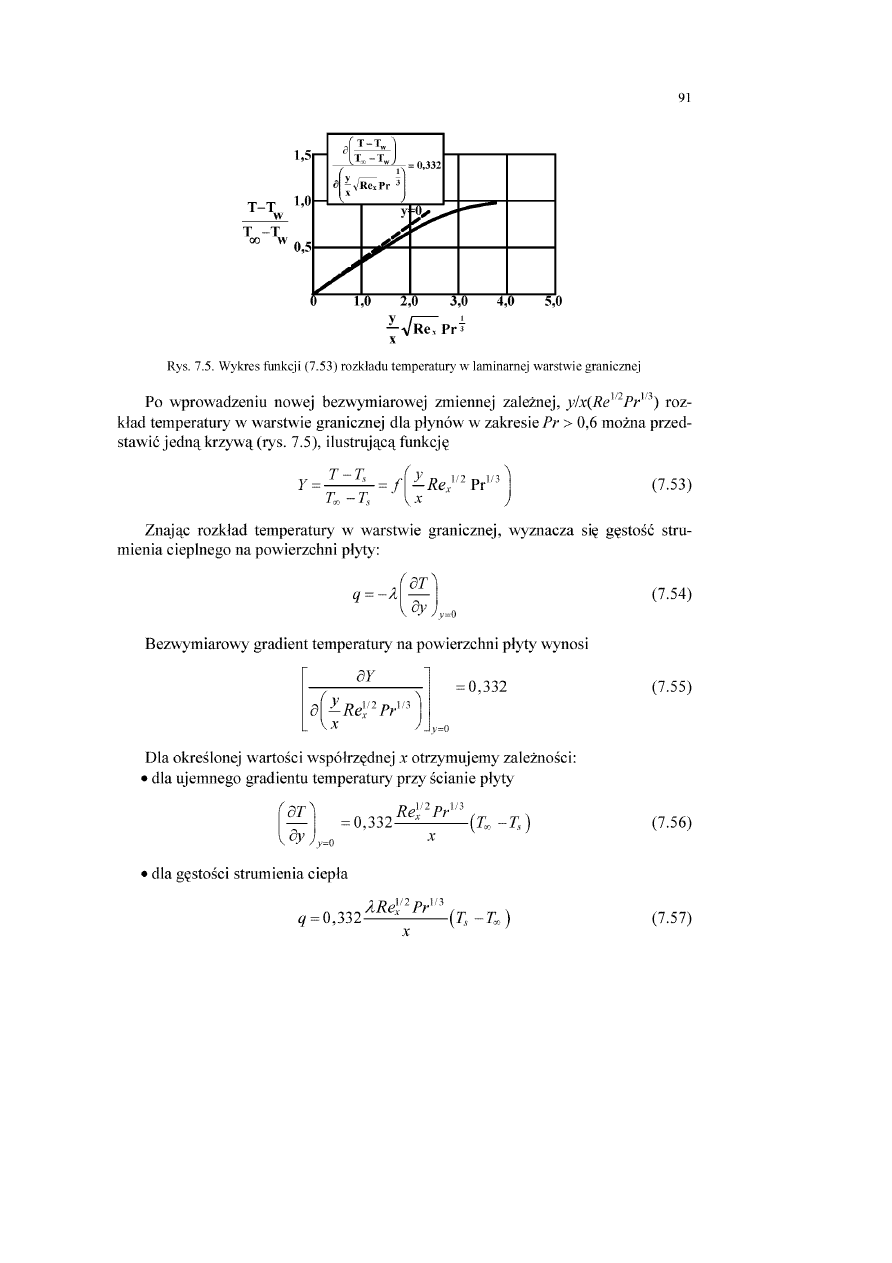
91
Rys. 7.5. W ykres funkcji (7.53) rozkładu tem peratury w laminarnej w arstwie granicznej
Po wprowadzeniu nowej bezwymiarowej zmiennej zależnej, y/x(Re]l
2
Pr]l3) roz
kład temperatury w warstwie granicznej dla płynów w zakresie Pr > 0,6 można przed
stawić jedną krzywą (rys. 7.5), ilustrującą funkcję
T ^ T S
T - T
1 c o
1 S
= f
y
12 n
1/ 3
R e ' Pr
(7.53)
Znając rozkład temperatury w warstwie granicznej, wyznacza się gęstość stru
mienia cieplnego na powierzchni płyty:
q - - A
r d T '
\ d y ) y =0
Bezwymiarowy gradient temperatury na powierzchni płyty wynosi
dY
(7.54)
51 —Rei
12
Pr
113
-0,332
(7.55)
r=o
Dla określonej wartości współrzędnej
jc
otrzymujemy zależności:
• dla ujemnego gradientu temperatury przy ścianie płyty
f d T \
0
1 dla gęstości strumienia ciepła
Re
= 0,332— i---------{T * -T s )
(7.56)
O Re1/2 P r y 3
g =0,332AK—
e Pr
[T
s
-T,»)
(7.57)

92
• dla współczynnika wnikania ciepła
a x = — - — = 0,332- R e x 2PrV3
(7.58)
Ts - T
k
x
Po wprowadzeniu liczby Nusselta (Nux = axx!X) otrzymuje się równanie bezwy
miarowe
Nux =0,332Rex
2
Pr
113
(7.59)
Średni współczynnik wnikania ciepła dla płyty długości L otrzymamy przez scał-
kowanie równania (7.58):
1 f
n
XRH
x 2
Pr
V3
dx
a = — I a xax = 0,332 I------------------
(7.60)
T J
J
Y
L o
a następnie
gdzie
a = 0,664^R e!/2/ V /3
(7.61)
Re,, = —
(7.62)
v
Po przekształceniu uzyskujemy korelację dla średniej liczby Nusselta
fy J
Nu -----= 0,664R e p Pr
V2
(7.63)
X
Z porównania równań (7.59) i (7.63) wynika, że średnia wartość współczynnika wni
kania ciepła jest dwukrotnie większa od wartości lokalnej przy końcu płyty, aśr = 2ax (li
czonej dla a- = L).
7.2.5.
Rozwiązanie równania energii
turbulentnej warstwy granicznej na płycie płaskiej
Przejście od przepływu laminamego do turbulentnego w warstwie granicznej na
płycie płaskiej zachodzi na pewnym odcinku (rys. 7.6). Wyniki badań doświadczal
nych wskazują, że występuje ono dla wartości liczby Reynoldsa od 104 do 4-106
(Rex = wKx/v). Wartość krytycznej odległości
dla której występują zakłócenia
ruchu laminamego (xtń), po czym stabilizuje się ruch burzliwy (a*.2), zależy od liczby
Reynoldsa oraz od stopnia turbulencji. Zazwyczaj jako typową wartość krytycznej
liczby Reynoldsa przyjmuje się dla tego przypadku Re = 400 000.

93
Rys. 7.6. W arstwa przyścienna w opływie ściany płaskiej: 1 - warstwa laminarna,
2 - obszar przejściowy, 3 - warstwa turbulentna, 4 - podwarstwa laminarna
R ozkład prędkości i tem peratury w turbulentnej w arstw ie granicznej opisują za
leżności potęgow e
21k
(
y ] / 7
y_
k
S
j
(7.64)
oraz
Tw - T
TW ~Ty,
y
n
(7.65)
Do w yznaczenia zależności opisującej liczby N usselta w ruchu turbulentnym , gdy
płyn opływ a rów nolegle płytę płaską, korzysta się z rów nania całkow ego energii [5].
P rzyjm uje się, że dla płynów o liczbie P randtla bliskiej jedn ości stosunek grubości
w arstw y term icznej i hydrodynam icznej S , / S = 1. R ozw iązanie je s t oparte n a po dsta
w ieniu ró w nania rozkładu prędkości (7.64) i rozkładu tem peratury (7.65) do rów nania
całkow ego energii (7.36). K orzystając z zależności n a lokalny w spółczynnik w nikania
ciepła ą x dla płyty płaskiej
A
f d T \
a r
T - T
dy
7 v= o
(7.66 )
otrzym ujem y w yrażenie n a gradient tem peratury
f d T \
dy
= ^ ( T W- Ta>)
(7. 67)
Po podstaw ieniu tego w yrażenia do całkow ego rów n ania energii (7.36) otrzym ujem y
4 ~ \w.x ( T - T x )dy--
a x J
d T \
_ a x
.
Jv=0
cpp
{Tv - T „ )
( 7 .6 8 )

94
Po podzieleniu przez wx i przekształceniu otrzymujemy wyrażenie na liczbę Stantona
St = -
a
r
d r Wr T - T x
a r ir;
■dy
(7.69)
cp w* p
dx l w* Tw - Tx
do którego wprowadza się zależności na profile prędkości (7.64) i temperatury (7.65):
a x
S, f
\
n
cpwKp
d x JQ\ S
Po scałkowaniu otrzymuje się równanie
v
1/7
\
8
j
dy
(7.70)
7 dd
cpwx p
72 dx
do którego podstawiamy wyrażenie na grubość turbulentnej warstwy granicznej
(7.71 )
= 0,376 Re
1/5
(7.72)
i otrzymujemy następujące wyrażenie
_ J ^ = i „ , 3 7 6 i -
cpwKp
72
dx
z którego po zróżniczkowaniu otrzymujemy ostateczną postać funkcji
/
\
-1 /5 ‘
n
X
yw„xp
J
(7.73)
ffr
cpwx p
■
= 0,0292
(
V/5
n
p i y x p x
= 0,0292 Re;
(7.74)
Zależność tę dla przypadku, gdy liczba Prandtla jest równa jedności możemy zapisać
w postaci równania
a.x
Nllr
Nltr
cp wx p
Re, Pr
Re,
= 0,0292 Re]
1/5
(7.75)
z którego po pomnożeniu przez liczbę Re, otrzymujemy korelację
Re
Wyrażenie na średnią wartość liczby Nusselta na płycie o długości Z. jest całką
i
i
N u = - \ N u xdx
= — h,W192Rexlsfo = 0,0366R e f 5
(7.77)

Wyprowadzone równania obowiązują w następujących warunkach:
• warstwa graniczna jest turbulentna na całej płycie,
• liczba Prandtla Pr = 1,
• ruch ciepła występuje na całej płycie,
• właściwości płynu należy określać w temperaturze, którą oblicza się z zależności:
(” s)
W przypadkach liczb Prandtla większych od 0,6 należy stosować zależności kry-
terialne
Nux =Q,Q292ReĄ
x'5Prm
(7.79)
lub zależności do obliczania średnich wartości współczynników wnikania ciepła
Re
W innych przypadkach należy zastosować wzory zmodyfikowane [5].
7.3. Teoria podobieństwa i analiza wymiarowa
Metody doświadczalne wyznaczania współczynników wnikania ciepła są oparte
na zastosowaniu teorii podobieństwa do powiększania skali aparatu. Badania do
świadczalne są bowiem z reguły wykonywane z użyciem aparatów o małych rozmia
rach, a ich wyniki wykorzystuje się do obliczeń dużych jednostek.
95
mały aparat
duży aparat
Rys. 7.7. Podobieństw o trójkątów dla aparatów a i b
Pojęcie podobieństwa geometrycznego jest znane w geometrii. Jak wiadomo,
w figurach geometrycznie podobnych odpowiadające sobie kąty są równe, a długość
odpowiadających odcinków - proporcjonalna. Zgodnie z rys 7.7 zależność tę zapi
szemy następująco:
c0nSt
(7.81)
h
li
H

96
gdzie /], h i h odpowiadają długości boków trójkąta a (dla małego aparatu) oraz //, /2'
oraz U - długości odpowiadających im boków trójkąta podobnego b (dla dużego apa
ratu).
Pojęcie podobieństwa można także stosować w odniesieniu do zjawisk fizycz
nych. Dwa zjawiska fizyczne są podobne, gdy zachodzą w aparatach podobnych geo
metrycznie, a liczbowe wartości odpowiednich modułów bezwymiarowych charakte
ryzujących je są sobie równe. Wyprowadzenie oraz uzasadnienie sensu fizycznego
tych modułów opiera się na zastosowaniu analizy wymiarowej. Umożliwia ona spro
wadzanie złożonych funkcji wielu zmiennych opisujących dane zjawisko do prostych
równań korelacyjnych, zbudowanych z modułów bezwymiarowych. Przekształcenie
takie jest możliwe jedynie w odniesieniu do funkcji kompletnych i homogenicznych.
Funkcja kompletna obowiązuje w każdym układzie wymiarów. Jako przykład takiej
funkcji łłobler [4] przytoczył równanie opisujące swobodne spadanie ciał z wysoko
ści h na ziemię: h = 0,5gr2. Przykładem funkcji niekompletnej w tym przypadku jest
wzór h = 0,5x9,81 r 2, który obowiązuje w układzie m, s. Funkcja homogeniczna ma
ten sam wymiar po każdej stronie równania. W tym przykładzie wzór: h = 0,5gr,
spełnia oczywiście to wymaganie.
Analiza wymiarowa znalazła powszechne zastosowanie w nauce o ruchu ciepła.
Różniczkowe równania ruchu płynu i równania energii dla konwekcyjnego ruchu
ciepła są bowiem trudne do rozwiązania, a zależności empiryczne dla współczynni
ków wnikania ciepła okazały się stosunkowo prostymi zależnościami potęgowymi.
Zależność współczynnika wnikania ciepła od podstawowych parametrów dla prze
pływu wewnątrz rury w obszarze przepływu burzliwego
« = f { n A , P , c P,w ,d)
(7.82)
można na przykład przedstawić w postaci funkcji potęg podstawowych parametrów
a = const T]ai A
a2
p a:' cpat was d°b
(7.83)
Liczba i postać modułów bezwymiarowych wynika z twierdzenia Buckinghama .
według którego każde kompletne równanie homogeniczne wyrażające związek mię
dzy n parametrami wymiarowanymi można przedstawić za pomocą funkcji n - r mo
dułów bezwymiarowych, gdzie r jest liczbą zasadniczych wymiarów. W naszym
przykładzie dotyczącym przepływu płynu wewnątrz rury liczba parametrów n = 7,
r = 4 (kg, s, K, m). Liczba bezwymiarowych modułów n - r wynosi więc 3. Pierw
szym z nich jest zawsze liczba Nusselta, w której w liczniku mamy współczynnik
wnikania ciepła a.
Po wprowadzeniu wymiarów poszczególnych parametrów do równania (7.83)
otrzymujemy:
E. Buckingham, M odel experiments a nd the fo rm s o f em pirical equations, Trans. AS ME, 37 (1915)
263-296.

97
-3
-i
r
-i
-i i a‘ r
-3
- i i a2
kg • s • K = const kg • ni • s
x kg • ni • s • K
x | \ g • n T 3 J ' x j^ n i2 • s-2 • K T 1J 4 x j^ n i • s ~ 1 ] ' x [ m ] 3*
i po przekształceniu
kgi ,
, j^-1 _ ęoflSt kg^1
+a2 +a:' $ ~ ai ~ ^ a i - 2 aą -a $
j^-«2
- ^ 4
+¡72 -
3
«:,
+ 2 aą
+¡75
+a^ ę - j
g<j^
Z założenia o homogeniczności funkcji wynika, że wartości wykładników po
szczególnych zasadniczych wymiarów (kg, s, K, m) po obu stronach równania mus/ą
być sobie równe. Na tej podstawie otrzymujemy szereg równań algebraicznych:
• dla kilogramów (kg)
1 = a-i +
02
+
03
• dla sekund (s)
-3 = -O] - 3a2 - 2
oą
- as
• dla kelwinów (K)
- 1
= -
02
-
0
ą
• dla metrów (m)
0
= -
0 ] + 0 2 - 3 (1 }
+
2cIą
+ 0 5
+ 0 6
W naszym przykładzie po wyrażeniu wszystkich wykładników przez
oą
i a$
otrzymujemy:
• z równania dla kelwinów
02
= 1 - Oą
• z równania dla sekund:
a i = 3 - 3<o - 2o\ - 05 = 3 - 3 + 3a\ - 2o\
-0 5
=
04-05
• z równania dla kilogramów
0 2 =
1
-
O] ~ 0 2 = \ ~ O ą +
0 5
- \ + O ą =
05
• z równania dla metrów
0 6 = O] - 0 2 +
3
(
1
} ~
2
o ą - 0 5 = 0 4 - 0 5 -
1
+ 0 4 +
3
c O ~
2
o \ - 0 5 = -
1
+
0 5
Po wprowadzeniu tych wyrażeń do funkcji potęgowej (7.83) otrzymujemy
a' = const x
-°s A1^ p as cap>
d~]+as
(7.86)
Po przegrupowaniu parametrów wymiarowanych o tych samych wykładnikach
potęgowych otrzymujemy równanie korelacyjne liczb bezwymiarowych
( 7 .8 4 )

98
a d
■
= const
v
ycP
x
\ a A
wdp
( 7 .8 7 )
Ostatecznie przyjmujemy następującą zależność liczby Nusselta od liczby Rey
noldsa i liczby Prandtla z odpowiadającymi im wykładnikami a$ i ay.
Nu - const x Rea$ Praą
( 7 .8 8 )
Liczbowe wartości stałej const oraz wykładników potęgowych przy liczbie Reynoldsa
as i liczbie Prandtla
oą
wyznaczamy zawsze na podstawie danych doświadczalnych.
7.3.1. W yprowadzenie modułów podobieństwa z równania energii
Równanie energii, tj. różniczkowe równanie Fouriera-Kirchhoffa opisuje nieusta
lony, konwekcyjny ruch ciepła z przewodzeniem ciepła w płynach znajdujących się
w ruchu. Ma ono następującą postać
r
7"7
r
7"7
rri
rri
U l
U l
U l
U l
X-72rri
O A \
Hwy
hwv
hw, — ~aV T
(7.89)
d t
dx
} dy
' dz
Rozważmy dwa różne procesy nieustalonego wnikania ciepła w płynącej strudze.
Przyjmijmy, że wartości poszczególnych zmiennych wynoszą:
• w procesie 1: /. r, wx, wy, w., ,v. y, z, a,
• w procesie 11: T', r', wx', w /, w2', x', y', z', a'
Załóżmy, że zmienne w procesie 11 są równe odpowiednim zmiennym w proce
sie 1 pomnożonym przez stałe współczynniki:
T r
=
CjT,
T?
=
c zt
,
w x'
=
cww x,
Wy
=
cwWy,
w J
=
cww z,
x '
=
cjx,
y
=
c y ,
z '
= c/z,
a '
=
caa
Po podstawieniu tych wielkości do równania (7.89) otrzymujemy dla procesu 11:
1
wx
1
Wy
1
w , ---- = — — a \ 1
(7.90)
Jeśli obowiązuje równość grup współczynników
to równanie dla procesu 11 (7.90) sprowadza się do równania dla procesu 1 (7.89).
Równość grup odpowiednich współczynników (7.91) można przekształcić do po
staci sprowadzających się do jedności.

99
Z równości dwóch pierwszych grup
cr
cwcr
cT
q
otrzymujemy
Cu
CT
.
Ct
Z równości pierwszej i trzeciej grupy
C i
Ca C f
2
Cz
C/
otrzymujemy
Ca Cr
7
Cf
a z równości drugiej i trzeciej grupy
C‘w C f
Ca C r
(7.92)
(7.93)
(7.94)
(7.95)
(7.96)
wynika, że
CwCi
(7.97)
Warunkiem utrzymania stałości poszczególnych członów równań (7.89) i (7.90)
jest zatem zachowanie stałości odpowiednich modułów.
Z zależności (7.93) otrzymujemy zatem
trr
w V
z zależności (7.95)
a z zależności (7.97)
l
V
av
a V
= S
(7.98)
j ^ j r ^ Fo
i7- " )
wł
w'V
— - — — - Pe
(7.100)
a
a'
Warunkiem zachowania podobieństwa nieustalonego wnikania ciepła podczas
przepływu płynu jest równość następujących modułów:

100
• liczby Strouhala S, charakteryzującej przepływ nieustalony (np. pulsacyjny),
• liczby Fouriera Fo, charakteryzującej nieustalony ruch ciepła w płynie,
• liczby Pecleta Pe, którą można 'wyrazić iloczynem liczby Reynoldsa i liczby
Prandtla:
Pe = ^!Sp£_a= w l p S £ l = Rep r
(7.101)
A
rj
7]
A
W ogólnym przypadku mamy jednocześnie zachowaną równość modułu Nusselta
Nu = ad! A.
7.4.
Wnikanie ciepła podczas
wymuszonego przepływu burzliwego
Z wnikaniem ciepła w strumieniu wymuszonego przepływu burzliwego mamy do
czynienia, gdy prędkość masowa płynu jest dostatecznie duża, tak że liczba Reynoldsa
jest większa od 10 000. Prędkość ta przy określonym przekroju poprzecznym rury
zależy tylko od urządzenia tłoczącego, tj. pompy lub wentylatora, natomiast nie zależy
od procesu wymiany ciepła. Drugą istotną cechą tego przepływu jest burzliwość. Już
Hobler [4] na podstawie pracy Pannella wskazywał na fakt, że rozkład prędkości
i rozkład temperatury powietrza przepływającego przez ogrzewaną rurę (rys. 7.8) są
ze sobą związane.
^
A T max
►
--------- A T — ►
// / / / / / / / / / / / /
/
' / / / / / / / / / / / / / / z
w y
Wmax
^
\
\
T
M i
T max
/
2
i
/
/ / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / / ,
Rys. 7.8. Profile prędkości i tem peratury w edług Pannella
Jak widać z rys. 7.8, transport ciepła przez konwekcję w rdzeniu płynu napotyka
niewielki opór, o czym świadczy płaski profil temperatury. Główny spadek temperatu
ry występuje natomiast przy ścianie wskutek oporu cieplnego w laminamej warstewce
przyściennej.

101
D o k ła d n y o b r a z ro z k ła d u p r ę d k o ś c i i te m p e r a tu ry m o ż n a u z y s k a ć z o b lic z e ń z a p o
m o c ą p r o g ra m u k o m p u te ro w e g o F L U E N T 6.0. R o z w ią z a n ie u k ła d u r ó w n a ń p rz e p ły w u ,
tj. r ó w n a n ia N a v ie r a - S to k e s a o ra z r ó w n a n ia e n e rg ii w p r o g ra m a c h te g o ty p u w y m a g a
z a a w a n s o w a n y c h m e to d n u m e ry c z n y c h , n a jc z ę ś c ie j m e to d y o b ję to ś c i k o n tro ln e j P a ta n -
k a r a [9]. P rz y k ła d o w e o b lic z e n ia w y k o n a n o d la p rz e p ły w u w o d y w ru rz e p o z io m e j o
ś re d n ic y 0 ,0 5 m n a o d c in k u d łu g o ś c i 4 m z u ż y c ie m s ia tk i n ie s tru k tu ra ln e j (ry s. 7 .9 ).
W p r z y p a d k u d u ż e j śre d n ie j p r ę d k o ś c i w o d y (v = 0 ,2 5 6 m /s , ry s. 7 .1 0 ) lic z b a R e y n o ld
s a w y n o s i o k o ło 11 0 0 0 i p r o f ile p r ę d k o ś c i s ą w y r a ź n ie p ła s k ie z a r ó w n o u w lo tu (ry s.
7 .1 0 b ), j a k i n a w y lo c ie z r u r y (ry s. 7 .1 0 a ). P o d o b n ie r o z k ła d te m p e r a t u r y w o d y j e s t
d o ś ć w y r ó w n a n y (ry s. 7 .1 1 ), j e d n a k j e s t o n a z n a c z n ie n iż s z a o d te m p e r a t u r y ś c ia n k i
(tść = 55 °C ).
Rura 1 + 2
Siatka niestrukturalna
Rys. 7.9. Siatka niestrukturalna dla rury 1+2 (L = 1 m +3 m; d = 0,05 m)
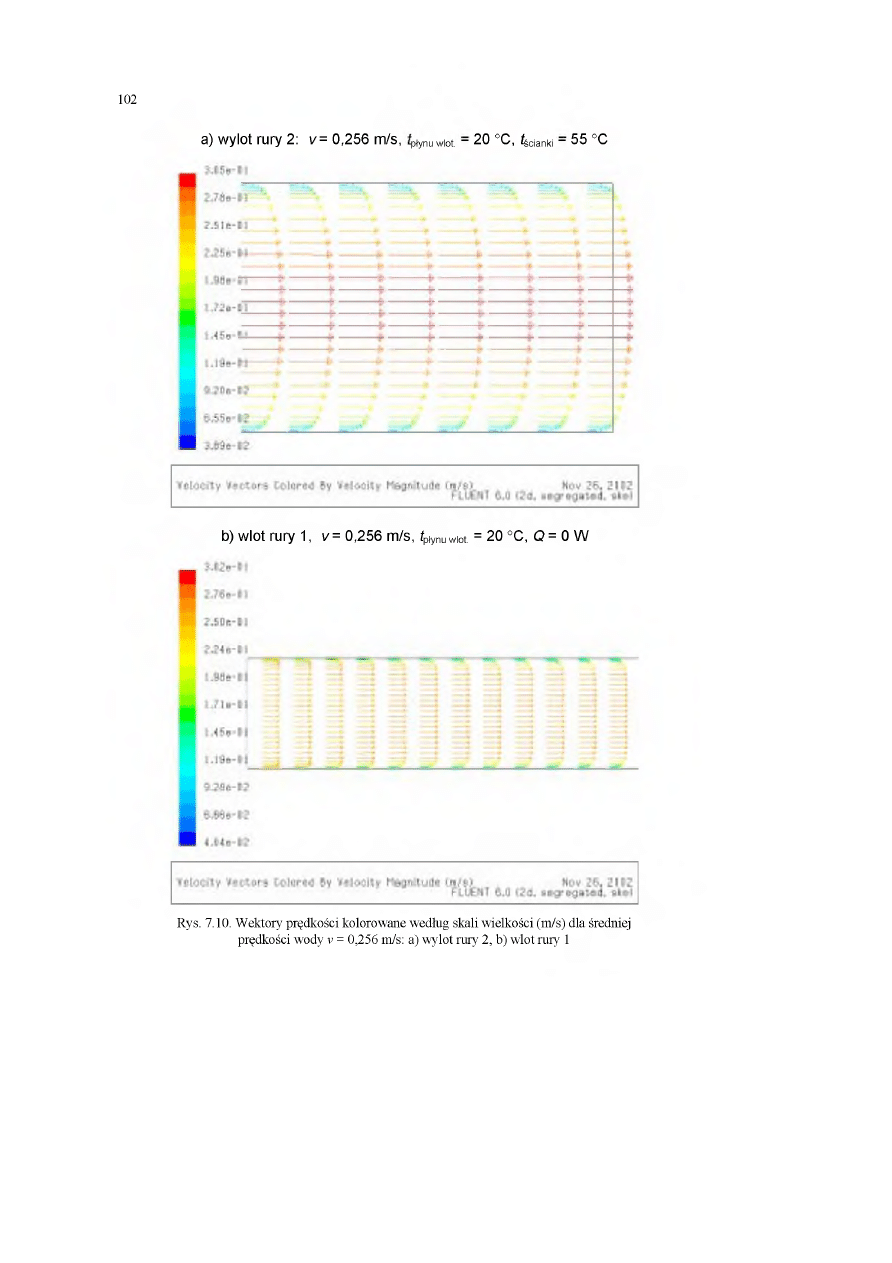
102
a) wylot rury 2: v - 0,256 m/s,
płynu wlot. - 2 0 ° C tścia nki - 5 5 ° C
b) wlot rury 1,
v
- 0,256 m/s,
tp
■płynu wlot.
- 20 °c ,
q
- 0 W
Rys. 7.10. Wektory prędkości kolorowane według skali wielkości (m/s) dla średniej
prędkości wody v = 0,256 m/s: a) wylot rury 2, b) wlot rury 1
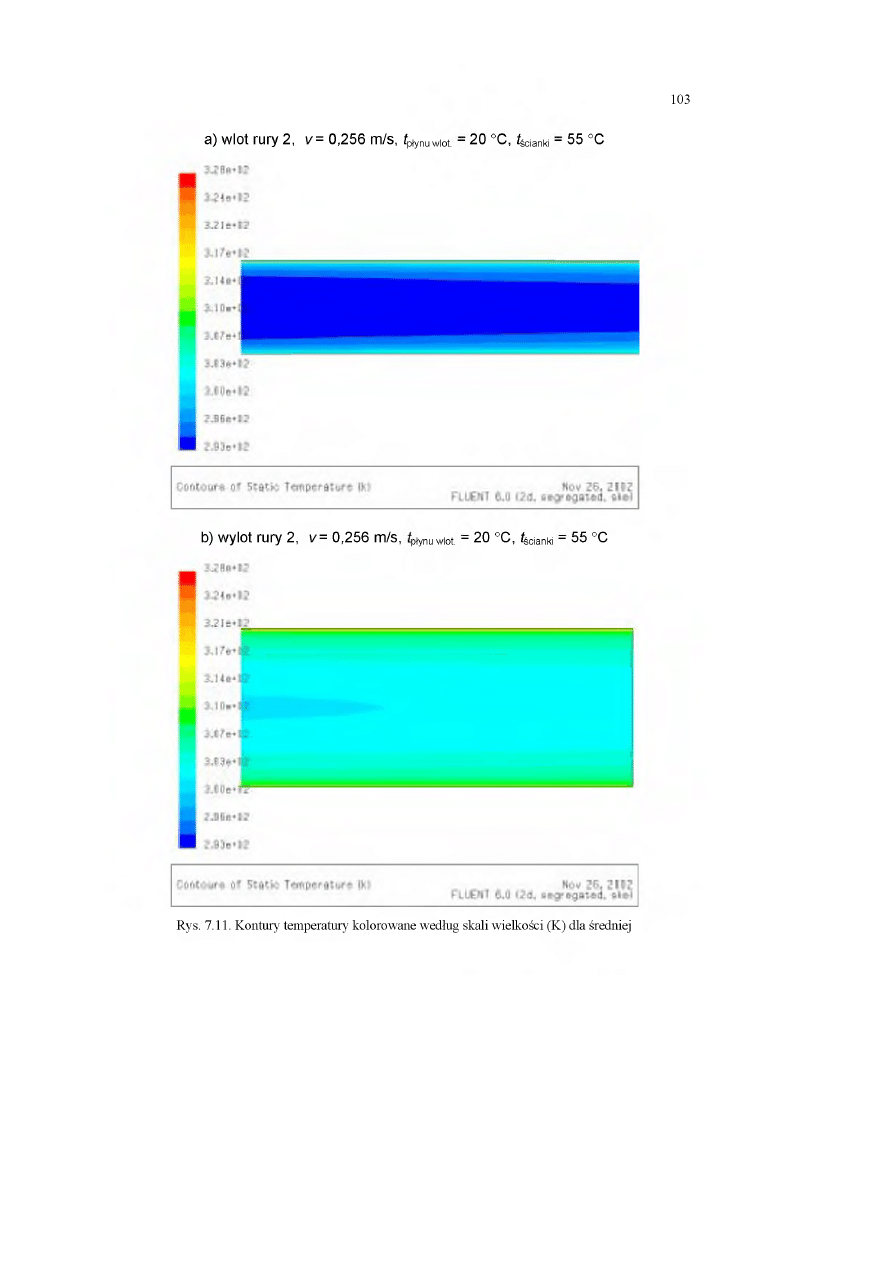
103
a) wlot rury 2,
v
= 0,256 m/s, tp,ynu wbt
= 2 0 ° C t ścia nki = 5 5 ° C
b) wylot rury 2, v = 0,256 m/s,
płynu wlot. = 2 0 ° C , tścia nki = 5 5 ° C
Rys. 7.11. Kontury temperatury kolorowane według skali wielkości (K) dla średniej

104
\ Ściana
Rys. 7.12. Schemat w nikania ciepła w edług Iłoblera
Najczęściej stosowaną metodą jest tradycyjna analiza wymiarowa. Wymaga ona
przede wszystkim ustalenia, od jakich zmiennych zależy przebieg procesu wnikania
ciepła. Dla przykładu rozważmy schemat wnikania ciepła w wymuszonym przepływie
burzliwym wewnątrz odcinka rury o powierzchni 1 m2, zaproponowany przez Hobłera
[4] (rys. 7.12). Założywszy, że liczba Reynoldsa jest w przybliżeniu stała wzdłuż dro
gi przepływu płynu, można przyjąć, że grubość warstewki przyściennej nie zmienia
się i tym samym współczynnik wnikania ciepła nie zależy od długości rury. Ciepło
jest przekazywane przez elementy płynu w strudze wirów poruszających się od rdze
nia do warstwy granicznej. Całkowita ilość ciepła przekazywana przez wszystkie
strugi na jednostkowej powierzchni wynosi
q = m ffcp (Ty-T2)
(7.102)
gdzie T[ i T
2
to temperatura płynu na wlocie i na wylocie analizowanego odcinka rury,
m'' natomiast jest prędkością masową płynu.
Dzięki założeniom, że ruch ciepła jest ustalony oraz że główny opór cieplny wy
stępuje w warstwie przyściennej, możemy napisać dla tej warstwy równanie Fouriera
q = - A T '
(7.103)
w którym x jest grubością warstwy granicznej, X - współczynnikiem przewodzenia
ciepła w płynie.
Sumaryczny proces wnikania ciepła opisuje równanie Newtona:
q = aAT
(7.104)
Z porównania równań (7.102) oraz (7.104) otrzymujemy

105
ATj-2
AT
(7.105)
z porównania zaś równań (7.103) i (7.104)
^
/"7 in ^
a -
(7.106)
x AT
Ponieważ stosunki różnic temperatury są bezwymiarowe, możemy je pominąć.
Z zależności grubości warstwy jc od liczby Reynoldsajc =f(rh", d,
t
f) otrzymujemy:
a = f { v A , c p ,m " ,d ) = f ( q , X , c p ,p , w , d )
(7.107)
Jak pokazano w poprzednim rozdziale, zależność tę za pomocą analizy wymiaro
wej można sprowadzić do korelacji liczb bezwymiarowych Nusselta, Reynoldsa
i Prandtla:
Nu - CRea Prh
(7.108)
Wartości stałej C i wykładników potęgowych a i b wyznaczono na podstawie wy
ników badań eksperymentalnych.
W pierwszych podręcznikach (por. np. McAdams [10]) rekomendowano następu
jące równanie korelacyjne
Nu = 0,023Re°'&
Prn
(7.109)
w którym:
• przyjmuje się, że n = 0,4 podczas ogrzewania płynu oraz n = 0,3 podczas jego
chłodzenia,
• wszystkie stałe fizyczne płynu określa się dla stałej temperatury płynu, wyzna
czonej jako jej średnia arytmetyczna,
• wartość liczby Reynoldsa powinna być większa od 104,
• liczba Prandtla Pr powinna mieścić się w zakresie od 0,7 do 100,
• stosunek długości rury do średnicy powinien być większy od 60. łncropera i de
Witt [11] przyjęli, że równanie to można stosować już dla LID > 10.
Równanie to początkowo przypisywano McAdamsowi [10], ale obecnie najczę
ściej jest nazywane równaniem Dittusa-Boeltera [3, 11, 12].
Równanie (7.108) można wykreślić w układzie podwójnie logarytmicznym jako
prostą lub zbiór prostych równoległych, zgodnie z funkcją
\g N u ^ \g C + a\gRe + b\gPr
(7.110)
Jeśli przyjmiemy stałą wartość liczby Prandtla, to zależność (7.110) da się spro
wadzić do równania linii prostej

106
\gNu = \gC" + a\gRe
(7.111)
w którym stała C" jest równa ( 'Pr'.
Jeżeli założymy stałą wartość liczby Reynoldsa, to równanie to również daje pro
stoliniową zależność
W szczególnych przypadkach stała C i wykładniki a i b równania korelacyjnego
(7.108) muszą być jednak wyznaczone doświadczalnie. Przykładowe zestawienie
danych dla różnych geometrii układu i różnego kształtu opływanych elementów ze
stawiono za podręcznikiem Hoblera [4] w tabeli 7.1.
Niekiedy, dla bardzo dużego zakresu wartości liczby Reynoldsa, np. gdy sięga
ona obszaru przepływu laminamego, wyniki doświadczeń są korelowane za pomocą
nieliniowej zależności:
Stałe C' i C oraz wykładniki a i b równania korelacyjnego (7.113) są wyznaczane
eksperymentalnie dla danego układu geometrycznego i kształtu opływanych elemen
tów. Przykładowe wartości zestawiono w tabeli 7.2. We wszystkich przypadkach
w odniesieniu do tych korelacji należy stosować parametry warstwy przyściennej.
Wnikanie ciepła podczas przepływu płynu wewnątrz rury w pewnym stopniu za
leży od kierunku. Wyniki pomiarów wskazują na większe wartości współczynników
wnikania ciepła podczas ogrzewania cieczy niż podczas jej chłodzenia. Podczas
ogrzewania cieczy temperatura w warstwie granicznej jest bowiem wyższa niż pod
czas chłodzenia, dzięki czemu współczynniki lepkości cieczy są mniejsze. Aby
uwzględnić ten efekt, Sieder i Tate wprowadzili poprawkę, która jest funkcją stosun
ku współczynnika lepkości w rdzeniu strumienia i] do współczynnika lepkości cieczy
przy samej ścianie //^(równanie 2 w tabeli 7.1).
W rozważaniach przepływu płynu przez rury wypełnione należy rozróżnić dwa
przypadki ruchu ciepła: wnikanie ciepła od płynu do ziarna lub odwrotnie oraz wni
kanie ciepła między ścianą rury i płynem. Można znaleźć wiele korelacji dla poszcze
gólnych przypadków, zwłaszcza w monografiach na temat fluidyzacji. W tabeli 7.1
przedstawiono dla przykładu korelacje Hougena i Watsona dla małych i dużych liczb
Reynoldsa. W tym przypadku zarówno liczba Reynoldsa, jak i liczba Nusselta są od
niesione do wymiaru liniowego będącego średnicą kulki o powierzchni ziarna.
\gNu = \gC"' + b\gPr
(7.112)
w której stała C'" jest równa CRea.
7.4.1. Przypadki szczególne
(7.113)
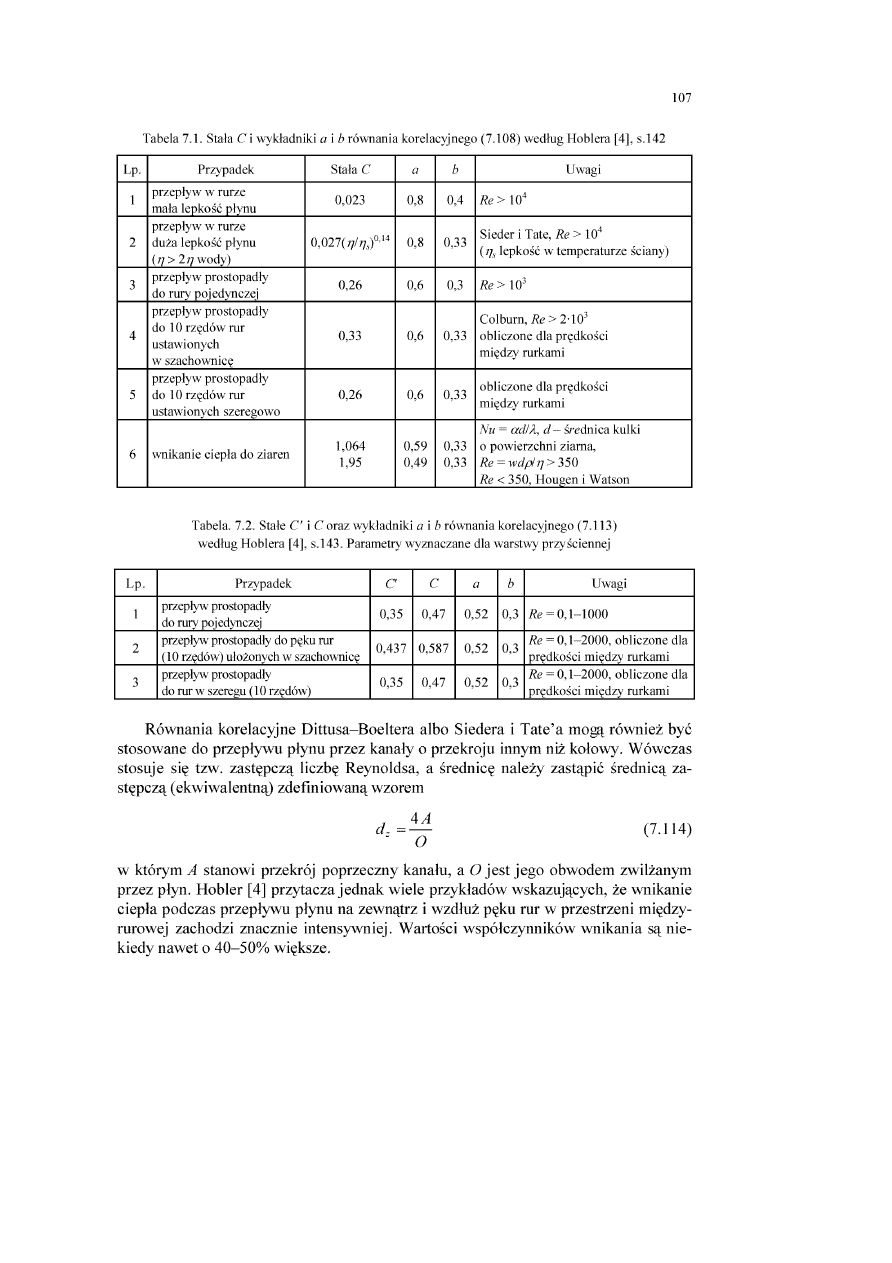
107
Tabela 7.1. Stała C i wykładniki a i
b rów nania korelacyjnego (7.108) według H oblera [4], s.142
Lp.
Przypadek
Stała C
a
b
Uwagi
1
przepływ w rurze
mała lepkość płynu
0,023
0,8
0,4
R e > 10
4
2
przepływ w rurze
duża lepkość płynu
(77
> 2
77
wody)
0
,
0 2 7
(
77
/
77,)014
0,8
0,33
Sieder i Tate, Re > 10
4
(
77
, lepkość w tem peraturze ściany)
3
przepływ prostopadły
do rury pojedynczej
0,26
0,6
0,3
R e > 10
3
4
przepływ prostopadły
do
10
rzędów rur
ustawionych
w szachownicę
0,33
0,6
0,33
Colburn, Re > 2-10
3
obliczone dla prędkości
między rurkami
5
przepływ prostopadły
do
10
rzędów rur
ustawionych szeregowo
0,26
0,6
0,33
obliczone dla prędkości
między rurkami
6
w nikanie ciepła do ziaren
1,064
1,95
0,59
0,49
0,33
0,33
N u = ad/A, d - ś/'ednica kulki
0
powierzchni ziarna,
Re = w dp/t]> 350
Re < 350, Hougen i Watson
Tabela. 7.2. Stałe C" i C oraz w ykładniki a i b rów nania korelacyjnego (7.113)
w edług H oblera
[
4
],
s.143. Parametry w yznaczane dla warstwy przyściennej
Lp.
Przypadek
C
C
a
b
Uwagi
1
przepływ prostopadły
do rury pojedynczej
0,35
0,47
0,52
0,3
Re = 0,1-1000
2
przepływ prostopadły do pęku rur
(10
rzędów) ułożonych w szachownicę
0,437
0,587
0,52
0,3
Re = 0,1-2000, obliczone dla
prędkości między rurkami
3
przepływ prostopadły
do rur w szeregu
(10
rzędów)
0,35
0,47
0,52
0,3
Re = 0,1-2000, obliczone dla
prędkości między rurkami
Równania korelacyjne Dittusa-Boeltera albo Siedera i Tate’a mogą również być
stosowane do przepływu płynu przez kanały o przekroju innym niż kołowy. Wówczas
stosuje się tzw. zastępczą liczbę Reynoldsa, a średnicę należy zastąpić średnicą za
stępczą (ekwiwalentną) zdefiniowaną wzorem
4 A
d , = —
(7.114)
*
O
w którym A stanowi przekrój poprzeczny kanału, a O jest jego obwodem zwilżanym
przez płyn. Hobler [4] przytacza jednak wiele przykładów wskazujących, że wnikanie
ciepła podczas przepływu płynu na zewnątrz i wzdłuż pęku rur w przestrzeni między-
rurowej zachodzi znacznie intensywniej. Wartości współczynników wnikania są nie
kiedy nawet o 40-50% większe.

108
Przytoczone korelacje obowiązują dla przepływów wewnątrz rur dostatecznie
długich (L/D > 60), gdyż wówczas profil prędkości jest ustalony. Dla niezbyt długich
przewodów lub gdy chcemy uwzględnić kształt odcinka wlotowego, należy wprowa
dzić współczynnik poprawkowy
S / ,.
W tabeli 7.3 zestawiono ich wartości dla dwóch
liczb Reynoldsa.
Tabela 7.3. W spółczynniki poprawkowe zL = f(L /d ) dla przepływu burzliwego
U d
1
2
5
10
15
20
30
40
50
Re = T 104
1,63
1,50
1,34
1,23
1,17
1,13
1,07
1,03
1,0
Re = 2-104
1,51
1,40
1,27
1,18
1,13
1,10
1,05
1,02
1,0
Dla przepływu wewnątrz wężownicy, gdy pewne znaczenie ma krętość rury, Jesz-
ke [2] podał wzór
a R = a pr^ 1+3,54-^j
(7.115)
w którym apr jest współczynnikiem wnikania dla przepływu w rurze prostej, r - pro
mieniem rury, R zaś promieniem wężownicy.
Szczególnym przypadkiem jest przepływ przez rury o zmiennym przekroju (rury
zgniatane). Według Hoblera [4] współczynniki wnikania ciepła mogą tu być zwięk
szone nawet do 40%.
W celu intensyfikacji wnikania ciepła stosuje się wiele metod, takich jak [3, 4]:
• zwiększanie prędkości masowej przepływu,
• stosowanie różnorodnych wypełnień,
• wprowadzanie przegród powodujących wielokrotną zmianę przepływu,
• stosowanie przepływów prostopadłych i skośnych do wiązki rur,
• wprowadzanie różnego rodzaju deformacji przekroju rury,
• mieszanie cieczy w aparacie.
Niektóre z nich są przedmiotem analizy w następnym rozdziale.
7.4.2. Wnikanie ciepła podczas przepływu
wokół różnorodnych elementów
Zagadnienie wnikania ciepła podczas przepływu prostopadłego do rury jest bardzo
złożone z wielu powodów. Po pierwsze, należy rozróżnić szereg przypadków takich jak
przepływ płynu wokół pojedynczej rury lub układu rurek ułożonych szeregowo lub na-
przemianlegle (w. układzie w szachownicę, tabele 7.1, 7.2). Wyniki badań opublikowane
w klasycznych pracach [2, 4] pokazują, że z jednej strony mamy tu do czynienia z prze
pływem o zmiennej prędkości, z drugiej zaś - z występowaniem charakterystycznych wi
rów z tyłu rury. Dokładny obraz struktury strugi ze wszystkich stron rury można uzyskać
jedynie w wyniku symulacj i komputerowej wykonanej za pomocą zaawansowanych pakie
tów oprogramowania.
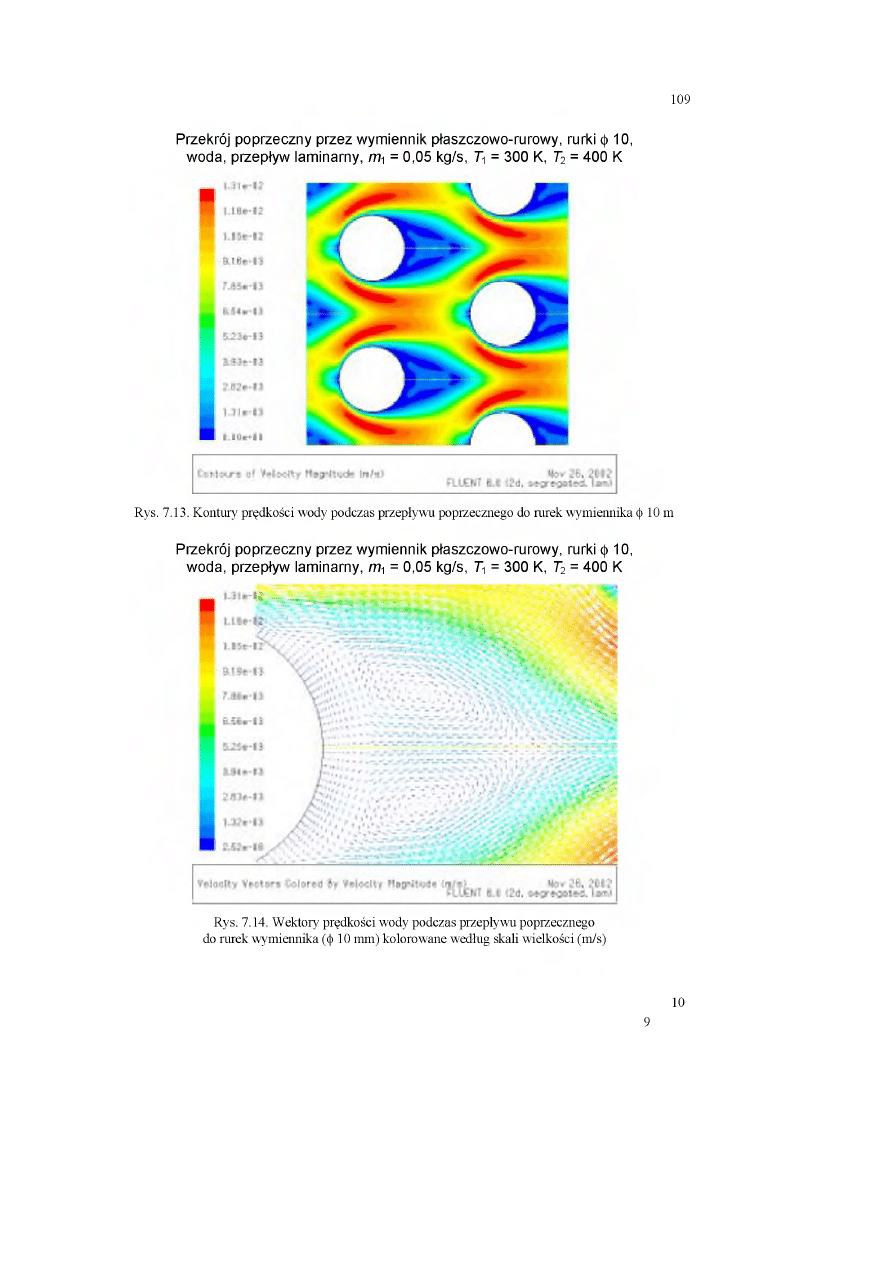
109
Przekrój poprzeczny przez wym iennik płaszczowo-rurowy, rurki $ 10,
woda, przepływ laminarny,
m1
= 0,05 kg/s,
T1
= 300 K, T2 = 400 K
Rys. 7.13. Kontury prędkości wody podczas przepływu poprzecznego do rurek wymiennika $ 10 m
Przekrój poprzeczny przez wym iennik płaszczowo-rurowy, rurki $ 10,
woda, przepływ laminarny,
m1
= 0,05 kg/s,
T1
= 300 K, T2 = 400 K
Rys. 7.14. Wektory prędkości wody podczas przepływu poprzecznego
do rurek wymiennika ($ 10 mm) kolorowane według skali wielkości (m/s)
10
9
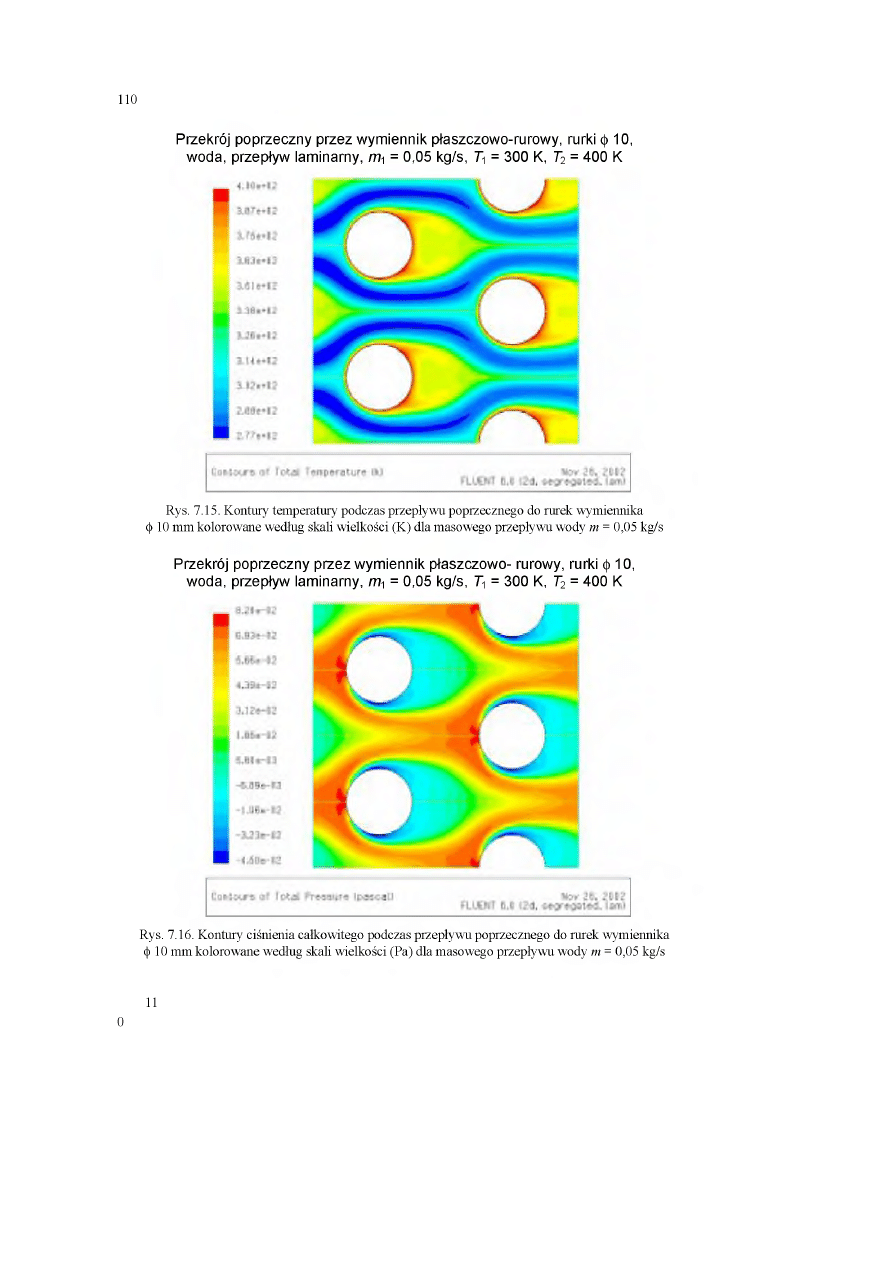
110
Przekrój poprzeczny przez wym iennik płaszczowo-rurowy, rurki $ 10,
woda, przepływ laminarny,
m1
= 0,05 kg/s,
T1
= 300 K, T2 = 400 K
Rys. 7.15. Kontury temperatury podczas przepływu poprzecznego do rurek wymiennika
$ 10 mm kolorowane według skali wielkości (K) dla masowego przepływu wody m = 0,05 kg/s
Przekrój poprzeczny przez wym iennik płaszczowo- rurowy, rurki $ 10,
woda, przepływ laminarny,
m1
= 0,05 kg/s,
T1
= 300 K, T2 = 400 K
Rys. 7.16. Kontury ciśnienia całkowitego podczas przepływu poprzecznego do rurek wymiennika
$ 10 mm kolorowane według skali wielkości (Pa) dla masowego przepływu wody m = 0,05 kg/s
11
0

111
Na rysunkach 7.13-7.16 pokazano rozkład prędkości, wektorów prędkości, tem
peratury i ciśnienia całkowitego podczas przepływu poprzecznego wody przez prze
stawny układ rurek (układ szachownicowy) o średnicy 10 mm. Dane te otrzymano
w wyniku rozwiązania układu równań przepływu Naviera-Stokesa oraz równania
energii metodą objętości kontrolnej Patankara [9] za pomocą oprogramowania Fluent
6.0. Od strony czołowej następuje uderzenie czynnika o ścianę rury (co wiąże się ze
zmniejszeniem prędkości i temperatury, ale ze zwiększeniem ciśnienia), po czym
prędkość się zwiększa, ciśnienie po bokach rury zmniejsza, a wreszcie występują wy
raźne wiry z tyłu rury.
Podczas przepływu płynu prostopadle do układu większej liczby rurek strugi są
ułożone rozmaicie w zależności od typu układu. Przyjmuje się, że układ rurek
w szachownicę (naprzemianległy) zapewnia większe wartości współczynników wni
kania ciepła od układu szeregowego. W obydwu zaś przypadkach współczynniki wni
kania są większe niż dla przepływu prostopadłego do rury pojedynczej. W literaturze
można również znaleźć wiele korelacji opisujących wnikanie ciepła podczas przepły
wu wokół rur o innym kształcie niż kołowy [2, 4].
Jeżeli czynnik nie dopływa do rurki pod kątem prostym do jej osi, to należy
wprowadzić poprawkę sę zależną od kąta napływu. Dla wszystkich omawianych przy
padkach układów rur stosuje się wzór
a v = aeę
(7.116)
Wartość poprawki sę odczytujemy z wykresów lub tabel (tabela 7.4).
Tabela 7.4. W spółczynniki poprawkowe eę = f{ ę ) dla przepływu pod kątem różnym od 90°
<p
90
80
70
60
50
40
30
20
10
£(p
1,0
1,0
0,98
0,94
0,88
0,78
0,67
0,52
0,42
7.5.
Wnikanie ciepła podczas
wymuszonego przepływu laminarnego
W procesach przemysłowych przepływ laminamy występuje znacznie rzadziej od
przepływu burzliwego. Niemniej jednak przepływ ten ma znaczenie w niektórych
rodzajach technologii, chociażby produkcji tworzyw sztucznych, przerobu węgla,
ropy naftowej, a obecnie biomasy.
Możemy założyć, że w przepływie czysto uwarstwionym wnikanie ciepła spro
wadza się jedynie do przewodzenia ciepła od rdzenia płynu do ściany lub odwrotnie.
Dla takiego przypadku otrzymano rozwiązania analityczne równania energii, oddziel
nie dla tzw. obszaru wlotowego (rozwiązania Graetza i Prandtla [4]) lub dla przepły

112
wu w pełni rozwiniętego. W tym ostatnim przypadku zakłada się, że gęstość strumie
nia ciepła lub temperatura ściany jest stała [11]. Rozwiązania teoretyczne stanowią
jednak tylko pewne przybliżenie, bo rzeczywisty proces wnikania ciepła podczas tego
przepływu jest o wiele bardziej skomplikowany. W warunkach wymiany ciepła, tzn.
istnienia pola temperatury, nie jest on izotermiczny. Paraboliczny rozkład prędkości
(rys. 7.17), który występowałby w przypadku idealnego laminamego przepływu (linia
I na rys. 7.17), deformuje się w wyniku zmian lepkości płynu w zależności od tempe
ratury w poszczególnych warstwach. Jeżeli temperatura ściany jest niższa od tempera
tury cieczy (chłodzenie), to warstwy płynące przy ścianie mają większą lepkość i po
ruszają się z mniejszą prędkością liniową (linia II na rys. 7.17). Z kolei podczas
ogrzewania jest odwrotnie i rozkład temperatury odpowiada linii III. Zmiany tempera
tury na drodze przepływu płynu powodują również zmiany jego gęstości i następuje
ruch ciepła w wyniku konwekcji naturalnej. Można oczekiwać, że większe deformacje
profilu prędkości wystąpią w przypadkach niezgodności kierunków ruchu wymuszo
nego i swobodnego.
Rys. 7.17. Profile prędkości płynu dla przepływu lam inam ego: I - przepływ izotermiczny
(stała lepkość), II -chłodzenie, III - ogrzewanie
Rys. 7.18. Rozwinięcie parabolicznego profilu prędkości u w lotu rury

113
Podstawową przyczyną trudności jest jednak występowanie tzw. odcinka rozbie
gowego (rys. 7.18), na którym zachodzi formowanie się profilu parabolicznego roz
kładu prędkości u wlotu do rury. Przy samym wlocie do rury tworzy się laminama
warstwa przyścienna, podczas gdy w rdzeniu płyn ma stałą prędkość. Warstwa lami
nama narasta stopniowo, aż w pewnej odległości dochodzi do osi rury, zapewniając
paraboliczny profil prędkości w kierunku promieniowym. Podobnie zmienia się rów
nież rozkład temperatury, zapewniając formowanie się tzw. termicznej warstwy gra
nicznej.
Dokładny obraz kształtowania się profili prędkości płynu (wody) oraz rozkładu tempe
ratury uzyskano za pomocą programu komputerowego FLUENT 6.0 (rys. 7.19-7.20).
Przykładowe obliczenia wykonano dla przepływu wody w rurze poziomej o średnicy
0,05 m na odcinku 4 m z użyciem siatki niestrukturalnej (rys. 7.9). Dla niewielkiej
prędkości v = 0,01025 m/s liczba Reynoldsa wynosi około 500, profile prędkości
(rys.7.19) i temperatury (rys.7.20) dość znacznie się zmieniają w przypadku wyższej
temperatury ścianki (/«. = 55 °C). Widać również kształtowanie się wzdłuż kolejnych
warstw różniących się temperaturą: gorących przy ścianie rury grzejnej, chłodnych
dalej od niej.
Długość odcinka rozbiegowego do ustabilizowania się prędkości (rys. 7.18) wy
nosi L = 0,02SSRedwedług Hoblera [4] orazZ, = 0,065ited według Boussinesąa [10],
Długość odcinka rozbiegowego d, na którym stabilizuje się rozkład temperatury
(długość termicznego odcinka wlotowego) można natomiast obliczyć ze wzoru
W literaturze można znaleźć wiele zależności korelacyjnych do określania współ
czynnika wnikania ciepła podczas wymuszonego przepływu laminamego w rurach.
Różnią się jednak bardzo pod względem budowy modułów liczb bezwymiarowych
oraz wartości stałych i wykładników potęgowych. Wynika to z przyczyn omówionych
na wstępie tego rozdziału.
Graetz [ 10] jako pierwszy w 1885 r. opublikował rozwiązanie równania ustalone
go przewodzenia ciepła w płynie podczas przepływu uwarstwionego. Po scałkowaniu
równania Fouriera-Poissona dla przewodzenia ciepła w kierunku promieniowym
otrzymał on zależność bezwymiarowej temperatury w postaci szeregu
d
) lam
0,05 Re o Pr
(7.118)
(7.119)
gdzie
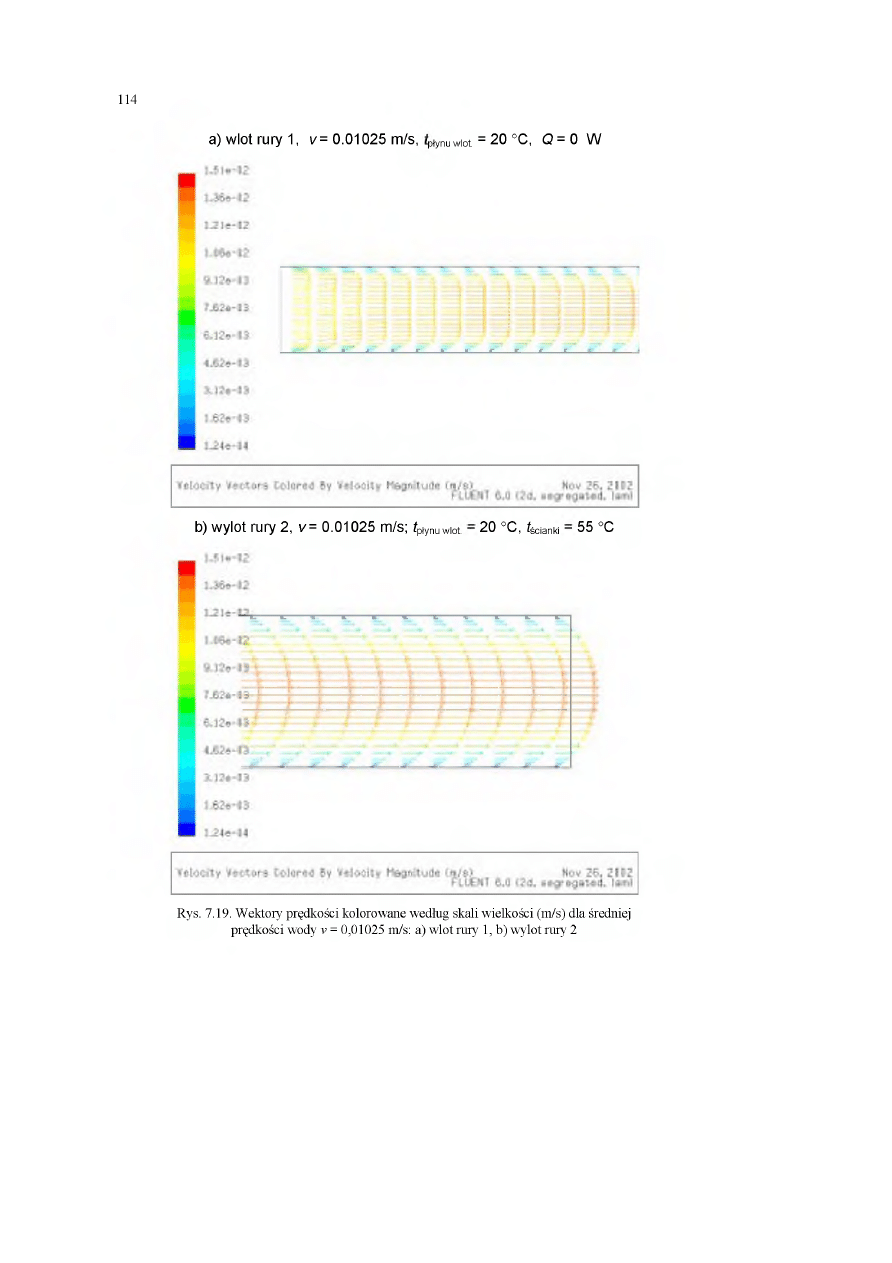
114
a) wlot rury 1, v = 0.01025 m/s,
płynu wlot.
= 20 °C,
q
= 0 W
b) wylot rury 2, v = 0.01025 m/s; t
p ły n u wlot. = 2 0 ° C t ścianki = 5 5 ° C
Rys. 7.19. Wektory prędkości kolorowane według skali wielkości (m/s) dla średniej
prędkości wody v = 0,01025 m/s: a) wlot rury 1, b) wylot rury 2
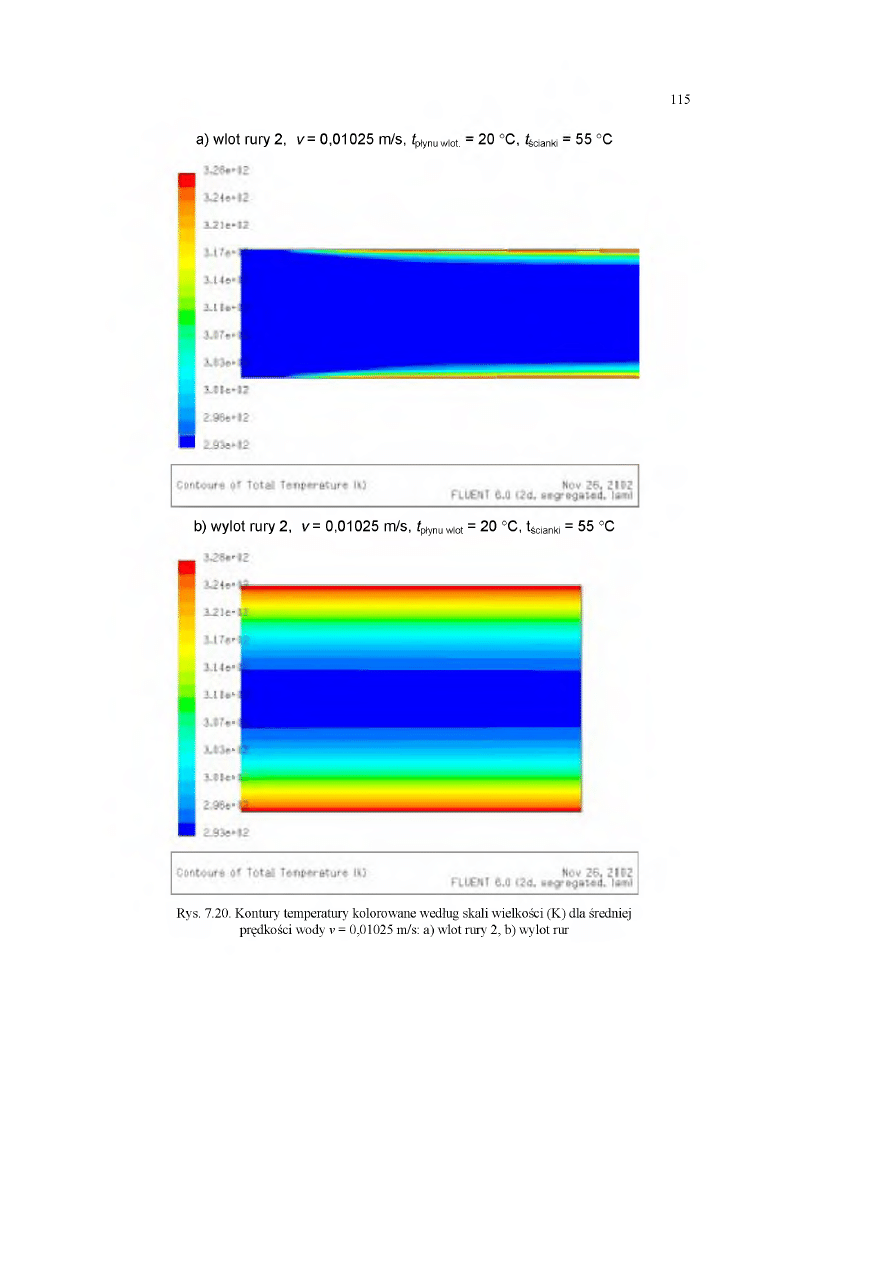
115
a) wlot rury 2,
v
= 0,01025 m/s, tp
płynu wlot. = 2 0 ° C tścia nki = 5 5 ° C
b) w ylot rury 2,
v
= 0,01025 m/s,
t
p
płynu w lot
= 20 °C, t
ś cia n ki
= 55 °C
Rys. 7.20. Kontury temperatury kolorowane według skali wielkości (K) dla średniej
prędkości wody v = 0,01025 m/s: a) wlot rury 2, b) wylot rur
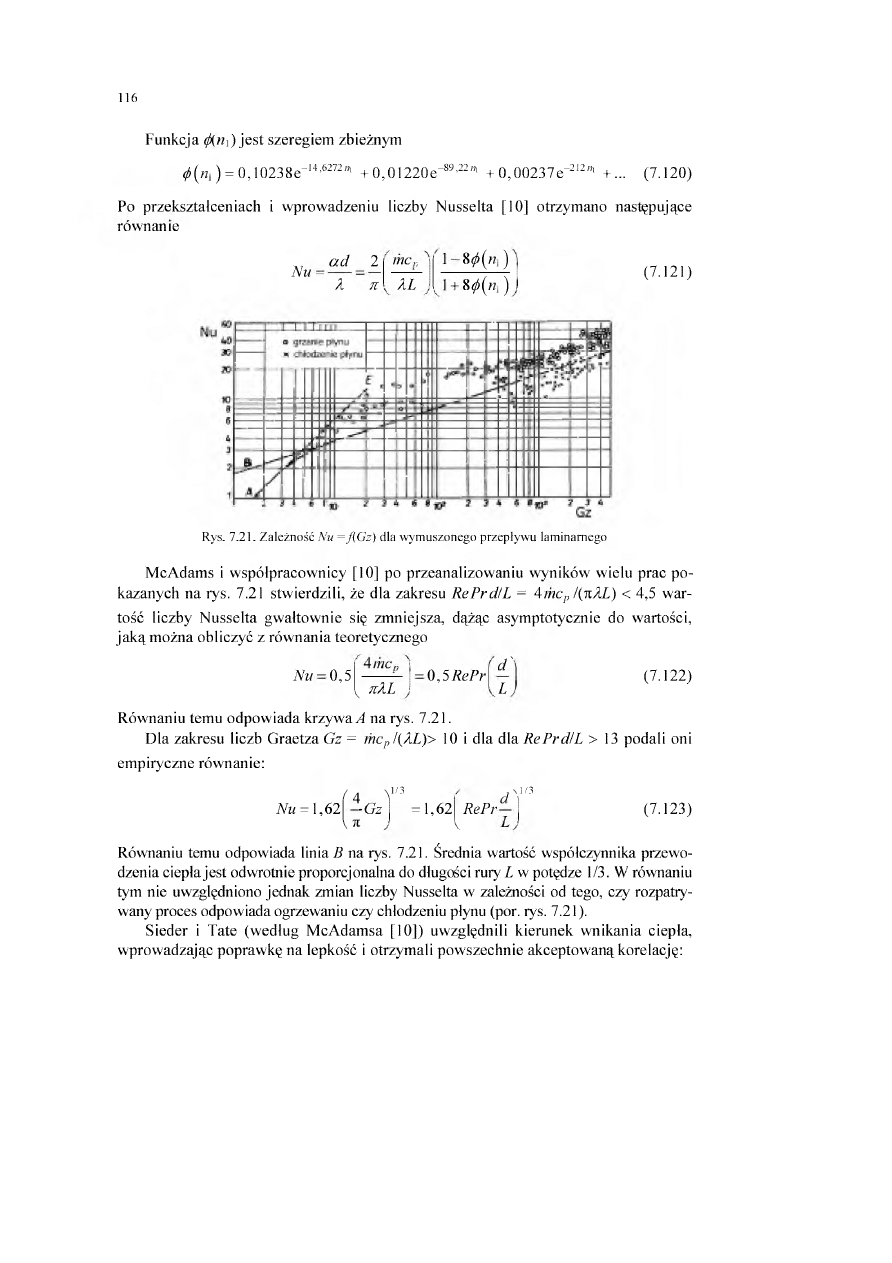
116
F unkcja $ » j ) je s t szeregiem zbieżnym
^ ( « i ) = 0,10238e~ l4-6272ni + 0 , 01220 e-89,22"1 + 0,00237e~ 2l2"‘ + ...
(7.120)
Po przekształceniach i w prow adzeniu liczby N usselta [10] otrzym ano następujące
rów nanie
N u —
a d _ 2
A
71
m c r
AL
■H{rh )
%(/>(»])
(7.121)
Rys. 7.21. Zależność Nu = f{G z) dla w ym uszonego przepływu lam inam ego
M cA dam s i w spółpracow nicy [10] po przeanalizow aniu w yników wielu prac p o
kazanych n a rys. 7.21 stw ierdzili, że dla zakresu Re P r dlL = 4 m c p /{nAL) < 4,5 w ar
tość liczby N usselta gw ałtow nie się zm niejsza, dążąc asym ptotycznie do w artości,
ja k ą m ożna obliczyć z rów nania teoretycznego
d '
N u ~ 0 , 5
\
nAL
- 0,5 Re P r
L
(7.122)
R ów naniu tem u odpow iada krzyw a A n a rys. 7.21.
D la zakresu liczb G raetza Gz = mcp /(AL)> 10 i dla dla Re P r dlL > 13 podali oni
em piryczne rów nanie:
N u = 1,62
/ 4
V'3
-Gz
{71
= 1,62 ReP r
d
x l/3
V
(7.123)
Równaniu temu odpowiada linia B na rys. 7.21. Średnia wartość współczynnika przewo
dzenia ciepła jest odwrotnie proporcjonalna do długości rury L w potędze 1/3. W równaniu
tym nie uwzględniono jednak zmian liczby Nusselta w zależności od tego, czy rozpatry
wany proces odpowiada ogrzewaniu czy chłodzeniu płynu (por. rys. 7.21).
Sieder i Tate (w edług M cA dam sa [10]) uw zględnili kierunek w nikania ciepła,
w prow adzając popraw kę n a lepkość i otrzym ali pow szechnie akceptow aną korelację:

117
\
0 ,1 4
JVw = l,86
T]_
Vvs)
-Gz
13
=
1 ,8 6
f
^ • 14
j L
k
V
s
)
RePr-
L
13
(7.124)
Korelacja ta obowiązuje dla zakresu RePrd/L > 13. Poprawkę oblicza się ze sto
sunku współczynników lepkości płynu w jego średniej temperaturze i w średniej tem
peraturze ścianki. Inne parametry fizyczne cieczy należy określić dla średniej tempe
ratury strumienia, obliczonej jako średnia arytmetyczna temperatury na wlocie i na
wylocie z aparatu.
Jeżeli założymy, że ogólną zależność dla wymuszonego przepływu wewnątrz rury
w zakresie przepływu laminamego można przedstawić w postaci
(7.125)
liczba podstawowych parametrów wymiarowanych wynosi 8, liczba zasadniczych
wymiarów zaś 4, to liczba modułów bezwymiarowych jest równa 4. W wyniku anali
zy wymiarowej otrzymuje się zależność między modułami bezwymiarowymi:
Nu = CRe Pr
rd_ Y
, L y
(7.126)
Na podstawie badań doświadczalnych ustalono, że wykładniki liczb bezwymiarowych
są sobie równe: a = b = c = 1/3.
Badacze rosyjscy (por. np. [3]) przyjęli, że podstawowym czynnikiem kształtują
cym rozkład prędkości i temperatury są siły wyporu, czyli konwekcja swobodna;
ogólna zależność ma zatem następującą postać:
« = f { w ,d ,V ,A ,P ,c P,g,& T,P)
(7.127)
Liczba podstawowych parametrów wymiarowanych wynosi 10, liczba zasadniczych
wymiarów 5, więc liczba modułów bezwymiarowych jest równa 5.
W wyniku analizy wymiarowej uzyskano następującą zależność modułów bez
wymiarowych
Nu - CRea Prh Gac Vd
gdzie V= NT/L Ga = gd\ p
2
h f .
Na podstawie danych doświadczalnych Michiejew [3] otrzymał korelację
(7.128)
Su - 0.15.7/ R ł -33Pr
0
-43Gr":
r />,. ^ - 25
Pi\
(7.129)
w której: Gr = GaV= g d \ p
2
ATj3hj
2
- liczba Grashofa, liczona dla średniej temperatu
ry płynu, Pr - liczba Prandtla liczona dla średniej temperatury płynu, Pi\ - liczba Prand-
tla liczona dla średniej temperatury ściany, AT - średnia różnica temperatury ściany i
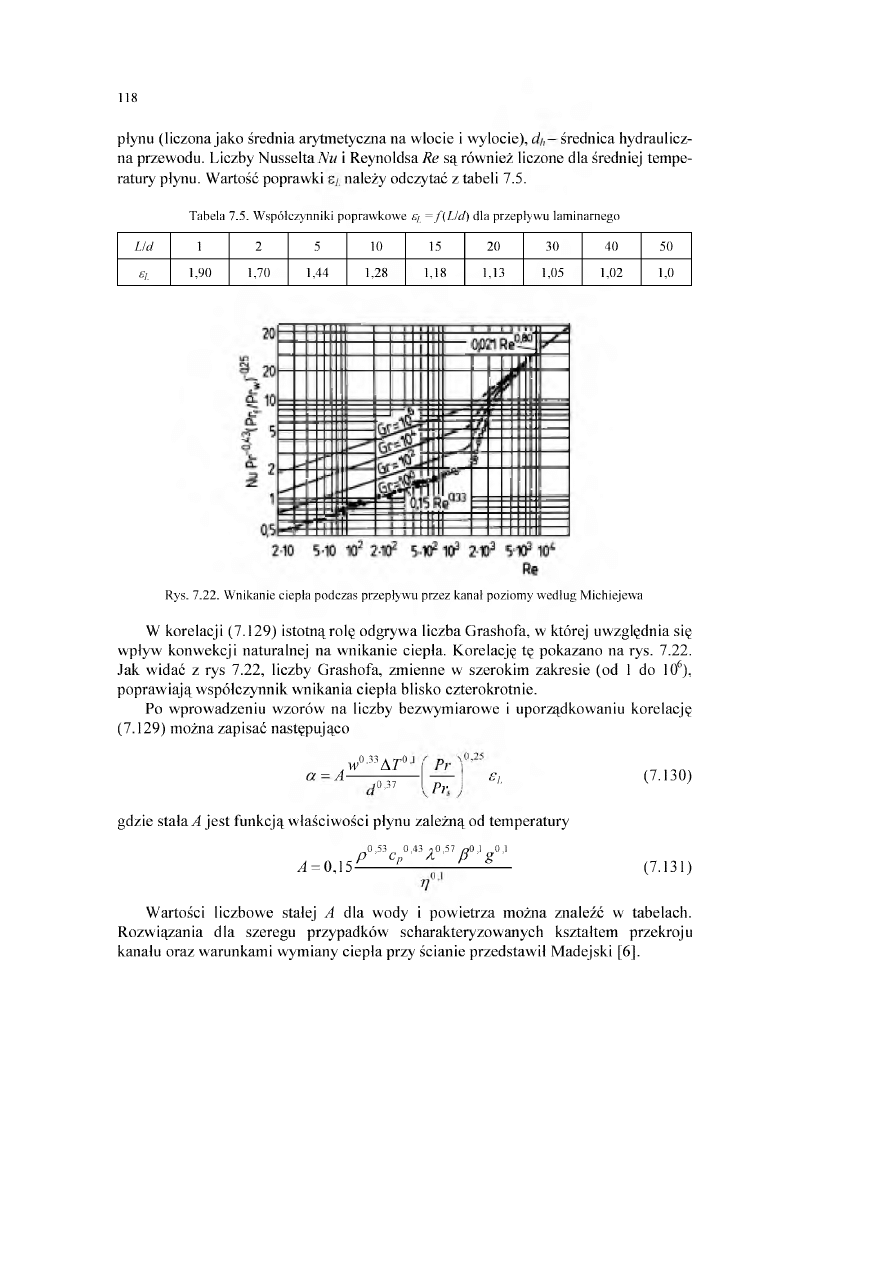
118
płynu (liczona jak o średnia arytm etyczna n a wlocie i wylocie),
d
średnica hydraulicz
n a przewodu. Liczby N usselta JVw i R eynoldsa ife są rów nież liczone dla średniej tem pe
ratury płynu. W artość popraw ki
należy odczytać z tabeli 7.5.
Tabela 7.5. Współczynniki poprawkowe
eL =f(L!d)
dla przepły wu laminarnego
U d
1
2
5
10
15
20
30
40
50
u
1,90
1,70
1,44
1,28
1,18
1,13
1,05
1,02
1,0
Rys.
7.22.
Wnikanie ciepła podczas przepływu przez kanał poziomy według Michiejewa
W korelacji (7.129) istotną rolę odgryw a liczba G rashofa, w której uw zględnia się
w pływ konw ekcji naturalnej n a w nikanie ciepła. K orelację tę pokazano n a rys. 7.22.
Jak w idać z rys 7.22, liczby G rashofa, zm ienne w szerokim zakresie (od 1 do 106),
po p raw iają w spółczynnik w nikania ciepła blisko czterokrotnie.
Po w prow adzeniu w zorów n a liczby bezw ym iarow e i uporządkow aniu korelację
(7.129) m ożna zapisać następująco
a ~ A
w
0-33AT0-
j0,37
P)\
Sl.
(7.130)
gdzie stała
A
je s t fu n k cją w łaściw ości płynu zależną od tem peratury
¿ = 0,15
/70-53c / - 43A°-57/ J g 0J
(7.131)
W artości liczbow e stałej
A
dla wody i pow ietrza m ożna znaleźć w tabelach.
R ozw iązania dla szeregu przypadków scharakteryzow anych kształtem przekroju
kanału oraz w arunkam i w ym iany ciepła przy ścianie przedstaw i! M adejski [6].

119
7.6. Wnikanie ciepła w obszarze przejściowym
Z godnie z zasadam i hydrodynam iki przejście od przepływ u lam inam ego do prze
pływ u burzliw ego następuje w zakresie liczb R eynoldsa około 2 1 0 0 -2 3 0 0 [4]. W y
stępuje je d n a k strefa przejściow a, w której przepływ lam inam y stopniow o zanika,
a przepływ staje się w pełni burzliw y dopiero dla
R e
= 104. Z ależność m odułu Nussel-
ta od liczby R eynoldsa w różnych obszarach przepływ u w ym uszonego w rurach dla
płynu o liczbie
P r
= 1 oraz
ij/i]s
= 1 przedstaw iono n a rys. 7.23. Poniew aż w obszarze
przejściow ym proces w nikania ciepła nie je s t ustabilizow any i w yniki pom iarów nie
są jednakow e, więc m ożna przyjąć dla tego zakresu liniow ą interpolację liczby Nus-
selta w układzie logarytm icznym . Interpolacji dokonujem y m iędzy w artościam i
N u
obliczonym i kolejno dla
R e
= 2100 z korelacji dla przepływ u lam inam ego oraz dla
R e
= 104 dla burzliw ego przepływ u. Podany sposób interpolacji je s t tylko przybliże
niem , poniew aż funkcja
\gN u = f{ \g R e )
nie je s t dokładnie pro stolinio w ą zależnością.
M cA dam s [10] p oleca korzystać z wykresu C o lb u m a (rys. 7.24), zw łaszcza dla
cieczy lepkich:
Hu
'
Fi Ina I* f lr e p iir in n w
^
-liu rz iw ^ _
K
2
IP1?™
V?
10®
R*
Rys. 7.23. Zależność
Nu =fiRe)
dla
Pr =
1 oraz
/]//], =
1
/
\0J4
= f { R e )
(7.132)
gdzie
j H
=
S t P r213
=
N u /(R e P r m ).
Hausen [4] dla przepływ u w szerokim zakresie liczb R eynoldsa (2300 < Re < 106)
opracow ał zależność korelacyjną
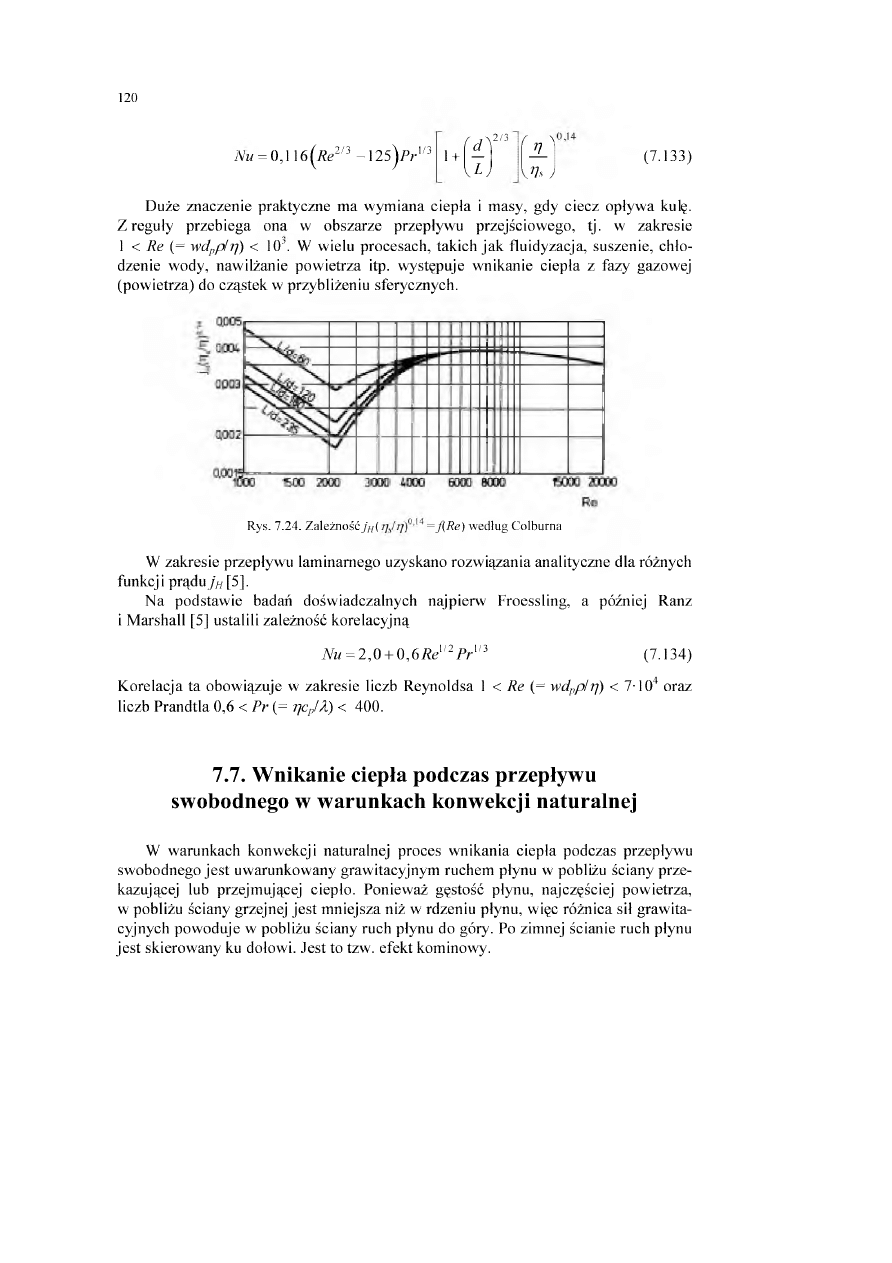
120
JVM = 0 , 1 1 6 ( t e 2/3 - 1 2 5
) P r 113
i l \
2 /3
f
\
^ A d
n
1+
—
U
j
W
)
(7.133)
D uże znaczenie praktyczne m a w ym iana ciep ła i m asy, gdy ciecz opływ a kulę.
Z reguły przebiega ona w obszarze przepływ u przejściow ego, tj. w zakresie
1 <
R e
(=
w dpp h j ) <
10'\ W wielu procesach, takich ja k fluidyzacja, suszenie, chło
dzenie wody, naw ilżanie p ow ietrza itp. w ystępuje w nikanie ciepła z fazy gazowej
(pow ietrza) do cząstek w przybliżeniu sferycznych.
Rys. 7.24. Zależność
j H( = f i R e )
według Colburna
W zakresie przepływ u lam inam ego uzyskano rozw iązania analityczne dla różnych
funkcji p rą d u
J h
[5].
N a podstaw ie badań dośw iadczalnych najpierw Froessling, a później R anz
i M arshall [5] ustalili zależność k orelacyjną
N u = 2 ,0 + 0 , 6 R e 112 P r 113
(7.134)
K orelacja ta obow iązuje w zakresie liczb R eynoldsa
1 <
R e
(= wdpphj) < 7-104
oraz
liczb P randtla 0,6 <
P r
(=
r/CpIA) <
400.
7.7.
Wnikanie ciepła podczas przepływu
swobodnego w warunkach konwekcji naturalnej
W w arunkach konw ekcji naturalnej proces w nikania ciepła podczas przepływ u
sw obodnego je s t uw arunkow any graw itacyjnym ruchem płynu w pobliżu ściany prze
kazującej lub przejm ującej ciepło. Poniew aż gęstość płynu, najczęściej pow ietrza,
w pobliżu ściany grzejnej je s t m niejsza niż w rdzeniu płynu, więc różn ica sil graw ita
cyjnych pow oduje w pobliżu ściany ruch płynu do góry. Po zim nej ścianie ruch płynu
je s t skierow any ku dołow i. Jest to tzw . efekt kom inow y.
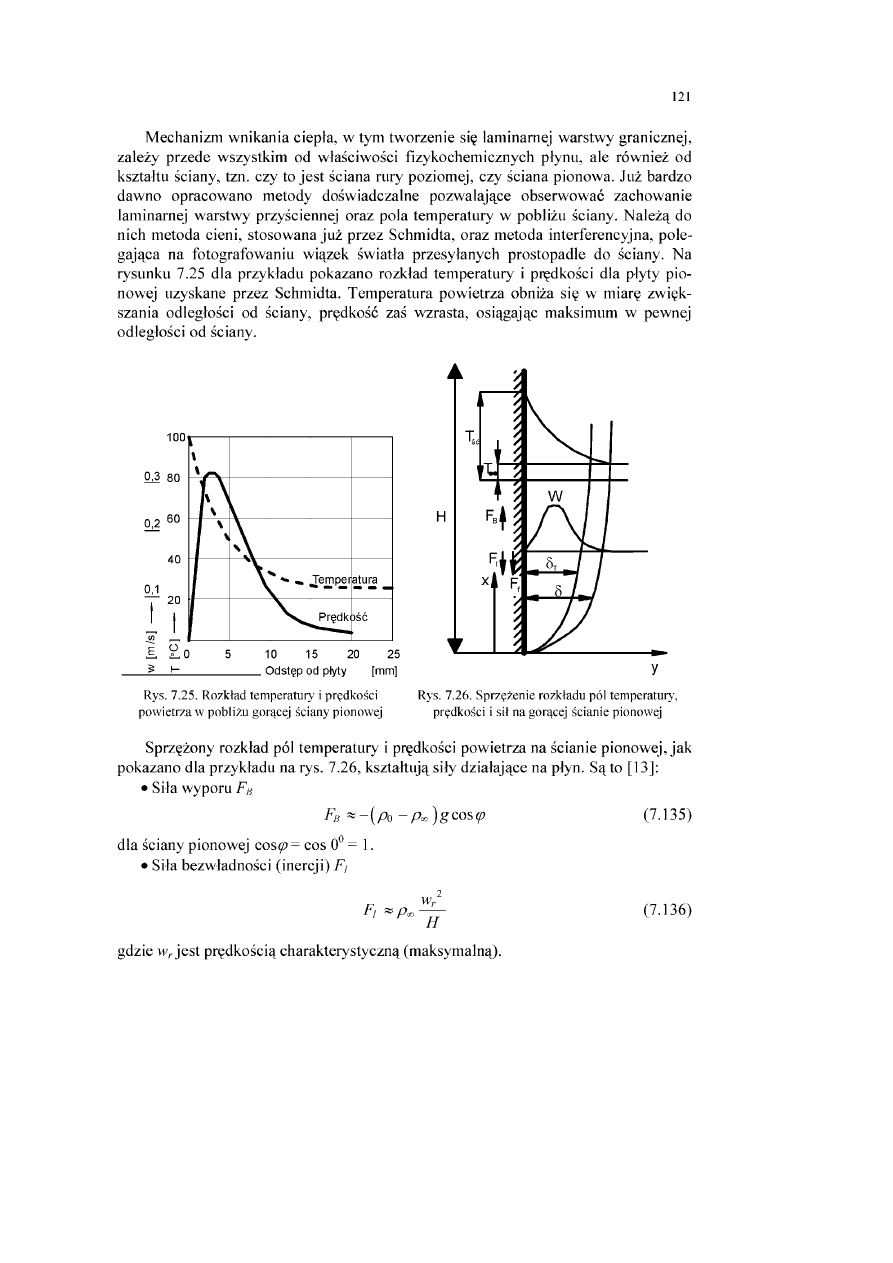
121
Mechanizm wnikania ciepła, w tym tworzenie się laminamej warstwy granicznej,
zależy przede wszystkim od właściwości fizykochemicznych płynu, ale również od
kształtu ściany, tzn. czy to jest ściana rury poziomej, czy ściana pionowa. Już bardzo
dawno opracowano metody doświadczalne pozwalające obserwować zachowanie
laminarnej warstwy przyściennej oraz pola temperatury w pobliżu ściany. Należą do
nich metoda cieni, stosowana już przez Schmidta, oraz metoda interferencyjna, pole
gająca na fotografowaniu wiązek światła przesyłanych prostopadle do ściany. Na
rysunku 7.25 dla przykładu pokazano rozkład temperatury i prędkości dla płyty pio
nowej uzyskane przez Schmidta. Temperatura powietrza obniża się w miarę zwięk
szania odległości od ściany, prędkość zaś wzrasta, osiągając maksimum w pewnej
odległości od ściany.
100
0,3 80
0,2
0,1
60
40
20
1
\
V \
\
\
\
\ \
%
T e m p e r atura
P rę d k i )ŚĆ
E. ¿Lo
10
15
20
25
O d s tę p od płyty
[m m ]
Rys. 7.25. Rozkład temperatury’ i prędkości
pow ietrza w pobliżu gorącej ściany pionowej
Rys. 7.26. Sprzężenie rozkładu pól temperatury’,
prędkości i sił na gorącej ścianie pionowej
Sprzężony rozkład pól temperatury i prędkości powietrza na ścianie pionowej, jak
pokazano dla przykładu na rys. 7.26, kształtują siły działające na płyn. Są to [13]:
• Siła wyporu FB
F
b
~ -(p o -A c)geosę>
(7.135)
dla ściany pionowej cos<^= cos 0° = 1.
• Siła bezwładności (inercji) Fj
w
r2
(7.136)
gdzie wr jest prędkością charakterystyczną (maksymalną).

122
Siła tarcia wewnętrznego Ff
Ff
kti
HV
J 2
(7.137)
W pobliżu ściany (w warstwie granicznej) siły inercji są takie same jak siły tarcia,
co można zapisać:
w,
w,
'■
v —
h
?
(7 J3 8 >
Po przekształceniu otrzymujemy równanie określające grubość laminamej warstwy
granicznej:
z
V/2
V
8
_
H
w, II
Również siły wyporu są porównywalne z siłami inercji, a zatem
7
W,
-(po - p x )gcos<p&px
H
Po przekształceniu otrzymujemy
w.
~(po - p x )H gcosę
Pm
12
Po podstawieniu tej zależności do równania (7.139) otrzymujemy
/
9
V/4
s_
H
v
/
\
gH~ cosę
Po
Ao)
Jeżeli wprowadzimy do wyrażenia różnicę gęstości
PO Po0
Po'j jlcO (^0 ^OO )
otrzymamy zależność określającą grubość warstwy granicznej
«,
(
9
V /4 /
.
\ l /4
O
V "
1
H ~ p n f a - T ^ g H * )
U os^y
a tym samym
(7.139)
(7.140)
(7.141)
(7.142)
(7.143)
(7.144)
(7.145)

123
Liczba Grashofa jest odwrotnością wyrażenia w poprzednim równaniu
Cr gH
3
(T
0
-T „ ) &
Grubość laminamej warstwy granicznej jest więc odwrotnie proporcjonalna do liczby
Grashofa w potędze 1/4, a wprost proporcjonalna do wysokości ściany.
Już w 1881 r. Lorenz [10] ustalił, od jakich wielkości zależy wnikanie ciepła
w warunkach konwekcji naturalnej. Po scałkowaniu różniczkowego równania prze
wodzenia ciepła w ruchomym płynie otrzymał on równanie bezwymiarowe
a H
~Y
- 0,548
i ncp \
( g f f 3p 2/ ? A T Y
y X )
1/4
(7.146)
Dla gazów idealnych /? = \/T. Wielu badaczy, między innymi Nusselt, skorzystali
z tej zależności do korelowania wyników badań w odniesieniu do rur. Zamiast wyso
kości ściany //podstawiali średnicę zewnętrzną dz.
Współczynnik wnikania ciepła podczas konwekcji naturalnej
a ^ f ( A , V , c p , A T , h , p , / 3 , g )
(7.147)
zależy od współczynnika przewodzenia ciepła X, lepkości p, ciepła właściwego cp,
różnicy temperatury AT, wymiaru liniowego h przedmiotu (dla rury poziomej h = d),
gęstości p, współczynnika rozszerzalności objętościowej płynu /3 i przyspieszenia
ziemskiego g.
W wyniku analizy wymiarowej (« = 9, r = 5 i m = 4) otrzymujemy równanie kry -
terialne:
Nu - C
ycp
X
\a
gfr p ‘
ł
]2
\ h
{pAT)C
(7.148)
w którym liczba NusseltaM/jest funkcją liczby Prandtla Pr. Galileusza Ga i liczby V.
Ponieważ doświadczalnie ustalono, że wykładniki potęgowe dla poszczególnych
liczb bezwymiarowych sąjednakowe, najczęściej spotyka się zapis w postaci
Nu = CGr'Pr‘ =CRd
(7.149)
gdzie: liczba Grashofa Gr = GaV, liczba Rayleigha (Strutta) Ra = GrPr.
Graficzną postać tej korelacji przedstawiono na rys. 7.27. W układzie podwójnie
logarytmicznym nie jest to linia prosta, więc dla lepszego przybliżenia krzywą podzie
lono na trzy odcinki; dla małych wartości X = GrPr przepływ swobodny jest laminar
ny, dla średnich - przejściowy, dla dużych - burzliwy.
Wartości wykładnika potęgowego i oraz stałej C dla różnych zakresów konwekcji
zestawiono w tabeli 7.6. Wszystkie parametry fizykochemiczne płynu wyznacza się
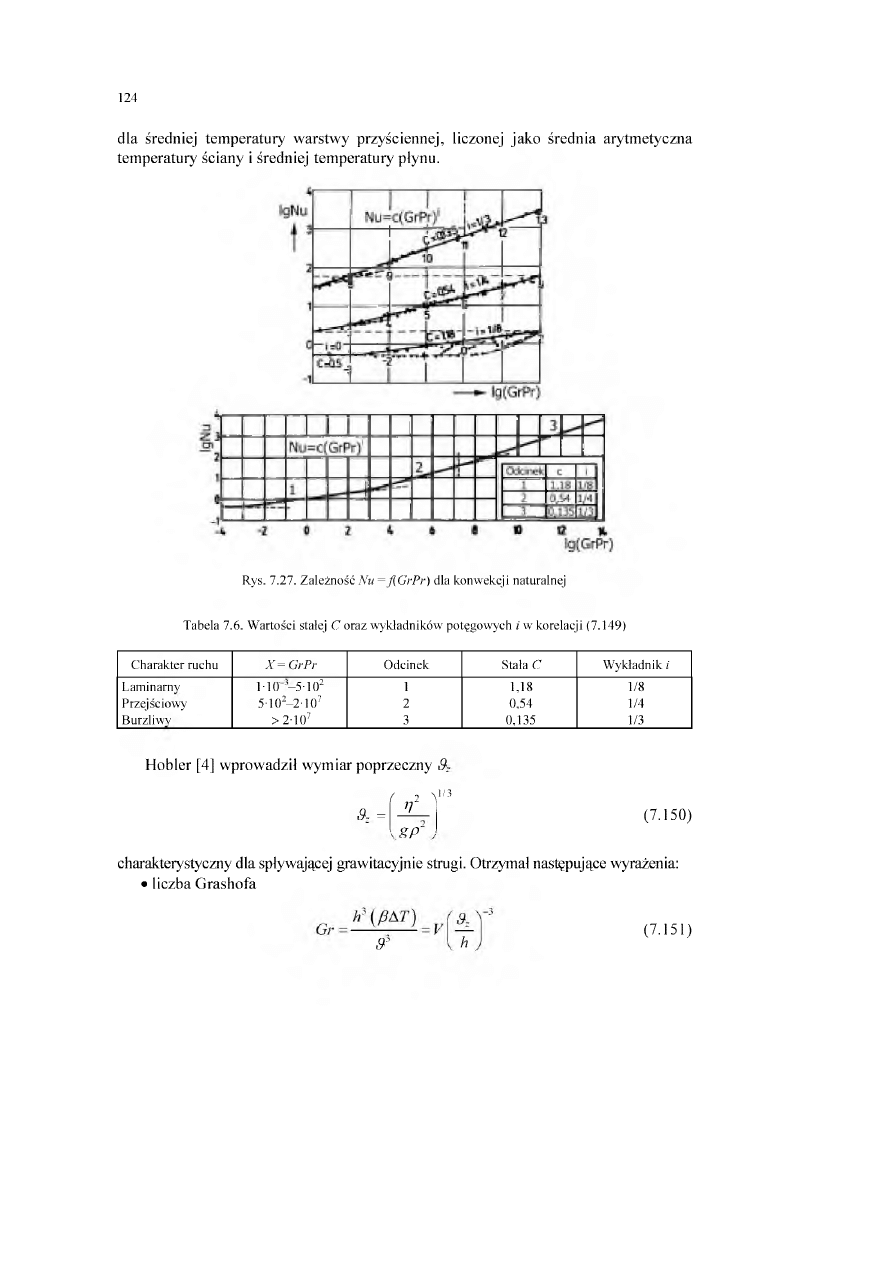
124
dla średniej tem peratury w arstw y przyściennej, liczonej jak o średnia arytm etyczna
tem peratury ściany i średniej tem peratury płynu.
Rys. 7.27. Zależność Nu = f(G rP r) dla konwekcji naturalnej
Tabela 7.6. W artości stałej C oraz w ykładników potęgowych i w korelacji (7.149)
Charakter ruchu
X = GrPr
O dcinek
Stała C
W ykładnik i
Laminarnv
M O -5 -1 0
2
1
1,18
1/8
Przejściowy
5-10
2
—2-10
7
2
0,54
1/4
Burzliwy
>
2
-
10 7
3
0,135
1/3
H obler [4] w prow adzi! w ym iar poprzeczny 3:
3- =
(
i \l/3
>f
8
P~
(7.150)
charakterystyczny dla spływającej grawitacyjnie strugi. Otrzyma! następujące wyrażenia:
• liczba G rashofa
3 3
h
(7.151)

125
• liczba V
Równanie (7.149) można więc przekształcić do następującej postaci:
V - (3AT
(7.152)
( a 3 z ^ h
— = CV
\ ż
,
3;
U J
dzięki czemu otrzymujemy zależność nowych modułów bezwymiarowych
f O V - 3('
fY
Q
JVm = — - = CV'Pr'
X
V
h j
(7.153)
Wartości stałej C dla różnych zakresów konwekcji i rozmaitych geometrii układu
zestawiono w tabeli 7.7.
Przez ograniczenie zakresu zastosowania równań uogólnionych można otrzymać
równania o prostej budowie, przydatne w praktyce. Dla ściany pionowej najczęściej
mamy do czynienia z obszarem przejściowym (5-102 < GrPr (= VPr(3z/h))~3 < 2-107),
gdzie i = 1/4, C = 0,54 oraz
a - A
r
A T \ y4
v h ,
[ W/(m -K)]
(7.154)
Równania (7.149) ¡(7.153) można wówczas sprowadzić do prostej postaci. Współ
czynnik A jest funkcją temperatury danego płynu. Wartości tego współczynnika dla
powietrza i wody zestawiono w tabelach 7.8 i 7.9.
Tabela 7.7. W artości stałej C d laW = G rP r= VPr(9Jh) (równ. (7.153))
Lp.
Układ
Od W,
Do W
2
C
Powyżej X 2
C
Źródło
1
Ściana pionowa,
cylinder pionowy
104
5-10
2
109
2
-
10 7
0,59
0,54
>
109
>
2
-
10 7
0,13
Weise, Saunders,
McAdams,
Michiejew
2
Rura pozioma,
drut
103
103
109
109
0,53
0,47
>
109
0,11
Eberle, Wamsler,
Koch, McAdams,
Rice,
Brown i Marco
3*
Płyta pozioma,
oddająca ciepło
do góry
105
2
-
10 7
0,54
>
2
-
10 7
0,14
Fishenden i Saunders
4
Płyta oddająca
ciepło w dół
103
109
0,35
>
109
0,08
Brown i Marco
‘Dla płyty poziomej h odpowiada krótszemu bokowi. Dla płyt, w których h > 0,6 m, należy przyjąć hmax = 0,6 m.
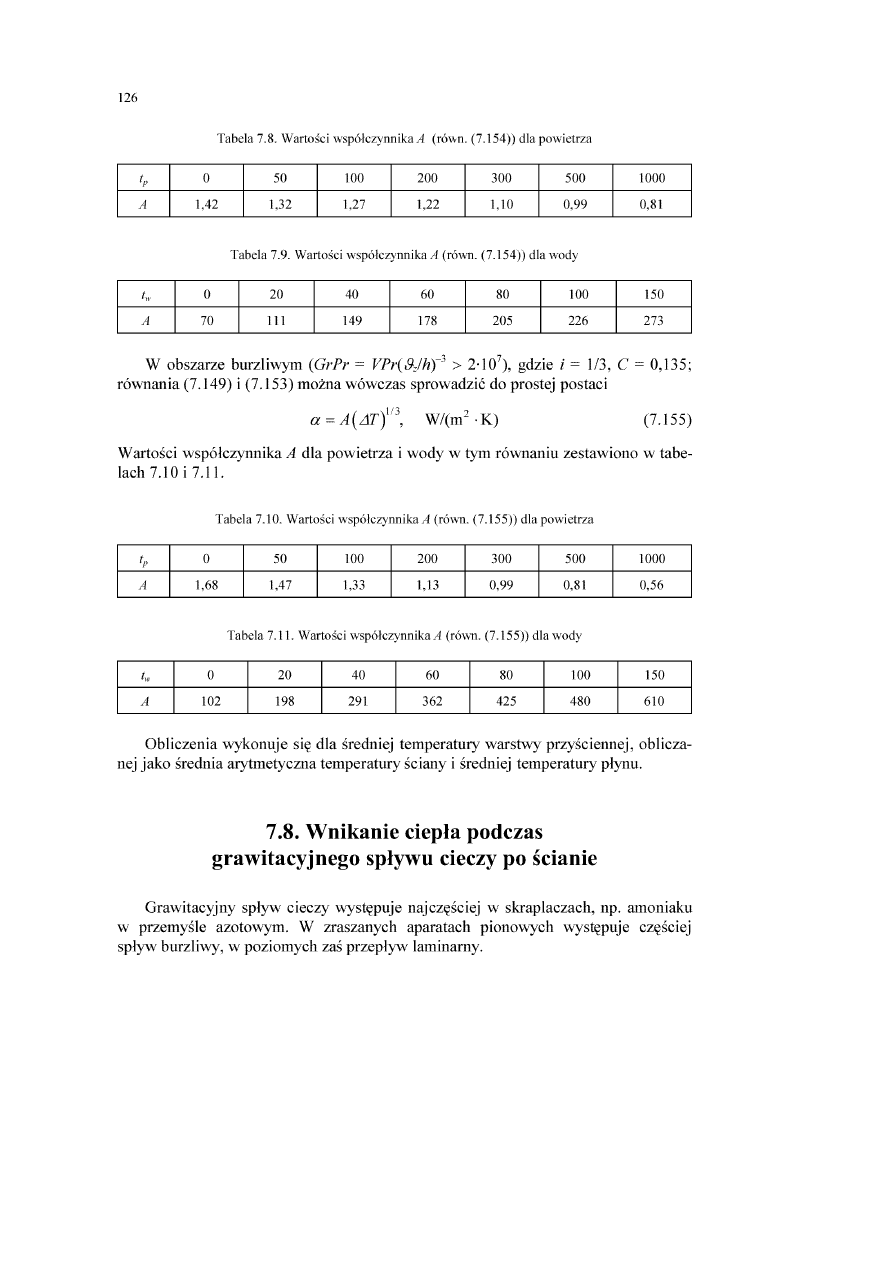
126
Tabela 7.8. W artości w spółczynnika A (równ. (7.154)) dla pow ietrza
tp
0
50
100
200
300
500
1000
A
1,42
1,32
1,27
1,22
1,10
0,99
0,81
Tabela 7.9. W artości w spółczynnika A (równ. (7.154)) dla wody
At
0
20
40
60
80
100
150
A
70
111
149
178
205
226
273
W obszarze burzliwym (GrPr = VPr(&Jh)3 > 2-10 ). gdzie i = 1/3, C = 0,135;
równania (7.149) i (7.153) można wówczas sprowadzić do prostej postaci
a - A ( A T ) 3,
W/(m2 -K)
(7.155)
Wartości współczynnika A dla powietrza i wody w tym równaniu zestawiono w tabe
lach 7.10 i 7.11.
Tabela 7.10. W artości w spółczynnika A (równ. (7.155)) dla pow ietrza
tp
0
50
100
200
300
500
1000
A
1,68
1,47
1,33
1,13
0,99
0,81
0,56
Tabela 7.11. W artości w spółczynnika A (równ. (7.155)) dla wody
At
0
20
40
60
80
100
150
A
102
198
291
362
425
480
610
Obliczenia wykonuje się dla średniej temperatury warstwy przyściennej, oblicza
nej jako średnia arytmetyczna temperatury ściany i średniej temperatury płynu.
7.8.
Wnikanie ciepła podczas
grawitacyjnego spływu cieczy po ścianie
Grawitacyjny spływ cieczy występuje najczęściej w skraplaczach, np. amoniaku
w przemyśle azotowym. W zraszanych aparatach pionowych występuje częściej
spływ burzliwy, w poziomych zaś przepływ laminamy.

127
N ajpierw rozw aża się opory cieplne podczas konw ekcji zachodzącej m iędzy p o
w ierzchnią ściany a gazem (pow ietrzem ), oddzielonym od ściany spływ ającą w arstw ą
cieczy (rys. 7.28). Jeżeli w arstw a ta je s t cienka, to przekazyw anie ciepła w zasadzie
zależy od w łaściw ości opływ ającego gazu, gdy natom iast je s t ona gruba, spływ cieczy
je s t z reguły burzliw y.
Rys. 7.28. Schem at w nikania ciepła
podczas grawitacyjnego spływu cieczy
Przyjm ijm y schem at rozkładu tem peratury ja k n a rys 7.28, gdzie ,v je s t średnią
grubością w arstw y cieczy. Strum ień ciepła m ożem y w yrazić za p o m ocą rów nania
N ew tona opisującego opór w nikania ciepła od gazu do cieczy
Q ^ a KA cA T '
(7.156)
Przew odzenie ciepła przez w arstw ę cieczy w przypadku ustalonego ruchu ciepła
opisuje rów nanie F ouriera
Q ^ - A A T "
(7.157)
,v
W w arstw ie cieczy niew ielkiej grubości niezależnie od kształtu pow ierzchni chłodzą
cej pow ierzchnia przekroju poprzecznego je s t stała A c = A.
Po przekształceniu rów n. (7.156) i (7.157) otrzym ujem y
A T ' = - 0 —
(7.158)
a KA
oraz
A A
(7.159)

128
Po dodaniu obu równań stronami otrzymujemy wzór na całkowitą różnicę tempe
ratury:
A T ^ A T ' + A T " ^ —
A Ka g
A j
(7.160)
Wprowadźmy zastępczy współczynnik wnikania ciepła, opisujący cały proces ru
chu ciepła
wówczas otrzymamy
a
a g
A
O = a A AT
(7.161)
(7.162)
Składową oporu cieplnego w procesie przewodzenia ciepła w warstwie cieczy
można opisać za pomocą zastępczego współczynnika wnikania:
Otrzymujemy równanie
a ■
■
a g + a z
(7.163)
(7.164)
Wyznaczenie zastępczego współczynnika wnikania ciepła a
2
w warstwie cieczy
spływającej grawitacyjnie wymaga określenia grubości tej warstwy.
Można ją obliczyć analitycznie, jeśli spływ cieczy jest uwarstwiony. Dostępne
w literaturze liczne wzory do obliczania zastępczej grubości warstwy cieczy można
zapisać w następującej postaci
sfr - — 3, Re J
13
C ‘
‘
(7.165)
gdzie:
f
O
V / 3
77"
y f g
A r
71
stała C = 1,47 dla skroplin na rurze pionowej oraz C = 1,2 dla skroplin na rurze po
ziomej .
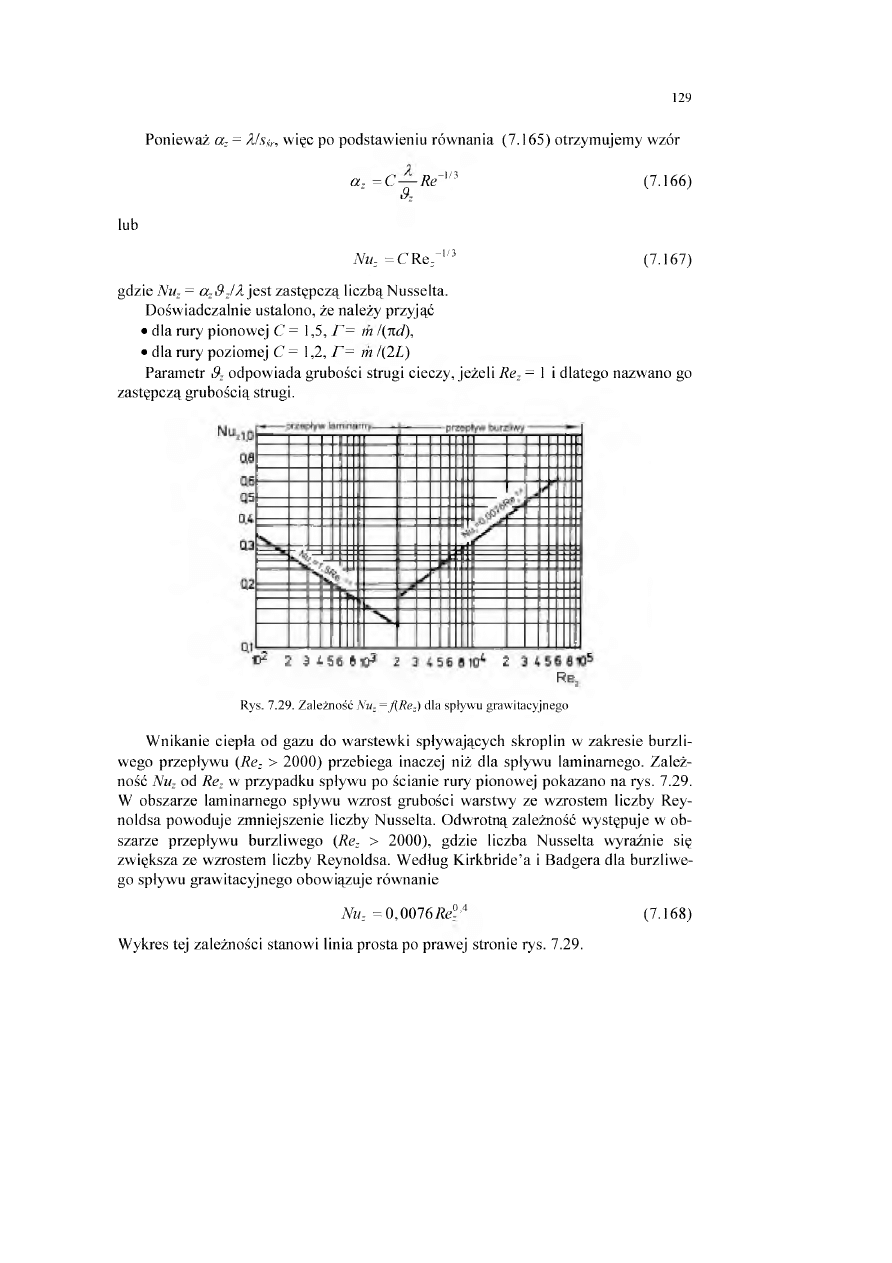
129
P oniew aż a : = AAv<r, więc po podstaw ieniu rów nania (7.165) otrzym ujem y wzór
a z = C — Re~m
(7.166)
9Z
lub
N u z = C R e / l/3
(7.167)
gdzie N u: = a : 3-JX je s t zastępczą liczbą N usselta.
D ośw iadczalnie ustalono, że należy przyjąć
• dla rury pionow ej C = 1,5, F = m l{nd),
• dla rury poziom ej C = 1,2, F = m /(2L)
Param etr 3Z odpow iada grubości strugi cieczy, jeżeli R e: = 1 i dlatego nazw ano go
zastęp czą grubością strugi.
v
2
3 4 S e i t f i
t
R
e
>:
Rys. 7.29. Zależność N u. = fiR e :) dla spływu grawitacyjnego
W nikanie ciepła od gazu do w arstew ki spływ ających skroplin w zakresie burzli
wego przepływ u {Rez > 2000) przebiega inaczej niż dla spływu lam inam ego. Z ależ
ność N u: od Re: w przypadku spływu po ścianie rury pionow ej pokazano n a rys. 7.29.
W obszarze lam inam ego spływu w zrost grubości w arstw y ze w zrostem liczby Rey
n oldsa pow oduje zm niejszenie liczby N usselta. O dw rotną zależność w ystępuje w ob
szarze przepływ u burzliw ego {Rez > 2000), gdzie liczba N usselta w yraźnie się
zw iększa ze w zrostem liczby R eynoldsa. W edług K irk b rid e’a i B adgera dla burzliw e
go spływu graw itacyjnego obow iązuje rów nanie
N u z
=0,0076/te?''4
(7.168)
W ykres tej zależności stanow i linia p ro sta po praw ej stronie rys. 7.29.

130
7.9. Wnikanie ciepła podczas skraplania pary nasyconej
Proces skraplania pary w ystępuje zaw sze, gdy p ara nasyco na styka się ze ścianą
o tem peraturze niższej od tem peratury n asycenia pary pod danym ciśnieniem . Pierw
sze kropelki cieczy tw o rzą się w m ikroskopijnych w głębieniach n a pow ierzchni ścia
ny. K olejne krople zlew ają się w cienką w arstw ę, tw orząc film (blonkę) kondensatu,
spływ ający graw itacyjnie w dół ściany. W ytw arza się jed nokierunkow y ruch cząste
czek pary w kierunku do ściany, a skraplanie pary zachodzi ju ż n a pow ierzchni film u
cieczy. T ow arzyszy tem u gw ałtow ne zm niejszenie objętości oraz przekazanie ciepła
skraplania do ściany. Proces ten, nazyw any w nikaniem ciepła podczas skraplania pary
nasyconej, je s t tym intensyw niejszy, im w iększa je s t ró żn ica m iędzy tem peratu rą pary
nasyconej a tem peraturą n a pow ierzchni ściany. G łów ny opór w nikania ciepła je s t
skoncentrow any w film ie kondensatu, w którym zachodzi przew odzenie ciepła. Waż
n ą rolę odgryw a zatem grubość film u kondensatu, która się zw iększa ku dołow i ścia
ny, co pow oduje zm niejszenie w artości lokalnych w spółczynników w nikania ciepła.
Jest to tzw . kondensacja film ow a, którą schem atycznie pokazano n a rys. 7.30. K on
densacja film ow a zachodzi wtedy, gdy ciecz kondensatu dobrze zw ilża pow ierzchnię
ściany, czyli siły adhezji p rzew ażają nad siłam i kohezji.
Gdy siły napięcia pow ierzchniow ego kropli (siły kohezji) są w iększe od sił adhe
zji (przylegania), kropelki kondensatu szybko odryw ają się od ściany i opadają, nie
tw orząc film u cieczy. T aką kondensację nazw ano kropelkow ą (perlistą). W ystępuje
ona zaw sze n a dolnej pow ierzchni płyty poziom ej oraz n a pow ierzchniach słabo zw il
Rys. 7.30. Schem at w nikania ciepła podczas
skraplania pary nasyconej na ścianie pionowej

131
żanych przez ciecz. Brak zwilżalności powierzchni można także uzyskać przez powle
kanie ściany takimi substancjami, jak np. kwasy tłuszczowe lub przez dodanie odpo
wiedniego składnika do pary. Podczas skraplania kropelkowego warstewka kondensa
tu praktycznie nie istnieje, co powoduje zmniejszenie oporu cieplnego i wzrost
współczynników wnikania ciepła. Są one wielokrotnie większe niż w kondensacji
filmowej, osiągając wartości 10' W/(m2-K). Zjawisko kondensacji kropelkowej jest
także charakterystyczne dla świeżych powierzchni. Jednak po pewnym czasie eksplo
atacji w wyniku powstawania wżerów, osadów czy zmycia powlekanej substancji na
powierzchni zachodzi kondensacja filmowa. Ma ona podstawowe znaczenie dla pracy
skraplaczy, nazywanych też kondensatorami.
Proces wnikania ciepła podczas kondensacji filmowej badano zarówno metodami
eksperymentalnymi, jak i analitycznymi (prace Nusselta). Najpierw rozpatruje się
równania empiryczne [4], w tym opisy modelowe procesu, aby ustalić zmienne zależ
ne. Na powierzchni ciekłego filmu spływającego po ścianie skrapla się strumień pary
ńip, z którego powstaje strumień kondensatu mk (rys. 7.30). Strumień ciepła odda
wany powierzchni filmu cieczy przez kondensującą się parę jest równy
Q = mpr
(7.169)
Jest on przewodzony przez warstwę kondensatu zgodnie z równaniem Fouriera
Q ^ — AAT
(7.170)
s
gdzie Ac jest współczynnikiem przewodzenia ciepła cieczy, W/(m-K), a s - średnią
grubością filmu cieczy.
Wnikanie ciepła w tym procesie opisujemy równaniem Newtona
Q = aA A T
(7.171)
gdzie AT= Ts - T ić.
Jeżeli para jest nasycona i nie zachodzi schładzanie kondensatu, to z porównania
równań (7.169) ¡(7.171) otrzymujemy
™Pr
mkr
a -
= ------
(7.172)
A M
AAT
a ponieważ w równaniu tym mk!A - m”, więc otrzymujemy
• " aA T
i ni \
mk -------------------------
(7.173)
r
Z porównania równań (7.170) i (7.171) otrzymujemy natomiast
a = —
(7.174)
s

132
Ogólnie jest to zależność funkcyjna
a = f { \ , s )
(7.175)
Ponieważ średnia grubość warstwy kondensatu zależy od intensywności spływu,
właściwości fizykochemicznych cieczy oraz od parametrów geometrycznych ściany
s = f{m'k',h,Tic ,p c,g )
(7.176)
więc po podstawieniu tego równania do wzoru (7.175) otrzymujemy ogólną zależność
funkcyjną
a = f(m 'k',^ ,V c ,P c ,h ,g )
Uwzględniając równanie (7.173), po podstawieniu otrzymujemy
a = f ( ^ c ,Xc ,p c ,r,H.T,h,g)
(7.177)
(7.178)
Zgodnie z twierdzeniem Buckinghama mamy 8 zmiennych wymiarowanych i 4 zasad
nicze wymiary, a zatem zależność ogólną można przedstawić jako związek 4 modułów
bezwymiarowych.
Na podstawie analizy wymiarowej otrzymuje się równanie
ah
~ T ~
lcCp
Y i
\ Ac j \CpAT j
czyli
Nu = CPra K hGac
(7.179)
(7.180)
Pr jest liczbą Prandtla, Ga liczbą Galileusza dla skroplin, K zaś liczbą kondensacji.
Doświadczalnie wykazano, że zgodnie z wynikami analitycznymi Nusselta, wy
kładniki potęgowe są sobie równe: a = b = c.
Stąd równania (7.179) i (7.180) dają związek
ah
17
= c
( ii
2
gn pć r
Acr/cAT
- CC,
IA
(7.181)
lub
a = C i
r p l Alg
r/c h AT
(7.182)
W korelacji (7.181) dla rur poziomych liczba Nusselta Nu = ad!Ac, Cv natomiast
jest liczbą skraplania Nusselta.

133
Wartości stałej C, zależnej od kształtu i położenia powierzchni, na której zacho
dzi skraplanie, zestawiono w tabeli 7.12.
Tabela 7.12. W spółczynnik C w równaniu (7.181)
Powierzchnia
C
Uwagi
Ściana pionowa, rura pionow a
Rura pozioma, skraplanie zewnętrzne
N rur poziomych jed n a pod drugą
Rura żebrow ana pozioma, skraplanie zewnętrzne
1,13
0,725
0,725Ah/4
0,689
h - wysokość
h = d - średnica
h = D zastępcze
Hobler [4] przekształcił równanie (7.181) przez wprowadzenie zastępczego wy
miaru poprzecznego spływającej warstwy kondensatu
&2
= (vc2/g)1/3. Otrzymał on
wyrażenie na liczbę skraplania
Pc2 r g
r ?i ccc
' h
' 3
A
c
7]cAT C
c AT
Ą
&
■c
J
czyli
Cv =
K
Prc
/ a v 3
y h j
Po podstawieniu tego równania do równania (7.181) przyjmie ono postać
—
^CKyĄPrL
V
Ą
f ^ -
X,
{ h
-3/4
(7.183)
(7.184)
(7.185)
a po obustronnym pomnożeniu przez 9Jh otrzymamy
i n V 3/4
I I
I I
JL
r
Ą_
y h j
h
(7.186)
W równaniu tym występuje zastępcza liczba Nusselta, którą zapiszemy w postaci
Nu, —
CK]I4 PrJ14
r & y !Ą
(7.187)
v n /
7.9.1. Teoria Nusselta
Nusselt już w 1916 r. wyprowadził równanie określające współczynnik wnikania
ciepła podczas kondensacji filmowej. Analizował spływającą błonkę skroplin według

134
schematu przedstawionego na rys. 7.31. Grubość filmu s =f(x) jest zmienna; dla jc = 0
(u góry) jest równa zero i zwiększa się ku dołowi.
Rys. 7.31. Spływ warstwy skroplin
Na podstawie równania Fouriera gęstość strumienia ciepła przewodzonego przez
warstwę skroplin w odległości
jc
wynosi:
qx = - { T s - T i£) = ^ T
(7.188)
s
s
Ten sam strumień ciepła wnikający do ścianki opisuje równanie Newtona
qx = a x (r, - Tśi) = a x AT
(7.189)
Z porównania tych równań wynika definicja lokalnego współczynnika wnikania ciepła:
a x =—
(7.190)
s
Najtrudniejsze było określenie lokalnej grubości filmu. Przyjęto, że temperatura
ścianki oraz różnica temperatury są stałe na całej wysokości ściany. Aby wyznaczyć
rozkład prędkości, analizowano wycinek różniczkowej objętości
o wysokości dx
i szerokości dy oraz skończonej długości b (rys. 7.32). Podlega on działaniu sił cięż
kości Fc oraz sił tarcia wewnętrznego F,. Dla ruchu jednostajnego można przyjąć, że
drFc + d
2
F, =0
(7.191)

135
Poszczególne człony równania (7.191) są następujące:
• różniczkowa siła ciężkości
d 2 Fc =ycbdxdy
1 ciężar właściwy skroplin
d 2 F = bdxdT
Y
c
= gP
c
(7.192)
(7.193)
(7.194)
W równaniu (7.193) naprężenie styczne Tjest siłą tarcia działającą na jednostkę
powierzchni.
Rys. 7.32. Rozkład prędkości
i naprężeń w warstwie skroplin
Następnie analizuje się jest zależność naprężenia stycznego od właściwości fizy
kochemicznych i prędkości płynu. Z równania (7.193) otrzymujemy
dT =
d 2 Ft
bdx
z równania (7.191) mamy natomiast
d 2 Ft = - d 2 Fc
(7.195)
(7.196)
Po podstawieniu do równania (7.195) i przekształceniach otrzymuje się następujące
równanie

136
(7.197)
Pochodna naprężenia stycznego rwzględem y wynosi
(7.198)
Po uwzględnieniu prawa Newtona
dw
T - T /
-------
(7.199)
otrzymuje się przez zróżniczkowanie
Z porównania równań (7.198) i (7.200) otrzymujemy wyrażenie
dy
2
ii
które całkujemy dwukrotnie względem y i otrzymujemy wzór na rozkład prędkości
w filmie cieczy
() . C
2
są stałymi całkowania. Wyznaczamy je z warunków brzegowych:
• Przy ścianie, gdy y = 0, w = 0, zatem Ci = 0.
• Na powierzchni błonki kondensatu y = s oraz dw/dy = 0. Po zróżniczkowaniu
równania rozkładu prędkości (7.202) względem y i przyrównaniu do zera otrzymuje
się wyrażenie
-
= - ^ - y + Q =0
(7.203)
dy
t
/
c
z którego wyznaczamy stałą Ci
dc
Po podstawieniu wyrażenia na stałą C] oraz C
2
= 0 do równania (7.202) otrzymujemy
równanie określające profil prędkości:
2
t/c
(7.202)
(7.204)

137
Yc
2
, n - S
n n r \
w = - - — >• +
y
(7.205)
2?7c
V c
Równanie średniej prędkości strugi kondensatu wyprowadza się z całki:
Wir = “
S
| wdy ■
(
2
2
\
yc s~ t
YcS
s~
v
2
t jc
3
T]c
2
J
Yc s
1
(7.206)
3/7,
Następnie ustalamy związek przyrostu masowego strumienia kondensatu z grubo
ścią filmu.
Z definicji masowego natężenia przepływu mamy
iii - bswir p c
(7.207)
po podstawieniu wzoru na średnią prędkość otrzymujemy
•
YcPcb 3
g p c b 3
ono\
m = --------5 = ---------5
(7.208)
3?7c
3 7]c
Po zróżniczkowaniu tego równania otrzymuje się wyrażenie na przyrost strumienia
masowego na drodze dx
2
i
d m ^ ^ — s2ds
(7.209)
n,
Przyrost ten następuje w wyniku skroplenia pary przez odebranie strumienia ciepła
o gęstości qx, co można zapisać następująco:
dm - bdxm" - — bdx
(7.210)
r
Po wprowadzeniu równania Fouriera (7.188) otrzymujemy
dm - —— ATdx
(7.211)
s r
Z porównania równań (7.209) i (7.211) wynika związek
dx ~ ^ Y>c— s3ds
(7.212)
¿cTicA T
Po scałkowaniu obu stron równania otrzymuje się
9
AXci]ctsT
Ponieważ dla jc = 0 grubość błonki s = 0, więc stała C = 0.
g p c r s4 + c
(7.213)

138
Po przekształceniu równania (7.213) otrzymuje się wzór na grubość filmu
/
\ 1/4
14 Xcr,c A
t
— x
v gpc~r
(7.214)
a po podstawieniu tego wyrażenia do równania (7.190) wzór na lokalny współczynnik
wnikania ciepła
a x
i
2
i 4 \ 1/4
gPc rAc
4rjcATx
(7.215)
Średni współczynnik wnikania ciepła dla ściany o wysokości h obliczamy jako
średnią całkową
a ■
■ - 1 a xdx
i J
(7.216)
Przyjmując wyrażenie na stałą
A =
(
2
* 4 V/4
4łjcAT
w wyniku całkowania otrzymujemy równanie
(7.217)
a - A —{x VĄdx -
h i
A
h3/4 =
3/4 h
4 A
3 h
/4
g p i r f c
4r/cATh
\ 1/4
(7.218)
którego postać końcowa nazywa się wzorem Nusselta
a ~ 0,943
f
4 , 4 V/4
g P P rlg
rjcATh
(7.219)
Na podstawie badań doświadczalnych stałą C w tym równaniu należy skorygować
do wartości 1,13. Według Walta i Kroegera [13] spływ skroplin odbywa się ruchem
falowym, co wymaga wprowadzenia przelicznika 1,15.
W przypadku skraplania na ścianie nachylonej pod kątem ^do poziomu równanie
(7.192) skorygujemy następująco
d 7 Fc = yc sin ęSdxdy
(7.220)
Uwzględnienie tego równania prowadzi do określenia współczynnika korekcyjnego
dla kąta (j) :

139
a,$ =a$J sin^
(7.221)
« jest współczynnikiem wnikania ciepła dla ściany pionowej.
Podczas skraplania pary na rurze poziomej zewnętrzną powierzchnię rury można
traktować jak płaszczyzny wielkości różniczkowej, nachylone pod kątem (/). Po scał-
kowaniu w zakresie 0 < (j) < 180° otrzymamy wzór
a ~ 0,725
f
7 .
7
V/4
gPc~rAc-
v tjcATd
(7.222)
w którym d jest średnicą zewnętrzną rury. Wzór ten został potwierdzony doświad
czalnie.
7.9.2. Wpływ intensywności skraplania na wnikanie ciepła
Aby określić zależność współczynnika wnikania ciepła od intensywności spływu
skroplin, należy sformułować bilans energii dla kondensatu. Bilans ilości ciepła dla
rury poziomej ma postać
wir - aATudL
(7.223)
Ze wzoru (7.222) zaś otrzymujemy
A T =
a
v 0,725 j
dcd
(7.224)
Po podstawieniu tego równania do równania bilansowego (7.223) i przekształceniach
otrzymujemy
a
X
(
7 y/3
>id
K p c g )
- 0,959
f ■
v 1/3
m
\V cL j
(7.225)
lub inaczej zapisaną zależność modułów bezwymiarowych
a&.
■ =
1,51
r 4 r , v 1/3
Vc
(7.226)
gdzie f = m //..
Z bilansu energii dla kondensacj i na ścianie pionowej o wysokości h wynika:
wir - aATbh
(7.227)

140
Ponieważ ze wzoru (7.222) otrzymujemy wyrażenie
v-4
AT
a
0,943
gpc2r l l
ilch
( 7 .2 2 8 )
więc po podstawieniu do równania bilansowego (7.223) i po przekształceniach otrzy
mujemy równanie
f
2
y /3
lc
\ p c g
lub w postaci zależności kryterialnej
aP-
0,925
i • V 1/3
m
\Jlcb)
(7.229)
0,925
r
n-i/3
f r \
Khcj
1,47
r
n-i/3
V
h c
y
(7.230)
w którym T= m!b.
Porównanie otrzymanych zależności dla ściany poziomej (7.222) i dla ściany pio
nowej (7.119) daje możliwość oceny intensywności wnikania ciepła w zależności od
ustawienia ściany. Z podzielenia tych wzorów stronami otrzymujemy
a
poziom
a
pion
0,7721
h
1/4
(7.231)
Długość rury L jest dla rury pionowej wysokością h.
7.9.3.
Wpływ prędkości i kierunku ruchu pary
na wnikanie ciepła podczas kondensacji filmowej
Zależność współczynników wnikania ciepła od prędkości i kierunku ruchu pary
podczas kondensacji filmowej występuje dopiero dla większych wartości prędkości
Rys. 7.33. Zależność a ja ® = ftw )'■
a w - współczynnik w nikania dla
danej prędkości pary, a 0 - w spółczynnik w nikania dla prędkości zero
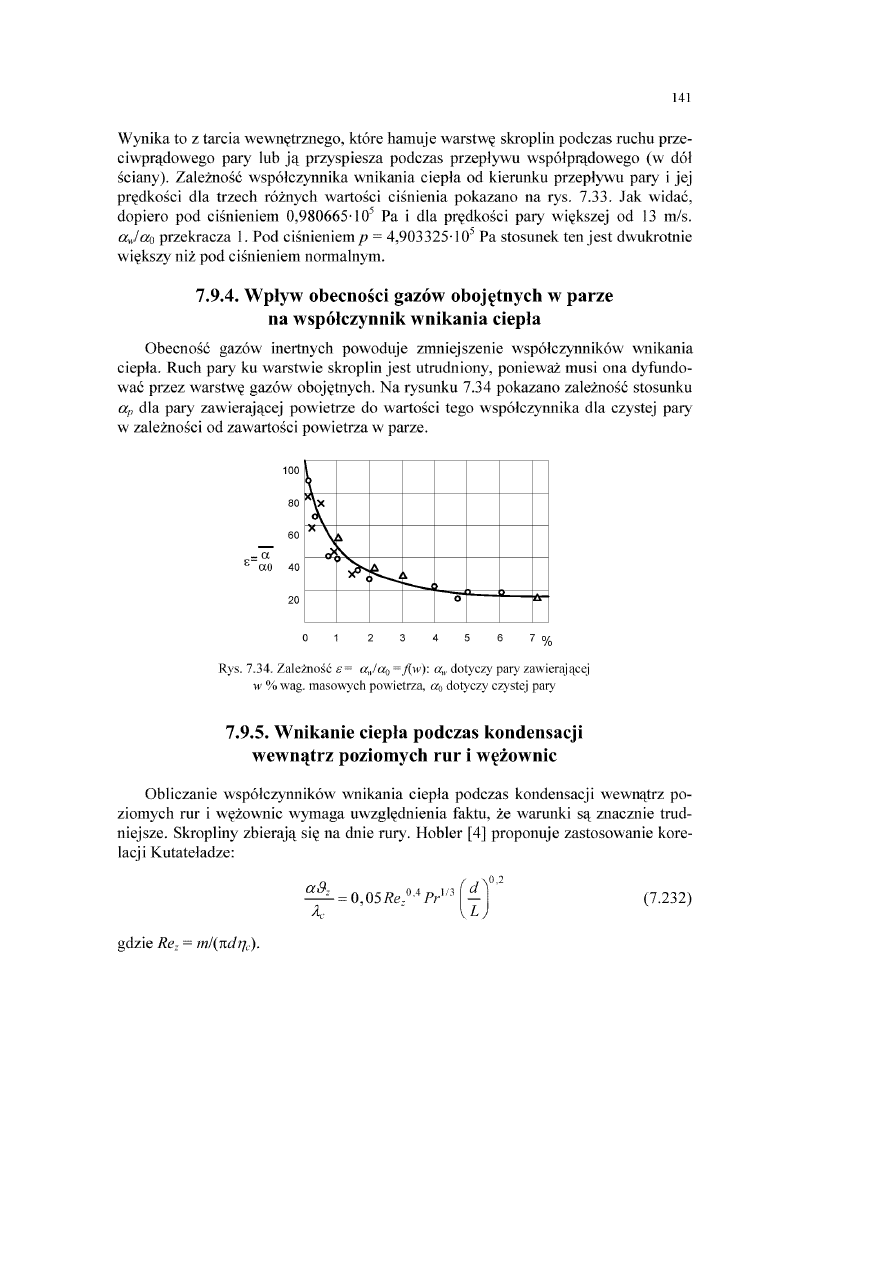
141
Wynika to z tarcia wewnętrznego, które hamuje warstwę skroplin podczas ruchu prze
ciw praylow ego pary lub ją przyspiesza podczas przepływu współ prądow ego (w dół
ściany). Zależność współczynnika wnikania ciepła od kierunku przepływu pary i jej
prędkości dla trzech różnych wartości ciśnienia pokazano na rys. 7.33. Jak widać,
dopiero pod ciśnieniem 0,980665-10' Pa i dla prędkości pary większej od 13 m/s.
a ja o przekracza 1. Pod ciśnieniem p = 4,903325-10' Pa stosunek ten jest dwukrotnie
większy niż pod ciśnieniem normalnym.
7.9.4. Wpływ obecności gazów obojętnych w parze
na współczynnik wnikania ciepła
Obecność gazów inertnych powoduje zmniejszenie współczynników wnikania
ciepła. Ruch pary ku warstwie skroplin jest utrudniony, ponieważ musi ona dyfundo-
wać przez warstwę gazów obojętnych. Na rysunku 7.34 pokazano zależność stosunku
Op dla pary zawierającej powietrze do wartości tego współczynnika dla czystej pary
w zależności od zawartości powietrza w parze.
100
60
= a
a o
40
20
* \ x
X \
^ <
i
--— i i
o
ts r
0
1
2
3
4
5
6
7 o/0
Rys. 7.34. Zależność
e= ajao =AW): <*w
dotyczy pary zawierającej
w
% wag. masowych pow ietrzą
a
0
dotyczy czystej pary
7.9.5. Wnikanie ciepła podczas kondensacji
wewnątrz poziomych rur i wężownic
Obliczanie współczynników wnikania ciepła podczas kondensacji wewnątrz po
ziomych rur i wężownic wymaga uwzględnienia faktu, że warunki są znacznie trud
niejsze. Skropliny zbierają się na dnie rury. Hobler [4] proponuje zastosowanie kore
lacji Kutateładze:
a 9
z - = 0 ,0 5 R e , 0’4 P r 13
A,
d_
\ L j
( 7 .2 3 2 )
gdzie Rez = m/(ndr/c).

142
7.9.6. Obliczenia uproszczone dla kondensacji filmowej
Biorąc pod uwagę, że parametry p c, ijc, Xc we wzorach obliczeniowych należy
przyjmować w odniesieniu do średniej temperatury skroplin, ciepło parowania r zaś
do temperatury pary nasyconej dla danego ciśnienia pary, opracowano wzory uprosz
czone określające współczynniki wnikania ciepła.
Współczynnik ten dla ściany pionowej obliczamy ze wzoru
a = C ęrVA{hW )~VA
(7.233)
Dla rur poziomych należy przyjąć h = d. Wartość współczynnika C dobieramy na
podstawie podanych wcześniej wzorów. Wartości ę i r 1/4 odczytujemy z tabeli 7.13.
Tabela. 7.13. W artości ^ i / - 1/4dla pary wodnej
t,°C
0
20
40
60
80
100
120
140
160
180
200
<p
174,9
214,0
247,2
276,1
299,3
318,1
332,5
342,7
347,0
349,9
351,3
r m
39,66
39,50
39,42
39,25
39,01
38,77
38,61
38,29
38,05
37,65
37,32
7.10. Warunki parowania i wrzenia cieczy
Proces parowania cieczy przebiega na granicy faz. Zachodzi on w całym zakresie
temperatury; w temperaturze niższej od temperatury krzepnięcia cieczy przebiega
proces sublimacji, od temperatury krzepnięcia do temperatury wrzenia mówimy o
parowaniu cieczy, w temperaturze wrzenia - o wrzeniu cieczy.
W fizyce cieczy przyjmuje się, że proces wrzenia przebiega przy temperaturze
wrzenia cieczy równej temperaturze pary nasyconej (Twrz =
co jest związane
z warunkiem, że prężność pary nasyconej tej cieczy jest równa ciśnieniu zewnętrzne
mu. W rzeczywistych warunkach warstwa cieczy pewnej grubości wywiera ciśnienie
hydrostatyczne (P/, = ghp) i aby nastąpiło jej wrzenie, musi być spełniony warunek, że
prężność pary nasyconej cieczy p", jest większa od sumy ciśnienia zewnętrznego P
i ciśnienia hydrostatycznego Pp
p \ > / ’ = / ’ • A
(7.234)
Spełnienie tego warunku jest związane z przegrzaniem cieczy.
Proces parowania przebiega z kolei w takiej temperaturze, że prężność pary nasy
conej danej cieczy A jest mniejsza lub równa ciśnieniu zewnętrznemu
P U K
(7.235)

143
Ciecz wieloskładnikowa wrze w temperaturze, w której suma prężności parcjal
nych jej składników przewyższa ciśnienie zewnętrzne wokół pęcherzyków pary
i=n
> P — P, + Ą
(7.236)
<=i
Dla procesu parowania mieszaniny cieczy musi być natomiast spełniony warunek
^ P i < R
(7.237)
<=i
Proces parowania cieczy ma podstawowe znaczenie w takich operacji jednostko
wych, jak destylacja molekularna lub suszenie.
7.10.1. Szybkość parowania cieczy
W procesie parowania cząsteczki cieczy znajdujące się tuż przy granicy faz prze
chodzą do fazy gazowej, część z nich natomiast kondensuje i przechodzi do fazy cie
kłej. W stanie równowagi, gdy ciśnienie cząstkowe składnika w fazie parowej jest
równe jego prężności pary nasyconej, efektywna szybkość parowania jest równa zero.
Szybkość parowania można określić na podstawie teorii kinetycznej gazów w od
niesieniu zarówno do fazy ciekłej, jak i parowej.
Ułamek ogólnej liczby cząsteczek gazu doskonałego o danej prędkości określa
funkcja rozkładu energii kinetycznej cząsteczek Maxwella-Boltzmanna:
N
f kT
e- ““2/2W’
(7.238)
Nc
\ 2 mu
gdzie: N - liczba cząsteczek przechodząca w ciągu 1 s z fazy ciekłej do fazy parowej
na powierzchni 1 cm2, Nc - liczba cząsteczek w 1 cm3 cieczy, m - masa cząsteczki
w kg, u — minimalna (graniczna) wartość składowej prędkości w kierunku prostopa
dłym do powierzchni cieczy, dla której zachodzi przejście cząsteczki do fazy parowej,
w m/s, k - stała Boltzmanna (k = R/N
0
= 1,38-10 23 J/K), R - stała gazowa (8,31432
J-rnol '-K ' ). No - stała Avogadra (6,022-1023 mol ' ).
Ułamek liczby cząsteczek podlegających kondensacji na 1 cm2 powierzchni cie
czy wciągu 1 sjest równy
N '
( kT N°’5
(7.239)
gdzie Ng jest liczbą cząsteczek w 1 cm3 fazy parowej.

144
Jeżeli założymy, że faza parowa jest gazem doskonałym, to
pV
p
Ng - ng N
0
^ — No = —
RT
kT
gdzie: //.. - liczba moli w 1 cm3 fazy parowej, V= 1 cm3, k = R/No.
Po podstawieniu do równania (7.239) otrzymujemy wyrażenie
N ’ =
P_
kT
kT
2
xm
\ 0 , 5
( 7 .2 4 0 )
(7.241)
Efektywna liczba cząsteczek cieczy opuszczających powierzchnię 1 cm7 w ciągu 1 s,
stanowiąca szybkość parowania, jest równa różnicy
- ± * L = N - N ' J * L 1
A d r
l lian
0,5 /
JWe~
kT
(7.242)
gdzie: A - powierzchnia cieczy w cm", d N /d r- szybkość parowania.
W stanie równowagi dynamicznej efektywna szybkość parowania jest równa zero,
więc
P _ a
r
- m u 2 / 2 k T
kT ~ c
(7.243)
Po podstawieniu tej zależności do równania (7.242) otrzymujemy wyrażenie na szyb
kość parowania
1 dN
A dr
-■(2rnnkT')°':‘ ^p° - /? )
(7.244)
W przypadku odparowywania w próżni, gdy p = 0, szybkości parowania jest mak
symalna, równa iloczynowi:p (2nmkT)
7.11. Wnikanie ciepła podczas wrzenia cieczy
Wrzenie cieczy ma podstawowe znaczenie w rozmaitych urządzeniach, takich jak
wyparki, kotły parowe oraz parowniki urządzeń chłodniczych. Warunkiem osiągnięcia
stanu wrzenia cieczy jest doprowadzenie dostatecznej ilości ciepła, aby temperatura
ścianki była wyższa od temperatury nasycenia pary pod danym ciśnieniem. Podczas
wrzenia para tworzy się w całej objętości cieczy, zwłaszcza na powierzchni ściany
grzejnej w postaci pęcherzyków (rys. 7.35). Ich liczba, kształt i szybkość narastania
zależą od intensywności ogrzewania i właściwości fizykochemicznych cieczy i pary,
ale również od szorstkości powierzchni i zdolności zwilżania jej przez ciecz. Pęche
rzyki powstające przy ścianie grzejnej mają kształt kulisty, po oderwaniu się unoszą

145
się do góry pod działaniem siły wyporu, ich objętość rośnie i ulegają spłaszczeniu;
każdy z nich kształtem przypomina grzyb. Para zamknięta w pęcherzyku ma wyższe
ciśnienie od ciśnienia otaczającej cieczy. Nadwyżka ciśnienia Ap = p r - p zależy od
promienia pęcherzyka r i od napięcia powierzchniowego cieczy er. Jeżeli założymy, że
pęcherzyk ma kształt kulisty, to w warunkach równowagi sił rozrywających pęcherzyk
i sił napięcia powierzchniowego mamy
nr {Pr - p) = 2TirS
i nadciśnienie wewnątrz pęcherzyka wynosi
(7.245)
(7.246)
Rys. 7.35. Schemat wnikania ciepła podczas w rzenia cieczy
Pęcherzyki powstają na rozmaitych krzywiznach na ścianie grzejnej lub na drob
nych ciałach stałych, stanowiących miejsca zarodkowe. Powstanie i wzrost pęcherzy
ka wymaga spełnienia warunku, że dp > 2 cr/r. Uwzględniwszy poprawkę Thomsona
na zwiększenie ciśnienia nasycenia nad zakrzywionym meniskiem oraz że dp =
(dp/dt)nA I' równanie określające promień r zapiszemy następująco:
2A
P
± \
a t p
-
p
dt
(7.247)
gdzie: / / , p " - gęstość cieczy i pary nasyconej pod danym ciśnieniem cieczy, AT
- nadwyżka temperatury cieczy nad temperaturą nasycenia. Wielkość (dp/dt)n można
obliczać z równania Clausiusa-Clapeyrona
r dp^
\ dt j
r y ’p "
T ,,{ p '- P " )
(7.248)
gdzie ciężar właściwy w stanie nasycenia y' = SP-
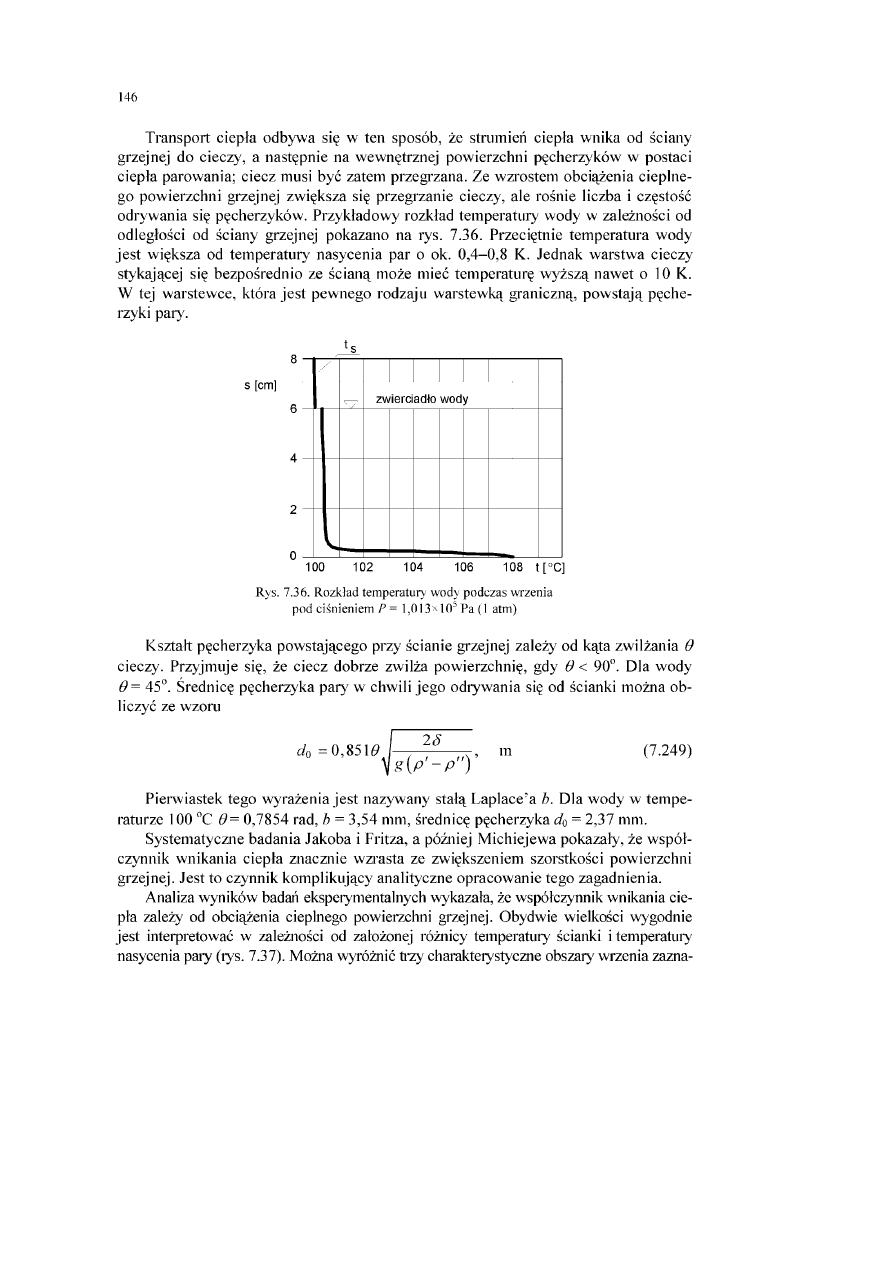
146
Transport ciepła odbywa się w ten sposób, że strumień ciepła wnika od ściany
grzejnej do cieczy, a następnie na wewnętrznej powierzchni pęcherzyków w postaci
ciepła parowania; ciecz musi być zatem przegrzana. Ze wzrostem obciążenia cieplne
go powierzchni grzejnej zwiększa się przegrzanie cieczy, ale rośnie liczba i częstość
odrywania się pęcherzyków. Przykładowy rozkład temperatury wody w zależności od
odległości od ściany grzejnej pokazano na rys. 7.36. Przeciętnie temperatura wody
jest większa od temperatury nasycenia par o ok. 0,4-0,8 K. Jednak warstwa cieczy
stykającej się bezpośrednio ze ścianą może mieć temperaturę wyższą nawet o 10 K.
W tej warstewce, która jest pewnego rodzaju warstewką graniczną, powstają pęche
rzyki pary.
z w ie rc ia d ło w o d y
100
102
104
106
108 t [ ° C
Rys. 7.36. Rozkład temperatury wody podczas wrzenia
pod ciśnieniem P = 1,013><105 Pa (1 atm)
Kształt pęcherzyka powstającego przy ścianie grzejnej zależy od kąta zwilżania
6
cieczy. Przyjmuje się, że ciecz dobrze zwilża powierzchnię, gdy 0 < 90°. Dla wody
6
= 45°. Średnicę pęcherzyka pary w chwili jego odrywania się od ścianki można ob
liczyć ze wzoru
4>=0,851g
2 5
m
(7.249)
\ g ( P - P )
Pierwiastek tego wyrażenia jest nazywany stałą Laplace’a h. Dla wody w tempe
raturze 100 °C
6
= 0,7854 rad, b = 3,54 mm, średnicę pęcherzyka d
0
= 2,37 mm.
Systematyczne badania Jakoba i Fritza, a później Michiejewa pokazały, że współ
czynnik wnikania ciepła znacznie wzrasta ze zwiększeniem szorstkości powierzchni
grzejnej. Jest to czynnik komplikujący analityczne opracowanie tego zagadnienia.
Analiza wyników badań eksperymentalnych wykazała, że współczynnik wnikania cie
pła zależy od obciążenia cieplnego powierzchni grzejnej. Obydwie wielkości wygodnie
jest interpretować w zależności od założonej różnicy temperatury ścianki i temperatury
nasycenia pary (rys. 7.37). Można wyróżnić trzy charakterystyczne obszary wrzenia zazna
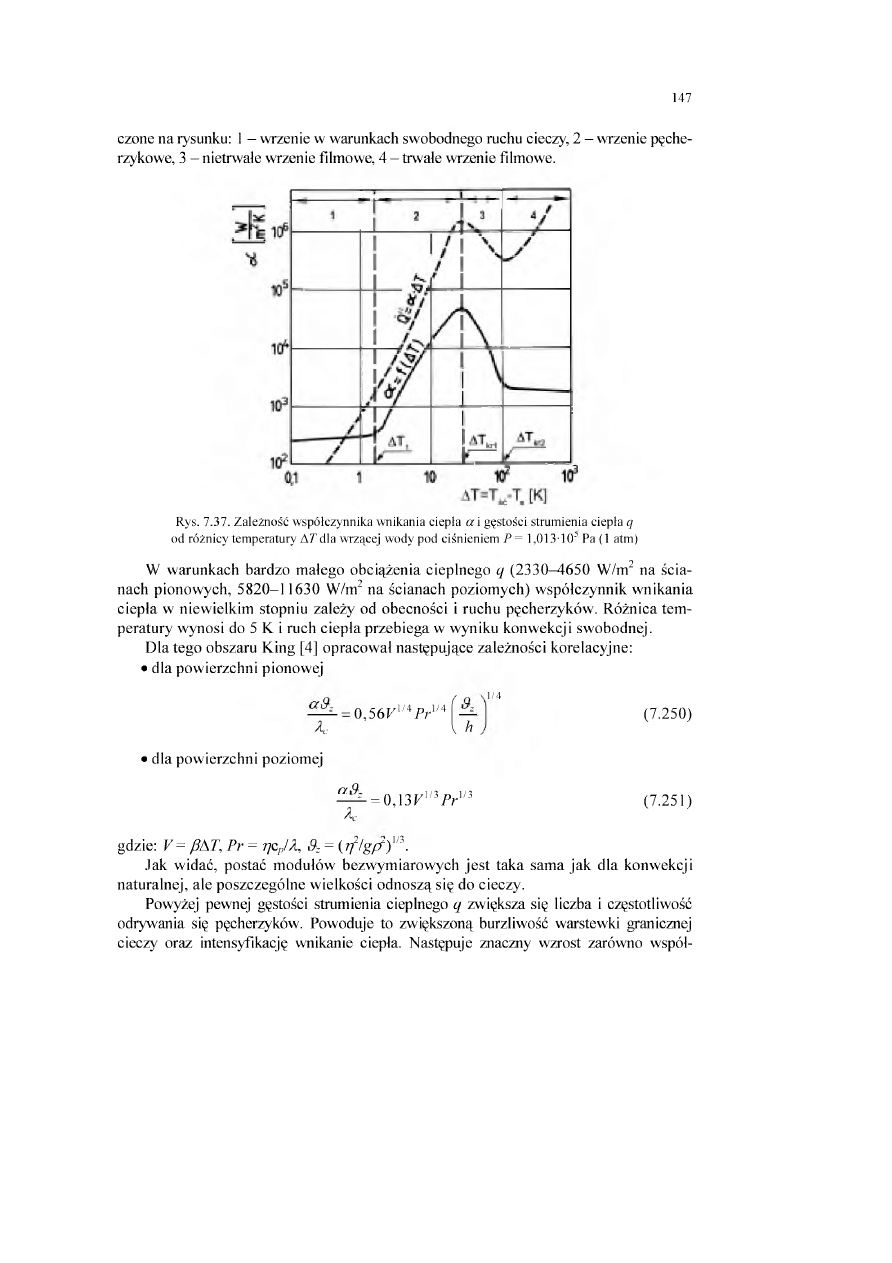
147
czone n a rysunku: 1 - wrzenie w warunkach swobodnego ruchu cieczy, 2 - wrzenie pęche
rzykowe, 3 - nietrwale wrzenie filmowe, 4 - tr w a le wrzenie filmowe.
Rys. 7.37. Zależność w spółczynnika w nikania ciepła a i gęstości strumienia ciepła ą
od różnicy tem peratury A T dla wrzącej wody pod ciśnieniem P = 1,013-10' Pa (1 atm)
W w arunkach bardzo m ałego obciążenia cieplnego q (2 3 3 0 -4 6 5 0 W /m2 n a ścia
nach pionow ych, 582 0 -1 1 6 3 0 W/m2 n a ścianach poziom ych) w spółczynnik w nikania
ciepła w niew ielkim stopniu zależy od obecności i ruchu pęcherzyków . R óżnica tem
peratury w ynosi do 5 K i ruch ciepła p rzebiega w wyniku konw ekcji sw obodnej.
D la te g o obszaru K ing [4] opracow ał następujące zależności korelacyjne:
• dla pow ierzchni pionow ej
- 0 ,5 6 F 1/4/ V /4 f —
A:
{ h
1/4
(7.250)
• dla pow ierzchni poziom ej
a 9
— - = 0 ,1 3 F 1/3/V 1/3
(7.251)
A-
gdzie: V= J3AT, P r = i]cp/ l , 3: = ( r f l g / f ) v\
Jak w idać, postać m odułów bezw ym iarow ych je s t tak a sam a ja k dla konw ekcji
naturalnej, ale poszczególne w ielkości o dnoszą się do cieczy.
Powyżej pewnej gęstości strumienia cieplnego q zwiększa się liczba i częstotliwość
odrywania się pęcherzyków. Powoduje to zwiększoną burzliwość warstewki granicznej
cieczy oraz intensyfikację wnikanie ciepła. Następuje znaczny wzrost zarówno współ-

148
czynników wnikania ciepła a, jak i gęstości strumienia cieplnego q (rys. 7.37). Ten obszar
wrzenia nazwano wrzeniem pęcherzykowym. Zakres wrzenia pęcherzykowego odpowiada
różnicy temperatury (dla wody) 5 < AT < 25 K. Gdy różnica temperatury przybiera bardzo
duże wartości (od 25 K dla wody), liczba tworzących się pęcherzyków jest tak duża, że
łączą się one tuż przy ścianie grzejnej, tworząc film (błonkę parową). Powoduje to wpro
wadzenie dodatkowego oporu przewodzenia ciepła przez błonkę pary, co zmniejsza za
równo wartość współczynnika wnikania ciepła, jak gęstość strumienia ciepła, nawet gdy
nadal zwiększa się różnica temperatury. Przejście od wrzenia pęcherzykowego do wrzenia
filmowego następuje dla pewnej charakterystycznej dla danej cieczy różnicy temperatury,
zwanej temperaturą krytyczną.
Dla tego obszaru wrzenia opracowano wiele zależności empirycznych. Ogólnie
sprowadzają się one do zależności
Do obliczeń tych współczynników Michiejew [4] zaleca równania Krużylina, wy
prowadzone teoretycznie i uściślone doświadczalnie w odniesieniu do wrzenia cieczy
dobrze zwilżających powierzchnię w dużej objętości. Mają one postać zależności
modułów bezwymiarowych. Dla wnikania ciepła jest to równanie
gdzie S - wymiar charakterystyczny, proporcjonalny do wielkości pęcherzyka w chwi
li odrywania się od ścianki, określony wzorem
a = f ( q )
(7.252)
lub
a = f ( A T )
(7.253)
Nu^Q, Q15Kq0J K u]nPr-°'5
(7.254)
dla krytycznej gęstości strumienia ciepła zaś
Kq =995 Ku-°'
66
Arl/ĄPr
0'5
(7.255)
W równaniach tych mamy następujące moduły:
• liczba Nusselta
(7.256)
(7.257)
• liczba Archimedesa
(7.258)

149
liczba Prandtla dla cieczy
P r
ycP
A
(7.259)
• Kq - liczba znamienna, związana z liczbą czynnych miejsc powstawania pęche
rzyków
Kq =
P ' 8 2 p ' ^ p "
Acr
p '
gdzie p' jest pochodną na linii nasycenia według równania Clausiusa-Clapeyrona
(7.260)
dp
\ d t j
ry p
rg p 'p "
T { p ' ~ p " )
T { p ' - p " )
1 Ku - liczba znamienna związana z częstością odrywania się pęcherzyków
p '
c p <j
p '
(7.261)
K„ =-
p " r S p ' p ' - p "
(7.262)
W równaniach tych występują następujące parametry fizykochemiczne cieczy: ciepło
właściwe cp, lepkość //. współczynnik przewodzenia ciepła X, napięcie powierzch
niowe <7. ciężar właściwy f , gęstość p ' .
Wygodniejsze do stosowania są szczegółowe równania Krużylina, które otrzyma
no po rozpisaniu i przekształceniu względem a:
a - 0,0686
p r
\ p ' - p " )
0 ,0 3 3
,
x
1 / 3
i 0 , 8
0, 7
P_
\< y)
0 , 5
1 / 6
t
0, 3 7
V
L p
1
(7.263)
oraz
X * * { p ' - p " T IU {p "rT)m J I1A
n ' 1 0 / 2 4
1/6
H
qkr = 2940
(7.264)
W odniesieniu do wody równanie Krużylina upraszcza się do prostego związku
a = 2. 656/ / ’
’
(7.265)
lub
a = 2 5 ,8 8 /- 58A r2-33
(7.266)

150
W literaturze można znaleźć wiele korelacji dla wyparek oraz innych aparatów.
Praktyczne znaczenie może mieć również wzór podany przez Kutateładze, sprawdzo
ny w zakresie wartości ciśnienia od 0,2 do 10 barów dla różnego rodzaju cieczy:
a = 2,1 5 ęp 0’4 q
0,1
(7.267)
gdzie q wyrażamy w W/m2, p zaś w barach.
Wartości współczynnika ę zestawiono w tabeli 7.14.
Tabela 7.14. W spółczynnik ^ d o w zoru (7.267)
Płyn
<P
Płyn
<P
W oda
1
A lkohol etvlowv
0,45
Nafta
0,31-0,56
A lkohol metvlowv
0,36
Benzen
0,31
24% roztw ór wodnv NaCl
0,62
25% roztw ór cukru
0,57
9% roztw ór wodny NaCl
0 ,8 6
Szczegółowe wzory dla innych substanej i można znaleźć w literaturze [3,4].

8. Zatężanie roztworów nielotnych
substancji. Wyparki
Proces odparowywania, czyli zmiany stanu ciekłego na stan gazowy, przebiega
pod ciśnieniem cząstkowym pary niższym od ciśnienia pary nasyconej w danej tempe
raturze cieczy. Podwyższając temperaturę cieczy lub obniżając ciśnienie całkowite,
doprowadzimy roztwór do wrzenia. Wytworzoną parę po oddzieleniu od cieczy moż
na odprowadzać do atmosfery, wykorzystać jako czynnik grzejny w kolejnym stopniu
lub poddać skropleniu. Odparowanie pod ciśnieniem wyższym od ciśnienia atmosfe
rycznego jest stosowane w celu wykorzystania par do ogrzewania. Odparowanie pod
ciśnieniem niższym od atmosferycznego jest natomiast uzasadnione wówczas gdy pro
cesowi temu poddajemy roztwory wrażliwe na działanie podwyższonej temperatury.
Odparowanie polega na doprowadzeniu do cieczy określonej ilości energii ciepl
nej w celu ogrzania cieczy, a następnie zmiany jej stanu skupienia, aby osiągnąć żą
dane zatężenie roztworu. Aby zapewnić prawidłową i efektywną pracę instalacji, mu
simy określić warunki operacyjne, tj. ciśnienie i temperaturę, ale również parametry
ruchowe.
8.1. Bilans masowy procesu odparowania
Podstawowym elementem projektowania instalacji wypamej jest bilans masowy
substancji. Bilans masowy sporządza się dla ustalonego przepływu substancji, a więc
stałych parametrów procesu odparowania: temperatury, ciśnienia, stężenia roztworu,
intensywności wymiany ciepła itp.
Schematy konstrukcji typowych aparatów wypamych, tj. odpowiednio zaprojek
towanych wymienników ciepła, można znaleźć w literaturze [14]. Na rys 8.1 przed
stawiono podstawowy typ płaszczowo-rurkowej wyparki jednostopniowej. Jest ona
zbudowana z walczaka o dość dużej średnicy, zamkniętego od dołu i od góry dnami
z króćcami do dopływu surowca i odpływu pary rozpuszczalnika, wsadu rurkowego
oraz króćców - umocowanych z boku - do dopływu pary grzejnej i odprowadzania
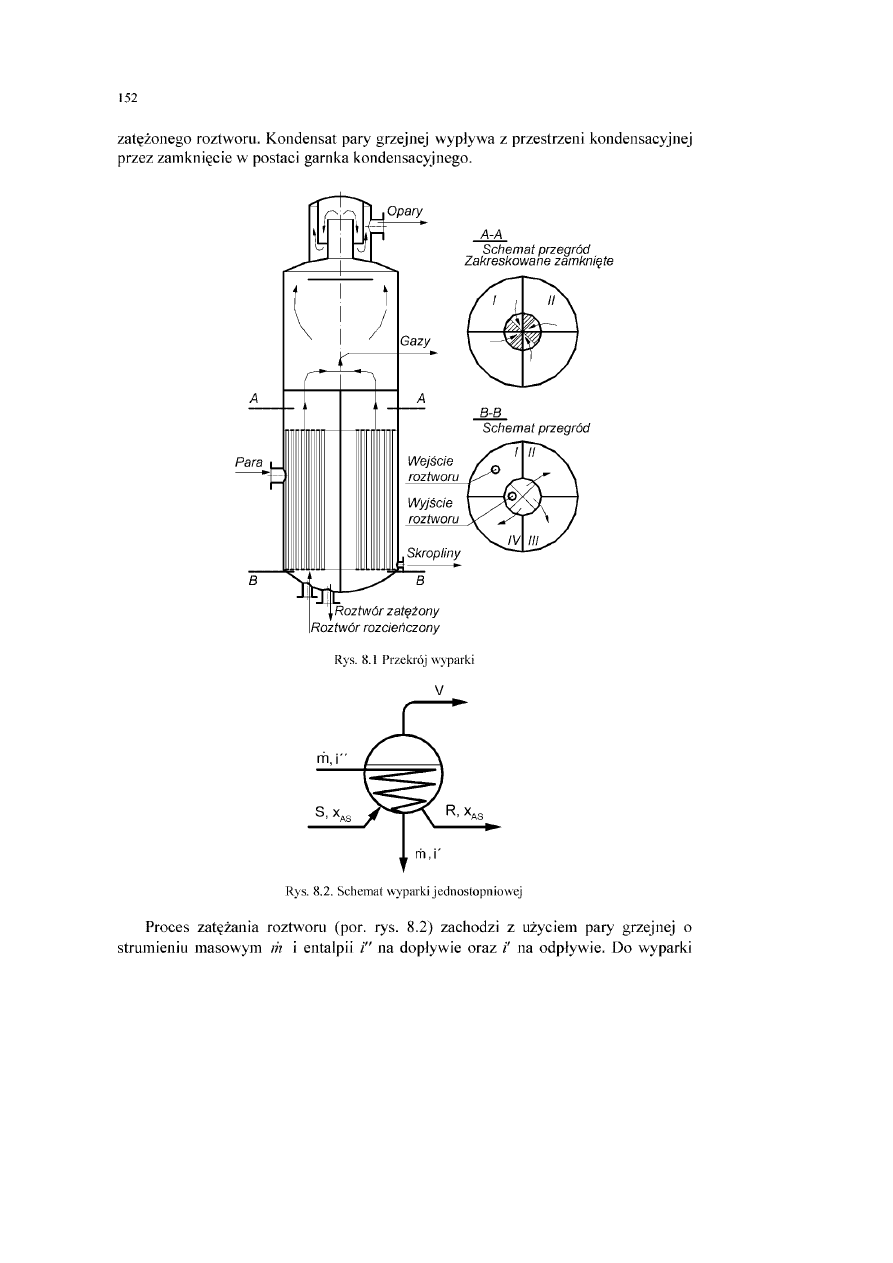
152
zatężonego roztworu. Kondensat pary grzejnej wypływa z przestrzeni kondensacyjnej
przez zamknięcie w postaci garnka kondensacyjnego.
i r ™ '
Rys. 8.2. Schemat wyparki jednostopniow ej
Proces zatężania roztworu (por. rys. 8.2) zachodzi z użyciem pary grzejnej o
strumieniu masowym m i entalpii i" na dopływie oraz i' na odpływie. Do wyparki

153
dopływa S kg roztworu o stężeniu składnika nielotnego A równym X
as
(kg A/kg S).
Z wyparki wypływa R kg zatężonego roztworu o stężeniu składnika A równym
xar
(kg A/kg R) oraz F kg oparów czystego rozpuszczalnika (yAv= 0). Zaniedbuje się stra
ty roztworu związane z unoszeniem roztworu w postaci kropel. Równanie bilansu
masowego można zapisać więc w prostej postaci
S ~ R + V
(8.1)
Równanie bilansowe nielotnego składnika A jest następujące
S
x a s
^ R
xar
(8.2)
Po podstawieniu R = S - V do drugiego równania i przekształceniu otrzymuje się rów
nanie określające ilość oparów
V ^ S
X
a r
(8.3)
Bilans masowy wielodziałowej instalacji wypamej wykonuje się oddzielnie dla
poszczególnych działów.
8.2. Wielostopniowe instalacje wyparne
Zatężanie roztworów prowadzi się na ogół w tzw. wielodziałowych instalacjach
wypamych. Umożliwia to z jednej strony odparowanie dużych ilości rozpuszczalnika,
z drugiej zaś wielokrotne wykorzystanie powstających oparów do ogrzewania kolej
nych działów wyparki. W instalacjach tego typu jest więc realizowana zasada wielo
krotnego odparowania, którą można nazwać również zasadą wielokrotnego wykorzy
stania energii cieplnej.
Zasadę wielokrotnego wykorzystania energii wygodnie jest interpretować za po
mocą schematu instalacji jak na rys. 8.3. Przedstawia on układ połączeń baterii trzy
stopniowej. Para wytworzona na pierwszym stopniu jest parą grzejną dla drugiego
stopnia, a para wytworzona na drugim stopniu - parą grzejną dla trzeciego stopnia.
Temperatura i ciśnienie na każdym stopniu są inne. Ciśnienie na drugim stopniu musi
być np. dostatecznie niskie, aby w temperaturze cieczy T
2
zachodziła wymiana ciepła
od kondensującej się pary rozpuszczalnika (T
g2
> T2) oraz wrzenie roztworu.
Efektywne zużycie pary wodnej na 1 kg odparowywanej wody wynosi:
• 1,10 kg/kg w wyparce jednostopniowej,
• 0,57 kg/kg w baterii dwustopniowej,
• 0,40 kg/kg w baterii trójstopniowej,
• 0,30 kg/kg w baterii czterostopniowej,
• 0,27 kg/kg w baterii pięciostopniowej.
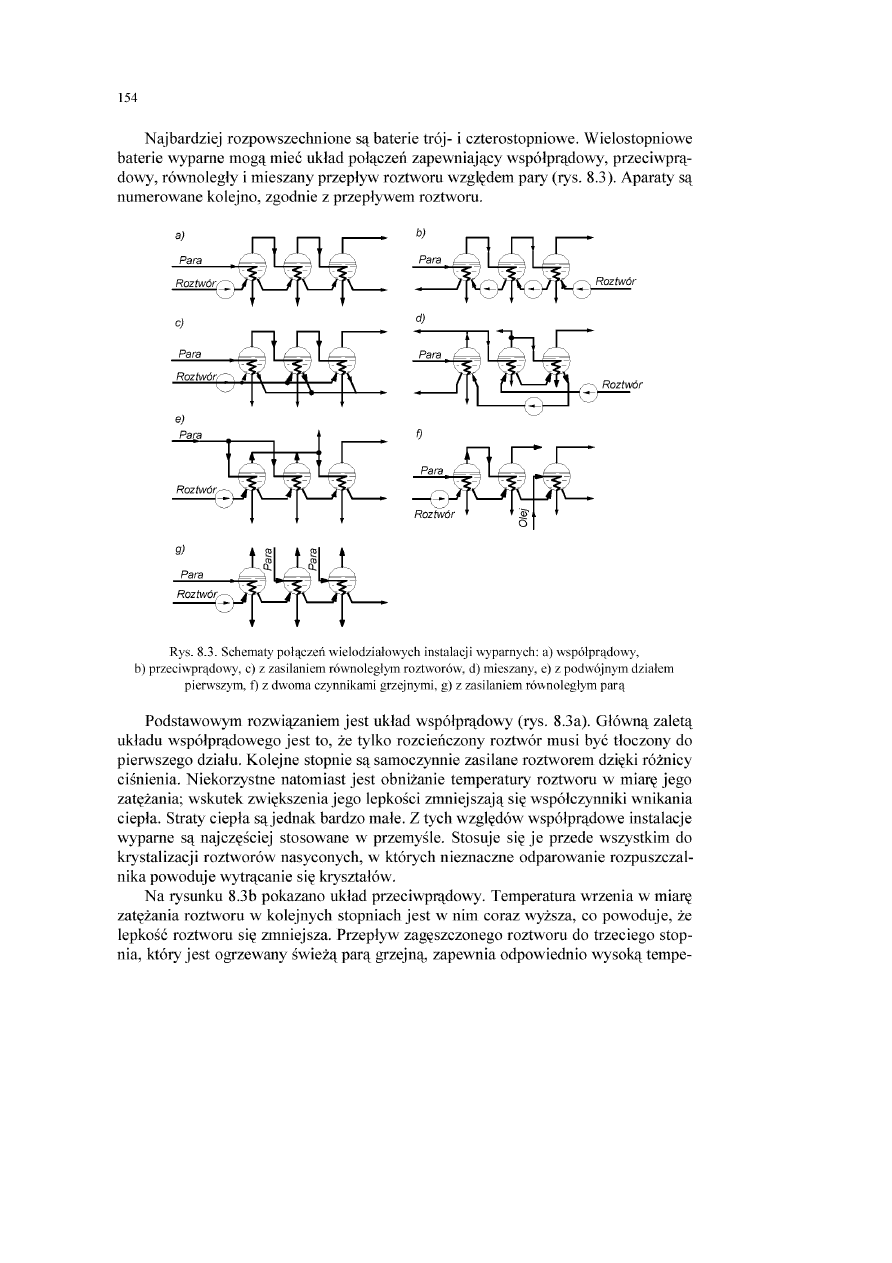
154
Najbardziej rozpowszechnione są baterie trój- i czterostopniowe. Wielostopniowe
baterie wyparne mogą mieć układ połączeń zapewniający współprądowy, przeć iw prą
dowy. równoległy i mieszany przepływ roztworu względem pary (rys. 8.3). Aparaty są
numerowane kolejno, zgodnie z przepływem roztworu.
Rys. 8.3. Schematy połączeń w ielodziałowych instalacji wyparnych: a) w spółprądowy,
b) przeciwprądowy, c) z zasilaniem równoległym roztworów, d) mieszany, e) z podwójnym działem
pierwszym, f) z dw om a czynnikami grzejnymi, g) z zasilaniem równoległym p arą
Podstawowym rozwiązaniem jest układ współprądowy (rys. 8.3a). Główną zaletą
układu współprądowego jest to, że tylko rozcieńczony roztwór musi być tłoczony do
pierwszego działu. Kolejne stopnie są samoczynnie zasilane roztworem dzięki różnicy
ciśnienia. Niekorzystne natomiast jest obniżanie temperatury roztworu w miarę jego
zatężania; wskutek zwiększenia jego lepkości zmniejszają się współczynniki wnikania
ciepła. Straty ciepła sąjednak bardzo małe. Z tych względów współprądowe instalacje
wyparne są najczęściej stosowane w przemyśle. Stosuje się je przede wszystkim do
krystalizacji roztworów nasyconych, w których nieznaczne odparowanie rozpuszczal
nika powoduje wytrącanie się kryształów.
Na rysunku 8.3b pokazano układ przeciwprądowy. Temperatura wrzenia w miarę
zatężania roztworu w kolejnych stopniach jest w nim coraz wyższa, co powoduje, że
lepkość roztworu się zmniejsza. Przepływ zagęszczonego roztworu do trzeciego stop
nia, który jest ogrzewany świeżą parą grzejną, zapewnia odpowiednio wysoką tempe-

155
raturę roztworu już zagęszczonego. Układ ten jest zalecany do zatężania bardzo lep
kich roztworów. Jego wadą jest konieczność instalowania pomp między kolejnymi
stopniami do przetłaczania roztworu do aparatów o coraz wyższym ciśnieniu pracy.
Powoduje to znaczne zwiększenie kosztów inwestycyjnych i ruchowych. W wyniku
strat ciepła układ ten wykazuje również duże zużycie pary grzejnej, około 5-10%.
Instalacje z równoległym zasilaniem roztworu (rys. 8.3c) są stosowane do krysta
lizacji roztworów nasyconych.
Układy mieszane (rys. 8.3d) stosuje się bardzo rzadko, wówczas gdy niezbędne
jest wyeliminowanie wad układów omówionych poprzednio [14]. Układ z dwoma
czynnikami grzejnymi (rys. 8.3f) jest np. stosowany, gdy należy zwiększyć temperatu
rę w ostatnim stopniu. Równoległe łączenie aparatów wypamych w odniesieniu do
pary grzejnej (rys. 8.3e) jest stosowane wówczas, gdy stosuje się parę grzejną nisko
ciśnieniową, a wymagana jest duża wydajność instalacji.
W wyjątkowych przypadkach konieczne jest równoległe zasilanie parą grzejną do
uzyskania wysokiej temperatury wrzenia roztworu (rys. 8.3g).
Liczbę działów przyjmuje się tym większą, im wyższe jest ciśnienie pary grzejnej
i mniejsze obniżenie temperatury roztworu. Pewną rolę odgrywa również wartość
całkowitej różnicy temperatury. Liczbę działów instalacji wypamej najlepiej jest do
bierać na podstawie analizy techniczno-ekonomicznej.
Całkowity spadek temperatury AT
0
w wyparce lub baterii wyparek jest równy
różnicy między temperaturą pary grzejnej w pierwszym stopniu, TPir] a temperaturą
skraplającej się pary z ostatniej wyparki (dla układu próżniowego na wlocie do skra
placza) Tskl
W warunkach rzeczywistych różnica ta jest pomniejszona o straty temperatury
wynikające z fizykochemicznej, hydrostatycznej i hydraulicznej depresji temperatu
rowej. Użyteczna różnica temperatury jest zatem równa całkowitej różnicy temperatu
ry pomniejszonej o całkowitą stratę temperatury
Dla «-stopniowej baterii wypamej użyteczna różnica temperatury jest sumą uży
tecznych różnic temperatury poszczególnych działów
8.3. Obliczanie całkowitej różnicy
temperatury instalacji wyparnej
Ar0 —Tp gl —Tsix
(8.4)
A’/,", —
A?o —
A TstI
(8.5)
(8.6)

156
Całkowita strata temperatury jest zatem sumą
AT^tr ~
5" AZ? + AZ)
(8.7)
gdzie: AZ) - fizykochemiczna depresja temperatury, AZ) - hydrostatyczna depresja
temperatury, AZ) - hydrauliczna depresja temperatury.
Fizykochemiczna depresja temperatury jest wynikiem podwyższenia temperatury
wrzenia roztworu względem temperatury wrzenia rozpuszczalnika (wody)
AZ] —Tr — Tw
(8.8)
Temperatura wrzenia roztworu zależy od ciśnienia, ale również od składu chemiczne
go i stężenia roztworu.
Fizykochemiczną depresję temperatury oblicza się z wzoru Gelperina
AZ) =
RT2
(8.9)
r
1
- a x
gdzie: R - uniwersalna stała gazowa, kJ/(kmol-K), 7 - temperatura wrzenia, K, r - cie
pło parowania, kJ/kg, jc - stężenie roztworu, kg/kg, a - stała wyznaczona doświadczalnie
dla danego roztworu.
W praktyce przemysłowej proces zagęszczania prowadzi się pod obniżonym ci
śnieniem. W takich przypadkach depresję temperatury należy określić na podstawie
przybliżonego wzoru Tiszczenki
T
AZj =0,01362— AT]'
r
(
8
.
10
)
gdzie: A Z) - szukana depresja temperatury pod danym ciśnieniem, A Z]'- depresja
temperatury pod ciśnieniem atmosferycznym, T - temperatura wrzenia czystego roz
tworu, K , r - ciepło parowania wody pod danym ciśnieniem odparowania, kJ/kg.
Prężność par cieczy można obliczać z równania
lg(p + l) = 0,3016>0-935
(8.1 1)
w którym wyznaczamy
P :
•g
•g
J L
l, Pkr J
7
7
Pb_
Pkr )
(
8
.
12
)
W równaniu tym
•g
0
— -
•g
yTfa- j
f rp \
J-h
(8.13)
\Tkr )

157
T jest temperaturą wrzenia pod ciśnieniem p, k . 1), - temperaturą wrzenia pod ciśnie
niem atmosferycznym pi„ k. T/,r - temperaturą krytyczną, k ,p tr~ ciśnieniem krytycz
nym, bar.
Znając wartości temperatury wrzenia roztworu o określonym stężeniu pod dwoma
różnymi ciśnieniami, temperaturę wrzenia pod jakimś innym ciśnieniem można wy
znaczyć z wzoru Duehringa
rp f
rp f f
1 ~ 1 = const
(8.14)
J
t
f
rpff
'
Z
2 —
±2
gdzie: T\ - T ”- różnica temperatury wrzenia danej cieczy pod dwoma określonymi
ciśnieniami, T{ - T " - różnica temperatury wrzenia dowolnej cieczy (wody) pod tymi
ciśnieniami.
Depresja hydrostatyczna temperatury AT
2
występuje w wyparkach z wysokim
słupem cieczy (powyżej lm). Temperaturę wrzenia roztworu w wyparce należy obli
czać jako temperaturę nasycenia dla ciśnienia na średniej wysokości słupa cieczy
P ~ Pm ~ ~ ~
(8.15)
gdzie: p m - ciśnienie w przestrzeni opar, Pa,
11
wysokość słupa cieczy, m, p - gę
stość cieczy, kg/m3, g - przyspieszenie ziemskie (9.81 m/s2).
Dla obliczonego tym wzorem ciśnienia znajdujemy temperaturę nasycenia pary
wodnej na podstawie tablic, przy czym temperatura wrzenia roztworu będzie wynosić
tr /n.ss* A'/'|.
Opisana metoda daje przybliżone wyniki, ponieważ we wzorze (8.15) wprowa
dzamy gęstość roztworu, a należałoby stosować gęstość mieszaniny ciecz-para, której
wartość zależy nie tylko od intensywności grzania, ale i od intensywności cyrkulacji
w wyparce.
Wartości depresji hydrostatycznej temperatury dla wyparek z intensywną cyrku
lacją można określić z równania
A r, = HkAT"
(8.16)
'
0,5 wpdc
gdzie: H - wysokość rur w komorze grzejnej, m,
współczynnik przenikania ciepła,
W/(m2-k), ATm - średnia logarytmiczna różnica temperatury między parą grzejną
a wrzącym roztworem, k , w - prędkość przepływu roztworu, m/s, d - średnica rury, m
c - ciepło właściwe roztworu, J/(kg-k), p — gęstość roztworu, kg/m3.
Jeżeli wrzenie roztworu występuje jedynie nad komorą grzejną, depresja hydro
statyczna nie jest istotna.
Depresja hydrauliczna temperatury Ar3 stanowi obniżenie temperatury związane
ze stratą ciśnienia na tarcie i opory miejscowe w przewodach łączących działy wy par
ne. W praktyce należy przyjmować A / j = 1 °C dla każdego działu.

158
8.4. Obliczanie użytecznej różnicy
temperatury instalacji wyparnej
Zgodnie z równaniem (8.5), użyteczna różnica temperatury jest równa całkowitej
różnicy temperatury pomniejszonej o całkowitą stratę temperatury. Zmniejsza się ona
wraz ze wzrostem liczby działów instalacji wyparnej [14]. Suma użytecznych spad
ków temperatury nie może być mniejsza od pewnej minimalnej wartości ,\T„ = 5 °C.
Przyjęcie dużej użytecznej różnicy temperatury w jednym dziale wpływa na wzrost
intensywności wymiany ciepła, ale również może być powodem porywania kropel
roztworu przez opary.
Powierzchnia grzejna «-stopniowej baterii wyparnej jest równa sumie powierzch
ni wszystkich stopni:
n
n
- 4 j -
(8.17)
/—
1
/=] KiZUi
gdzie: At - powierzchnia grzejna na i-tym stopniu, m2, (), - strumień ciepła na i-tym
stopniu ((), = mf), W, ki - współczynnik przenikania ciepła na i-tym stopniu,
W/(m2-K), A Ti - użyteczna różnica temperatury na i-tym stopniu, K.
Projektowanie wielodziałowych instalacji wypamych może być oparte na założeniu:
• minimalnej sumarycznej powierzchni grzejna całej instalacji (baterii),
• jednakowych powierzchni grzejnych wszystkich działów (stopni baterii),
• minimalnej całkowitej powierzchni wymiany ciepła i jednakowych powierzchni
grzejnych w każdym dziale.
8.4.1. Założenie minimalnej powierzchni wymiany ciepła
Założenie minimalnej powierzchni wymiany ciepła wiąże się z wysokimi kosztami
inwestycyjnymi wynikającymi z cen drogich metali, a zwłaszcza metali szlachetnych.
Zanalizujmy dwudziałową instalację wypamą. Całkowita powierzchnia wymiany
ciepła jest równa
Qi
Q>
4. = 4 +A,
+
(8.18)
'
kATj
k
2
AT
2
W celu wyeliminowania użytecznej różnicy działu drugiego, podstawiamy
AT
2
= ATu- A T ]
i otrzymujemy
Q]
Q
4 . * = - ^ + — 7— -------
(8.19)
k]AT]
k
2
(ATu -A T ,)

159
Minimalną powierzchnię wymiany ciepła wielodziałowej instalacji wypamej wy
znaczamy, szukając minimum funkcji Ac = /(A7j). Po zróżniczkowaniu równania
(8.19) i przyrównaniu do zera otrzymujemy wyrażenie
dA;
0
,
Qi
lub inaczej
4 A70
h ( m )
2
k
2
(±Tu - w )
d A
_
0
+
0
d ( ^ )
k ( m )
2
k2 ( m
)2
Z ostatniego wyrażenia otrzymuje się zależność
0
&
h {A7i )
k
2
(&t
2
f
z której po dalszym przekształceniu
■
= 0
(
8
.
20
)
(
8
.
2 1
)
(
8
.
22
)
otrzymujemy
0
ki
A T,
A T
2
(8.23)
(8.24)
Dla «-stopniowej baterii wypamej stosunek użytecznych spadków temperatury
opisuje równanie
ATj
Q_ K_
a rn
] j a h
Analogicznie zaś do równania (8.24) otrzymuje się związek
(8.25)
A T„
"
n
,=1
/=1 '
0
ki
(8.26)

160
W wyniku takiego podziału powierzchnie wymiany ciepła w poszczególnych
działach instalacji są niejednakowe.
8.4.2. Założenie równych powierzchni wymiany ciepła
Założenie równych powierzchni wymiany ciepła zapewnia ekonomiczne rozwią
zanie konstrukcyjne ze względu na identyczną budowę wyparek, co daje niższe koszty
zarówno inwestycyjne, jak i eksploatacyjne.
Użyteczne różnice temperatury w poszczególnych działach wynoszą:
• dla pierwszego stopnia
Założywszy równość powierzchni A x = A
2
= ... = A„ = A, po zsumowaniu użytecznych
różnic temperatury otrzymuje się
(8.27)
• dla n-tego stopnia
k n An
(8.28)
(8.29)
lub
n
n
(8.30)
z czego wynika, że
n
(8.31)
A
A Tx =
(8.32)
n

161
oraz dla
M-tego
działu związek
(8.33)
Po podzieleniu stronami dwóch ostatnich równań otrzymuje się warunek rozdzia
łu różnic temperatury dla równych powierzchni grzejnych:
8.4.3. Założenie minimalnej całkowitej powierzchni wymiany ciepła
i jednakowych powierzchni w każdym dziale
Uzyskanie jednakowych powierzchni wymiany ciepła wymaga spełnienia
zależ
ności
(8.33), osiągnięcie minimalnej całkowitej powierzchni wymiany ciepła nato
miast zależności (8.25). Z porównania obydwu warunków otrzymujemy:
Spełnienie tego warunku jest możliwe jedynie wtedy, gdy użyteczne różnice tempera
tury w poszczególnych działach są jednakowe: A'/j = A T
2
= A T„, a wówczas
Obciążenia cieplne są zatem wprost proporcjonalne do współczynników przenikania
ciepła. Spełnienie wszystkich tych założeń wymaga odpowiedniej regulacj i przepływu
oparów.
(8.35)
Qn = kn
Qi
*1
(8.36)

9. Analogia między ruchem ciepła
a ruchem pędu
9.1. Analogia Reynoldsa
Olbrzymie trudności w teoretycznym opracowaniu zagadnień ruchu ciepła,
a zwłaszcza w rozwiązywaniu równania energii dla przepływów burzliwych, skłaniają
do korzystania z wyników badań doświadczalnych. Jedną z takich metod doświad
czalnych jest metoda oparta na analogii zjawisk cieplnych i hydrodynamicznych.
Umożliwia ona badanie procesu wnikania ciepła na podstawie analizy hydrodynamiki
przepływu. Równanie ruchu w laminamej warstwie granicznej na płaskiej płycie jest
analogiczne do odpowiedniego równania energii dla tej warstwy pod warunkiem, że
lepkość kinematyczna jest równa przewodnictwu temperaturowemu (współczynniko
wi dyfuzyjności cieplnej); wówczas Pr = v/a = 1. Jak wiadomo z poprzednich
rozdziałów, również warunki brzegowe dla obu procesów są wówczas analogiczne.
Reynolds w 1874 r. jako pierwszy stwierdził podobieństwo mechanizmów trans
portu energii i pędu. W pracy opublikowanej w 1883 r. przedstawił wyniki analizy
oporu hydrodynamicznego podczas przepływu płynu w rurze, dając możliwość ilo
ściowego opisu analogii między obydwoma zjawiskami. Analogia Reynoldsa opiera
się na założeniu, że profile rozkładu prędkości i temperatury są podobne. Rozpatrując
laminamą warstwę graniczną na płycie płaskiej (rys. 9.1), przyjmujemy, że wx i Tm
oznaczają prędkość i temperaturę w rdzeniu płynu, natomiast Tw - temperaturę po
wierzchni płyty. Gdy liczba Prandtla Pr = 1, gradienty bezwymiarowej prędkości
i bezwymiarowej temperatury względem y są jednakowe:
d ( wy - wy _ d ( T - T r A
dy \ wy - wy J dy\T„ - T r ,
(9.1)
wartości wy i Tr odpowiadają przekrojowi w odległości jy od ściany.
Po przekształceniu równanie (9.1) możemy zapisać w postaci
1
dwx
1
dT
wy - wy dy
T> - T r dy
dT
(9.2)
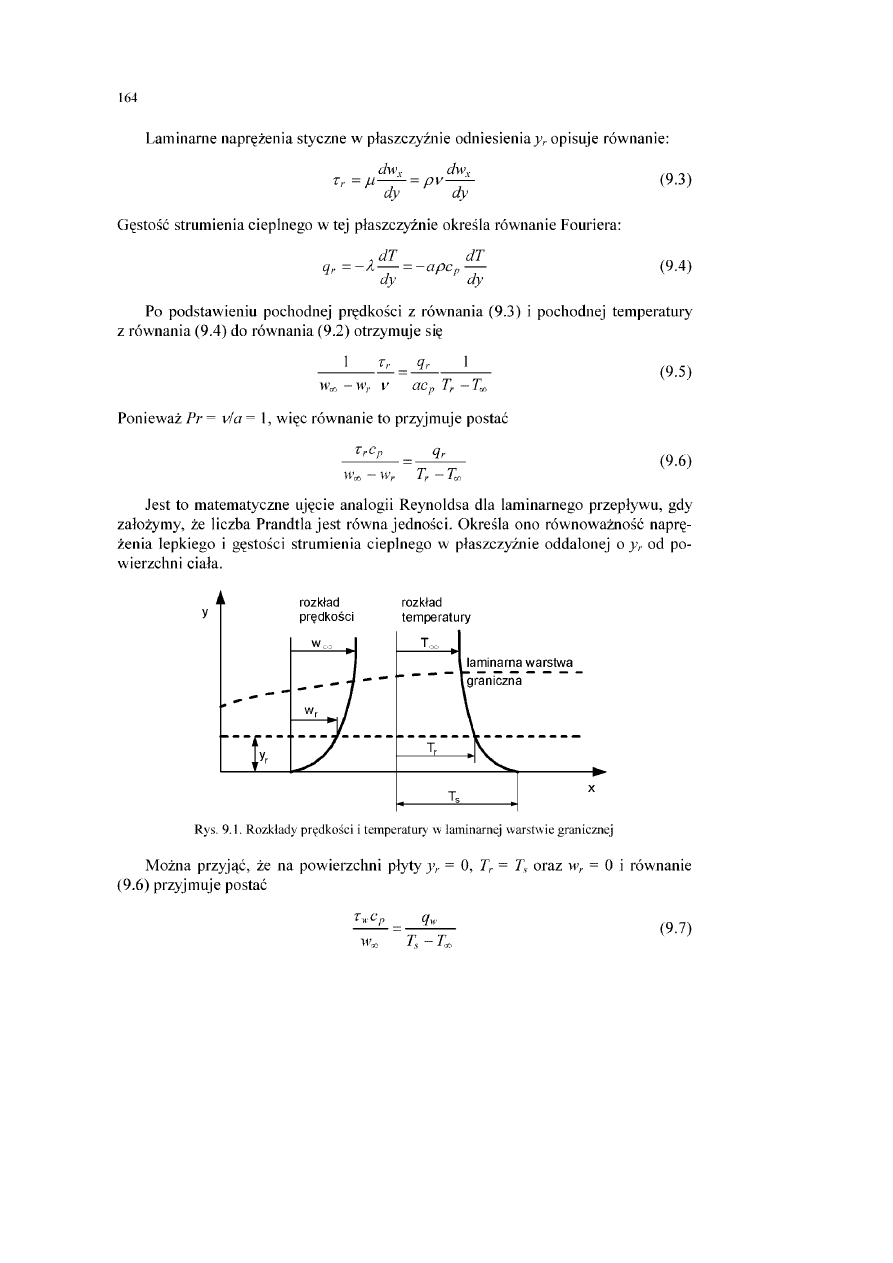
164
Laminarne naprężenia styczne w płaszczyźnie odniesieniay r opisuje równanie:
(9.3)
dwx
dw,
Tr = p — - = pv-
Gęstość strumienia cieplnego w tej płaszczyźnie określa równanie Fouriera:
(9.4)
Po podstawieniu pochodnej prędkości z równania (9.3) i pochodnej temperatury
z równania (9.4) do równania (9.2) otrzymuje się
qr
w«, - wr v
acp
- T,
Ponieważ Pr = v!a= 1, więc równanie to przyjmuje postać
T y C p
C[r
Wr„
W/-
Ty
Tr/y
(9.5)
(9.6)
Jest to matematyczne ujęcie analogii Reynoldsa dla laminarnego przepływu, gdy
założymy, że liczba Prandtla jest równa jedności. Określa ono równoważność naprę
żenia lepkiego i gęstości strumienia cieplnego w płaszczyźnie oddalonej o y r od po
wierzchni ciała.
Rys. 9.1. Rozkłady prędkości i tem peratury w laminarnej warstwie granicznej
Można przyjąć, że na powierzchni płyty y r = 0, Tr = Ts oraz wr = 0 i równanie
(9.6) przyjmuje postać
wa
T - T
-L
C
-Ł QO
(9.7)

165
Ponieważ po prawej stronie tego równania mamy współczynnik wnikania, więc
« =
(9.8)
Wco
Współczynnik wnikania ciepła można wyznaczyć po podstawieniu zależności na na
prężenie styczne, które jest stosunkowo łatwe do określenia. W literaturze anglosa
skiej można znaleźć następującą funkcję:
(9.9)
Po podstawieniu jej do równania (9.8) i przekształceniu otrzymuje się
" - = S t = ^ ~
(9.10)
wx cpp
2
Jest to analogia Reynoldsa w ujęciu liczb bezwymiarowych (St = Nu/(RePr)) oraz
współczynnika oporu hydrodynamicznego C/. Należy pamiętać o ograniczeniu, że
Pr = 1 oraz nie ma oporu wynikającego z kształtu. W literaturze polskiej podaje się
wartość C/ = Zo/4.
Z warunku równowagi pracy tarcia i pracy ciśnienia wynika bowiem
TwAw = FAp
(9.11)
gdzie: A jest powierzchnią omywaną rury, m2, 9 - objętościowym natężeniem prze
pływu, m3/s, Ap - spadkiem ciśnienia, Pa. Z równania tego mamy:
VAp
rw =— +-
(9.12)
Aw
Dla przepływu wewnątrz rury można wprowadzić następujące wzory:
• powierzchnia opływana
A ^itd L
(9.13)
• objętościowe natężenie przepływu
32
V = —
w
(9.14)
4
• spadek ciśnienia
L w
2
p
m K ,
A p ^ l o - — —
(9.15)
a 2
Po przekształceniach uzyskuje się związek:

166
rw —
w~ p
(9.16)
O
Z porównania równań (9.16) i (9.9) wynika, że C/ = hJA.
Po podstawieniu równania (9.16) do równania (9.8) i przekształceniu analogię
Reynoldsa dla przepływu w rurze można zapisać w postaci
a . = S t = —
(9.17)
WCpP
Uwzględniwszy, że St = uf (Re Pr) oraz Pr = 1, otrzymuje się
X
q
Nu - — Re
(9.18)
lub
Su,: - —^ - — Re
(9.19)
X
2
dla przepływu wzdłuż płyty.
Interesujące jest sprawdzenie możliwości wykorzystania równania analogii Rey
noldsa w praktyce. Może to dotyczyć dwu przypadków: przepływu wzdłuż płyty pła
skiej lub przepływu wewnątrz rur. Po podstawieniu zależności na lokalny współczyn
nik oporu podczas przepływu wzdłuż płyty
(9.20)
N i p
2
do równania (9.19) otrzymuje się
Nux =0,332 Rei
12
(9.21)
Jak widzimy, jest to zależność taka sama jak równanie Pohlhausena (dla Pr = 1),
wynikające z rozwiązania matematycznego tego zagadnienia.
9.2. Analogia Prandtla
W praktyce wartość liczby Prandtla znacznie różni się od jedności, więc należy
uwzględnić laminamą i turbulentną strefę strumienia. Prandtl zaproponował uwzględ
nienie rozkładu prędkości i temperatury w turbulentnej warstwie granicznej przez
wprowadzenie turbulentnej lepkości kinematycznej (lepkości wirowej) s.
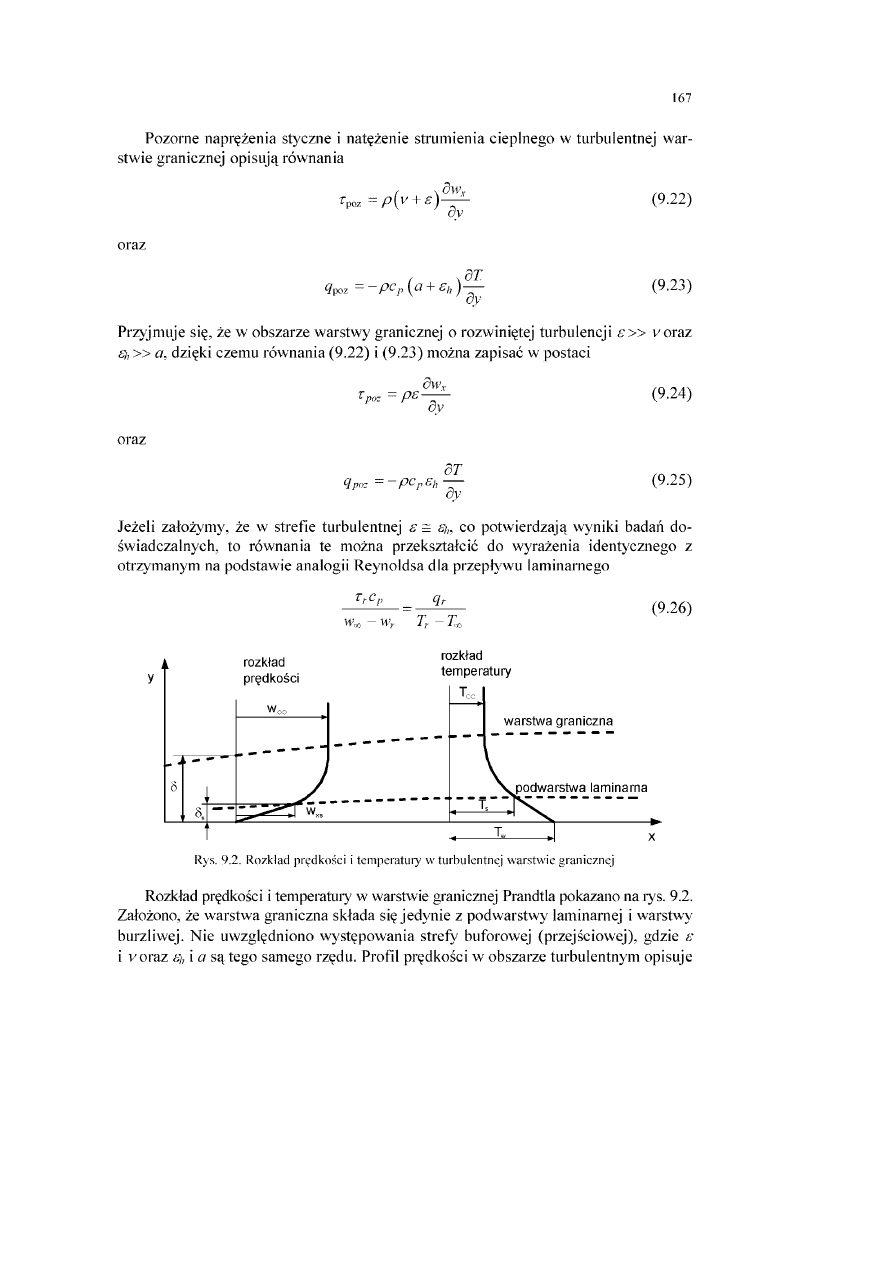
167
Pozorne naprężenia styczne i natężenie strumienia cieplnego w turbulentnej war
stwie granicznej opisują równania
*poz
p ( v + e)
dwx
dy
(9.22)
oraz
^poz
PCp
"t" &h )
dT_
dy
(9.23)
Przyjmuje się, że w obszarze warstwy granicznej o rozwiniętej turbulencji s » voraz
Sh» a, dzięki czemu równania (9.22) i (9.23) można zapisać w postaci
' poz
ps-
dw x
dy
(9.24)
oraz
Q p o i ~
P C p
dT_
dy
(9.25)
Jeżeli założymy, że w strefie turbulentnej s = Sh, co potwierdzają wyniki badań do
świadczalnych, to równania te można przekształcić do wyrażenia identycznego z
otrzymanym na podstawie analogii Reynoldsa dla przepływu laminarnego
qr
Woo
—
Wr
Tr
Tr
(9.26)
Rys. 9.2. Rozkład prędkości i tem peratury w turbulentnej warstwie granicznej
Rozkład prędkości i temperatury w warstwie granicznej Prandtla pokazano na rys. 9.2.
Założono, że warstwa graniczna składa się jedynie z podwarstwy laminamej i warstwy
burzliwej. Nie uwzględniono występowania strefy buforowej (przejściowej), gdzie s
i voraz sh i a są tego samego rzędu. Profil prędkości w obszarze turbulentnym opisuje

168
funkcja potęgowa, można natomiast przyjąć, że w laminamej podwarstwie jest on
liniowy. Nachylenie krzywej rozkładu prędkości w pobliżu ściany zależy od lokalne
go współczynnika oporu C/, który dla płyty płaskiej w zakresie przepływu burzliwego
(5-10' < Rex < 107) oblicza się z równania Blasiusa
Cf = ---- — = 0,0456
i n d .
r
V/2
v
\ 11', d'
(9.27)
Rozkład temperatury w podwarstwie laminamej jest również liniowy. Gęstość
strumienia ciepła można więc opisać za pomocą równania:
qw ~ ( T w - T s )
(9.28)
O.s
Jeżeli założymy, że płaszczyzna odniesienia r (równ. (9.26)) znajduje się na gra
nicy laminamej podwarstwy, to analogię Reynoldsa dla obszaru warstwy granicznej
zawartego między y =
8
S i obszarem przepływu potencjalnego opisuje równanie
r, c„
qs
P
(9.29)
w« - w TS
Ts - Tx
w którym rs i qs oznaczają naprężenia styczne i gęstość strumienia cieplnego dlay = Ss.
Ponieważ zmiany prędkości i temperatury w podwarstwie są liniowe, więc warto
ści r i q dla y =
8
S są równe ich wartościom dla r = 0. Równanie (9.29) można zatem
zapisać następująco:
T r
n
(9.30)
Wcrj - w xs
Ts
Po podstawieniu współczynnika wnikania ciepła
a = — - —
(9.31)
Tw ^
do równania na gęstość strumienia ciepła (9.28) otrzymujemy
^ Tw - Ts
a - -------------
(9.32)
O rr-t
rr-t
'
‘
o, l\v ~
1
qo
Z równania (9.30) wynika natomiast zależność
qw ——
— (Ts —Tk )
(9.33)
w® ~wxs
która podstawiona do równania (9.31) daje równanie
169
a -
Tw cp
Ts - T x
wx. — wxs Tw - T m
w«) -Wxę V
Przekształcenie równania (9.32) daje natomiast zależność
Tw - T s _ aSs
Tw —T
k
X
którą podstawiamy do równania (9.34) i otrzymujemy
T - T
1 W
1 S
T
_
T
J - w
00
a -
Tw^p
f t O- Ó\
( 9 .3 4 )
(9.35)
(9.36)
wx - tv rt V
X
Dla liniowego rozkładu prędkości w podwarstwie laminamej można przyjąć, że
w.
= 77
r dw x N
V
dy
>1
Jy=0
S s
z czego wynika, że
os
----
Tw
Po podstawieniu tego równania do równania (9.36) otrzymamy
(9.37)
(9.38)
a -
wx +wr.
\
ncP
x
Licznik i mianownik tego równania dzielimy przez w*
c„
Tw
a ~ —
wx
l + - ( P r - l )
w.
(9.39)
(9.40)
Równanie to jest matematycznym zapisem analogii Prandtla. Po dalszych prze
kształceniach otrzymujemy równania korelacyjne dla wymiany ciepła.
Równanie (9.40) mnożymy obustronnie przez x!X {x jest lokalną współrzędną
wzdłuż płyty):
a x
Nux - — =
X
Tw CPX
W«, A
Tw
V c p ~Wx X p
pvŁ k
rj
— CfPrRex
2 ;
1 + — ( P r - l )
1+ — ( ^ - l )
1 + — ( P r - 1 )
Woo
Woo
Woo
( 9 .4 1 )

170
Po wprowadzeniu wzoru na liczbę Stantona równanie to można zapisać w postaci
- c t
St = ------- ----------
(9.42)
1+— (P r-1)
Należy teraz określić stosunek prędkości wxs/wx. Wiemy [12], że na granicy pod-
warstwy laminamej zachodzi równość bezwymiarowych prędkości i współrzędnej y
w+=y +=
5
(9.43)
Na podstawie definicji bezwymiarowej prędkości
w + -
-
5
(
9
.
4 4
)
i z defmicj i współczynnika tarcia
r
PWZ:
Cf =
r
(9.45)
otrzymuje się wyrażenie
r
I ^ f
J - = w” \ h r
(9A 6)
\ p
V
2
które podstawiamy do równania (9.44) i przekształcamy:
— = 5 , & -
(9.47)
V
2
Po podstawieniu do równania (9.42) otrzymujemy wzór na lokalną liczbę Stantona:
- C f
Stx =------- 3 = ---------
(9-48)
\c
l +
5
J ^ - ( F r ^ 1)
Zależność ta, nazywana analogią Prandtla [12], określająca lokalną liczbę Stantona
podczas przepływu wzdłuż płyty, daje wyniki zgodne z wynikami badań doświadczal
nych wnikania ciepła w obszarze burzliwym.
W literaturze można znaleźć kilka innych rozwiązań do opisu stosunku prędkości
wxs/wx, uwzględniających warstwę pośrednią (buforową), na przykład analogie Ka-

171
miana i Martinelliego [4, 6]. Zależność uzyskana przez Karmana, zwana analogią
Karmana, ma następującą postać
St = -
- C f
2 1
Ic
1 +
j/V - 1 + ln
1 + — (Pr - 1)
(9.49)
W literaturze niemieckojęzycznej [15] polecane jest natomiast rozwiązanie Frien-
da i Metznera
St =
U ,
(9.50)
1,20 + 11,8 Pr~l/
3
( P r - l ) J —
Takie samo równanie zostało wyprowadzone do opisu analogii transportu pędu
i masy. Brauer [15] zastosował tę zależność do analizy wielu zagadnień dotyczących
zarówno wymiany ciepła, jak i wymiany masy.
9.3. Analogia Colburna
Założenie, że liczba
Pr = 1
powoduje znaczne ograniczenie zastosowania analogii
Reynoldsa. Colbum zaproponował wprowadzenie empirycznej funkcji liczby Prandtla
i otrzymał następujące wyrażenie
— = StPr2/3
(9.51)
8
w którym: Z0 - współczynnik oporu hydrodynamicznego,
Pr
- liczba Prandtla, S ł - licz
ba Stantona.
Obliczenia Colburna na podstawie wielu danych dla różnorodnych przepływów
i geometrii układów
wykazały dobrą ich zgodność dla zakresu liczb
Prandtla
0,5 < Pr < 50 pod warunkiem braku oporu kształtu. Wyrażenie to często zapisuje się
w postaci
^ = ./»
(9.52)
8
W.L. Friend, A.B. Metzner, Turbulent heat transfer inside tubes a nd the analogy between heat,
mass, a nd momentum transfer, A ICHE J. 4 (1958) 393-402.

172
gdzie
ja = StPr
213
(9.53)
nazywamy czynnikiem Colbuma dla wymiany ciepła.
Jak widać z równania (9.53), dla Pr = 1 analogia Colbuma przechodzi w analogię
Reynoldsa. Tym samym analogia Colbuma stanowi rozszerzenie analogii Reynoldsa
w zakresie liczb Prandtla od 0,5 do 50. Graniczne liczby Prandtla odpowiadają warto
ściom charakterystycznym dla ciekłych metali (małe wartości) oraz ciężkich frakcji
olejowych (duże wartości).

10. Promieniowanie cieplne
10.1. Wprowadzenie
P rom ieniow anie cieplne je s t przekazyw ane od w szystkich cial stałych o tem pera
turze wyższej od zera kelw inów . Intensyw ność prom ienio w ania zależy od tem peratury
ciała, ale rów nież od w łaściw ości m ateriału. Stosow ane są dw ie teo rie do opisu em i
sji, przenoszenia i absorpcji energii prom ieniow ania: klasyczna teo ria przenoszenia
fal elektrom agnetycznych i kw antow a teo ria fotonów . Teorie te nie w ykluczają się,
a raczej uzupełniają.
Fale elektrom agnetyczne są falam i poprzecznym i, które oscylują prostopadle do
kierunku ich rozchodzenia. W próżni przyjm ują prędkość św iatła Co = 299 792 458 m/s.
W ośrodku m aterialnym ich prędkość c je s t m niejsza, częstotliw ość natom iast je s t
taka sam a. S tosunek prędkości n = co/c > 1 je s t w spółczynnikiem załam ania św iatła
danego m ateriału.
: u i ± i (!■>' p r /y . ,- . i1 u
Rys. 10.1. Zakres promieniowania elektrom agnetycznego
Iloczyn długość fali i częstotliw ości je s t rów ny jej prędkości
A v ^ c
(10.1)
N a rysunku 10.1 pokazano zakres prom ienio w an ia elektrom agnetycznego. Zakres
m ałych długości fali (A < 0,01 pm ) odpow iada prom ieniow aniu kosm icznem u, p ro

174
m ieniow aniu y oraz X. Nie je s t ono w zbudzane cieplnie, więc nie należy do prom ie
niow ania cieplnego. Fale radiow e (A > 1(F pm ) rów nież nie n ależ ą do prom ieniow a
n ia cieplnego. O bszar prom ieniow ania cieplnego rozciąga się w zakresie od 0,1 pm do
1000 pm . P rom ieniow anie to je s t przekazyw ane przez ciała o tem peraturze od kilku
stopni K elvina do 2-104 K. W tym zakresie m ieści się rów nież św iatło w idzialne, ro z
pościerające się od fioletow ego (0,38 pm ) do podczerw onego (0,78 pm ). Zakres dłu
gości fali 0 ,0 1 -0 ,3 8 pm odpow iada światłu ultrafioletow em u, nato m iast od 0,78 pm
do 1000 pm prom ieniow aniu podczerw onem u, które je s t podstaw ow ym obszarem
prom ieniow ania cieplnego.
10.2. Właściwości promieniowania cieplnego
W łaściw ości optyczne prom ieniow ania cieplnego są takie sam e ja k w łaściw ości
prom ieniow ania w idzialnego. P rom ieniow anie cieplne padające n a pow ierzchnię (rys.
10.2) m oże zostać zaabsorbow ane, odbite bądź przepuszczone przez ciało stale. Jeżeli
ułam ki energii prom ieniow ania Q padającego n a pow ierzchnię ciała określim y jak o
Qu, Qb, Qc, to otrzym amy:
(? = & + & + &
(10-1)
lub inaczej
1 ^ a + b + c
(10.2)
gdzie: a = Q J Q je s t zd olnością absorpcji prom ieniow ania, b = QiJQ - zd oln ością
odbijania prom ieniow ania, c = Q J Q - zd oln ością p rzepuszczania prom ieniow ania
przez dane ciało.
o d a *
p a d a ją »
Rys. 10.2. O braz prom ieniowania padającego na pow ierzchnię
P rom ieniow ania m oże być odbite od pow ierzchni pod określonym kątem (odbicie
spekulam e) bądź rozproszone (W elty i in. [12]). N a rysunku 10.2 pokazano odbicie
spekulam e. W iększość cial rozprasza prom ieniow anie we w szystkich kierunkach.
A bsorpcja prom ieniow ania w ciałach stałych zachodzi n a niew ielkiej głębokości,
ok. 1 pm w elektrycznych przew odnikach oraz ok. 1 m m w półprzew odnikach.

175
Przepuszczalność większości ciał stałych jest równa zero (c = 0) i równanie (10.2)
sprowadza się do postaci
a + b = 1
W przypadku idealnie absorbującego ciała mamy a = 1. Takie ciało nazywamy
doskonale czarnym. Ponieważ nie przepuszcza ono ani nie odbija promieniowania,
widzimy je jako czarne. Oko ludzkie odbiera tylko odbite promieniowanie. Taką rolę
„czarnej dziury” odgrywa otwór małych rozmiarów w powierzchni ograniczającej
objętość większych rozmiarów. Promieniowanie wpadające nie ma możliwości wyj
ścia z powrotem.
Całkowitą energię w\ promien¡owywaną we wszystkich kierunkach przez po
wierzchnię jednostkową ciała nazywamy jego zdolnością promieniowania i oznacza
się literą £ (ang. total emissive power).
Zdolność emisyjna <?jest ściśle związana ze zdolnością promieniowania ciała. Jest
ona definiowana jako stosunek zdolności promieniowania ciała szarego do zdolności
promieniowania ciała doskonale czarnego:
Energia promieniowania Ex o długości fali w przedziale X, X + dX jest mono
chromatyczną zdolnością promieniowania. Całkowita oraz monochromatyczna zdol
ność promieniowania są zdefiniowane w następujący sposób:
• w postaci różniczkowej
d l i - E ;.dX
(10.4)
• w postaci całkowej
i»
E = ^E xdX
(10.5)
0
Monochromatyczną zdolność emisyjną sx wyrażamy wzorem:
d = - | r -
(10.6)
-¿a o
gdzie Exo jest monochromatyczną zdolnością promieniowania ciała doskonale czarne
go o długości fali Z w danej temperaturze.
Monochromatyczną zdolność absorpcji promieniowania, ax definiuje się jako sto
sunek zdolności absorpcji promieniowania o długości fali X do zdolności absorpcji
ciała doskonale czarnego dla tej samej długości fali i w tej samej temperaturze.

176
10.3. Podstawowe prawa promieniowania
10.3.1. Prawo Kirchhoffa
Z w iązek m iędzy zd olnością p rom ieniow ania ciała
E
i jeg o zd olno ścią absorpcji
a
określa praw o K irchhoffa, zgodnie z którym w zględna zdolność em isyjna i absorpcyj
n a układu w stanie rów now agi term odynam icznej są sobie rów ne:
s = a
lub
£; = ax.
Rys. 10.3. Schemat bilansu emisji promieniowania
między ciałem szarym i doskonale czarnym
R ozpatrzm y bilans em isji prom ien iow an ia m iędzy ciałem doskonale czarnym
a dow olnym ciałem szarym (rys. 10.3). Jeżeli E] je s t em isją ciała szarego (1), a E 0
em isją ciała doskonale czarnego, to ciepło w ym ienione przez prom ieniow anie w ynosi
q0_{ = E 0 - E { - E 0
( l - a t )
(10.7)
Po pew nym czasie tem peratura obu cial w yrów nuje się, a zatem
q
0.i = 0, z czego
w ynika
Ei = E 0 ( \ - \ + al ) = a lE 0
(10.8)
D la w szystkich cial o tej samej tem peraturze zapisujem y ogólnie:
— = —
= - = Eo = f ( T )
(10.9)
ai
a2
a
Stosunek energii em itow anej przez jednostkę pow ierzchni ciała do jeg o zdolności
absorpcji prom ieniow ania m a taką sam ą w artość dla w szystkich cial i je s t rów ny
zdolności prom ieniow ania ciała doskonale czarnego w danej tem peraturze.
10.3.2. Prawo Lamberta
E m isja prom ieniow ania ciała m oże być nierów nom iernie rozłożona w przestrzeni,
ale skierow ana pod pew nym kątem
0,
m ierzonym od norm alnej do danej pow ierzchni
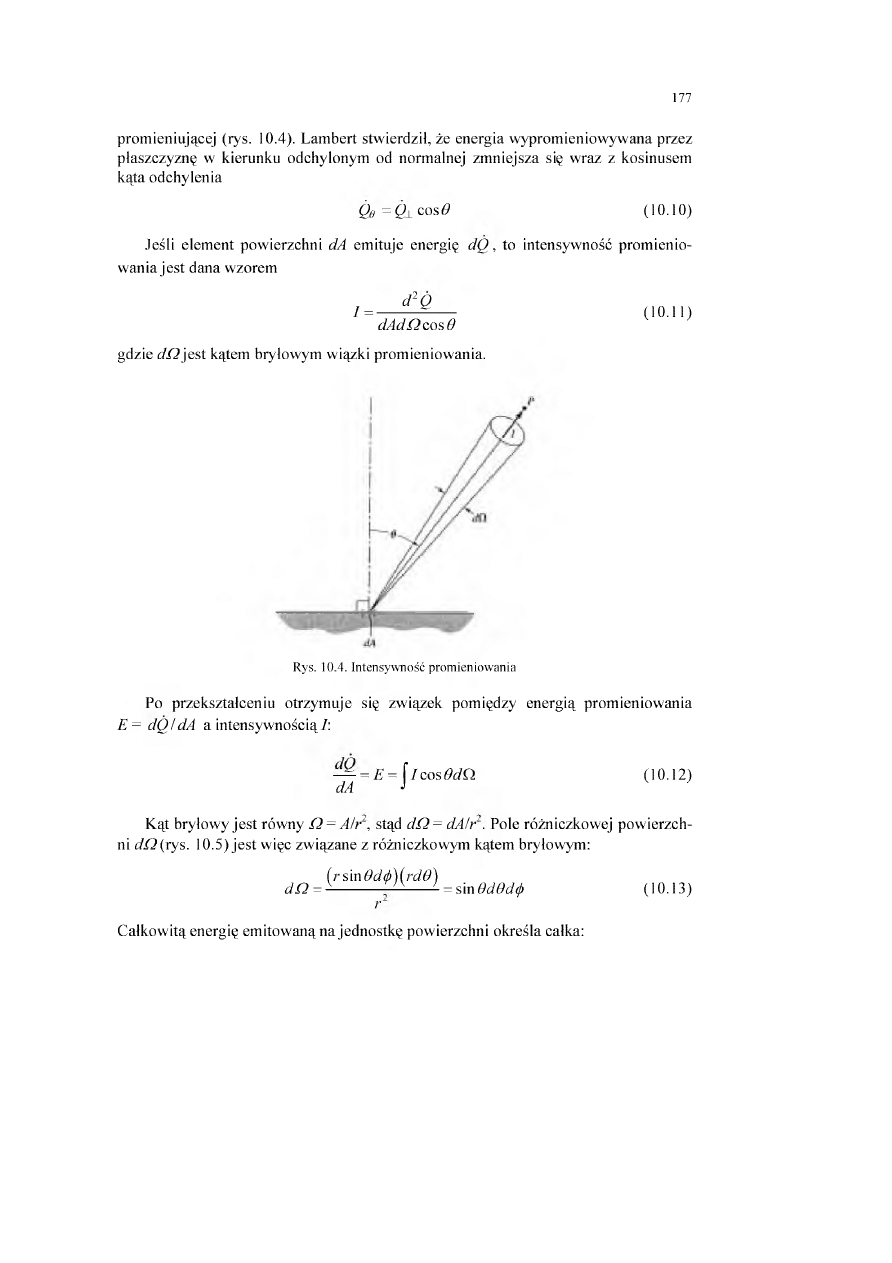
177
prom ieniującej (rys. 10.4). L am bert stw ierdził, że energia w yprom ieniow yw ana przez
płaszczyznę w kierunku odchylonym od norm alnej zm niejsza się w raz z kosinusem
kąta odchylenia
Q o = Q ± c o s O
(10.10)
Jeśli elem ent pow ierzchni
dA
em ituje energię
d Q
, to intensyw ność prom ienio
w ania je s t dana w zorem
i2
.
£ Q _
d Q
c<
gdzie
d Q
je s t kątem bryłow ym wiązki prom ieniow ania.
1
=
-
(
10
.
11
)
d A d O c o s O
Rys. 10.4. Intensywność promieniowania
Po przekształceniu otrzym uje się zw iązek pom iędzy en erg ią prom ieniow ania
E = d Q ! d A
a inten sy w n o ścią/:
—
= E = [ l c o s 0 d Q
(10.12)
dA
i
K ąt bryłow y je s t rów ny
£2 = Air
,
stąd
d fl = dAIr
,
Pole różniczkow ej po w ierzch
ni <7/2 (rys. 10.5) je s t więc zw iązane z różniczkow ym kątem bryłowym :
( r sin
9dd> )(rd9)
d Q = ±
U l
7 = sin
6d6d(/)
(10.13)
r '
C ałkow itą energię em itow aną n a jednostk ę pow ierzchni określa całka:

178
Rys. 10.5. Całkowanie intensywności promieniowania według kąta bryłowego
E ^ I ^ c o s d d D - I
| |
cosdsmdddd<f>
(10.14)
o o
Po scałkow aniu otrzym ujem y
E = i d
(10.15)
Jest to w ażna zależność energii em isji prom ien iow an ia od jeg o intensywności.
W 1900 r. P lanck opublikow ał teorię, w edług której energia prom ien io w an ia je s t
em itow ana w postaci kw antów . Przyjął on, że intensyw ność prom ieniow ania m ono
chrom atycznego ciała doskonale czarnego
I
qa
±
określa p ochodna
w której
d E 0±
stanow i część p ro m ien io w a n ia o długości fali w zakresie
dA.
Z n ak
_L
oznacza, że w ielkość ta dotyczy p ro m ien io w a n ia p ro sto p ad łeg o do je d n o stk i p o
w ierzchni pro m ien iu jącej,
h
oznacza sta lą P lancka,
c
p rędk ość św iatła,
k
s ta lą B ol
tzm ann a.
C ałkow ita intensyw ność prom ieniow ania m onochrom atycznego ciała doskonale
czarnego objętego pó łk u lą zakreśloną nad p ow ierzch nią i skierow anego pod w szyst
kim i kątam i zgodnie z praw em L am berta wynosi:
10.3.3. Prawo Plancka
r
_ d E 01 _
2 hc2r 5
E/.± —— ~ ~ —------------------
(10.16)
h x — nh/.L
( 1 0 .1 7 )
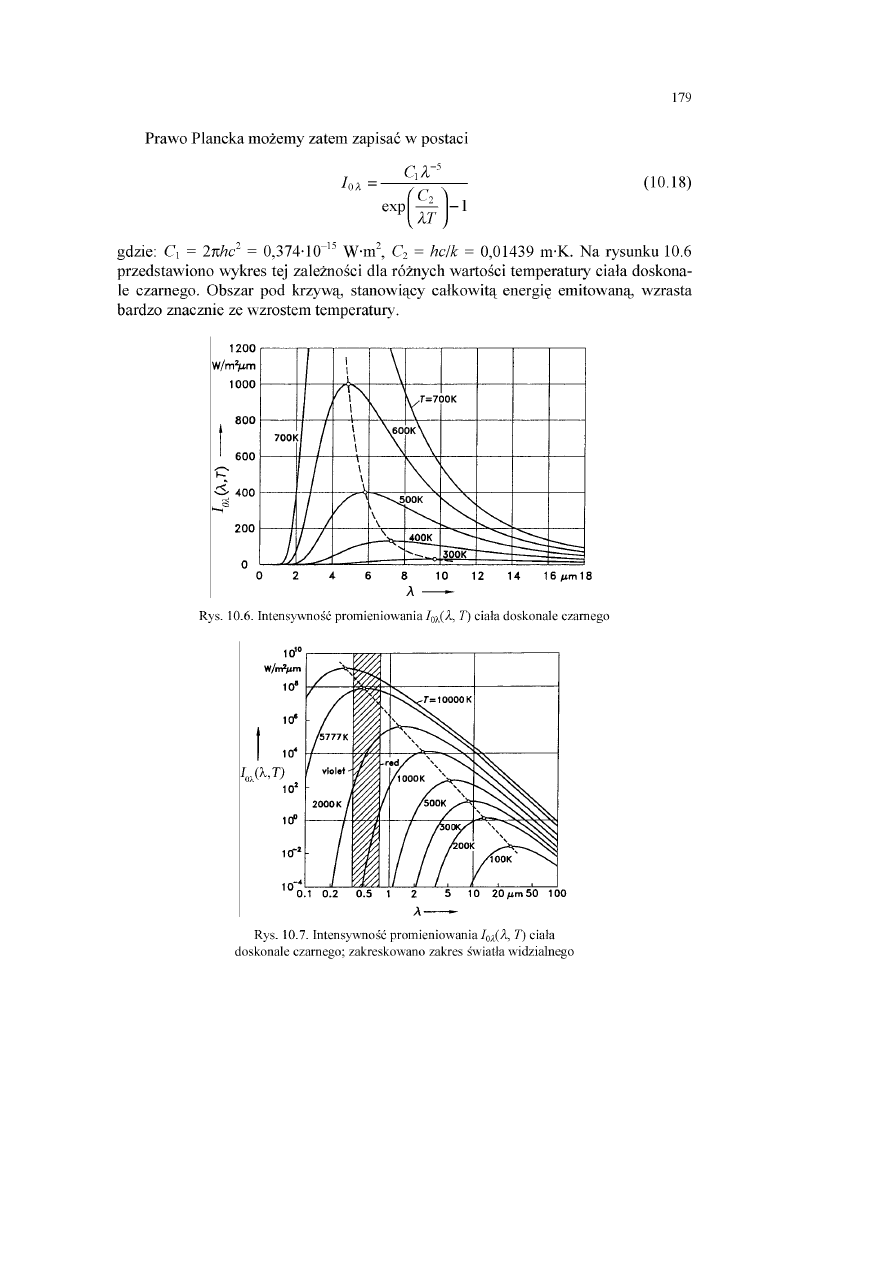
179
Prawo Plancka możemy zatem zapisać w postaci
1 0
a —
■
c , r
exp
AT
(10.18)
-1
gdzie: C
1
= 2nhc
2
= 0,374-10-15 W m 2, C
2
= hc/k = 0,01439 m-K. Na rysunku 10.6
przedstawiono wykres tej zależności dla różnych wartości temperatury ciała doskona
le czarnego. Obszar pod krzywą, stanowiący całkowitą energię emitowaną, wzrasta
bardzo znacznie ze wzrostem temperatury.
Rys. 10.6. Intensywność promieniowania I0A(A,
T
ciała doskonale czarnego
Rys. 10.7. Intensywność promieniowania I0A(A,
T
ciała
doskonale czarnego; zakreskowano zakres światła widzialnego
5

180
Energia wypromieniowywana przez ciało doskonale czarne, E0, W/m2 w zakresie
długości fal od A] do Ai_ jest proporcjonalna do pola powierzchni pod krzywą Plancka
(rys. 10.6) i określona całką:
^2
E
0
^ j l 01dA
(10.19)
A
Na rysunku 10.7 pokazano zależność intensywności promieniowania ciała dosko
nale czarnego z zaznaczonym zakresem światła widzialnego dla kilku wartości tempe
ratury. Gdy temperatura ciała doskonale czarnego jest równa temperaturze po
wierzchni słońca (5800 K), większość energii jest emitowana w zakresie długości fal
odpowiadającej światłu widzialnemu (0,4-0,7 pm).
10.3.4. Prawo Wiena
Maksimum intensywności promieniowania ciała doskonale czarnego oraz maksi
mum energii przesuwa się ku falom krótszym ze wzrostem temperatury ciała (por. rys.
10.6 i 10.7). Maksimum energii występuje dla Am^T = 2897,6 pm-K, co można po
twierdzić przez określenie maksimum funkcj¡(10.18).
Już w 1883 r. Wien ustalił doświadczalnie związek
/,„,s7' = 2.897-10 \
m -K
(10.20)
Jest to tzw. prawo przesunięć Wiena i służy do obliczania długości fali odpowia
dającej maksimum promieniowania w określonej temperaturze. Gdy na przykład
T= 1000 K, Amm = 2,9-1 (T6 m = 2,9 pm.
10.3.5. Prawo Stefana-Boltzmanna
Energię w\ promien¡owywaną przez jednostkową powierzchnię ciała doskonale
czarnego można otrzymać jako całkę funkcji Plancka w zakresie długości fali od zera
do nieskończoności
E o = ] l o x d A =
i
C
]
/
- C
0
i~~1
(10-
21)
L
¿ 0exp^ _
,
Wielkość C0 nazywamy stałą promieniowania ciała doskonale czarnego. Jej war
tość liczbowa wynosi 5,676 W/(m2-K4). Jest ona kombinacją innych stałych występu
jących w funkcj i Plancka (C0 = lic k
4
/(15c
2
h3)-108).
Prawo to, nazywane prawem Stefana-Boltzmanna, stwierdza, że energia wypro-
mieniowana przez ciało doskonale czarne jest proporcjonalna do czwartej potęgi tern-

181
peratury absolutnej. Zostało ono ustalone eksperymentalnie przez Stefana w 1879 r.
i potwierdzone na gruncie termodynamiki przez Boltzmanna w 1884 r. Dokładna war
tość stałej Co i jej związek z innymi stałymi zostały jednak ustalone na podstawie
prawa Plancka.
Ciała rzeczywiste emitują mniejszą energię w danej temperaturze (por. równ.
(10.3)). Z przekształcenia równania (10.3) otrzymujemy
100
(
10
.
22
)
Jest to prawo Stefana-Boltzmanna dla ciał szarych. Możemy je również zapisać
w postaci:
E ^ C
i rp \ 4
V
100
(10.23)
gdzie C = <sC0.
Rys. 10.8. Proporcjonalność intensywności prom ieniowania
Ciało, dla którego dla każdej długości fali stosunek intensywności promieniowa
nia do intensywności promieniowania ciała doskonale czarnego jest stały i wynosi s,
nazywamy ciałem idealnie szarym (rys. 10.8). Stałe promieniowania C ciał szarych
lub ich emisyjności s są podawane w tabelach.
10.4. Promieniowanie cieplne między ciałami stałymi
Na podstawie dotychczas wyprowadzonych praw można przyjąć, że wymiana
ciepła między dwoma ciałami stałymi zależy przede wszystkim od ich temperatury
i emisyjności powierzchni. Okazuje się jednak, że podstawowe znaczenie ma geome
tria ciał i ułożenie względem siebie. W kolejnych rozdziałach omówiono podstawowe
charakterystyczne przypadki.

182
10.4.1. Wymiana ciepła między dwoma równoległymi płytami
Zanalizujmy wyidealizowany układ nieskończenie dużych płyt szarych (rys.
10.9), tak że całe ich promieniowanie ulega wymianie. Płyta 1 ma temperaturę wyższą
od temperatury płyty 2. Można przyjąć, że z jednostkowej powierzchni płyty 1 jest
emitowana energia E
1
. Powierzchnia chłodniejsza (płyta 2) absorbuje energię
Rys. 10.9. Schemat bilansu emisji promieniowania między dwoma ciałami szarymi
równą a
2
Eh odbija zaś energię (1 - a2)E1. Z tej energii z kolei powierzchnia 1 absor
buje a 1(1 - a2)E1, odbija natomiast (1 - a 1)(1 - a2)Ei. Powierzchnia 2 pochłania ener
gię a2(1 - ai)(1 - a
2
)Eu a odbija (1 - ai)(1 - a
2
)2E
1
. Sumując otrzymane w ten sposób
kolejne ilości zaabsorbowanej energii przez płytę, otrzymujemy szereg:
qa
2
= a
2
Ej + a
2
E (1 - ax )(1 - a
2
) + a
2
E (1 - ax )2 (1 - a
2
)2
(10.24)
+— = a
2
E\ (1 + p + p 2 +— )
gdzie p = (1 - a:)(1 - a
2
).
- p
a2E1
/i n
qa 2 = -----
(10.25)
1 - P
y-
tę 2, otrzymamy podobne równanie określające energię zaabsorbowaną przez płyę 1:
qa
1
= 0 - ^
(10.26)
1 - P
Końcowy bilans energii stanowi ciepło uzyskane przez płytę 2:

183
0 - 2 — 0> 2 — 0 j]
¿2?
C[
0 £7
1 ~ p
1 ~ p
Wyrażenie (1 - p ) można zapisać w postaci
p )
= 1 - (1 -
0
) ( \ - a 2 ) = a2
+ 0
- a {a2
Po jego podstawieniu do równania (10.26) otrzymujemy
a
2
E] - a\E
2
0 - 2
a
2
+ 0
- ą a
2
(10.27)
(10.28)
(10.29)
Wartości £) i E
2
zastępujemy odpowiednimi wyrażeniami z prawa Stefana
-Boltzmanna i otrzymujemy:
0 -2
a ,0 C o | —
I
- 0 a ,C o | —
100
J
‘
l 100
ąa2
a
2
+
0
- 0 o 2
Co
(10.30)
ya
2
+ 0
-
0
a
2
7
i po dalszych przekształceniach mamy:
A J - ( A .
100J
i 100
0 -2
/
Co
.4
r
x4
7j V
( T
2
x
Co
1007
u 00
.4
s
.4
Ti V
( T>
1007
U 00
(10.31)
7
<61
S
2
Strumień ciepła przekazanego od płyty 1 do płyty 2 o powierzchni A wynosi za-
tem
81-2
- £ -.A C o
A .
100
t
2
100
w
(10.32)
Zastępczą zdolność emisj i układu dwóch płyt równoległych opisuje równanie
(10.33)
£\
£2

184
10.4.2. Wymiana ciepła od powierzchni
A \
zamkniętej przez powierzchnię A2
W wyniku podobnej jak poprzednio analizy (rozdz. 10.4.1) wymiany ciepła przez
promieniowanie od powierzchni A\ otoczonej przez powierzchnię zamkniętą ,-L (rys.
10.10) otrzymuje się wzór Christiansena
W przypadku gdy powierzchnia/L jest bardzo duża w porównaniu z powierzchnią Ah
zastępcza zdolność emisj i jest równa zdolności emisj i powierzchni A h tj. s'z ~S\.
10.4.3. Wymiana ciepła między dwoma powierzchniami
dowolnie ustawionymi
W przypadku dwu płaszczyzn ustawionych dowolnie względem siebie (rys. 10.11)
można na podstawie prawa Lamberta wyprowadzić następujące równanie
(10.34)
gdzie zastępcza zdolność emisji jest dana wzorem
(10.35)
$
Rys. 10.10. Schem at układu z pow ierzchnią.4,
w ewnątrz pow ierzchni A 2
(10.36)
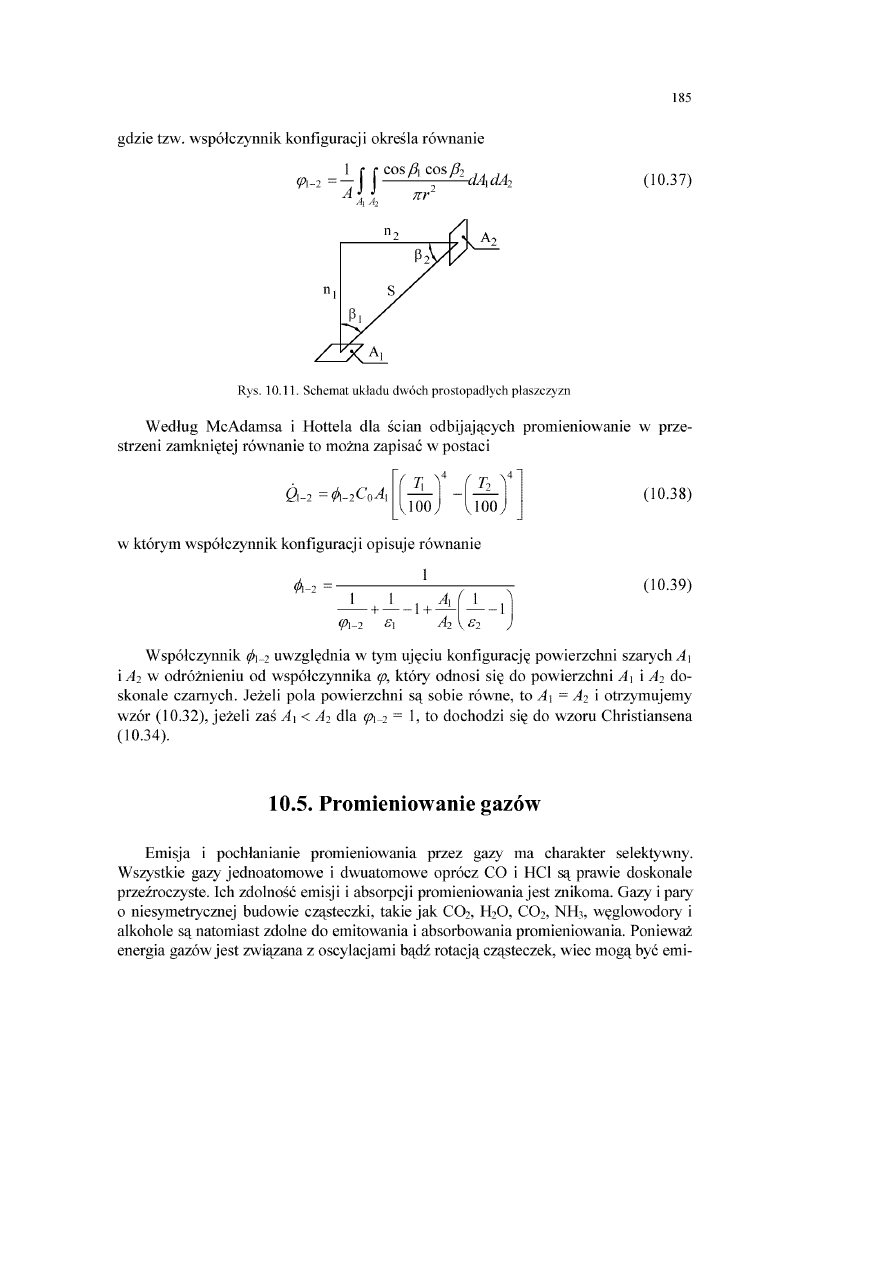
185
gdzie tzw. współczynnik konfiguracji określa równanie
cosfy cos/?;
1
f f
J
-
dĄ dA
2
(10.37)
A
Tir
Rys. 10.11. Schemat układu dwóch prostopadłych płaszczyzn
Według McAdamsa i Hottela dla ścian odbijających promieniowanie w prze
strzeni zamkniętej równanie to można zapisać w postaci
0 i - 2
^(/h-iC^Ai
w którym współczynnik konfiguracji opisuje równanie
J L
100
t
2
100
(10.38)
<Pi-2
A
a
2
(10.39)
\ £2
Współczynnik $_2 uwzględnia w tym ujęciu konfigurację powierzchni szarych A\
i A
2
w
odróżnieniu od współczynnika ę, który odnosi się do powierzchni A\ i A
2
do
skonale czarnych. Jeżeli pola powierzchni są sobie równe, to A] = A
2
i otrzymujemy
wzór (10.32), jeżeli zaś A\ < A
2
dla (p
\-2
= 1, to dochodzi się do wzoru Christiansena
(10.34).
10.5. Promieniowanie gazów
Emisja i pochłanianie promieniowania przez gazy ma charakter selektywny.
Wszystkie gazy jednoatomowe i dwuatomowe oprócz CO i HC1 są prawie doskonale
przeźroczyste. Ich zdolność emisji i absorpcji promieniowania jest znikoma. Gazy i pary
o niesymetrycznej budowie cząsteczki, takie jak CTK 11 (). C(K \1 E. węglowodory i
alkohole są natomiast zdolne do emitowania i absorbowania promieniowania. Ponieważ
energia gazów jest związana z oscylacjami bądź rotacją cząsteczek, wiec mogą być emi-

186
towane lub absorbowane kwanty promieniowania odpowiadające różnicy energii mię
dzy dozwolonymi stanami. Dla przykładu pasma promieniowania CO? odpowiadają
następującym wartościom długości fali X (w pm): 2,64-2,84, 4,13—4,47 oraz 13,0-17,0,
pomijając fale krótsze, świetlne, dające niewielkie ilości energii cieplnej.
Podobnie promieniowanie pary wodnej składa się z pasm o długościach fali X
(wpm): 2,24-3,27, 4,80-8,50 oraz 12,0-25,0. Gazy te są produktami spalania węglo
wodorów oraz innych ciał stałych (m.in. węgla).
Istotna różnica pomiędzy promieniowaniem gazów i ciał stałych polega również
na tym, że w gazach emisja i pochłanianie promieniowania zachodzą w całej objęto
ści. W przypadku wiązki promieniowania monochromatycznego o intensywności Ix
przechodzącego przez płaską warstwę gazu grubości s, pochłanianie energii następuje
zgodnie z zależnością
w którym: Ix - intensywność promieniowania w odległości jc od początku warstwy,
kx - współczynnik pochłaniania, zależny od ciśnienia i temperatury gazu.
Po scałkowaniu równania (10.39) w granicach od 0 do s otrzymujmy
stanowiącą energię zaabsorbowaną przez warstwę gazu.
Wielkość w nawiasie kwadratowym oznacza współczynnik absorpcji promienio
wania gazu /•.. dla długości fali X, który zgodnie z prawem Kirchhoffa jest równy emi-
syjności sgX. Całkowite wartości tych współczynników otrzymuje się przez ich zsumo
wanie w zakresie długości fali pasma promieniowania. Wielkości sgX i ZAg zależą od
kształtu i wymiarów warstwy gazu. Dla całego zakresu promieniowania s = j{T, p, s)
odczytuje się z odpowiednich wykresów (rys. 10.12 i 10.13).
Według wielu autorów prac doświadczalnych energia promieniowania gazów nie
podlega prawu Stefana-Boltzmanna. Otrzymane zależności mają zatem postać:
dIXs = - kxhxdx
(10.40)
IXs = h e x p (-ł} s)
(10.41)
oraz rozmcę
(10.42)
• dla CO
3,5
(10.43)
• dla pary H20
( 1 0 .4 4 )
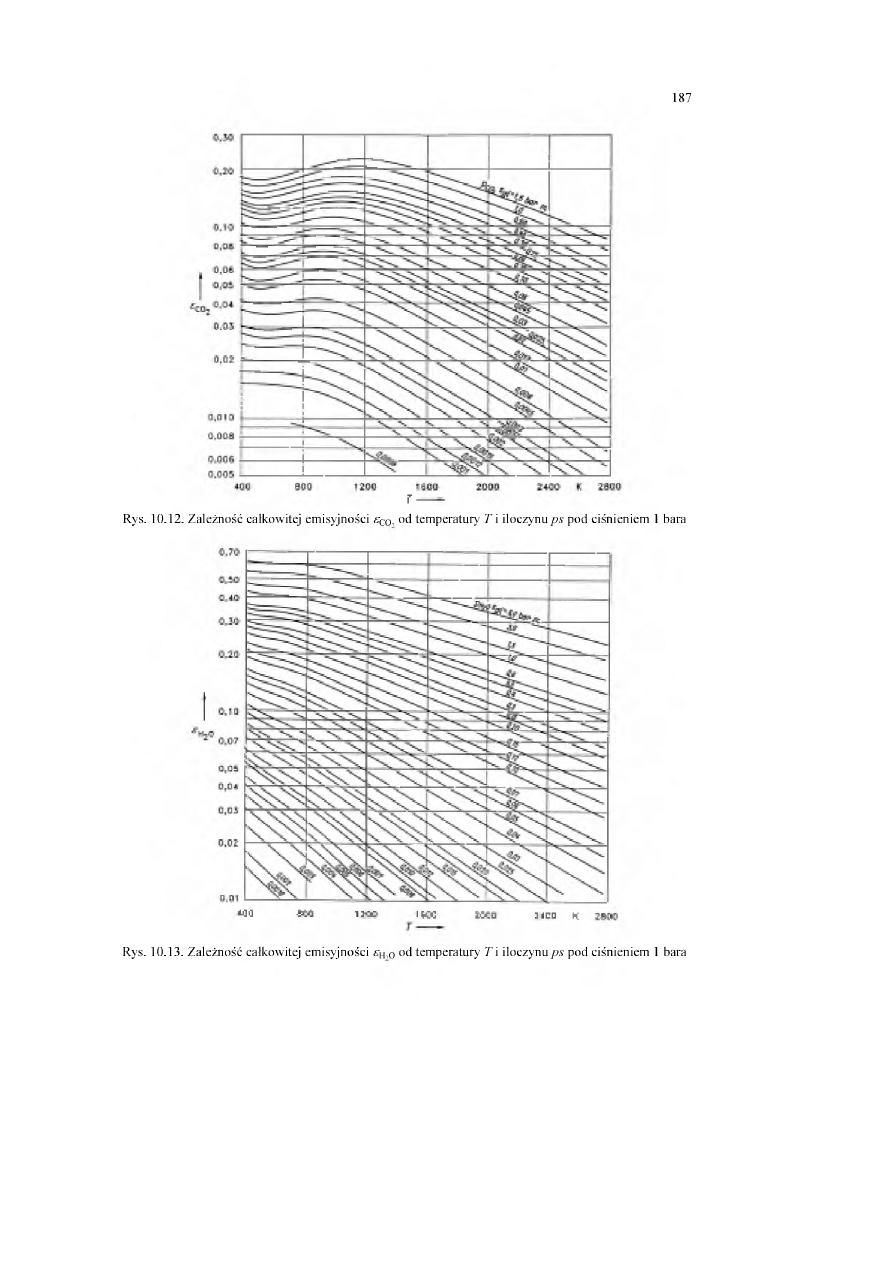
187
r
Rys. 10.12. Zależność całkowitej emisyjności f Co, ° d tem peratury T i iloczynu p s pod ciśnieniem 1 bara
« 0
i «
1TOO
l « K
1 « U
?
riCD
K
Rys. 10.13. Zależność całkowitej emisyjności f H,o od tem peratury T i iloczynu p s pod ciśnieniem 1 bara
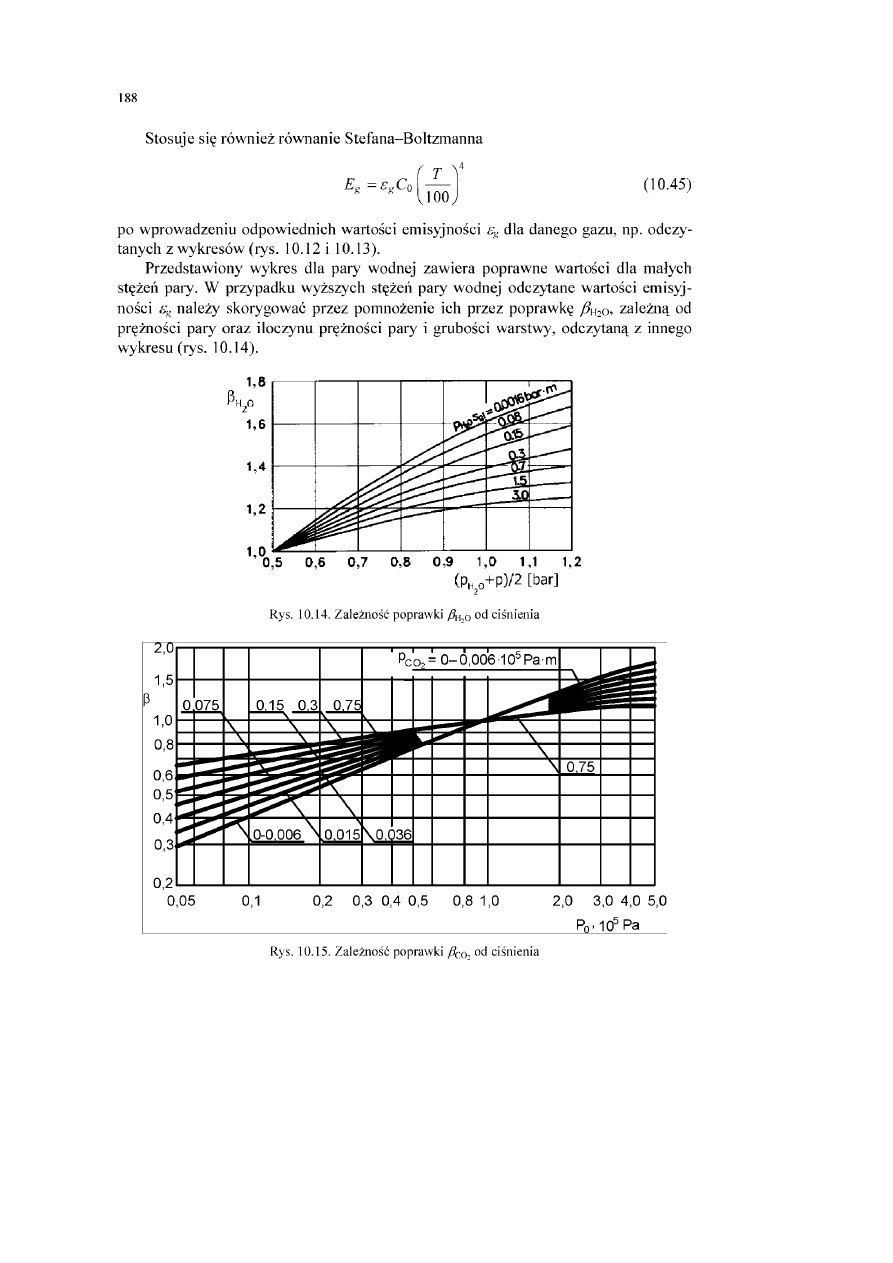
188
Stosuje się również równanie Stefana-Boltzmanna
= % C0
f rp
v100y
( 1 0 .4 5 )
po wprowadzeniu odpowiednich wartości emisyjności sg dla danego gazu, np. odczy
tanych z wykresów (rys. 10.12 i 10.13).
Przedstawiony wykres dla pary wodnej zawiera poprawne wartości dla małych
stężeń pary. W przypadku wyższych stężeń pary wodnej odczytane wartości emisyj
ności sg należy skorygować przez pomnożenie ich przez poprawkę /?h2o> zależną od
prężności pary oraz iloczynu prężności pary i grubości warstwy, odczytaną z innego
wykresu (rys. 10.14).
Rys. 10.14. Zależność poprawki /?H
0
od ciśnienia
Rys. 10.15. Zależność poprawki (3COl od ciśnienia
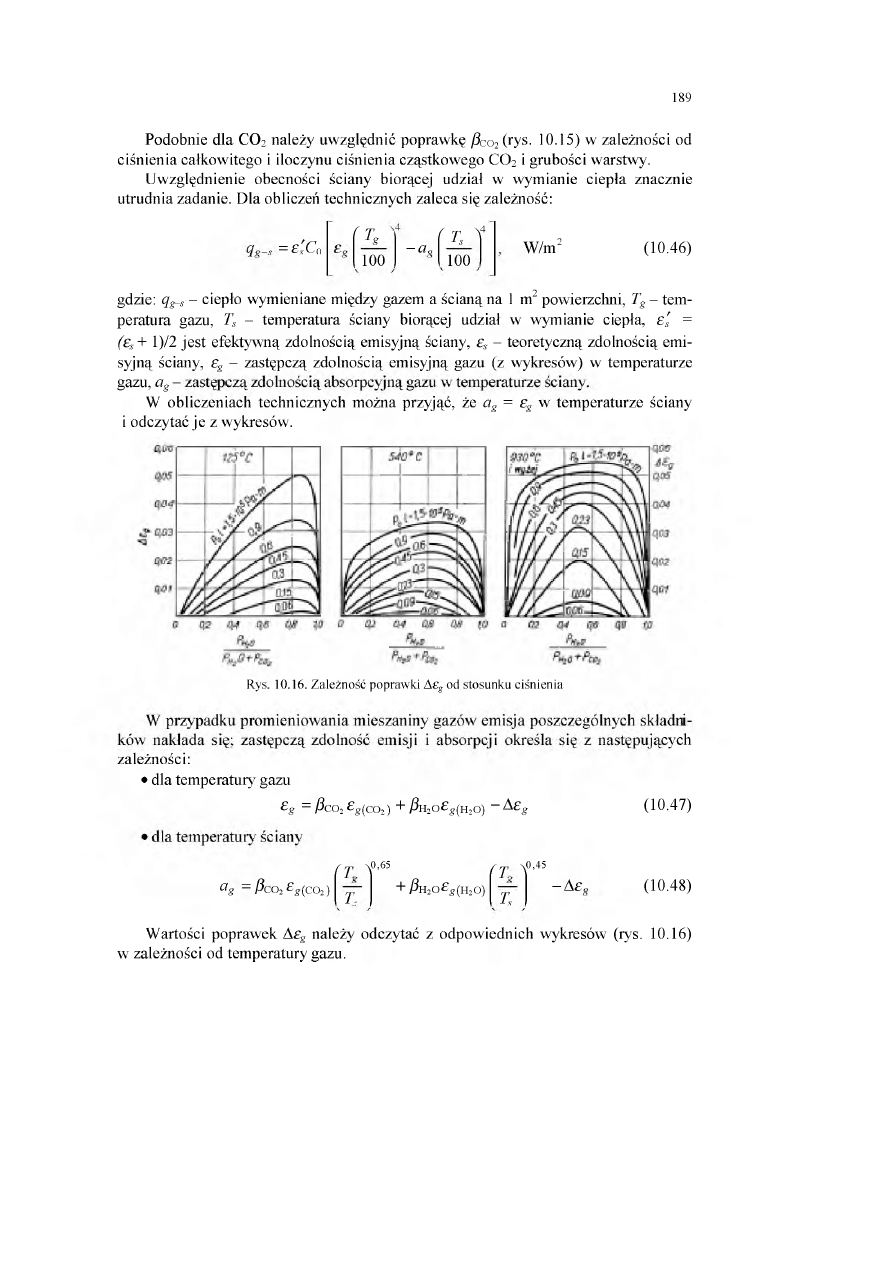
189
Podobnie dla CO2 należy uwzględnić poprawkę ¡3
CO2
(rys- 10.15) w zależności od
ciśnienia całkowitego i iloczynu ciśnienia cząstkowego C 02 i grubości warstwy.
Uwzględnienie obecności ściany biorącej udział w wymianie ciepła znacznie
utrudnia zadanie. Dla obliczeń technicznych zaleca się zależność:
=£.:cn
i T
Tg
100
- ag
/ T \4
T s
100
W/m2
(10.46)
gdzie: qg-s - ciepło wymieniane między gazem a ścianą na 1 m2 powierzchni, Tg - tem
peratura gazu, Ts - temperatura ściany biorącej udział w wymianie cie^a, e's =
(es + 1)/2 jest efektywną zdolnością emisyjną ściany, es - teoretyczną zdolnością emi
syjną ściany, eg - zastępczą zdolnością emisyjną gazu (z wykresów) w temperaturze
gazu, ag -
p
W obliczeniach technicznych można przyjąć, że ag = eg w temperaturze ściany
i odczytać je z wykresów.
Rys. 10.16. Zależność poprawki
Aeg od stosunku ciśnienia
i-
cych
zależności:
• dla temperatury gazu
Eg =Pco
2
Eg(CO
2
) + A^oCg(H
2
O) - A e g
(10.47)
a g
=
P c O 2 E g
(CO
2
)
^T \°,65
T
+ ^H
2
OEg (H
2
O)
/^
t
A0’45
T
s
-A E
g
(10.48)
Wartości poprawek AEg należy odczytać z odpowiednich wykresów (rys. 10.16)
w zależności od temperatury gazu.

11. Obliczanie wymienników ciepła
11.1. Klasyfikacja wymienników ciepła
Wymienniki ciepła są to urządzenia, w których zachodzi przekazywanie energii
między dwoma płynami. Ze względu na sposób działania dzielimy je na trzy rodzaje.
Podstawową grupę (według Hoblera) stanowią wymienniki powierzchniowe, ina
czej przeponowe lub rekuperatory. Go racy czynnik, oddający ciepło, oraz zimny płyn
przejmujący ciepło, przepływają rozdzielone wzdłuż ściany rury albo ściany płaskiej,
lub zakrzywionej. Wymiana energii zachodzi kolejno od gorącego płynu do ściany
przez konwekcję, następnie przez przewodzenie w ścianie i w końcu ponownie przez
kon
ustalonej wymiany ciepła z utrzymaniem czystości płynów bez ich mieszania się.
eniem.
W aparatach tych znajduje się wypełnienie z ciała stałego w postaci kształtek, kul lub
blach, nieruchomych albo będących w ruchu. Czynnik gorący i zimny płyn
przepływają przez wolną objętość wypełnienia naprzemian. Czynnik gorący oddaje
energię cieplną do wypełnienia, po czym zimny płyn przejmuje ją. Ruch ciepła jest z
zasady nieustalony, tj. temperatura zmienia się w czasie. Do tej grupy należą
regeneratory pieców Siemensa-Martina oraz niektóre generatory gazu.
k-
torem.
Trzecią grupę stanowią wymienniki ciepła bezprzeponowe mokre (mieszankowe).
d-
nym czynnikiem jest gaz, drugi znajduje się w fazie ciekłej. Ciecz spływa po wypel-
nienia.
o
u
a-
chodzi w sposób ciągły, ustalony. Zaletą takich wymienników jest duża intensywność
- mie
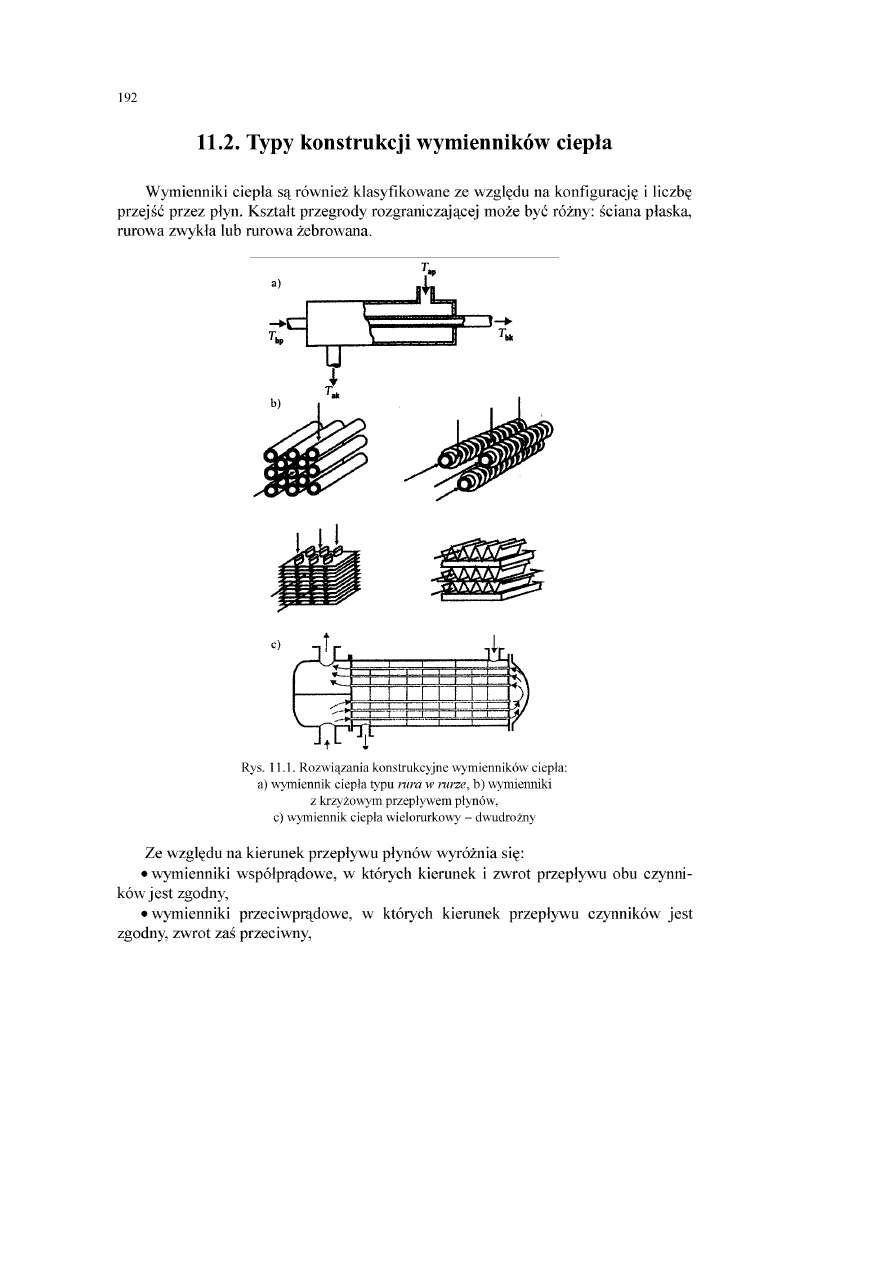
192
11.2. Typy konstrukcji wymienników ciepła
Wymienniki ciepła są również klasyfikowane ze względu na konfigurację i liczbę
przejść przez płyn. Kształt przegrody rozgraniczającej może być różny: ściana płaska,
rurowa zwykła lub rurowa żebrowana.
Rys. 11.1. Rozwiązania konstrukcyjne wymienników ciepła:
a) wymiennik ciepła typu
rura w rurze,
b) wymienniki
z krzyżowym przepływem płynów,
c) wymiennik ciepła wielorurkowy - dwudrożny
Ze względu na kierunek przepływu płynów wyróżnia się:
• wymienniki współprądowe, w których kierunek i zwrot przepływu obu czynni
ków jest zgodny,
zgod

193
• wymienniki krzyżowe, w których kierunek i prędkość przepływu czynników są
prostopadłe.
0-
razowy. Typowym przykładem takiej konfiguracji jest wymiennik typu rura w mrze,
przedstawiony schematycznie na rys. 11.1a. Schemat wymienników z przepływem krzy
żowym pokazano na rys. 11.1 b.
W rozwiązaniach przedstawionych na rys. 11.1 a i b płyny przepływają oddzielnie
u-
gim -
u
u-
mieniami płynu o różnej temperaturze.
j-
1-
guracyjnego z dwu- lub wielokrotnym przepływem czynnika. Typowym przykładem
e-
rurek, drugi natomiast -
o
n-
ników ciepła, będą omówione w następnym rozdziale.
11.3. Warunki pracy wymienników ciepła
e-
pływu płynów względem siebie. Rozróżnia się:
czynników są zgodne,
•
czynników jest zgodny, a zwrot przeciwny,
•
o-
stopadłe lub inne.
Schematy wymienników ciepła i rozkładu temperatury płynów dla przepływu
współprądowego i przećiwprądowego przedstawiono na rys. 11.2 i rys. 11.3. Jeżeli
przyjmiemy jednakowe wartości współczynników wnikania ciepła po obu stronach
i-
odsta
o-
dzić czynnik a do temperatury niższej od temperatury końcowej czynnika b (rys.
11.3), czynnik b natomiast możemy podgrzać do temperatury wyższej od temperatury
ko cowej czynnika a
^^
a
(przeciwp.) ^^^
a
(wspólp.)
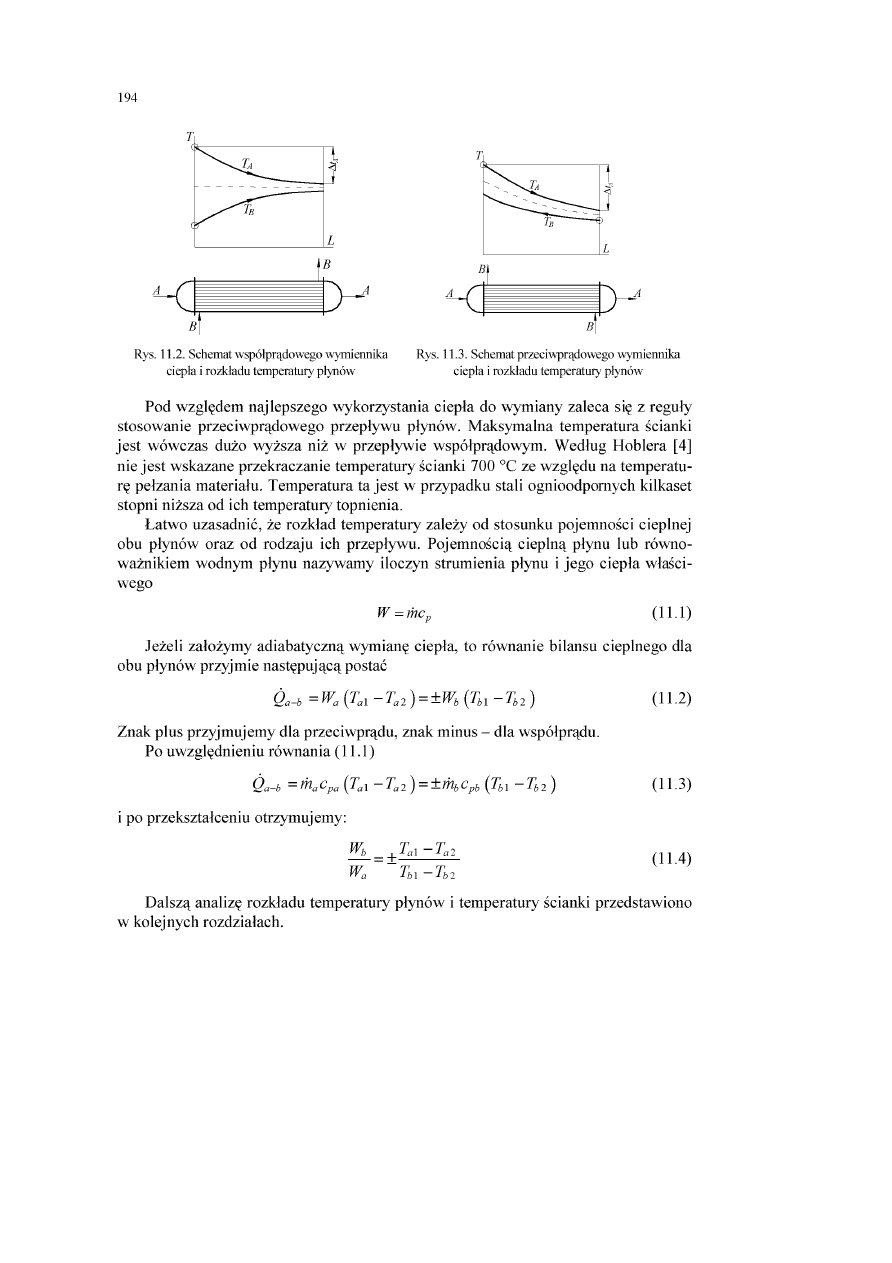
194
B
Rys. 11.2. Schemat współprądowego wymiennika
ciepła i rozkładu temperatury płynów
Rys. 11.3. Schemat przeciwprądowego wymiennika
ciepła i rozkładu temperatuty płynów
Pod względem najlepszego wykorzystania ciepła do wymiany zaleca się z reguły
stosowanie przeciwprądowego przepływu płynów. Maksymalna temperatura ścianki
jest wówczas dużo wyższa niż w przepływie współprądowym. Według Hoblera [4]
nie jest wskazane przekraczanie temperatury ścianki 700 °
C ze względu
na temperatu
rę pełzania materiału. Temperatura ta jest w przypadku stali ognioodpornych kilkaset
stopni niższa od ich temperatury topnienia.
Łatwo uzasadnić, że rozkład temperatury zależy od stosunku pojemności cieplnej
0-
1-
wego
W = mcp
(111)
Jeżeli założymy adiabatyczną wymianę ciepła, to równanie bilansu cieplnego dla
obu płynów przyjmie następującą postać
Qa-b = Wa (Ta
1
- Ta
2
)=±Wb (Tbl - Tb
2
)
Znak plus przyjmujemy dla przeciwprądu, znak minus - dla współprądu.
Po uwzględnieniu równania (11.1)
Qa-b = macpa (Ta 1 - Ta 2 ) = ± mbCpb (T>1 - Tb 2 )
i po przekształceniu otrzymujemy:
WL = ± Ta 1 - Ta
2
Wa
Tm - Tb 2
(11.2)
(11.3)
(11.4)
Dalszą analizę rozkładu temperatury płynów i temperatury ścianki przedstawiono
w kolejnych rozdziałach.
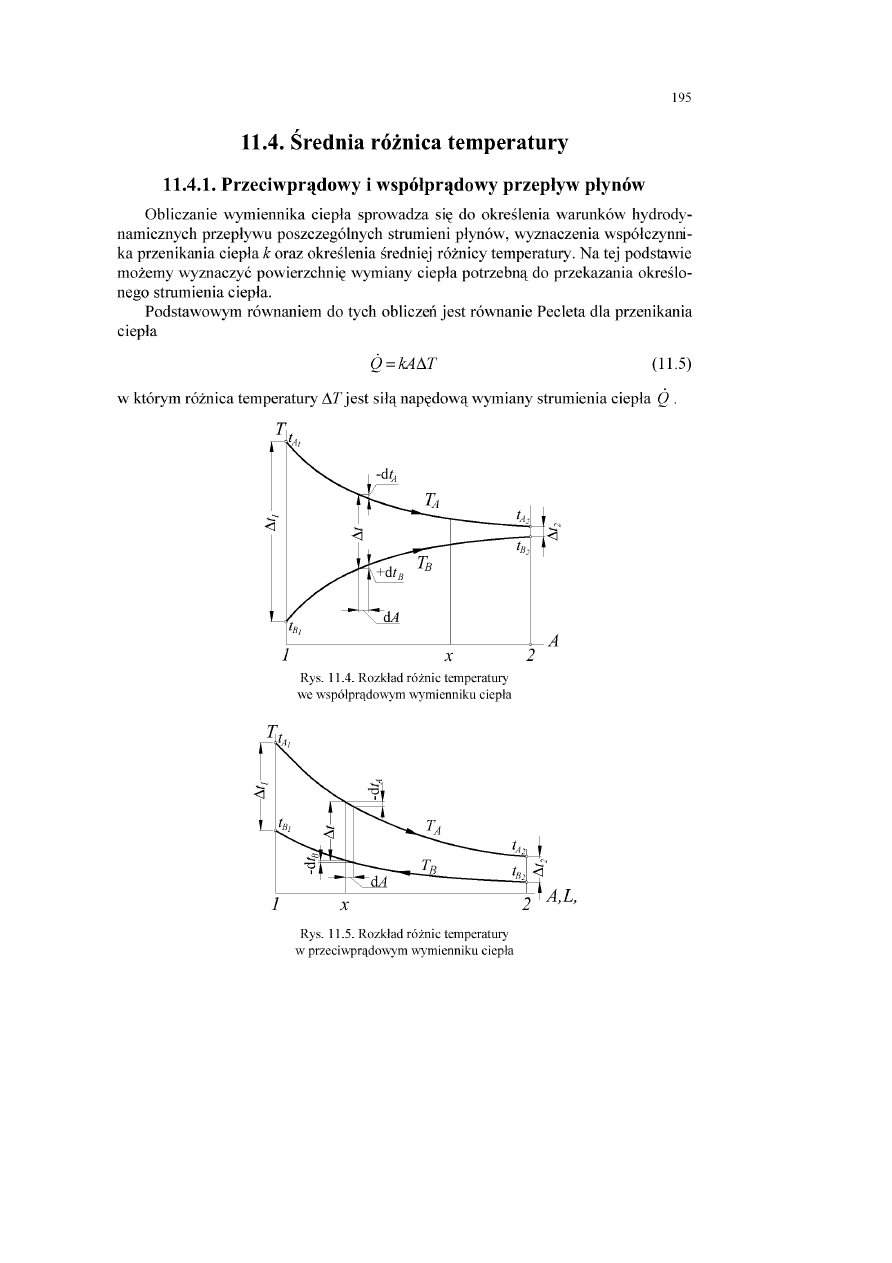
195
r
11.4. Średnia różnica temperatury
11.4.1. Przeciwprądowy i współprądowy przepływ płynów
Obliczanie wymiennika ciepła sprowadza się do określenia warunków hydrody
namicznych przepływu poszczególnych strumieni płynów, wyznaczenia współczynni
ka przenikania ciepła k oraz określenia średniej różnicy temperatury. Na tej podstawie
możemy wyznaczyć powierzchnię wymiany ciepła potrzebną do przekazania określo
nego strumienia ciepła.
Podstawowym równaniem do tych obliczeń jest równanie Pecleta dla przenikania
ciepła
Q = k A M
(11.5)
w którym różnica temperatury AT jest siłą napędową wymiany strumienia ciepła Q .
Rys. 11.4. Rozkład różnic temperatury
we wspólprądowym wymienniku ciepła
Rys. 11.5. Rozkład różnic temperatury
y

196
wierzchni i drogi wymiany ciepła. Jedynie w szczególnym przypadku, jakim jest wy
parka, w której po jednej stronie ścianki ciecz wrze, a po drugiej skrapla się nasycona
para grzejna, ta różnica temperatury jest stała. Najczęściej jednak różnica temperatury
płynów AT = Ta - Tb zmienia się wzdłuż drogi przepływu, jak pokazano na rys. 11.4
i 11.5 dla współprądowego i przećiwprądowego wymiennika ciepła. W każdym prze
kroju różnica temperatury płynów jest inna. Jedynym możliwym rozwiązaniem jest
ATm
a
nie Pecleta
Q = kAATm
(11.6)
W celu wyprowadzenia wzorów na średnią różnicę temperatury rozpatruje się
wiele równań. Na różniczkowej powierzchni wymiennika ciepła dA gorący płyn odda
je w jednostce czasu różniczkową ilość ciepła dQa:
dQa = -m aCpadTa
(11.7)
Całkowity strumień ciepła przekazany na całej powierzchni A, tzn. na drodze od prze
kroju 1 do przekroju 2 (rys. 11.5), wynosi
Ta 2
Qa =-ma
J
CpadTa
(11.8)
o-
Ta
a 1
W równaniach tych mamy znak - dla przeć iwprądu oraz znak + dla współprądu.
Strumienie ciepła można opisać ze względu na wymianę ciepła między czynnikami:
• w odniesieniu do elementu powierzchni dA
dQa -b = kdAAT
(11.9)
•
A
Qa-b = A (kAT )m
(11.10)
Równanie (11.9) przekształcamy do postaci
dA = d ^
(11.11)
kAT
Można przyjąć, że w adiabatycznym wymienniku ciepła dQa = dQa-b oraz Qa = Qa-b .
Po podstawieniu wzoru (11.7) do (11.11), otrzymujemy
ma cpa dTa
dA =-------------
kAT
(11.12)

197
oraz po scałkowaniu
A = -m
a
f —
—
—
(11.13)
J
kAT
y
'
T
a 1
Ta
2
iT
Po podstawieniu ostatniego wyrażenia do wzoru (11.10)
r2 c dT
Qa-b = ma
( t ó T )m
( 1114)
T
kAT
Ta 1
i porównaniu równania (11.14) z równaniem (11.8) otrzymujemy
- ma f c
p
adTa = —ma f -
p
^ ( k A T )
m
(11.15)
JT
JT kM
T
a 1
T
a 1
po przekształceniu zaś
f cpadTa
(kAT )m = £ ----- —
( 1116)
c dT
pa
a
kAT
Ta1
oraz założeniu, że cp = const mamy:
M ) = T
Ta2 dTa
(kAT )m = § 2 - ^
(11.17)
j kAT
Ta 1
dla k = const zaś
Ta 2 —
Ta 1
Tr2 dTa
ATm =~
T
~----- 21
(11.18)
T
a 2
T
T
T
a 1
Jeżeli założymy, że k = const, to z równania (11.10) otrzymujemy równanie Pec-
leta w ogólnej postaci:
Q = kAAT
m
(1119)
o-
mość zależności AT = f (Ta). Zależność ta jest najczęściej liniowa. Wyjątek stanowi
chłodzenie przeponowe mieszaniny gazu i pary, kiedy część pary się wykrapla. Jeżeli

198
założymy prostoliniową zależność: AT = aTa + b (tj. równanie y = ax + b), to po prze
kształceniu otrzymujemy:
rri
rri
rri
rri
rri
rri
rri
rri
ATm = Ta2 - Ta 1 = Ta2 - Ta 1 = Ta2 - Ta 1 = aTa2 -
aTa1
(11.20)
1
dTa
T dTa
l i n ^^a2 +b
^ AT2
AT
1
aT
a
+ b
a
aT
a
\ +b
A?j
T
a 1
T
a 1
a po dodaniu w liczniku stałych b i -b mamy
ATm = ^ TL-T T -
(11.21)
i n ^ _
T
Jest to tzw. średnia logarytmiczna różnica temperatury płynów. Wyrażenie to obowią
zuje również, gdy jedna z wartości temperatury jest stała (linia Tb), jak np. podczas
kondensacji czy odparowania. Taką samą postać równania otrzymujemy dla współ-
e
w-
naniem (11.6) iub (11.7). W szczególnym przypadku, gdy wyrażenie {kAT) zmienia
się liniowo w zależności od Ta iub Tb, rozwiązanie otrzymuje się jako średnią loga
rytmiczną:
, j k ą
- y p
,
(
1 1
.
22
)
V
>m
(kAT)
in ------ —
(kAT ,1
Częściej współczynnik k i różnica temperatury AT są o d rę b n y i liniowy mi funk
cjami temperatury czynnika a. Obowiązuje wówczas wzór Colbuma:
(kAT) =
kAT2
- k lA T
(11.23)
v
,m
ki AT2
k2A T
Całkowanie możemy wykonać metodą graficzną lub innymi przybliżonymi metodami.
11.4.2. Prądy skrzyżowane i mieszane
y-
żowy. Zasadę działania wymiennika z przepływem krzyżowym pokazano na rys. 11.6.
o-
wadzamy poprawkę e. Poprawka £ jest wskaźnikiem zmiany intensywności wymiany
ciepła. Wykres zmian temperatury dla zastępczego układu przepływu krzyżowego
pokazano na rys. 11.7.
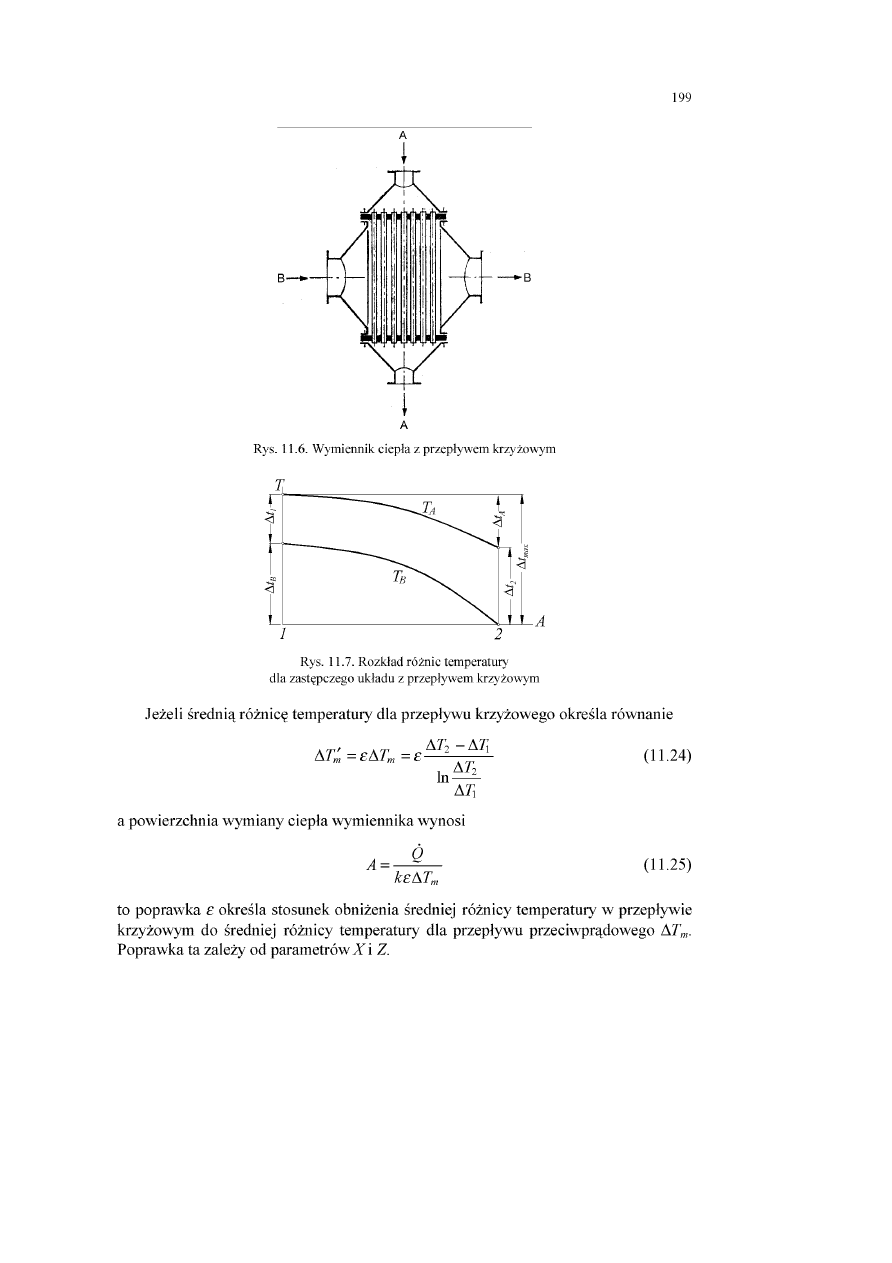
199
Rys. 11.6. Wymiennik ciepła z przepływem krzyżowym
Rys. 11.7. Rozkład różnic temperatury
dla zastępczego układu z przepływem krzyżowym
e
AT
2
—
A T
ATm' =eA Tm =e-
ln
AT;
AT
1
(11.24)
a powierzchnia wymiany ciepła wymiennika wynosi
Q
A = ■
k£A Tm
(11.25)
to poprawka £ określa stosunek obniżenia średniej różnicy temperatury w przepływie
krzyżowym do średniej różnicy temperatury dla przepływu przećiwprądowego ATm.
Poprawka ta zależy od parametrów X i Z.

200
Rys. 11.8. Zależności
£
=
f
(X,
Z
dla różnych
przypadków przepływu krzyżowego (wewnątrz
rurek i prostopadle do nich według schematu)
Rys. 11.9. Zależności
£
=
f
(X, Z)
e
Parametr X
o
wej czynnika b (ogrzanie czynnika b, ATb
eratury
w układzie ATmax, parametr Z zaś jako stosunek różnicy temperatury początkowej
i końcowej czynnika a (ochłodzenie czynnika a, ATb) do maksymalnej różnicy tempe
ratury ATmax:
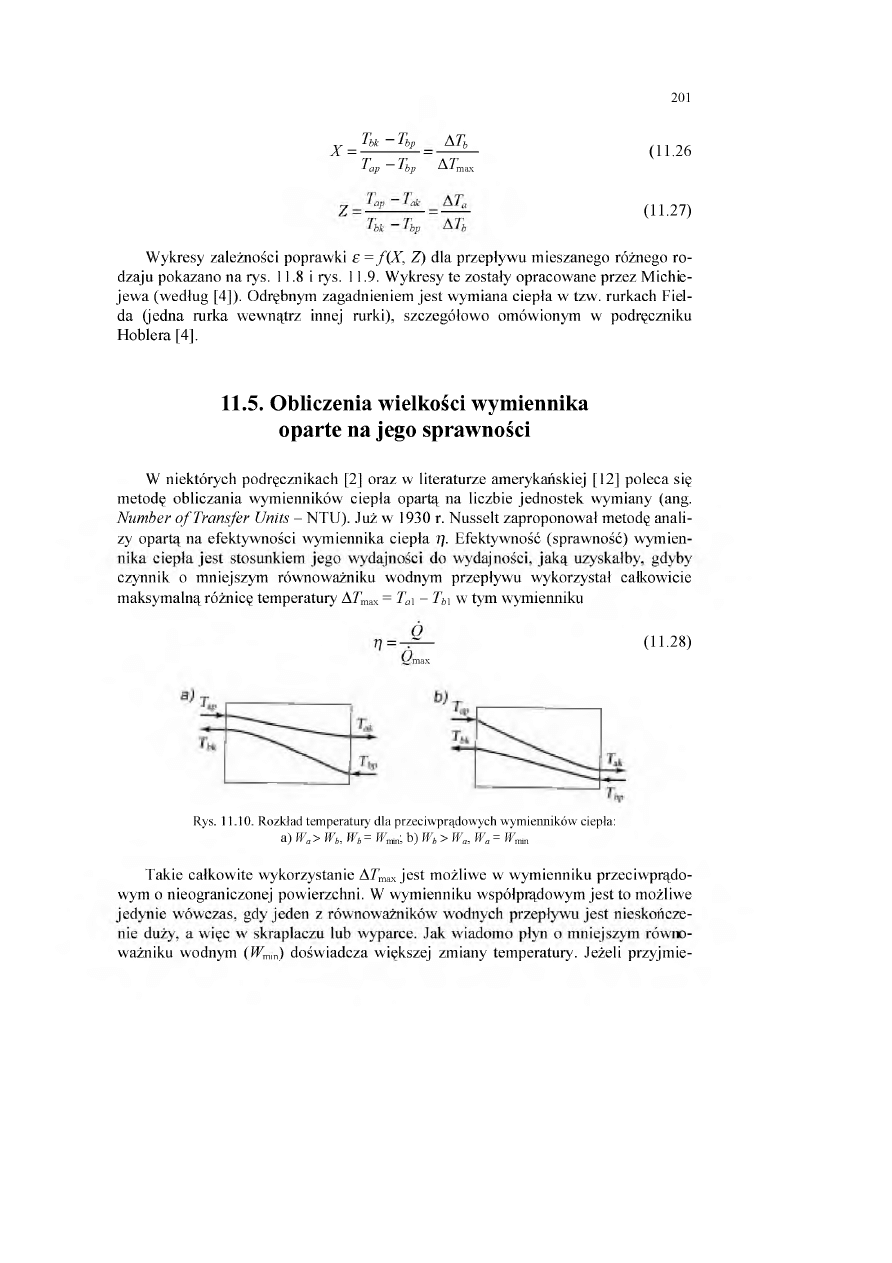
201
v _ T bk —Tbp
ATb
X —---------- —
-------
(11.26
T — T
AT
1
ap 1bp
L^1
nmax
(11.27)
Wykresy zależności poprawki £ = f (X, Z) dla przepływu mieszanego różnego ro
dzaju pokazano na rys. 11.8 i rys. 11.9. Wykresy te zostały opracowane przez Michie-
jewa (według [4]). Odrębnym zagadnieniem jest wymiana ciepła w tzw. rurkach Fiel-
da (jedna rurka wewnątrz innej rurki), szczegółowo omówionym w podręczniku
Hoblera [4].
W niektórych podręcznikach [2] oraz w literaturze amerykańskiej [12] poleca się
metodę obliczania wymienników ciepła opartą na liczbie jednostek wymiany (ang.
Number o f Transfer Units - NTU). Już w 1930 r. Nusselt zaproponował metodę anali
zy opartą na efektywności wymiennika ciepła n Efektywność (sprawność) wymien-
j
czynnik o mniejszym równoważniku wodnym przepływu wykorzystał całkowicie
maksymalną różnicę temperatury ATmax = Ta
1
- Tb
1
w tym wymienniku
Takie całkowite wykorzystanie ATmax jest możliwe w wymienniku przeciwprądo-
wym o nieograniczonej powierzchni. W wymienniku współprądowym jest to możliwe
e-
o-
ważniku wodnym (Wmm) doświadcza większej zmiany temperatury. Jeżeli przyjmie
11.5. Obliczenia wielkości wymiennika
oparte na jego sprawności
max
(11.28)
Rys. 11.10. Rozkład temperatury dla przeciwprądowych wymienników ciepła:
a)
W
a >
W
b
, W
b
= W
mn
; b)
W
b >
W
a
, Wa
=
Wmn

202
my, że Wb = Wmin ^ak na rys. 11.10a dla przeciwprądu), to w przypadku nieskończenie
dużej powierzchni wymiany temperatura płynu b na f l o c i e będzie równa temperatu
rze wlotowej płynu a. Zgodnie z definicją mamy
Q
m a x
= W
m in
(Tap — Tbp ) = W
m in
AT
m a x
(11.29)
a następnie
Q = Wnax (ap — Tak ) = Wnax ATmm
(1 1.30)
oraz
Wa (Tap — Tak ) Wmax
(ap ~ Tak )
n =— r - p—
= -------TJp------- k
(1131)
Wb (bk — Tbp )max
Wmin (Tap — Tbp )
enie
przyjmie postać
Wb (bk — Tbp )
Wmax (bk — Tbp )
n = ---- ^
= ------ t---------H
(11.32)
Wa (Tap — Tak )max
Wmin (Tap — Tbp )
Ponieważ w licznikach tych wzorów mamy strumień ciepła Q,więc możemy na
pisać, że
Q =nW
m in
(Tap — Tbp )
(11.33)
Jeżeli płyn zimny jest płynem minimum, to dla przećiwprądowego wymiennika
mamy:
Q W (
T ) kA (Ta1 —
Tb1 ) — (Ta2 —
Tb2 )
(1134)
Q = Wb ( b
2
—
Tb 1 ) = kA--------
(11.34)
ln la 1 —
T 1
v Ta 2 —
Tb 2
Z równania (11.33) otrzymujemy wyrażenie określające sprawność wymiennika:
(
u
Wmin ( 2 —
Tb 1 )
Wb = Wmin
Ta 2 = Tb 1 +--- (Tb 2 —
Tb
1
)
(11.36)
n
a następnie odejmiemy stronami Tb2, to
203
Ta 2 —
Tb 2 —
Tb
1
— Tb 2 +---- (Tb 2 —
Tb
1
) —
n
X —
A
(Tb
2 —
Tb 1
)
Ponieważ
Wb
Ta 2 —
Ta
1
Wa
Tb 2 —
Tb 1
więc po przekształceniu otrzymamy
W
' ' m
J
t
rr7
’ ’ min / m
rri \
a 1 —
Ta 2
--- ( b 2 —
Tb 1 )
max
(11.37)
(11.38)
(11.39)
oraz
W
J
T
'T'
'T'
'T'
min / m
m \
a 1 —
Tb 1 —
Ta 2 —
Tb 1 —
~ --- \Tb 2 —
Tb \)
W
’ • may
Z równania (11.36) otrzymujemy zależność
1
Ta 2 —
Tb
1
—~(Tb 2 —
Tb 1 )
n
którą podstawiamy do równania (11.40):
1
W
J
t
m
(T
T \
min / m T' \ _
a 1 —
Tb 1 ——{-tb 2 —
Tb1 ) —
------- ( Tb 2 —
Tb 1 ) —
n
Wmax
^ 1
W ■
^
min
(11.40)
(11.41)
n
Wm
a następnie zależności (11.37) i (11.42) podstawiamy do równania (11.34)
(Tb
2
—
Tb
1
) (11.42)
1
Wm
ln
n
Wma
1 —
1
n
kA
Wm
Wm
Wm
ceniu otrzymamy ostatecznie
(11.43)
1 —
exp
kA
Wm
Wm
Wm
Wmin
1
exp
Wmax
kA
Wm
1 —
Wm
Wm
(11.44)
Wyrażenie kA/Wmin
nazywamy
liczbą
jednostek
wymiany NT U. Stosunek Wmin/Wma
oznaczymy jako R i dla przeciwprądowego im ie n n ik a ciepła otrzymamy równanie:
n

204
t
- NTU(1-R)
Vp =
------ r ^ r
(1145)
1
- Re- NTU(1-R)
Dla współprądowego wymiennika ciepła w wyniku podobnego wyprowadzenia
[2, 12] uzyskuje się wyrażenie
,
- NTU(1+ R)
n . = 1 - e,
'
(11.46)
1 + R
a-
itych konstrukcji wymienników ciepła.
11.6. Rozkład temperatury płynów i ściany
11.6.1. Temperatura płynów
ienniku
o-
wierzchni wymiany ciepła. Jak pokazano w rozdziale 11.3, charakter krzywych
T = f (A) lub T = f (L), gdzie A jest powierzchnią, L zaś długością wymiennika zależy
od stosu
m-
ności cieplnej drugiego płynu (równ. (11.4)). W dalszych rozważaniach zostanie
przedstawiony rozkład zmian temperatury dla adiabatycznego wymiennika ciepła
(z
otoczenia, dQa = dQb = dQ) w przeciwpr dowym
i współprądowym przepływie płynów.
dla
przećiwprądowego możemy zapisać różniczkowy bilans ciepła (dotyczący powierzch-
dA):
dQ = -m acpadTa
(11.47)
dQ = -mbcpbdTb
(11.48)
t-
szej postaci:
dQ = -W adTa
(11.49)
d Q = - W bdTb
(11.50)
i otrzymam

205
dTa
— —
dTh —
■
dQ
Wa
dQ
'
Wb
z
AT = Ta - Tb
d (A T ) —
dTa —
dTb
którą podstawiamy do równań (11.51) i (11.52)
d (A T ) ——
dQ
Wa
Wb
Po wprowadzeniu różniczkowej postaci równania Pecleta
dQ —
kdAAT
otrzymujemy
d (A T ) —
—
kdAAT ' X —_ L A
Wa
Wb
(11.52)
(11.53)
(11.54)
(11.55)
(11.56)
(11.51)
i po przekształceniu mamy
d (A T )
T
—
—k
' _ L —J _ A
Wa
Wb
A
1
= 0 do A
2
oraz od AT
1
do AT
2
(zakładamy, że k = const)
T2
ln------—
—kA2
AT
1
Wa
Wb
(11.57)
i po przekształceniu otrzymujemy
AT
2
—
A 71 e
-
^2
1 —
1
Wa Wb
(11.58)
Jest to wzór określający różnicę temperatury płynów na wylocie wymiennika jako
e
go równoważnika wodnego (wzór Hudlera [2])

206
AT2 =A Tje- kA2/Wz
(11.59)
ynów w dowolnym prze
kroju wymiennika (w odległości x od wlotu), to możemy ją obliczyć na podstawie AT1
z równania otrzymanego w wyniku całkowania
ATx = A Tje- kAx/Wz
(11.60)
y
t-
nia. Dla przeciwprądu, gdy W1 < W2, mamy zatem:
W ~ W ~ W
jeżeli zaś W1 > W2, to
(11.61)
(11.62)
Dla współprądowego przepływu płynów różniczki temperatury płynów mają
przeciwne znaki (równania (11.47)-(11.52)); dTb jest dodatnie, więc zastępczy rów-
y
— = — + —
(11.63)
Wz
W
W2
podczas skrapla
nia pary w skraplaczu lub odparowywania w wyparce, to przyjmujemy, że jego po
jemność cieplna jest nieskończenie duża (W =
i zastępczy równoważnik wodny
prze
Wz = W
(11.64)
w skraplac
Wz = W2
(11.65)
We wzorach Hudlera (11.59)—
(11.60) AT1 należy przyjmować po stronie wlotu
kszej
mperatury.
Z równań tych możemy obliczać również temperaturę poszczególnych płynów.
Zasada postępowania polega na tym, że jeżeli znamy warunki w przekroju wlotowym
płynu gorącego (stan 1), to szukamy np. temperatury Tb1 dla przeciwprądu. Obliczamy
najpierw AT2:

207
AT2 —
Ta 2 —Tb 2
(11.66)
Tb 2 —
Ta 2 —
AT
2
(11.67)
Po wyeliminowaniu temperatury na podstawie równania bilansu cieplnego (11.2) mamy:
W
Ta 1 —Ta
2
—
W-(Tb 1 —Tb2)
(11.68)
Wa
Tb
2
a następnie
W
Ta2 —
Ta
1
— - ^ (Tb 1 —Tb2)
(11.69)
a
Po podstawieniu tego wy
W.
W
Tb 2 —
Ta 1 —
-bT b 1 + - f T b 2 —
AT
2
(11.70)
Wa
Wa
i uporządkowaniu otrzymujemy
W
Ta 1 —-^T b 1 —
AT
2
^ 2 —
W \
-
0 1 7 1 )
1 Wa
\
a /
AT2
AT1
otrzy
Tb 2 —
f (
,Ta 1 Tb 1)
(11.72)
Tb lub Ta w dowolnym przekroju wy
miennika: Tb = f(AT1,
Ta1, Tb1). W tym celu należy wyznaczyć odpowiednie AT
w
o-
czątkową
Wa (Ta 1 Ta ) —±Wb (Tb
1
—% )
(11.73)
Znak plus mamy dla przeciwprądu, a znak minus zaś dla współprądu.
ków wodnych płynów na rozkład temperatury w wymienniku ciepła.
i-

208
11.6.2. Temperatura ścianki
o
rze materiału konstrukcyjnego.
a
Q = aaA (Ta - Ta )
(11.74)
czynnik b zaś pobiera strumień ciepła
Q = abA (Tb - Tb)
(11.75)
określony równaniem Pecleta
Q = kAAT
(11.76)
i po przekształceniach wyznaczamy temperaturę ścianki
k AT
Ta = Ta
(11.77)
a a
oraz
kAT
Tb = Tb +-----
(11.78)
ab
Jeżeli przyjmiemy, że Tsa = Tsb =TS, to po przekształceniu otrzymujemy
Ta -Ts =—
(11.79)
Ts - "Tb
—a
a następnie
Ts = —aTa +—bTb
(11.80)
aa +ab
Temperaturę ścianki Ts możemy znacznie obniżyć, zwiększając współczynnik
wnikania ciepła po stronie płynu (gazu) zimniejszego.
11.7. Wskazówki do projektowania wymienników ciepła
any
o-
gicznego. Obliczenia projektowe składają się z następujących etapów:
1. Podstawą obliczeń jest sporządzenie bilansu cieplnego z ewentualnym
ariantów.

209
skupienia (w przeci
Ta
1
> Ta
2
, Tb
1
> Tb
2
)
opisuje znane nam równanie
Q —
m
a
C
p a
(T
a
1
—T
a
2
) —
m
b
C
p b
(T
b
1
—T
b
2
)
(11.81)
w którym indeksy a i b
a
na jako średnia w danym przedziale temperatury.
1.2. Gdy po jednej stronie wymiennika zachodzi zmiana stanu skupienia czynni
ka, np. w skraplaczu pary chłodzonym wodą (Tb2 > Tb1) lub w wyparce ogrzewanej
spa
Q —
m
a
r
a
—
m
b
C
p b
( 2 —T
b
1 )
(11.82)
1.3. Jeżeli zmiana
stanu skupienia zachodzi po obu stronach, np. w wyparce
ogrzewanej parą, to mamy
Q —m
a
r
a
—
m
b
r
(11.83)
o-
a-
Ta1 > Ta2, Tb2 > Tb1, ia1 > ia2)
przyjmuje po
Q —
m
i
C
p i
(T
i
1
—T
i
2
) + mt (X
a
1 i
a
1 —
Xa
2
i
a
2 ) —
Ki
k
—
m
b
C
p b
(
2
—
T.1 ) (11.84)
gdzie xa
suchego, K, kg/s, masowy stru
i
2.
Określamy średnią różnicę temperatury dla procesu wymiany ciepła. Najczę
ściej posługujemy się średnią logarytmiczną skrajnych różnic temperatury. Niekiedy,
gdy AT1/AT2 < 2, stosujemy średnią arytmetyczną.
a-
wartości pary wodnej, stosujemy metodę obliczeń polecaną przez Kerna i Hoblera [4]:
a) obliczyć ciepło oddawane przez gaz i ciepło kondensacji pary; ich sumę należy
pr
b) zastosować współczynnik wnikania ciepła, obliczony jak dla gazu,
c) użyć średniej logarytmicznej jako średniej różnicy temperatury, biorąc pod
uwagę skrajne temperatury gazu i wody chłodzącej,
W przypadku wyparki należy z kolei sprawdzić, czy obciążenie cieplne q, W/m2,
jest dostatecznie małe w porównaniu z qkr.
e-
biega równocześnie kilka różnych procesów, to dla każdego wykonujemy osobne
oblic
e-
niem mieści się w granicach od 8 do 30 m/s, cieczy natomiast nie przekracza 1,5 m/s.
Im droższy jest materiał konstrukcyjny, tym zaleca się większe wartości prędkości
1.1.

210
maga też założenia typu konstrukcyjnego wymiennika.
e
e-
ymiennik
o
11.8. Obliczanie wymienników dla wybranych
przypadków nieustalonej wymiany ciepła
W praktyc
e-
pła, zwłaszcza w urządzeniach pracujących w reżimie okresowym. W związku z tym
po
zbiornika napełnionego cieczą.
11.8.1. Ogrzewanie (chłodzenie) cieczy przez ścianę zbiornika
w stałej temperaturze czynnika grzejnego (chłodz ącego)
Bilans ciepła w procesie ogrzewania (chłodzenia) cieczy przez ścianę zbiornika
w
dwóch pod
y-
Równanie (11.85) określa ilość ciepła przekazywaną przez przenikanie w czasie
dT od czynnika a w stałej temperaturze Ta do cieczy b w zmiennej temperaturze T.
Gdy Ta < T, następuje chłodzenie cieczy b. Równanie (11.86) opisuje zmianę entalpii
cieczy b o masie mb w tym samym czasie dT. Po przyrównaniu prawych stron obu
równań
dQ = kA(Ta - T)dT
(11.85)
oraz
dQ = mb cpb dT
(11.86)
kA(Ta - T)dT = mbcpbdT
(11.87)
zy
A
,
dT
------- dT =— -------- -
mbCpb
k(Ta - T )
(11.88)

211
Równanie to całkujemy granicach od 0 do T po lewej stronie oraz od temperatury
początkowej Tp do końcowej Tk po prawej stronie
Nie uwzględnia się masy ściany metalowego zbiornika, ponieważ czas jej nagrzewa
nia jest bardzo krótki. Rozwiązanie równania (11.89) umożliwia obliczenie czasu
trwania procesu ogrzewania lub chłodzenia albo powierzchni wymiany ciepła dla
o
a
nia ciepła k.
1.
Gdy współczynniki wnikania ciepła po obu stronach ściany są bardzo duże
(ogrzewanie parą cieczy mieszanej w zbiorniku) przyjmuje się: Ta = const; k = const
i
a
dużym zmianom i współczynnik przenikania ciepła k jest zmienny, jak np. podczas
anie
ciepła po obu stronach następuje w wyniku konwekcji naturalnej. W celu wykonania
o
i na podstawie zasady rozdzielania całki sumy na sumę całek po podstawieniu równa
nia (11.91) do równania (11.89) i przekształceniu otrzymuje się
Rozwiązanie całek po lewej stronie równania wymaga określenia związków opisują-
e
Spadek temperatury po obu stronach ścianki można wyznaczyć ze wzoru (por.
rozdz. 11.6):
(11.89)
(11.90)
1 1
5
1
- = — + —+ —
(11.91)
k
a a
X ab
(11.92)
a aTa +abT
(11.93)
a a + ab

212
z którego otrzymuje się
*T _ T
T a aTa +abT
T _ T - Ta
¿iT a —
T s Ta
—
Ta —
Oa + ab
a a
,
—
+1
ab
oraz
ATh _ T - Ts _ T-
aaTa + abT
T - Ta
a a + a b
1
+ a
aa
(11.94)
(11.95)
Przyjmujemy, że stosunek współczynników wnikania wynosi x = Ob,/aa i otrzymujemy:
T - Ta
ATa _ x-
oraz
Tb _
x +1
T - Ta
x +1
(11.96)
(11.97)
e
stronach w warunkach konwekcji naturalnej. Dla obu przypadków współczynnik wni
kania ciepła zależy od założonej różnicy temperatury
a a _ LA T'
oraz
O
b
_ NAT
bn
y
oraz
a a _ Lx”
ab _ N
x + 1
f
T - Ta
x +1
(11.98)
(11.99)
(11.100)
(11.101)
Zmienna x (x = a b/a a) jest w niektórych przypadkach stała. Przyjąwszy jej wartość
a
w zależności (11.92):

213
Tr
dT
_ l
l a a (T - T ) _ j
X + 1
d T
L (T - Ta )m (Ta - T )
\m
1
Tjc
x
) L
dT
X +1 Y 1 r _________
L f (T - Ta )m+1
f X +11
m 1
1
1
l X i Lm _(Tk - Ta )m
(Tp - Ta )m _
(11.102)
sdT
_ - S ln Ja - Tk
f
dT
_ f
l a b (Ta - T ) I
n
(T - Ta )n (Ta - T )
J l(Ta - T )
X Ta - Tp
Tk
(
x
+ 1)n
dT
(
x
+ 1)n
Tt
(11.103)
dT
N
i (T - Ta )n+1
(X + 1)n
nN
1
1
(Tk - Ta )n
(Tp - Ta )n
(11.104)
Jeżeli przyjmiemy, że (Tp - Ta) = 0 p oraz (Tk - Ta) = 0 k, to wzór (11.92), określający
czas chłodzenia, zapiszemy w postaci:
t
A
1
f
1
+ x ^
m
mb cpb
Lm
X
1
1
&
k m
0
n
S . 0k +(1 + X )n
—ln----- 1----------
X
0
„
nN
1
1
\
n
0
p n
v
F /
(11.105)
Podobne równanie otrzymuje się dla ogrzewania cieczy w zbiorniku; przyjmuje
my wówczas oznaczenia: (Ta - Tp) = 0 p oraz (Ta - Tk) = 0 k.
11.8.1.1. Chłodzenie cieczy w zbiorniku na wolnym powietrzu
Rozważmy chłodzenie cieczy w zbiorniku umieszczonym na wolnym powietrzu
(rys. 11.11). Temperatura powietrza jest stała, Ta = const, a temperatura cieczy
w
obu stronach ścianki w wyniku konwekcji naturalnej i współczynniki wnikania można
opis
m przy
różnicy temperatury wynosi najczęściej 1/3, rzadziej 1/4. Jeżeli założymy, że wykład-
m = n
ostaci
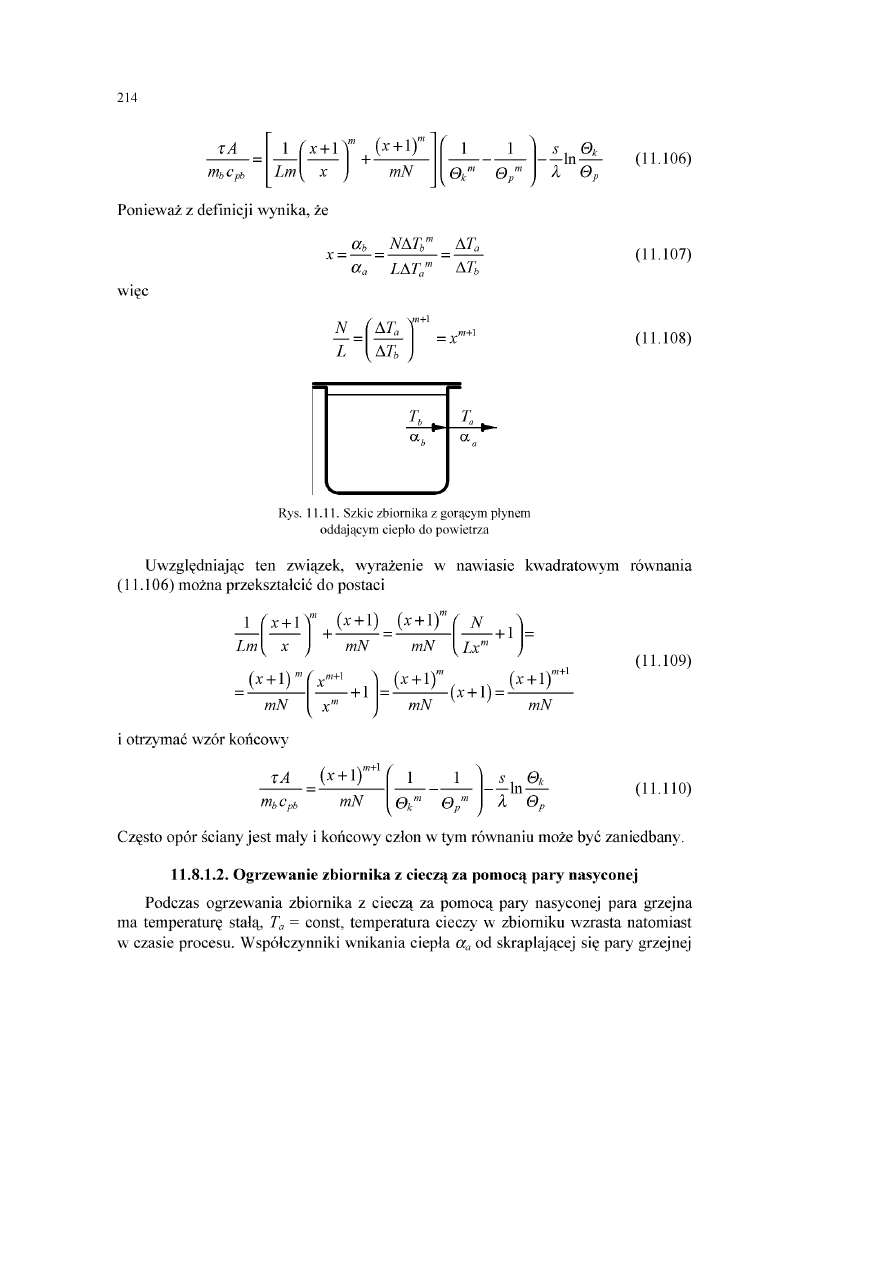
214
t
A
mb cpb
Lm
+
(x +!)
mN
&
km
&
p
Ponieważ z definicji wynika, że
x = -
ab
NATbm
ATa
a a
LATam
AT,
- - l n 0
(11.106)
X
0„
(11.107)
więc
N
L
z A Ta m1
ATbb
= x
(11.108)
Rys. 11.11. Szkic zbiornika z gorącym płynem
oddającym ciepło do pow ietrza
Uwzględniając ten związek, wyrażenie w nawiasie kwadratowym równania
(11.106) można przekształcić do postaci
1
x +1
Lm
x
V
(x +1)
1
+
(x +1)
(x + 1 )
mN
k xm+1
mN
cowy
t
A
+1
mN
m
(x +1)
mN
N
Lxm
+1
(x + 1) =
(x +1)
m+1
(11.109)
mN
( x + 1)
m
+1
mbcpb
mN
0
k
0
p
- - ln 0
X
0
p
(11.110)
Często opór ściany jest mały i końcowy człon w tym równaniu może być zaniedbany.
11.8.1.2. Ogrzewanie zbiornika z cieczą za pomocą pary nasyconej
Podczas ogrzewania zbiornika z cieczą za pomocą pary nasyconej para grzejna
Ta = const, temperatura cieczy w zbiorniku wzrasta natomiast
w czasie procesu. Współczynniki wnikania ciepła aa od skraplającej się pary grzejnej

215
do ścianki oraz ab od ścianki zbiornika do
ogrzewanej
cieczy zależą od spadków tem
peratury: aa = f (ATa) oraz ab = f (ATb).
Jednak wartości wykładników m i n
są różne. Dla
kondensacji pary m = -1/4, dla
konwekcj i
naturalnej
zaś n = 1/3.
Należy
skorzystać z równania (11.105), przyjmując
X
e-
mniej jednak możliwe jest pewne przybliżenie, ponieważ aa >> ab i
stąd
x = ab/a a =
0. Dla skraplania wielkość L
jest rzędu
104, co dla m = -1/4 daje:
1
Lm
m
x
+1
v X
'
x
^ 25
X + 1
^ 0
Dlatego w równaniu ogólnym (11.105) można pominąć pierwszy człon i otrzymać
przy
A
t
1
m b C p b
n N
0
1
0
p
—ln —^
(11.111)
X
0p
Chociaż błąd obliczenia nie przekracza kilku procent, obliczoną wartość czasu
ogrzewania należy zwiększyć o 10-20% [4].
11.8.2. Ogrzewanie (oziębianie) cieczy medium grzejnym
(chłodzącym) w zmiennej temperaturze
j
z
Ta
1
= const,
zmienną natomiast na wylocie (Ta2). Bilans cieplny takiego procesu opiszemy za po-
a
• dla płynu ogrzewanego w zbiorniku
dQ _ mbcpbdTb
(11.112)
• dla p
dQ _ maCpa (Ta 1 - Ta )
(11.113)
dQ _ kAkTdT
(11.114)
Tbp, pod
Tbk
ym momencie jest
różnica temperatury:
• na wlocie cieczy grzejnej AT
1
= Ta
1
- Tb,
• na wylocie z płaszcza grzejnego AT2 = Ta - Tb.
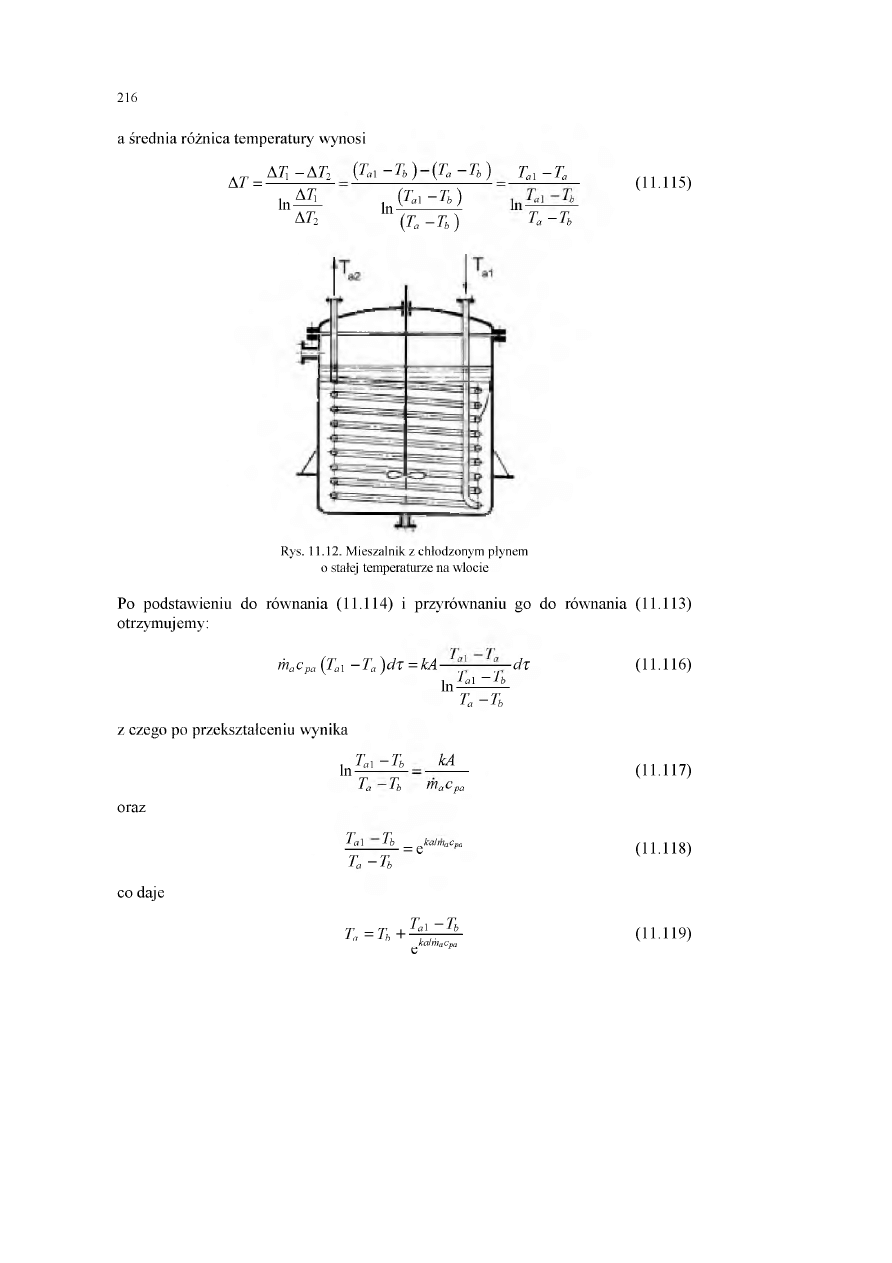
216
a średnia różnica tem peratury wynosi
ATI -AT2
(Tai - Tb ) (Ta - Tb )
Ta
1
- Ta
AT = -
1
^ĄTL
ln (Ta
1
- T )
A?2
(Ta - Tb )
Ta - Tb
Rys. 11.12. Mieszalnik z chłodzonym płynem
o stałej temperaturze na wlocie
Po podstawieniu do równania (11.114) i przyrównaniu go do równania
otrzymujemy:
maCpa (Ta 1 - Ta )dT = k
A
d
T
ln Zał^bL
Ta - Tb
z czego po przekształceniu w ynika
Ta 1 —
Tb
kA
ln-
Ta
Tb
mac pa
oraz
Ta 1 Tb kaimacpa
Ta - Tb ~
6
co daje
Ta 1 - Tb
Ta _ Tb + ka/macpa
e
(11.115)
(11.113)
(11.116)
(11.117)
(11.118)
(11.119)

217
Przyjmijmy oznaczenie K = QkalmaCpa [ równanie określające temperaturę cieczy
grzejnej na wylocie zapiszmy w postaci
Ta = Tb +
Ta1 - Tb
K
(11.120)
Po podstawieniu tej zależności do bilansu (11.113) i przyrównaniu do równania
(11.112) otrzymuje się
mb c pb dTb
ma c p
{Ta 1 - Tb )
Ta 1 -
rri Ta 1
Tb
Tb +
K
1
1
K
dT =
K -1
(11.121)
dT
ma cpa
{Ta 1 Tb ) ) T
K
Rozdzielenie zmiennych i całkowanie daje
K - 1T
mbCpb Tbc
dTb
K
i
t
=mbciL r
Po rozwiązaniu całki mamy ostatecznie
maCpa T Ta 1 - Tb
mbCpb in Ta
1
- Tbk
mac pa
Ta 1 Tbp
(11.122)
(11.123)
gdzie: T
a1
- Tbp = ATJp jest spadkiem tem peratur na wlocie cieczy grzejnej na począt
ku procesu, T
a1
- Tbk = ATJk - spadkiem temperatury na wlocie cieczy grzejnej na
końcu procesu.
Temperaturę cieczy grzejnej na wylocie z płaszcza grzejnego na początku procesu
( t = 0) i końcu procesu ogrzewania możemy obliczyć z równania (11.120) po podsta
wieniu Tbp lub Tbk za Tb:
oraz
Tap = Tbp +
Tak = Tbk +
Ta 1 - Tbp
K
Ta 1 - Tb
bk
K
(11.124)
(11.125)
zczem zastosujemy
n-
tyczny z równaniem (11.123), jedynie zmieniają się definicje spadków temperatury
Tbp - Ta
1
= = AT
1
p oraz na
esu Tbk - Ta
1
= = AT
1
k.
T

218
11.8.3. Ogrzewanie (oziębianie) cieczy za pomocą zewnętrznego
wymiennika ciepła o stałej temperaturze medium
Gdy zbiornik ma dużą pojemność lub gdy wymiana ciepła przez ściankę jest
utrudniona, a wężownica niewskazana, zaleca się stosowanie dodatkowego wymien
nika ciepła. Do rozważań przyjmijmy rozwiązanie przedstawione na rys. 11.13, w
którym ciecz należy ogrzać do temperatury Tbk w zewnętrznym wymienniku ciepła za
pomocą nasyconej pary wodnej o temperaturze Ta1. Masowe natężenie przepływu
cieczy w wymienniku jest równe mb = const. Przyjmuje się, że temperatura w prze
strzeni zbiornika jest zmienna, ale wyrównana, równa temperaturze cieczy obiegowej
na wlocie do wymiennika Tb. Temperatura cieczy na wylocie z wymiennika Tb jest
także zmienna, ale wyższa od temperatury Tb.
Rys. 11.13. Schemat instalacji do ogrzewania mieszalnika
za pomocą osobnego wymiennika ciepła
cyc
• dla cieczy w zbiorniku
dQ = mbcpbdTb
(11.126)
dQ = mbCpb (Tb-Tb )dT
(11.127)
dQ = kAATdt
(11.128)
rocesu jest równa Tbp, pod
Tbk
różnica temperatury:

219
• na wlocie cieczy do wymiennika
AT1 = Ta1 - Tb
• na wylocie z wymiennika
AT2 = Ta1 - Tb
Średnia różnica temperatury wynosi zatem
\ T = ATl -AT2 = {Ta 1 - Tb ) - { a 1 - Tb ) = Tb - Tb
( ,, 129)
= l n ^ =
l n
i ^
= l n
^
'
AT2
{Ta
1
- Tb' )
Ta 1 - Tb
Po podstawieniu do równania na przenikanie ciepła (11.128) i przyrównaniu go
do równania (11.127)
mbCpb {Tb - Tb )dT = kA Tb ~ T\ , dT
(11.130)
ln
Ta 1 - Tb
i po przekształceniu otrzymuje się
ln Ta 1 - T\ = ——
(11.131)
a następnie
Ta 1
Tb
mbc pb
kA
Ta 1 - Tb
co daje
---- = embCpb
(11.132)
Ta 1 - Tb
Tb = T* -
( 11133)
e
Jeżeli przyjmiemy, że K =eka
1
mbCpb , to równanie na temperaturę cieczy grzejnej na
wylocie zapiszemy w postaci
Tb = Ta
1
- Ta 1 ~ Th
(11.134)
K
Po podstawieniu tego wyrażenia do bilansu (11.127) i przyrównaniu do równania
(11.126) otrzymuje się

220
—
mb cpb (Ta 1
Tb ) 1
dT
K
(11.135)
Rozdzielenie zmiennych
K -1
K
(11.136)
i całkowanie daje
K —
1 —
mb in Ta
1
—
Tbk
(11.137)
K J
mb
Ta
1
- Tbp
gdzie: Ta\ - Tbp = ATJp jest spadkiem temperatury na wlocie cieczy do wymiennika na
początku procesu, Ta
1
- Tbk = AT
1
k jest spadkiem temperatury na wlocie cieczy przy
końcu procesu.
Temperaturę cieczy na wylocie z wymiennika T/ na początku procesu ( t = 0)
i końcu proces u ogrzewania (
t
) możemy obliczyć z równania (11.134) po podstawie
niu za Tb Tbp lub Tbk
W przypadku chłofenia płynem o stałej temperaturze TaX wzór jest identyczny
z
ymiennika:
na poc^tku procesu Tbp - T
a1
= = ATJp o ^ na końcu procesu Tbk - T
a1
= AT1k.
(11.138)
oraz
(11.139)
Tbk — T a 1 —
11.9. Obliczanie regeneratorów ciepła
a-
dowego, tzn. energii cieplnej gazów odlotowych (np. spalin). Regeneracyjne podgrze
wacze powietrza, zwane podgrzewaczami Ljungstroema, są na przykład stosowane w

221
kotłach parowych. Wsad stanowiący wypełnienie, zwykle w postaci cegieł ceramicz
nych, jest ogrzewany przez gorące spaliny, a następnie jest chłodzony powietrzem. W
niektórych regeneratorach wsad może być zestawem blach metalowych.
Metodę obliczeń idealnego regeneratora opracował Hausen [2]. Analizował on
regenerator, w którym współczynnik przewodzenia ciepła w wypełnieniu jest anizo
tropowy. W kierunku przepływu gazów (wzdłuż osi x) ma o t skończoną wartość X,
a w kierunku do niego prostopadłym - nieskończenie dużą. Można wówczas przyjąć,
że temperatura wypełnienia w przekroju poprzecznym do przepływu ma wartość stałą.
Hausen [2] wyprowadził następujące równania różniczkowe:
• dla gazów
gdzie: Ts, Tg - temperatura wypełnienia regeneratora i gazów, Aj - zewnętrzna, opły
wana przez gazy powierzchnia wypełnienia regeneratora długości 1 m, mg - strumień
masowy gazów, cpg - ciepło właściwe pod stałym ciśnieniem, C - pojemność cieplna
1 m wypełnienia.
Gdy regenerator jest długi, a współczynniki wnikania ciepła dla obydwu gazów
i
w
czas z analizy wynika, że w połowie długości regeneratora pochodne temperatury
gazów względem x oraz pochodne tem peratur wypełnienia względem czasu są stałe.
Ciepło przekazane do wypełnienia przez czynnik grzejący B jest przejęte przez
czynnik ogrze
• dla okresu chłodzenia wypełnienia
ta
gdzie Q wyrażamy w J/cykl.
Po przekształceniu równań (11.142) i (11.143), tak aby po prawej stronie były
ró
(11.140)
• ora; dla wypełnienia
(11.141)
Q = a AA (Ts - TgA )m
ta
(11.142)
• dla okresu grzania wypełnienia
tb
Q - a BA (TgB - Ts )m TB
(11.143)
Q -
1
‘
|
A TgB - TA )m
(11.144)
1--------
a ATA
a BTB

222
ciepła dla regeneratora idealnego:
1 — - ^
+ —^
(11.145)
k
a AT A a BTB
i równanie (11.144) przyjmie wówczas postać
Q — kA (TgB — TgA )m — kAATm
(11.146)
gdzie ATm = (ATi+AT2)/2 jest średnią wartością różnic temperatury na wlocie i na
wylocie z regeneratora.
11.10.
Wybór typu konstrukcji
przeponowego wymiennika ciepła
Projektowanie aparatury jest procesem złożonym, wymagającym od projektanta
zarówno wiedzy merytorycznej po
o-
wać aparat, konieczne jest określenie zarówno parametrów konstrukcyjnych, jak
i
omii
a-
kości.
Przez określenie typ konstrukcji należy rozumieć grupę rozwiązań o podobnej
koncepcji do zrealizowania założonych ustaleń i wyników obliczeń. Podstawowym
rodzajem konstrukcyjnym jest tzw. wymiennik wielorurkowy. Do tej grupy wymien-
t
i-
aniem rur od
i
Odrębną grupę stanowią tzw. konstrukcje specjalne. Są to wymienniki spiralne,
np. według patentów Rosenblada. Do rozwiązań specjalnych są również zaliczane
wymienniki z grafitu impregnowanego żywicami syntetycznymi, stosowane do cieczy
silnie korozyjnych oraz wymienniki płytowe, zbudowane z pakietów blach metalo-
e-
a-
dzona w kolektorach: wlotowym i wylotowym. Na rynku jest oferowanych wiele
nicowanych cenach.
Istotnym czynnikiem jest także koszt wykonania wymiennika ciepła danego typu.
z-
ty inwestycyjne.
ania

223
Przystępując do obliczenia wymiennika ciepła, projektujący musi obrać pewien
typ rozwiązania konstrukcyjnego. Innych wzorów należy użyć do obliczenia współ
-
d-
umieni oraz
o
y-
miennika, tj. stosunku jego długości do średnicy wewnętrznej rur, S = L/d [4]. Kolejne
za
elementów aparatury.

Oznaczenia
A
- pole przekroju, powierzchnia, m
2
a
- dyfuzyjność cieplna, m
2
-s^‘
b
- szerokość, m
C
- stała prom ieniowania dla ciała szarego, W-nT^KC
1
Co
- stała prom ieniowania dla ciała doskonale czarnego, W-nT
2
-IC
4
C
,_2
- zastępcza stała prom ieniowania dla układu pow ierzchni 1 i 2, W-nT2-IC
Cf
- w spółczynnik tarcia
cp
- ciepło właściwe pod stałym ciśnieniem, J-kg_l-K_l
d
- średnica, m
E
- zdolność prom ieniowania ciała, W-nT
2
g
- przyspieszenie ziemskie, n r s
^2
h
- wysokość, m
h
- intensywność prom ieniowania monochromatycznego, W-nT
3
k
- w spółczynnik przenikania ciepła, W-m_
2
-K_l
L
- długość, m
m
- masa, kg
m
- strumień masy, kg-s
^1
m "
- gęstość strumienia masy, kg-m_
2
-s_l
N
- liczba cząsteczek przechodząca w ciągu
1
s z pow ierzchni
1
cm
2
No
- stała Avogadra, N 0= 6,022-10
23
m o k
1
P
- ciśnienie, Pa
Q
- energia cieplna, J
Q
- strumień energii cieplnej, W
<i
- gęstość strum ienia ciepła, W-nT
2
p
- prężność parcjalna, Pa
p
°
prężność pary nasyconej, Pa
R
- opór cieplny, K-W
^1
R
- masa roztworu, kg
R
- uniw ersalna stała gazowa, R = 8,31432 J-mol^-KT
1
r
- ciepło parowania, J-kg
^1
r
- promień rury, m
S
- masa surowca, kg
s
- grubość warstwy, m
T
- tem peratura, K
U
- obwód, m
V
- masa fazy parowej, kg

226
V
- objętościowy strumień płynu, m
3
-s^‘
w
- rów noważnik wodny płynu, W-K2
1
w
- liniow a prędkość przepływu, m-s
^1
x, y, z - w spółrzędne prostokątne, m
a
- w spółczynnik wnikania ciepła, W -nT ^IC
1
P
- w spółczynnik rozszerzalności objętościowej, K2
1
e
- w zględna zdolność emisyjna
e
- w spółczynnik poprawkowy na przepływ mieszany
G
- zastępcza w zględna zdolność emisyjna
il
- dynamiczny współczynnik lepkości, Pa-s
T]
- dzielność izolacji
0
- kąt zwilżania, rad
&
- zastępczy w ymiar poprzeczny, m
2
- w spółczynnik przew odzenia ciepła, W-m_l-K_l
2
- długość fali elektromagnetycznej, pm
2
o
- w spółczynnik oporu przepływu
V
- kinematyczny w spółczynnik lepkości, m
2
-s^‘
P
- gęstość, kg-nT
3
er
- napięcie powierzchniowe, N -nT
1
z
- czas, s
z
- naprężenie styczne, N-nT
2
V
- w spółczynnik konfiguracji
r
- strumień masy odniesiony do jednostki długości, kg-nT
1
-s
^1
Moduły podobieństwa
Bi
- liczba Biota, asIX
Fo
- liczba Fouriera, az/s2
Ga
- liczba Galileusza, g c ł / T h f
Gr
- liczba Grashofa, g d 3/X /iA T /tf
Gz
- liczba Graetza, mcp/AL
Nu
- liczba Nusselta, ad/A
Pe
- liczba Pecleta, RePr
Pr
- liczba Prandtla, i]cp/A
Ra
- liczba Rayleigha, GrPr
Re
- liczba Reynoldsa, wdplr]
Re._
- liczba Reynoldsa dla grawitacyjnego spływu po ścianie,
477/7
S
- liczba Strouhala, w z/L
St
- liczba Stantona, N u/(RePr)
j l i
- czynnik C olbum a dla wymiany ciepła, S tP F 13

Piśmiennictwo cytowane
[1]
W
i ś n i e w s k i
S., T.S.
W
i ś n i e w s k i
,
Wymiana ciepła, w ydanie czwarte, WNT, Warszawa, 1997.
[2] K
alinowski
E., Przekazywanie ciepła i wymienniki, Ofic. Wyd. PWr., Wrocław, 1995.
[3]
S
k o c z y l a s
A., Przenoszenie ciepła, Ofic. Wyd. PWr., Wrocław, 1999.
[4]
H
o b l e r
T., Ruch ciepła i wymienniki, w ydanie czwarte, WNT, Warszawa, 1971.
[5]
K
e m b ł o w s k i
Z ., M
i c h a ł o w s k i
S.,
S
t r u m i ł ł o
C ., Z
a r z y c k i
R .,
P odstaw y teoretyczne inżynierii
chem icznej i procesowej, WNT, Warszawa, 1985.
[6]
M
a d e j s k i
J .,
Teoria w ym iany ciepła, PWN, Warszawa, 1963.
[7]
S
t a n i s z e w s k i
B., Wymiana ciepła, PWN, Warszawa, 1979.
[8]
B
e j a n
A., H eat Transfer, Wiley, N ew York, 1993.
[9]
P a t a n k a r
S.V., N umerical H eat Transfer a nd F luid Flow, M c-Graw-Hill, N ew York,
1980.
[10] M
c
A
dams
W.H., H eat Transmission, Second Edition, McGraw-Hill, New York, 1942, s. 168.
[11]
I
n c r o p e r a
F.P.,
D
e
W
i t t
D.P., Introduction to H eat Transfer, Second Edition, Wiley, N ew York,
1990, s. 456.
[12]
W e l t y J .R ., W i c k s C .E ., W i l s o n R .E ., R o r r e r G .L .,
Fundam entals o f Momentum, H eat an d Mass
Transfer, Fourth Edition, Wiley, N ew York, 2001,
s. 323.
[13]
B a e h r
H.D.,
S t e p h a n
K., H eat a nd Mass Transfer, Springer-Verlag, Berlin, 1998,
s. 373.
[14]
K u b a s i e w i c z a . ,
Wyparki: konstrukcja i obliczanie, WNT, Warszawa,
1977.
[15]
B r a u e r
H., Stoffaustausch, Sauerlaender AG, Aarau, Schweiz,
1971.
Wyszukiwarka
Podobne podstrony:
Energetyka - 36 Pyt i odp, INŻYNIERIA PROCESOWA, T. cieplna
A4 1 Procesy cieplne Ruch ciepła – pojęcia podstawowe
Procesy cieplne inzynieria Zajr Nieznany
zad na kolosa2, nauka, PW, sem 6, sterowanie procesami cieplnymi
Zadania z wymienników, INŻYNIERIA PROCESOWA, T. cieplna, wymienniki
PRZYKADOWE OBLICZENIA, INŻYNIERIA PROCESOWA, T. cieplna
Przyklady zadań - procesy cieplne, INŻYNIERIA PROCESOWA
Projekt - wymiennik 2, uniwersytet warmińsko-mazurski, inżynieria chemiczna i procesowa, rok III sem
OCZYSZCZALNIA ŚCIEKÓW „CZAJKA” - sprawozdanie 2, INŻYNIERIA PROCESOWA, T. cieplna
Energetyka - Ściąga, INŻYNIERIA PROCESOWA, T. cieplna
1.1 Procesy cieplne w technologii gastronomicznej
wzory do obliczeń grzejników, INŻYNIERIA PROCESOWA, T. cieplna
Badanie urządzeń chłodniczych, INŻYNIERIA PROCESOWA, T. cieplna
Procesy cieplne
Spalanie paliw a ochrona środowiska, INŻYNIERIA PROCESOWA, T. cieplna
A4 2 Procesy cieplne Wnikanie, Przewodzenie, Przenikanie, Promieniowanie
Energetyka - Egzamin, INŻYNIERIA PROCESOWA, T. cieplna
więcej podobnych podstron