
1

Przekładnie z paskiem zębatym
Przekładnie z paskiem zębatym (rys. 10.22) są najczęściej stosowanym rodzajem przekładni z cięgnem
kształtowym. W przeciwieństwie do przekładni cięgnowych ciernych przekładnie z cięgnem kształtowym
zapewniają bezpoślizgowe przenoszenie napędu z członu czynnego na bierny. Przekładnie z paskiem
zębatym znajdują w szerokim zakresie zastosowanie zarówno w maszynach (m.in. w silnikach
spalinowych), jak i w urządzeniach precyzyjnych, np. w maszynach biurowych, kopiarkach, sprzęcie
informatycznym, projektorach filmowych, zmechanizowanym sprzęcie gospodarstwa domowego itp. Paski
zębate nadają się jednak tylko do przekładni o osiach równoległych.
2
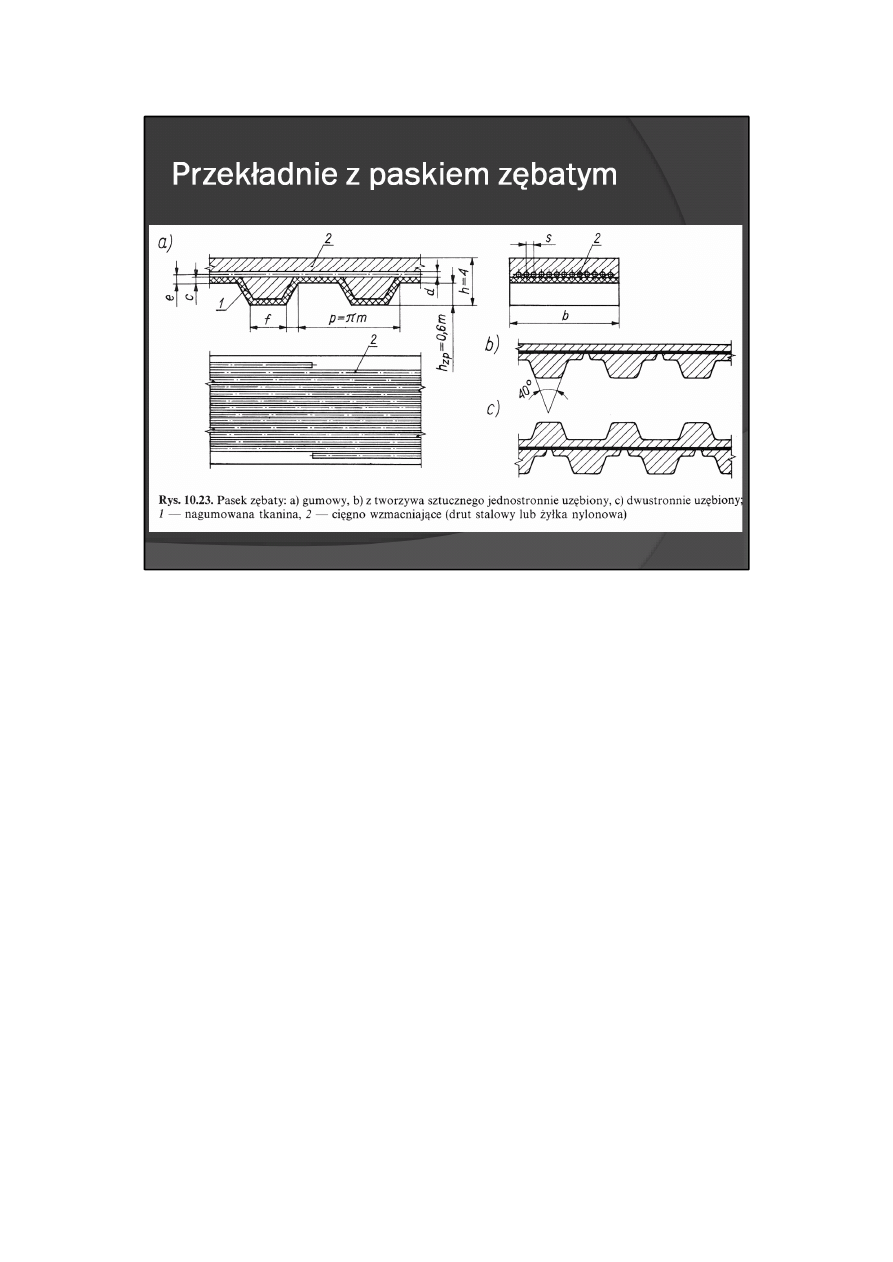
Paski zębate są wykonywane ze specjalnych rodzajów gumy lub innych tworzyw o dużej wytrzymałości na
ścinanie i odpornych na zużycie. W celu zwiększenia wytrzymałości paska na rozciąganie, w jego wnętrzu
są umieszczane cięgna zwykle stalowe lub nylonowe (rys. 10.23), wskutek czego wydłużenie paska przy
przenoszeniu obciążenia jest bardzo małe. Wytrzymałość zębów paska na ścinanie jest tak dobrana, aby
przy współpracy z kołem co najmniej sześciu zębów podczas przeciążenia przekładni nastąpiło zerwanie
paska, a nie ścięcie zębów.
Oprócz pasków uzębionych jednostronnie (rys. 10.23a, b) stosuje się też paski uzębione obustronnie (rys.
10.23c). Umożliwiają one napędzanie jednym paskiem trzech lub nawet większej liczby kół zębatych (koła
znajdujące się po zewnętrznej stronie paska mają wtedy przeciwny kierunek obrotów). Ze względu jednak
na to, że pasek uzębiony obustronnie ulega obustronnemu zginaniu, trwałość takich pasków jest mniejsza
niż uzębionych jednostronnie.
3
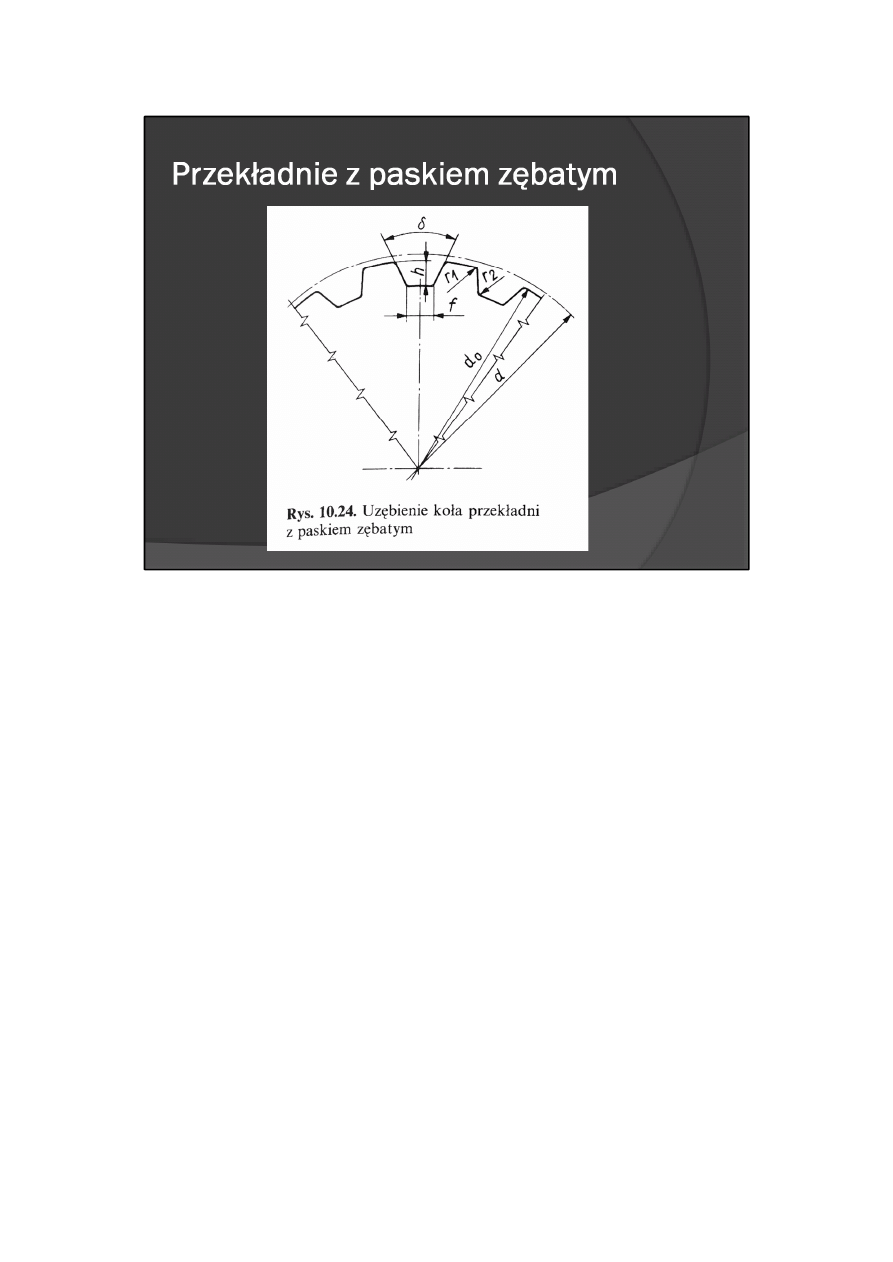
Podziałkę paska zębatego i jego długość znamionową mierzy się wzdłuż osi cięgna wzmacniającego. Oś ta
pokrywa się z kołem podziałowym koła zębatego i znajduje się powyżej jego koła wierzchołków zębów
(rys. 10.24).
4

Koła zębate współpracujące z paskami zębatymi najczęściej wykonuje się ze stopów aluminium lub z
tworzyw sztucznych, a niekiedy także ze stali. W celu zabezpieczenia paska przed spadnięciem, koła
zębate są zaopatrzone w obrzeża (rys. 10.25). Przy małych odległościach osi kół sprzęgniętych paskiem
zębatym wystarczy, aby tylko jedno koło (mniejsze) miało obrzeża. Przy większych przełożeniach (i≥3) i
dużych odległościach osi (a≥8d
01
, gdzie d
01
— średnica wierzchołków mniejszego koła), lub przy osiach kół
o innym położeniu niż poziome jest konieczne zastosowanie obu kół zaopatrzonych w obrzeża.
W przypadku zastosowania pasków zębatych o większej długości niż to wynika z obliczenia, bądź jeśli nie
można z góry dokładnie określić odległości osi kół sprzęgniętych paskiem, konieczne jest zastosowanie
naprężacza paska. Funkcję naprężacza może spełniać gładka rolka, umieszczona po zewnętrznej stronie
paska lub uzębiona, znajdująca się po stronie wewnętrznej. Średnica rolki naprężacza umieszczonego po
zewnętrznej stronie paska powinna być większa o ok. 30% od średnicy d
01
mniejszego koła, a średnica rolki
naprężacza wewnętrznego nie powinna być mniejsza od d
01
.
5
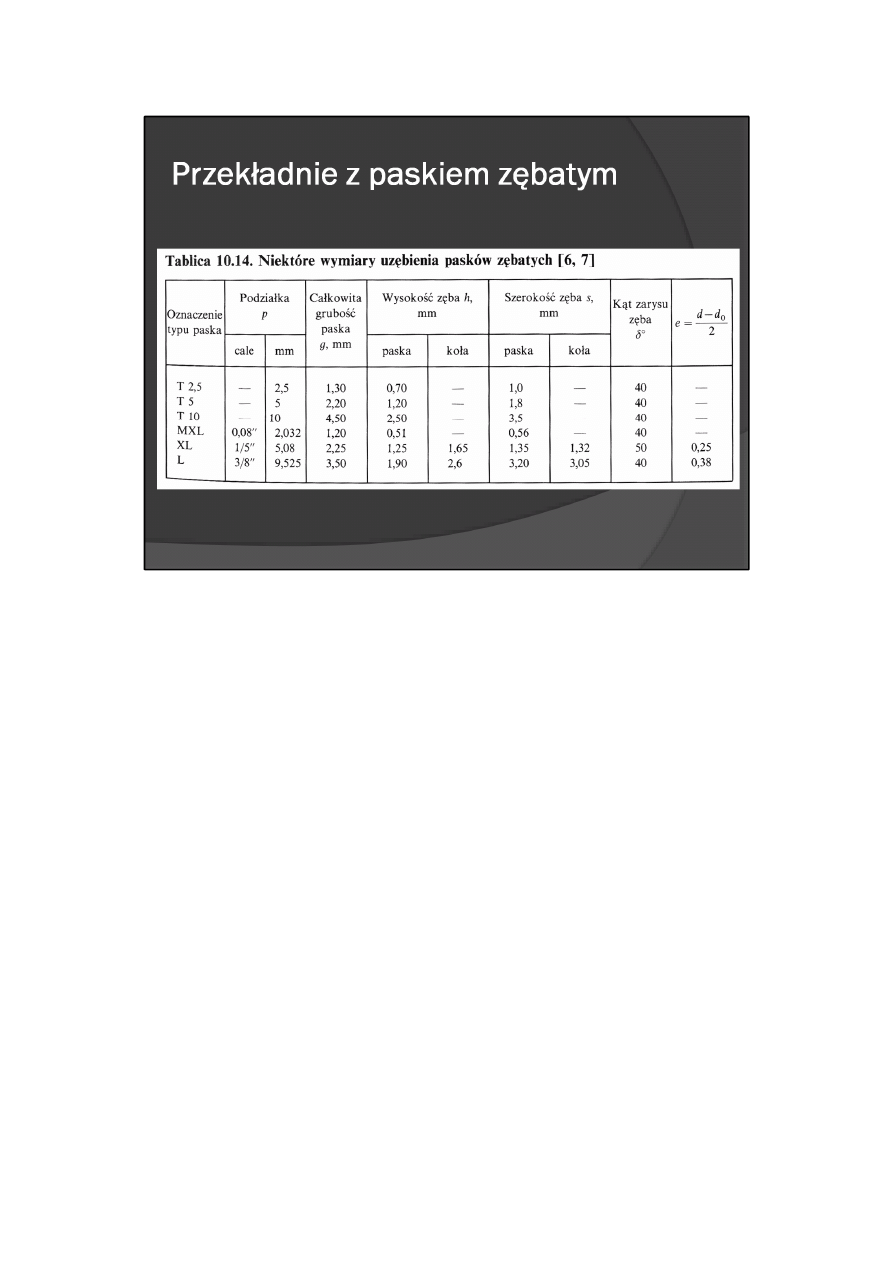
Paski zębate są produkowane przez wyspecjalizowane firmy w różnych odmianach i wymiarach. W
zależności od potrzeby stosuje się paski zębate o podziałkach od 2 mm do 22,225 mm i długościach
znamionowych od 90 mm do 9 m oraz szerokościach od 4 do 102 mm. W tablicy 10.14 podano niektóre
parametry geometryczne najczęściej stosowanych pasków zębatych oraz współpracujących z nimi kół.
Paski zębate mogą pracować z bardzo dużymi prędkościami v ≤ 80 m/s i prędkościami obrotowymi n ≤
10000 obr/min. Zalecana najmniejsza liczba zębów małego koła wynosi 12. Jednak w przekładniach
niedociążonych, pracujących z niewielkimi prędkościami, liczby zębów kół mogą być mniejsze, np. 8.
6

Obliczanie przekładni z paskiem zębatym
Do obliczenia wymiarów paska zębatego i kół zębatych są potrzebne następujące dane wyjściowe:
- moc średnia przenoszona przez przekładnię P
o
w [W],
- prędkość kątowa koła napędzającego ω
1
[rad/s],
- przełożenie przekładni i = z
2
/z
1
,
- odległość osi wałków przekładni a w [mm],
- warunki pracy i charakter obciążenia przekładni.
7

Przebieg obliczeń paska zębatego jest następujący:
1. Obliczenie prędkości kątowej mniejszego koła. W przypadku reduktora ω = ω
1
a dla przekładni
przyśpieszającej
ω = ω
1
/i
2. Przyjęcie współczynnika przeciążenia k. W tablicy 10.15 w zależności od charakteru pracy przekładni
redukcyjnych podano wartości współczynnika przeciążenia k. Współczynnik k powinien być powiększony
dla przekładni przyśpieszających przy przełożeniach i = 1/1,25 - 1/2,49 o wartość 0,2, przy i = 1/2,5 -
1/3,49 — o wartość 0,3, a przy i < 3,5 — o wartość 0,4. Jeśli przekładnia jest wyposażona w naprężacz
paska, wtedy współczynnik k powinien być dodatkowo powiększony o wartość 0,2 (zarówno w przypadku
reduktorów, jak i przekładni przyśpieszających).
8

3. Obliczenie mocy maksymalnej. Maksymalną moc przenoszoną przez przekładnię oblicza się ze wzoru
Pm = kP0
4. Określenie rodzaju paska. Rodzaj paska określa się na podstawie wykresu przedstawionego na rys.
10.26 przy obliczanej mocy maksymalnej P
m
i prędkości kątowej ω. Jest to pasek, którego krzywa znajduje
się najbliżej punktu przecięcia się współrzędnych P
m
i ω.
9
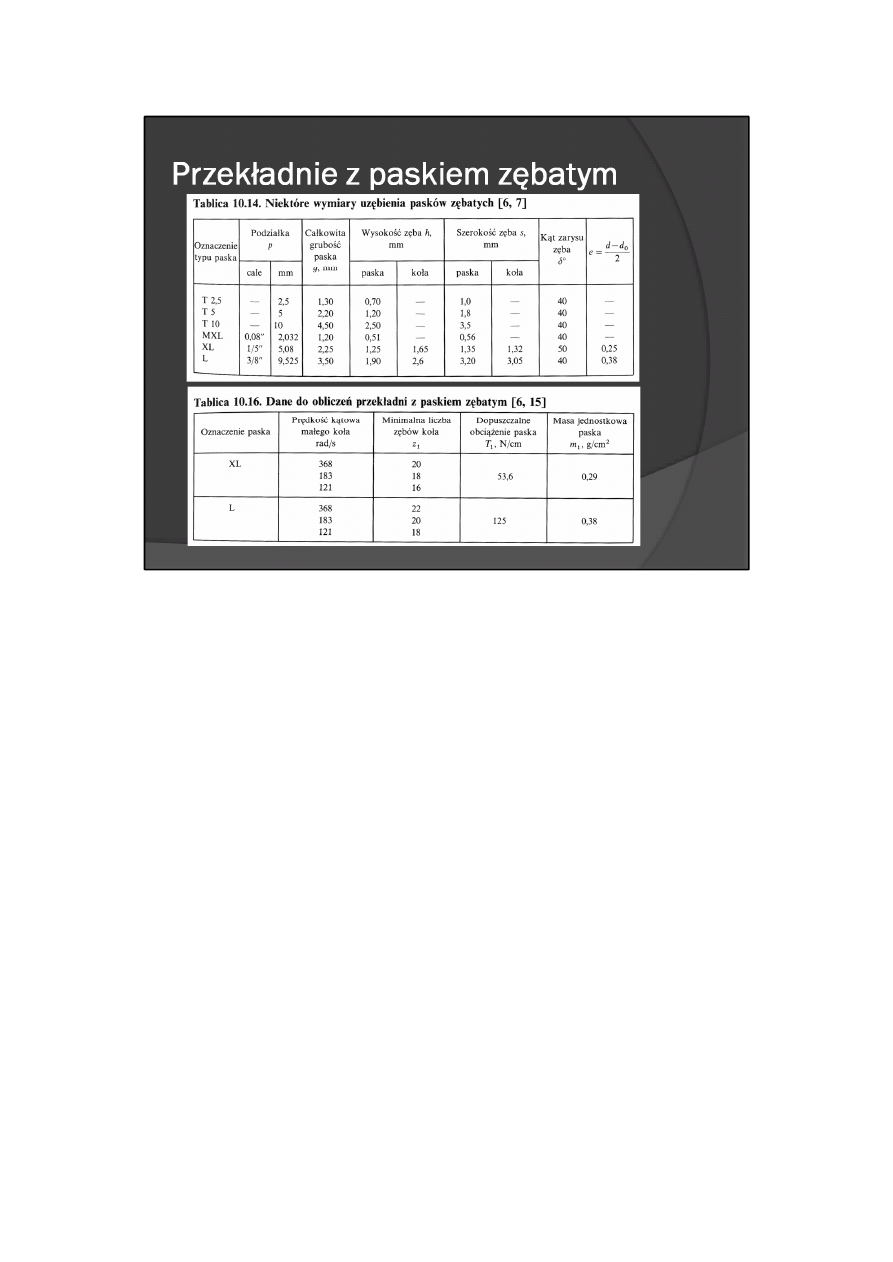
Podziałka p wybranego paska jest podana w tabl. 10.14.
5. Wyznaczenie minimalnej liczby zębów małego koła. Najmniejszą liczbę zębów małego koła przy danej
wartości prędkości kątowej co i wybranym rodzaju paska wyznacza się z tabl. 10.16. Jeśli z jakichkolwiek
przyczyn przyjmuje się liczbę zębów małego koła mniejszą od podanej w tablicy, należy liczyć się ze
zmniejszeniem się trwałości paska.
10
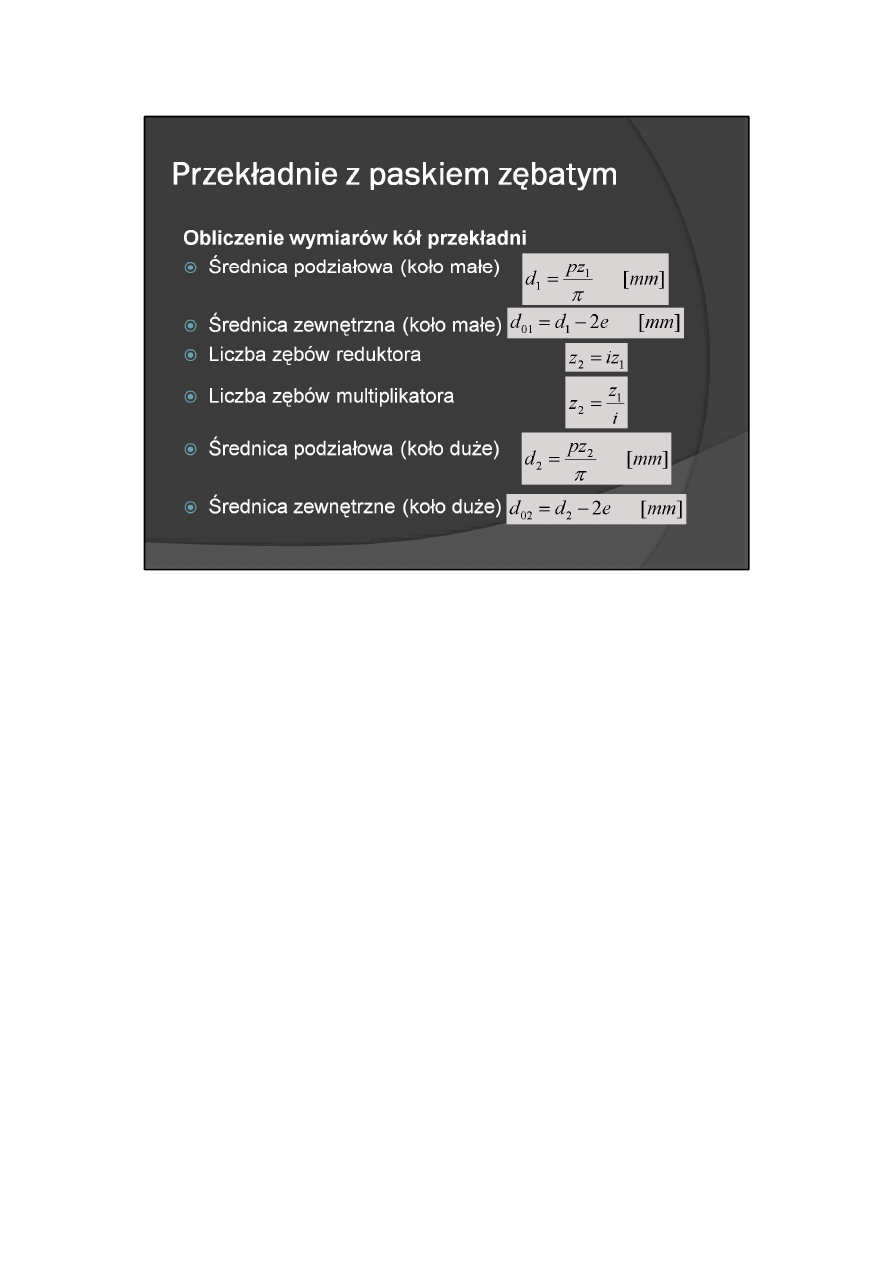
6. Obliczenie wymiarów kół przekładni. Koło małe (liczba zębów z
1
):
- średnica podziałowa
- średnica zewnętrzna
Wartości e i pozostałych parametrów geometrycznych kół są podane w tabl. 10.14.
Koło duże (liczba zębów z2):
- liczba zębów reduktora
- liczba zębów przekładni przyśpieszającej
- średnica podziałowa
- średnica zewnętrzna
11

7. Wyznaczenie obciążenia roboczego paska. Obciążenie robocze paska na jednostkę jego szerokości
wynosi
gdzie: T
1
— dopuszczalne obciążenie paska na jednostkę szerokości, T
2
— naciąg paska równoważący
działanie siły odśrodkowej
przy czym: m
1
— masa paska przypadająca na jednostkę jego powierzchni w g/cm2, ω — prędkość kątowa
w rad/s, d — średnica podziałowa jednego z kół przekładni w mm.
Uwaga: Dopuszczalne obciążenie na jednostkę szerokości T
1
oraz masa paska przypadająca na jednostkę
jego powierzchni m
1
mogą być różne dla pasków różnych firm i różnych rodzajów paska tej samej firmy. W
tablicy 10.16 podano przykładowo dane dla pasków zębatych firmy Good Year.
8. Obliczenie siły wynikającej z mocy przenoszonej przez pasek. Siła wynikająca z mocy przenoszonej przez
pasek zębaty wynosi
gdzie F
n
— naciąg wstępny paska w N (w przekładniach z paskiem zębatym może być F
n
= 0).
12

9. Wyznaczenie współczynnika osłabienia paska. Liczba zębów małego koła jednocześnie zazębianych z
paskiem wynosi
Jeśli n < 6, współczynnik osłabienia paska c oblicza się ze wzoru c = 0,2(n-1)
Jeśli n ^ 6, to przyjmuje się c = 1.
10. Założenie współczynnika bezpieczeństwa. Współczynnik bezpieczeństwa q w zależności od charakteru
i wymaganego stopnia pewności działania przekładni przyjmuje się w granicach q = 1-2
11. Obliczenie szerokości paska. Na podstawie obliczeń wykonanych wcześniej można obliczyć szerokość
paska zębatego. Otrzymaną wartość należy zaokrąglić w górę do najbliższej szerokości produkowanych
pasków.
12 Obliczenie długości paska zębatego. Długość paska zębatego oblicza się ze wzoru
Otrzymaną wartość należy zaokrąglić do najbliższej długości produkowanych pasków. Jeżeli długość ta
znacznie różni się od obliczonej, wtedy należy zmienić założoną odległość osi a, natomiast gdy różnica jest
nieznaczna — można zastosować naprężacz paska.
W celu uproszczenia obliczeń wymiarów pasków, wiele firm produkujących paski zębate podaje w swych
katalogach różnego rodzaju wykresy, nomogramy i tabele, na podstawie których można wybrać
odpowiedni pasek. Chociaż sposoby wyznaczania wymiarów pasków zębatych podawane przez różne
firmy niekiedy znacznie się różnią, to wyniki uzyskane według tych sposobów są w większości do siebie
zbliżone.
13

Sprzęgła
Wśród sprzęgieł rozróżniamy następujące ich rodzaje:
- sprzęgła nierozłączne, w których człon czynny i bierny są połączone ze sobą trwale,
- sprzęgła samoczynne, w których połączenie lub rozłączenie członów następuje samoczynnie na skutek
zmian zadanych parametrów pracy,
- sprzęgła sterowane, wyposażone w urządzenia umożliwiające obsługującemu połączenie lub rozłączenie
członów sprzęgła.
14
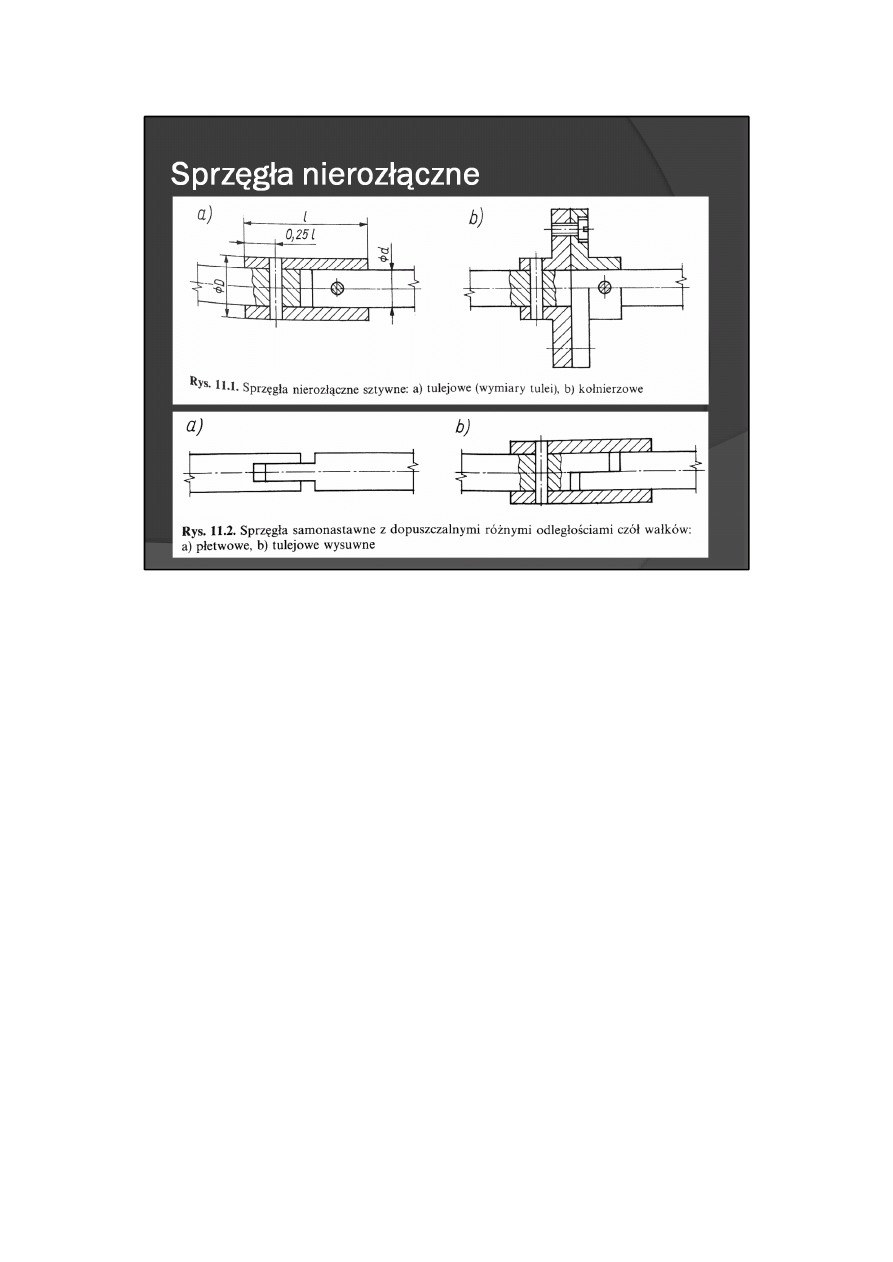
Do sprzęgieł nierozłącznych zalicza się:
- sprzęgła sztywne — sztywno łączące oba wałki bez możliwości jakiegokolwiek wzajemnego ich
przemieszczania podczas pracy (rys. 11.1),
- sprzęgła samonastawne — umożliwiające łączenie wałków w przypadku, gdy podczas pracy lub montażu
zmienia się odległość od siebie czół wałków (rys. 11.2),
15
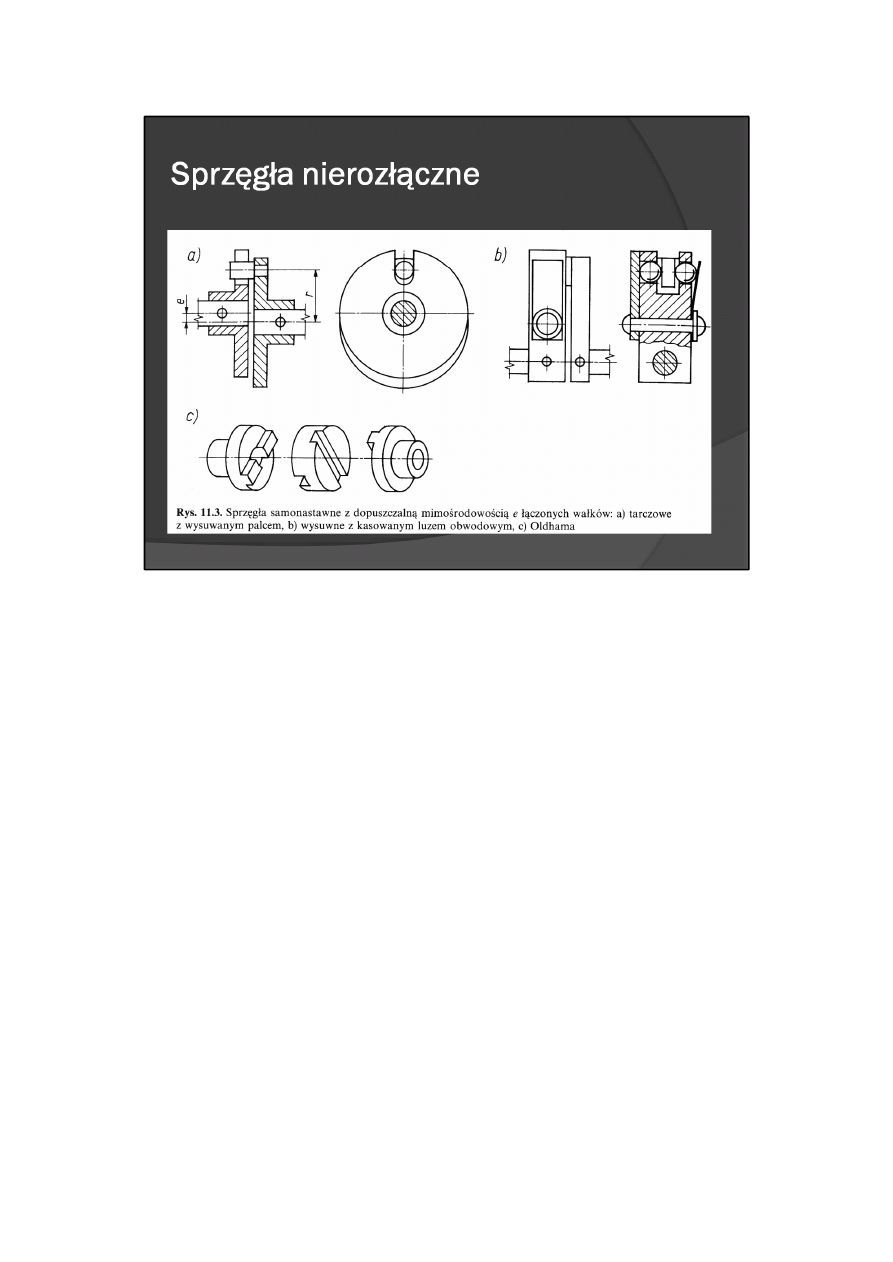
albo gdy osie wałków są względem siebie usytuowane mimośrodowo (rys. 11.3)
16
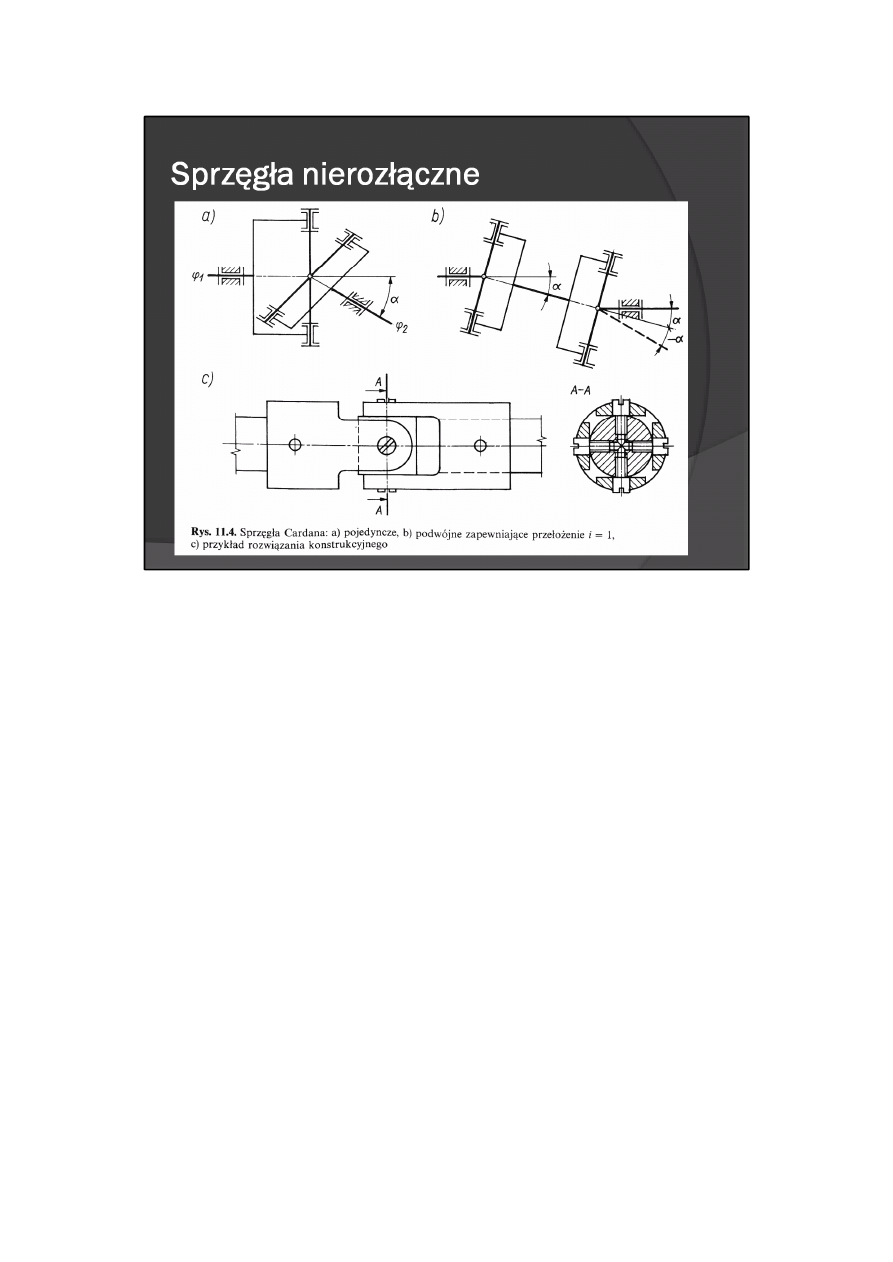
lub pod kątem, zwykle niewielkim (rys. 11.4),
17
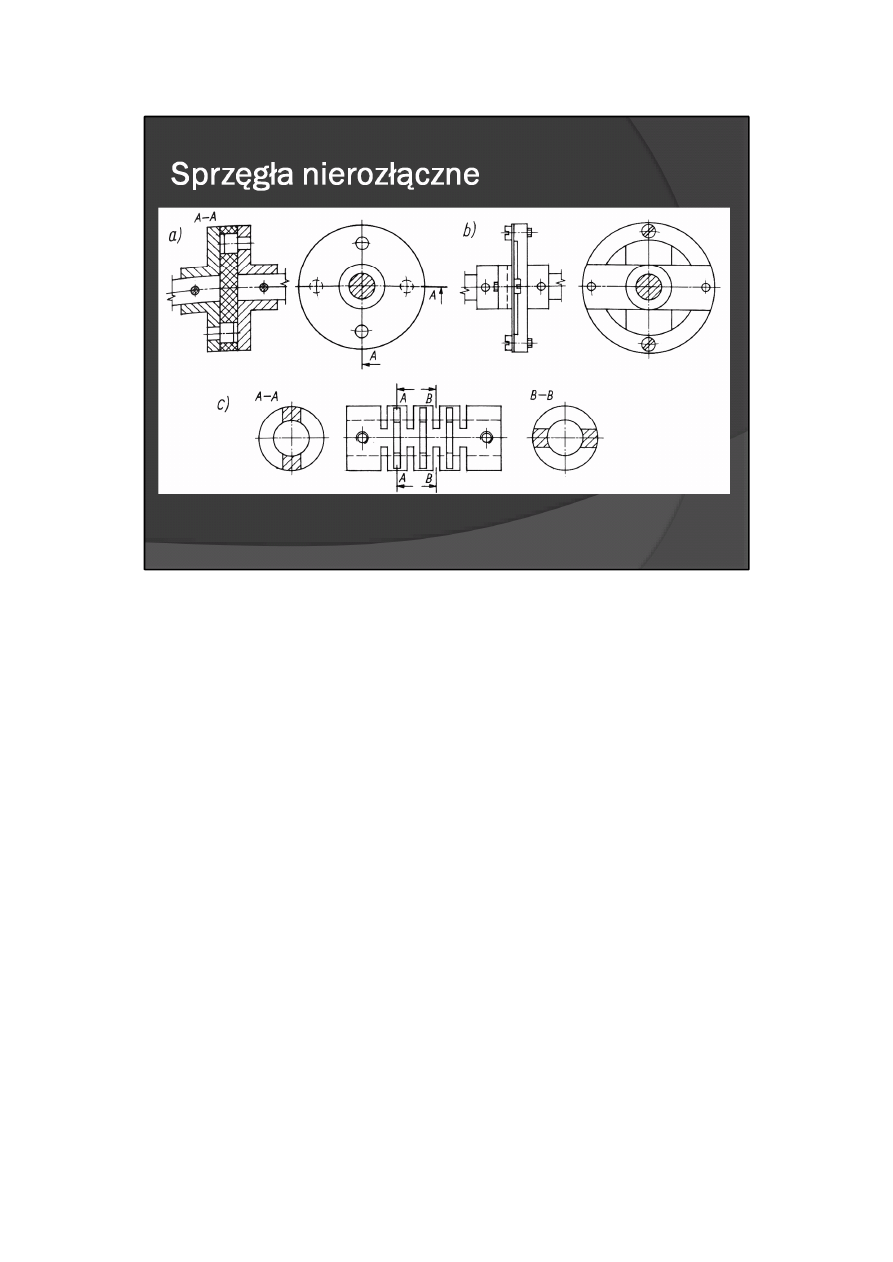
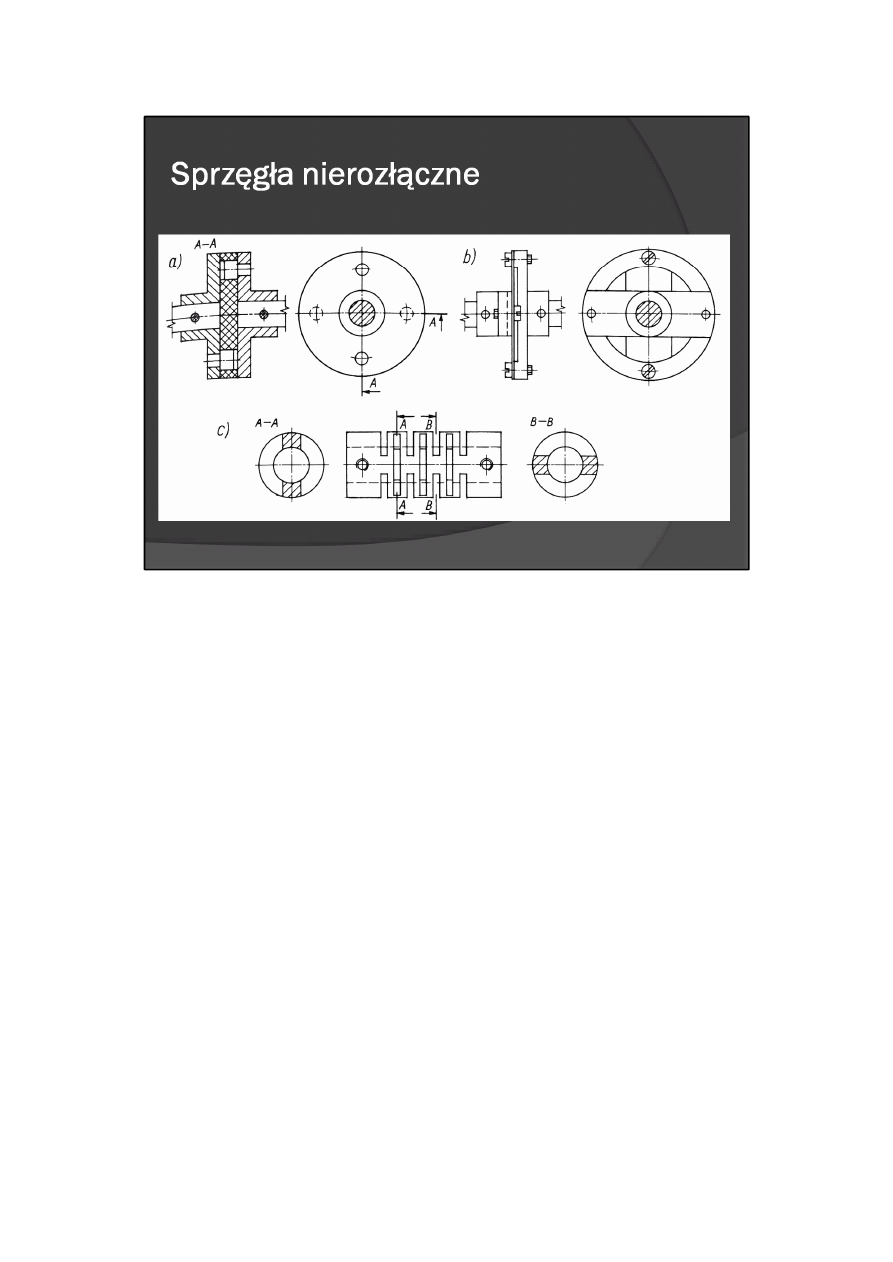
sprzęgła podatne (rys. 11.5) — zaopatrzone w podatny łącznik sprężysty, umożliwiający dynamiczne
oddzielenie członów czynnego i biernego oraz poprawną pracę mechanizmu pomimo względnego
przekoszenia wałków, powstającego wskutek niedokładnego wykonania i montażu elementów napędu
(wałków, sprzęgła, łożysk).
18
Przy użyciu sprzęgieł sztywnych niedokładności montażowe (przekoszenia czy nieosiowości łączonych
wałków) muszą być skompensowane odkształceniami sprężystymi elementów napędu. Wprowadza to
dodatkowe obciążenia łożysk, co przejawia się m.in. wzrostem oporów ruchu i cyklicznymi, o okresie 2π,
zmianami ich chwilowych wartości. Wspomniane niekorzystne zjawisko może być zmniejszone przez
zastosowanie sprzęgieł samonastawnych lub podatnych.
19
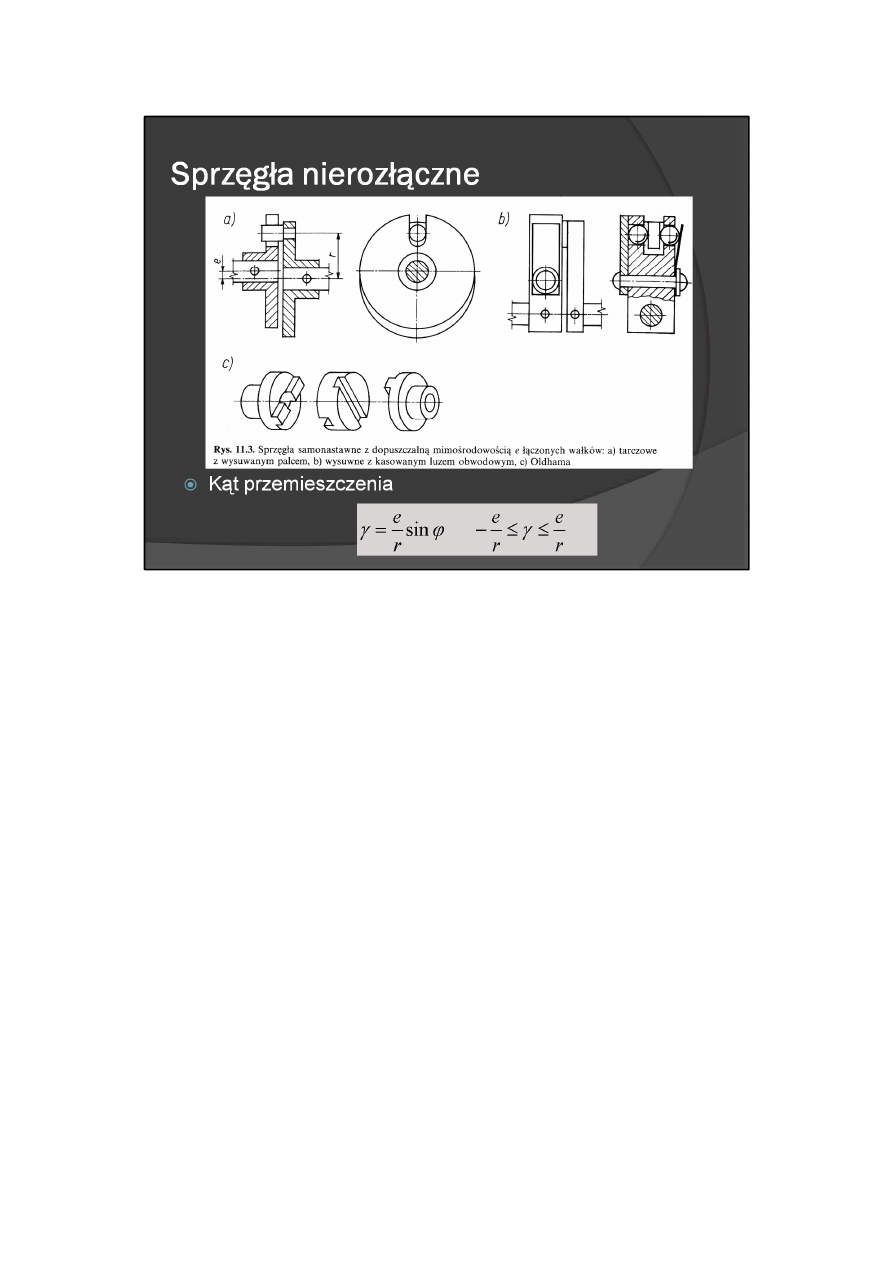
Jednakże w sprzęgłach samonastawnych przy zmianie kierunku napędu występuje martwy luz. Może on
być usunięty przez docisk sprężysty współpracujących elementów, np. jak w rozwiązaniu przedstawionym
na rys. 11.3b. Przy zastosowaniu sprzęgieł do łączenia wałków mimośrodowych (rys. 11.3a) występuje
podczas obrotu przemieszczanie kątowe wałków względem siebie (przełożenie sprzęgła i≠1). Kąt tego
przemieszczenia w przybliżeniu wynosi
gdzie ψ — bieżący kąt obrotu wałka.
Ponieważ, kąt przemieszczenia przyjmuje wartość między –e/r a e/r dlatego wartość stosunku e/r
powinna być mała. Przemieszczenie kątowe wałków nie występuje przy zastosowaniu sprzęgła Oldhama
(rys. 11.3c), jednakże w sprzęgle tym w większym stopniu niż w sprzęgle tarczowym z wysuwnym palcem
(rys. 11.3a) występują straty na tarcie wynikające z przemieszczania się podczas pracy — wewnętrznej
tarczy. Ogranicza to możliwość zastosowania sprzęgła Oldhama do przenoszenia dużych mocy.
Niektóre rodzaje sprzęgieł nierozłącznych oferowane są przez wytwórców do natychmiastowej sprzedaży;
informacje o ich wymiarach przedstawiono w tabl. 11.1 do 11.4.
20

Do łączenia wałków usytuowanych względem siebie pod kątem służy sprzęgło Cardana, zapewniające
łączonym wałkom dwa stopnie swobody (możliwości wychyleń kątowych w dwu wzajemnie prostopadłych
płaszczyznach). Zastosowanie pojedynczego sprzęgła (rys. 11.4a) powoduje, iż przełożenie między
wałkami jest zmienne i wynosi
gdzie: ω
1
, ω
2
— prędkości kątowe wałka czynnego i biernego, ψ — bieżący kąt obrotu wałka czynnego.
Stałe przełożenie można uzyskać przez zastosowania dwóch sprzęgieł Cardana Połączonych szeregowo wg
schematu pokazanego na rys. 11.4b.
W sprzedaży są oferowane sprzęgła Cardana do łączenia wałków o średnicy od 1/16" 5/8". Maksymalny
kąt wychylenia wałków jest ograniczony nie tylko konstrukcją sprzęgła, lecz również stratami mocy
(grzaniem się sprzęgła) zależnymi od kąta wzajemnego ustawienia wałków i od ich obciążenia.
Przykładowo maksymalny kąt ustawienia wałków w pojedynczym sprzęgle wynosi 30° przy założeniu, że
prędkość obrotowa wałka nie przekroczy 500 obr/min, a w sprzęgle podwójnym — 10° przy prędkości
obrotowej nie większej niż 1000 obr/min. Przy kątach mniejszych niż 3,5° nie stawia się ograniczeń
dotyczących prędkości obrotowej, lecz jedynie zmniejsza się wartość obciążenia. Maksymalny moment
obrotowy przenoszony przez sprzęgło, przy założeniu, że kąt położenia wałków nie przekracza 3,5°, wynosi
dla sprzęgła łączącego wałki o średnicy 1/16" — 0,05 Nm, a o średnicy 1/4" — 1,10 Nm.
21
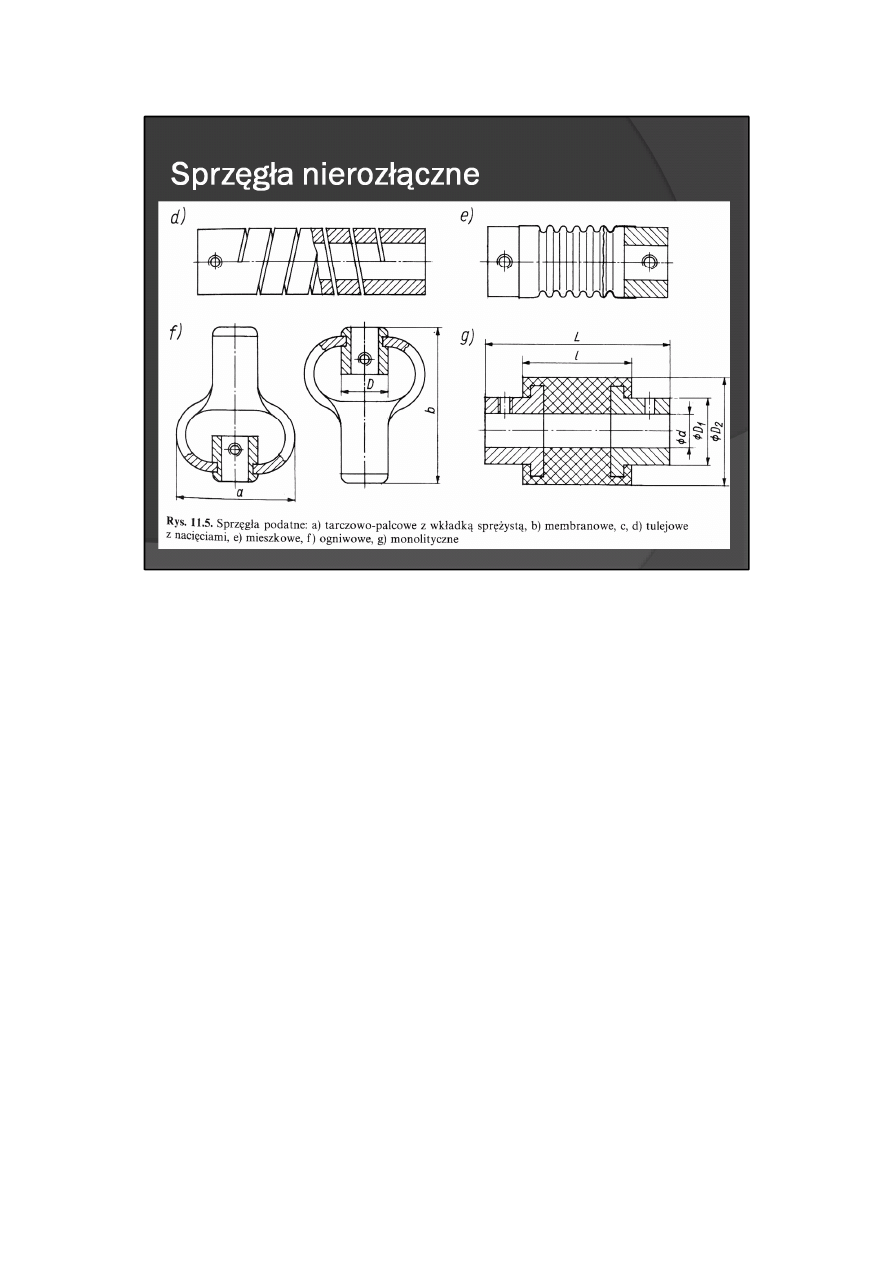
W sprzęgłach podatnych moment obrotowy jest przenoszony przez łącznik sprężynu. jacy, będący
odrębnym elementem sprzęgła lub fragmentem sztywnego członu uzyskanym przez wykonanie
specjalnych nacięć (rys. 11.5c, d). <spacja> Łącznik ten umożliwia dynamiczne oddzielenie łączonych
wałków oraz skompensowanie niezamierzonych nieosiowości wałków, wynikających z przyjętych tolerancji
wykonania i montażu.<spacja>
Obserwując częstość stosowania poszczególnych rodzajów sprzęgieł podatnych można dojść do wniosku,
że konstruktorzy preferują sprzęgła membranowe (rys. 11.5b) mieszkowe (rys. 11.5c) i monolityczne (rys.
11.5g).<spacja>
Sprzęgła membranowe, w celu zwiększenia podatności, mogą być wykonane z dwóch a nawet większej
liczby membran.
Sprzęgła mieszkowe są przeznaczone do łączenia wałków o średnicach od 0,12" do 1/4". Przy mieszku
połączonym z końcówkami przez zaciśnięcie lub przylutowanie sprzęgła te przenoszą moment nie większy
niż 0,36 Nm, a przy mieszku przynitowanym — moment nie większy niż 0,54 Nm. Mimośrodowości
wałków nie powinny być większe niż 0,25 mm, a kąty ich przekoszenia — nie większe niż 5°. Martwy luz
przy użyciu sprzęgieł mieszkowych jest niezauważalny.
Niektóre rodzaje sprzęgieł nierozłącznych oferowane są przez wytwórców do natychmiastowej sprzedaży;
informacje o ich wymiarach przedstawiono w tabl. 11.1 do 11.4.
22

Funkcje sprzęgła podatnego może pełnić wałek giętki, sprężysty, zwinięty z drutu (rys. 11.6), lub
cienkościenna rurka (polietylenowa, gumowa) wciśnięta na końce dwóch łączonych wałków. Przy
zastosowaniu tego typu sprzężenia należy się liczyć z zauważalną zmianą wzajemnego położenia kątowego
wałków w funkcji przenoszonego obciążenia lub przy zmianie kierunku napędu.
23
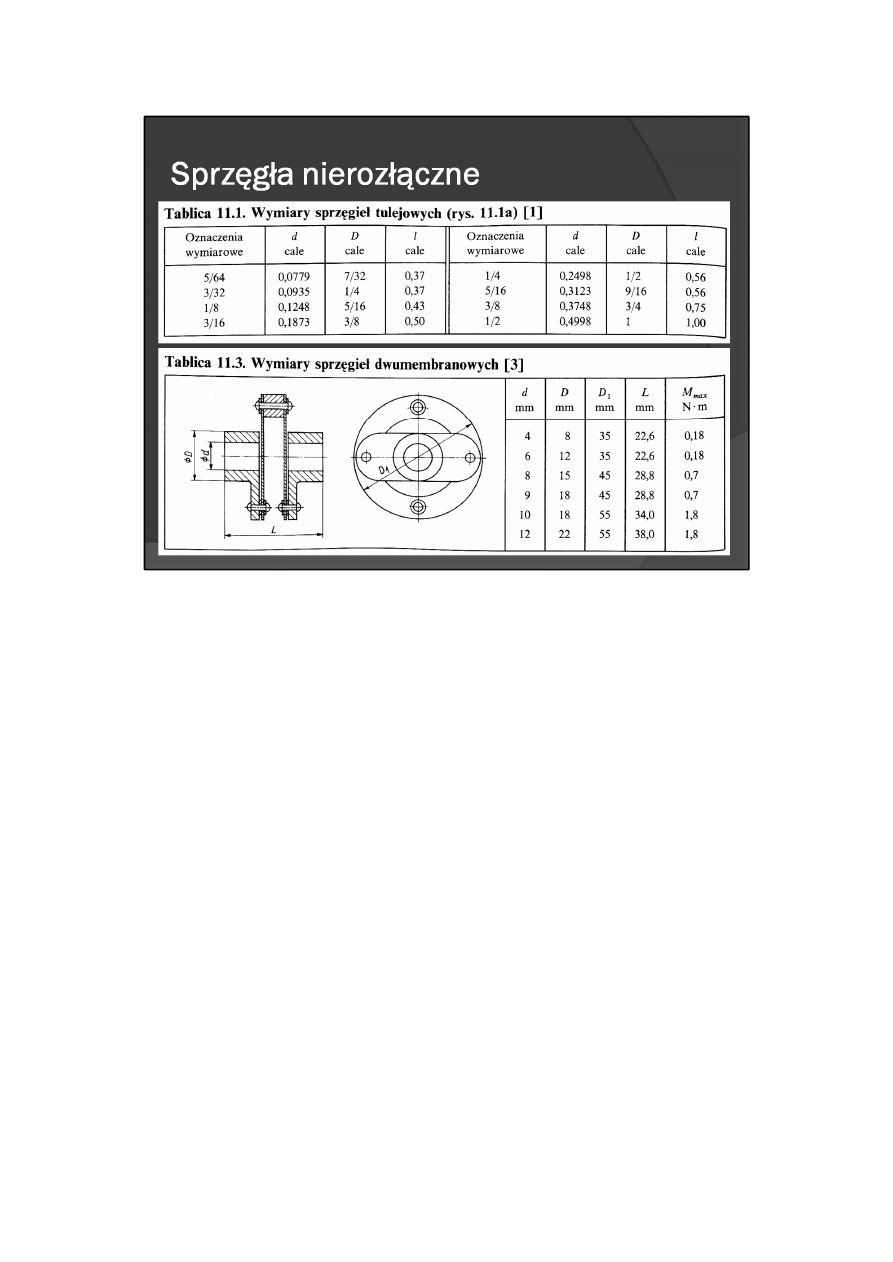
Niektóre rodzaje sprzęgieł nierozłącznych oferowane są przez wytwórców do natychmiastowej sprzedaży;
informacje o ich wymiarach przedstawiono w tabl. 11.1 do 11.4.
24

25
Sprzęgła samoczynne
Wśród sprzęgieł samoczynnych rozróżnia się:
- sprzęgła odśrodkowe — rozpoczynające sprzęganie wałków dopiero po osiągnięciu przez człon czynny
zadanej prędkości obrotowej,
- sprzęgła jednokierunkowe — przenoszące napęd tylko w jednym kierunku,
- sprzęgła bezpieczeństwa rozłączające wałki przy przekroczeniu określonej wartości momentu obciążenia
(rzadziej po przekroczeniu ustalonej temperatury).
Stosowane są rozwiązania konstrukcyjne sprzęgieł łączących funkcje dwóch wymienionych wyżej rodzajów
sprzęgieł, np. jednokierunkowych i bezpieczeństwa.
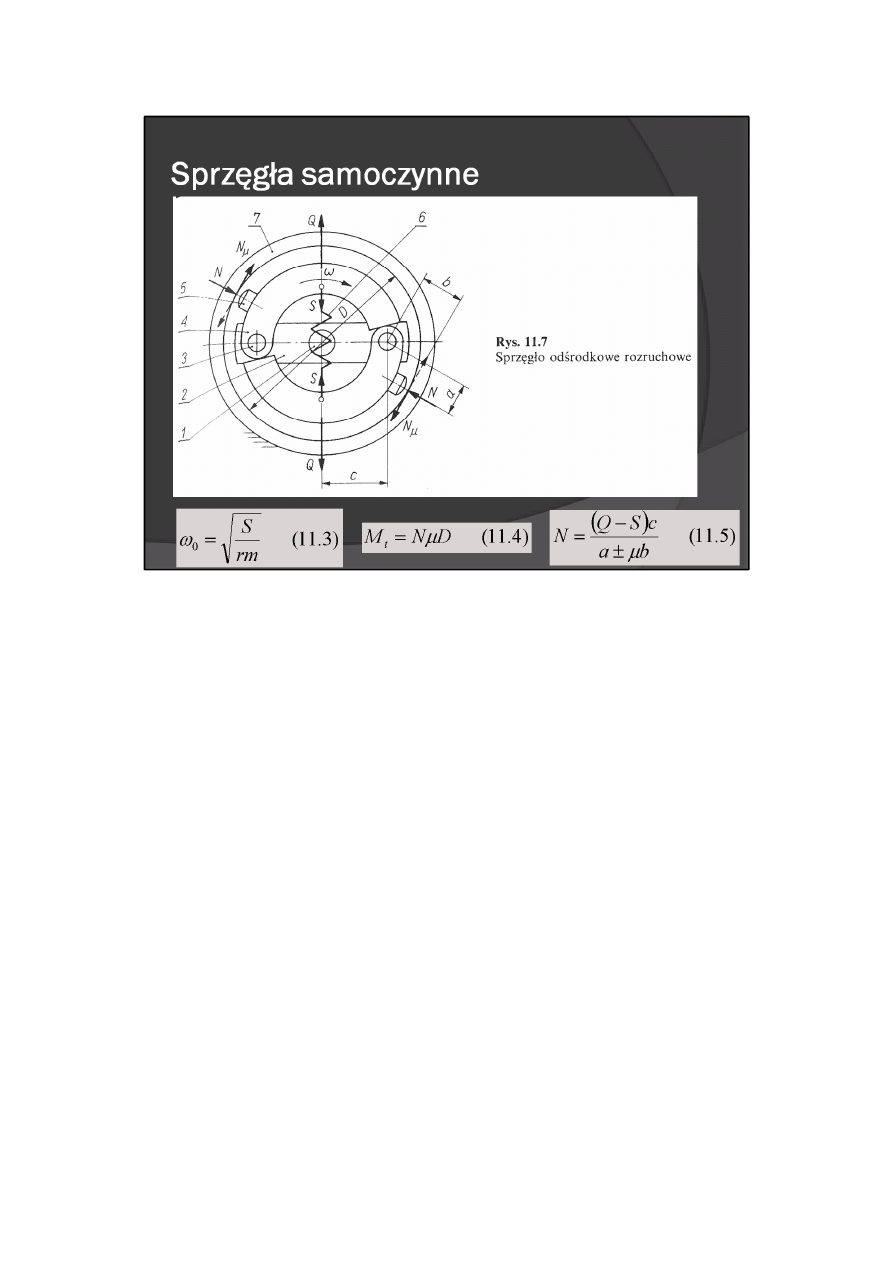
Sprzęgła odśrodkowe (rys. 11.7) mogą przekazywać napęd dopiero wtedy, gdy siła odśrodkowa Q
zrównoważy siłę S pochodzącą od sprężyny 6, ściągającej do środka wahniki 4. Przy założeniu, że sprężyna
jest zaczepiona w środku masy wahników, napęd jest przekazywany z prędkością kątową
gdzie: m — masa wahnika, r — odległość środka masy wahników od osi.
Dalszy wzrost prędkości kątowej wałka czynnego 1, na którym jest osadzona ruchoma część sprzęgła
(belka 2 z dwoma czopami 3 i ułożyskowanymi na nich wahnikami 4, zaopatrzonymi w nakładki cierne 5 i
sprężynę 6) powoduje odchylenie się wahników, zetknięcie nakładek ciernych z bębnem 7, osadzonym na
wałku biernym, i przekazywanie mu — poprzez siły tarcia — momentu M
t
pod działaniem siły N.
gdzie μ — współczynnik tarcia między nakładką cierną a bębnem.
W zależności (11.5) znak „ —" występuje przy obrotach sprzęgła w kierunku zaznaczonym strzałką na rys.
11.7, a znak „ + " — przy kierunku przeciwnym. Ruch członu biernego nastąpi dopiero wtedy, gdy moment
obliczony z zależności (11.4) będzie większy od momentu obciążenia. Należy zwrócić uwagę na możliwość
zakleszczenia się sprzęgła, lecz jedynie przy kierunku obrotów, przy którym w mianowniku zależności
(11.5) występuje znak „-". Nastąpi to wtedy, gdy a ≤ μb.
26
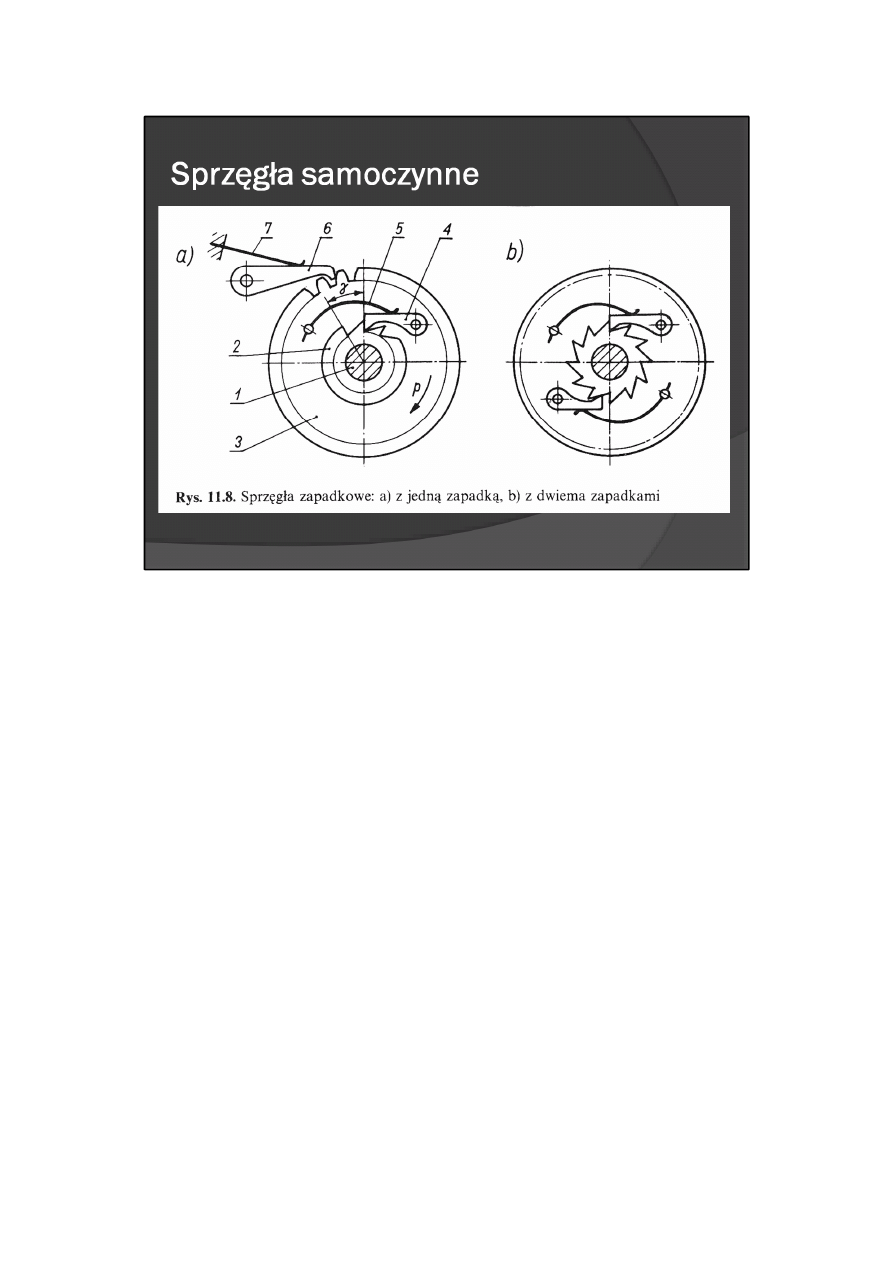
W sprzęgle jednokierunkowym zapadkowym (rys. 11.8) następuje sprzęganie członu czynnego wałka 1 z
osadzonym na nim kołem zapadkowym 2 z członem biernym (kołem zębatym 3) przy kierunku p
zaznaczonym na rysunku. Koło zębate 3 jest osadzone obrotowo na wałku 1. Na kole tym jest
ułożyskowana zapadka 4 oraz jest osadzona sprężyna 5 dociskająca zapadkę do koła zapadkowego 2.
Przeciwzapadka 6 dociskana do koła zębatego 3 sprężyną 7 unieruchamia je podczas jałowego ruchu
sprzęgła. Zmiana kierunku ruchu jałowego na kierunek pracy następuje po przebyciu przez człon czynny
kąta 0 < ψ < γ, gdzie γ jest podziałką kątową koła zapadkowego. Rozrzut wartości kąta ψ może być
zmniejszony do połowy przez stosowanie dwóch zapadek przesuniętych względem zębów koła
zapadkowego o kąt γ /2 (rys. 11.8b). W przypadku zastosowania w sprzęgle zapadkowym zapadek
podatnych (np. wykonanych z odkształcalnych tworzyw lub długich, smukłych) łagodzi się uderzenie po
zmianie napędu z jałowego na roboczy.
27

Sprzęgło jednokierunkowe cierne typu wolne koło może być wyposażone w rolki (rys. 11.9a, b) lub zapadki
cierne (rys. 11.9c). Rolki współpracują równocześnie z powierzchnią walca i krzywki, dzięki czemu jest
uzyskiwany żądany kąt zaklinowania a (rys. 11.9d). W celu poprawnego działania jednokierunkowego
sprzęgła ciernego jest wymagane, aby
gdzie: f – współczynnik tarcia tocznego rolki, ρ – kąt tarcia ślizgowego rolki.
28

W sprzęgle jednokierunkowym sprężynkowym (rys. 11.10) jest wykorzystany efekt zmniejszenia się
wymiaru średnicy sprężyny śrubowej obciążonej czynnym momentem skręcającym, przeciwnym do
kierunku nawinięcia zwojów. Tak więc obrót (w kierunku zaznaczonym na rysunku) wałka 1, na który jest
lekko wciśnięta sprężyna 2, powoduje, poprzez powstający moment tarcia obciążający sprężynę,
zmniejszenie jej średnicy i dodatkowy zacisk na wałku 1. Umożliwia to sprzęgnięcie wałka 1 ze sprężyną, a
więc także z drugim wałkiem 3, z którym sprężyna jest na trwale związana. Zmiana kierunku obrotów
wałka 1 powoduje zmianę kierunku momentu działającego na sprężynę 2, powiększenie jej średnicy i
swobodny obrót wałka w sprężynie 2.
Uzyskanie żądanego wstępnego zacisku sprężyny na wałku jest dość trudne. Rozrzut bowiem średnicy
wewnętrznej w poszczególnych egzemplarzach sprężyny jest duży. Z tego też względu opłaca się sprężynę
zwijać, tak aby uzyskać średnicę wewnętrzną nieco mniejszą od średnicy wałka, a następnie przeszlifować
ją na wymagany wymiar i wtedy wcisnąć na wałek (rys. 11.10b).
W przypadku sprzęgieł tego typu zaleca się, aby liczba zwojów obejmująca wałek wynosiła 5—10, a wcisk
— około 0,15 mm. Jeżeli sprzęgło pracuje bez smarowania, wówczas ocenia się, że współczynnik tarcia
drutu sprężyny o wałek μ = 0,15, przy smarowaniu smarem stałym — μ = 0,1, a przy pracy sprzęgła w oleju
— μ = 0,05. Podane wartości μ są stosowane do oszacowania oporu ruchu wałka przy jałowym kierunku
obrotów.
29
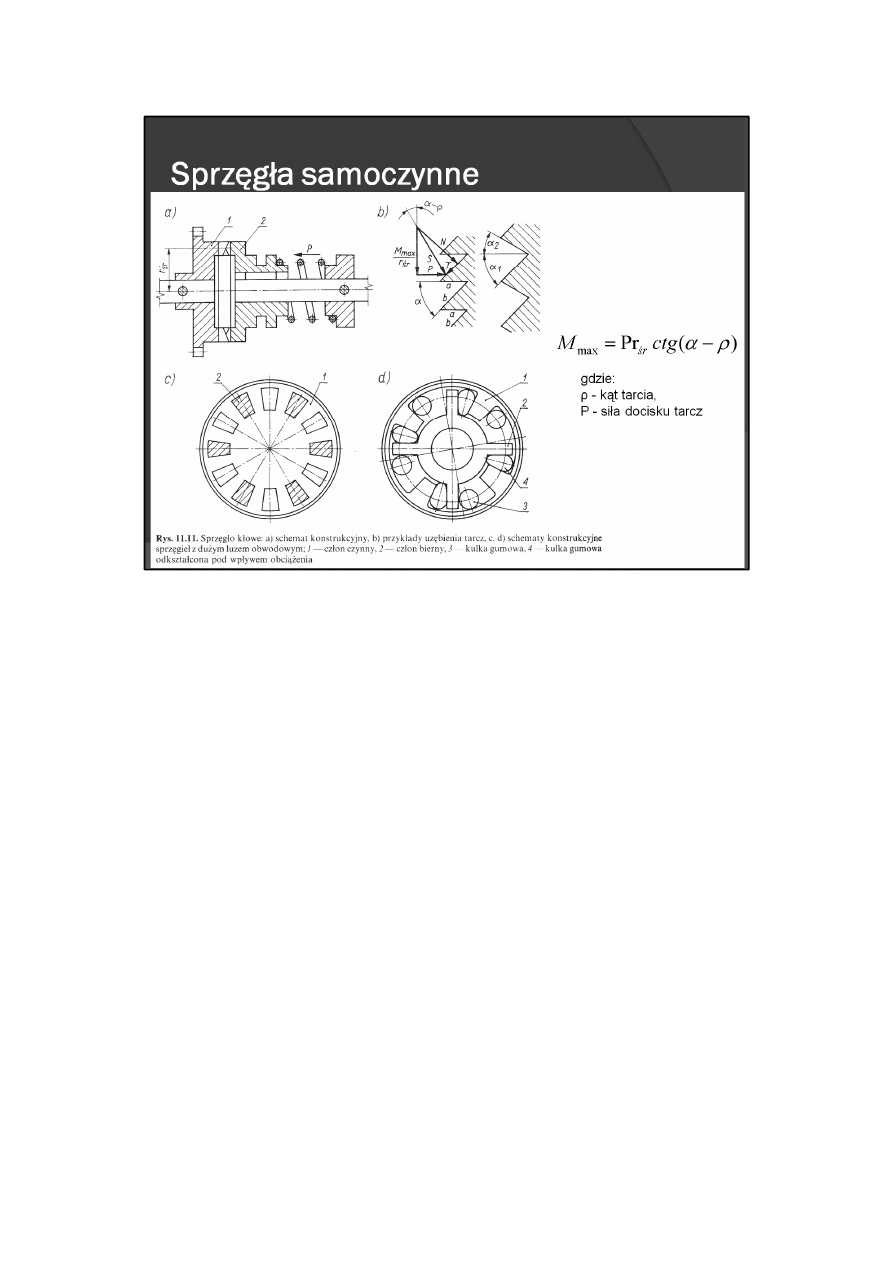
Sprzęgło kłowe (rys. 11.11) przy przenoszeniu obciążenia przez powierzchnie a uzębionych tarcz pracuje
jako sztywne, a przy przenoszeniu obciążenia przez powierzchnie b może przenosić jedynie ograniczony
moment
gdzie:ρ— kąt tarcia, P — siła docisku tarcz.
Jeżeli wartość momentu obciążenia jest większa od M
max
, wtedy następuje samoczynne odepchnięcie
tarczy i rozłączenia napędu. W takiej sytuacji sprzęgło grzechocze, informując obsługę, że napęd nie jest
przenoszony. Jeżeli natomiast moment obciążenia będzie mniejszy od wartości M
max
— sprzęgło powraca
do normalnej pracy.
Przyjmując różne kąty α
1
i α
2
, można uzyskać zróżnicowanie wartości momentów, zależnie od kierunku
napędu; w granicznym przypadku sprzęgło kłowe staje się sprzęgłem jednokierunkowym.
W specjalnych rozwiązaniach konstrukcyjnych sprzęgieł kłowych (nie pełnią wtedy one funkcji sprzęgieł
przeciążeniowych) jest stosowany bardzo duży luz obwodowy pomiędzy sprzęgającymi elementami członu
czynnego i biernego. Luz ten bywa wykorzystany do polepszenia warunków startu silników napędowych o
małej mocy lub do realizacji pewnych funkcji urządzenia w czasie zmiany kierunku napędu. Jednak wtedy,
w celu złagodzenia uderzenia następującego po usunięciu luzu, elementy sprzęgające są podatne na
odkształcenia (smukłe i wykonane z odkształcalnego tworzywa sztucznego — rys. 11.11c) lub między te
elementy wprowadza się dodatkowe elementy odkształcalne (np. gumowe kulki — rys. 11.11d).
30
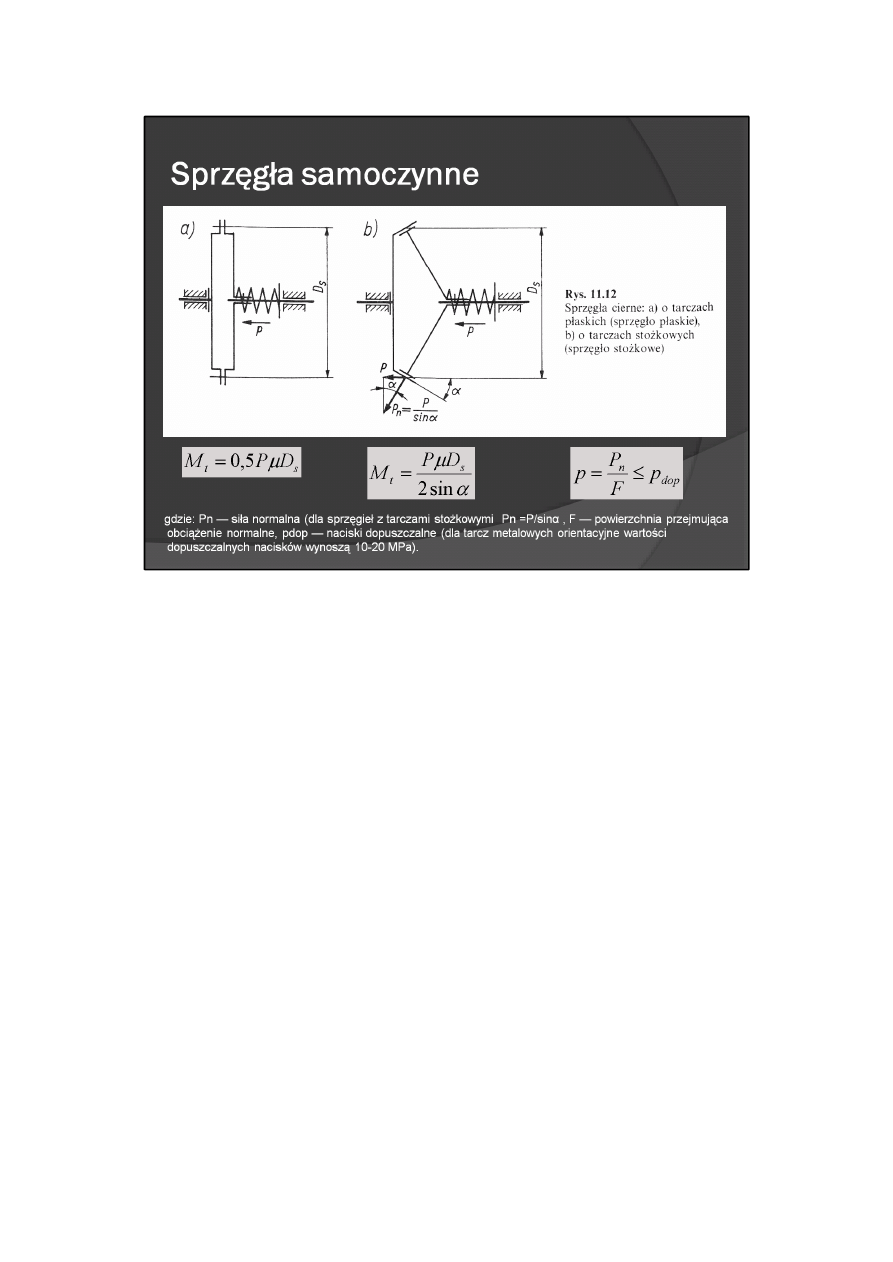
Sprzęgła bezpieczeństwa mają na celu rozłączenie napędu wtedy, gdy wartość momentu obciążającego
wzrośnie powyżej wartości momentu dopuszczalnego M
t
Najczęściej rolę takiego sprzęgła, zwanego
również sprzęgłem przeciążeniowym, pełni sprzęgło cierne o jednej powierzchni trącej (rys. 11.12).
Maksymalny moment przenoszony przez sprzęgło cierne o tarczach płaskich
a o tarczach stożkowych
gdzie μ — współczynnik tarcia tarcz.
Sprzęgła te z reguły pracują na sucho. Materiały współpracujących tarcz ciernych to:
Stal-stal, stal-mosiądz, metal-tworzywo sztuczne lub metal-filc. Nie są to więc materiały stosowane na
okładziny sprzęgieł maszynowych przenoszących duże moce.
Do wstępnych obliczeń przyjmuje się wartości współczynników tarcia 0,1-0,3. Dokładne wartości
współczynników tarcia bądź wartości momentów przenoszonych przez te sprzęgła wyznacza się
doświadczalnie.
Maksymalną siłę docisku tarcz Pn ogranicza wartość nacisków p
gdzie: P
n
— siła normalna (dla sprzęgieł z tarczami stożkowymi P
n
=P/sinα , F — powierzchnia przejmująca
obciążenie normalne, p
dop
— naciski dopuszczalne (dla tarcz metalowych orientacyjne wartości
dopuszczalnych nacisków wynoszą 10-20 MPa).
31
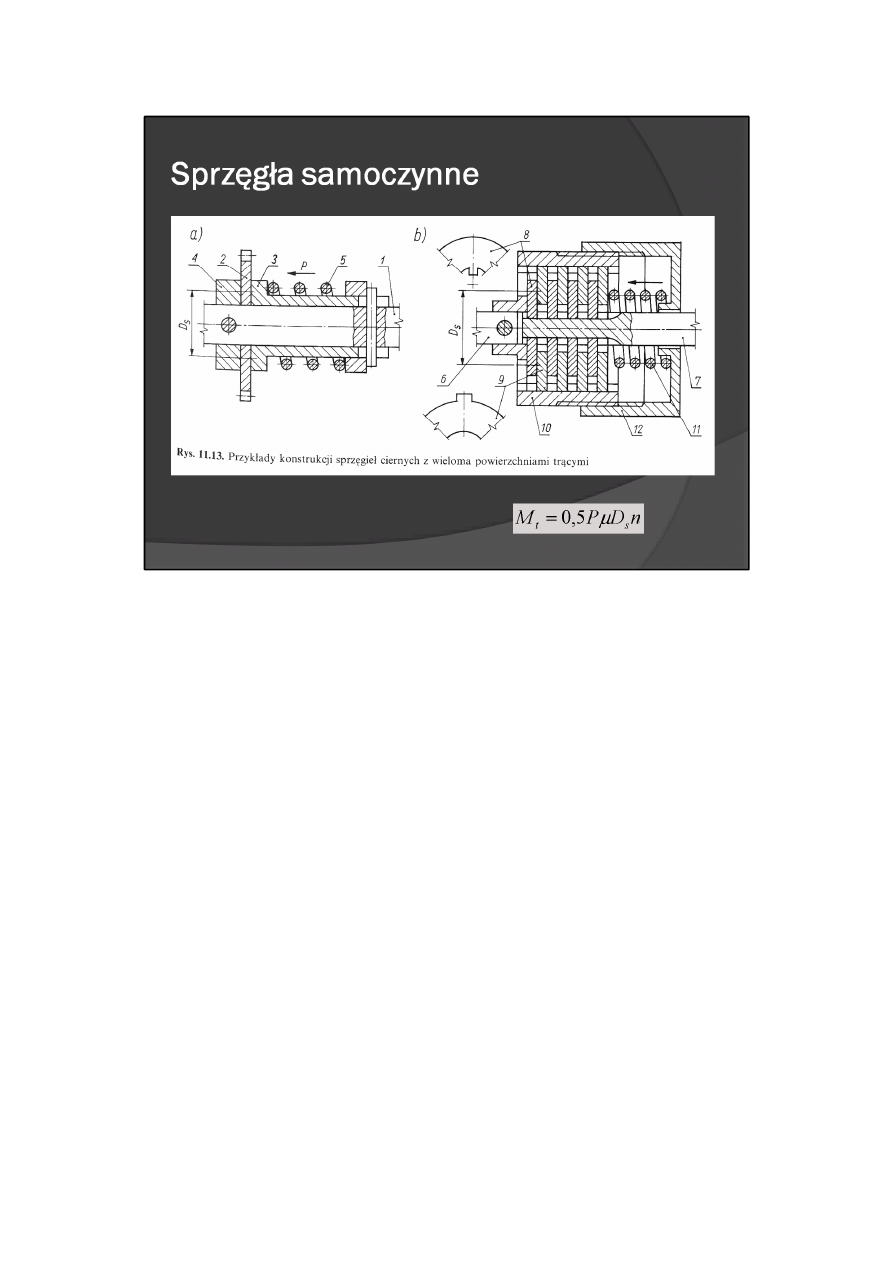
Przykład prostej konstrukcji sprzęgła ciernego umożliwiającego przeniesienie napędu wałka 1 na koło
zębate 2 przedstawiono na rys. 11.13a. W celu obrócenia wałka względem koła zębatego 2 należy
pokonać moment tarcia występujący na obu powierzchniach koła stykających się z pierścieniem 4 i tulejką
3, dociskaną do koła sprężyną 5. Zatem liczba powierzchni trących wynosi 2. W ogólnym przypadku liczba
powierzchni trących jest sumą czynnych płytek trących oraz biernych płytek pomniejszonych o 1.
Przykład sprzęgła ciernego z wieloma powierzchniami trącymi przedstawiono na rys. 11.13b. Na wałku
6jest osadzony bęben 10 z czynnymi płytkami trącymi 9. Płytki te dzięki występom, współpracującym z
wyjęciami w bębnie 10, mogą się w nim przemieszczać wzdłuż osi, ale nie mogą się obrócić. Płytki bierne
8, przedzielone płytkami 9, są osadzone na wałku 7 przesuwnie, bez możliwości obrotu. Płytki czynne 9 i
bierne 8 są dociskane do siebie sprężyną 11 z siłą P regulowaną za pomocą nakrętki 12. Sprzęgło cierne z n
powierzchniami trącymi przenosi moment
32
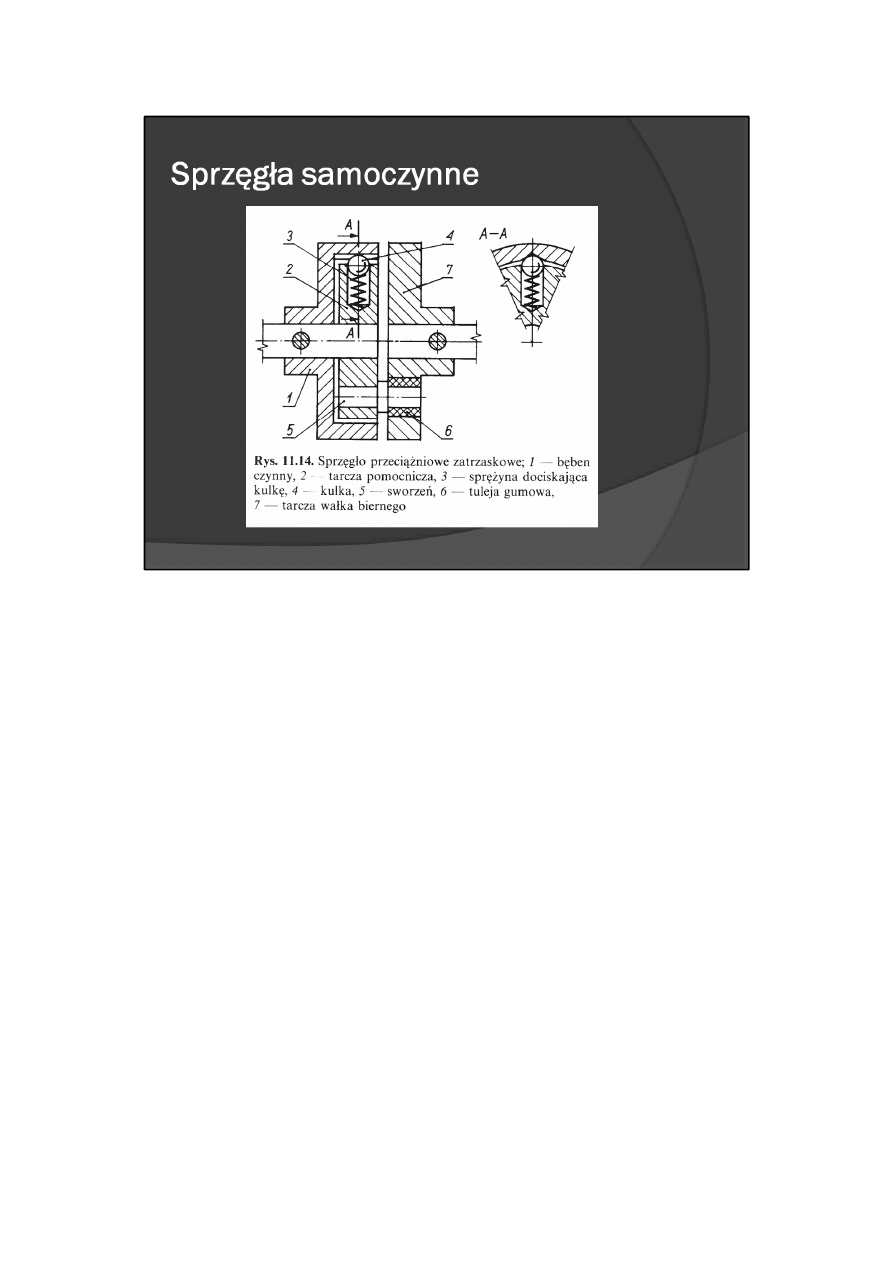
Rolę sprzęgła przeciążeniowego może również pełnić sprzęgło przedstawione na rys. 11.14 lub poprzednio
omówione sprzęgło kłowe (rys. 11.11), które jest przykładem łączenia funkcji sprzęgła jednokierunkowego
i sprzęgła bezpieczeństwa.
33
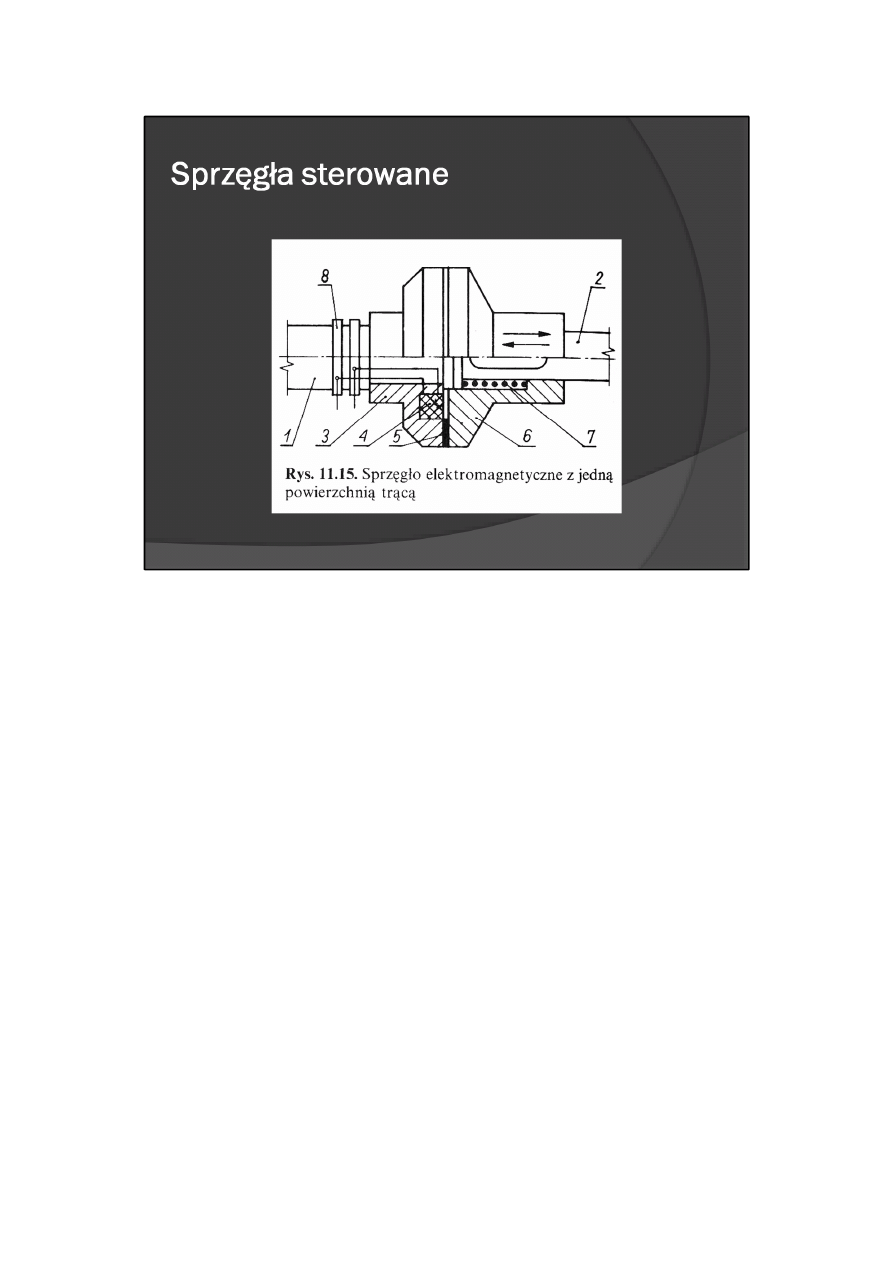
Do zdalnego sterowania sprzęganiem czy rozłączaniem wałków służą najczęściej sprzęgła
elektromagnetyczne, które mogą być budowane jako sprzęgła cierne lub indukcyjne.
Sprzęgło elektromagnetyczne cierne z jedną powierzchnią trącą przedstawiono na rys. 11.15. Na wałku
czynnym 1 jest osadzona tarcza 3, wykonana z materiału ferromagnetycznego, zaopatrzona w wykładzinę
cierną 5 i uzwojenie 4. Uzwojenie to jest zasilane poprzez szczotki współpracujące ze ślizgaczami 8.
Wytworzone pole elektromagnetyczne zamyka się przez tarczę 6, osadzoną przesuwnie na wałku biernym
2, i dociąga ją do tarczy 3. Docisk tarcz do siebie jest zależny od wytworzonych sił elektromagnetycznych
pomniejszonych o siłę sprężyny 7 wycofującej tarczę 6 po zaniknięciu pola elektromagnetycznego.
Omówione sprzęgło jest bardzo podobne do sprzęgła ciernego przedstawionego na rys. 11.12a. Siła
docisku tarcz pochodzi tu jednak nie od sprężyny, lecz od elektromagnesu i działa tylko w czasie zasilania
uzwojenia.
34
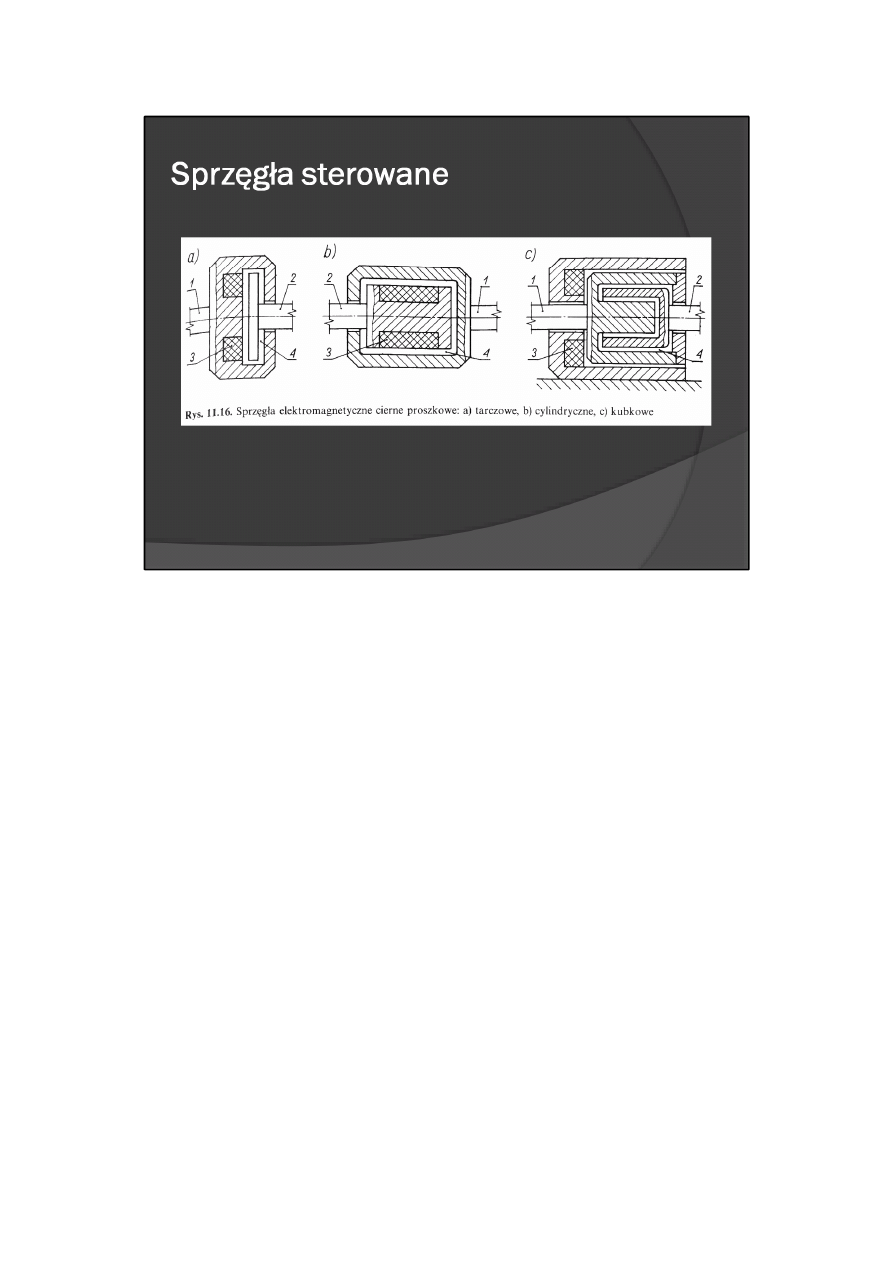
Inną formą sprzęgieł elektromagnetycznych ciernych są sprzęgła proszkowe. Przykładowe schematy
konstrukcyjne takich sprzęgieł przedstawiono na rys. 11.16. W przestrzeni 4 między członem czynnym 1 a
biernym 2 znajdują się drobnoziarniste proszki ferromagnetyczne zmieszane z substancjami
pomocniczymi. Pole magnetyczne, wytworzone przez uzwojenie 3 wirujące wraz z wałkiem (rys. 11.16a, b)
lub uzwojenie nieruchome (rys. 11.16c), zamyka się przez mieszaninę proszkową powodując zlepianie się
jej cząsteczek i sprzęgnięcie członu czynnego z biernym. Zanik tego pola umożliwia swobodny obrót
wałków względem siebie. Substancje pomocnicze służą do zmniejszania tarcia między proszkiem a
wirującymi elementami wałków i zabezpieczają proszek przed zlepianiem się w gruzełki. W sprzęgłach
„suchych" dodatkami tymi mogą być: grafit, talk, tlenek magnezu, tlenek cynku, dwusiarczek molibdenu,
zaś w sprzęgłach „ciekłych" — olej — najlepiej silikonowy.
35
Sprzęgło indukcyjne działa na podobnej zasadzie jak silnik indukcyjny asynchroniczny. Obrót wałka
czynnego powoduje wirowanie pola magnetycznego, wytworzonego przez elektromagnes czy magnes
trwały, które — przecinając wirnik (np. w postaci kubka) wykonany z materiału niemagnetycznego (Al, Cu)
o małej rezystywności — indukuje w nim prądy wirowe. Prądy te i związane z nimi pole magnetyczne
powodują porywanie wirnika w kierunku wirowania pola magnetycznego i wałka czynnego. Moment
przenoszony przez takie sprzęgło jest zależny od strumienia magnetycznego i od poślizgu (względnej
różnicy prędkości wałka czynnego i biernego).
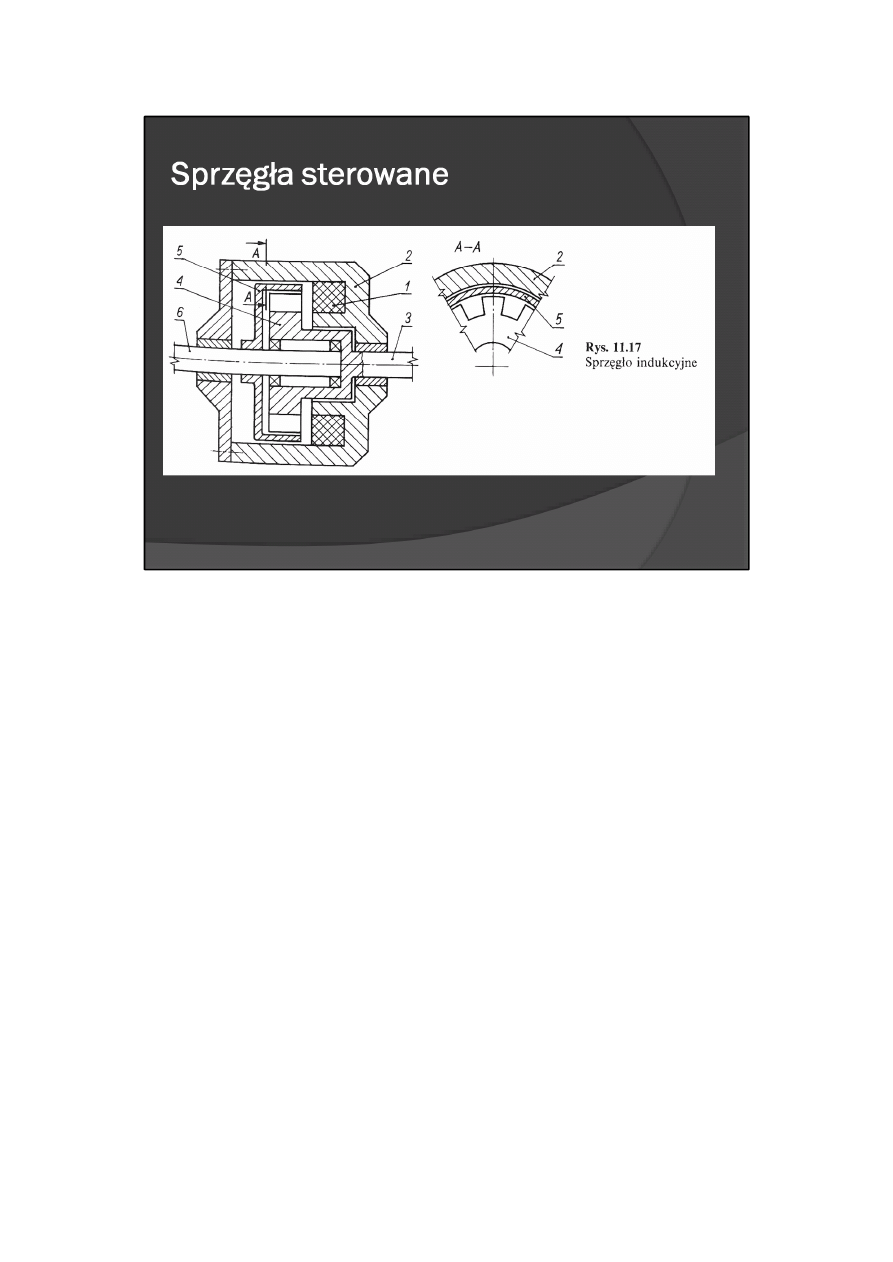
Schemat konstrukcyjny sprzęgła indukcyjnego przedstawiono na rys. 11.17. Strumień magnetyczny jest
wytwarzany przez cewkę 1 umieszczoną w stojanie 2. Zamyka się on przez zamocowany na wałku czynnym
3 uzębiony wirnik 4 oraz przez aluminiowy kubek 5 związany z wałkiem biernym 6. Uzębienie wirnika
powoduje, że przy jego obrocie pole magnetyczne wiruje, a więc w kubku 5 powstają prądy wirowe, a
związane z nimi pole magnetyczne napędza kubek i wałek bierny. Wzrost obciążenia sprzęgła powoduje
zwiększenie poślizgu, a w granicznym przypadku może doprowadzić do zatrzymania wałka biernego.
36
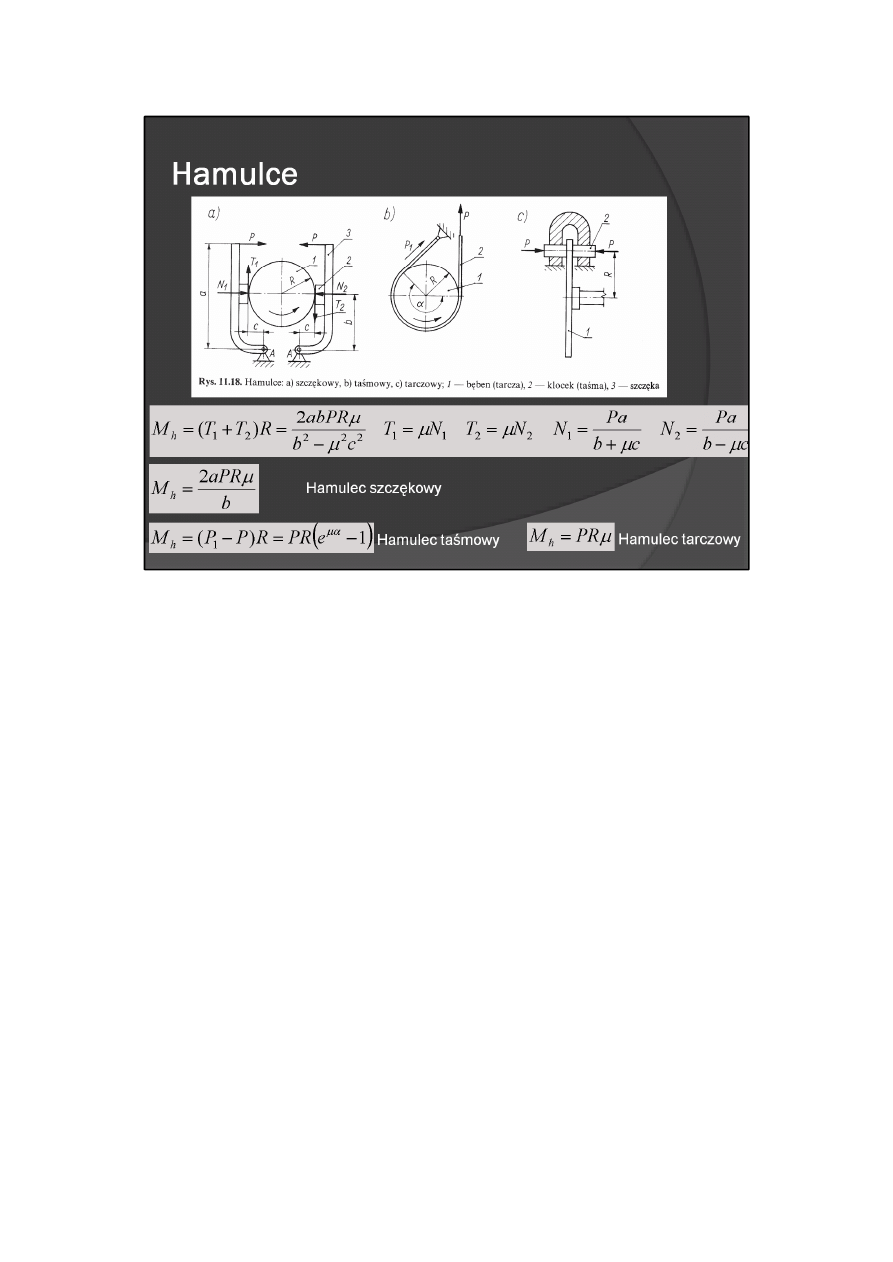
Schematy podstawowych rodzajów hamulców przedstawiono na rys. 11.18. Moment hamujący bęben w
hamulcu szczękowym (rys. 11.18a) wynosi
Z analizy rozkładów sił w hamulcu szczękowym i zależności (11.14) wynika, że w ogólnym przypadku siły T
1
i T
2
nie są równe, gdyż nakładki hamulcowe są dociskane do bębna z różnymi siłami (przy zaznaczonym na
rysunku kierunku obrotów bębna działająca na szczękę siła T
1
wywołuje moment odciągający szczękę od
bębna, a siły T
2
— moment dociskający szczękę). W przypadku gdy b ≤ μc, następuje zablokowanie
hamulca. Jeżeli punkty A obrotu szczęk zostaną tak dobrane, że c = 0, wówczas obie szczęki spowodują
jednakowy efekt hamowania oraz nie wystąpi niebezpieczeństwo zablokowania hamulca i wtedy moment
hamowania w hamulcu szczękowym
Moment hamowania w hamulcu taśmowym (rys. 11.18b)
zaś moment hamowania w hamulcu tarczowym (rys. 11.18c)
gdzie: e — podstawa logarytmu naturalnego, a — kąt opasania, μ — współczynnik tarcia między bębnem a
taśmą lub między tarczą a klockami.
W hamulcach taśmowych i tarczowych nie może wystąpić zakleszczenie hamulców.
W omówionych hamulcach siła P może pochodzić od sprężyny, obciążnika, elektromagnesu, siłownika
hydraulicznego, pneumatycznego itp.
Hamulce szczękowy i tarczowy mogą działać również przy jednostronnym docisku nakładki (klocka) do
bębna. Powoduje to jednak zmniejszenie momentu hamowania, ponadto zwiększenie obciążenia łożysk
bębna (tarczy).
37

Ustalacze są to mechanizmy służące do wzajemnego ustalania części w zamierzonym położeniu. Zmiana
tego położenia może odbywać się po zwolnieniu (odciągnięciu) ustalaka czy po przekroczeniu siły lub
momentu działającego na ustalany element. Ze względu na zasadę działania ustalacza rozróżnia się
ustalacze kształtowe i cierne (zwane zaciskami).
Ustalacze kształtowe służą do skokowego ustalania elementów przesuwnych lub obrotowych w
położeniach wyróżnionych kształtem ustalanego elementu i ustalaka. Ustalanie odbywa się najczęściej
przez zagłębienie ustalaka w otwór, wycięcie itp., przy czym ustalak jest utrzymywany w tym położeniu
przez dopasowania kształtu elementu i ustalaka, często z udziałem tarcia, lub przez docisk sprężyną.
Jeżeli ustalak 1, dociskany siłą P, ma być odwiedziony na skutek przyłożenia do ustalanej listwy 2 siły R
(rys. 11.19a), to musi być spełniony warunek
gdzie. W - siła oporu ruchu listwy, ρ — kąt tarcia ustalaka po wycięciu listwy.
Jeżeli ustalak ma sprowadzić listwę do pozycji zaznaczonej na rys. 11.19b linią Przerywaną, to
gdzie musi być spełniony warunek α > ρ.
uwaga: we wzorach (11.18) i (11.19) nie uwzględniono oporów ruchu ustalaka w jego wadnicy;
przyjmowane wartości sil czynnych powinny być zatem większe niż obliczone.
Jeżeli natomiast ustalak ma pełnić obie wyżej wymienione funkcje, wtedy kąt rozwarcia wycięcia a będzie
zawarty w przedziale ρ < α < 90° — ρ. W praktyce konstrukcyjnej dopuszcza się 15° < α < 75°; zwykle α =
45°, 60°.
38
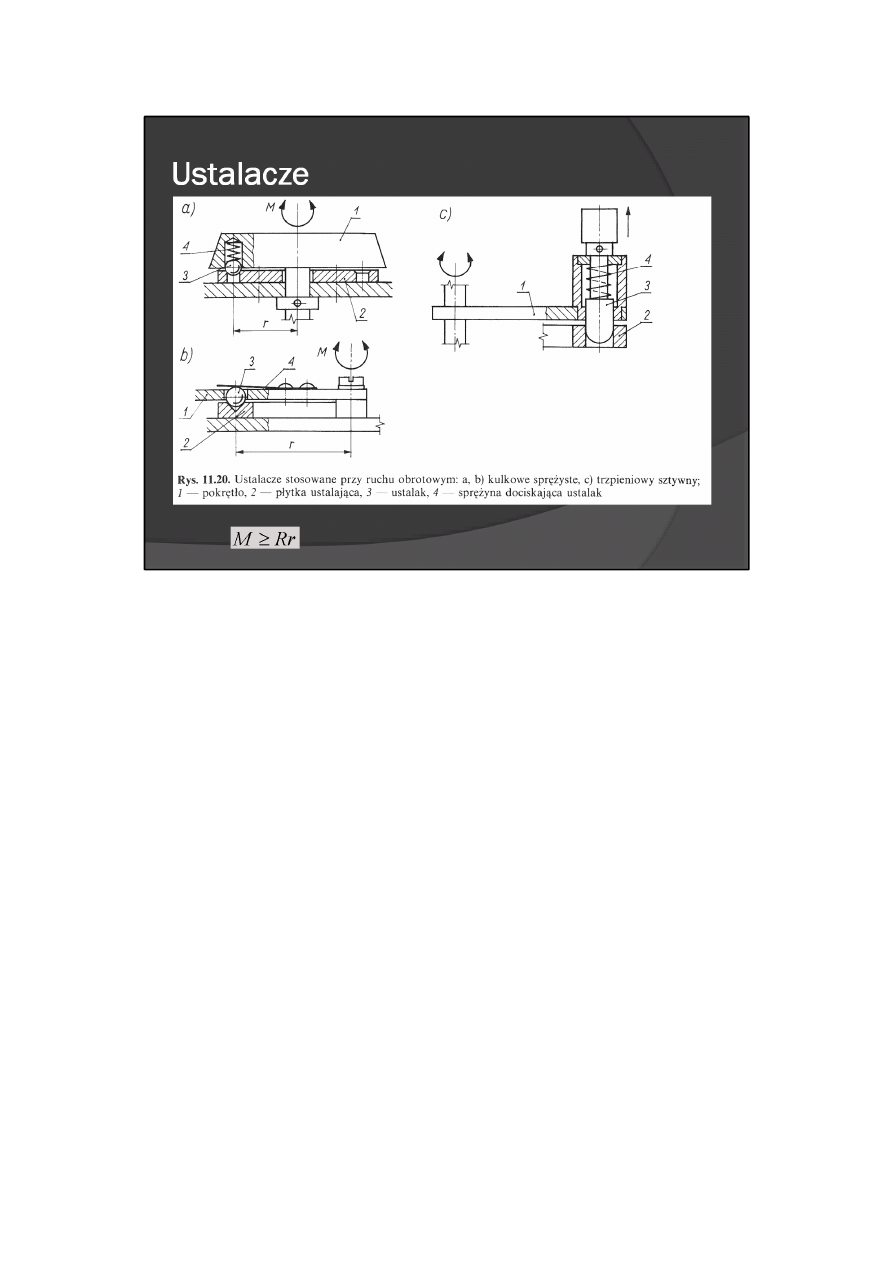
Przykłady ustalaczy przedstawiono na rys. 11.20. Ustalacze kulkowe (rys. 11.20a, b) umożliwiają zmianę
położenia po przyłożeniu momentu
Zmiana położenia w ustalaczu (rys. 11.20c) jest możliwa dopiero po odciągnięciu ustalaka w kierunku
zaznaczonym strzałką.
39
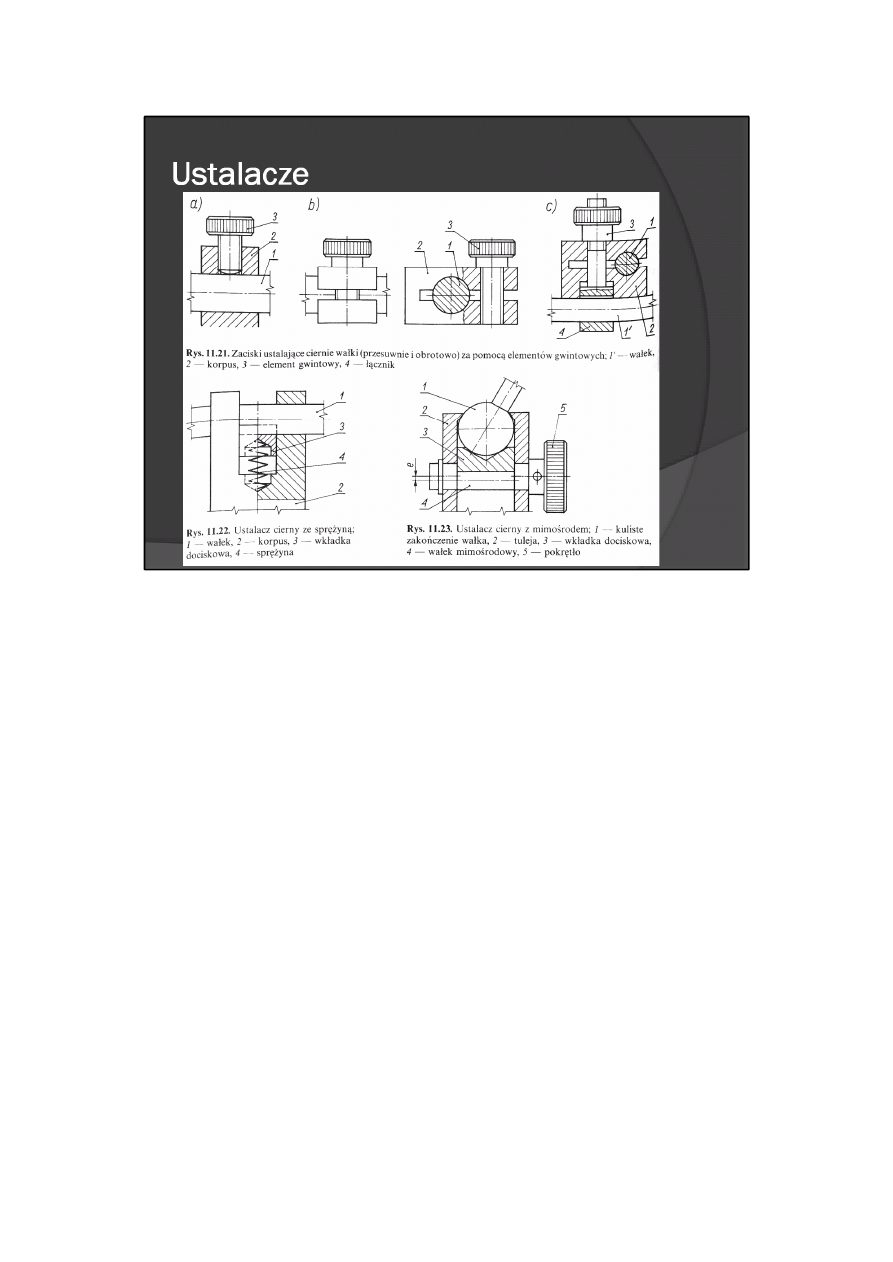
Ustalacze cierne (zaciski) służą do ustalenia elementów względem siebie w dowolnym położeniu z siłą lub
momentem wynikającymi z tarcia. Wymagany jest zatem docisk ustalanych elementów za pomocą
elementów gwintowych (rys. 11.21), sprężyny (rys. 11.22) lub mimośrodu (rys. 11.23).
40
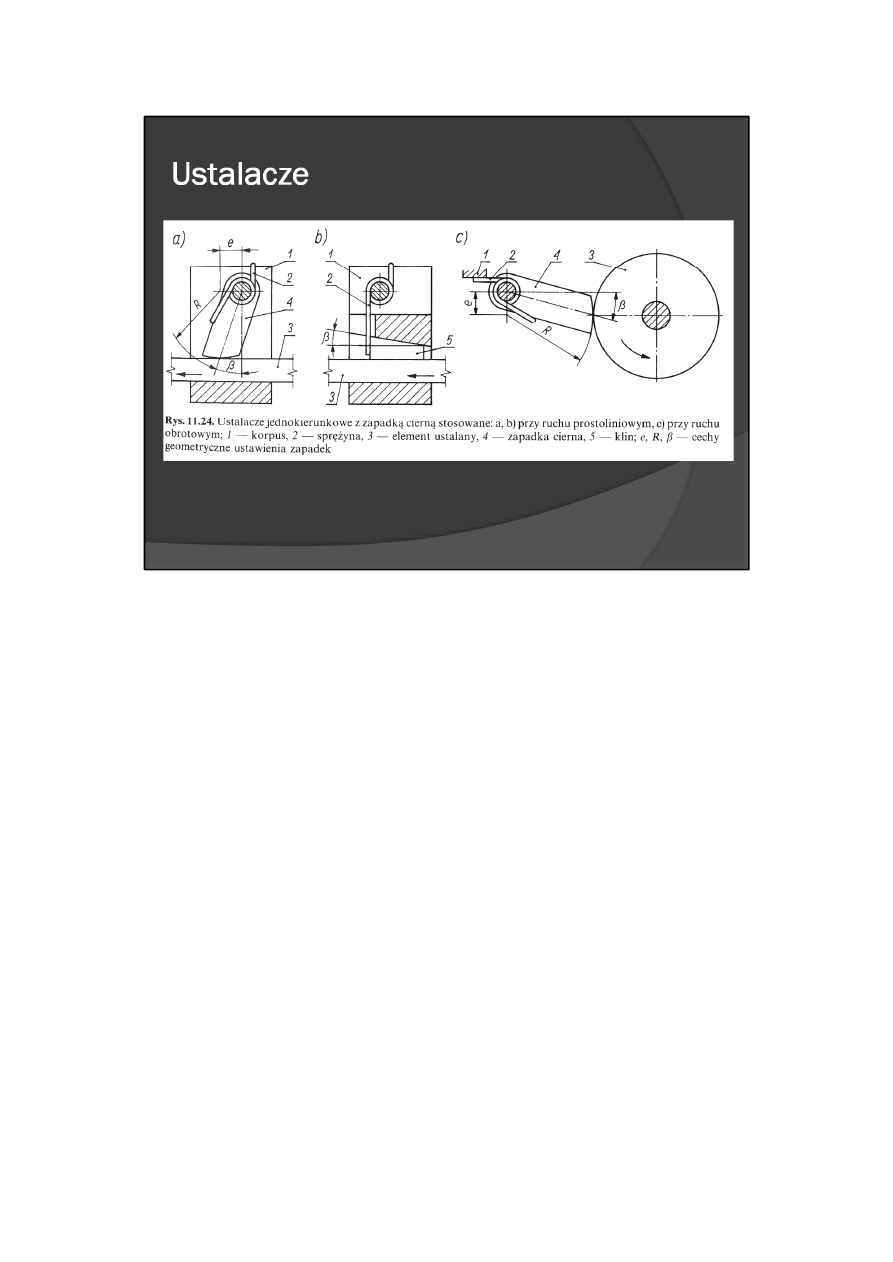
W celu ustalenia elementu przy jednokierunkowym obciążeniu czynnym można zastosować zapadki cierne
(rys. 11.24), które samoczynnie odwodzą się przy ruchu elementu ustalanego w kierunku strzałki.
Zakleszczenie zapadki ciernej następuje wtedy, gdy β < ρ, gdzie ρ — kąt tarcia.
41
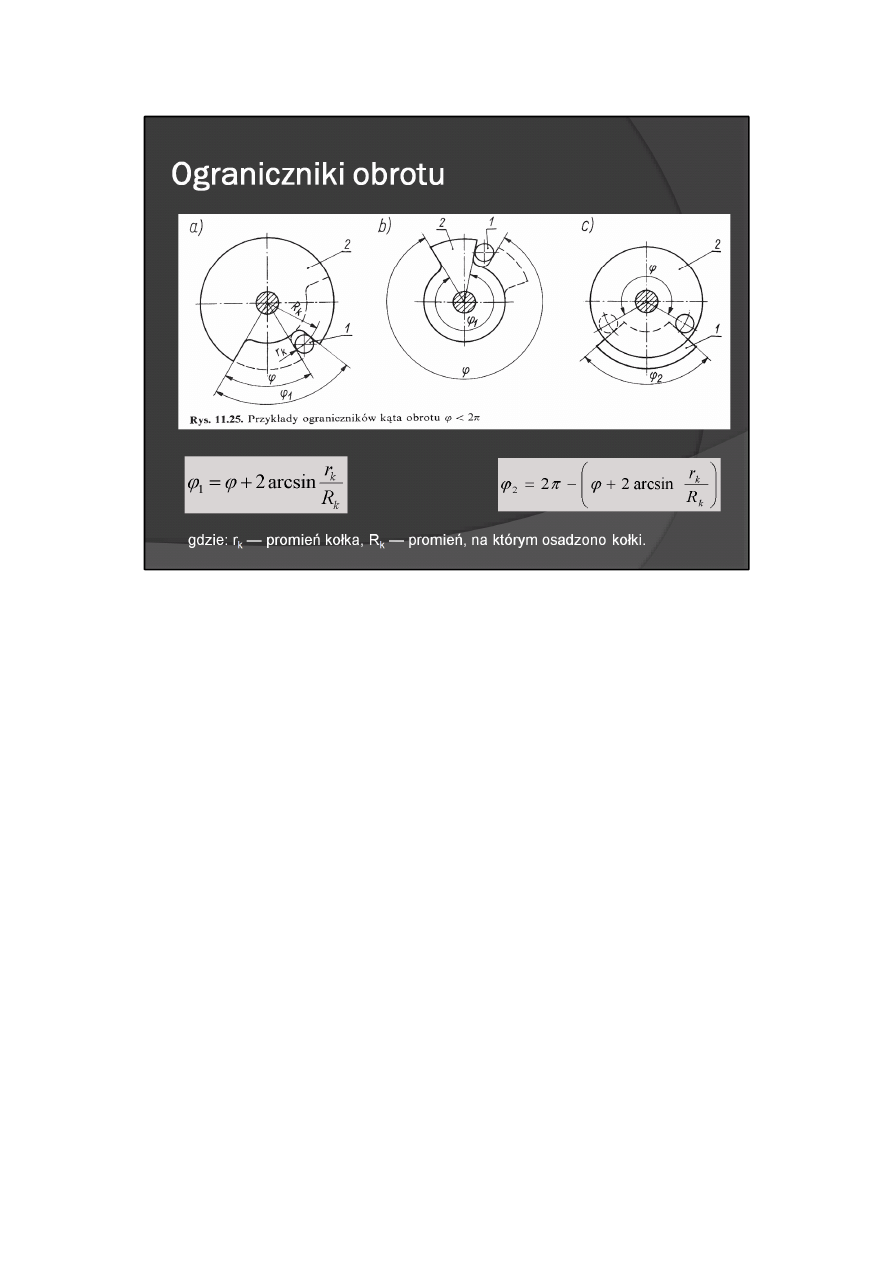
Ograniczniki obrotu
W celu zapewnienia wałkowi żądanego kąta obrotu ψ, należy zastosować ogranicznik obrotu. W
przypadku gdy ψ < 2π (rys. 11.25) ograniczniki obrotu mają postać zderzaków 2, zamocowanych na wałku,
współpracujących ze zderzakami 1, zamocowanymi w nieruchomym korpusie. Przy założonym kącie
obrotu ψ wałka, kąt wycięcia ψ
1
zderzaka (w postaci tarczy zamocowanej na wałku) wynosi (rys. 11.25a)
Zaś kąt ψ
2
płytki zderzakowej (rys. 11.25b)
gdzie: r
k
— promień kołka, R
k
— promień, na którym osadzono kołki.
42
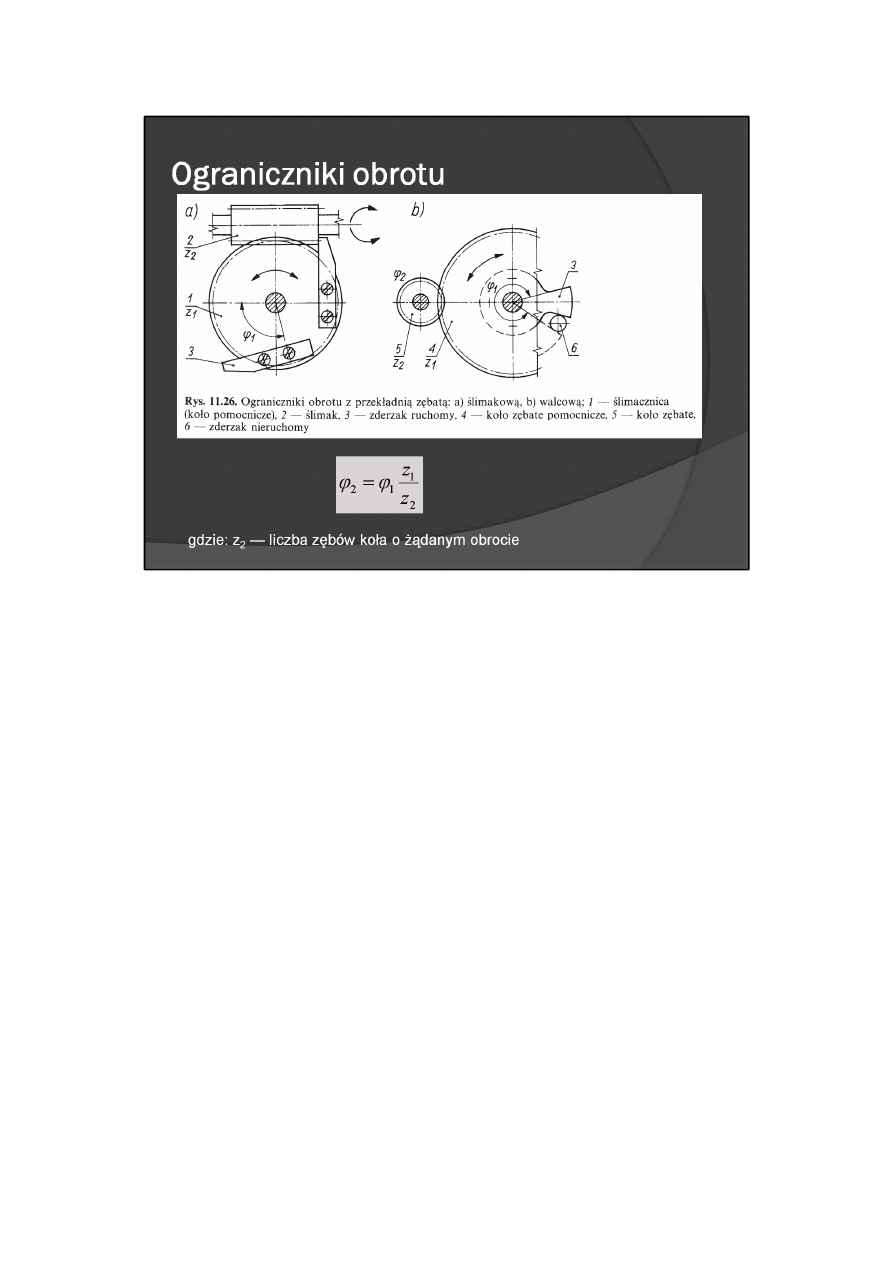
Jeżeli kąt obrotu ψ > 2π, wtedy w ogranicznikach obrotu można wykorzystać przekładnie zębate (rys.
11.26). Żądany kąt ψ
2
obrotu ślimaka bądź koła zębatego uzyskuje się przez wybór takiego kąta obrotu
ψ1<2π pomocniczego koła zębatego, o liczbie zwojów z
1
, przy którym jest spełniony warunek
gdzie: z
2
— liczba zębów koła o żądanym obrocie
43
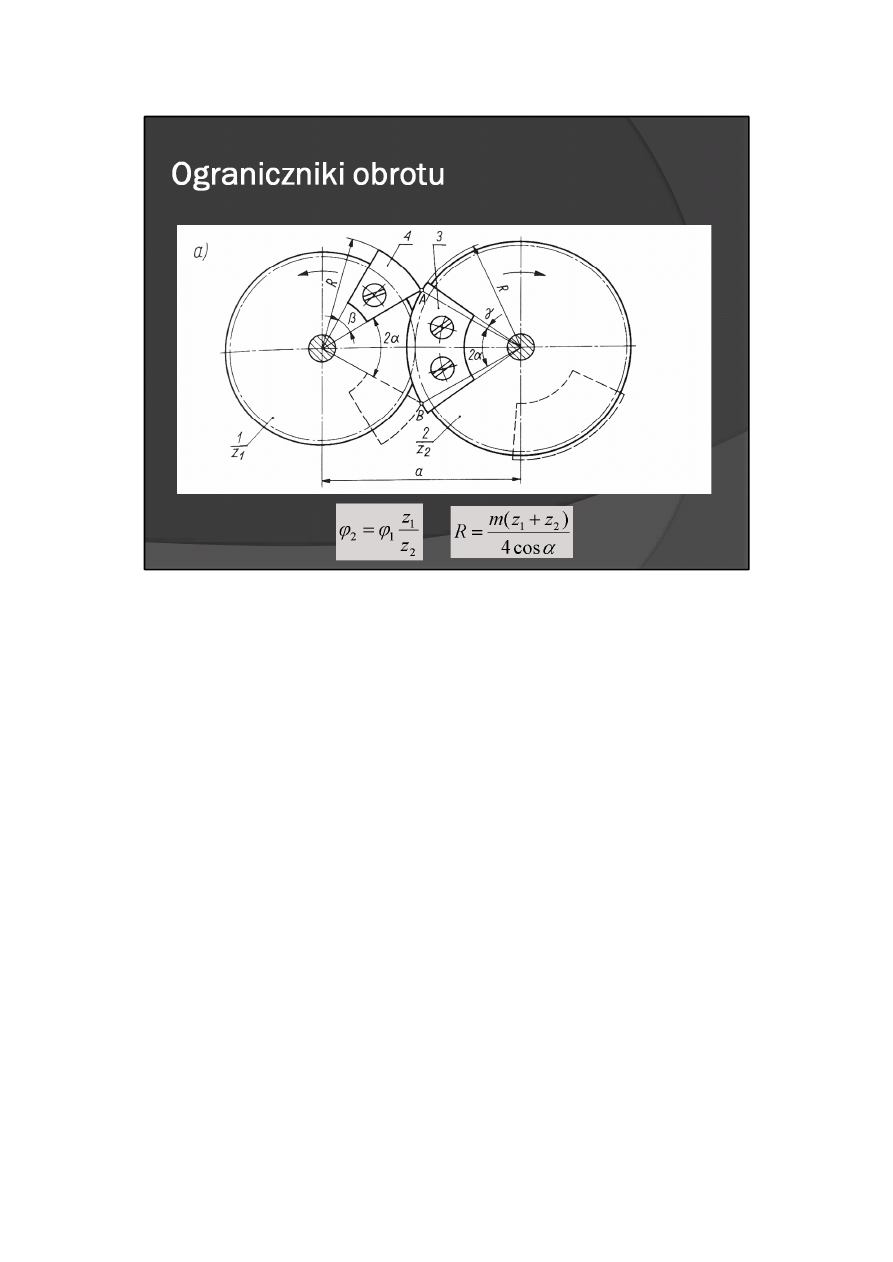
W innym rozwiązaniu konstrukcyjnym ogranicznika obrotu (rys. 11.27) przewidziano umieszczenie na
współpracujących kołach zębatych 1 i 2, o różnej liczbie zębów (z
1
< z
2
), segmentów łukowych 3 i 4, o
zewnętrznym promieniu R. Zakładając, że koło 2 ma wykonać całkowitą liczbę obrotów n
2
, należy tak
dobrać kąt β i kąty rozwarcia segmentów (2α + 2γ) (zwykle przyjmuje się kąt γ równy kilka stopni
kątowych) oraz przyjąć takie całkowite liczby zębów z
1,
z
2
współpracujących kół, aby była zachowana
równość
Promień zewnętrzny zderzaków R można obliczyć z zależności : |
gdzie: m — moduł kół zębatych, α — kąt przyporu.
44
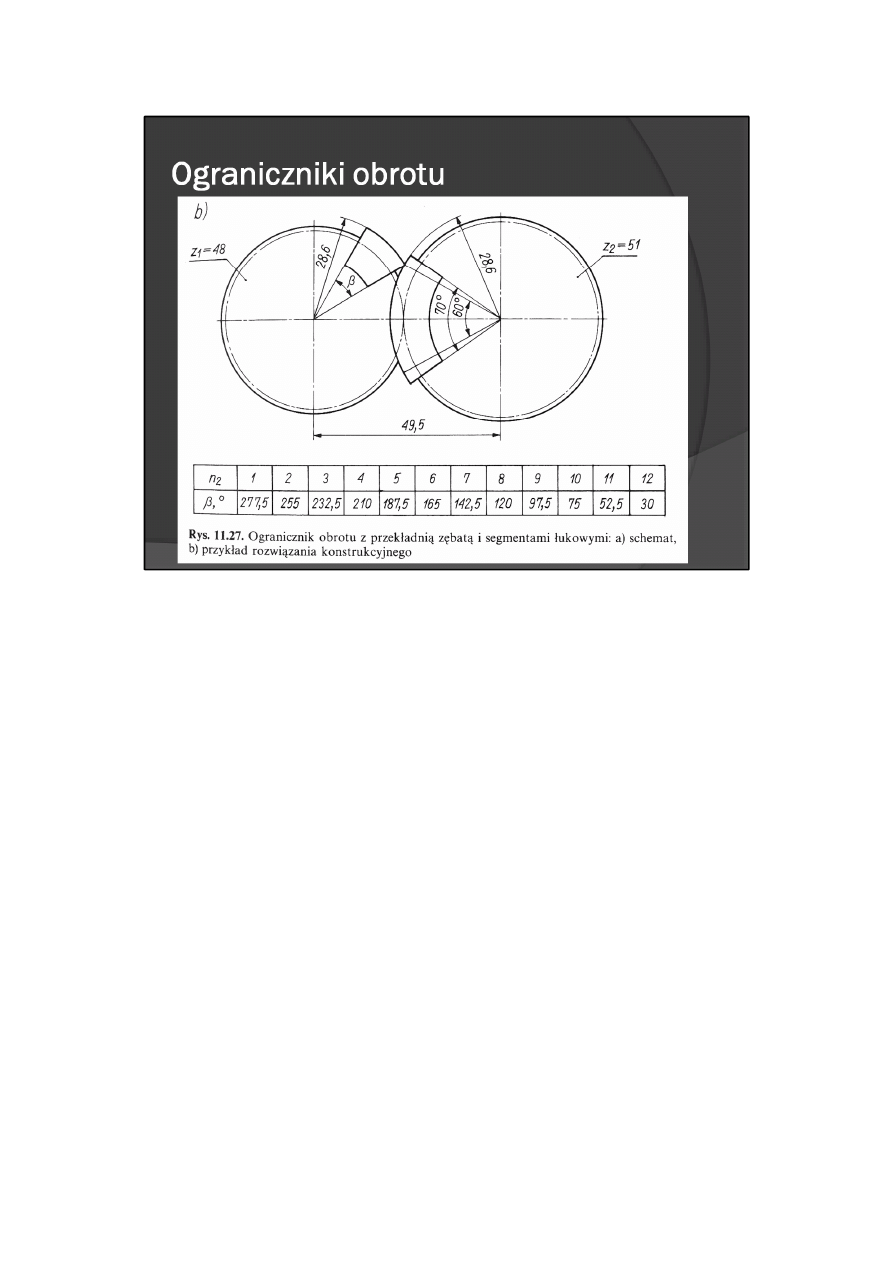
Przykładowe wymiary elementów ogranicznika obrotów zapewniających uzyskanie liczby obrotów 1 ≤ n
2
≤
12, z wykorzystaniem kół zębatych o znormalizowanym zarysie i module m = 1 mm, przedstawiono na rys.
11.27b.
45
Wyszukiwarka
Podobne podstrony:
Podstawy konstruowania urządzeń precyzyjnych 10
Podstawy konstruowania urządzeń precyzyjnych 09
Podstawy konstruowania urządzeń precyzyjnych 01
Podstawy konstruowania urządzeń precyzyjnych 11
Podstawy konstruowania urządzeń precyzyjnych 04
Podstawy konstruowania urządzeń precyzyjnych 03
Podstawy konstruowania urządzeń precyzyjnych 05
Podstawy konstruowania urządzeń precyzyjnych 08
Podstawy konstruowania urządzeń precyzyjnych 09
Podstawy konstruowania urządzeń precyzyjnych 11
Podstawy konstruowania urządzeń precyzyjnych 09
Podstawy konstruowania urządzeń precyzyjnych 08
Podstawy konstruowania urządzeń precyzyjnych 05
Podstawy konstruowania urządzeń precyzyjnych 01
Podstawy konstruowania urządzeń precyzyjnych 03
Podstawy konstruowania urządzeń precyzyjnych 04
podstawy konstrukcji urządzeń cyfrowych i mikroprocesorowych
Projektowanie i Konstrukcja Urządzeń, Ściąga, Funkcje konstruowania urządzeń- podstawową funkcja kon
13 Określanie konstrukcji wybranych urządzeń precyzyjnych
więcej podobnych podstron