1

BLOK II

PRAWA DOTYCZĄCE BIEGU PROMIENI ŚWIETLNYCH
ODBICIE ŚWIATŁA
Zjawisko odbicia zachodzi, gdy wiązka światła pada na powierzchnię odbijającą. Odbicie (regularne, czyli zwierciadlane) polega na zmianie kierunku
rozchodzenia się fali świetlnej na granicy środowisk bez jej przejścia do drugiego środowiska.

Prawo odbicia mówi, że kąt odbicia równy jest kątowi padania i oba te kąty leżą w jednej płaszczyźnie prostopadłej do powierzchni odbijającej
w miejscu padania fali.
Fala odbita niesie zazwyczaj tylko część energii fali padającej. Stosunek energii fali odbitej do padającej nazywamy współczynniki em odbicia fali
świetlnej r:

o

r

I

I

r



gdzie I

0

oznacza natężenie fali padającej, a I

r

— natężenie fali odbitej.

Współczynnik ten może być wyrażany również w procentach.
Jeżeli I

0

jest równe I

r

, zachodzi tak zwane całkowite odbicie. Powierzchnię odbijającą w ten sposób nazywamy doskonałym zwierciadłem.

ZAŁAMANIE ŚWIATŁA
Załamanie promienia świetlnego zachodzi, gdy światło pada na granicę dwóch przezroczystych ośrodków, z których każdy ma inną przepuszczalność
(tzn. fale świetlne mają w nim inną prędkość).

Promień padający pod kątem α do tzw. normalnej padania (umowna linia prostopadła do powierzchni, na którą pada światło) po przejściu granicy
ośrodków zmienia kierunek i biegnie pod kątem β.
Kąt β wzrasta ze wzrostem kąta α, kąty te jednak nie są do siebie proporcjonalne. Wprost proporcjonalne są do siebie sinusy kątów α i β.
Iloraz sinusów tych dwóch kątów jest stały dla każdego układu dwóch środowisk. Jest on nazywany względnym współczynnikiem załamania światła n
środowiska drugiego względem pierwszego (n

1→2

).

2

1

sin

sin





n





Wykazane zostało, że wartość współczynnika n jest zarazem ilorazem prędkości światła w ośrodku pierwszym do prędkości światła w ośrodku drugim.
Jest to prawo załamania światła:

2

1

2

1





n

v

v

Z powyższego zapisu wynika, że:

1.

gdy n > 1, to prędkość światła w ośrodku pierwszym jest większa od prędkości światła w ośrodku drugim, czyli ośrodek drugi jest op-
tycznie gęstszy (np. przejście z powietrza do wody). W tym przypadku kąt α jest większy od kąta β. Światło załamuje się do normalnej
padania.

2.

gdy n < 1, to prędkość światła w ośrodku pierwszym jest mniejsza od prędkości światła w ośrodku drugim, czyli ośrodek drugi jest op-
tycznie rzadszy (np. przejście ze szkła do powietrza). W tym przypadku kąt α jest mniejszy od kąta β. Światło załamuje się od normal-
nej padania.

Jeżeli środowiskiem pierwszym jest próżnia, a drugim dowolna inna substancja, na której granicę pada światło, współczynnik załamania wynosi:

substancji

w

światla

.

.

v

c

n

subst

pr





Dla dowolnej substancji współczynnik n jest w takim przypadku większy od zera, ponieważ w żadnym środowisku światło nie ma prędkości większej
niż w próżni. Współczynnik ten nazywamy bezwzględnym współczynnikiem załamania światła.

Na podstawie wartości tego współczynnika możemy przewidzieć zachowanie się promienia na granicy dowolnych dwóch środowisk. Im większy n, tym
większa optyczna gęstość środowiska, a zatem przechodząc ze ośrodka o mniejszym n do ośrodka o n większym światło będzie załamywało się do nor-
malnej padania — i odwrotnie.
Względny współczynnik załamania światła n

1→2

na granicy między tymi środowiskami obliczamy ze wzoru:

1

2

2

1

n

n

n





gdzie n

2

i n

1

są bezwzględnymi współczynnikami załamania światła obu ośrodków.

UKŁADY I PRZYRZĄDY OPTYCZNE

SOCZEWKI CIENKIE
Soczewkami nazywamy ciała przezroczyste ograniczone dwoma wycinkami powierzchni zakrzywionych. Najczęściej są to powierzchnie kuliste. Środki
tych powierzchni kulistych (O

1

i O

2

) nazywamy środkami krzywizn soczewki, a promienie (r

1

i r

2

) — promieniami krzywizny. Uważamy je za dodatnie,

jeżeli rozpatrywana powierzchnia jest wypukła, a za ujemne w przypadku powierzchni wklęsłej. Jedna z powierzchni soczewki może też być płaska —
wówczas odpowiedni promień uważamy za nieskończenie wielki. Prosta przechodząca przez punkty O

1

i O

2

jest nazywana główną osią optyczną so-

czewki.

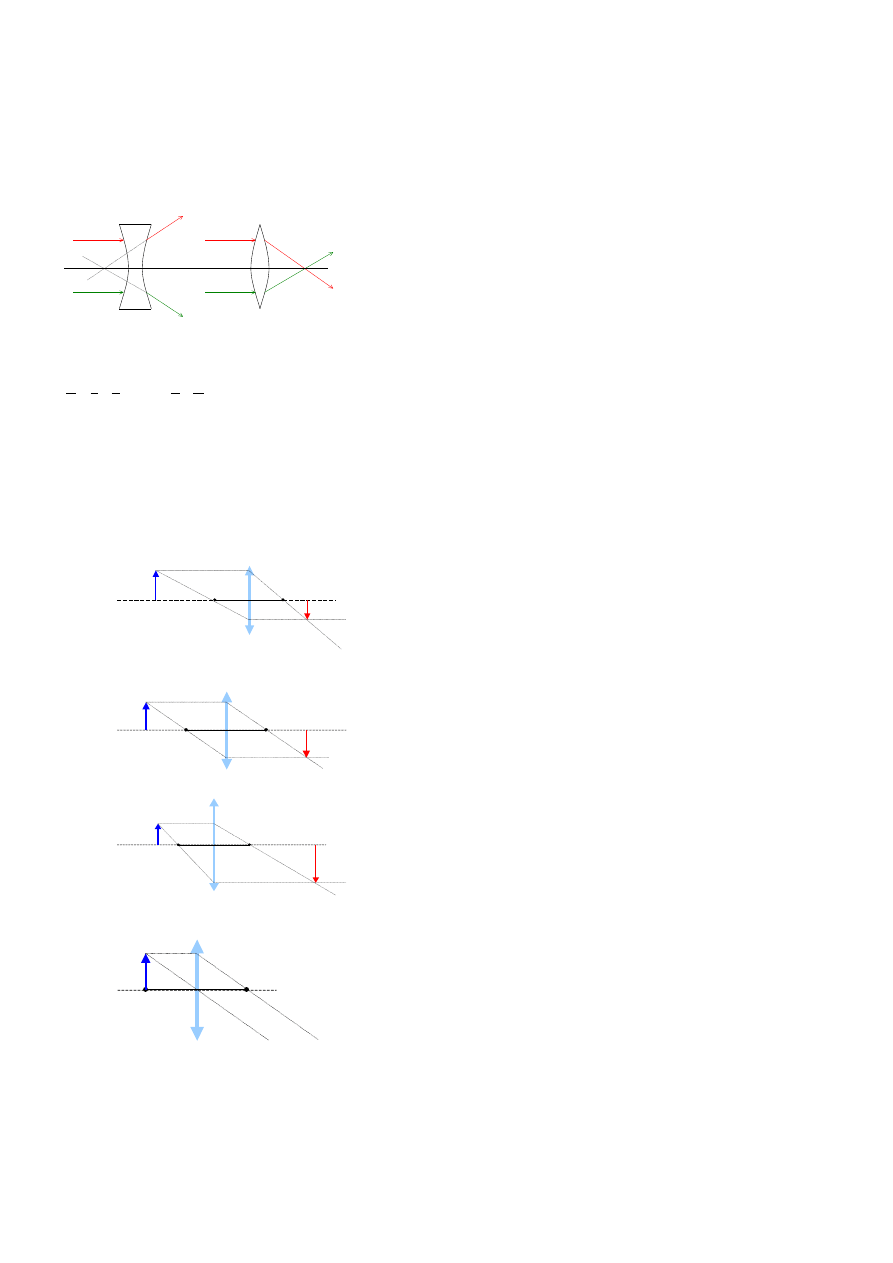
Jeżeli na dwuwypukłą soczewkę, np. szklaną, ustawioną w powietrzu rzucimy wiązkę światła równoległą do osi optycznej, to po załamaniu stanie się
ona wiązką zbieżną i wszystkie załamane promienie przetną oś optyczną w ognisku F. Taką soczewkę nazywamy skupiającą — ma ona dwa ogniska,
znajdujące się na osi optycznej symetrycznie po obu jej stronach.

α

β

powierzchnia odbijająca

Kolorem czerwonym oznaczono pro-
mień padający, kolorem zielonym pro-
mień odbity, linią przerywaną — nor-
malną powierzchni odbijającej.

2

W analogicznej sytuacji soczewka dwuwklęsła przekształci wiązkę równoległą w rozbieżną. Promienie załamane nie przetną się po wyjściu z soczewki.
Przecinają się jednak ich przedłużenia, tworząc na osi optycznej po przeciwnej stronie tzw. ognisko pozorne F’. Taką soczewkę nazywamy rozprasza-
jącą. Podobnie jak poprzednia, ma ona dwa symetrycznie rozmieszczone ogniska pozorne.
Warto dodać, że po umieszczeniu soczewki w środowisku o współczynniku załamania większym od materiału, z którego ją wykonano, jej właściwości
optyczne ulegają zmianie — soczewka dwuwklęsła skupia promienie świetlne, soczewka dwuwypukła zaś rozprasza je.
Każda soczewka posiada ponadto pewien szczególny punkt, leżący na osi optycznej i mający taką właściwość, że biegnący przezeń promień świetlny
nie zmienia swojego kierunku. Nazywamy go optycznym środkiem soczewki (O). Nie musi on znajdować się wewnątrz soczewki (jest tak np. w so-
czewkach wypukło-wklęsłych i wklęsło-wypukłych).
Odległość OF lub OF’ nazywamy ogniskową soczewki f. Ogniskowa jest wielkością charakteryzującą każdą soczewkę. Zależy od niej wzajemny sto-
sunek odległości przedmiotu (x) i jego obrazu (y) od soczewki. Ogniskowa soczewki skupiającej jest dodatnia, rozpraszającej — ujemna.

Ze względu na grubość soczewki dzielimy na cienkie i grube. Soczewkami cienkimi nazywamy takie, których grubość jest mała w porównaniu z czynną
średnicą i z ogniskową soczewki. Wzajemne zależności wartości x, y i ogniskowej f dla tych soczewek charakteryzuje następujący wzór, nazywany
wzorem soczewkowym:



























2

1

1

1

1

1

1

1

r

r

n

y

x

f

gdzie f jest ogniskową soczewki,
x — odległością przedmiotu od środka optycznego soczewki;
y — odległością obrazu od środka optycznego soczewki;
n — względnym współczynnikiem załamania światła soczewki względem ośrodka otaczającego;
a r

1

i r

2

są promieniami krzywizny soczewki.

KONSTRUKCJA OBRAZÓW W SOCZEWKACH CIENKICH
Na wszystkich poniższych rysunkach kolorem ciemnoniebieskim oznaczony został przedmiot, a kolorem czerwonym — jego obraz. Ogniska soczewki
zaznaczone są kropkami na osi optycznej.
Soczewki skupiające:

1.

Przedmiot znajduje się w odległości x > 2f od optycznego środka soczewki:

Uzyskany obraz jest: rzeczywisty (znajduje się po przeciwnej stronie soczewki niż przedmiot), pomniejszony i odwrócony.

2.

Przedmiot znajduje się w odległości x = 2f od optycznego środka soczewki:

Uzyskany obraz jest: rzeczywisty, naturalnej wielkości i odwrócony.

3.

Przedmiot znajduje się w odległości 2f > x > f od optycznego środka soczewki:

Uzyskany obraz jest: rzeczywisty, powiększony i odwrócony.

4.

Przedmiot znajduje się w odległości x = f od optycznego środka soczewki:

Obraz nie powstaje. Przedmiot znajduje się w jednym z ognisk soczewki. Po przejściu przez soczewkę promienie biegną równolegl e do sie-
bie i nigdzie się nie przecinają.

5.

Przedmiot znajduje się w odległości x < f od optycznego środka soczewki:

F

F’

3

Uzyskany obraz jest: pozorny (znajduje się po tej samej stronie soczewki, co przedmiot), powiększony i prosty.

Soczewki rozpraszające:

Uzyskany obraz jest: pozorny, pomniejszony i prosty.

ZDOLNOŚĆ SKUPIAJĄCA SOCZEWKI I UKŁADU SOCZEWEK
Zdolnością skupiającą (zbierającą) lub rozpraszającą soczewki nazywamy następującą wielkość D:

f

D

1



Zdolność skupiająca soczewki może być dodatnia (soczewki skupiające) lub ujemna (soczewki rozpraszające). Jej wartość wyrażamy w dioptriach (D).
Liczba dioptrii jest równa odwrotności ogniskowej (wyrażonej w metrach).

 

1

1

1







m

D

D

Zdolność skupiająca układu wielu soczewek cienkich, umieszczonych tuż obok siebie, jedna za drugą, na wspólnej osi optycznej, jest sumą zdolno-
ści zbierających poszczególnych soczewek (które mogą przyjmować wartości zarówno dodatnie, jak i ujemne):







n

i

ukl

D

D

1

Jeżeli natomiast układ stanowią dwie soczewki cienkie ustawione w odległości d od siebie, to jego zdolność skupiającą wyrażamy wzorem:

2

1

2

1

D

dD

D

D

D







MIKROSKOP OPTYCZNY — BUDOWA I ZASADA DZIAŁANIA

Układ optyczny mikroskopu tworzą w zasadzie dwie soczewki zbierające, których środki leżą na wspólnej osi optycznej. Soczewki te noszą nazwy
obiektywu i okularu.
Obiektyw jest soczewką o krótkiej (rzędu kilku milimetrów) ogniskowej, okular — soczewką o ogniskowej dłuższej (rzędu kilku centymetrów). Dzięki
odpowiedniemu ustawieniu obu tych soczewek względem siebie, przedmiot obserwowany umieszczony w niewielkiej odległości od obiektywu może
zostać powiększony od kilkudziesięciu do około dwóch tysięcy razy.
Schemat obserwacji przedmiotu w mikroskopie optycznym jest następujący:



Przedmiot obserwowany umieszczamy przed obiektywem w odległości x

1

(2f

ob

> x

1

> f

ob

) i uzyskujemy obraz rzeczywisty, powiększony i

odwrócony.



Uzyskany w obiektywie obraz staje się przedmiotem powiększanym przez okular.



Obraz ten znajduje się przed okularem w odległości x

2

(x

2

< f

ok

), w wyniku uzyskujemy zatem obraz pozorny, powiększony i prosty.



Obraz uzyskany w mikroskopie (obiektyw + okular) jest pozorny, powiększony i odwrócony. Po wybiegnięciu z okularu promienie za-
łamują się na siatkówce oka obserwatora, dając w efekcie obraz rzeczywisty.

Bieg promieni w mikroskopie optycznym przedstawia się następująco:

Mniejszą soczewką na obrazie jest obiektyw, którego ogniskowa zaznaczona jest kropkami na osi optycznej.
Większa soczewka to okular, którego ogniskową zaznaczono na osi optycznej kwadracikami.
Kolorem niebieskim zaznaczony został przedmiot obserwowany.
Kolorem zielonym — obraz powstały w obiektywie, a zarazem przedmiot powiększenia okularu.
Kolorem czerwonym — obraz uzyskany w okularze, czyli widziany przez obserwatora w mikroskopie.

POWIĘKSZENIE MIKROSKOPU
Powiększenie P mikroskopu jest iloczynem powiększeń obiektywu i okularu. Wyrażamy je wzorem:

ok

ob

ok

ob

f

f

d

L

P

P

P











gdzie P

ob

jest powiększeniem obiektywu,

P

ok

— powiększeniem okularu

f

ob

— ogniskową obiektywu

4

f

ok

— ogniskową okularu

L — długością tubusu, czyli odległością między obiektywem a okularem
d — tzw. odległością dobrego widzenia (około 25 cm).


ZDOLNOŚĆ ROZDZIELCZA MIKROSKOPU
Uzyskiwanie coraz znaczniejszych powiększeń oglądanych przedmiotów powoduje postępujące zmniejszanie wyrazistości szczegółów ich budowy.
Zjawiska dyfrakcyjne, zachodzące na drobnych elementach preparatu, powodują bowiem zniekształcenie odwzorowania.
Zdolnością rozdzielczą D mikroskopu nazywamy odwrotność najmniejszej odległości d dzielącej na powierzchni przedmiotu obserwowanego dwa

punkty, które na obrazie możemy rozróżnić jeszcze jako oddzielne.

d

D

1



FOTOMETRIA

DEFINICJA FOTOMETRII. RODZAJE ŹRÓDEŁ ŚWIATŁA.
Fotometrią nazywamy dziedzinę fizyki zajmującą się pomiarami energii przenoszonej przez fale świetlne i wielkościami związanymi z tą energią.
Źródła światła w fotometrii dzielimy na punktowe i rozciągłe. Źródłem punktowym nazywamy takie, którego odległość od obserwatora lub przyrządu
pomiarowego jest na tyle duża, aby można było powiedzieć, że energia świetlna z nich emitowana rozchodzi się równomiernie we wszystkich kieru n-
kach w postaci fali kulistej. Źródła rozciągłe z kolei emitują światło nierównomiernie, w zależności od miejsca na powierzchni i kierunku; rzecz jasna,
każde źródło punktowe obserwowane z bliska staje się źródłem rozciągłym.

WIELKOŚCI FOTOMETRYCZNE



Światłość źródła (I) — dawniej nazywana natężeniem źródła światła).
Jest to wielkość, charakteryzująca źródło światła pod względem energetycznym. Wyrażamy ją w kandelach (1 cd). Kandela jest jedną z jednostek
podstawowych w układzie SI, a jej naukowa definicja to: światłość, jaką ma w kierunku prostopadłym powierzchnia 1/600 000 m

2

promiennika

zupełnego w temperaturze krzepnięcia platyny pod ciśnieniem 101 325 Pa.
Warto dodać, że światłość źródła rozciągłego zmienia się w zależności od kąta obserwacji proporcjonalnie do cos α (gdzie α oznacza kąt zawarty
między kierunkiem obserwacji a normalną do powierzchni obserwowanej).



Strumień świetlny (Ф).
Wielkość ta wiąże się ze światłością źródła, a wyraża się wzorem:











I

gdzie I oznacza światłość źródła mierzoną w kandelach,
a ∆ω— kąt bryłowy, w którym rozchodzi się strumień.
Jednostką strumienia świetlnego jest lumen (1 lm). Jest to strumień świetlny wysyłany w kącie bryłowym 1 steradiana przez umieszczone w
wierzchołku tego kąta punktowe, emitujące izotropowo źródło światła o światłości 1 kandeli.
Strumień świetlny można mierzyć także ilością energii przechodzącej w jednostce czasu przez powierzchnię S znajdującą się w polu świetlnym, a
więc wyrażać go w watach.
Na podstawie wzoru definiującego strumień świetlny możemy obliczyć światłość źródła:









I

Zauważmy, że dla źródła punktowego o światłości 1 cd strumień świetlny emitowany w pełnym kącie bryłowym wynosi 4π lumenów. Jeżeli ma-
my do czynienia ze źródłem rozciągłym, jego światłość oceniamy dzieląc je na drobne (w przybliżeniu punktowe) elementy powier zchniowe i ob-
liczając z powyższego wzoru światłość każdego z nich. Otrzymane wartości światłości następnie sumujemy.



Luminancja (B) — inaczej zwana blaskiem lub jasnością powierzchniową.
Luminancja jest wielkością służącą do fotometrycznego opisu źródeł rozciągłych. Luminancję charakteryzuje promieniowanie, które rozpatrywana
powierzchnia wysyła w określonym kierunku.
Rozpatrzmy powierzchnię S, emitującą w danym kierunku promieniowanie o światłości I. Rzut tej powierzchni na płaszczyznę prostopadłą do te-
go kierunku nazwijmy S’. Luminancją powierzchni S źródła rozciągłego nazwiemy stosunek światłości I do wielkości S’. Obliczamy ją, znając
wielkość powierzchni S oraz wartość kąta α pomiędzy normalną do niej a wybranym kierunkiem promieniowania.



cos

'

S

I

S

I

B





Jednostką luminancji jest kandela na metr kwadratowy. Jest to luminancja powierzchni o światłości 1 cd, jeżeli powierzchnia rzutu S’ prostopa-
dła do wyróżnionego kierunku wynosi 1 m

2

.

Luminancji dotyczy jedno z praw fotometrycznych, prawo Lamberta, mówiące, że luminancja powierzchni emitującej jest niezależna od kąta, pod
jakim tę powierzchnię obserwujemy. Jest to zrozumiałe, ponieważ światłość źródła I obserwowanego pod kątem α jest proporcjonalna co cos α, a
z drugiej strony powierzchnia świecąca, obserwowana pod tymże kątem, doznaje perspektywicznego skrótu w stosunku cos α: S’ = S cos α .



Natężenie oświetlenia (E)
Natężeniem oświetlenia nazywamy stosunek strumienia świetlnego padającego na powierzchnię S ustawioną prostopadle do kierunku strumienia,
do wielkości tej powierzchni. Jednostką natężenia oświetlenia jest luks (1 lx). Jest to natężenia oświetlenia powierzchni 1 m2, przez którą prze-
chodzi strumień świetlny o wartości 1 lm.

S

E





   

2

m

1

lm

1

lx

1





E

Podstawiając do powyższego wzoru wartość strumienia, otrzymujemy:

S

I

E







Jeżeli odległość r powierzchni oświetlanej o wielkości S od źródła światła jest na tyle duża, aby powierzchnię tę można było potraktować jako wy-
cinek kuli, w miejsce ω możemy podstawić:

2

r

S





Powstaje wówczas końcowy wzór:

2

r

I

E



Natężenie oświetlenia jest zatem wprost proporcjonalne do światłości źródła i odwrotnie proporcjonalne do kwadratu odległości między
źródłem a powierzchnią oświetlaną.
Zależność tę wykorzystujemy, porównując oświetlenie dwóch powierzchni odległych od tego samego źródła światła o r

1

i r

2

:

5

2

1

2

2

2

1

r

r

E

E



Powyższe równanie nosi nazwę prawa odwrotnych kwadratów.
Natężenie oświetlenia zależy również od kąta padania promieni na oświetlaną powierzchnię. Wyraża to zależność:

2

cos

r

I

E





.

gdzie α jest kątem pomiędzy kierunkiem padania promieni a normalną do powierzchni oświetlanej.
Jest to podstawowe prawo fotometrii, z którego wynika, że gdy światło pada na powierzchnię prostopadle (α = 0˚, cos α = 1), natężenie oświ e-
tlenia przybiera wartość maksymalną, natomiast gdy wiązka jest do powierzchni równoległa (α = 90˚, cos α = 0), natężenie oświetlenia E jest rów-
ne 0.



Naświetlenie (H), zwane też ekspozycją.
Jest to iloczyn natężenia oświetlenia E i czasu ekspozycji (oświetlania) danej powierzchni.

t

E

H





 

s

1

lx

1





H

BUDOWA I ZASADA DZIAŁANIA FOTOOGNIWA
Wiele urządzeń stosowanych we współczesnej technice pomiarowej wykorzystuje korpuskularny charakter wiązki świetlnej. Podstawą działania części
tych urządzeń są zjawiska fotoelektryczne. Zachodzą one, gdy wiązka światła o określonej energii pada na jakąś powierzchnię. Może wówczas nastąpić
przekazanie całej energii fotonu jednemu z elektronów substancji naświetlanej, co powoduje albo opuszczenie powierzchni tej substancji przez elektron
(zjawisko fotoelektryczne zewnętrzne), albo oderwanie tego elektronu od atomu, lecz bez jego wyjścia poza obręb substancji — zachodzi wówczas
zwiększenie jej przewodnictwa (zjawisko fotoelektryczne wewnętrzne). Może również występować tzw. efekt fotowoltaiczny, polegający na powstawa-
niu różnicy potencjałów na złączu dwóch półprzewodników lub metalu i półprzewodnika.
Fotoogniwo jest urządzeniem, wykorzystującym w swoim działaniu zjawisko fotoelektryczne wewnętrzne, zjawisko powstawania kontaktowej różnicy
potencjałów oraz szczególne własności przewodzące półprzewodników (tzw. przewodnictwo elektronowo-dziurowe). Jego budowa przedstawia się na-
stępująco: jest to naniesiony na metalową płytkę, pełniącą rolę elektrody, półprzewodnik, pokryty cienką warstwą drugiego półprzewodnika lub metalu.
Do całości podłączony jest obwód, w którym po zamknięciu może płynąć prąd fotoelektryczny.

Obszar oznaczony zygzakowatą linią oznacza warstwę półprzewodnika.
Obszar zakreskowany ukośnie oznacza warstwę pokrywającego go metalu lub drugiego półprzewodnika.
Strzałki (hv) wskazują kierunek padania promieni świetlnych.
W najczęściej stosowanym fotoogniwie selenowym układ półprzewodnik – metal składa się z cieniutkiej (rzędu 0,1 mm) warstewki selenu, na którą na-
pylona jest przezroczysta dla światła warstewka ołowiu lub srebra (czasem można spotkać także inne metale). Po oświetleniu takiej powierzchni od
strony metalu, pary elektron – dziura (czyli ładunek ujemny i odpowiadający mu ładunek dodatni) znajdujące się w półprzewodniku są rozdzielane na
skutek istnienia kontaktowej różnicy potencjałów na złączu. Powstaje w ten sposób SEM fotoelektryczna, która po zamknięciu ob wodu zewnętrznego
powoduje przepływ prądu, zwanego prądem fotoelektrycznym. Natężenie tego prądu jest (w pewnym zakresie) proporcjonalne do natężenia światła pa-
dającego na powierzchnię fotoogniwa. Natężenie to dla różnych materiałów może wynosić od kilku do kilkudziesięciu mikroamperów na lumen.
W fotoogniwach następuje bezpośrednie przetworzenie energii świetlnej w elektryczną. Sprawność tego procesu osiąga nawet do 15%! Ma to szczegól-
ne znaczenie przy konstrukcji baterii słonecznych, zaopatrujących w energię zarówno urządzenia naziemne, jak i statki, sondy kosmiczne itp. Zastoso-
wania fotoogniw są zresztą bardzo rozległe — mogą one zastępować fotokomórki próżniowe, są stosowane w fotometrii obiektywnej w takich przyrzą-
dach pomiarowych, jak fotometry, luksomierze i fotokolorymetry, posługujemy się nimi także w kinie dźwiękowym i noktowizji.

RUCH FALOWY

DEFINICJA FALI
Falą nazywamy proces rozchodzenia się zaburzeń w środowisku. Część przestrzeni objętą w danej chwili zaburzeniem nazywamy polem falowym.
Powierzchnię, na której we wszystkich punktach zaburzenie ma tę samą fazę, nazywamy powierzchnią fali. Powierzchnię falową, odgraniczającą pole
falowe od niezaburzonego jeszcze środowiska nazywamy czołem fali. Kierunek rozchodzenia się energii niesionej przez falę nazywamy promieniem
fali. Element przestrzeni, który wysyła zaburzenia, nazywamy źródłem fali.
W zależności od kierunku drgań cząsteczek ośrodka lub innych zmian parametrów fali fale dzielimy na podłużne i poprzeczne. O pierwszych mówimy,
gdy drgania te są równoległe do kierunku rozchodzenia się fali, o drugich — gdy drgania te są prostopadłe do tego kierunku. Większość fal nie jest jed-
nak ani podłużna, ani poprzeczna — drgania nie zachodzą wzdłuż prostych, lecz np. po okręgach, elipsach i krzywych jeszcze bardziej skomplikowa-
nych. Mówimy wówczas o drganiach złożonych (ze składowych podłużnych i poprzecznych).
Wśród fal wyróżniamy elektromagnetyczne i mechaniczne. Te z kolei podzielić możemy na płaskie (takie, dla których powierzchnia falowa jest linią
prostą), koliste (takie, których powierzchnia falowa jest okręgiem) i kuliste (takie, których powierzchnia falowa jest sferą). Podział ten jest oczywiście
przybliżony. Powierzchnia falowa, jak wspomniano wyżej, może być jakąkolwiek krzywą lub powierzchnią; czasami, gdy mamy do cz ynienia ze źró-
dłem fali o nieregularnym kształcie, przypominający je kształt powierzchni fali również jest całkowicie nieregularny. W miarę oddalania się od źródła
fala stopniowo traci jego kształt, a zbliża się formą do kuli. W dostatecznie dużej odległości niewielkie wycinki powierzchni falowych kulistych można
traktować jako fale płaskie.

PARAMETRY OKREŚLAJĄCE FALĘ



Długością fali λ nazywamy odległość liczoną wzdłuż promienia między sąsiednimi punkami będącymi w tej samej fazie drgań.



Prędkością fazową fali v nazywamy prędkość rozchodzenia się danej fazy zaburzenia w środowisku.



Okresem T nazywamy czas, w którym cząstka drgająca wykona pełne drganie (lub inny parametr po całkowitej okresowej przemianie powróci do
położenia początkowego) .



Częstością fali υ nazywamy odwrotność okresu, czyli ilość zmian położenia cząstki drgającej (lub innego parametru) przypadającą na jednostkę
czasu.

Powyższe parametry łączymy w jedno zależnością:

hv

E
L
E
K
T
R
O
D
A

SCHEMAT
FOTOOGNIWA

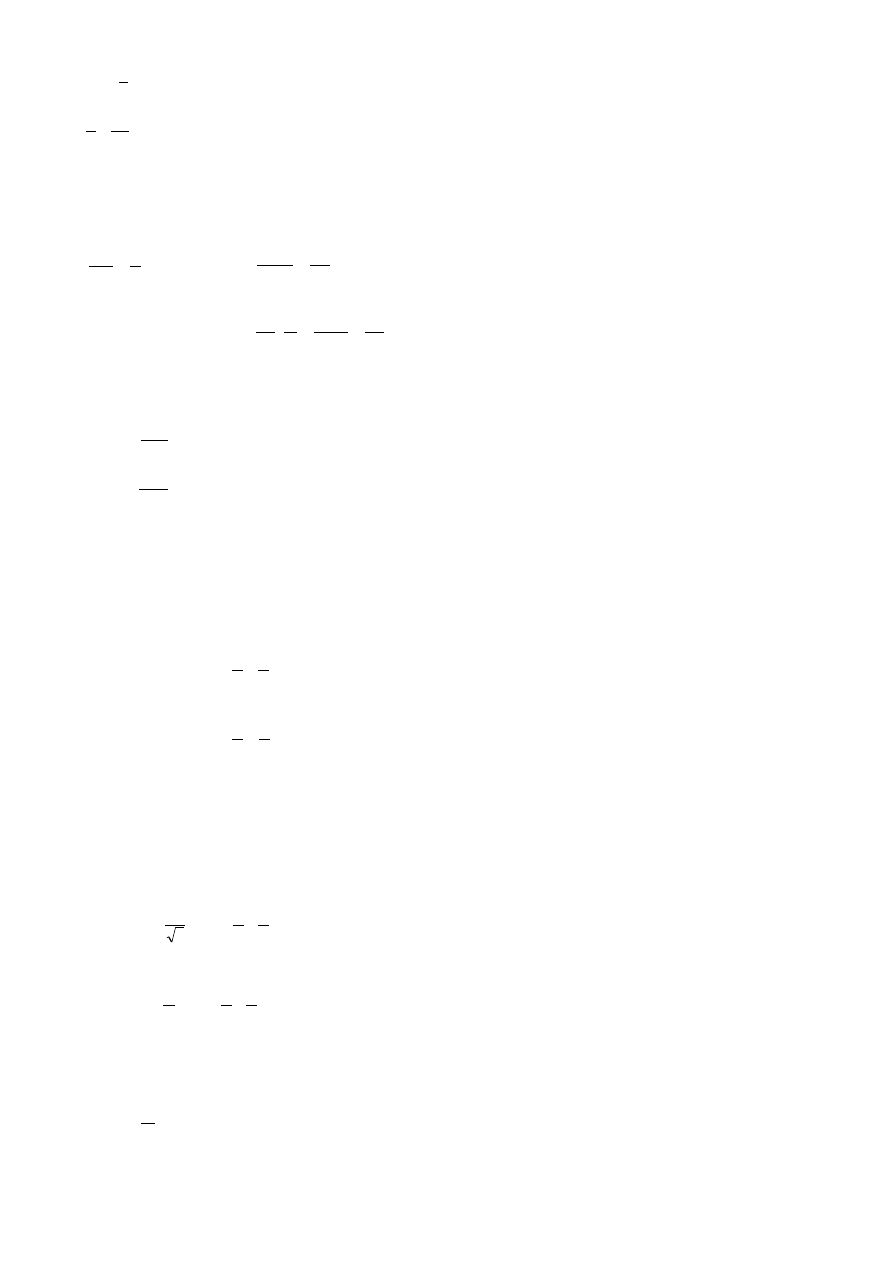
6





v

vT





Jeżeli wprowadzimy do niej częstość kołową drgań źródła fali ω = 2πυ, możemy przedstawić ją w postaci:







2





T

v

Widzimy zatem, że częstość fali zależy od częstości drgań jej źródła.
Prędkość rozchodzenia się fali zależy od właściwości środowiska. Zależność tej prędkości od częstości fali nazywamy dyspersją, a środowisko, w któ-
rym ta zależność zachodzi, nazywa się dyspersyjnym. Pod względem prędkości rozchodzenia się fali środowiska podzielić możemy na izotropowe (ta-
kie, w których fala rozchodzi się z jednakową prędkością w każdym kierunku) i anizotropowe (takie, w których prędkość fali jest różna w zależności
od wybranego kierunku).
Wielkością charakteryzującą energię fali jest natężenie (I). Mierzy się je ilością energii przechodzącej w jednostce czasu przez jednostkową powierzch-
nię ustawioną prostopadle do promienia fali (albo inaczej jednostką mocy źródła fali przechodzącej przez tę powierzchnię).

S

P

t

S

E

I







 

2

2

m

W

s

m

J

I







Natężenie fali możemy określić również posługując się pojęciem gęstości energii w, którą określamy jako ilość energii (np. kinetycznej i potencjalnej
ruchu drgającego) zawartej w jednostce objętości, i prędkością fali v:

wv

I



 

2

2

3

m

W

s

m

J

s

m

m

J

I











Ponieważ prędkość fali jest wielkością wektorową, natężenie fali również możemy traktować jako wektor, którego kierunek i zwr ot są zgodne z kierun-
kiem przenoszenia energii (promieniem fali).
Warto zauważyć, że natężenie fali płaskiej rozchodzącej się w środowisku nieabsorbującym (przezroczystym) jest stałe. W tych samych warunkach na-
tężenia fal dwu- i trójwymiarowych maleją, gdyż niesiona przez falę ilość energii rozkłada się na coraz to większą powierzchnię.
W przypadku fali kolistej natężenie wyniesie:

rt

E

I



2



,

a w przypadku fali kulistej:

t

r

E

I

2

4





gdzie jako r oznaczamy promień okręgu lub sfery.

RÓWNANIE FALI MECHANICZNEJ
Jeżeli w polu falowym parametry określające stan środowiska zmieniają się periodycznie i sinusoidalnie, to fale takie nazywamy sinusoidalnymi lub harmonicz-
nymi. Wychylenie Ψ takiej fali, będące funkcją czasu, opisać możemy równaniem., które nazywamy równaniem fali sinusoidalnej.



Równanie fali płaskiej.
Równanie to opisuje wartość wychylenia wybranego punktu fali (oddalenie punktu od położenia równowagi) po upływie określonego czasu t od roz-

poczęcia drgań. Przyjmujemy oczywiście, że w chwili rozpoczęcia drgań punkt znajdował się w położeniu równowagi. Kierunek rozchodzenia się fali
nakładamy na oś x układu współrzędnych, wartość wychylenia mierzymy na osi y.

Równanie fali płaskiej będzie wyglądało nieco inaczej w zależności od tego, w którym kierunku biegnie fala.

Jeżeli przyjmiemy, że zaburzenie rozchodzi się „w prawo”, czyli zgodnie z dodatnim zwrotem osi x, równanie fali płaskiej przy biera postać:

 











 











x

T

t

A

t

x

2

sin

,

Jeżeli zaburzenie rozchodzi się „w lewo”, czyli zgodnie z ujemnym zwrotem osi x, wartości prędkości fali (będącej oczywiście wektorem), należy
przypisać wartość ujemną. Zmienia to postać równania w następujący sposób:

 











 











x

T

t

A

t

x

2

sin

,

Wielkości występujące w powyższych wzorach oznaczają:

Ψ — wychylenie punktu
λ — długość fali
x — odległość punktu od źródła fali
T — okres drgań punktu
A — amplituda drgań.



Równanie fali kolistej.
Dla fali dwuwymiarowej pojawia się dodatkowa współrzędna przestrzenna — fala nie rozchodzi się już w jednym kierunku, lecz w pewnej płaszczyź-
nie. Kolejne powierzchnie falowe są okręgami o coraz większych promieniach.
Równanie takiej fali ma postać:











 









r

T

t

r

A

t

r

2

sin

)

,

(

Zauważmy, że odległość x punktu od źródła fali, występująca w równaniu fali płaskiej, została zastąpiona promieniem r powierzchni falowej.



Równanie fali kulistej.

Fala kulista jest falą trójwymiarową. Powierzchnia falowa ma kształt sfery — zaburzenie rozchodzi się we wszystkich kierunkach przestrzeni.











 









r

T

t

r

A

t

r

2

sin

)

,

(

ODBICIE I ZAŁAMANIE FAL
Jeżeli fale biegnące w określonym środowisku napotykają na swojej drodze gładką powierzchnię graniczną innego środowiska, w którym prędkość fali jest różna
od prędkości w środowisku pierwszym, to na tej granicy zachodzą zjawiska odbicia i załamania fal.
Odbicie polega na zmianie kierunku rozchodzenia się fali padającej na granicę środowisk, przy czym fala odbita pozostaje w środowisku pierwotnym. Zazwyczaj
fala odbita niesie tylko część energii fali padającej. Stosunek energii fali odbitej do padającej nazywamy współczynnikiem odbicia fali r:

o

r

I

I

r



gdzie I

0

oznacza natężenie fali padającej, a I

r

— natężenie fali odbitej.

Współczynnik ten może być wyrażany również w procentach.

7

Jeżeli I

0

jest równe I

r

, zachodzi tak zwane całkowite odbicie. Powierzchnię odbijającą w ten sposób nazywamy doskonałym zwierciadłem.

Wartość r dla fal mechanicznych zależy od tzw. oporów akustycznych obu środowisk. Oporem akustycznym ośrodka nazywamy iloczyn gęstości ośrodka ρ i
prędkości fali v w tym ośrodku. Jeżeli opory akustyczne obydwu środowisk są jednakowe, odbicie fali nie zachodzi.
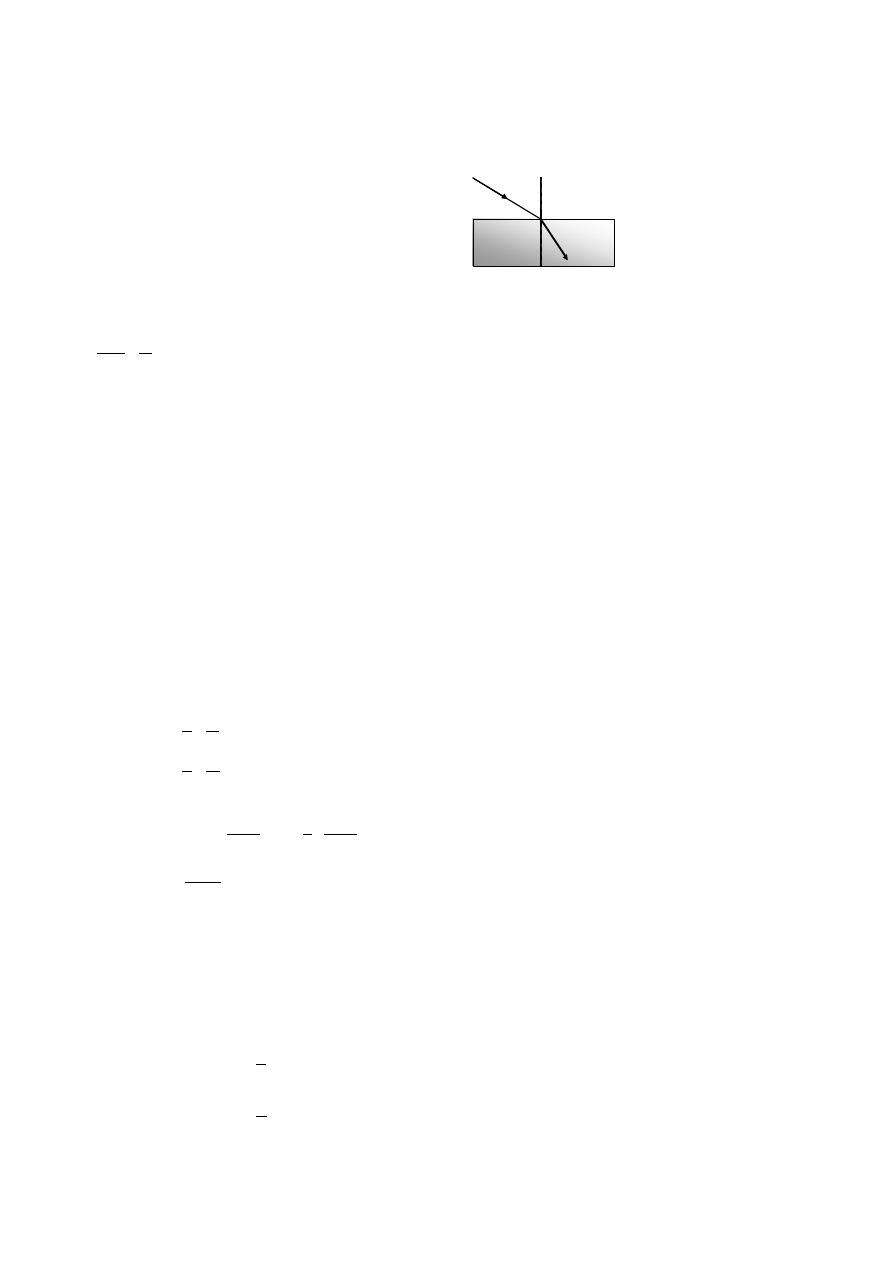
Prawo odbicia głosi, że kąt odbicia jest równy kątowi padania i oba te kąty leżą w jednej płaszczyźnie przechodzącej przez prostopadłą do powierzchni
odbijającej w miejscu padania fali (tzw. normalną).
Podczas odbicia może nastąpić skokowa (o π) zmiana fazy fali odbitej. Następuje ona wówczas, gdy fala odbija się od środowisk a o większym oporze akustycz-
nym lub takiego, w którym jej prędkość jest mniejsza niż w środowisku, w którym biegła do tej pory.

Załamanie zachodzi, gdy fala padająca na granicę środowisk przechodzi
z jednego do drugiego z nich. Zmienia się wówczas jej kierunek
rozchodzenia się (wyjątek stanowi przypadek, gdy kąt padania jest
równy zeru).

Promień padający pod kątem α do tzw. normalnej padania
(umowna linia prostopadła do powierzchni, na którą pada fala)
po przejściu granicy ośrodków zmienia kierunek i biegnie pod kątem β.
Kąty te nie są do siebie proporcjonalne, choć kąt β wzrasta ze wzrostem
kąta α.Dowiedziono jednak, że proporcjonalne do siebie są ich sinusy.
Prawo załamania orzeka, że stosunek sinusa kąta padania α do kąta załamania β dla danej pary środowisk jest wielkością stałą, tzn. że nie zależy od war-
tości obu kątów i równa się stosunkowi prędkości fali w środowisku 1 (tym, w którym biegła przed załamaniem) do prędkości fali w środowisku 2 (tym, w którym
biegnie po załamaniu).

2

1

2

1

sin

sin









n

const

v

v





Wielkość n jest nazywana współczynnikiem załamania fali środowiska drugiego względem pierwszego. Przy przechodzeniu z jednego do drugiego środowiska
zmieniają się zarówno prędkość fali, jak i jej długość, zmianie nie ulegają natomiast jej okres i częstość.


DYFRAKCJA FAL MECHANICZNYCH
Dyfrakcja, czyli uginanie fal polega na odstępstwach od ich prostoliniowego rozchodzenia się, podobnie jak w przypadku załamania. Charakter i przyczyna tego
zjawiska są jednak zupełnie inne niż w przypadku załamania. Załamanie fal zachodzi przy przejściu fali z jednego środowiska do drugiego, dyfrakcja natomiast
polega na zmianie kształtu i kierunku rozchodzenia się fali bez zmiany ośrodka.
Zjawisko dyfrakcji fal wiąże się z zasadą Huygensa, mówiącą, że dowolny punkt pola falowego (ośrodka, w którym rozchodzi się fala płaska) może stać się
źródłem nowej elementarnej fali kolistej (na płaszczyźnie) bądź kulistej (w przestrzeni).
Ugięcie fali rozchodzącej się w środowisku jednorodnym następuje wtedy, gdy napotyka ona na swej drodze nieprzezroczystą prze szkodę odpowiednich rozmia-
rów i kształtu. Zachodzące wówczas efekty dyfrakcyjne mogą być różne dla różnych długości fali i rozmiarów przeszkody:

1.

jeżeli rozmiary przeszkody są porównywalne z długością fali, efekty dyfrakcyjne są najsilniejsze — fala płaska zostaje przekształcona w falę kulistą
lub kolistą;

2.

jeżeli rozmiary przeszkody kilkakrotnie przekraczają długość fali, dyfrakcja zachodzi jedynie na jej krawędziach;

3.

jeżeli rozmiary przeszkody wielokrotnie przekraczają długość fali, efekty dyfrakcyjne są tak znikome, że można je zaniedbać.

INTERFERENCJA FAL MECHANICZNYCH
Zjawisko interferencji występuje przy wzajemnym nakładaniu się pól falowych. Innymi słowy, jest to superpozycja fal rozchodzących się w tym samym ośrodku i
działających na te same cząsteczki.
Fale wytwarzane przez źródła o tej samej częstości drgań i stałej w czasie różnicy faz (zwłaszcza równej zeru, kiedy to faza obydwu fal jest identyczna) oraz ma-
jące jednakową amplitudę nazywamy spójnymi. Nakładaniu się fal spójnych, wyemitowanych przez dwa różne źródła, towarzyszy powstawanie nowej fali wy-
padkowej. Częstość i okres drgań tej fali są takie same, jak obu fal interferujących, inna natomiast jest jej amplituda.
Wychylenie fali wypadkowej w danym punkcie pola falowego zależy od jego odległości od obu źródeł. Rozważmy punkt P, odległy od źródła 1 o x

1

, a od źródła

2 o x

2

. Równania ruchu drgającego tego punktu po upływie określonego czasu t przedstawiają się następująco:











 









1

1

2

sin

x

T

t

A

(wychylenie fali emitowanej przez źródło 1)











 









2

2

2

sin

x

T

t

A

(wychylenie fali emitowanej przez źródło 2)

Ponieważ długość, amplituda i częstość drgań obydwu fal interferujących są jednakowe, a różnica ich faz stała, możemy połączyć obydwa ró wnania we wzorze na
wychylenie wypadkowe:



























 





















2

2

sin

2

2

cos

2

2

1

2

1

2

1

x

x

T

t

x

x

A

w

Po uproszczeniu możemy przedstawić go następująco:











 









2

2

cos

2

2

1

x

x

A

w

W zależności od wzajemnego stosunku odległości x

1

i x

2

możemy wyróżnić dwa skrajne przypadki:

1.

Jeżeli różnica (x

1

– x

2

) jest równa całkowitej wielokrotności długości fal, wyrażenie na wychylenie Ψ fali wypadkowej przybiera postać:

A

w

2





Wychylenie Ψ jest wówczas największe. Nazywamy je amplitudą fali wypadkowej — widać, że jest ona dwukrotnie większa od amplitudy drgań in-
terferujących. O punkcie, w którym wychylenie to osiąga maksymalną wartość, mówimy, że zachodzi w nim wzmocnienie fal interferujących.









n

x

x

2

1

gdzie

N

n



(warunek wzmocnienia fal interferujących).
W praktyce oznacza to, że obydwie fale interferujące w danym punkcie znajdują się w maksymalnym wychyleniu o jednakowej fazie.

2.

Jeżeli różnica (x

1

– x

2

) jest równa nieparzystej wielokrotności połówek długości fal, wyrażenie na wychylenie Ψ fali wypadkowej przybiera postać:

0

2

cos

2

























n

A

w

Wychylenie Ψ osiąga wartość 0. Mówimy wówczas, że w danym punkcie zachodzi wygaszenie fal interferujących.





2

1

2

2

1











n

x

x

gdzie

N

n



(warunek wygaszenia fal interferujących).
W praktyce oznacza to, że obydwie fale interferujące w danym punkcie znajdują się w maksymalnym wychyleniu, lecz w przeciwnej fazie.

α

β

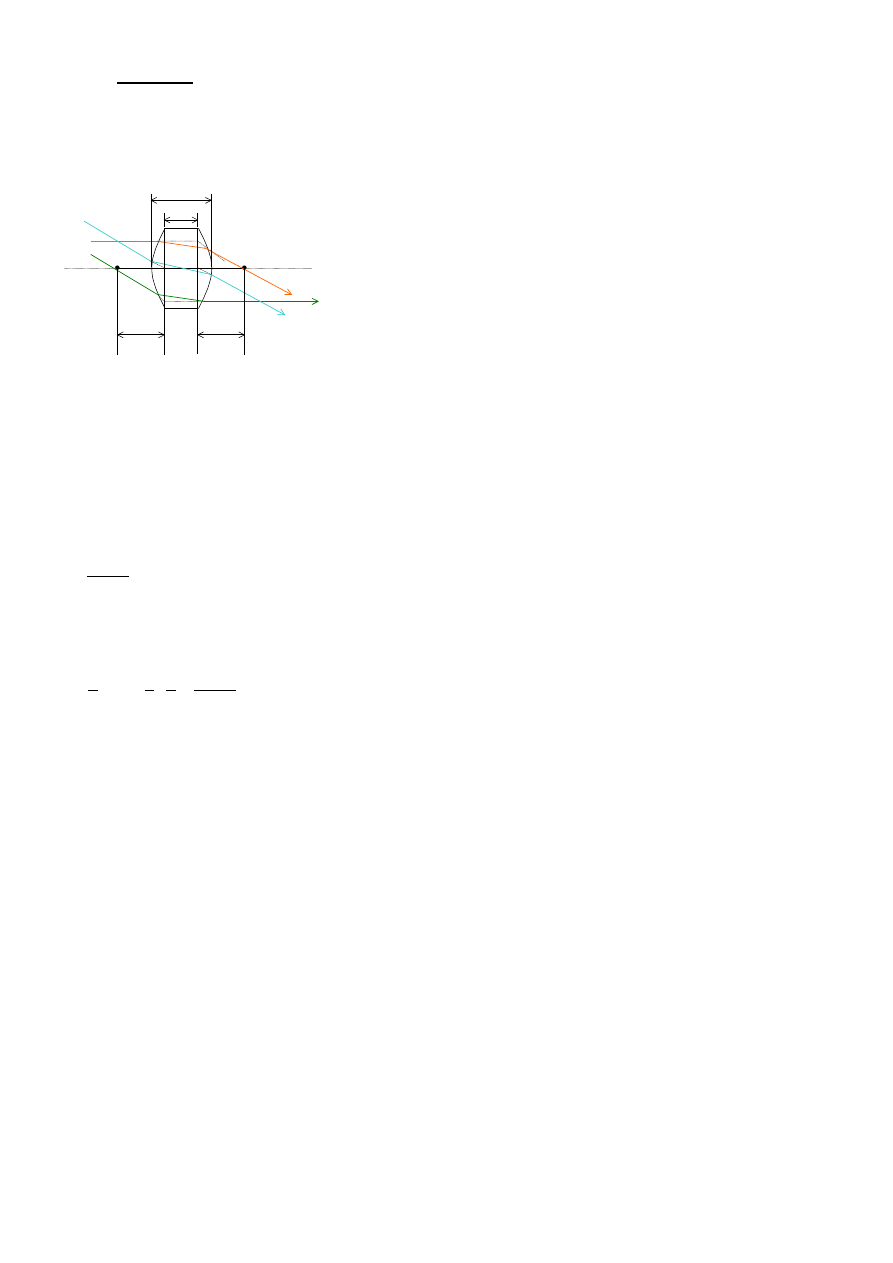
8

CZĘŚĆ B

ĆWICZENIE 21

SOCZEWKI GRUBE

Soczewki grube, czyli takie, których grubości nie można zaniedbać w porównaniu z ich średnicą i ogniskową, stanowią większość so-
czewek rzeczywistych (należy do nich m.in. soczewka oka).
Schemat biegu promieni w soczewce grubej przedstawia rysunek:

Promień 1, padający równolegle do osi optycznej soczewki, załamuje się dwukrotnie na jej powierzchniach, po czym wychodzi z niej
przez ognisko soczewki F

2

. Przedłużenia promieni padającego i wychodzącego przecinają się w punkcie C

2

. Prostopadła do osi so-

czewki poprowadzona z tego punktu przecina ją w punkcie G

2

, zwanym punktem głównym (obrazowym). Płaszczyzna poprowadzona

przez punkty C

2

i G

2

nazywana jest płaszczyzną główną (obrazową) soczewki.

Promień 2 biegnie odwrotnie do promienia 1 — przed wejściem do soczewki przechodzi przez ognisko F

1

, a wychodzi z soczewki

równolegle do osi optycznej. Z przecięcia przedłużeń promieni padającego i wychodzącego wyznaczamy punkt C

1

, a prowadząc pro-

stopadłą — punkt G

1

. Punkt G

1

nazywa się punktem głównym (przedmiotowym), a płaszczyzna poprowadzona przez punkty C

1

i G

1

—

płaszczyzną główną (przedmiotową) soczewki.
Promień 3, padający na powierzchnię soczewki tak, że jego przedłużenie przecina punkt G

1

, załamuje się w niej dwukrotnie i wychodzi

tak, że jego przedłużenie przecina punkt G

2

. Po wyjściu z soczewki biegnie zatem równolegle do swego biegu początkowego, lecz do-

znaje przesunięcia o odległość a (G

1

–G

2

). Można wykazać, że odległość ta jest zależna od grubości soczewki d oraz od współczynnika

załamania światła, co prezentuje przybliżona zależność:





n

n

d

a

1





Odległość a jest zarazem odległością, na jaką rozsunięte są ogniskowe soczewki f

1

(ogniskowa przedmiotowa) i f

2

(ogniskowa obrazo-

wa), definiowane jako odległości F

1

–G

1

i F

2

–G

2

. Ogniskowe te są sobie równe, gdy soczewka umieszczona jest w środowisku jedno-

rodnym. Jeżeli współczynniki załamania światła środowisk, w których biegną promienie świetlne przed wejściem i po wyjściu z so-
czewki, są różne, wówczas różnią się także ich ogniskowe.
Wzór soczewkowy dla soczewek grubych przybiera wartość:









2

1

2

2

1

1

1

1

1

1

r

nr

d

n

r

r

n

f

D

























gdzie f jest ogniskową soczewki (zakładamy, że soczewki umieszczona jest w jednorodnym ośrodku otaczającym);
x — odległością przedmiotu od środka optycznego soczewki;
y — odległością obrazu od środka optycznego soczewki;
n — względnym współczynnikiem załamania światła soczewki względem ośrodka otaczającego;
r

1

i r

2

są promieniami krzywizny soczewki,

a d — jej grubością.


WADY ODWZOROWAŃ SOCZEWEK I ICH KORYGOWANIE
Wady odwzorowań soczewek występują zawsze. Przyczyną tego nie są techniczne niedokładności w ich wykonaniu, lecz prawa fizyki,
z których wynika niemożność idealnie dokładnego odwzorowania pewnego skończonego obszaru przestrzeni (przedmiotu) za pomocą
wiązek światła załamanego na powierzchni kulistej.
Do najczęściej spotykanych wad soczewek należą: aberracja chromatyczna, aberracja sferyczna i astygmatyzm. Innymi spotykanymi
wadami odwzorowań są jeszcze: dystorsja, koma, krzywizna pola obrazu itp.

1.

Aberracja chromatyczna.
Wada ta jest wynikiem rozszczepiania światła białego. Wskutek tego procesu punkt wysyłający światło białe nie daje obrazu
punktowego, lecz nieskończenie wiele obrazów jednobarwnych, położonych w różnych miejscach i częściowo się pokrywa-
jących. Obraz, jaki otrzymujemy na ekranie, jest nieostrą plamką otoczoną barwną obwódką. Kolor zarówno plamki, jak i
obwódki, zależy od położenia ekranu względem soczewki.
Z praw załamania wynika, że ogniskowa soczewki dla promieni fioletowych (o mniejszej długości fali) jest krótsza, czyli że
ognisko tych promieni znajduje się bliżej, a dla promieni czerwonych (o większej długości fali) — dłuższa, co odpowiada
ognisku położonemu dalej. Miarą aberracji chromatycznej jest odległość między tymi ogniskami.
Wadę tę korygujemy, stosując układy optyczne złożone z soczewki skupiającej z lekkiego szkła potasowego (crownu, o ma-
łej dyspersji) oraz rozpraszającej ze szkła ołowiowego (flintu, o większej dyspersji). Ponieważ odchylenie promieni wywoła-
ne przez obie soczewki zachodzi w przeciwnych kierunkach, przy doborze odpowiednich wartości krzywizn i współczynni-
ków załamania rozszczepienie powodowane przez pierwszą z nich może zostać praktycznie zniesione przez drugą.

2.

Aberracja sferyczna.
Wada ta polega na tym, że w soczewce w inny sposób ulegają załamaniu promienie brzegowe i osiowe (wiązki światła bie-
gnące najdalej i najbliżej osi optycznej). Promienie brzegowe załamywane są mocniej niż osiowe, co powoduje powstanie

9

dwóch ognisk soczewki i zniekształcenie obrazu. Ulega on rozmyciu, z obrazu punktowego przekształcając się w niewyraźną
jasną plamkę.

Wadę tę możemy zmniejszać, stosując odpowiednie przesłony (diafragmy) zasłaniające brzegowe części soczewki. Powoduje
to jednak zmniejszanie ilości energii świetlnej przechodzącej przez soczewkę, co odbija się niekorzystnie na jasności obrazu.
Ponadto im mniejszy jest otwór, przez który światło przechodzi, tym bardziej znaczące stają się efekty dyfrakcyjne, sprawi a-
jące, że obraz staje się nieostry. Dlatego też lepszym sposobem niż stosowanie diafragm jest zestawianie soczewek w układy
o odpowiednio dobranych krzywiznach i wzajemnych odległościach.

3.

Astygmatyzm.

Wada ta polega na tym, że po przejściu światła przez soczewkę odwzorowaniem pojedynczego punktu stają się dwa odcinki,
wzajemnie prostopadłe i nieco od siebie nawzajem oddalone.
Astygmatyzm występuje w dwóch przypadkach. Może być spowodowany techniczną niedoskonałością soczewki — gdy jej
powierzchnie nie są idealnie kuliste, lecz np. elipsoidalne, tak że promienie krzywizny soczewki są różne w różnych płasz-
czyznach. Może również pojawiać się w wyniku skośnego w stosunku do głównej osi optycznej soczewki padania promieni
świetlnych (tzw. astygmatyzm wiązek skośnych).
Gdy promienie krzywizny soczewki są niejednakowe, w swoich różnych przekrojach ma ona różne zdolności skupiające, co
przekłada się na różne ogniskowe. Każdemu przekrojowi odpowiada zatem inny kierunek i odległość odwzorowania.
Astygmatyzm wiązek skośnych jest znacznie trudniejszy do wyeliminowania, a jego pojawianiu się nie przeciwdziała nawet
najdoskonalej kulisty kształt soczewki. Gdy promienie świetlne padają na soczewkę z punktu umieszczonego na jej osi op-
tycznej, kąt obejmujący całą jej średnicę ma dużą rozwartość, a więc krzywizna „widziana” od strony źródła światła jest
normalna. Kiedy natomiast światło pada na soczewkę z innego miejsca, promienie obejmują ją pod innym kątem, co powodu-
je, że każdy z nich przebiega przez fragment o innej pozornej krzywiźnie. Dla każdego elementu wiązki soczewka ma zatem
inną zdolność skupiającą i ogniskową. Daje to taki efekt, jak gdyby soczewka miała różne promienie krzywizny.
Ponieważ w przyrządach optycznych nie można zrezygnować z udziału wiązek skośnych w tworzeniu obrazu, celem korekcji
astygmatyzmu stosuje się układy soczewek.

UKŁAD OPTYCZNY OKA
Układ optyczny oka składa się z rogówki i soczewki oka, przy czym ośrodki optyczne graniczące z tym układem (powietrze, ciecz
wodnista i ciało szkliste) są różne, co powoduje powstawanie różnic ogniskowych obrazowych i przedmiotowych w obydwu soczew-
kach.
Głównym elementem układu optycznego oka jest soczewka. Ma ona specyficzną budowę, gdyż współczynniki załamania światła w jej
poszczególnych warstwach różnią się między sobą (przy czym największy współczynnik załamania obserwujemy w centrum, czyli w
jądrze soczewki). Ponadto dzięki napinaniu się i zwalnianiu mięśnia soczewki może się ona stawać bardziej lub mniej wypukła, czyli
zmieniać swój promień krzywizny. Zmiana tego promienia pociąga za sobą zmiany zdolności skupiającej oka, co przy praktycznie sta-
łej odległości między układem optycznym a siatkówką oka umożliwia tworzenie na siatkówce odpowiednio ostrych obrazów przed-
miotów tak bliskich, jak i dalekich. Zdolność tę nazywamy akomodacją oka.
Akomodacja oka mieści się oczywiście w pewnym zakresie i jest ograniczona skrajnymi położeniami soczewki. Gdy soczewka jest
najbardziej płaska, zdolność skupiająca oka jest najmniejsza. Rejestruje ono wówczas obraz najdalej położonego punktu, zwanego
punktem dalekim lub punktem dali (D). Gdy soczewka najmocniej się uwypukla, jej zdolność skupiająca rośnie. Na siatkówce poja-
wia się obraz najbliższego wyraźnie widzianego punktu — punktu bliskiego lub punktu bliży (B). Punkt daleki oka zdrowego czło-
wieka znajduje się w nieskończoności, punkt bliski w młodości w odległości około 10 cm (w miarę starzenia odległość ta powiększa
się wskutek sztywnienia soczewki i zmniejszania jej zdolności akomodacyjnej). W optyce często posługujemy się również inną wielko-
ścią, tak zwaną odległością dobrego widzenia, wynoszącą około 25 cm, przy której wysiłek akomodacyjny oka jest najmniejszy.

Odwrotność odległości S

D

punktu dalekiego od oka nazywana jest refrakcją oka R, mierzoną w dioptriach.

D

S

R

1



 

D

R

1



Gdy refrakcja oka jest równa zeru, tzn. S

D

→ ∞, mówimy, że oko jest miarowe. Dla oka miarowego zdolność skupiająca równa jest

refrakcji. W przypadku wad układu optycznego refrakcja staje się dodatnia lub ujemna, a jej wartość jest miarą odpowiedniej wady.

Inną wielkością związaną z odległościami punktu dalekiego i bliskiego od oka jest amplituda akomodacji oka A. Jest ona niezależna
od refrakcji, a definiujemy ją jako różnicę między odwrotnościami odległości punktu dalekiego i bliskiego:

B

D

S

S

A

1

1





Amplituda akomodacji oka maleje z wiekiem.
„Ostrość” obrazu pojawiającego się na siatkówce oka charakteryzujemy, tak jak w przypadku wszystkich innych układów optycznych,
wielkością zwaną zdolnością rozdzielczą. Przy opisie zdolności rozdzielczej oka d posługujemy się pojęciem zdolności rozdzielczej
kątowej, danej wzorem:





22

,

1

1

źr

d

d





gdzie d oznacza kątową zdolność rozdzielczą oka;
α — kąt, pod jakim widziane są ze źrenicy dwa punkty obserwowanego przedmiotu, jeszcze rozdzielane przez układ optyczny oka
(najmniejszemu kątowi odpowiadają obrazy tych punktów na dwóch sąsiadujących czopkach);
d

źr

— średnicę źrenicy;

a λ — długość fali światła.
Jak widać, kątowa zdolność rozdzielcza oka jest odwrotnością kąta α.
Wzór powyższy wynika z tak zwanego kryterium Rayleigha, które mówi, że dwa punkty są jeszcze rozdzielane przez układ op-
tyczny, gdy maksimum główne jednego z punktów pokrywa się z pierwszym minimum drugiego. Wymienione maksima i minima
odnoszą się do efektów dyfrakcyjnych, związanych z powstawaniem obrazu będącego sumą wielu nakładających się obrazów punkto-
wych.

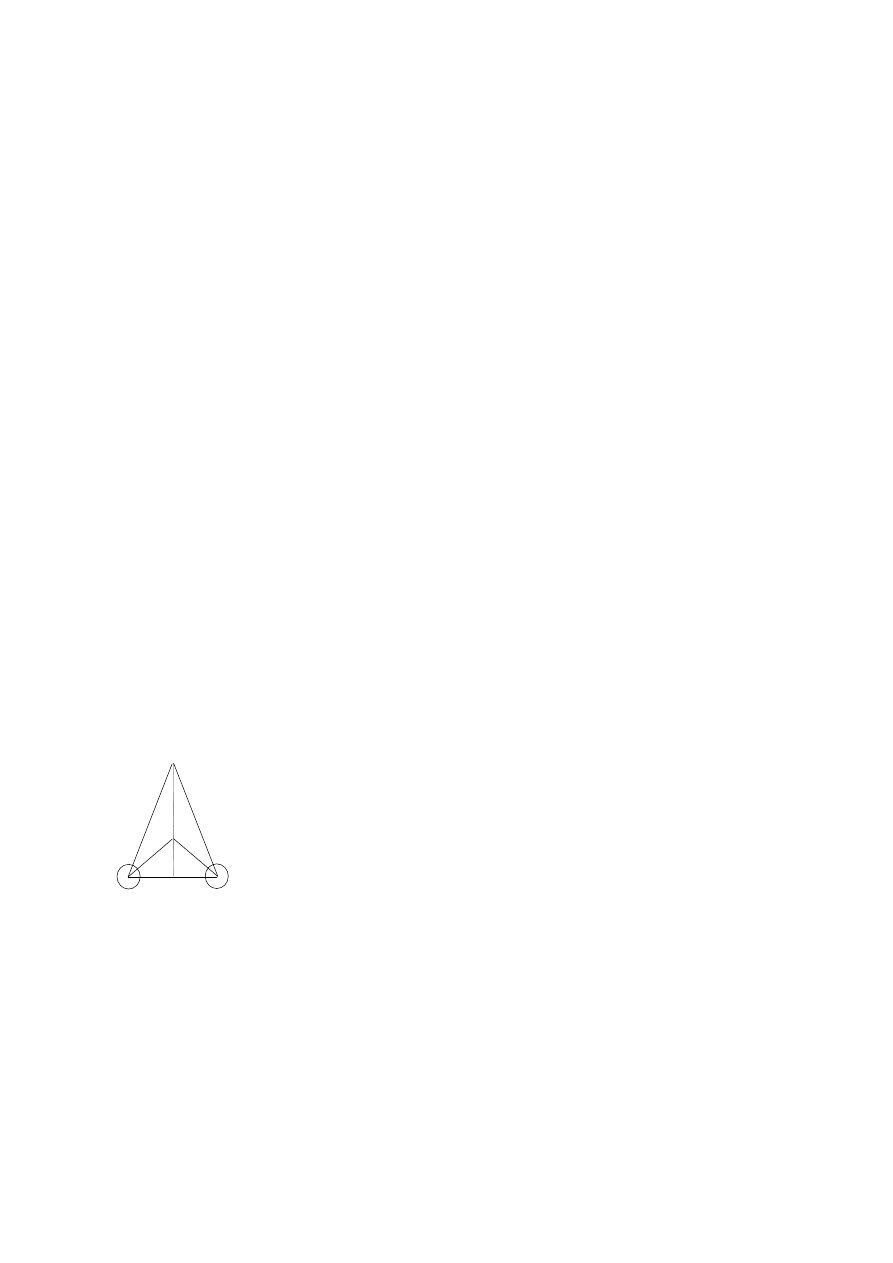
10

Zdolność rozdzielcza oka zależy od warunków oświetlenia oglądanego przedmiotu — maleje, gdy zmniejsza się natężenie oświetlenia
— a także od budowy układu optycznego oka i od czułości receptorów siatkówki.
Oko ludzkie jest narządem bardzo czułym. Może rozróżniać różne natężenia światła i barw dzięki sprawnym mechanizmom adaptacji.
Jeden z nich, o którym warto wspomnieć, to regulacja średnicy źrenicy. Źrenica jest otworem w tęczówce oka, przez który światło do-
staje się do jego wnętrza i który dzięki działaniu odpowiednich mięśni może być powiększany lub zmniejszany (odpowiednio dla świa-
tła o mniejszych i większym natężeniu). Drugi mechanizm adaptacji wiąże się z czynnością komórek światłoczułych.

WADY WZROKU I ICH KORYGOWANIE
Trzy spotykane wady wzroku, wynikające z niedoskonałości układu optycznego oka, to: krótkowzroczność, dalekowzroczność (nad-
wzroczność) i astygmatyzm.
Korekcja wad wzroku polega na dobraniu odpowiednich okularów, czyli soczewek, które załamują promienie świetlne jeszcze przed
rogówką tak, aby ich kolejne załamanie wewnątrz oka doprowadziło do powstania na siatkówce prawidłowego obrazu.

1.

Krótkowzroczność występuje, gdy promienie światła wpadające do oka są załamywane zbyt mocno, w efekcie czego ich
ognisko znajduje się przed siatkówką. Powoduje to, że przedmioty znajdujące się daleko od oka są widziane niewyraźnie.
Punkt D oka krótkowzrocznego znajduje się bliżej niż w nieskończoności, punkt B — bliżej niż u oka zdrowego. Refrakcja
oka krótkowzrocznego jest ujemna.

Wadę tę korygujemy dzięki szkłom (okularom) rozpraszającym.

2.

Dalekowzroczność jest efektem zbyt słabego załamywania światła we wnętrzu oka — promienie nie skupiają się na siat-
kówce, lecz padają na nią w pewnych odległościach jedne od drugich. Przedłużenia promieni skupiałyby się za siatkówką.
Powoduje to utrudnienia w widzeniu przedmiotów blisko położonych. Czasami, w skrajnej dalekowzroczności, punkt D oka
jest przesunięty daleko poza nieskończoność — wówczas nawet punkty nieskończenie dalekie (np. gwiazdy) nie są widziane
dostatecznie wyraźnie. Punkt B oka dalekowzrocznego znajduje się dalej niż u oka zdrowego. Refrakcja takiego oka jest do-
datnia.

Wadę tę korygujemy, stosując dodatkowe szkła skupiające.

3.

Astygmatyzm oka polega na niedokładnościach w odwzorowaniu obrazu na siatkówce wskutek nieregularności budowy
układu optycznego. Występuje on, gdy dla różnych przekrojów głównych oka mamy do czynienia z różnymi wartościami re-
frakcji.

Wyróżniamy astygmatyzm krótko- i dalekowzroczny. Astygmatyzm krótkowzroczny występuje wówczas, gdy w jednym
przekroju głównym oko jest miarowe, a w drugim refrakcja jest ujemna. Jeżeli natomiast oko jest miarowe w jednym prze-
kroju głównym, a w drugim refrakcja jest dodatnia, mówimy o astygmatyzmie dalekowzrocznym. Możemy mieć do czynie-
nia również z astygmatyzmem złożonym: kiedy obydwa przekroje główne oka są niemiarowe. Jeżeli dla obydwu przekrojów
R < 0, jest to astygmatyzm złożony krótkowzroczny, jeżeli dla obydwu R > 0 — astygmatyzm złożony dalekowzroczny.
(Oczywiście dla obydwu przekrojów głównych wartości refrakcji muszą się różnić. W przeciwnym razie mamy do czynienia
nie z astygmatyzmem, ale po prostu z krótko- lub dalekowzrocznością). Istnieje także astygmatyzm złożony mieszany —
kiedy w jednym przekroju głównym oka refrakcja jest większa, a w drugim mniejsza od zera.
Astygmatyzm oka koryguje się soczewkami lekko cylindrycznymi lub sferocylindrycznymi (jeżeli ponadto oko jest niewy-
miarowe). Soczewki te oszlifowane są tak, że w obu przekrojach głównych mają różne zdolności skupiające, dobrane tak, aby
korygować refrakcję w odpowiednich przekrojach oka.

WIDZENIE STEREOSKOPOWE

Wiemy z codziennych doświadczeń, że przy pomocy jednego oka nie jesteśmy w stanie precyzyjnie określać odległości i położenia
różnych przedmiotów. Za widzenie stereoskopowe, czyli przestrzenne, odpowiada dopiero para oczu. Dzieje się tak dlatego, że zbież-
ność (konwergencja) osi oczu dla obiektów bliższych jest mniejsza niż dla dalszych. Innymi słowy, gdy patrzymy na obiekty położone
blisko nas, główne osie optyczne oczu przecinają się pod nieco większym kątem (α) niż gdy patrzymy na obiekty oddalone (kąt β).

Obrazy przedmiotu przestrzennego, dawane przez oboje oczu, nie są jednak identyczne. Dzieje się tak tylko wtedy, gdy jedno i drugie
oko patrzy nań pod tym samym kątem, tak jak na rysunku powyżej (czyli że przedmiot leży na linii prostopadłej do prostej łączącej ob-
oje oczu). Przesunięcie przedmiotu w prawo spowodowałoby odpowiednio zwiększenie kątów α i β dla prawego, a zmniejszenie ich
dla lewego oka. Przy przesunięciu w lewo sytuacja będzie odwrotna.
Wynika z tego różnica między obrazami odbieranymi przez oboje oczu. Miarą widzenia stereoskopowego γ jest bezwzględna różni-
ca kątów widzenia dla obojga oczu dwóch przedmiotów, które odróżniamy jeszcze jako oddalone od siebie. Zwróćmy uwagę, że
widzenie stereoskopowe zależy od kąta, pod jakim patrzymy na przedmiot. Wyjaśnia to fakt, dlaczego człowiek widzi przestrzennie
tylko w pewnym obszarze przestrzeni z przodu i po bokach głowy.


APARAT RECEPTOROWY OKA

Promienie załamywane w układzie optycznym oka przechodzą przez ciało szkliste i padają na siatkówkę, powodując powstawanie ob-
razu. Jego przetwarzanie na konkretne wrażenia wzrokowe odbywa się dopiero w mózgu, dokąd impulsy biegną za pośrednictwem
nerwu wzrokowego. Wewnątrz oka obraz odbierany jest przez receptory, czyli komórki fotoczułe. Zaliczamy do nich, dokładnie opisa-
ne niżej, pręciki i czopki. Receptory te łączą się z zakończeniami rozgałęzień nerwu wzrokowego i do niego przekazują to, co zostanie
w nich zarejestrowane. Pręciki rozmieszczone są najgęściej w brzegowych obszarach siatkówki, czopki znajdują się w jej części środ-
kowej.

oko lewe

oko prawe

11

CZUŁOŚĆ OKA. BEZWZGLĘDNY PRÓG CZUŁOŚCI.

Czułość receptorów świetlnych oka wiąże się z natężeniem światła wpadającego do układu optycznego i rejestrowanego na siatkówce.
Jest ona tym większa, im mniejsze natężenie zostaje zarejestrowane jako efekt wzrokowy.
Bezwzględnym progiem czułości nazywa się najmniejszą porcję energii (najmniejsze natężenie światła), której dostarczenie do oka
spowoduje rejestrację efektu wzrokowego. Na drodze doświadczeń ustalono, że bezwzględny próg czułości przeciętnego zdrowego oka
wynosi

ok.

4 · 10

-17

J. Przy długości fali światła λ = 510 nm odpowiada to około 100 kwantom energii, z których jedynie 8 dociera do siatkówki

oka (pozostałe ulegają odbiciom od powierzchni optycznych i absorpcji w ośrodkach przeziernych oka). Ponieważ nie padają one na
jeden pręcik, a na ich grupę, można przyjąć, że w skrajnym przypadku jeden kwant powoduje pobudzenie jednego pręcika. Bez-
względny próg czułości siatkówki wynosi zatem zaledwie od 1 do 8 kwantów energii świetlnej!
Względnym progiem czułości receptorów oka, czyli pręcików i czopków, nazywamy najmniejszą ilość energii potrzebną do pobudze-
nia danego receptora. Okazuje się, że jest ona zależna od długości fali światła padającego, co przedstawiają tzw. krzywe wrażliwości
widmowej, omówione poniżej.


WIDZENIE SKOTOPOWE I FOTOPOWE
Za widzenie skotopowe, czyli ciemne lub pręcikowe, odpowiadają komórki fotoczułe oka zwane pręcikami. Zawierają one fotopig-
ment rodopsynę, która pod wpływem światła rozkłada się błyskawicznie na cząsteczkę białka i retyninę (pochodną witaminy A). Po-
woduje to zmniejszanie czułości pręcika, a powstała podczas rozkładu energia zużyta jest na pobudzenie nerwu wzrokowego. W cie m-
ności następuje odtwarzanie fotopigmentu, a zatem czułość pręcika ponownie wzrasta. W związku z dużą wrażliwością tego rodzaju
komórek fotoczułych na zmiany natężenia światła, odpowiadają one za rejestrowanie nawet minimalnych zmian tego natężenia. Ma to
duże znaczenie dla widzenia w świetle przyćmionym i w ciemności.
Wykres absorpcji światła przez rodopsynę pręcików pokrywa się z tzw. krzywą wrażliwości widmowej w widzeniu ciemnym. Krzywa
ta przedstawia zależność względnego progu wrażliwości pręcików na światło w zależności od długości fali padającej. Jej maksimum
(maksymalny względny próg wrażliwości pręcików) przypada na fale o długości ok. 500 nm. Oznacza to, że dla fal o tej długości ilość
energii potrzebna do pobudzenia pręcika jest największa.
Drugi rodzaj komórek światłoczułych — czopki — działa precyzyjnie tylko przy stosunkowo dużych natężeniach światła padającego,
dlatego też mówimy, że czopki biorą udział w widzeniu fotopowym (jasnym, czopkowym). Są one odpowiedzialne za odróżnianie
barw i rzeczywiście zachodzi ono tylko przy ich pełnej czynności — oko zaadaptowane do ciemności (widzenie skotopowe) barw nie
rozróżnia. Mechanizm widzenia barwnego jest prawdopodobnie procesem ogromnie złożonym, którego jeszcze dokładnie nie poznali-
śmy. Na razie wiemy, że z pewnością bierze w nim udział więcej niż jeden rodzaj receptorów lub barwników — prawdopodobnie trzy.
Mają one maksimum pochłaniania dla trzech różnych barw i wskutek swoich kombinacji dają wszystkie pozostałe barwy, a także wra-
żenie światła białego (teoria Younga – Helmholtza i wiele innych).
Krzywa wrażliwości widmowej dla widzenia skotopowego jest przesunięta w stosunku do krzywej dla światła fotopowego w stronę fal
o większej długości. Maksimum tej krzywej (maksymalny względny próg wrażliwości czopków) przypada na fale o długości ok. 560
nm. Oznacza to, że ilość energii potrzebna do pobudzenia czopka jest największa dla fal o tej właśnie długości.
Fakt, że krzywe wrażliwości widmowej pręcików i czopków są przesunięte względem siebie, powoduje, że względną jasność ogląda-
nego przedmiotu oko ocenia inaczej przy adaptacji jasnej (widzenie fotopowe) i ciemnej (widzenie skotopowe). Falom o długości 560
nm odpowiada barwa zielonożółta, falom o długości 510 nm — barwa zielona. Tłumaczy to, dlaczego barwy widziane w świetle
dziennym jako zielone i niebieskie robią wtedy wrażenie jaśniejszych niż oglądane wieczorem (do wywołania wrażenia wzrokowego
potrzebna jest mniejsza ilość energii). Efekt ten nosi nazwę zjawiska Purkinjego.


ĆWICZENIE 22
KĄT APERTUROWY. APERTURA NUMERYCZNA MIKROSKOPU.

Ilość światła wchodząca do układu optycznego mikroskopu jest tym większa, im większy jest kąt aperturowy obiektywu. Kątem aper-
turowym α nazywamy kąt rozwartości stożka świetlnego wchodzącego do obiektywu (inaczej mówiąc: jest to połowa kąta, jaki
tworzą dwa promienie rozpoczynające się na osi optycznej przedmiotu obserwowanego i wchodzące jeszcze do obiektywu). Kąt ten
może ulegać zmianie w zależności od rodzaju środowiska znajdującego się między obiektywem a przedmiotem obserwowanym (a
konkretnie: od współczynnika załamania światła tego środowiska).
Wielkością bezpośrednio powiązaną w kątem aperturowym jest apertura numeryczna A mikroskopu. Jest ona iloczynem współ-
czynnika załamania środowiska znajdującego się między przedmiotem obserwacji a obiektywem i sinusa kąta aperturowego dla tego
środowiska.



sin





n

A

Kąt aperturowy mikroskopu może ulegać wyraźnemu ograniczeniu w przypadku, gdy przestrzeń między obserwowanym przedmiotem
a obiektywem wypełniona jest przez powietrze. Współczynnik załamania powietrza jest mniejszy niż szkła, co powoduje, że na granicy
tych dwu środowisk nader często pojawia się całkowite wewnętrzne odbicie. Zmniejsza to wydatnie ilość światła wchodzącego do
obiektywu, a w konsekwencji — niekorzystnie wpływa na jasność obrazu.
W technice optycznej dąży się do rozwiązania tego problemu, wykorzystując zjawisko immersji. Zjawisko to polega na wprowadzeniu
między przedmiot obserwowany a obiektyw cieczy (woda, gliceryna, olejek cedrowy) o współczynniku załamania światła możliwie
bliskim współczynnikowi załamania szkła. Sprawia to, że zjawisko całkowitego wewnętrznego odbicia przestaje zachodzić lub znacz-
nie zmniejsza się jego zakres, a w konsekwencji — większa ilość światła dostaje się do obiektywu. Ciecz, którą wprowadzamy między
obiektyw a przedmiot obserwowany, nazywamy cieczą immersyjną, a obiektyw taki — obiektywem immersyjnym.


ZWIĄZEK ZDOLNOŚCI ROZDZIELCZEJ Z APERTURĄ MIKROSKOPU
Jak wspomniano przy opisie zdolności rozdzielczej mikroskopu, obserwowany przez nas obraz danego przedmiotu jest efektem nało-
żenia się szeregu obrazów dyfrakcyjnych zarejestrowanych przez mikroskop. Z teorii opracowanej przez Abbego w II połowie XIX w.
wynika, że im więcej jest tych obrazów (im więcej wiązek świetlnych ugiętych na drobnych niejednorodnościach wchodzi do obiekty-

12

wu), tym lepsze odwzorowanie przedmiotu przez obiektyw. Aby odwzorowanie to było dostatecznie dobre, do obiektywu musi wejść
przynajmniej wiązka rzędu zerowego (centralna) i dwie wiązki I rzędu.
Aby zebrane w płaszczyźnie ogniskowej obiektywu wiązki ugięte wzmocniły się przez interferencję, musi zajść warunek:





sin



d

gdzie d jest stałą siatki (czyli najmniejszą odległością dwóch punktów widzianych jeszcze jako oddzielne),
λ — długością fali świetlnej,
α — kątem ugięcia wiązki I rzędu.

Rzecz jasna, kąt aperturowy obiektywu (który od tej chwili dla odróżnienia określać będziemy jako kąt β) nie może być mniejszy od
kąta ugięcia wiązki I rzędu, a tylko równy bądź większy od niej. Wynika z tego, że:





sin



d

Miarą zdolności rozdzielczej jest więc:





sin

1





d

D

Ze wzoru tego wynika, że zwiększanie kąta aperturowego mikroskopu zwiększa jego zdolność rozdzielczą. Wzór ten odnosi się jednak
wyłącznie do obiektywów nieimmersyjnych, tzn. takich, w których nie mamy do czynienia z żadnymi zmianami długości fali światła
(a, jak to wynika ze wzoru, długość ta również wpływa na zdolność rozdzielczą mikroskopu).
Rozważmy wobec tego obiektyw immersyjny. Wiemy skądinąd, że długość fali światła maleje n-krotnie podczas przechodzenia przez
środowisko o współczynniku załamania światła n. Gdy w takim razie wypełnimy przestrzeń między preparatem a obiektywem cieczą
immersyjną o takim współczynniku załamania, otrzymamy powyższy wzór w zmienionej postaci:





sin

1







n

d

D

Widzimy zatem, że obiektywy immersyjne zwiększają zdolność rozdzielczą mikroskopu niejako podwójnie: powiększając kąt apertu-
rowy β, a zarazem zmniejszając długość fali światła λ.
Ponieważ, jak pamiętamy, iloczyn n ·sin β oznacza aperturę numeryczną mikroskopu, między tą wielkością a zdolnością rozdzielczą
zachodzi związek:



A

d

D





1

W dotychczasowych rozważaniach zakładaliśmy, że promienie świetlne padają na przedmiot obserwowany równolegle do osi optycz-
nej. Jeżeli kierunek ich padania nie jest równoległy, lecz skośny, musimy nieco zmodyfikować powyższy wzór:







A

n

D

2

sin

2







MIKROSKOP Z CIEMNYM POLEM WIDZENIA

Mikroskopy z jasnym polem widzenia (do których należy m.in. powszechnie używany mikroskop optyczny) pozwalają oglądać

poszczególne fragmenty obserwowanego przedmiotu dzięki różnicom w natężeniu światła przez nie przepuszczanego. Dla wzmocnie-
nia tego efektu stosuje się odpowiednie barwienie preparatów, których różne elementy w sposób zróżnicowany przyjmują barwniki.

Zdarza się jednak, że kontrasty na preparacie są małe, niemal niewidoczne, nawet po zabarwieniu, albo że barwienie preparatu z

jakiegoś względu jest niepożądane. Stosuje się wówczas obserwację w tzw. ciemnym polu widzenia. Nazwa pochodzi stąd, że — od-
wrotnie niż w przypadku mikroskopów z jasnym polem widzenia — obserwujemy jasne fragmenty lub kontury struktur na tle ciemne-
go pola. Sytuację taką otrzymujemy, oświetlając preparat boczną wiązką, prostopadłą do osi optycznej tubusu. Do obiektywu wchodzi
wówczas wyłącznie światło rozproszone na drobnych elementach struktury przedmiotu. Mikroskopy takie, zwane również ultramikro-
skopami, stosuje się również wtedy, gdy cząstki lub fragmenty przedmiotu są bardzo małe. Dzięki ich użyciu możemy obserwować
nawet poszczególne cząsteczki koloidów o rozmiarach rzędu 5 · 10

-8

m. Niestety, dokładność takiej obserwacji jest niewielka — inte-

resujące nas obiekty zazwyczaj widzimy jako jasne punkty na ciemnym tle — toteż zamiast oświetlenia bocznego stosuje się często
specjalne kondensory ciemnego pola, które dają wiązki oświetlające dany mały obszar obejmujący obiekty obserwowane, lecz nie
wchodzą bezpośrednio do obiektywu, omijając go z boku. Do obiektywu dostaje się natomiast światło ugięte na oświetlonych mikroob-
iektach.

MIKROSKOP Z KONTRASTEM FAZOWYM

Poszczególne elementy subtelnych struktur, zwłaszcza biologicznych, często nie różnią się swoimi własnościami absorpcyjnymi, a je-
dynie współczynnikami załamania światła lub grubością — dlatego też w jasnym polu widzenia nie wyróżniają się lub nawet są niewi-
doczne na tle otaczającej cieczy.
Podczas przechodzenia przez elementy o różnym współczynniku załamania lub grubości, fala świetlna ulega jednak minimalnej zmia-
nie fazy. Zmiana ta nie jest dostrzegalna dla oka ani możliwa do zarejestrowania na kliszy fotograficznej, ale specjalne urzą dzenia
zwane mikroskopami z kontrastem fazowym, pozwalają ten niewidoczny obraz fazowy przekształcić w obraz „amplitudowy”, czyli
kontrastowy — zróżnicowany pod względem przechodzącego natężenia światła.
Spróbujmy w wielkim uproszczeniu opisać istotę ich działania.
Okazuje się, że fala przechodząca przez obiekt (1) wskutek różnic współczynników załamania zmienia fazę drgań o niewielką wartość
∆φ w stosunku do fali biegnącej obok obiektu (2). W ujęciu geometrycznym odpowiada to powstaniu nowej fali ugiętej (3), o niewiel-
kiej amplitudzie i przesuniętej względem fali 2 o π/2 — innymi słowy, fala 1 jest geometrycznym złożeniem fal 2 i 3.
Fala 2 jest falą oświetlającą pole widzenia — ma dużą amplitudę i jednakową fazę w całym polu. Chcąc uzyskać większy kontrast fa-
zowy między nią a falą 3, musimy po pierwsze zmienić różnicę faz między nimi o π/2 (zlikwidować ją lub zwiększyć do π), a po drugie
— osłabić jej natężenie.
Dokonujemy tego za pomocą specjalnej płytki, zwanej płytką fazową, umieszczonej w płaszczyźnie ogniskowej obiektywu. Płytka ta w
maleńkim krążku w swej części środkowej (lub w wąskim pierścieniu okalającym środek) przechwytuje całość promieniowania oświe-

13

tlającego, po czym osłabia je przez absorpcję w warstewce napylonego metalu i jednocześnie wprowadza żądaną zmianę fazy, np.
wskutek nieco innej grubości płytki w tym miejscu. Światło ugięte przez obserwowany obiekt przechodzi natomiast niezakłócone przez
odpowiednie części płytki fazowej, a następnie tworzy przed okularem pożądany obraz kontrastowy.
Formą ulepszoną mikroskopu z kontrastem fazowym jest mikroskop interferencyjny. Ponadto w wielu przypadkach wzmocnienie
kontrastowości obrazów można uzyskać w mikroskopie polaryzacyjnym. Wykorzystuje się tu fakt, że wiele struktur organicznych sta-
nowi środowisko optycznie anizotropowe. W mikroskopach polaryzacyjnych, podobnie jak w polarymetrach, stały element budowy
stanowią dwa nikole. Polaryzator umieszczony jest przed kondensorem, a ruchomy analizator znajduje się wewnątrz tubusu między
obiektywem a okularem. Poprzez zmiany położenia płaszczyzn głównych obydwu polaryzatorów względem siebie oraz odległości
obiektu od pierwszego polaryzatora można uzyskać pojawiające się i znikające kontrasty różnych części obiektu.

MIKROSKOP ELEKTRONOWY

Zostało już nadmienione, że zmniejszanie długości fali stosowanego światła powoduje wzrost zdolności rozdzielczej mikroskopu. W
jednych z najdoskonalszych urządzeń optycznych, jakie znamy — mikroskopach elektronowych — wykorzystuje się w tym celu falo-
we właściwości materii, a konkretnie elektronów. Długość fal de Broglie’a dla elektronów, opisana wzorem:

mv

h

p

h







gdzie λ oznacza długość fali
h — stałą Plancka
m — masę ciała lub cząstki
a v — jego prędkość,

jest o kilka rzędów wielkości mniejsza od długości fal świetlnych.
Źródłem elektronów w mikroskopie jest tzw. działo elektronowe. Katodą jest rozżarzony drucik wolframowy; natężenia prądu elektro-
nowego są rzędu 100 mA, a napięcie przyspieszające (które musi się odznaczać doskonałą stałością) wynosi od kilkudziesięciu do 1000
kV. Po wyjściu z wyrzutni i przyspieszeniu przez anodę elektrony przechodzą przez pierwszą „soczewkę” mikroskopu (elektryczną lub
magnetyczną, spełniającą rolę kondensora) i dochodzą do preparatu. Podczas przechodzenia przez preparat, elektrony ulegają rozpro-
szeniu i pochłanianiu (tym większemu, im większa grubość preparatu i liczba masowa atomów danego fragmentu) na jego niejedno-
rodnej strukturze.
Preparat taki musi być dostatecznie cienki (10-100 nm, zależnie od materiału), elektrony zaś muszą mieć dostatecznie duże energie. W
przeciwnym razie znaczący odsetek elektronów ulega spowolnieniu wskutek zderzeń podczas przejścia przez preparat, a to powoduj e
dużą aberrację chromatyczną.
Obiektyw skupia elektrony, tworząc powiększony obraz przedmiotu, i kieruje je do soczewki projekcyjnej. Po przejściu przez nią elek-
trony tworzą obraz na ekranie pokrytym specjalną fluoryzującą substancją, emitującą pod ich wpływem promieniowanie widzialne. W
ten sposób „obraz elektronowy” jest przetwarzany na obraz widzialny, który można obserwować bezpośrednio lub fotografować.
Wszystkie elementy mikroskopu elektronowego umieszczone są wewnątrz obudowy, we wnętrzu której istnieje wysoka próżnia (od 10

-

5

do 10

-6

Pa), konieczna, aby wyelimnować zderzenia elektronów z cząsteczkami jakiegokolwiek gazu na drodze pomiędzy źródłem a

ekranem
Mikroskopy elektronowe dają znakomite powiększenia, nawet rzędu 500 tysięcy razy. Ich zdolność rozdzielcza również jest bardzo
dobra, aczkolwiek nie taka, jakiej można byłoby się spodziewać na podstawie analizy długości fal de Broglie’a. Teoretycznie mogłaby
być nawet stokroć większa! Niestety, zdolność rzeczywista jest mniejsza ze względu na wady soczewek magnetycznych — o wiele
bardziej znaczące, niż wady soczewek szklanych.
Obecnie prowadzi się również badania nad mikroskopami protonowymi. Na podstawie równania opisującego fale de Broglie’a może-
my stwierdzić, że cząstki cięższe od elektronów pozwalałyby uzyskać jeszcze mniejsze długości fal, a co za tym idzie — mikroskopy
opierające na nich swe działanie miałyby doskonalsze zdolności optyczne. Na razie jednak trudności techniczne wykluczają możliwość
ich użycia.

ĆWICZENIE 23
DEFINICJA FALI AKUSTYCZNEJ

Fale akustyczne (głosowe) są to mechaniczne fale podłużne w środowiskach wszystkich trzech stanów skupienia. W gazach i cieczach
rozchodzenie się tych fal polega na przenoszeniu się ruchu drgającego cząsteczek środowiska w kierunku promienia. Powoduje to roz-
chodzenie się wzdłuż promienia obszarów zagęszczenia i rozrzedzenia ośrodka, co przekłada się na naprzemienne zwiększanie się i
zmniejszanie ciśnienia. W ciałach stałych fale akustyczne mogą być również falami poprzecznymi (np. stojąca fala poprzeczna na drga-
jącej strunie).
Żródłem fal akustycznych może być dowolne ciało drgające z odpowiednią częstością i z dostatecznie dużą amplitudą. Możemy roz-
ważać źródła jedno-, dwu- i trójwymiarowe (drgające struny, błony czy objętości powietrza w rezonatorach). Realizacja źródła punk-
towego jest w akustyce znacznie trudniejsza niż w optyce.
Zmysł słuchu człowieka rejestruje drgania w zakresie od 16 Hz (λ ≈ 21 m) do 1 kHz (λ ≈ 0,017 m) i nimi zajmuje się akustyka w zna-
czeniu węższym. Akustyka w znaczeniu szerszym obejmuje również ultradźwięki (υ > ok. 20 kHz), hiperdźwięki (υ > 10

9

Hz) i infra-

dźwięki (υ < ok. 16 Hz).


CIŚNIENIE AKUSTYCZNE

Zmiany gęstości cieczy lub gazu, w których rozchodzi się dźwięk, są spowodowane naprzemiennym ściskaniem i rozprężaniem war-
stwy ośrodka przez ciało drgające będące jego źródłem. Zmiany te, jak już wyżej wspomniano, wywołują w ośrodku zmiany ciśnienia,
którego wartość chwilowa osiąga większą lub mniejszą wartość od ciśnienia atmosferycznego. Różnicę tych dwu ciśnień nazywamy ci-
śnieniem akustycznym p.
Ciśnienie akustyczne w danym punkcie przestrzeni jest funkcją czasu — zmienia się sinusoidalnie. W chwili maksymalnego odchyle-
nia punktu ośrodka od położenia równowagi jego wartość jest największa. Nazywamy ją amplitudą ciśnienia akustycznego.
Chwilowe ciśnienie akustyczne w danym punkcie przestrzeni zależy zarówno od stałej prędkości fali dźwiękowej w danym ośrodku,
jak i od zmiennej w czasie prędkości cząsteczek ośrodka (prędkości te nie są równoważne!), a wyrażane jest wzorem:

14

)

(

)

(

t

cv

t

p





NATĘŻENIE DŹWIĘKU

Natężenie dźwięku I wyraża stosunek mocy P dźwięku przechodzącego przez powierzchnię jednostkową. Moc P dźwięku jest równa
mocy źródła, które go emituje.

S

P

I



 

2

m

W

I



Z gęstością energii dźwięku łączy je wzór:

wv

I



gdzie w jest ilością energii przypadającą na jednostkę objętości ośrodka,
a v — prędkością dźwięku w tym ośrodku.

Z ciśnieniem akustycznym natomiast natężenie dźwięku wiąże się zależnością:

c

p

I

ak



2



gdzie ρ oznacza gęstość ośrodka,
a c — prędkość dźwięku w tym ośrodku.

Widzimy zatem, że natężenie dźwięku jest proporcjonalne do kwadratu ciśnienia akustycznego, a mówiąc ściśle — jego średniej war-
tości (ponieważ moc dźwięku jest pracą wykonaną przez zmieniające się ciśnienie w jednostce czasu).
Najmniejsza wartość natężenia dźwięku odbieranego przez ucho ludzkie wynosi ok. 10

-12

W/m

2

(dla częstotliwości ok. 1 kHz). War-

tość największa, która nie powoduje jeszcze trwałego uszkodzenia słuchu (choć może wywoływać ból), wynosi ok. 1 W/m

2

. Iloraz

największego i najmniejszego natężenia dźwięku, jakie może odebrać ucho, wynosi zatem ok. 10

12

i nazywany jest zakresem dyna-

micznym ucha.
Ponieważ, jak widać, zakres dynamiczny ucha jest bardzo duży, dla wygody opisu ciśnienia akustycznego i natężenia dźwięku wybra-
no skalę logarytmiczną. Posługujemy się nią przy porównaniu natężenia obiektywnego zjawisk głosowych, nie określamy jednak abso-
lutnego natężenia danego głosu, lecz logarytm stosunku jego natężenia I do natężenia I

0

, pełniącego rolę wzorca. Liczbę jednostek tego

względnego natężenia głosu wyznaczamy ze wzoru:

0

ln

I

I

k

L





,

gdzie k jest współczynnikiem proporcjonalności, mającym zazwyczaj wartość 1 lub 10, a wartość L nazywamy poziomem natężenia
dźwięku (słowo „poziom” sugeruje nam, że mamy do czynienia z wielkością odnoszoną do pewnej wielkości wzorcowej).

Jednostką skali logarytmicznej jest 1 bel. Dla k = 1 dźwięki o natężeniu I i I

0

różnią się o 1 bel wtedy, gdy stosunek

10

0



I

I

, tzn. gdy

natężenie dźwięku wzorcowego jest dziesięciokrotnie mniejsze niż natężenie, które oceniamy.
Ponieważ bel jest jednostką dosyć dużą, w praktyce częściej posługujemy się decybelem (wówczas k = 10). 1 bel równa się 10 decybe-
lom.
Jako

natężenie

wzorcowe,

czyli

tzw.

natężenie

odniesienia,

przyjęto

w

fizyce

wartość

równą

10

-12

W/m

2

, co odpowiada ciśnieniu o wartości 20 μPa (2 · 10

-5

N/m

2

). Logarytm stosunku ciśnienia akustycznego dźwięku do takiego

ciśnienia odniesienia nazywany jest poziomem ciśnienia akustycznego dźwięku.

0

ln

p

p

k

L

p





[dB SPL] z ang. sound pressure level

Wartość ciśnienia odniesienia została dobrana tak, aby odpowiadała progowi słyszalności (progowi absolutnemu) dla dźwięku sinusoi-
dalnego o częstotliwości 1 kHz.
Warto dodać, że obiektywną wartością natężenia dźwięku posługujemy się rzadko, ponieważ w praktyce ma ona niewielkie znaczeni e
— ten sam obiektywny wzrost natężenia w różnych okolicznościach możemy odbierać zupełnie inną zmianę siły głosu, a ponadto od-
biór wrażeń słuchowych przez ucho ludzkie zależy nie tylko od natężenia, ale także od częstości dźwięku.


ODBICIE, POCHŁANIANIE I ZAŁAMANIE FALI AKUSTYCZNEJ
Zjawisko odbicia fal w akustyce znamy pod nazwą echa oraz pogłosu — wielokrotnych odbić i chaotycznego nakładania się fal odbi-
tych najczęściej od gładkich ścian dużej sali. Na ogół jest to zjawisko niekorzystne dla akustyki wnętrz, ponieważ zakłóca odbiór mu-
zyki, zrozumiałość mowy itp. Aby zapobiec pogłosowi, stosuje się materiały silnie tłumiące dźwięki przy odbiciu — np. tkaniny, per-
forowane wykładziny ścian itp.
Akustyka sal zależy m.in. od tak zwanego czasu rewerberancji. Jest to odstęp czasu, po którym natężenie głosu (po umilknięciu źró-
dła) maleje 10

6

razy w stosunku do natężenia początkowego. Im mniejszy jest ten czas, tym lepsza akustyka pomieszczenia, i przeci w-

nie — dłuższy czas rewerberancji (będący skutkiem pogłosu) powoduje pogorszenie akustyki wnętrza. Czas rewerberancji nie powi-
nien jednak być zbyt krótki, ponieważ osłabiałoby to globalną energię dźwięku docierającą do słuchaczy.
W pewnych ośrodkach zachodzić może pochłanianie fali akustycznej, czyli tłumienie dźwięku. Proces pochłaniania fali dźwiękowej
przebiega zgodnie z prawem Lamberta:

kd

o

e

I

I





co oznacza, że natężenie dźwięku maleje wykładniczo podczas przechodzenia przez warstwę tłumiącą.
Fale akustyczne ulegają również ugięciu i załamaniu. Ugięcie występuje bardzo powszechnie, ponieważ większość przeszkód i otwo-
rów, jakie fale te napotykają na swojej drodze (okna, mury, drzewa) ma rozmiar porównywalny z długością fal — z tej przyczyny mo-
żemy słyszeć rozmowę odbywającą się za ścianą, nawet jeżeli nie znajdujemy się naprzeciw drzwi. Załamanie fal następuje na przy-
kład w powietrzu o niejednakowej gęstości, dajmy na to, na otwartym terenie w słoneczny dzień. Poszczególne warstwy powierza w
zależności od odległości od nagrzanej ziemi mają różne temperatury, a więc i gęstości, promień przechodzącej fali dźwiękowej może
zatem ulegać w nich zakrzywieniu.

15

Jako fale mechaniczne, fale akustyczne ulegają również i wielu innym zjawiskom — np. interferencji. Obserwujemy także rezonans
akustyczny i efekt Dopplera.

PRAWO WEBERA–FECHNERA.

Prawo to mówi, że elementarna odczuwalna zmiana głośności ∆G zależy od stosunku zmiany natężenia dźwięku ∆I od wartości
tego natężenia I i jest do tego stosunku wprost proporcjonalna.

I

I

k

G







gdzie k jest współczynnikiem proporcjonalności.
Prawo to jest sprawdzalne jedynie w pewnym ograniczonym zakresie częstotliwości i poziomów natężenia dźwięku — od około 500
Hz i 20 dB do 5000 Hz i 100 dB.

GŁOŚNOŚĆ DŹWIĘKU. PRÓG SŁYSZALNOŚCI I PRÓG BÓLU.

Jeżeli natężenie dźwięku I

0

(o danej częstotliwości υ) jest małe i nie jesteśmy pewni, czy odbieramy jakieś wrażenie słuchowe, czy nie,

a zmiana natężenia o ∆I powoduje odpowiedź pozytywną lub negatywną, to takie wrażenie nazywamy progowym lub po prostu pro-
giem słyszalności. Innymi słowy: próg słyszalności (próg absolutny) jest minimalnym poziomem dźwięku, jaki może być spo-
strzeżony wobec braku innych dźwięków zewnętrznych. Wartość natężenia dźwięku I

0

nazywamy wówczas wartością progową.

Jeżeli natężenie dźwięku wzrośnie od wartości progowej I

0

do wartości I, to głośność G tego dźwięku znajdziemy, całkując matema-

tyczny zapis prawa Webera–Fechnera w granicach od I

0

do I. Wyniesie ona wówczas:

0

ln

I

I

k

G



Zakładamy przy tym, że progowi słyszalności przypisujemy wartość G = 0 (dźwięk niesłyszalny ma zerową głośność), a odpo-
wiednie natężenie obiektywne I

0

nazywamy natężeniem progowym.

Głośność dźwięku odbierana przez narząd słuchu zależy od jego częstotliwości. W pomiarach głośności różnych zjawisk akustyczn ych
umówiono się określać ich głośność przez porównanie z głośnością tonu o częstotliwości υ

0

= 1000 Hz. Jednostką głośności jest fon.

Głośność badanego dźwięku wynosi tyle fonów, ile decybeli ma dźwięk o częstotliwości υ

0

(1000 Hz) równogłośny z badanym wraże-

niem.
Zależność głośności dźwięku od jego natężenia i częstotliwości przedstawia zbiór krzywych jednakowej głośności, czyli izofon (na
osi rzędnych wykresu, w którym umieszczamy krzywe, odłożony jest poziom natężenia dźwięku, a na osi odciętych — częstości υ w
skali logarytmicznej). Krzywe te łączą punkty wykresu, których głośność jest jednakowa, mimo że ich natężenia obiektywne i częst o-
tliwości mogą być różne.
Z wykresu krzywych jednakowej głośności, zwanego też wykresem czułości ucha w funkcji częstotliwości, wynika, że ucho wykazuje
różną wrażliwość na dźwięki. Dwa dźwięki, z których jeden ma częstotliwość 1000 Hz, a drugi 200 Hz, muszą różnić się natężeniem
aż o 15 dB, aby ucho oceniło je jako jednakowo głośne! Oznacza to, że ucho jest znacznie mniej wrażliwe na ton 200 Hz niż na 1000
Hz.
Jak już wspomniano, próg słyszalności wyznacza izofona, dla której głośność wynosi 0 fonów. Dźwięków o wartościach natężenia i
częstotliwości mieszczących się na wykresie poniżej tej krzywej ucho ludzkie nie odbiera. Izofonę 120 fonów (dla υ

0

: 12 beli) nazy-

wamy często progiem przykrości (dźwięki o odpowiadającej jej głośności są nieprzyjemne dla słuchającego), a izofony 130 – 140 fo-
nów — progiem bólu. Dźwięki o wartościach natężenia i częstotliwości mieszczących się na wykresie powyżej tej krzywej mogą
spowodować trwałe mechaniczne uszkodzenie narządu słuchu.

FIZYCZNE I FIZJOLOGICZNE CECHY DŹWIĘKU
Cechy dźwięku dzielimy na fizyczne (obiektywne) i odpowiadające im fizjologiczne (subiektywne), czyli odbierane w odmienny spo-
sób przez różnych ludzi.
Fizyczną cechą dźwięku jest jego częstotliwość. Odpowiadająca jej cecha fizjologiczna to wysokość dźwięku — większej częstotliwo-
ści odpowiada wyższy dźwięk i na odwrót.
Kolejna fizyczna cecha dźwięku to natężenie. Odpowiada jej cecha subiektywna — głośność. Przy stałej częstotliwości dźwięku wyż-
szemu natężeniu odpowiada większa głośność i odwrotnie. Przy zmiennej częstotliwości zależność głośności od niej i od natężenia
dźwięku opisują scharakteryzowane już krzywe jednakowej głośności.
Ostatnią z fizycznych cech dźwięku jest jego struktura widmowa. Wymaga ona krótkiego omówienia, a mianowicie przedstawienia
słyszanego przez nas dźwięku jako sumy pewnych zjawisk głosowych, czyli tonów, dzielonych przez nas na podstawowe i harmonicz-
ne.
Tonem nazywamy zjawisko głosowe wywołane przez falę harmoniczną o jednej, określonej częstości. Każdy dźwięk rzeczywisty jest
mieszaniną wielu tonów, ponieważ rzadko kiedy mamy do czynienia ze źródłem dźwięku emitującym fale o jednej tylko częstości.
Najłatwiej wytłumaczyć to na przykładzie struny instrumentu. Kiedy wprawiamy ją w drganie, wytwarza się na niej fala stojąca, której
węzły znajdują się na końcach struny. Ton emitowany w takich warunkach nazywamy podstawowym. Ta sama struna może jednak
drgać inaczej — fala stojąca może mieć więcej niż dwa węzły, co odpowiada wyższej częstotliwości. Takie fale i odpowiadające im
tony nazywamy harmonicznymi. Gdy struna zaczyna drgać, tony podstawowy i harmoniczne nakładają się na siebie — struna jest
wówczas źródłem fali złożonej, czyli dźwięku.
Odkładając na osi odciętych częstość fali stojącej i przypisując każdej częstości określoną długość fali, otrzymujemy zbiór odcinków
tworzących tzw. widmo akustyczne. Jest ono zmienne w czasie, gdyż wszystkie tony składające się na dźwięk nie muszą pojawiać się
jednocześnie; mogą następować jeden po drugim.
Liczba i natężenie, a także kolejność i odstęp w pojawianiu się tonów harmonicznych nałożonych na ton podstawowy decyduje o ostat-
niej cesze fizjologicznej, odpowiadającej widmowej strukturze dźwięku — jego barwie.

UBYTEK SŁUCHU. POZIOM UBYTKU SŁUCHU.
Ubytkiem słuchu określa się pogorszenie słuchu, powodujące podwyższenie progu słyszalności, czyli zmniejszenie wrażliwości ucha
na dźwięk o danym natężeniu. Ubytek słuchu opisujemy, posługując się pojęciem poziomu ubytku słuchu. Jest on opisany wzorem:

0

ln

10

I

I

L

u



[dB HL]

gdzie L oznacza poziom ubytku słuchu,

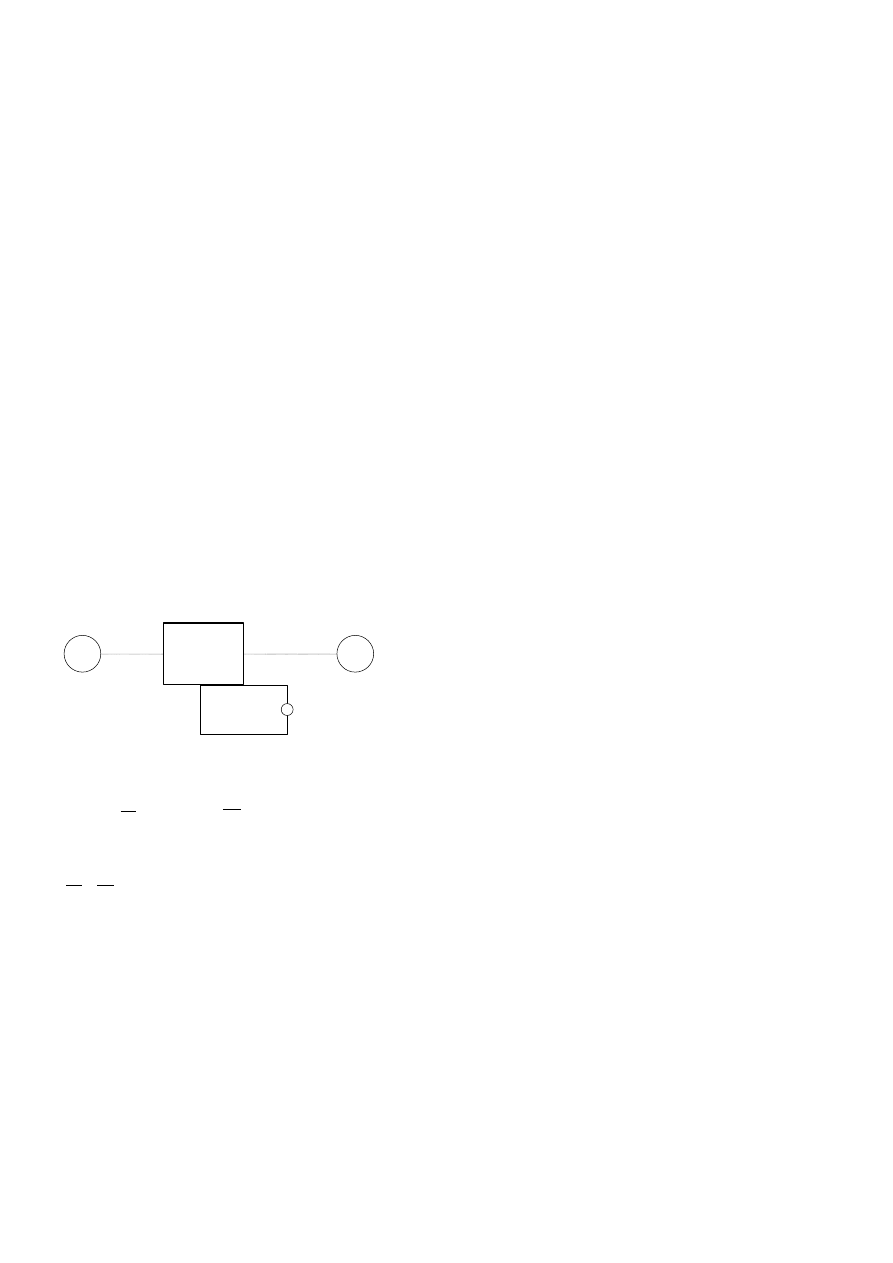
16

I

u

— próg słyszalności dla ucha badanego,

a I

0

— próg słyszalności dla ucha zdrowego.

Poziom ubytku słuchu określamy w „decybelach poziomu słyszalności” (z ang. hearing level). W praktyce oznacza to, że próg słyszal-
ności pacjenta z ubytkiem słuchu 40 dB HL dla 1 kHz jest podwyższony o 40 dB w stosunku do ucha zdrowego, młodego człowieka (z
„normalnym” słuchem).

MIERZENIE POZIOMU UBYTKU SŁUCHU. AUDIOMETRIA.
Audiometria progowa jest techniką badania stanu słuchu poprzez dźwięki leżące na granicy słyszenia, czyli najsłabsze, jakie jeszcze re-
jestruje ucho badanego. Sam audiometr — przyrząd służący do tego badania — jest bardzo złożonym przyrządem, jego zasada działa-
nia jest jednak prosta. Za jego pomocą określamy wartości minimalnego natężenia dźwięku odbieranego przez prawe i lewe ucho ba-
danego — czyli progi słyszalności uszu.
Progi słyszalności mogą być określone za pomocą audiometrii przewodnictwa powietrznego i kostnego. W audiometrii przewodnictwa
powietrznego sygnał testowy podawany jest pacjentowi poprzez słuchawki, w audiometrii przewodnictwa kostnego — poprzez wibra-
tor kostny, umieszczony na wyrostku sutkowym lub na czole badanego pacjenta.
Celem audiometrii przewodnictwa powietrznego jest określenie zdolności słyszenia dla różnych częstotliwości. Badanie może ujawnić
utratę słuchu, lecz nie może określić ubytku słuchu. Celem badania przewodnictwa kostnego jest natomiast podanie tonu testowego
bezpośrednio do ucha wewnętrznego (z pominięciem kanału usznego), w celu określenia progu słyszalności dla tej części ucha.
Wykonując badanie poziomu ubytku słuchu za pomocą audiometru, mierzymy najpierw przewodnictwo powietrzne, a następnie kost-
ne. Różnica między progiem słyszalności AC (powietrznym) a progiem BC (kostnym), nazywana „AC-BC gap” jest utratą słuchu ucha
środkowego, czyli niedosłuchem ślimakowym.
Wyniki badania audiometrycznego wykreśla się na tzw. audiogramie, będącym graficznym przedstawieniem poziomu ubytku słuchu.
Na osi odciętych takiego wykresu odkładamy częstotliwości tonów podawanych, a na osi rzędnych — wartości ubytku słuchu.

ĆWICZENIE 24
ZASADA POMIARU ŚWIATŁOŚCI ŹRÓDŁA METODĄ FOTOMETRYCZNĄ
Pomiarów fotometrycznych możemy dokonywać na dwa sposoby — mogą to być pomiary subiektywne, gdy rolę detektora promie-
niowania gra oko obserwatora, bądź obiektywne — gdy do oceny promieniowania używamy bardziej precyzyjnych urządzeń (takich
jak fotokomórka, fotoogniwo, fotopowielacz, klisza fotograficzna, termostosy itp.). Pomiary obiektywne polegają najczęściej na po-
równywaniu wartości mierzonych z innymi, które są nam znane (np. oceniamy stężenie koloidu, porównując „na oko” ilość rozprasza-
nego przezeń światła z ilością światła rozpraszanego przez koloidy o znanych stężeniach). W pomiarach obiektywnych odpowiednie
wartości odczytujemy z wybranej skali.
Pomiaru światłości źródła możemy dokonać za pomocą fotometru, składającego się ze źródła światła Z

1

o znanej światłości I

1

, fotoo-

gniwa F połączonego z mikroamperomierzem A oraz ze źródła światła Z

2

o nieznanej światłości I

2

, którą chcemy zmierzyć. Pomiaru

dokonujemy, przesuwając źródło światła o nieznanej światłości względem powierzchni fotoogniwa F tak długo, dopóki natężenia
oświetlenia E powierzchni fotoogniwa nie zrówna się z natężeniem światła emitowanego przez źródło o znanej światłości.

Korzystamy wówczas z następującej zależności: jeżeli natężenie oświetlenia E na powierzchni fotoogniwa jest jednakowe dla obydwu
źródeł światła, to zachodzi związek:

2

1

E

E



a że



cos

2

1

1

1

r

I

E



, a



cos

2

2

2

2

r

I

E



to dla α

1

= α

2

otrzymujemy równość:

2

2

2

2

1

1

r

I

r

I



Z równości tej, znając wartość odległości r obydwu źródeł światła od powierzchni fotoogniwa, możemy wyliczyć wartość I

2

.

ĆWICZENIE 25
ROZPRASZANIE ŚWIATŁA W ROZTWORACH KOLOIDOWYCH
Efektem Tyndalla nazywamy rozpraszanie światła podczas jego przechodzenia przez przezroczyste środowisko niejednorodne. Może
to być gaz, ciecz lub ciało stałe. Efekt Tyndalla najlepiej można zaobserwować w roztworach koloidowych, tzn. takich, w których roz-
miary cząsteczek fazy rozpraszanej mieszczą się między 10

-7

a 10

-9

m. Cząsteczki takie mają rozmiary porównywalne z długością fali

światła widzialnego, toteż dyfrakcja tych fal zachodzi na nich najmocniej. Zjawisko to obserwujemy w postaci powstającej wiązki
świetlnej o stożkowatym kształcie. Podobnie dzieje się w przypadku światła rozpraszanego np. przez mgłę (mikroskopijne krople wo-
dy) lub pyłki kurzu unoszące się w powietrzu.
Zjawisko rozpraszania światła przez koloid wykorzystywane jest w urządzeniu zwanym elektrohemoskopem Hellige’a, służącym do
pomiaru natężenia światła rozproszonego przez elementy morfotyczne krwi (erytrocyty, leukocyty i płytki krwi) zawieszone w izoto-
nicznej cieczy — jest to tzw. metoda turbidymetryczna. Ponieważ w osoczu krwi znajdują się zawieszone w nim elementy morfotycz-
ne, światło przechodzące przez krew ulega na nich rozproszeniu. Oceniając stopień rozproszenia światła, możemy zbadać liczbę tych
elementów i stwierdzić, czy jest ona prawidłowa.

Z

1

Z

2

A

F

17

Zasada działania elektrohemoskopu jest następująca: z otworu O wychodzi wiązka światła, która jest skupiana przez soczewkę S usta-
wioną tak, aby światło padało na pochłaniającą je przesłonę P. Jeżeli naczynie N jest wypełnione cieczą całkowicie przezroczystą, to
niemal całe światło skupione przez soczewkę zostaje pochłonięte w przesłonie, a tylko niewielka jego ilość pada na fotoop ornik, co
powoduje że natężenie prądu wskazywane przez mikroamperomierz jest nieznaczne. Jeżeli do cieczy znajdującej się w naczyniu N
wprowadzimy krwinki, zajdzie zjawisko rozproszenia światła, które zamiast na przesłonę pada na fotoopornik, powodując wzrost natę-
żenia prądu wskazywanego przez mikroamperomierz. Wzrost ten, zgodnie z prawem Beera, jest proporcjonalny do ilości rozproszone-
go światła, a zatem i stężenia koloidu — oczywiście do momentu, gdy stężenie to stanie się tak wysokie, że światło zamiast rozprasza-
niu zacznie ulegać pochłanianiu (nastąpi wówczas ponowny spadek wartości odczytywanych natężeń).