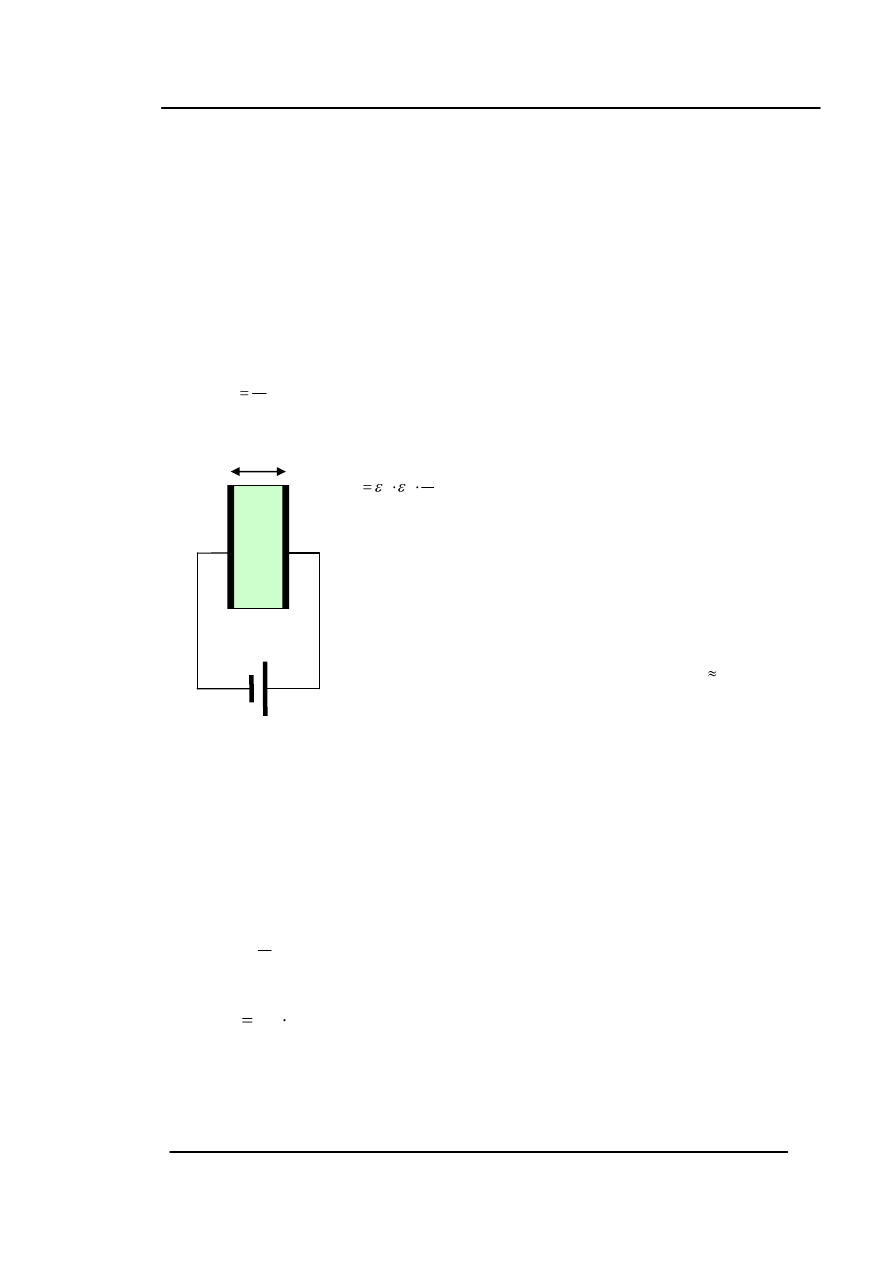
Laboratorium Fizyki; Ćwiczenie E-01. Badanie właściwości elektrycznych kondensatora płaskiego.

Katedra Podstaw Elektroniki, WEiI PK. Koszalin 2011.

1

E-01. Badanie właściwości elektrycznych kondensatora płaskiego

Cel eksperymentu

 Wyznaczanie pojemności kondensatora w funkcji powierzchni jego okładek
 Wyznaczanie pojemności kondensatora z różnymi dielektrykami między jego okładkami
 Wyznaczanie pojemności kondensatora w funkcji odległości między jego okładkami

1. Wiadomości teoretyczne

Wiadomo, że pojemność elektryczna kondensatora C jest stosunkiem ładunku elektrycznego Q do napię-
cia U między jego okładkami,

U

Q

C

.

(1)

Najprostszym kondensatorem elektrycznym jest kondensator płaski. Jego
pojemność elektryczna C dana jest wzorem,

d

A

C

r

0

,

(2)

gdzie
A - powierzchnia okładek kondensatora,
d – odległość między okładkami kondensatora,
ε

r

- przenikalność elektryczna względna materiału znajdującego się miedzy

okładkami kondensatora,
ε

0

= 8,85·10

-12

F/m jest przenikalnością elektryczną próżni.

Przenikalność elektryczna względna ε

r

uwzględnia zmianę pojemności kon-

densatora, spowodowaną wprowadzeniem materiału między okładkami, w
odniesieniu do próżni. Dla suchego, czystego powietrza ε

r

1, co oznacza,

że pojemności kondensatora w próżni i powietrzu są jednakowe.

Zależność (2) będzie badana eksperymentalnie z zastosowaniem kondensa-

tora o zmiennej geometrii. Do eksperymentu będą użyte okładki o powierzchniach A = 400 cm

2

i

A = 800 cm

2

. Odległość miedzy okładkami będzie zmieniana w odstępach 1 mm. Najpierw będzie mie-

rzony ładunek elektryczny Q, zgromadzony na okładkach kondensatora, w funkcji przyłożonego napięcia
U. Pojemność elektryczną C wyznaczamy z nachylenia prostej powstałej z punktów Q=f(U).
Proporcjonalność pojemności elektrycznej C do powierzchni okładek A

A

C ~

potwierdzona będzie pomiarami pojemności kondensatora przy zmiennej odległości między okładzinami
i dla różnych powierzchni okładzin A.
Dodatkowo, poprzez umieszczenie dielektryków miedzy okładkami kondensatora, będą wyznaczone
przenikalności elektryczne ε

r

różnych materiałów. Zmiana odległości między okładkami kondensatora

pozwoli na potwierdzenie proporcjonalności,

d

C

1

~

Ładunek zgromadzony na kondensatorze jest mierzony za pomocą elektrometru. Mierzony ładunek rów-
ny jest iloczynowi pojemności pomiarowej elektrometru i mierzonego napięcia.

A

A

U

C

Q

Na przykład, dla pojemności pomiarowej C

A

=10nF i mierzonego napięcia U

A

=1V mierzony ładunek

wynosi Q=10 nAs. Na stanowisku dostępne są dwa kondensatory pomiarowe C

A

o pojemnościach 10nF i

100nF. Uwaga!!! Jeżeli napięcie wskazywane przez elektrometr wynosi ok. 8V i więcej to należy
zmienić kondensator pomiarowy na większy, a pomiary zarejestrowane przy takich wskazaniach
należy powtórzyć.

ε

r

d

Q

-Q

A

Laboratorium Fizyki; Ćwiczenie E-01. Badanie właściwości elektrycznych kondensatora płaskiego.

Katedra Podstaw Elektroniki, WEiI PK. Koszalin 2011.

2

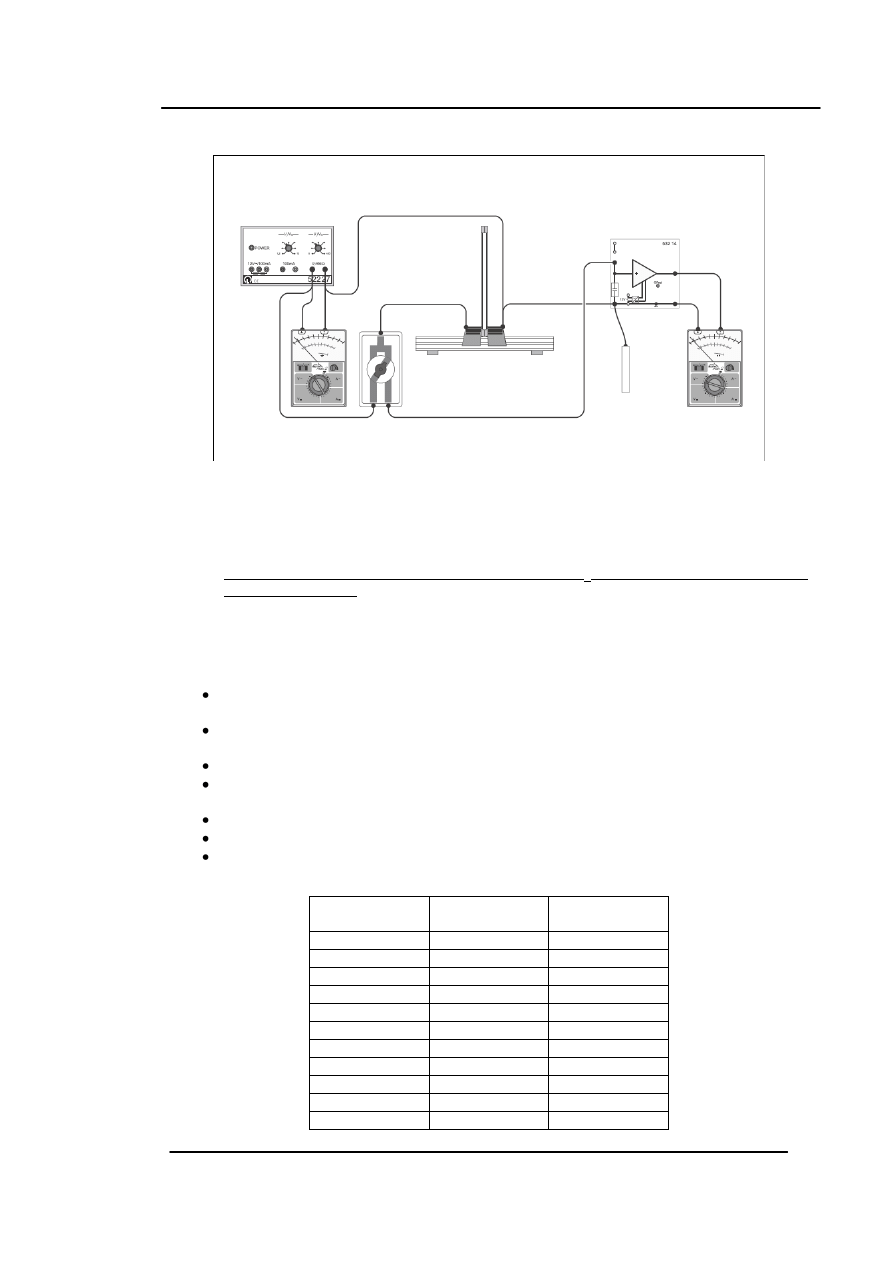
2. Opis aparatury pomiarowej

 Mniejsze okładki kondensatora (A=40cm

2

) ustawione są w odległości 4mm od siebie.

 Ujemny kontakt zasilacza 450V podłączony jest do okładziny prawej i do masy elektrometru.

Do masy elektrometru podłączony jest również kabel uziemiający.

 Dodatni kontakt zasilacza 450V podłączony jest do złącza B przełącznika
 Złącze A przełącznika podłączone jest do lewej okładziny kondensatora a złącze C do wejścia

elektrometru

 Do elektrometru podłączony jest kondensator pomiarowy C

A

=10nF (100nF), a do wyjścia podłą-

czony jest woltomierz

 Do zasilacza 450V podłączony jest woltomierz mierzący napięcie U.

3. Przebieg eksperymentu

3.1 Pomiar zależności ładunku kondensatora w funkcji przyłożonego napięcia dla różnych powierzchni
okładek kondensatora

Ustaw przełącznik w położenie A-C, rozładuj kondensator za pomocą przewodu uziemiającego,
sprawdź zero na mierniku ładunku

Weź w rękę przewód uziemiający, przełącznik ustaw w pozycję A-B i ustaw U=50V na zasila-
czu.

Ustaw przełącznik w pozycję A-C i zmierz wartość ładunku Q a następnie rozładuj kondensator

Powtórz pomiary dla innych wartości napięć U. Uwaga!!! Używaj napięć nie większych niż
300V

Wyłącz zasilacz 450V i zmień okładki kondensatora na większe (A=80cm

2

i d=4mm).

Włącz zasilacz 450V. Ustaw przełącznik w pozycję A-C i rozładuj kondensator

Trzymając kabel uziemiający wykonaj drugą serię pomiarów.

Tabela 1: Ładunek Q w funkcji napięcia U i pojemności C dla różnych powierzchni okładek A.

U [V]

Q

400

[nAs]

(A=400cm

2

)

Q

800

[nAs]

(A=800cm

2

)

50

75

100

125

150

175

200

225

250

275

300

Laboratorium Fizyki; Ćwiczenie E-01. Badanie właściwości elektrycznych kondensatora płaskiego.

Katedra Podstaw Elektroniki, WEiI PK. Koszalin 2011.

3

3.2 Pomiar zależności ładunku kondensatora w funkcji przyłożonego napięcia dla różnych dielektry-

ków

Przełącznik musi być w pozycji A-C

Umieść polistyren między dużymi okładkami kondensatora (okładki powinny przylegać
dokładnie do polistyrenu)

Ustaw przełącznik w pozycji A-C i rozładuj kondensator

Trzymając kabel uziemiający, zmierz ładunek Q w funkcji napięcia U (wykonuj czyn-
ności w kolejności jak w punkcie a, Pamiętaj o używaniu napięcia niewiększego niż
300V)

Zamień polistyren na szkło, ustaw przełącznik w pozycję A-C i rozładuj kondensator.

Trzymają kabel uziemiający wykonaj drugą serię pomiarów.

Tabela 2: Ładunek Q w funkcji napięcia U i pojemności C dla różnych dielektryków.

U [V]

Q [nAs]

powietrze

Q [nAs]

polistyren

Q [nAs]

szkło

50

75

100

125

150

175

200

225

250

275

300

3.3 Wyznaczanie pojemności kondensatora w funkcji odległości między okładkami

Przełącznik musi być w pozycji A-C

Ustaw napięcie na 300V

Usuń szkło znajdujące się miedzy okładkami kondensatora i ustaw odległość między
okładkami na d=6mm

Rozładuj kondensator

Trzymając w ręce kabel uziemiający. Naładuj kondensator poprzez ustawienie prze-
łącznika w pozycji A-B.

Ustaw przełącznik w pozycji A-C, zmierz ładunek Q i zapisz wynik.

Zmieniaj odległość na 4,3,2 i 1mm, ładuj kondensator i mierz ładunek.

Tabela 3: Ładunek Q (przy U=300V) i pojemność C w funkcji odległości d między okładkami
kondensatora (A=800cm

2

)

d [mm]

Q [nAs]

6

5

4

3

2

1

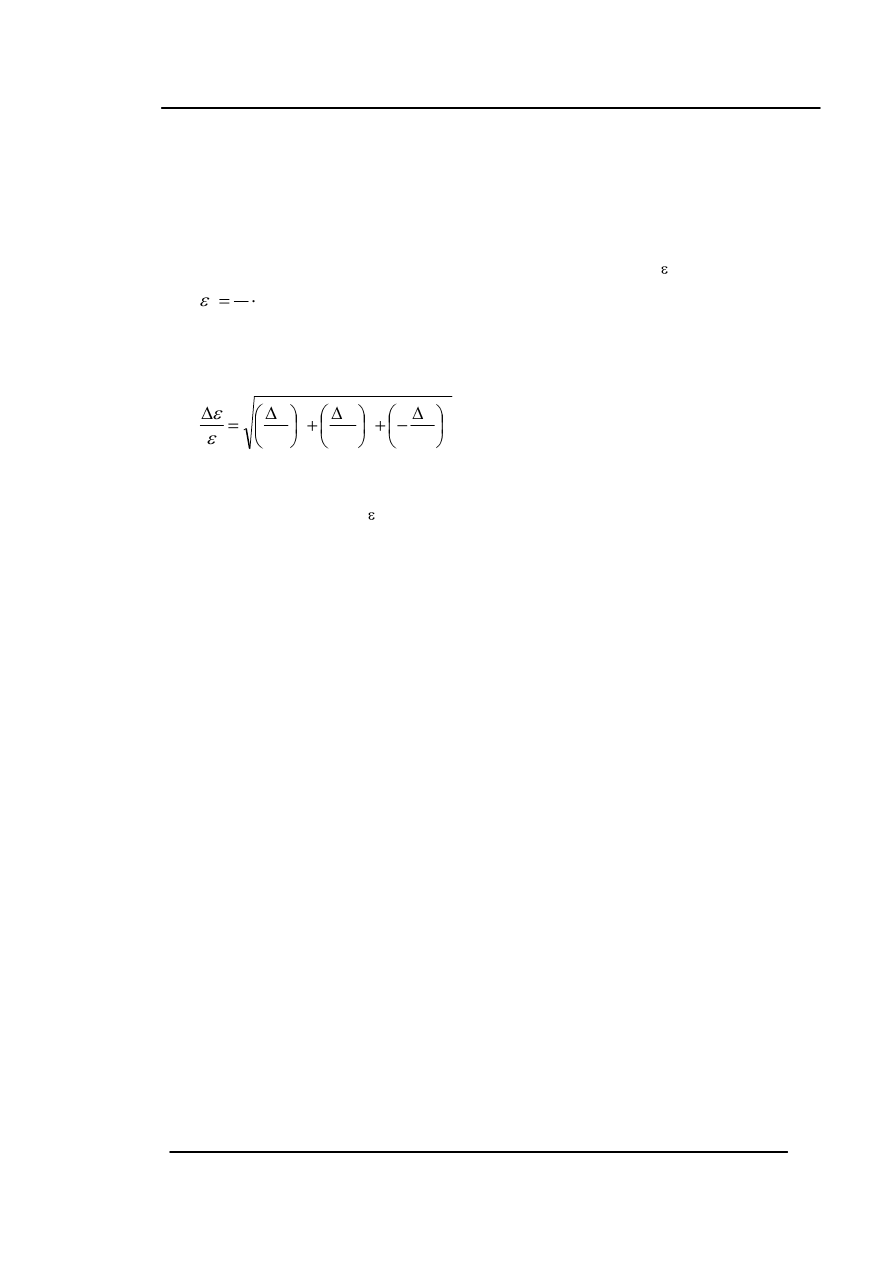
Laboratorium Fizyki; Ćwiczenie E-01. Badanie właściwości elektrycznych kondensatora płaskiego.

Katedra Podstaw Elektroniki, WEiI PK. Koszalin 2011.

4

4. Opracowanie wyników pomiarów

1. Wykonaj wykresy zależności ładunku Q od wartości napięcia U dla kondensatorów C

400

i C

800

na

bazie danych tabeli 1.

2. Z nachylenia prostych, przechodzących przez punkty pomiarowe, wyznacz pojemności kondensato-

rów C

400

i C

800

. Wyznacz również ich niepewności pomiarowe ΔC

400

i ΔC

800

. Wykorzystaj metodę

najmniejszych kwadratów.

3. Sprawdź proporcjonalność pojemności kondensatorów C

400

i C

800

do powierzchni ich okładek A.

4. Wyznacz doświadczalną wartość współczynnika przenikalności elektrycznej

0

korzystając ze wzoru:

C

A

d

0

gdzie jest współczynnikiem nachylenia prostej Q=f(U) wyznaczonym w pkt.2

5. Oszacuj niepewność pomiaru powierzchni okładek ΔA i odległości między okładkami Δd. Wyznacz

niepewność pomiaru współczynnika przenikalności elektrycznej dla każdego z badanych kondensa-
torów:

2

2

2

A

A

C

C

d

d

6. Oceń wpływ niedokładności poszczególnych parametrów (Δd, ΔA, ΔC) na niedokładność pomiaru

przenikalności elektrycznej.

7. Porównaj uzyskaną wartość

0

z wartością katalogową.

8. Wykonaj wykresy zależności ładunku Q od napięcia U na dużym kondensatorze (A=800cm

2

) dla

różnych dielektryków (powietrze, polistyren, szkło). Z nachylenia prostych przechodzących przez
punkty pomiarowe wyznacz pojemności kondensatorów C i ze stosunku C

szkło

/C

pow

i C

poly

/C

pow

wy-

znacz współczynniki przenikalności elektrycznej względnej ε

r

dla szkła i polistyrenu. Określ niepew-

ność pomiaru współczynnika przenikalności elektrycznej względnej ε

r

. Porównaj otrzymane wartości

z danymi katalogowymi.

9. Przeanalizuj otrzymane wyniki badań i sformułuj odpowiednie wnioski.

Laboratorium Fizyki; Ćwiczenie E-01. Badanie właściwości elektrycznych kondensatora płaskiego.

Katedra Podstaw Elektroniki, WEiI PK. Koszalin 2011.

5

Protokół pomiarowy

Ćw. E-01.

Laboratorium z fizyki

Rok akadem:

Temat:
Badanie właściwości elektrycznych kondensatora pła-
skiego

Kierunek:

Grupa:

Imię i Nazwisko:

Ocena

Data Zaliczenia

Podpis

L

S

K

Tabela 1: Ładunek Q w funkcji napięcia U i pojemności C dla różnych powierzchni okładek A.

U [V]

Q

400

[nAs] (A=400cm

2

) Q

800

[nAs] (A=800cm

2

)

50

75

100

125

150

175

200

225

250

275

300

Tabela 2: Ładunek Q w funkcji napięcia U i pojemności C dla różnych dielektryków.

U [V]

Q [nAs]
powietrze

Q [nAs]
polistyren

Q [nAs]
szkło

50

75

100

125

150

175

200

225

250

275

300

Tabela 3: Ładunek Q (przy U=300V) i pojemność C w funkcji odległości d między okładkami kondensa-
tora (A=800cm

2

)

d [mm]

Q [nAs]

1

2

3

4

5

6