Zagadnienia statycznie niewyznaczalne

 

 

Energia sprężysta prętów 

W zasadzie energii, która zakłada równość przyrostu energii kinetycznej ciała i pracy sił 

działających  na  ciało  odkształcalne,  należy  uwzględnić  zarówno  siły  zewnętrzne,  jak  i  też 

wewnętrzne.  

∆E = L + A 

gdzie: 

∆E – przyrost energii kinetycznej, 

L – praca sił zewnętrznych, 

A – praca sił wewnętrznych. 

Praca sił wewnętrznych w materiale doskonale sprężystym jest odwracalna i określa się 

ją  jako  energię  potencjalną  wewnętrznych  sił  sprężystości  lub  krócej  energią  sprężystą. 

Podstawiając: 

A = -U 

uzyskujemy: 

∆E + U = L. 

Energia  sprężysta  w  stanie  nienaprężonym  i  nieodkształconym  jest  równa  zero. 

Ponieważ energię sprężystą obliczać będziemy dla stanu równowagi więc: 

∆E = 0, 

wówczas: 

U = L. 

Energia  sprężysta  równa  jest  pracy  sił  zewnętrznych  i  do  obliczenia  tej  pracy  musimy 

sobie wyobrazić, że proces obciążenia siłami odbywa się w sposób statyczny, to znaczy, że w 

każdej  chwili  była  zachowana  równowaga  między  siłami  zewnętrznymi  i  wewnętrznymi. 

Czas  takiego  idealnego  procesu  jest  nieskończenie  wielki,  natomiast  szybkość  narastania 

odkształcenia – równa zero.  

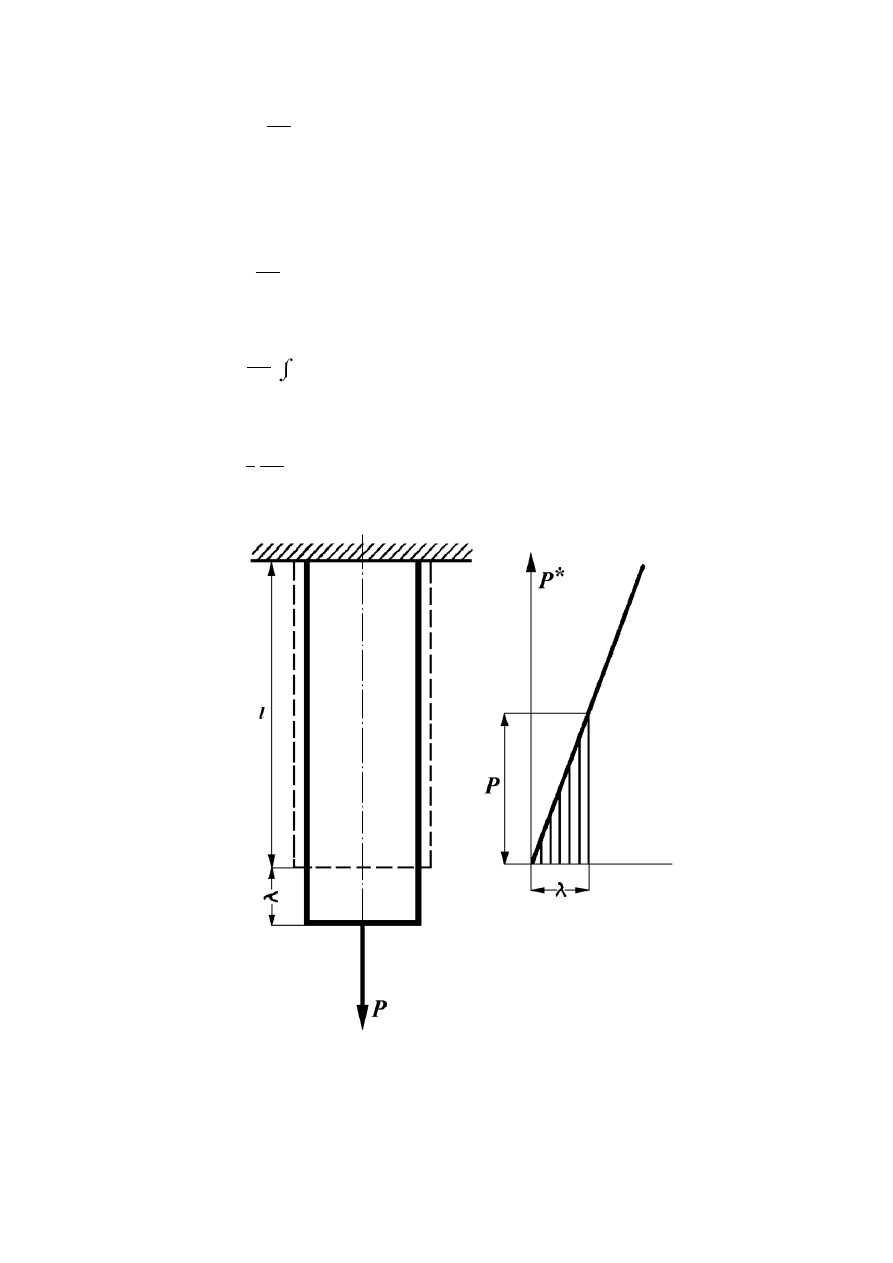
Wychodząc z tego założenia, obliczymy  energię  sprężystą pręta rozciąganego siłą  P o 

wydłużeniu  λ  (rys.  8.1).  Pod  P

*

  i  λ

*

  będziemy  rozumieli  wielkości  zmienne  w  czasie 

statycznego obciążenia.  

Praca elementarna wynosi: 

dL = P

*

 dλ

*

, 

po podstawieniu: 

P

*

 = λ

* 

EA

l

 

, 

oraz: 

L = U, 

otrzymamy: 

dU = 

EA

l

 λ

*

 dλ

*

, 

i po scałkowaniu wyrażenia; 

U = 

EA

l

  

0

λ

λ

*

 dλ

*

 , 

otrzymamy: 

U = 

1
2

 

EA

l

 λ

2

.   

 

 

 

 

 

 

 

(8.1) 

 

 

 

 

 

 

 

 

 

 

 

 

 

Rys. 8.1 

 

Podstawiając zgodnie z prawem Hooke’a (wzór 5.4): 

λ = 

Pl

EA

 

,

 

otrzymujemy: 

U = 

1
2

 ·

P

2

l

EA

  

 

 

 

 

 

 

 

 

(8.2) 

lub: 

U = 

1
2

 P λ 

 

 

 

 

 

 

 

 

(8.3) 

Do  identycznego  wyniku  dojdziemy  wyliczając  prace  wprost  z  wykresu  rozciągania 

(powierzchnia zakreskowanego trójkąta - rys. 8.1). 

Wzór  ten  jest  również  ważny  dla  ściskania.  Pozostałe  wzory  na  energię  sprężystą 

jednostki długości pręta napiszemy przez analogię. 

W liczniku wyrażenia (8.2) występuje kwadrat siły (P) a w mianowniku sztywność.  

Wartość energii sprężystej w przypadku zginania wynosi: 

 

 

U

Mg

 = 

M

g

2

 

2 ·E ·J    

 

 

 

 

 

 

 

(8.3) 

natomiast dla skręcania: 

 

 

U

Ms

 = 

M

s

2

 

2 ·G ·J

o

   

 

 

 

 

 

 

 

(8.4) 

 

Twierdzenie A. Castigliano

 

Pochodna cząstkowa  energii sprężystej  całego układu  liniowo  - sprężystego względem 

jednej  z  niezależnie  działających  sił  obciążających  jest  równa  odpowiadającemu  tej  sile 

przemieszczeniu. 

 

 

δU

δP = p  

 

 

 

 

 

 

 

 

(8.5) 

Powyższa  formuła  wyraża  twierdzenie  Castigliano.  Uważając  energię  sprężystą  za 

jednorodną  kwadratową  funkcję  przemieszczeń,  traktowanych  jako  zmienne  niezależne, 

możemy twierdzenie Castigliano odwrocić: 

 

 

δU

δp = P  

 

 

 

 

 

 

 

 

(8.6) 

Pochodna  cząstkowa  energii  sprężystej  względem  przemieszczenia  równa  się 

odpowiadającej  mu  sile.  Jako  energię  sprężystą  uwzględniamy  energię  pochodzącą  od 

zginania,  gdyż  część  energii,  wynikająca  z  istnienia  siły  poprzecznej  T,  jest  nieznaczna  w 

porównaniu  z  energią  pochodzącą  od  zginania;  wobec  tego  ograniczamy  się  tylko  do  tej 

pierwszej. 

Jeżeli w zagadnieniu poszukiwane przemieszczenie odpowiada rzeczywiście działającej 

sile,  zastosowanie  do  jego  wyznaczenia  twierdzenia  Castigliano  nie  nastręcza  żadnych 

trudności.  Gdy natomiast poszukujemy przemieszczenia, dla którego brak rzeczywistej siły, 

należy  założyć  w  schemacie  obciążeń  fikcyjną  siłę  P

*

  odpowiadającą  poszukiwanemu 

przemieszczeniu, aby w ostatecznym wyniku podstawić jej rzeczywistą wartość równą zeru. 

 

Twierdzenie o minimum energii Menabrea – Castigliano

 

Wskutek  obciążenia  układu  siłami  czynnymi  P

i

  w  podporach  (więzach)  powstają 

reakcje  R

i

.  Jeżeli  podparcie  jest  sztywne  i  bez  tarcia,  to  przemieszczenie  odpowiadające 

reakcji wynosi zero.  

Korzystając z twierdzenia Castigliano możemy to wyrazić w następujący sposób: 

 

 

δU
δR = 0, 

 

 

 

 

 

 

 

 

(8.7) 

gdyż przemieszczenie w kierunku działania reakcji jest równe zero. 

Wzór  (8.7)  wyraża  nam  twierdzenie  Menabrea-Castigliano:  w  układzie  liniowo  - 

sprężystym  sztywnie  podpartym  pochodna  cząstkowa  energii  sprężystej  całego  układu 

względem wielkości podporowej – statycznie niewyznaczalnej - jest równa zero. 

Twierdzenie Menabrea  –  Castigliano nazywane jest  również twierdzeniem  o minimum 

energii układów liniowo - sprężystych lub krócej – zasadą najmniejszości energii. 

Metodyka  postępowania  przy  stosowaniu  twierdzenia  Menabrea  –  Castigliano  jest 

następująca: 

-  zaznaczamy reakcje oraz piszemy warunki równowagi, 

-  stwierdzamy krotność statycznej niewyznaczalności układu, 

-  obieramy wielkości statycznie niewyznaczalne, 

-  wyrażamy  energię  sprężystą  jako  funkcję  sił  czynnych  i  tych  reakcji,  które  w  punkcie 

poprzednim uznaliśmy za statycznie niewyznaczalne, 

-  piszemy  zgodnie  z  twierdzeniem  Menabrea  –  Castigliano  równania 

δU

δR =  0  i  z  nich 

wyznaczamy wielkości statycznie niewyznaczalne, 

-  pozostałe wielkości podporowe wyznaczamy z równań równowagi. 

Główną  zaletą  tej  metody  jest  to,  że  sam  sposób  rozwiązywania  równań  jest 

schematyczny i nie wymaga wielkiego nakładu sił.