203

Przykłady (twierdzenie A. Castigliano)

Zadanie 8.4.1

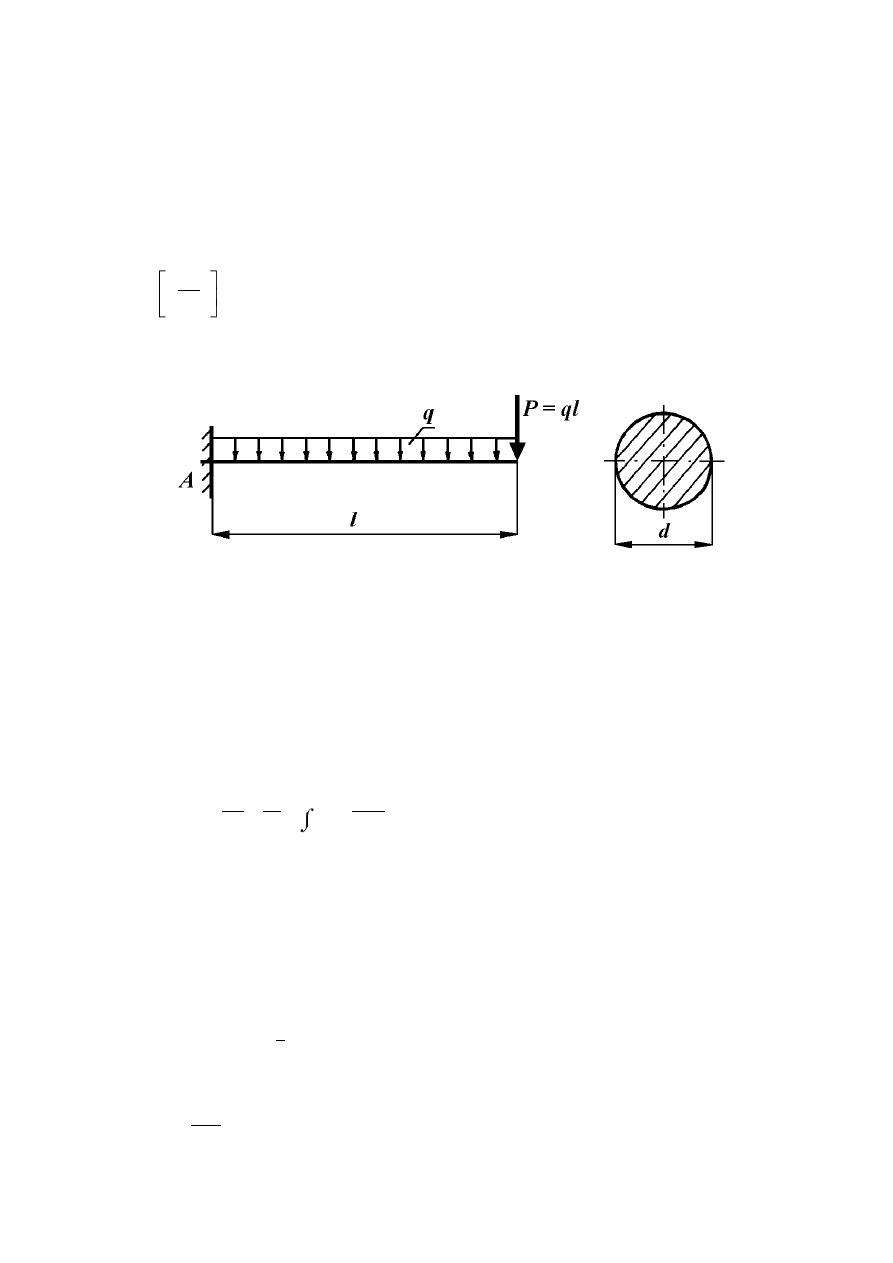
Obliczyć maksymalne ugięcie belki przedstawionej na rysunku (8.2). Do obliczeń

przyjąć następujące dane:

q = 10

kN

m

, l = 1 [m], E = 2 ·10

7

[Pa], d = 4 [cm], P = ql.

W obliczeniach pominąć wpływ siły poprzecznej T.

Rys. 8.2

Rozwiązanie:

Energia sprężysta przedstawionego układu zależy od funkcji momentu zginającego (siły

normalne i momenty skręcające nie występują).

Zgodnie z twierdzeniem Castigliano współrzędna uogólniona przemieszczenia p

i

odpowiadająca sile uogólnionej P

i

, jest równa pochodnej cząstkowej energii sprężystej U

danego układu względem tej siły (dla stałej sztywności zginania EJ).

p

i

=

δU
δP

i

=

1

EJ

Σ

l

i

M

gi

·

δM

gi

δP

i

d

xi

Maksymalne ugięcie dla belki wystąpi w punkcie przyłożenia siły P, więc siłą

uogólnioną odpowiadającą maksymalnemu przemieszczeniu (ugięciu) będzie siła P.

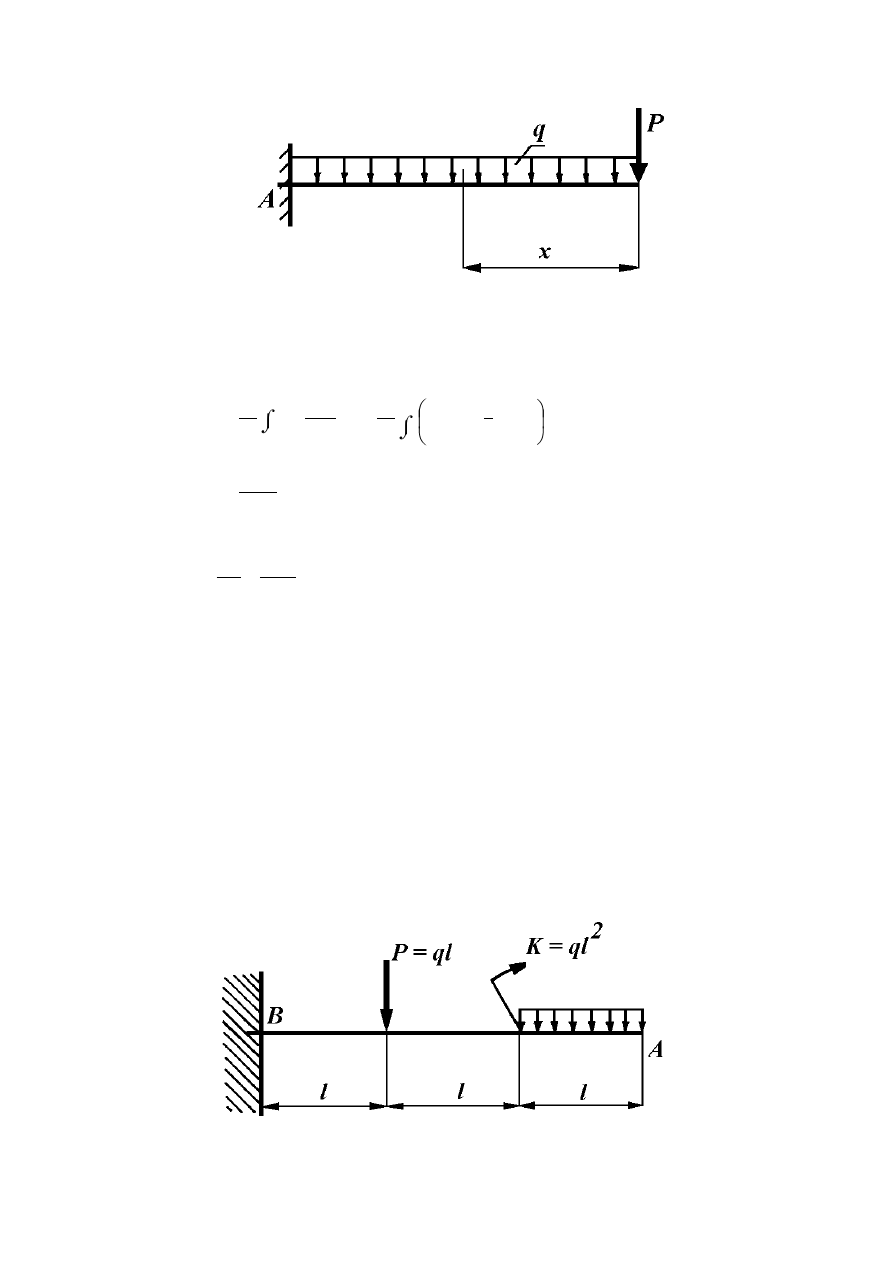
Funkcja momentu zginającego oraz pochodna cząstkowa momentu zginającego podług

siły P (rys. 8.3) wynosi dla:

0 ≤ x ≤ l

M

g

= - Px -

1
2

·qx

2

,

stąd:

δM

g

δP

i

= - x

204

Rys. 8.3

Maksymalne ugięcie wynosi:

p

max

=

1

EJ

0

l

M

g

·

δM

g

δP dx =

1

EJ

0

l

- Px -

1
2

·qx

2

(- x) dx

p

max

=

11ql

2

24EJ

Po wstawieniu danych z tematu zadania oraz przyjęciu, że:

J =

πd

4

64

=

π(4)

4

64

J = 12,56 [cm

4

],

otrzymamy:

p

max

= 1,82 [cm].

Zadanie 8.4.2

Obliczyć ugięcie w punkcie A belki o sztywności EJ przedstawionej na rysunku 8.4.

Wpływ sił poprzecznych na ugięcie belki pominąć.

Dane: q. L. EJ.

Rys. 8.4

205

Rozwiązanie:

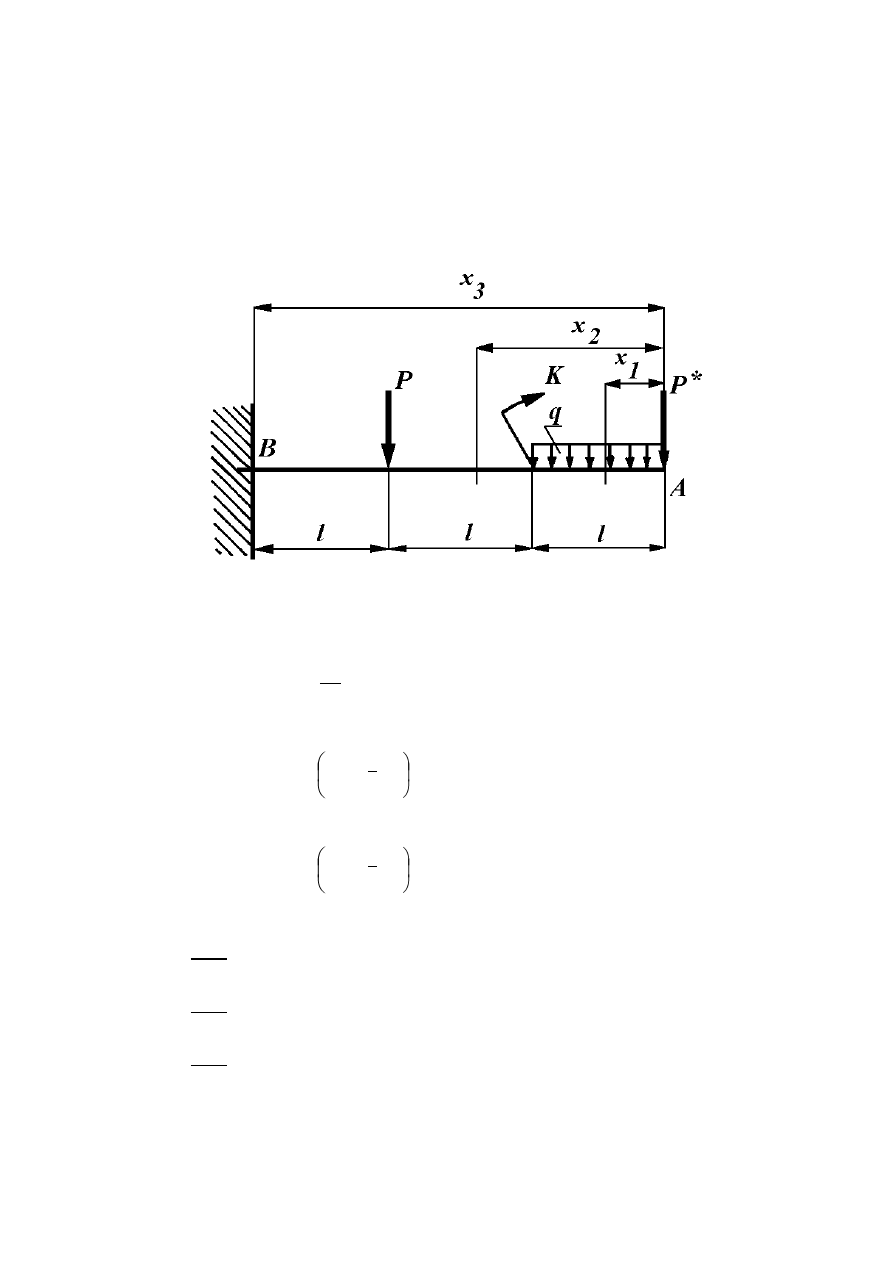
W celu wyznaczenia ugięcia belki w punkcie A, przykładamy siłę fikcyjną P

*

= 0

(rys. 8.5), o kierunku szukanego przemieszczenia. Funkcje wielkości sił wewnętrznych

(momentów zginających) w poszczególnych przedziałach wynoszą odpowiednio:

Rys. 8.5

0 ≤ x

1

≤ l

M

g1

= - P

*

x

1

– q ·

x

2

1

2

,

l ≤ x

2

≤ 2l

M

g2

= - P

*

x

2

– ql

x

2

-

1
2

·l

– K,

2l ≤ x

3

≤ 3l

M

g3

= - P

*

x

3

– ql

x

3

-

1
2

·l

– K – P(x

3

– 2l).

Pochodne cząstkowe podług siły fikcyjnej P

*

wynoszą:

δM

g1

δP

*

= - x

1

,

δM

g2

δP

*

= - x

2

,

δM

g3

δP

*

= - x

3

.

Ugięcie w punkcie A wynosi więc:

206

p

A

=

1

EJ

0

l

M

g1

·

δM

g1

δP

*

dx

1

+

l

2l

M

g2

·

δM

g2

δP

*

dx

2

+

2l

3l

M

g3

·

δM

g3

δP

*

dx

3

Po wstawieniu odpowiednich wartości liczbowych i scałkowaniu otrzymamy:

p

A

=

579ql

2

24EJ

.

Zadanie 8.4.3

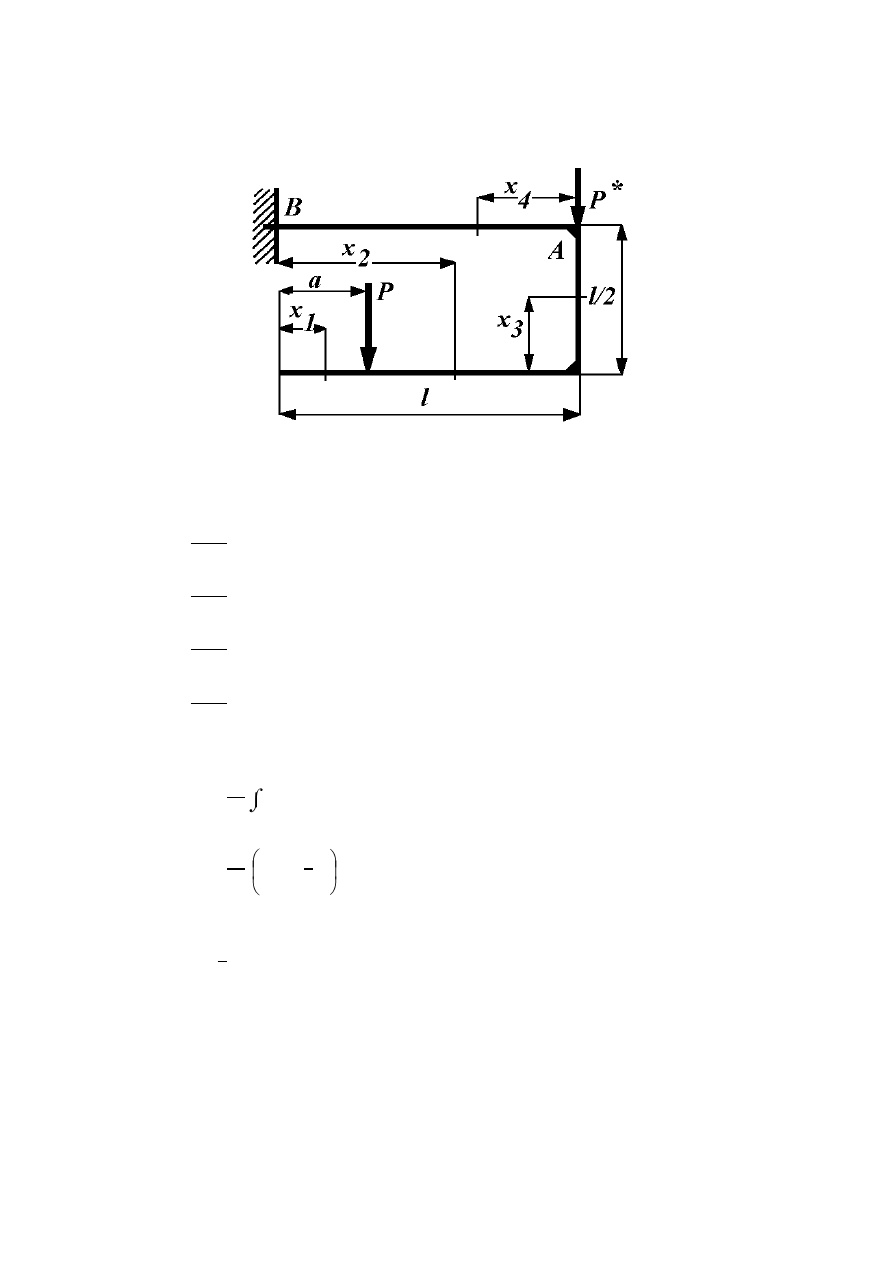
W jakiej odległości a od końca pręta (rys. 8.6), należy przyłożyć siłę aby

przemieszczenie punktu A było równe zero ?.

Dane: P, l, EJ = const.

Rys. 8.6

Rozwiązanie:

Aby obliczyć przemieszczenie punktu A, przykładamy w tym punkcie fikcyjną siłę P

*

o

wartości równej zero (rys. 8.7). Wartości momentów zginających w poszczególnych

przedziałach ramy wynoszą odpowiednio:

0 ≤ x

1

≤ a

M

g1

= 0

a ≤ x

2

≤ 2l

M

g2

= - P(x

2

– a)

0 ≤ x

3

≤ l

M

g3

= - P(2l – a)

0 ≤ x

4

≤ 2l

207

M

g4

= - P(2l – a – x

4

) – P

*

x

4

Rys. 8.7

Pochodne cząstkowe podług siły fikcyjnej P

*

wynoszą odpowiednio:

δM

g1

δP

*

= 0,

δM

g2

δP

*

= 0,

δM

g3

δP

*

= 0,

δM

g4

δP

*

= - x

4

,

czyli ugięcie w punkcie A będzie wynosiło:

p

A

=

1

EJ

0

l

[P(2l - a - x

4

)] ( - x

4

) dx

4

p

A

=

P

EJ

2a -

4
3

l

.

Ugięcie punktu A będzie równe wtedy zero, kiedy siła P będzie przyłożona w odległości a:

a =

2
3

l (od swobodnego końca belki).

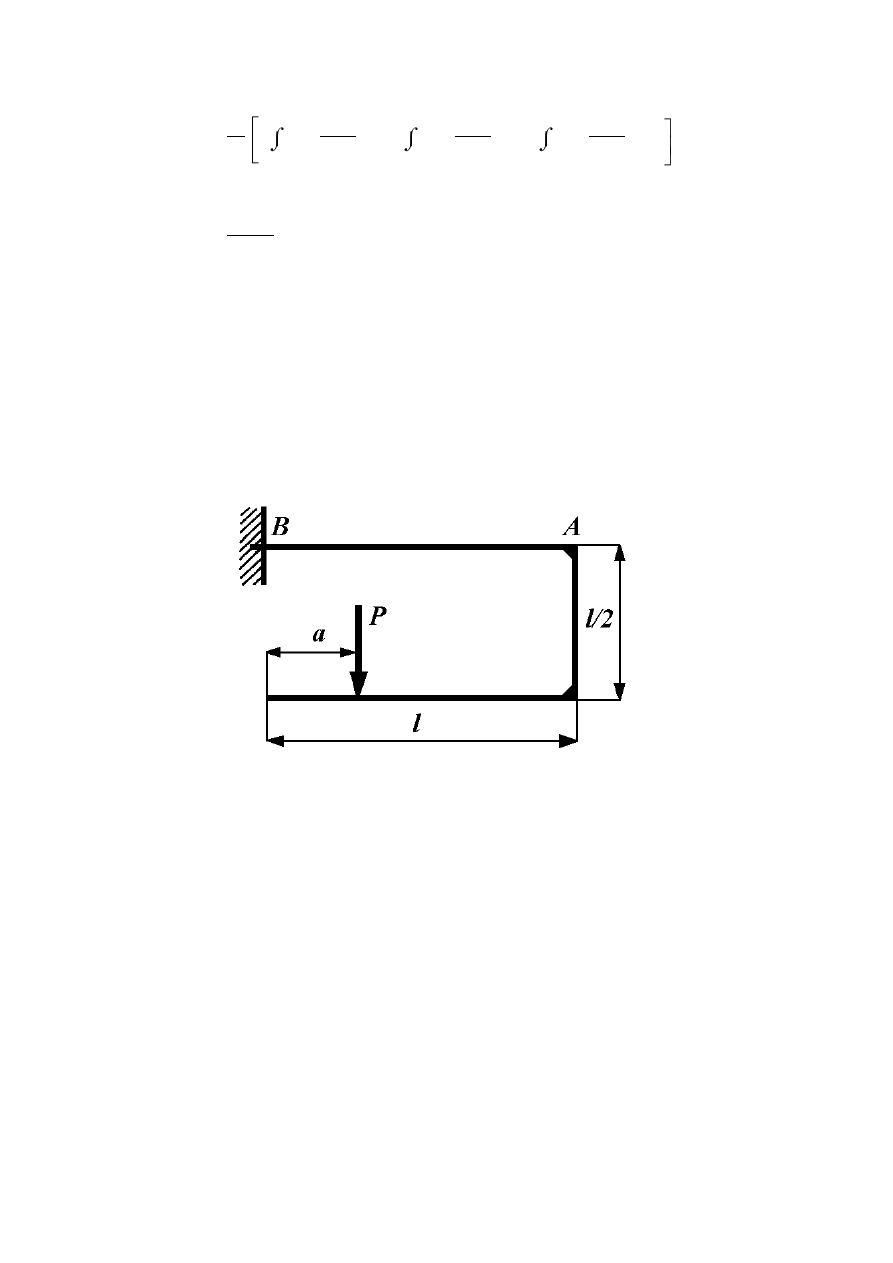
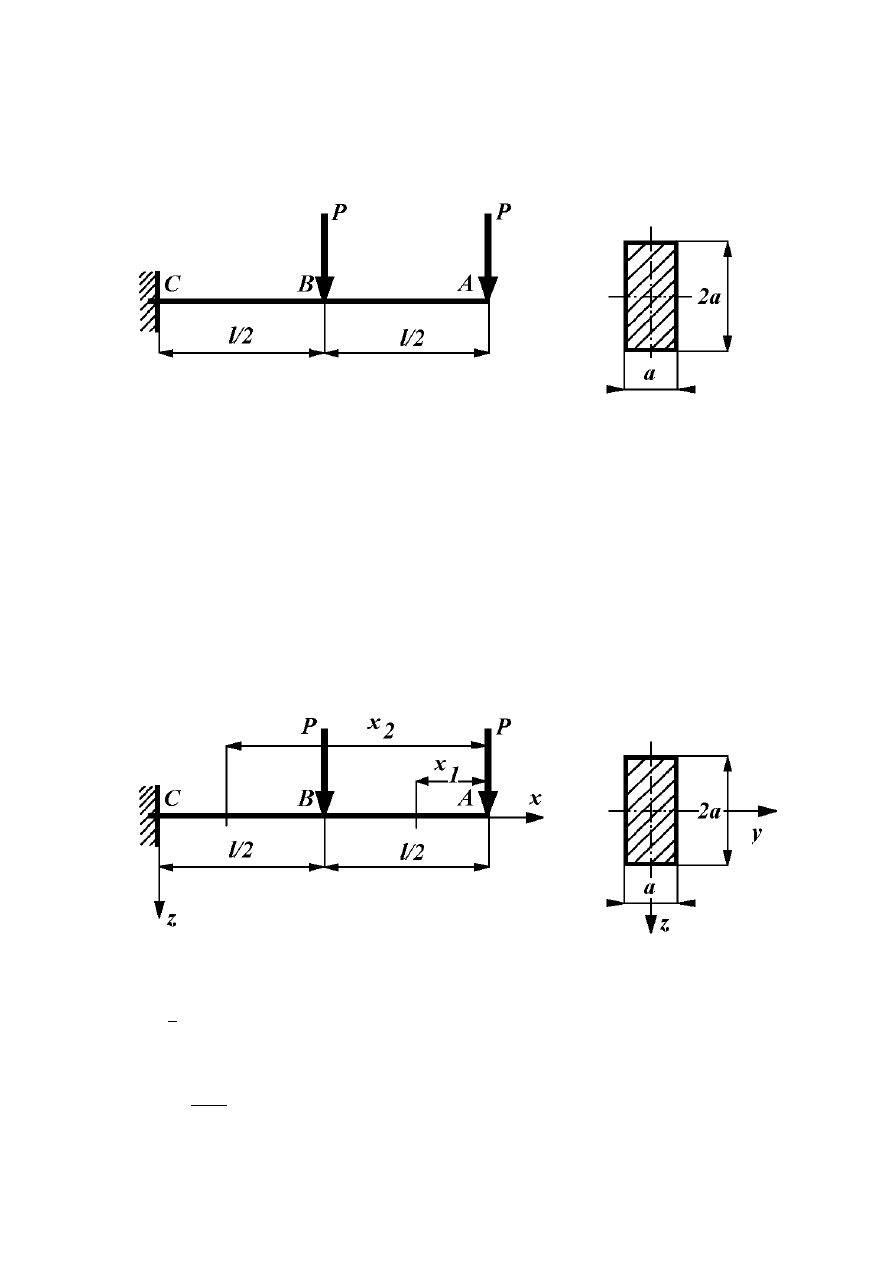
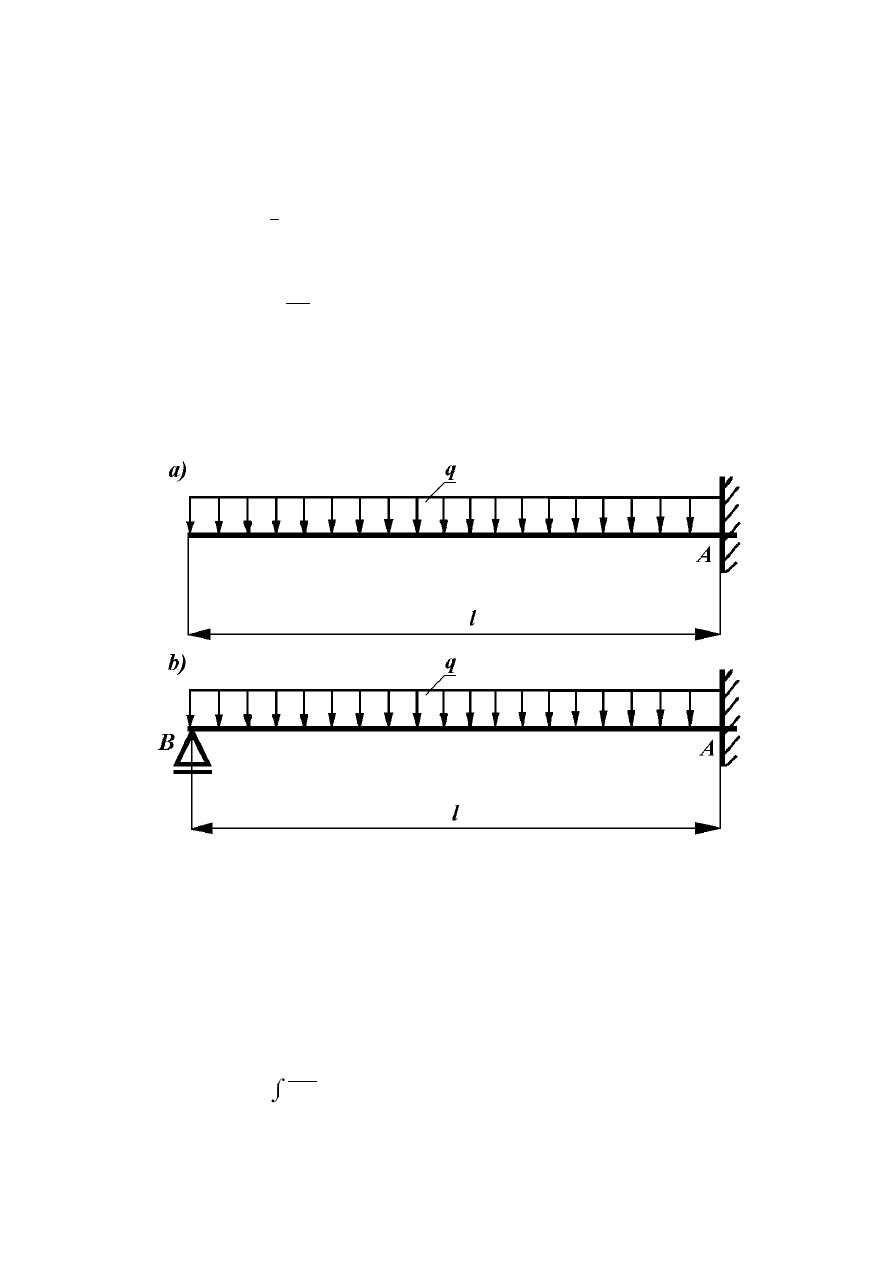
Zadanie 8.4.4

Zaprojektować przekrój stalowej belki zamocowanej i obciążonej jak na rysunku (8.8)

wiedząc, że dopuszczalne maksymalne ugięcie może wynosić p

dop

= 0,25 [cm].

208

Przyjąć, że naprężenia maksymalne nie mogą przekroczyć wartości k

g

= 28 [Pa].

Dane: P = 10 [kN], l = 2 [m], EJ = const, E = 2 ·10

5

[MPa].

Rys. 8.8

Rozwiązanie:

W celu zaprojektowania przekroju belki należy wyznaczyć rzeczywiste maksymalne

ugięcie wywołane obciążeniem zewnętrznym. Ugięcie to nie może przekroczyć ugięcia

dopuszczalnego p

dop

. Z charakteru obciążenia wynika, że maksymalne ugięcie belki wystąpi

w punkcie A.

Funkcje momentów zginających w poszczególnych przedziałach (rys. 8.9) i ich

pochodne cząstkowe podług siły P wynoszą:

Rys. 8.9

0 ≤ x

1

≤

1
2

M

g1

= - Px

1

,

δM

g1

δP = - x

1

,

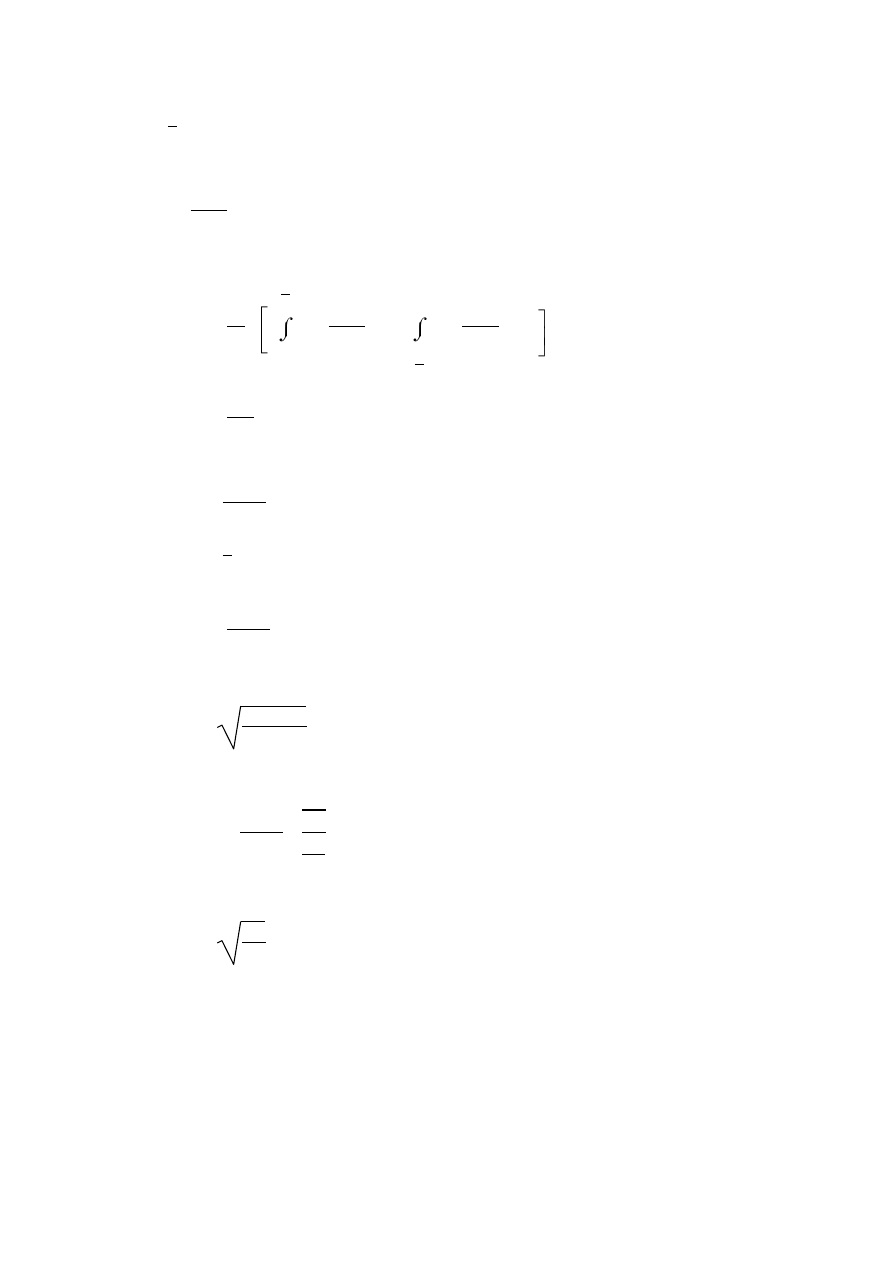
209

0 ≤ x

1

≤

1
2

M

g2

= - Px

2

– P(x

2

– 1),

δM

g2

δP = - x

2

.

Przemieszczenie punktu A wynosi:

p

A

=

1

EJ

·

0

l

2

M

g1

·

δM

g1

δP dx

1

+

l

2

l

M

g2

·

δM

g2

δP dx

2

p

A

=

Pl

3

4EJ

.

Moment bezwładności przekroju względem osi y wynosi:

J

y

=

a(2a)

3

12

J

y

=

2
3

·a

4

,

czyli:

p

A

=

3Pl

3

8E ·a

4

≤ p

dop

stąd:

a ≥

4

3Pl

3

8 ·E ·p

dop

.

Naprężenia maksymalne wystąpią w punkcie C i wyniosą:

σ

max

=

M

gmax

W

g

=

3Pl

2

2a

3

3

≤ k

g

,

czyli:

a ≥

3 9Pl

4k

g

.

Po podstawieniu wartości podanych w temacie zadania otrzymamy:

- z warunku na dopuszczalny kąt ugięcia:

a ≥ 8,81 [cm],

- z warunku na dopuszczalne naprężenie:

a ≥ 5,44 [cm].

Ostatecznie przyjmujemy: a = 9 [cm].

210

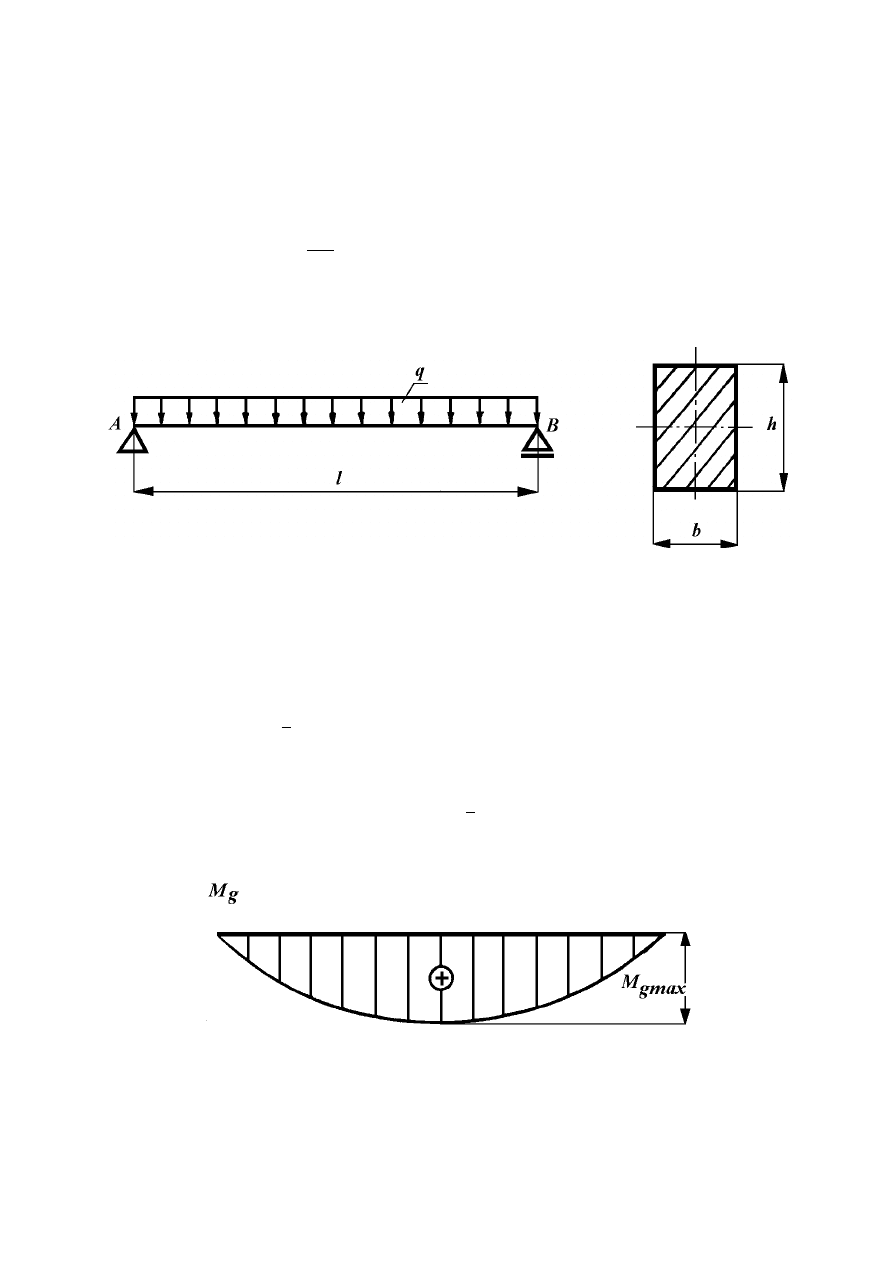
Zadanie 8.4.5

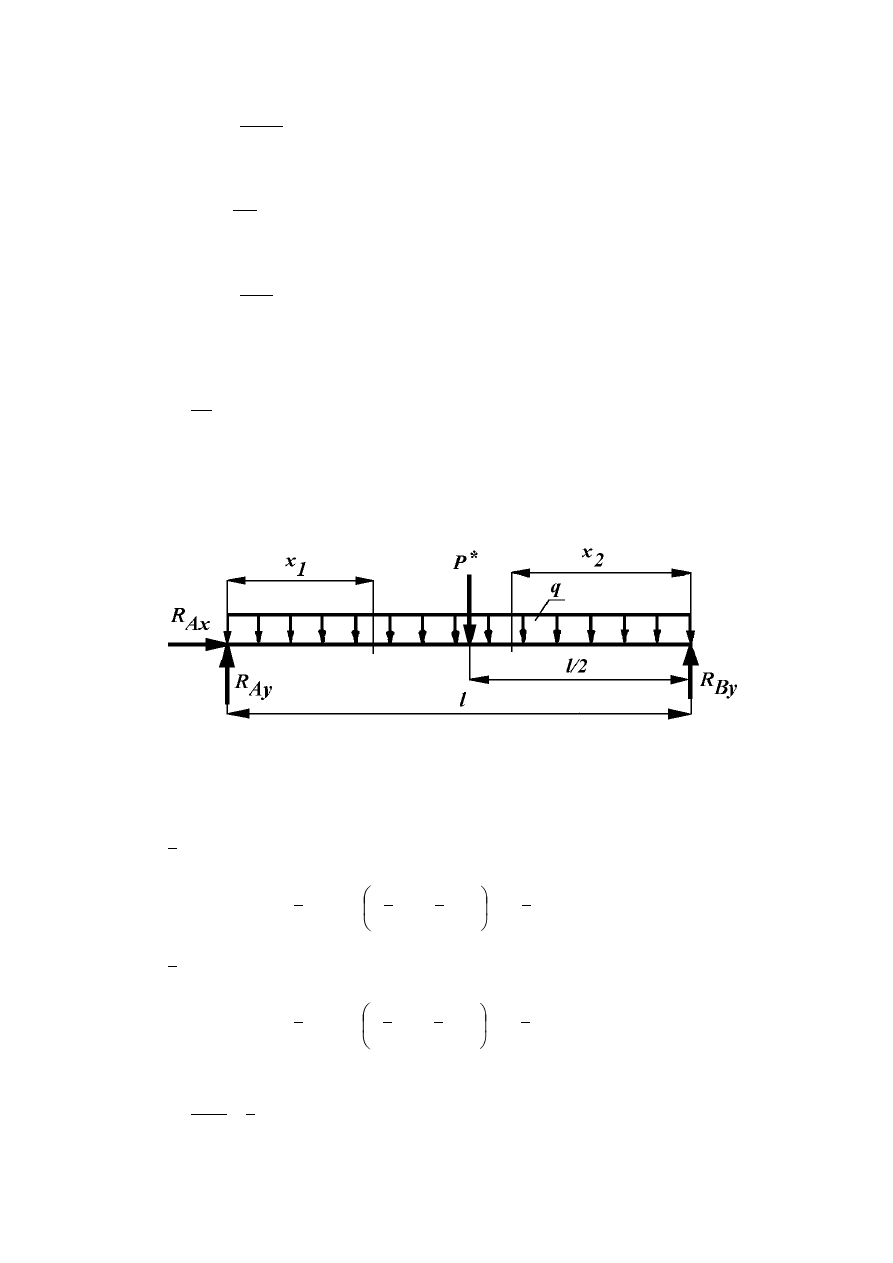
Stalowa belka o przekroju prostokątnym i długości l, podparta w dwóch miejscach

obciążona jest w sposób równomierny obciążeniem ciągłym q (rys. 8.10). Maksymalne

naprężenia normalne powstałe w przekroju poprzecznym wynoszą σ

max

= 6000 [Pa], a

maksymalne ugięcie p

max

=

l

600

.

Określić stosunek wysokości belki h do jej długości l.

Rys. 8.10

Rozwiązanie:

Wartości reakcji podporowych wyznaczone z równań równowagi wynoszą:

R

Ax

= 0

R

Ay

= R

By

=

1
2

·ql.

Z wykresu momentu zginającego przedstawionego na rys. 8.11 wynika, że maksymalne

naprężenia wystąpią w środku belki, czyli dla x =

1
2

l.

Rys. 8.11

Naprężenia normalne wywołane momentem zginającym wynoszą:

211

σ

max

=

M

gmax

W

g

≤ k

g

Wskaźnik zginania dla belki o przekroju prostokątnym wynosi:

W

g

=

bh

2

6

czyli:

σ

max

=

3ql

2

4bh

2

σ

max

= 6000 [Pa].

Maksymalne ugięcie wyznaczymy stosując twierdzenie Castigliano (wzór 8.5):

δU

δP = p.

Z charakteru obciążenia wynika, że maksymalne ugięcie wystąpi w środku belki.

Przykładamy więc w tym miejscu siłę fikcyjną P

*

= 0 (rys. 8.12).

Rys. 8.12

Funkcje momentów zginających w poszczególnych przedziałach wynoszą:

0 ≤ x

1

≤

1
2

l

M

g1

= R

Ay

x

1

-

1
2

·qx

2

1

=

1
2

·ql +

1
2

·P

*

x

1

-

1
2

·qx

2

1

0 ≤ x

2

≤

1
2

l

M

g2

= R

By

x

2

-

1
2

·qx

2

2

=

1
2

·ql +

1
2

·P

*

x

2

-

1
2

·qx

2

2

Pochodne cząstkowe podług uogólnionej siły P

*

wynoszą:

δM

g1

δP

*

=

1
2

·x

1

,

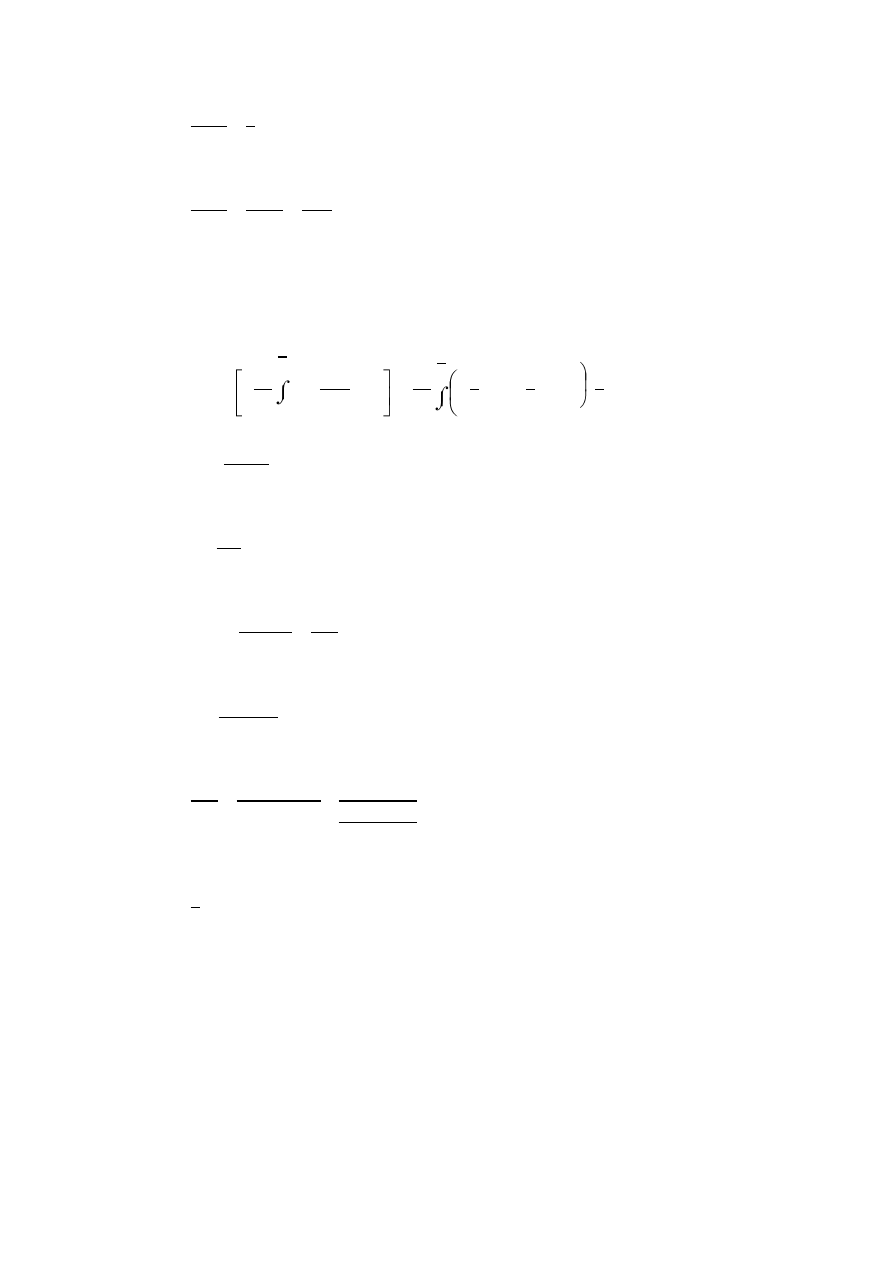
212

δM

g2

δP

*

=

1
2

·x

2

.

Uwzględniając symetrię układu, czyli:

δM

g1

δP

*

=

δM

g2

δP

*

=

δM

g

δP

*

,

oraz, że:

P

*

= 0,

ugięcie w punkcie C jest równe:

p

c

= 2

1

EJ

0

l

2

M

g

·

δM

g

δP

*

dx

=

2

EJ

0

l

2

1
2

·qlx -

1
2

·qx

2

1
2

·xdx

p

c

=

5gl

4

384EJ

= p

max

Moment bezwładności przekroju dla prostokąta wynosi:

J =

bh

3

12

,

czyli:

p

max

=

5gl

4

32bh

3

E

=

l

600

Obliczamy szerokość przekroju b ze wzoru na maksymalne naprężenia:

b =

3ql

2

600 ·4h

2

i podstawiając do wzoru na maksymalne ugięcie otrzymamy:

l

600

=

5gl

4

32h

3

·2 ·10

7

·

1

3ql

2

6000 ·4 ·h

2

Po uporządkowaniu i obliczeniu otrzymujemy:

h

l

= 0,0375.

213

Przykłady (twierdzenie Menabrea-Castigliano)

Zadanie 8.5.1

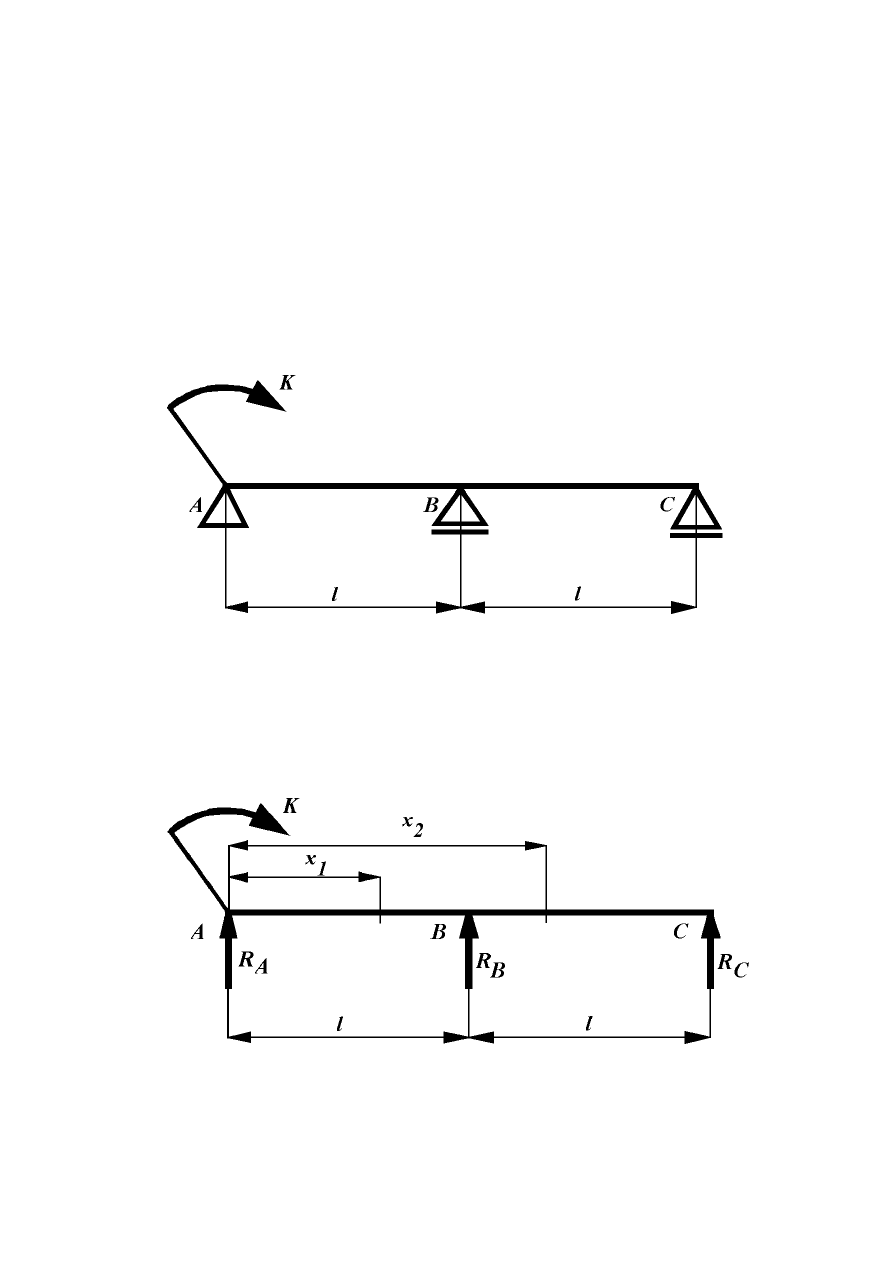
Dla belki dwuprzęsłowej (rys. 8.23) obciążonej na podporze A momentem skupionym

K, obliczyć reakcje podporowe oraz sporządzić wykres momentów zginających.

Dane: K, l, EJ = const.

Rys. 8.23

Rozwiązanie:

Belka stanowi układ jednokrotnie statycznie niewyznaczalny. Za wielkość

hiperstatyczną przyjmujemy reakcję R

A

(rys. 8.24).

Rys. 8.24

Funkcje momentów zginających w poszczególnych przedziałach mają postać:

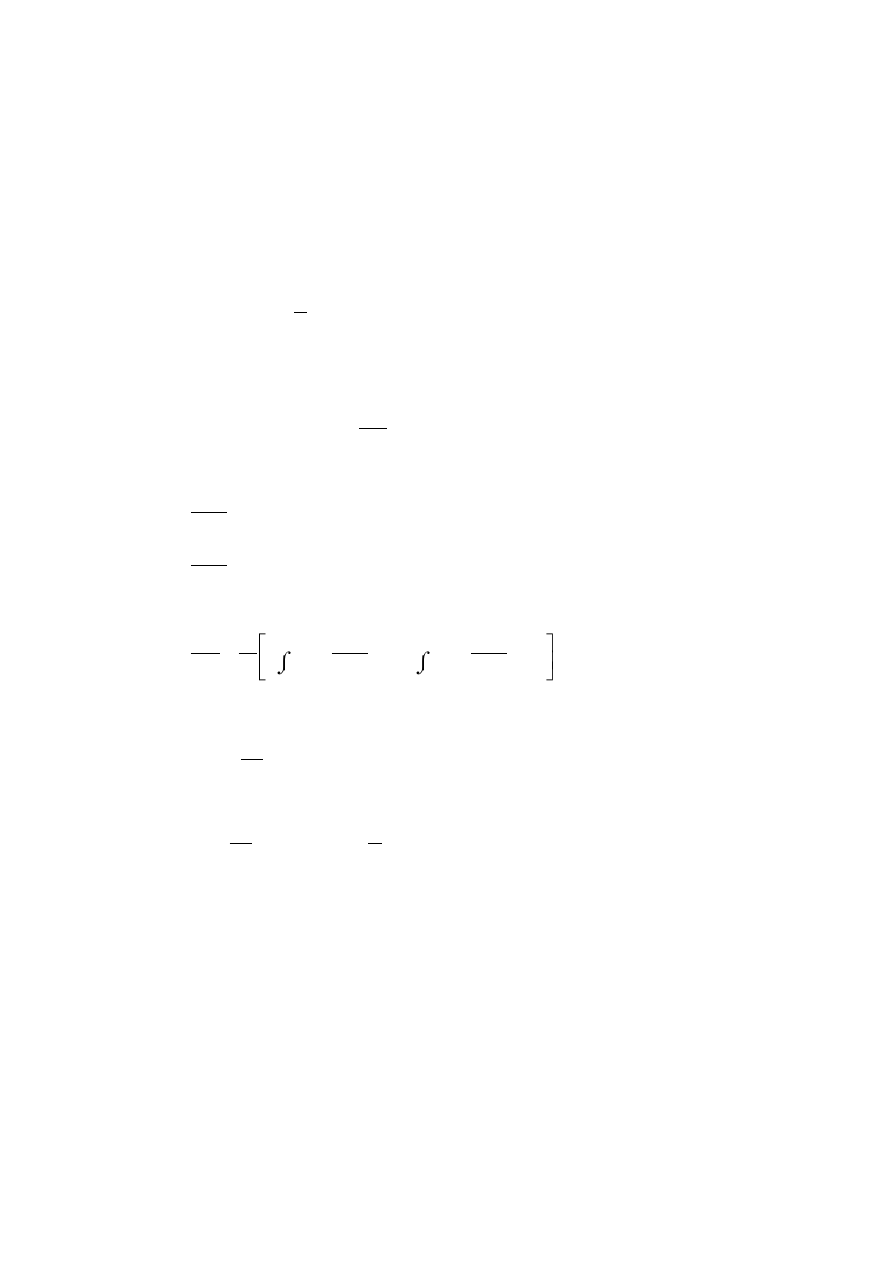
214

0 ≤ x

1

≤ l

M

g1

= R

A

x

1

+ K

l ≤ x

2

≤ 2l

M

g2

= R

A

x

2

+ K + R

B

(x

2

– l)

Występującą w równaniach reakcję R

B

wyrazimy za pomocą reakcji hiperstatycznej R

A

(korzystając z równań równowagi):

R

B

= - 2 ·R

A

-

K

l

,

czyli równania określające momenty zginające mają postać:

M

g1

= R

A

+ K,

M

g2

= 2 ·R

A

·l – R

A

x

2

-

Kx

2

l

+ 2 ·K.

Pochodne cząstkowe podług reakcji hiperstatycznej R

A

wynoszą:

δM

g1

δR

A

= x

1

,

δM

g2

δR

A

= 2l – x

2

.

Wykorzystując twierdzenie Menabrea-Castigliano otrzymujemy (wzór 8.7):

δU

δR

A

=

1

EJ

0

l

M

g1

·

δM

g1

δR

A

dx

1

+

l

2l

M

g2

·

δM

g2

δR

A

dx

2

= 0

Po podstawieniu wartości i scałkowaniu otrzymamy:

R

A

= -

5K

4l

.

Pozostałe reakcje zostały wyznaczone z równań równowagi i wynoszą:

R

B

=

3K

2l

,

R

C

= -

K

4l

.

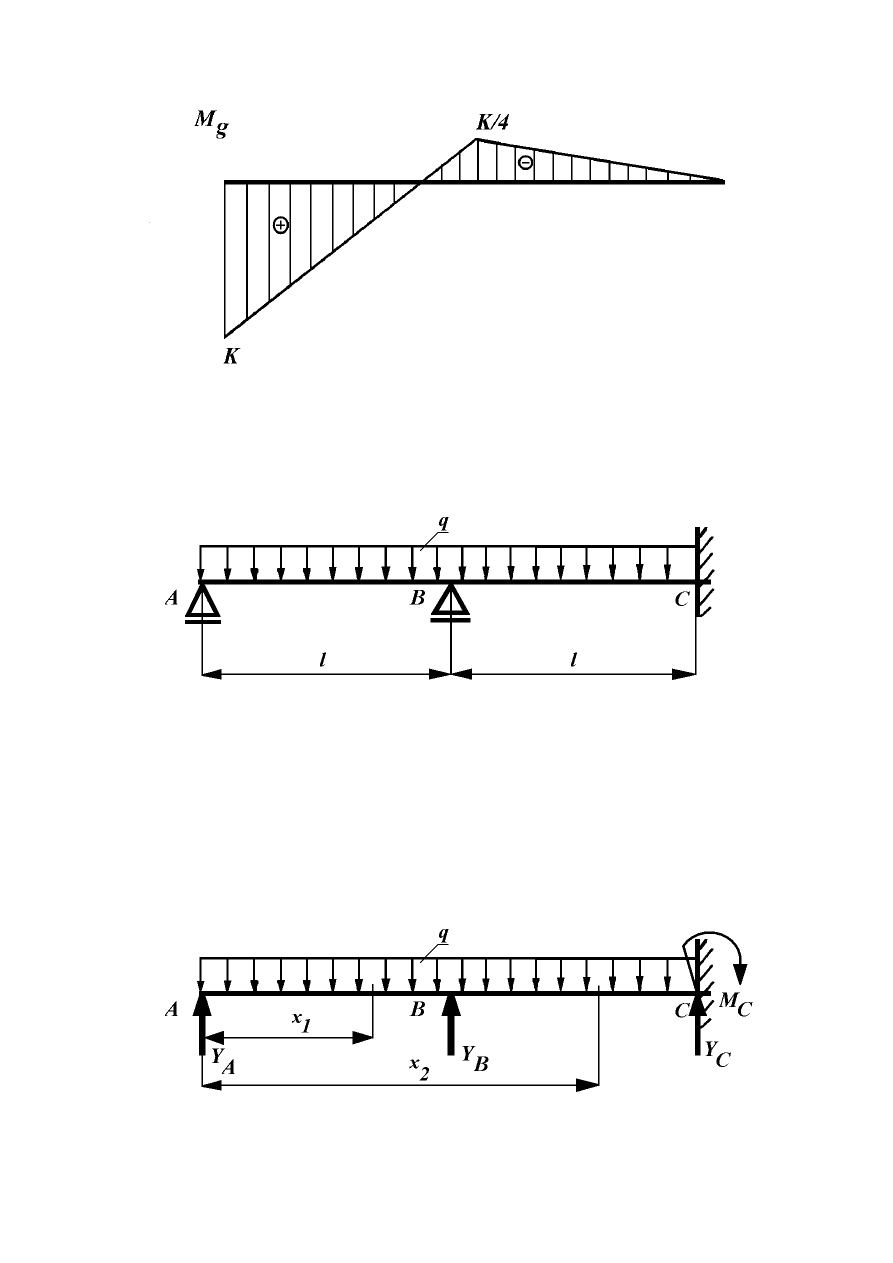
Wykres momentów zginających przestawiony został na rysunku 8.25.

215

Rys. 8.25

Zadanie 8.5.2

Wyznaczyć wielkości podporowe (reakcje) dla belki jak na rysunku 8.26.

Dane: q, l, EJ = const.

Rys. 8.26

Rozwiązanie:

Równania równowagi dla danego układu mają postać (rys. 8.27):

Y

A

+ Y

B

+ Y

C

– 2 ·ql = 0

- Y

A

·2l – Y

B

·l + 2 ·ql

2

+ M

C

= 0

Rys. 8.27

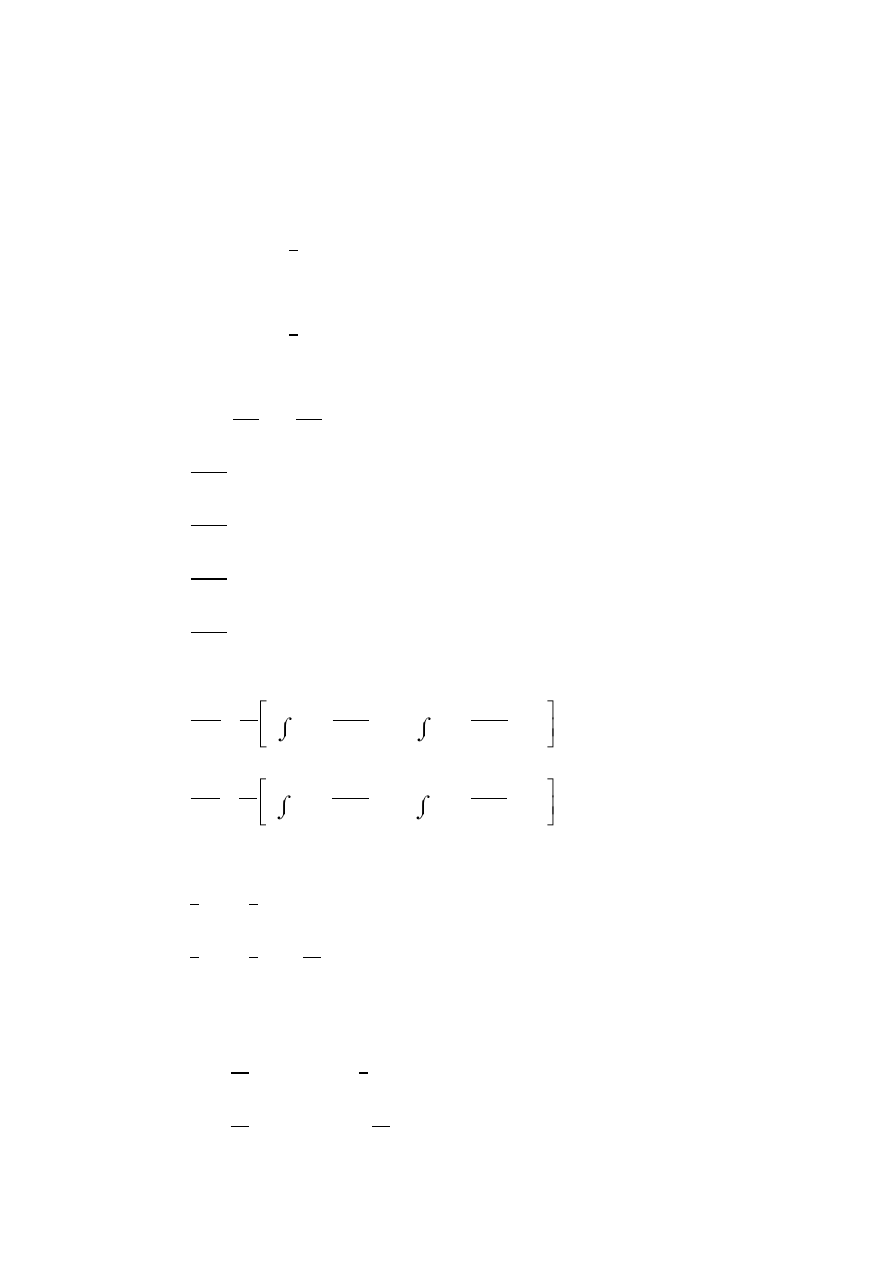
216

Układ jest dwukrotnie statycznie niewyznaczalny. Jako reakcje hiperstatyczne

przyjmujemy reakcje Y

A

oraz Y

B

. Dla określonych przedziałów zmienności obciążenia

(rys. 8.27) wypisujemy funkcje sił wewnętrznych w poszczególnych przedziałach:

0 ≤ x

1

≤ l

M

g1

= Y

A

x

1

-

1
2

·qx

2

1

l ≤ x

2

≤ 2l

M

g2

= Y

A

x

2

-

1
2

·qx

2

2

+ Y

B

(x

2

– l)

Pochodne cząstkowe podług reakcji hiperstatycznych (wielkości hiperstatyczne są od

siebie niezależne

δY

A

δY

B

= 0,

δY

B

δY

A

= 0) wynoszą:

δM

g1

δY

A

= x

1

,

δM

g2

δY

A

= x

2

,

δM

g1

δY

B

= 0,

δM

g2

δY

B

= x

2

–1.

Stosujemy dwukrotnie twierdzenie Menabrea-Castigliano i otrzymujemy:

δU

δY

A

=

1

EJ

0

l

M

g1

·

δM

g1

δY

A

dx

1

+

l

2l

M

g2

·

δM

g2

δY

A

dx

2

= 0

δU

δY

B

=

1

EJ

0

l

M

g1

·

δM

g1

δY

B

dx

1

+

l

2l

M

g2

·

δM

g2

δY

B

dx

2

= 0

Po podstawieniu danych i scałkowaniu otrzymujemy:

8
3

·Y

A

+

5
6

·Y

B

– 2 ·ql = 0,

5
6

·Y

A

+

1
3

·Y

B

-

17
24

·ql = 0.

Powyższe równania wraz z równaniami równowagi pozwalają na określenie wartości

wielkości podporowych, które wynoszą:

Y

A

=

11
28

·ql,

Y

B

=

8
7

·ql,

Y

C

=

13
28

·ql,

M

C

= -

1

14

·ql

2

.

217

Zadanie 8.5.3

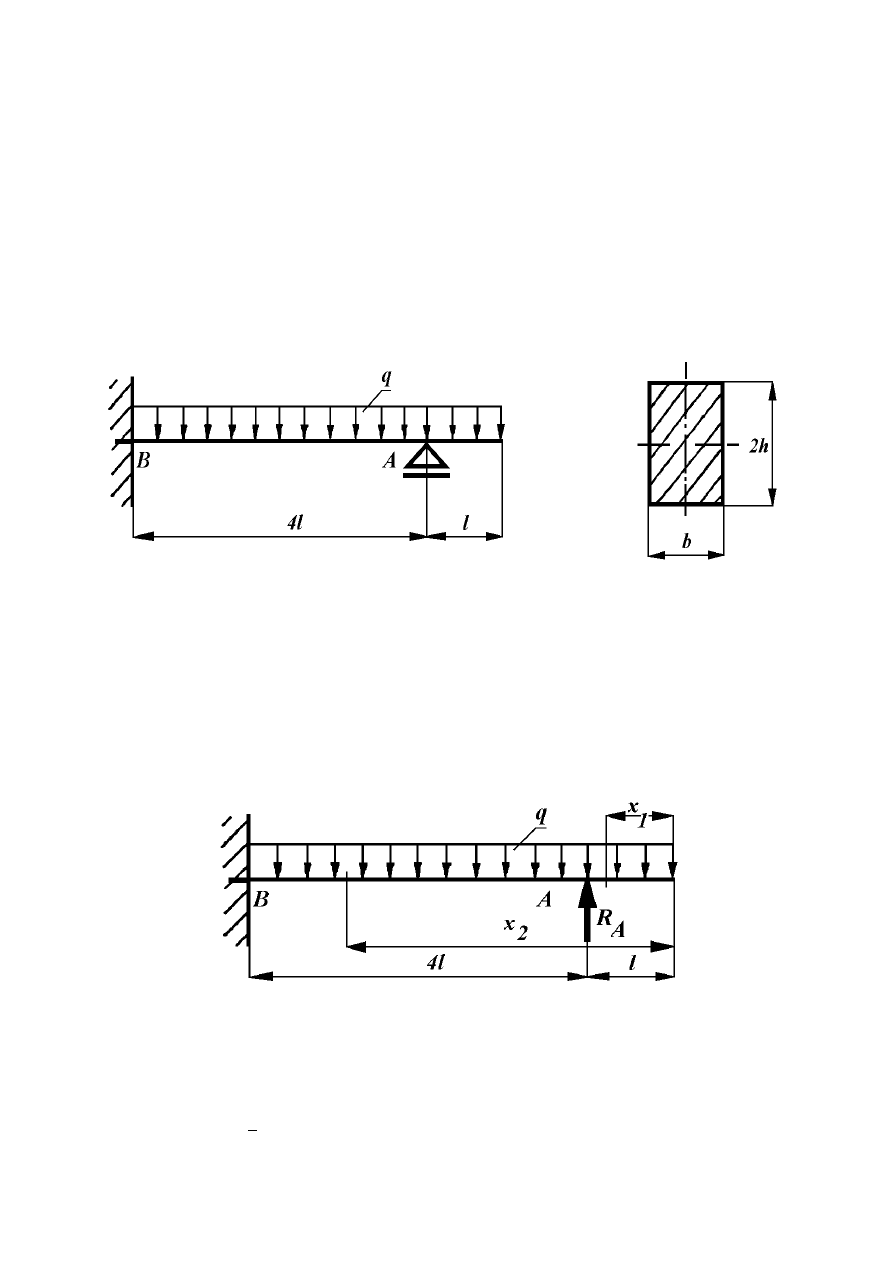
Dla belki jak na rysunku (8.28) obliczyć dopuszczalne obciążenie q, stosując metodę na

dopuszczalne naprężenie.

Dane: b, h, l, k

g

.

Rys. 8.28

Rozwiązanie:

Układ jest jednokrotnie statycznie niewyznaczalny. Dodatkowe równanie potrzebne do

rozwiązania przedstawionego układu dostarczy twierdzenie Menabrea-Castigliano. Jako

wartość hiperstatyczną przyjmujemy reakcję R

A

(rys. 8.29).

Rys. 8.29

Funkcje momentów zginających w poszczególnych przedziałach mają postać:

0 ≤ x

1

≤ l

M

g1

= -

1
2

·qx

2

1

218

l ≤ x

2

≤ 5l

M

g2

= -

1
2

·qx

2

2

+ R

A

(x

2

– l)

Pochodne cząstkowe momentów zginających podług reakcji hiperstatycznej R

A

wynoszą:

δM

g1

δR

A

= 0,

δM

g2

δR

A

= x

2

- l

Po zastosowaniu twierdzenia Menabrea-Castigliano:

δU

δR

A

=

1

EJ

0

l

M

g1

·

δM

g1

δR

A

dx

1

+

l

5l

M

g2

·

δM

g2

δR

A

dx

2

= 0

δU

δR

A

=

1

EJ

l

5l

-

1
2

·qx

2

2

+ R

A

(x

2

– l)

(x

2

– l)

dx

2

= 0

otrzymamy:

R

A

= 2,66 ·ql.

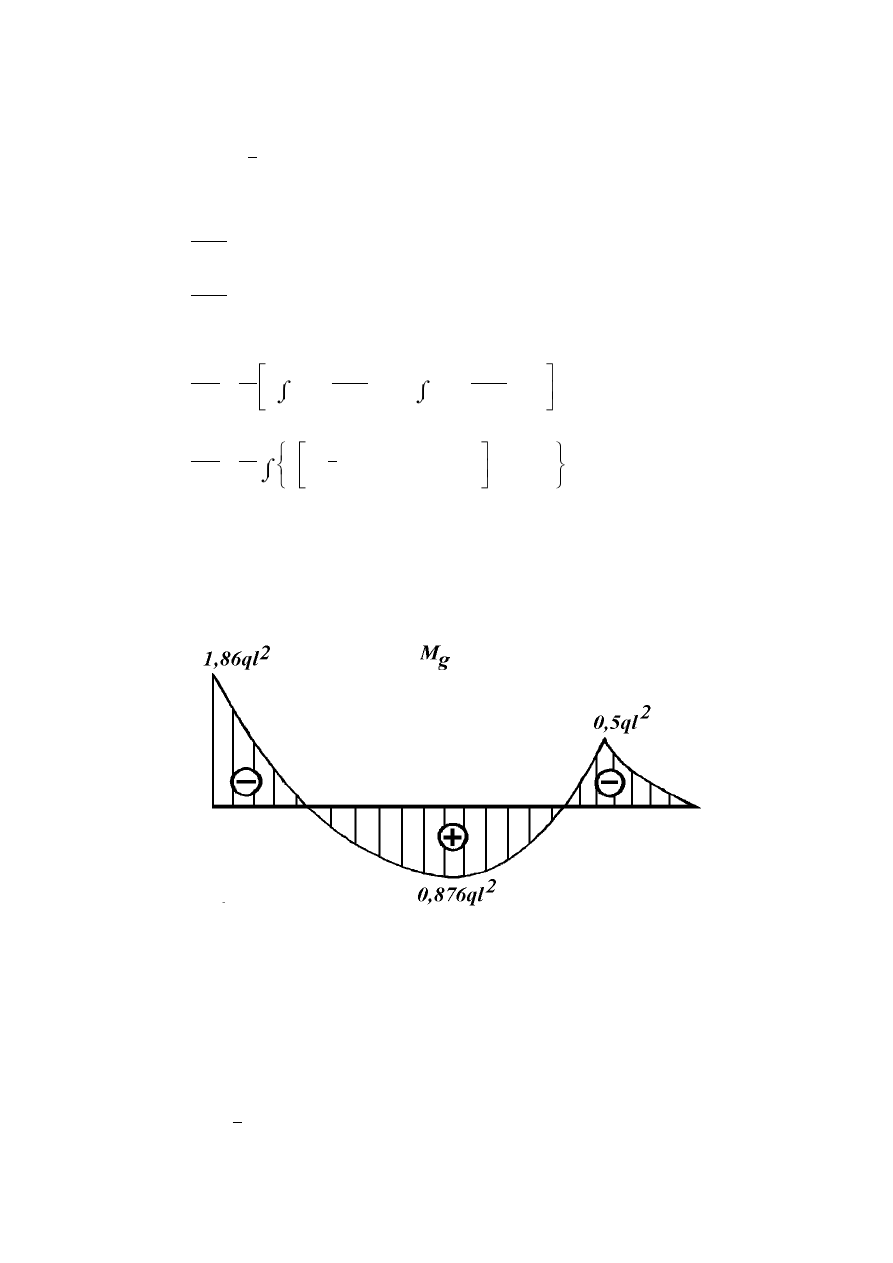
Na rysunku (8.30) został przedstawiony wykres momentów zginających Mg

.

Rys. 8.30

Maksymalny moment zginający (wartość bezwzględna) wynosi:

M

gmax

= 1,86 ·ql

2

.

Wskaźnik zginania sprężystego dla przekroju prostokątnego o wymiarach jak na

rysunku (8.28) wynosi:

W

g

=

2
3

bh

3

.

219

Korzystając ze wzoru:

M

gmax

≤ W

g

·k

g

,

czyli:

1,86 ·ql

2

≤

2
3

bh

3

·k

g

.

Stąd wyznaczamy dopuszczalne obciążenie q, które wynosi:

q

dop

≤ 0,358 ·

bh

3

l

2

·k

g

.

Zadanie 8.5.4

Porównać energie sprężyste pochodzące od zginania dla układów jak na rysunku (8.31).

Dla obu belek przyjąć stałą sztywność zginania równą EJ.

Rys. 8.31

Rozwiązanie:

Energię sprężystą układu obliczymy z zależności:

U = U

N

+ U

T

+ U

Mg

+ U

Ms

Ponieważ obliczamy tylko energię sprężystą pochodzącą od zginania, w naszym przypadku

będzie:

U = U

Mg

=

l

M

2

g

2EJ

dl.

Funkcje momentów zginających dla poszczególnych belek mają postać (rys. 8.32):

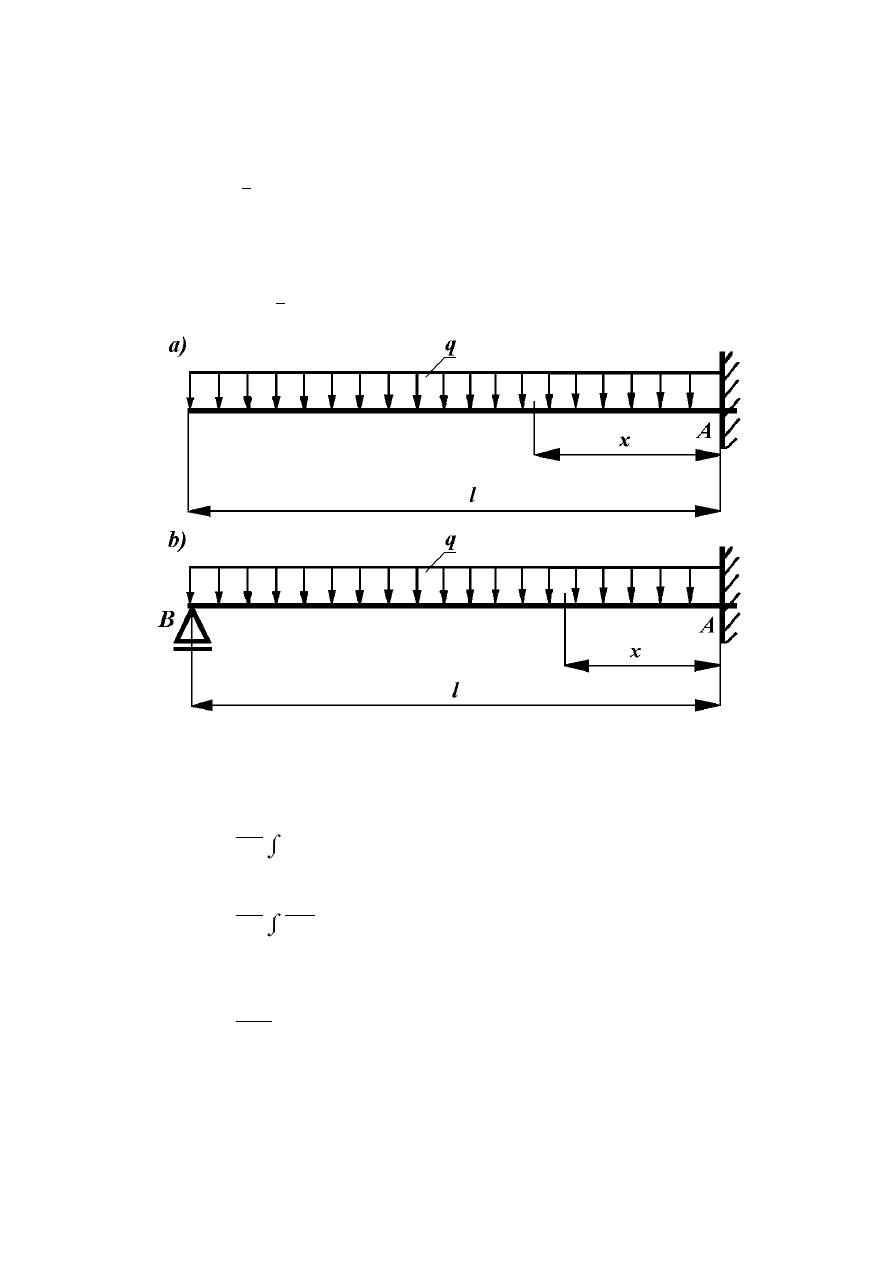
220

belka a:

0 ≤ x ≤ l

M

g

= -

1
2

·qx

2

belka b:

0 ≤ x ≤ l

M

g

= R

B

x -

1
2

·qx

2

,

Rys. 8.32

Czyli energia sprężysta dla układu a (statycznie wyznaczalnego, rys. 8.32a) wynosi:

U

(a)

=

1

2EJ

0

l

M

2

g

dx

U

(a)

=

1

2EJ

0

l

q

2

x

4

4

.

Po scałkowaniu otrzymujemy:

U

(a)

=

q

2

l

5

40EJ

.

Układ drugi stanowi belka jednokrotnie statycznie niewyznaczalna. Aby obliczyć jej

energię sprężystą, należy najpierw wyznaczyć wielkości podporowe. W tym celu skorzystamy

z twierdzenia Menabrea-Castigliano. Jako reakcję hiperstatyczną przyjmujemy R

B

. Funkcja

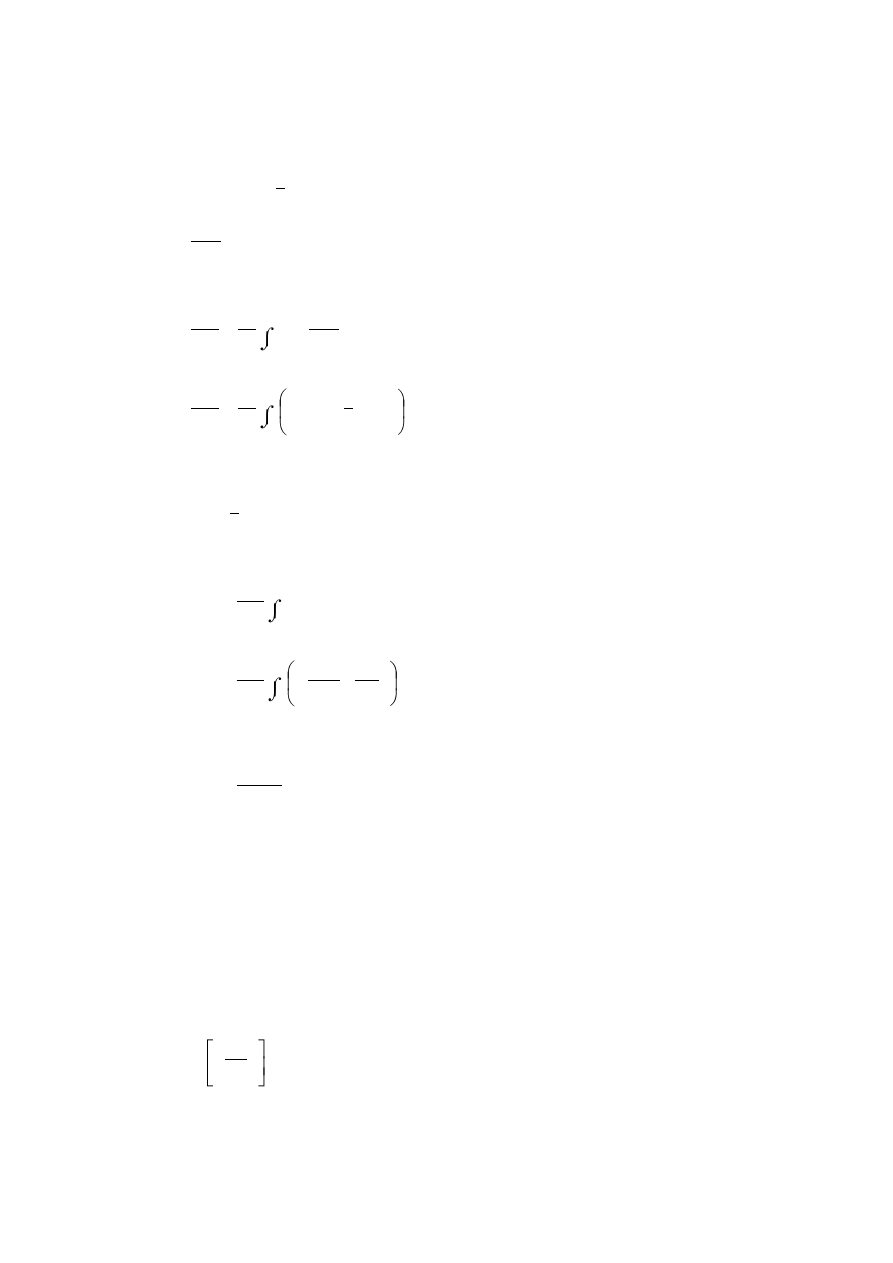
221

momentu zginającego i pochodna cząstkowa podług reakcji hiperstatycznej wynoszą

(rys. 8.32b):

M

g

= R

B

x -

1
2

·qx

2

δM

g

δR

B

= x

Wykorzystując twierdzenie Menabrea-Castigliano otrzymamy:

δU

δR

B

=

1

EJ

0

l

M

g

·

δM

g

δR

B

dx = 0

δU

δR

B

=

1

EJ

0

l

R

B

x -

1
2

·qx

2

xdx = 0.

Po scałkowaniu i rozwiązaniu otrzymamy:

R

B

=

3
8

·ql.

Energia sprężysta dla układu b (statycznie niewyznaczalnego) wynosi:

U

(b)

=

1

2EJ

0

l

M

2

g

dx

U

(b)

=

1

2EJ

0

l

3qlx

8

-

qx

2

2

.

Po uporządkowaniu i scałkowaniu otrzymamy:

U

(b)

=

q

2

l

5

320EJ

.

Jak z powyższego wynika, energia układu drugiego (b) jest osiem razy mniejsza od

energii układu pierwszego (a).

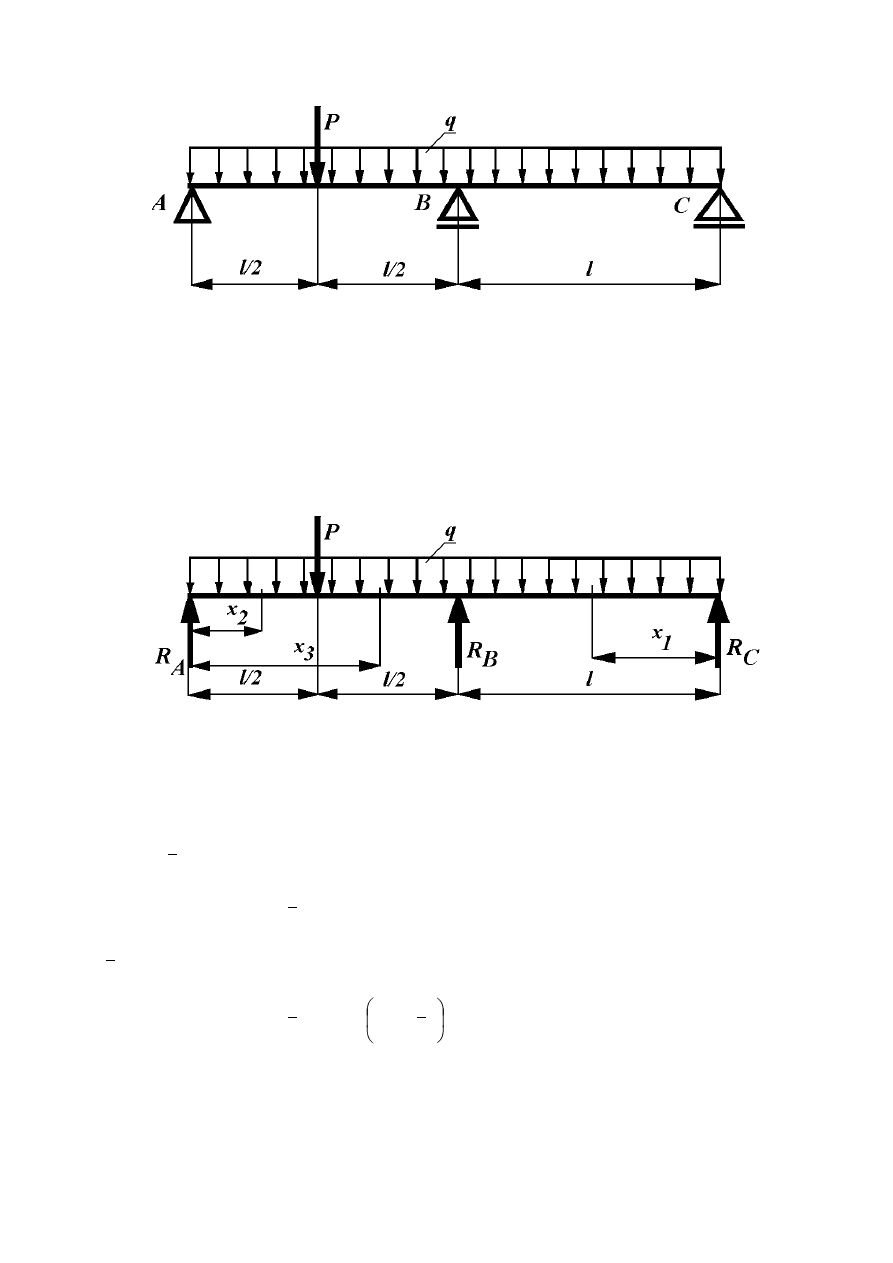
Zadanie 8.5.5

Jaka wartość powinna mieć siła P, aby reakcja w prawej podporze była równa zero.

Schemat belki przedstawiono na rysunku 8.33.

Dane: q = 10

kN

m

, l = 1 [m], EJ = const.

222

Rys. 8.33

Rozwiązanie:

Belka stanowi układ jednokrotnie statycznie niewyznaczalny. Jako wielkość

hiperstatyczną przyjęto reakcję R

C

(rys. 8.34) prawej podpory, która przy danej sile P

powinna być równa zero.

Momenty zginające w poszczególnych przedziałach belki mają postać (rys. 8.34):

Rys. 8.34

0 ≤ x

1

≤ l

M

g1

= R

C

x

1

0 ≤ x

2

≤

l

2

M

g2

= R

A

x

2

-

1
2

·qx

2

2

,

l

2

≤ x

2

≤ l

M

g3

= R

A

x

3

-

1
2

·qx

2

3

– P

x

3

-

l

2

,

Ponieważ występująca w równaniach rekcja R

A

jest wielkością niewiadomą nie

hiperstatyczną, należy ją przedstawić za pomocą reakcji hiperstatycznej R

C

. W tym celu

skorzystamy z równań równowagi i otrzymamy:

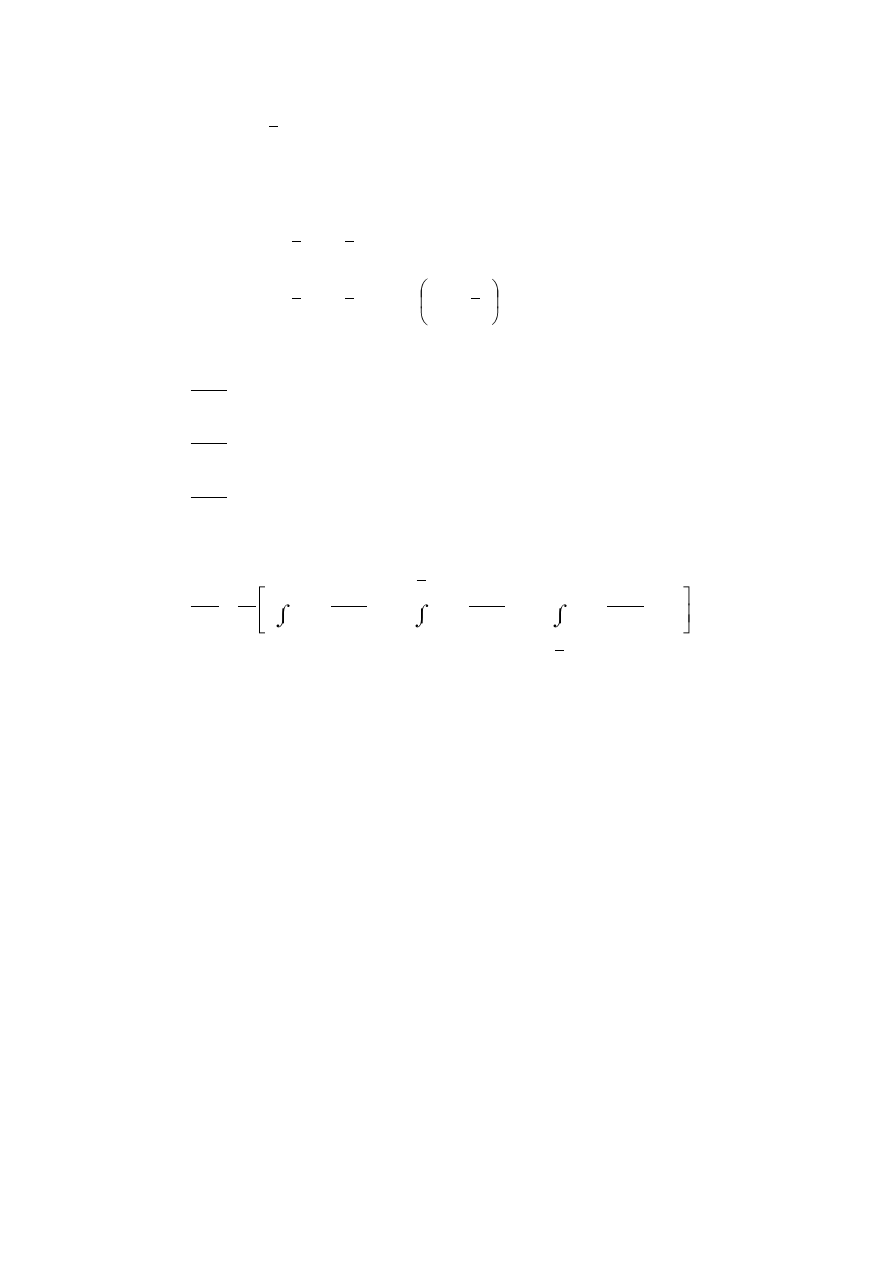
223

R

A

= R

C

+

1
2

·P

Po wstawieniu do równań sił wewnętrznych otrzymamy:

M

g1

= R

C

x

1

,

M

g2

= R

C

x

2

+

1
2

Px

2

-

1
2

·qx

2

2

,

M

g3

= R

C

x

3

+

1
2

Px

3

-

1
2

·qx

2

3

- P

x

3

-

l

2

.

Pochodne cząstkowe podług reakcji hiperstatycznej wynoszą odpowiednio:

δM

g1

δR

C

= x

1

δM

g2

δR

C

= x

2

δM

g3

δR

C

= x

3

Wykorzystując twierdzenie Menabrea-Castigliano możemy napisać:

δU

δR

C

=

1

EJ

0

l

M

g1

·

δM

g1

δR

C

dx

1

+

0

l

2

M

g2

·

δM

g2

δR

C

dx

2

+

l

2

l

M

g3

·

δM

g3

δR

C

dx

3

= 0

Po podstawieniu wartości, scałkowaniu i uwzględnieniu, że R

C

= 0, otrzymujemy wartość siły

P, która wynosi:

P = 4 ·ql

P = 40 [kN].