SPRAWOZDANIE Z LABORATORIUM
Z FIZYKI
TEMAT
Wyznaczanie szerokości przerwy energetycznej metodą termiczną
INFORMATYKA GR. 5, SEKCJA 2
PLEWA ŁUKASZ
STYŁA ROBERT
ŚLOSARCZYK PRZEMYSŁAW
1.Wstęp teoretyczny.
Przewodnictwo elektryczne półprzewodników związane jest z ruchem elektronów w paśmie przewodnictwa i okien w paśmie walencyjnym. W niskich temperaturach pasmo przewodnictwa jest całkowicie pozbawione elektronów, zaś pasmo walencyjne jest nimi całkowicie zapełnione. W wyższych temperaturach energia ruchu cieplnego pewnej ilości elektronów przekracza wartość przerwy energetycznej i elektrony te przechodzą do pasma przewodnictwa. Ilość takich elektronów rośnie wraz ze wzrostem temperatury. Koncentracja elektronów w paśmie przewodnictwa (n) i dziur w paśmie walencyjnym (p) zależna jest od stosunku T/Δgdzie ΔE jest energią aktywacji zależną od rodzaju materiału i stopnia domieszkowania półprzewodnika. Zależność tę opisują równania:
gdzie k - stała Boltzmana, T - temperatura w skali bezwzględnej.
Dla półprzewodnika samoistnego energie aktywacji i dziur są jednakowe i równe połowie szerokości przerwy energetycznej. Związek między przewodnictwem elektrycznym półprzewodnika a temperaturą można wyrazić równaniem:
gdzie ΔE jest odpowiednią dla danego półprzewodnika energią aktywacji. Ponadto z powyższego równania wynika, że:
co oznacza, że wykres powyższej zależności dla półprzewodnika powinien być linią prostą, której nachylenie zależy od wielkości energii aktywacji.
2.Wyniki pomiarów, wykresy
Temperatura [°C] |
Opór podczas ogrzewania[kΩ] |
Opór podczas chłodzenia [kΩ] |
23 |
13,5 |
- |
26 |
- |
11,8 |
30 |
9,9 |
10,3 |
40 |
6,76 |
7,45 |
50 |
4,6 |
5,33 |
60 |
3,2 |
3,84 |
70 |
2,26 |
2,83 |
80 |
1,65 |
2,1 |
90 |
1,2 |
1,57 |
100 |
0,88 |
1,19 |
110 |
0,64 |
0,937 |
120 |
0,49 |
0,728 |
130 |
0,401 |
0,573 |
140 |
0,311 |
0,46 |
150 |
0,245 |
0,365 |
160 |
0,196 |
0,296 |
170 |
0,158 |
0,238 |
180 |
0,129 |
0,195 |
190 |
0,105 |
0,105 |
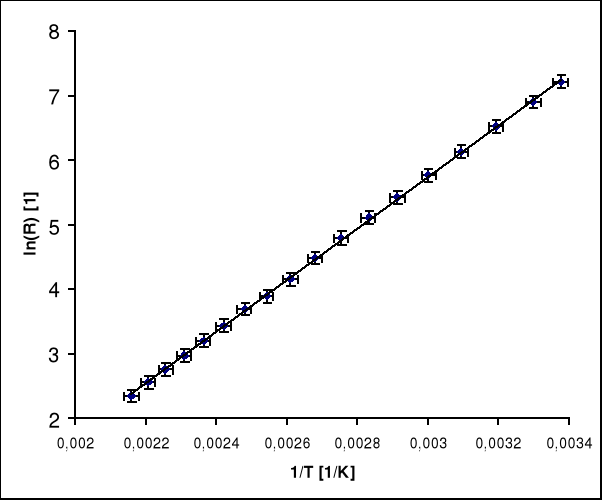
Powyższe dane zostały przekształcone w żądany sposób tzn. temperatura została zamieniona na skale Kelwina i wyznaczono jej odwrotność a opór został zlogarytmowany. Dane te zostały naniesione na wykresy:
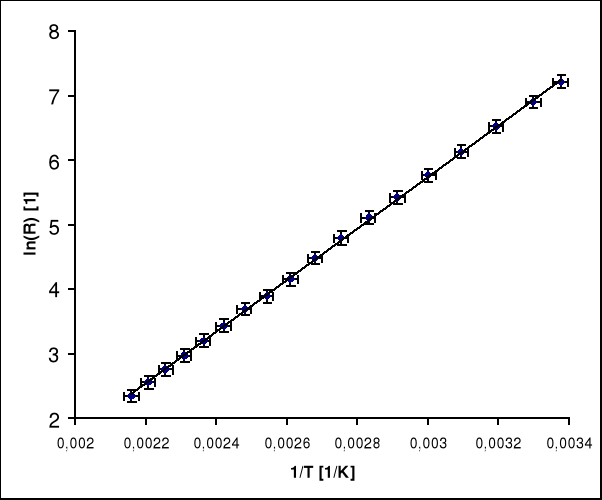
Wykres zależności podczas ogrzewania.
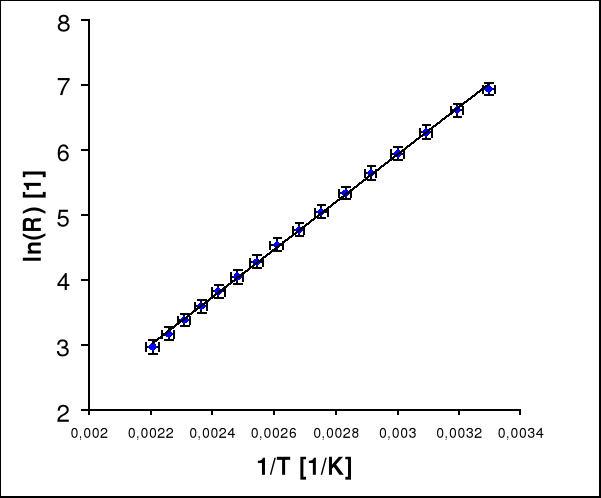
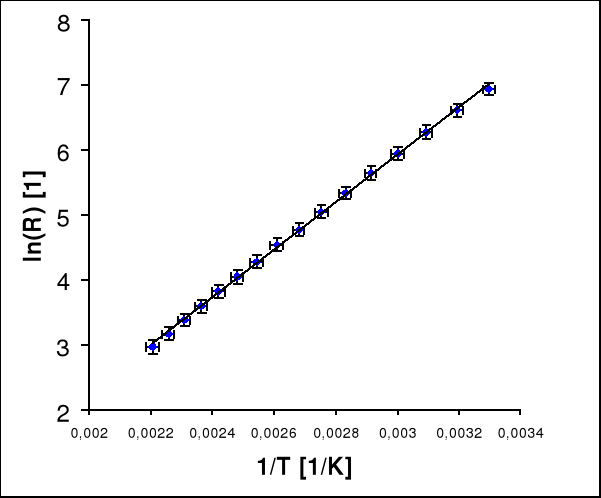
Wykres zależności podczas schładzania.
3. Obliczenia
Możemy wyznaczyć równania prostych metodą regresji liniowej.
y = ax + b
Dla pomiarów dokonanych przy wzroście temperatury :
a = 4010 [ K ]
b = -6,283 ,
natomiast dla pomiarów przy spadku temperatury :
a = 3653
b = -5,037 0,075
Przerwę energetyczną wyliczamy ze wzoru :
E = ka
gdzie k - stała Boltzmana k=1,38*10-23 [J/K]
Przy ogrzewaniu:
E = 1,38 * 10-23 *4010
E = 5,533 * 10-20 [J]
E = 0,3458 [eV] (1[J] = 0,625 * 1020 eV)
błąd :
(E) = k* a
(E) = 1,38 * 10-23 * 16
(E) = 0,022 * 10-20 [J]
(E) = 0,0013 [eV]
Przy schładzaniu:
E = 1,38 * 10-23 *3653
E = 5,041 * 10-20 [J]
E = 0,3150 [eV]
błąd :
(E) = k* a
(E) = 1,38 * 10-23 * 27
(E) = 0,037 * 10-20 [J]
(E) = 0,0023 [eV]
4. Wnioski.
W wyniku przeprowadzenia doświadczenia wyznaczona została szerokość przerwy energetycznej. W związku z tym, że wyniki pomiarów wykonanych przy podgrzewaniu i chłodzeniu termistora różniły się między sobą, zostały one uśrednione arytmetycznie:
E = ( 5,287 0,029 )* 10-20 [J]
E = 0,3304 0,0018 [eV]
Wyszukiwarka
Podobne podstrony:
lab2 ~$znaczanie przerwy energ met termiczna?
Wyznaczanie szerokości przerwy energetycznej metodą termiczną, Polibuda, Fiza, Fizyka sprawozdania (
laborka37, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!!LABORKI - sprawozdani
Wyznaczanie szerokości przerwy energetycznej metodą termiczną, PRZERWAE, Wydzia˙: AEI
Wyznaczanie współczynnika załamania, Pollub MiBM, fizyka sprawozdania
kospekt12, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, 12 Wyznaczanie
Atom- Wyznaczanie stałej Plancka i pracy wyjścia elektronów(1), Sprawozdania - Fizyka
Wyznaczanie gęstości cieczy, Pollub MiBM, fizyka sprawozdania
Wyznaczanie stałej Planca z wykorzystaniem zjawiska fotoelektrycznego, Sprawozdania
Wyznaczanie wspólczynnika załamania za pomocą refraktometru, Sprawolki
Pomiar napięć okres zmiennych met analog przetw, Sprawolki
Wyznaczanie gęstości za pomocą piometru, STUDIA, sprawozdania, Fizyka
Cw 11 - Wyznaczenie współczynnika rozszerzalności liniowej ciał stałych, Sprawozdania fizyka
więcej podobnych podstron