SPRAWOZDANIE Z LABORATORIUM

TECHNIKI CYFROWEJ

Ocena:

Bienieck

-termin-

-data-

1. Zapoznanie z programami Xilinx i ModelSim

1.1. Pierwszy „projekt”

W celu zapoznania się z programem Xilinx stworzyliśmy model układu logicznego składającego się z jednego, podstawowego, funktora – bramki AND. W pierwszej kolejności stworzyliśmy plik o rozszerzeniu .sch w którym powstał schemat ( Rys. 1). Po opisaniu wejść i wyjść w sposób nam odpowiadający przeszliśmy do

utworzenia pliku .vhd z kodem VHDL potrzebnego do

przeprowadzenia symulacji. W pliku tym ustaliliśmy w

jaki sposób będzie podawany sygnał na wejścia bramki.

Zrobiliśmy to analogicznie do przykładu podanego w

instrukcji do laboratorium, tj.

We_1 <= ‘0’, ‘1’ after 100 ns, ‘0’ after 300 ns;

We_2 <= ‘0’, ‘1’ after 200 ns, ‘0’ after 400 ns;.

Polecenie to spowodowało, że na oba wejścia zostaną podane zera, po 100ns (200ns dla We_2) zostanie podana jedynka, a po 300ns (400ns dla We_2) znowu zero. Po dopisaniu powyższych dwóch linii i usunięciu kilku niepotrzebnych można było przejść do symulacji.

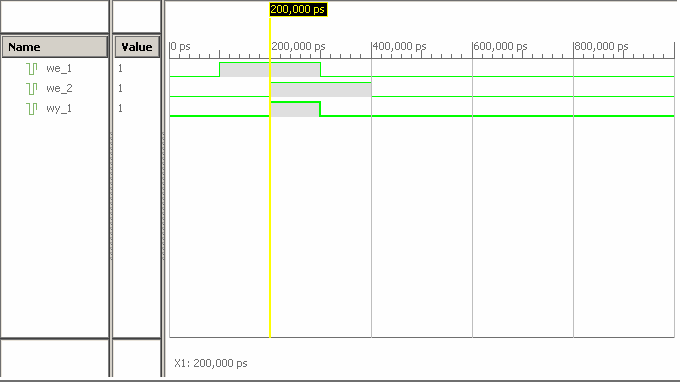
Efekt symulacji przedstawia poniższy rysunek.

Rys. 2. Efekt symulacji bramki AND (zmodyfikowany wizualnie)

Na rysunku podświetlony jest stan dla 200ns (200 000ps), czyli chwila w której na wejściu naszej bramki znajdują się jedynki. Zgodnie z oczekiwaniami na wyjściu również pojawiła się jedynka. Po przeanalizowaniu symulacji widać, że nasz funktor działa należycie.

1

2. Transkoder

2.1. Przygotowanie

Głównym celem laboratoriów, dla naszej grupy, było wykonanie schematu

translatora kodu NKB na +3 (4 bity) i zasymulowanie go. Główną część tego zadania opracowaliśmy przed laboratoriami tj. minimalizację funkcji boolowskich metodą Karnaugh i schemat w Xilinx.

Jako że projektowany przez nas

układ cyfrowy ma za zadanie zamianę kodu Tabela 1. Reprezentacja liczb w różnych zapisach NKB na +3 to w pierwszej kolejności

DEC

NKB

+3

należało zapoznać się z reprezentacją liczb

--

DCBA

WXYZ

w powy

0

0000

0011

ższych kodach ( Tabela 1).

1

0001

0100

Ze względu na to, że kod +3 na 4

2

0010

0101

bitach nie ma wartości dla 13

3

0011

0110

DEC, 14DEC i

15

4

0100

0111

DEC to nasz transkoder będzie zamieniał

te liczby na 0000 czyli słowo bitowe które

5

0101

1000

w kodzie +3 nie reprezentuje żadnej liczby.

6

0110

1001

7

0111

1010

8

1000

1011

9

1001

1100

10

1010

1101

11

1011

1110

12

1100

1111

13

1101

-

14

1110

-

15

1111

-

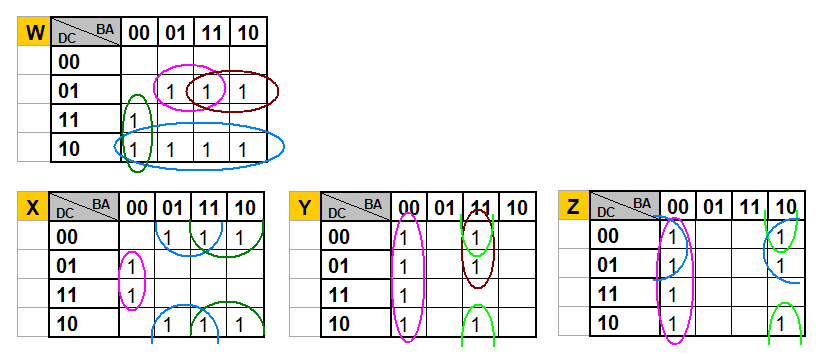
Rys. 3. Minimalizacja funkcji boolowskich przy pomocy tablic Karnaugh W wyniku minimalizacji otrzymujemy

W = C

D A + C

D B + DB A + DC

X = C B A + CA + CB

.

Y = B A + CBA + B

D A

Z = CB A + D A + B A

2

2.2. Schemat

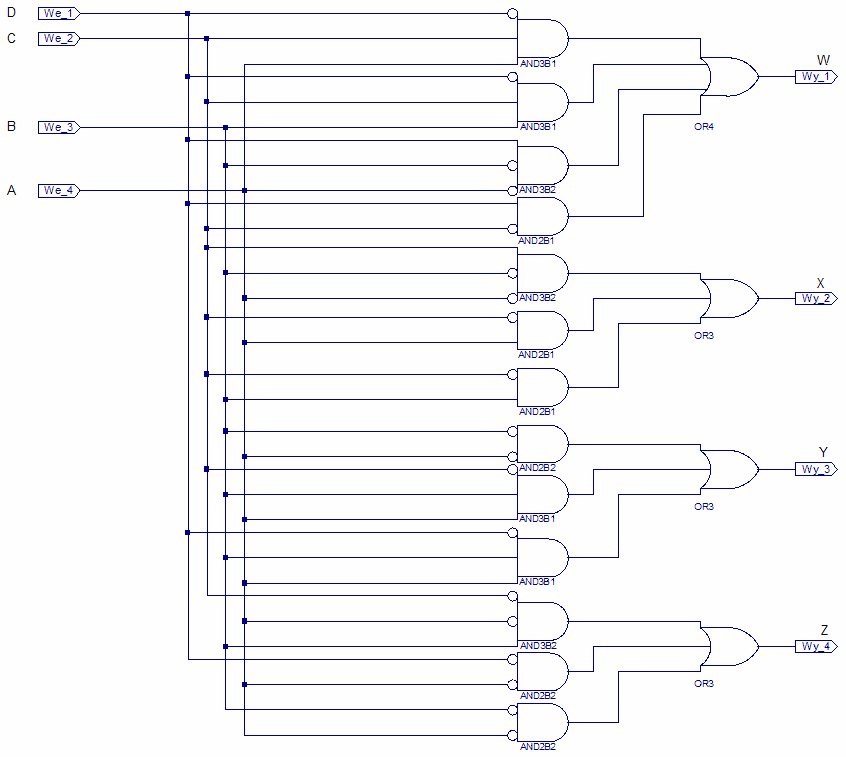
Nasz schemat składa się z 4 bramek OR oraz 13 bramek AND. Wynika to m.in. stąd, że przy minimalizacji posłużono się kanoniczną postacią sumy. Gdyby minimalizację robić zapisując w kanonicznej postaci iloczynu proporcje bramek byłyby odwrotne. Warto zwrócić uwagę na to, że w przypadku realizacji rzeczywistego układu ma się swoistą ograniczoną dowolność w konstrukcji określonych urządzeń i można, w zależności od np. dostępności pewnych funktorów, przeprojektować układ.

Rys. 4. Schemat Transkodera (wejścia po lewej)

Kod VHDL dla jednostki testowej uzupełniono o instrukcje przypisania pobudzeń dla wejść w sposób przedstawiony poniżej.

We_1 <= ‘0’, ‘1’ after 100 ns, ‘0’ after 500 ns;

We_2 <= ‘0’, ‘1’ after 200 ns, ‘0’ after 600 ns;

We_3 <= ‘0’, ‘1’ after 300 ns, ‘0’ after 700 ns;

We_4 <= ‘0’, ‘1’ after 400 ns, ‘0’ after 800 ns;

END;

3

2.3. Symulacja

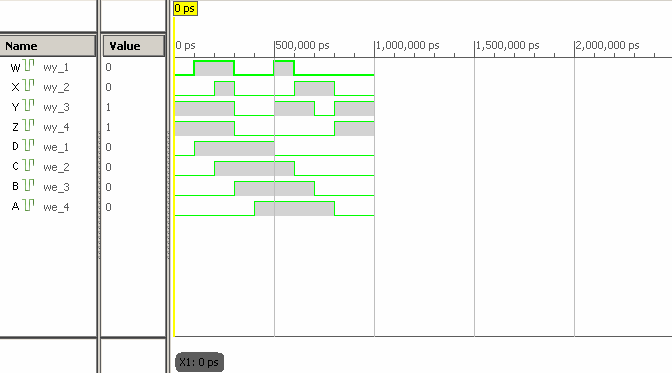
Efekt symulacji translatora kodu był zgodny z oczekiwaniami tj. zamieniał kod NKB

na kod +3 zgodnie z tabelą 5 oraz zamieniał wartości 1101, 1110 i 1111 na 0000.

Rys. 5. Symulacja Transkodera (zmodyfikowano wizualnie)

3. Podsumowanie i wnioski

Przy pomocy programu Xilinx i ModelSim można zaprojektować i zasymulować dowolny układ cyfrowy. W tym celu należy stworzyć wstępny projekt z odpowiednimi funkcjami boolowskimi, następnie schemat oparty o te funkcje i opisać odpowiednio wejścia i wyjścia, przypisując im pobudzenia. W ten sposób otrzymuje się gotowy projekt, w którym można wyszukiwać niepotrzebne lub niewłaściwie działające elementy i eliminować je.

Podczas projektowania transkodera pojawił się problem w postaci wartości które nie występują dla 4 bitowego +3. Problem ten rozwiązaliśmy w taki sposób, że wartościom tym przypisaliśmy 0000 w celu poinformowania użytkownika, że został przekroczony zakres.

Podczas projektowania transkoder został wysunięty wniosek, że nasz wariant nie jest jedynym który doprowadzi do założonego celu i gdy zajdzie potrzeba zaprojektowania rzeczywistego układu to minimalizację funkcji boolowskich będzie można wykonać pod określone proporcje funktorów jakimi będzie się dysponować, np. gdy będziemy posiadać więcej bramek OR to minimalizowaną funkcję zapiszemy w KPI, gdyż w takim przypadku będzie ich potrzeba więcej niż przy KPS. Można by również wykonać samą minimalizację inną metodą niż przy pomocy tablic Karnaugh’a i ocenić co jest bardziej opłacalne.

Największy problem na laboratorium sprawił nam sam Xilinx. Pomimo tego, że układ był niemal gotowy to uruchomienie go na zajęciach zajęło dużo czasu. W związku z powyższym doszliśmy do wniosku, że mniejsze projekty możemy tworzyć w programie Circuit którego obsługa jest banalna (co jest jednocześnie zaletą i wadą), a następnie gotowe układy przekonwertowywać do Xilinx’a.

Ostatecznym wnioskiem jest fakt, że nasz układ zadziałał zgodnie z oczekiwaniami z czego jesteśmy ze wszech miar dumni.

4