Wprowadzenie do informatyki - ć wiczenia Reprezentacja

Reprezentacja liczb ca

łkowitych

§ Jak kodowany jest znak liczby?

Kod uzupe

łnień do 2 (U2)

§ Omó wimy dwa sposoby kodowania liczb ze znakiem:

§ kod znak-moduł (ZM),

§ kod uzupełnień do dwu (U2).

dr inż . Izabela Szczęch

WSNHiD 2010/2011

Ćwiczenia z wprowadzenia do informatyki 2

Plan

Plan zaj

ęć

n

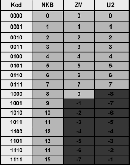
Kod

Kod U2

– definicja

definicja i konwersja

n

Zakresy

Zakresy liczb reprezentowanych liczb reprezentowanych w kodzie w kodzie U2

n

Arytmetyka

Arytmetyka w

w kodzie

kodzie U2

Kod

Kod uzupe

łnień

nie do dwu -

definicja i konwersja

3

Kod

Kod uzupe

łnień

nie do 2

do 2 (U2)

Kod uzupe

łnień

nie do 2 (U2)

§ Motywacja

00001110 (+14 )

28 - 00001110

10

+ 11110010 (-14 )

=100000000 – 00001110

00001110 (+14 )

000011

0000

10

11

10

10

10

00000000 (0)

=11110010

+ 1xxxxxxx (-14 )

+ 11110010

111

10

00000000 (0)

00000000

§ drugi składnik sumy jest uzupełnieniem dwó jkowym liczby prow

pro adzim

adzi y

y obliczenia na 8

-miu

iu bitach,

14 zapisanej na 8-miu bitach

więc

ę

c po

m

po ijam

ija y przeniesienie 1 na 9

y

-ty bit.

y

§ Uzupełnieniem dwó jkowym (ang. 2C - Two's T

Complement)

§ chcemy by najstarszy bit informował o znaku liczby liczby x zapisanej za pomocą n bitó w nazywamy liczbę

§ chcemy tak zapisać -14, aby wykonać powyż sze ró wną 2n – x(U2)

dodawanie w systemie dwó jkowym bez zastanawiania się

§ Kod U2 ułatwia realizację podstawowych operacji czy któ ryś bit jest znakiem czy nie arytmetycznych, gdyż nie wymaga oddzielnego obsługiwania bitu znaku (jak to jest w przypadku kodu ZM) 5

6

Izabela Szczęch

1

Wprowadzenie do informatyki - ć wiczenia Konwersja z

z kodu

kodu U2

Konwersja

Konwersja z kodu

U2

na

na system

system dziesi

ętny

na

na system

system dziesi

ętny

Wartość

Warto

dziesi

ętną

tn liczby w kodzie

liczby w kodzie U2

obliczamy nast

ępująco:

§ Jeśli

ś bit znaku

bit znaku jest r

ó wny 0, to liczba jest

dodatnia i resztę

§

zapisu

zapisu mo

ż emy potraktować jak

jak liczb

ę w naturalnym

cyfry mno

ż ymy przez wagi pozycji, na kt ó

pozycji, na kt rych si

ę znajdują

znajduj i

systemie dw

ó jkowym,

jkowym, bo waga

bitu znaku

i tak zniknie

dodajemy

dodajemy otrzymane

otrzymane iloczyn

y

iloczyn . Waga

y

. Waga bitu znakowego

bitu znakowego jest

przy

przy mno

ż

mno eniu

eniu przez bit znaku

przez bit znaku czyli 0.

ujemna

ujemna i wynosi

(-2n-1).

c

c

c

...c c c

=

Przykł

Przyk ad dla zapisu 8

dla zapisu -mio bitowego

n-1 n-2 n-3

2 1 0 (U2)

c

(-2n-1)

) +

c

2n-2 + ... + c 22 + c 21 + c 20

011010

1

11(U2)

n-1

n-2

2

1

0

(10)

= 0*(-27) + 1*26 + 1*25 + 0*24 + 1*23 + 0*22 + 1*21 + 1*20

gdzie,

c - cyfra dwó jkowa

jkowa 0 lub 1

= 26 + 25 + 23 + 21 + 20

n - liczba

liczba bit

ó

bit w w

w w zapisie

zapisie liczby

=64

=64 + 32 + 8 + 2

+ 1 = 107

.

(10)

7

8

Konwersja

Konwersja z

z kodu

kodu U2

Wyznaczanie liczby przeciwnej w U2

na

na system

dziesi

ętny

SPOSÓ

SPOS B 1:

§ Liczb

Lic

ę pr

ę

z

pr eci

z

wn

eci

ą

ą do x moż na

na wyzna

wyz

c

na zać z

z definicji

§ Jeśli

ś bit znaku jest ró wny 1

wny , to liczba

, to liczba ma warto

ść

ma warto

ujemną.

uz

u upe

z

ł

upe nienia

nienia dwó

dw jkow

jko ego

w

ego jako 2n – x

, gdzie n oznacza

(U2)

§ Bit znaku

Bit znaku ma

ma wag

ę (-2n-1), gdzie n oznacza liczb ę

liczb bitó

bit w w

liczbę bitó w w przyjętym formacie.

wybranym

wybranym formacie

formacie U2.

Przykł

Przyk ad:

§ Reszta

Reszta bit

ó w

w jest zwyk

łą liczb

ą

liczb w naturalnym kodzie

Rozwa

Ro

ż

zwa my

y zapis

z

apis na cz

na c terech

z

terech bitach:

dwó jkowym. Wagę bitu znakowego i warto

ść pozosta

łych

§

Niech x = 0101. Uz

Niech x = 0101. U upe

z

ł

upe nieniem

nieniem dwó

dw jkowy

jko

m

wy

m jest

bitó

bit w

w sumujemy

sumujemy otrzymuj

ą

otrzymuj c

c warto

ść liczby

U2.

x

= 24 - 0101

0101 =10000 - 0101 = 101

0101 = 10 1.

1

(U2)

Przykł

Przyk ad dla zapisu 8

dla zapisu -mio

mio bitowego

§

Niech y

Niech = 10

y

1

= 10 1. U

1

z

1. U upe

z

łnieniem

nieniem dwó

dw jkowy

jko

m

wy

m jest

y

= 24 - 101

10 1 = 0101.

1

111010

1

11

1010

(U2)

(U2)

Otrzy

Otr

ma

zy

li

ma śm

ś y

m

y zatem,

z

ż e y

= x. Poniewa

= x. Ponie

ż jednak y

jednak = x

y

,

= 1*(-27) + 1*26

6 + 1*25 + 0*24 + 1*23 + 0*22 + 1*21 + 1*20

(U2)

(U2)

więc ostatec

ę

z

c ostatec nie mo

z

ż emy

em

y zapisa

z

ć , ż e

e (x

)

= x.

(U2) (U2)

=-128+64+32+8+2+1 = -128

128 + 107

+ 107 = (

-21)

.

Zatem uz

u upe

z

ł

upe nienie

nienie dwó

dw jkow

jko e

w

e danej l

danej ic

l z

ic b

z y

b

y reprez

repre entuje

z

l

entuje ic

l zb

ic

ę

ę

(10)

do niej prz

do niej pr eci

z

wną

wn .

9

10

Wyznaczanie liczby przeciwnej w U2

Wyznaczanie liczby przeciwnej w U2

SPOSÓ

SPOS B 3:

SPOSÓ

SPOS B 2:

1. Anal

Ana iz

l ę

iz

ę roz

ro poc

z

zyna

zy

m

na y

y od praw

pra ej

w strony

stron zapisu

z

lic

l zb

z y

b .

y

§ Zanegować

wa ws

w zystkie

zy

stkie bity

bit

y z

apisu

z

l

apisu ic

l z

ic b

z y

b

y w

w U2

2. Do wyniku

wy

prz

pr episujem

z

y

episujem kol

ko ejne

l

ejne bity

bit o w

o arto

w

ści

ś 0

§ Do wy

Do

niku

wy

dodać

doda 1

wra

w z

ra

z z

z pierw

pier s

w zy

s

m

zy

m napotkany

napotkan m

y

m bitem o warto

w

ści

ś 1.

3. Wszy

s

stkie

zy

poz

po osta

z

ł

osta e

e bity

bit prz

pr episujem

z

y

episujem ,

y zmieniaj

z

ąc ich

ą

ść

ą

Przykł

Przyk ad:

warto

w

ść na prz

na pr eci

z

wn

eci

.

Znajdź

ź liczb

ę

liczb przeciwna

przeciwna do

do 0101

.

(U2)

Przykł

Przyk ad:

§

ź

ę

Zanegować wszystkie

wszystkie bity:

1010

Znajdź liczb

przeciwna do

1

100

1

1

100 100

1

1100

1

.

(U2)

§ Dodać 1: 1010+1=

1011

10

punkt 1

punkt -2:

2:

100

(U2)

punkt

punkt 3:

001

00 100

1

110

1

100(U2)

Sprawdzeni

Sprawdzen e

i

e wy

w n

y i

n ku:

i

ku: 0101

Spraw

Spra dzenie

dzenie w

yniku:

y

1

niku: 100

1

1

100 100

1

1100

1

=-2048+1024+128+64+8+4=-820

;

(U2)=4+1=5(10);

; 10

11

10

(U2)=-8+2+1=-5(10)

(U2)

(10)

001

00 100

1

1

100 10100

1

=512+256+32+16+4=820

(U2)

(10)

11

12

Izabela Szczęch

2

Wprowadzenie do informatyki - ć wiczenia Zadania

Konwersja

Konwersja dodatnich

dodatnich liczb

dziesiętnych na

na zapis

zapis U2

Zadania:

Oblicz

Oblicz warto

ść dziesi

ętną

tn nast

ępujących

cych liczb 8

-mio

ę

ó

ą

ś

bitowych w

reprezentacji

U2, a

nast

ępnie

pnie znajd

ź do

ź

do nich

§ Znajdujemy reprezentacj

ę dw

ó jkową danej warto

ci

liczby

liczby przeciwne

przeciwne (w

(w reprezentacji

U2):

liczbowej

§ Uzupełniamy ją

j z przodu

z przodu bitami 0 do

długości

ś zadanego

a) 10000001

formatu kodu

kodu U2.

(U2)

b) 11111111(U2)

c) 01111111(U2)

d) 01010100

Przykł

Przyk ad:

(U2)

Wyznaczyć

yznaczy 8-mio bitowy kod

kod U2 dla

U2 dla liczby dziesi

ętnej

tnej 27

.

(10)

27

= 16

= 16 + 8 + 2 + 1 =

1

+ 8 + 2 + 1 = 10

1

11

10

= 000110

1

11

10

(10)

(2)

(U2).

13

14

Konwersja

Konwersja ujemnych

ujemnych liczb

Konwersja

Konwersja ujemnych liczb

dziesiętnych

tnych na

na zapis

zapis U2

dziesiętnych na

na zapis

zapis U2

SPOSÓ

SPOS B 1:

SPOSÓ

SPOS B 2

B :

§ Wyznac

yz

zam

z

y

am

y z

apis

z

dwó

dw jkowy

wy modułu l

u ic

l zb

z y

b

§ Jeśli

ś do

do liczby 2

n (n - ilość bit

ó

bit w w formacie

U2)

dodamy

§ Otrzy

Otr

man

zy

y

man

y kod dwó

kod dw jkowy

jko

wy uz

u upe

z

łniamy

niam

y z pr

z

z

pr odu

z

odu w

w miarę

ę

przetwarzaną liczb

ę dziesi

ętną

tn , to zapisany dw

ó

to zapisany dw jkowo

potrz

potr eb

z

z

eb erami do ro

z

z

erami do ro miaru formatu U2

z

wynik będzie ró

dzie r wnoważ ny bitowo (tzn. o takiej samej

§ Wyznac

yz

z

nac am

z

y

am

y l

ic

l zbę

ę przeci

z

wną

ą (w

( do

w

w

do o

w l

o n

l y

y sposó b)

postaci)

postaci) kodowi

kodowi U2

przetwarzanej

liczb

y.

liczb

Prz

Pr yk

z

ł

yk ad: Wyzn

y

ac

zn

zy

ac

ć

zy 8-mi

m o

o b

i

b towy

towy kod U2

d

la

a li

cz

c by

z

-45(10).

Przykł

Przyk ad:

§ Wyzn

y

ac

zn

z

ac amy

z

amy kod b

i

kod b nar

n n

ar y

n

y moduł

modu u li

u cz

c by:

z

by: 45

(10)=101

=10 101

1

(2)

Wyznaczyć

yznaczy 8-mio bitowy kod

kod U2 dla

U2 dla liczby dziesi

ętnej -45

.

§

(10)

Kod uzu

Kod

pe

uzu

ł

pe ni

n amy

amy bi

b tami 0 do wymaga

ne

n j

e dł

d ugo

u

ś

go c

ś i

c 8-mi

m u b

u it

b ó

it w:

00101

0010 101

1

§

28 + (-45)

45) = 256

- 45

45 = 2

11

1

1 =

1

= 10100

1

11

10100

.

Wyzn

y

ac

zn

z

ac amy

z

amy li

czb

c

ę

zb

ę pr

z

pr ec

z

i

ec wną

wn do 0010

ą

1

do 0010 101

1

(2)

(U2): 1

10100

1

11(U2)

§

Stą

St d (

d -45)

= 1

= 10100

1

11

10100

Stą

St d

ą (-45)

(10)

(U2)

(10) = 1

= 10100

1

11

10100

(U2)

15

16

Zakres

Zakres liczb

w

w kodzie

U2

Jaka

Jaka jest

najmniejsza

najmniejsza i najwi

ększa

ksza warto

ści

ś

ci liczb

y

liczb , kt

y

ó

, kt rą da

się przedstawi

ć w

w danym formacie

kodu

kodu U2?

§ Liczba najwi

ększa w

U2 powstaje

U2 powstaje przy bicie

znaku

ró wnym 0, i przy pozosta

ł

0, i przy pozosta ych bitach

ró wnych 1.

§ Liczba najmniejsza

najmniejsza w

w U2 powstaje

U2 powstaje przy bicie

przy bicie znaku

ró wnym 1, i przy pozosta

ł

1, i przy pozosta ych bitach

ró wnych 0.

Zakres

Zakres liczb

Zadania:

w kodzie

w kodzie U2

1. Wyznacz

yznacz zakres

liczb dziesi

ętnych

tnych reprezentowanych

reprezentowanych w

kodzie

kodzie U2

U2 na 4, 8 i 16 bitach.

2. Podaj og

ó lny wz

ó

wz r na okre

ślaj

ś ący zakres

n-bitowych liczb

w

w kodzie

U2.

18

Izabela Szczęch

3

Wprowadzenie do informatyki - ć wiczenia Zakres liczb

liczb w

w kodzie

kodzie U2

Poró

Por wnanie

wnanie kodó w

§ Zakres n-bitowej liczby w kodzie liczby w kodzie ZM

określony

ś

lony jest

wzorem:

Poró wnanie

interpretacji wartości

Z

= <-2n-1, 2n-1 - 1>

(U2)

słó w kodu binarnego w

ró ż nych systemach

zapisu liczb ze znakiem

§ W por

ó wnaniu

wnaniu z kodem

z kodem znak

-moduł,

ł, kod

kod U2

U2 jest

niesymetryczny

niesymetryczn ,

y bo

bo na

n-bitach moż na

na zapisa

ć w nim

o

jedną wi

ęcej

cej liczb

ę ujemn

ą ni

ż liczb dodatnich.

19

20

Dodawanie i iodejmowanie w U2

§ Liczby U2 dodajemy i odejmujemy wg zasad dla naturalnego systemu dwó jkowego.

§ Przeniesienia poza bit znaku ignorujemy (w rzeczywistości takie przeniesienia czy poż yczki mogą być wykorzystywane przez procesor do dodawania liczb o wielokrotnej precyzji).

Arytmetyka

§ Przykłady dla 8-mio bitowego formatu U2:

-5 + 100=95

-100 - 5=-105

w kodzie

w kodzie U2

1 1 1 1 1 0 1 1

1 0 0 1 1 1 0 0

+

0 1 1 0 0 1 0 0

-

0 0 0 0 0 1 0 1

1 0 1 0 1 1 1 1 1

1 0 0 1 0 1 1 1

przeniesienie poza bit znaku

ignorujemy

22

Kod

Kod U2

– nadmiar

nadmiar i iniedomiar

Arytmetyka

Arytmetyka w

w kodzie

kodzie U2

-zadania

§ Poniewa

i

ż

ewa liczb

li

y

y zapisane

i

w system

y

ie

i

e U2 posi

U2 pos adaj

i

ą

adaj

ą ustal

usta on

l

y

on

y format

(ilość

ilo

bitó w jest sta

j

ła),

ł to prz

y

y wykonywan

y

iu

i operacji

operac

ji arytmet

y

y

tmet czn

y

ych

y

Zadania:

moż

mo e dochodzić

e dochodzi do nadmi

nadm ar

i ó

ar w (wy

(w n

y i

n k

i

k wię

wi ksz

ę

y

ksz

y niż

ni moż

mo na

ą

ó

ą

ę

przedstawić

przedstawi za pomocą

za pomoc dost

ą

ępn

ę y

pn ch b

y

it

ch b ó w

w moduł

modu u)

ł

u) lub

l

ni

n edom

i

i

edom ar

i ó

ar w.

Stosując dw

ó jkową reprezentacj

U2

na 8

-miu bitach

zapisz

następujące

ce liczby ca

łkowite i wykonaj

dzia

łania:

§ Nadmi

Nadm ar

i

ar (ni

(n edom

i

i

edom ar)

i

wy

w st

y ą

st p

ą i

p ,

i

, gdy

gd

y w U2 suma dwó

w U2 suma dw ch li

ch czb

li

czb dodatni

dodatn ch

i

(uj

(u emn

j

y

emn ch)

y

ch) daj

da e

j

e w wy

w w n

y i

n ku

i

ku liczb

li

ę

czb

ę uj

u emn

j

ą

emn

ą (dodatnią

(dodatni ).

ą

§ Nadmi

Nadm ar

i

ar i

i ni

n edom

i

i

edom ar

i ni

n e

i wy

w st

y ę

st puj

ę

ą

puj

ą przy

prz

y dodawani

dodawan u

i

u liczb

li

czb o

a) 18

18 + 20

przeci

przec wn

i

y

wn ch

y

ch znakach

b) -30

30 + (

-25)

§

c) -20 + 60

Przykłady dla 8-mio bitowego formatu U2: d) 120

120 + 32

100+40=nadmiar

-100 + (-40)=niedomiar

e) -65 + (

-84)

0 1 1 0 0 1 0 0

1 0 0 1 1 1 0 0

+

0 0 1 0 1 0 0 0

+

1 1 0 1 1 0 0 0

1 0 0 0 1 1 0 0

0 1 1 1 0 1 0 0

suma liczb dodatnich

suma liczb ujemnych

dała liczbę ujemną

dała liczbę dodatnią

23

24

Izabela Szczęch

4