Experimental study of drying kinetics by forced convection

of aromatic plants

A. Belghit

a,

*, M. Kouhila

b

, B.C. Boutaleb

a

a

Laboratoire de MeÂcanique des Fluides et EnergeÂtique, Faculte des Sciences Semlalia, Avenue Moulay Abdallah, B.P.

2390, Marrakech, Morocco

b

Laboratoire d'Energie Solaire, Ecole Normale SupeÂrieure, B.P. 2400, Marrakech, Morocco

Received 31 March 1999; accepted 20 September 1999

Abstract

This paper has the objectives to determine the isotherms of sorption and the drying kinetics of

verbena, which is the most consumed aromatic plant in Morocco. The experiments undertaken consist

of examining the e€ects of drying air velocity, temperature of drying air and air moisture content on the

drying kinetics of verbena in a laboratory drying tunnel working by forced convection. The results

veri®ed, with good reproducibility, that temperature is the main factor in controlling the rate of drying.

The expression of the drying rate is determined empirically from the characteristic curve of drying. 7 2000

Elsevier Science Ltd. All rights reserved.

Keywords: Drying; Isotherms of sorption; Verbena; Drying rate

1. Introduction

Optimization of the drying operation must answer two essential imperatives which are

the restricted consumption of the necessary energy and the safeguard of the biologic

quality of the dried products. These considerations have led to many works at di€erent

levels of the drying process: the drier, the product and the economical cost [1]. In the

same orientation, we study in this paper the isotherms of sorption and the drying kinetics

Energy Conversion & Management 41 (2000) 1303±1321

0196-8904/00/$ - see front matter 7 2000 Elsevier Science Ltd. All rights reserved.

PII: S0196-8904(99)00162-4

www.elsevier.com/locate/enconman

* Corresponding author. Tel.: [phone]; fax: [phone].

E-mail address: [e-mail] (A. Belghit).

of verbena so as to contribute to the understanding of the drying mechanism of aromatic

herbs and to the design of dryers adapted to this kind of product and working partially

or completely with solar energy.

Arti®cial thermal drying is adopted in this study. This kind of drying is often used in

the alimentary domain in order to avoid deterioration of the fresh products and in the

industrial domain in order to create new products (such as powder of milk, for example).

In other cases, drying is used to reduce the product weight and the cost of transport.

When we dry products, especially in the agricultural domain, we are often confronted with

the following diculties: the ®rst diculty comes from the fact that every product has its own

drying kinetics. Besides, the evaporative power of hot and humid air increases the process of

biological deterioration. The second diculty is technical. It is due to the experimental set up.

So, a bad control of the drying process involves some undesirable modi®cations. In addition,

some modi®cations of shape and structure appear during the drying of most alimentary

products.

The product studied in this work is verbena. This choice is justi®ed by its abundance and its

importance for the agriculturists of the region of Marrakesh (Ourika and central Haouz in

Nomenclature

a

B.E.T. constant

A

w

activity of water in product

db

dry basis

dm

dry matter

HR

air moisture content, %

M

w

mass of wet matter, kg

M

d

mass of dry matter, kg

k, n

Henderson constants

n'

number of adsorbed monolayers

t

time, s

T1

dry bulb temperature, 8C

T

h

wet bulb temperature, 8C

T'

temperature of thermostated bath, 8C

T

temperature of drying air, 8C

V

drying air velocity, ms

ÿ1

X ˆ …M

w

ÿ M

d

†=M

d

water content (db), kg water/(kg dm)

X

in

initial water content (db), kg water /(kg dm)

X

®n

®nal water content (db), kg water/(kg dm)

X

eq

equilibrium water content (db), kg water/(kg dm)

X

dimensionless water content

X

M

water content adsorbed on monolayer, kg water /(kg dm)

_X

i

ˆ …ÿdX=dt†

i

initial drying rate, kg water/(kg dm/mn)

_X ˆ ÿdX=dt

drying rate, kg water/(kg dm/mn)

A. Belghit et al. / Energy Conversion & Management 41 (2000) 1303±1321

1304

south Morocco) because of the produced quantity (about 520 tons per year) and the exported

quantity (88 tons to France). The undertaken experiments aim at the drying of verbena so as

to assure good conservation and quality of the product by respecting the international norms.

Determination of the isotherms of sorption is an indispensable stage in the study of drying

of every product. It gives precious information about the hygroscopic equilibrium of the

product and allows us to know the domain of stability of the products after drying. It is the

objective of the ®rst part of this work. The second part deals with the drying kinetics of

verbena in a laboratory-drying tunnel. The experimental results permit us to determine the

characteristic curve of drying (C C D), which is necessary for calculation of the drying rate of

the product [2].

2. Isotherms of sorption

An isotherm of sorption is usually described by a curve, which illustrates the evolution of

the product water content X

eq

as a function of the moisture content HR of the air surrounding

the product. This can be expressed by the equation X

eq

ˆ f…HR†: These curves are determined

by following the evolution of water adsorption in a product, which is, exposed to an air

atmosphere whose moisture content HR is imposed. The hygroscope equilibrium could be

achieved by a dynamic or static method.

Although the isotherms of sorption and desorption have similar rates, the methods

permitting their obtainment are completely di€erent. Indeed, for a product, which is previously

dry and put in humid air, the system encourages ®xation by the product of a part of the water

contained in the air. The equilibrium is, therefore, due to the sorption, and the relation

between the air moisture content and the equilibrium water content of the product constitutes

an isotherm of sorption of this product. In the case where the humid product is maintained at

constant temperature and placed in a vacuum medium, we follow the variation of pressure,

which increases, from a weak value to an equilibrium value due to evaporation of the water

contained in the product. So, the relation between the product water content and the

corresponding equilibrium vapor pressure constitutes the isotherm of desorption. The two

curves present a hysteresis in most cases [3].

2.1. Material and experimental procedure

In the present work, we use saturated salt solutions in a static method. Although this

method requires a long time for the hygroscopic equilibrium to be attained, it has the

advantage of presenting a more restricted domain of the water content variation [4]. The

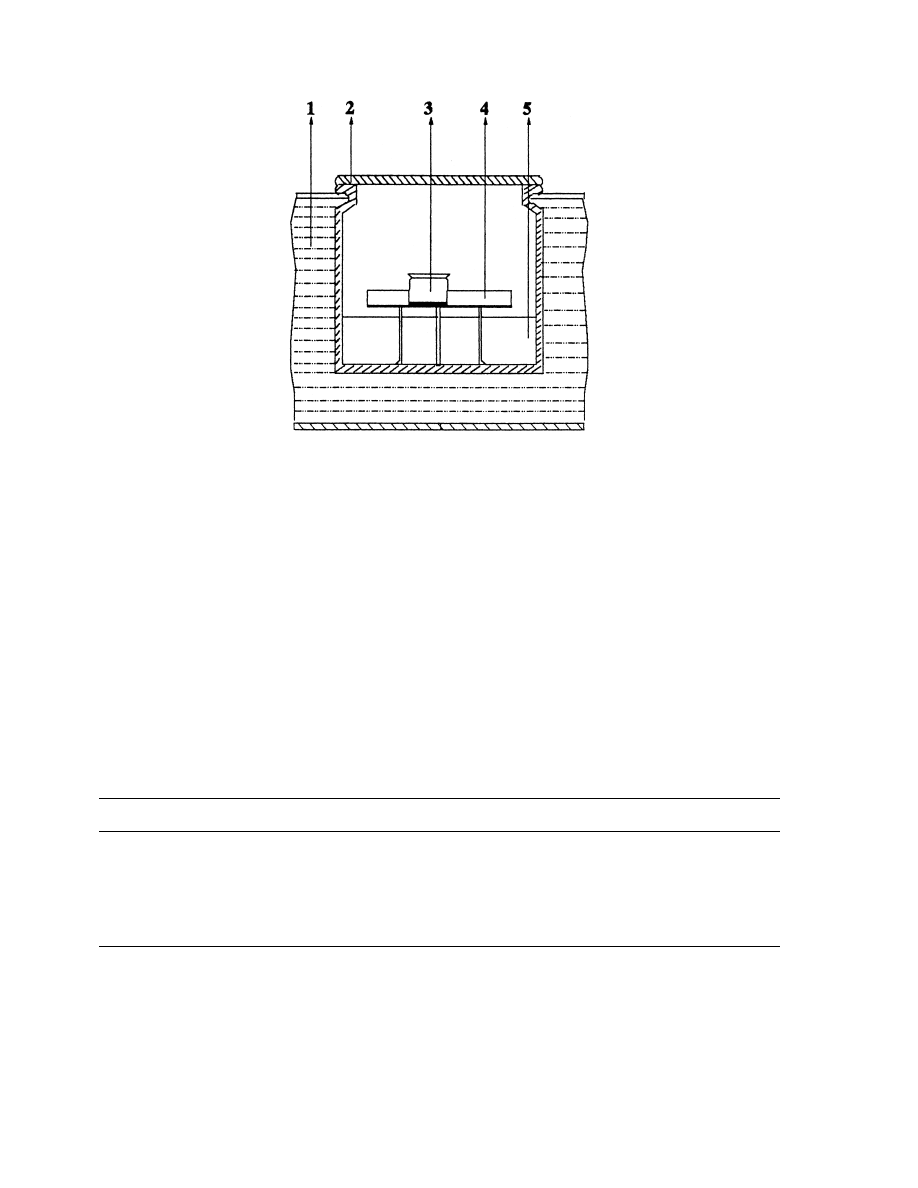
experimental apparatus is presented in Fig. 1. It consists of six bottles of one liter each with an

insulated closing. Every bottle is ®lled to quarter depth with a saturated salt. A ¯ask

containing 0.1 g of verbena is put on a tripod, which is introduced in the bottle. Each bottle

contains a di€erent salt solution (KOH, MgCl

2

, K

2

CO

3

, NaNO

3

, KCl, BaCl

2

) so as to have an

air moisture content which varies from 3% to 90%. Table 1 gathers di€erent salt solutions and

there activities of water at T ˆ 408C.

The bottles are immersed in a thermostated water bath adjusted at a ®xed temperature

A. Belghit et al. / Energy Conversion & Management 41 (2000) 1303±1321

1305

during 24 h so as to adapt the salt solutions with a stationary temperature. Before putting the

six samples of product in the bottles, they are submitted to dehydration in an oven regulated at

a temperature of 508C until reaching maximum dehydration. Water is added to the

thermostated bath every week so as to substitute for the evaporated quantity.

The six samples are weighed every ®ve days in order to determine their water content X

eq

.

Every sample is then placed in the ¯ask and put again into the bottle.

As soon as the six masses become stationary, the experiment is stopped, and the samples are

weighed and placed in a drying oven whose temperature is ®xed at 1058C. This operation lasts

six or seven hours, until the six masses do not vary anymore with time. The objective of this

last operation is to determine the dry masses of the six samples. The di€erence of mass before

and after drying in the oven allows us to have the water content of the product at hygroscopic

equilibrium X

eq

ˆ …M

w

ÿ M

d

†=M

d

: The results of this experiment are presented in Fig. 2.

Fig. 1. Experimental apparatus for the sorption isotherms measurement: (1) thermostated bath, (2) bottle containing

salt solution, (3) ¯ask containing product, (4) tripod and (5) salt solution.

Table 1

Standard values of air moisture content given for di€erent salts

Salt

Activity of water A

w

(%) at 408C

KOH

6.26

MgCl

2

31.59

K

2

CO

3

42.30

NaNO

3

71.00

KCl

82.32

BaCl

2

89.10

A. Belghit et al. / Energy Conversion & Management 41 (2000) 1303±1321

1306

2.2. Modeling of isotherms of sorption

To model the curves of sorption, several correlations exist in the scienti®c literature. Among

these models, we chose Henderson's and the B.E.T. ones.

2.2.1. Henderson's model

To take into account the in¯uence of temperature on hygroscopic equilibrium and make

interpolations, we use Henderson's model [5] because it has the advantage of describing the

whole isotherm of sorption for di€erent temperatures. The equation expressing this model is

given below:

X

eq

ÿ

T

0

, HR

ˆ

ÿln…1 ÿ HR†

k…1:8T

0

‡ 492†

1=n

…1†

This equation allows us to calculate the isotherms of sorption for every value of temperature.

The constants k and n in Eq. (1) depend on the temperature and characterize the product. In

order to determine k and n, we write Eq. (1) under the form:

nln

ÿ

X

eq

‡ ln…k† ˆ ln… ÿ ln…1 ÿ HR†† ÿ ln…1:8T

0

‡ 492†

…2†

Eq. (2) has the shape of a straight line equation: Y ˆ nX ‡ b, with k ˆ exp…b†: By plotting Y as

a function of X, we obtain a regression straight line which allows us to determine the

coecients k and n for T ˆ 408C. The tracing of this function, illustrates clearly the existence

of two straight lines with di€erent slopes. This shows that the modelization should be made at

di€erent intervals of activity of water:
. For 0RA

w

R0:35, we have the values of k and n as follows:

k ˆ 52 10

ÿ6

& n ˆ 2:014

. For 0:35RA

w

R1, we have the values of k and n as follows:

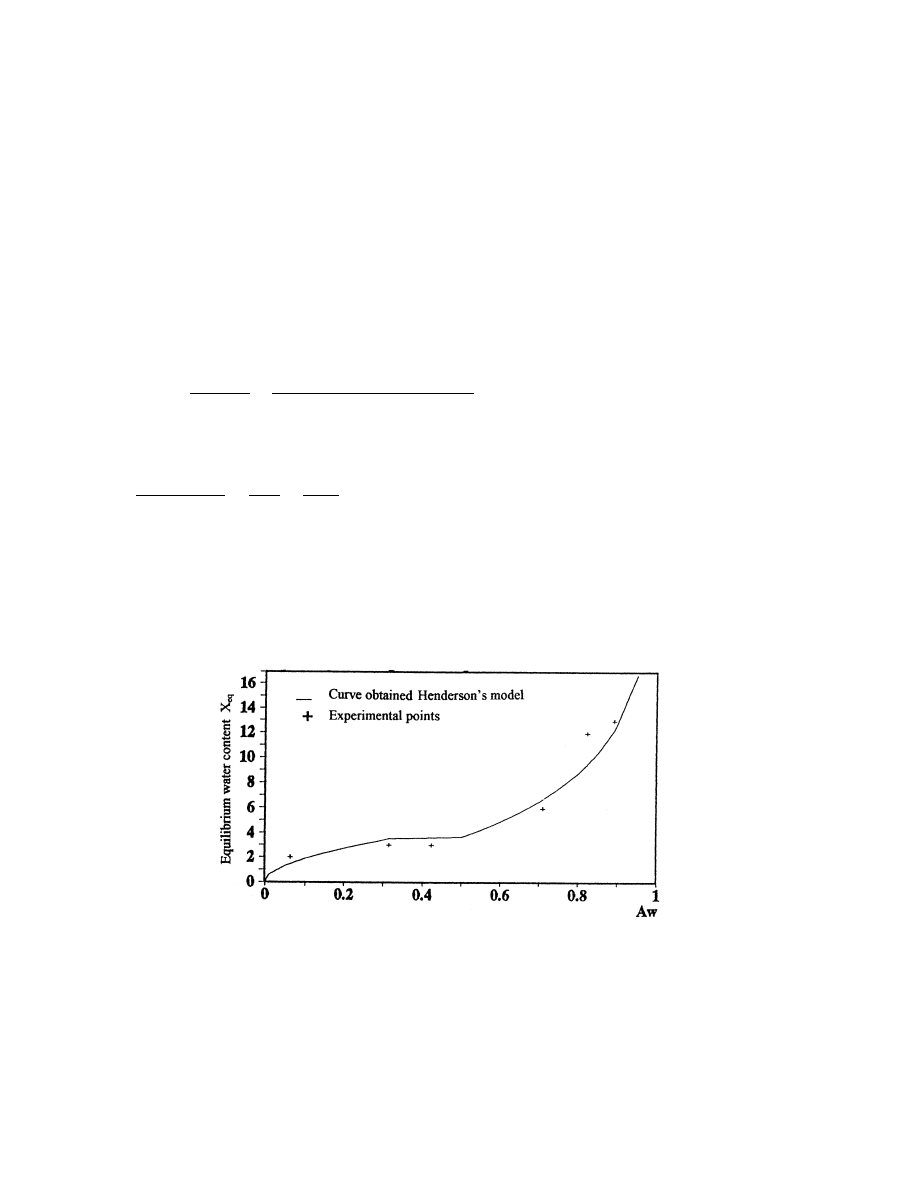
Fig. 2. Isotherm of sorption of verbena obtained at 408C.

A. Belghit et al. / Energy Conversion & Management 41 (2000) 1303±1321

1307

k ˆ 345 10

ÿ6

& n ˆ 0:97

From these coecients, we calculated the curve of sorption at T ˆ 408C. The representation of

these results is shown in Fig. 3, on which we notice that the calculated curve by Henderson's

model and the experimental points have practically the same rate.

In order to study the in¯uence of temperature, we calculated the curves of sorption at other

temperatures. Fig. 4 shows that the equilibrium water content decreases somewhat when the

temperature increases.

2.2.2. B.E.T model

In order to understand how the sorption occurs in our product, we use the model suggested

by Brunauer, Emmet and Teller (noted B.E.T.) [6]. This model allows us to examining the

phenomenon of ®xation and liberation of water molecules. The general equation expressing

this model is given by:

X

eq

ˆ

HR X

M

a

1 ÿ HR

1 ÿ …n

0

‡ 1†HR

n

0

‡ n

0

HR

n

0

‡1

1 ‡ …a ÿ 1†HR ‡ aHR

n

0

‡1

…3†

If we take into account only the adsorbed monolayers …n

0

ˆ 1† and if we neglect the square

terms of air moisture, Eq. (3) becomes:

HR

…1 ÿ HR†X

eq

ˆ

1

aX

M

‡

a ÿ 1

aX

M

HR

…4†

By plotting the quantity HR=‰…1 ÿ HR†X

eq

Š as a function of HR, we obtain a straight line for

which the slope …a ÿ 1†=…aX

M

† and intercept is 1=…aX

M

†: This allows us to calculate the

constants X

M

and a:

a ˆ 45:76 and X

M

ˆ 2:292 kg water=…kg dm†

Fig. 3. Curve of sorption calculated with Henderson's model at T ˆ 408C.

A. Belghit et al. / Energy Conversion & Management 41 (2000) 1303±1321

1308

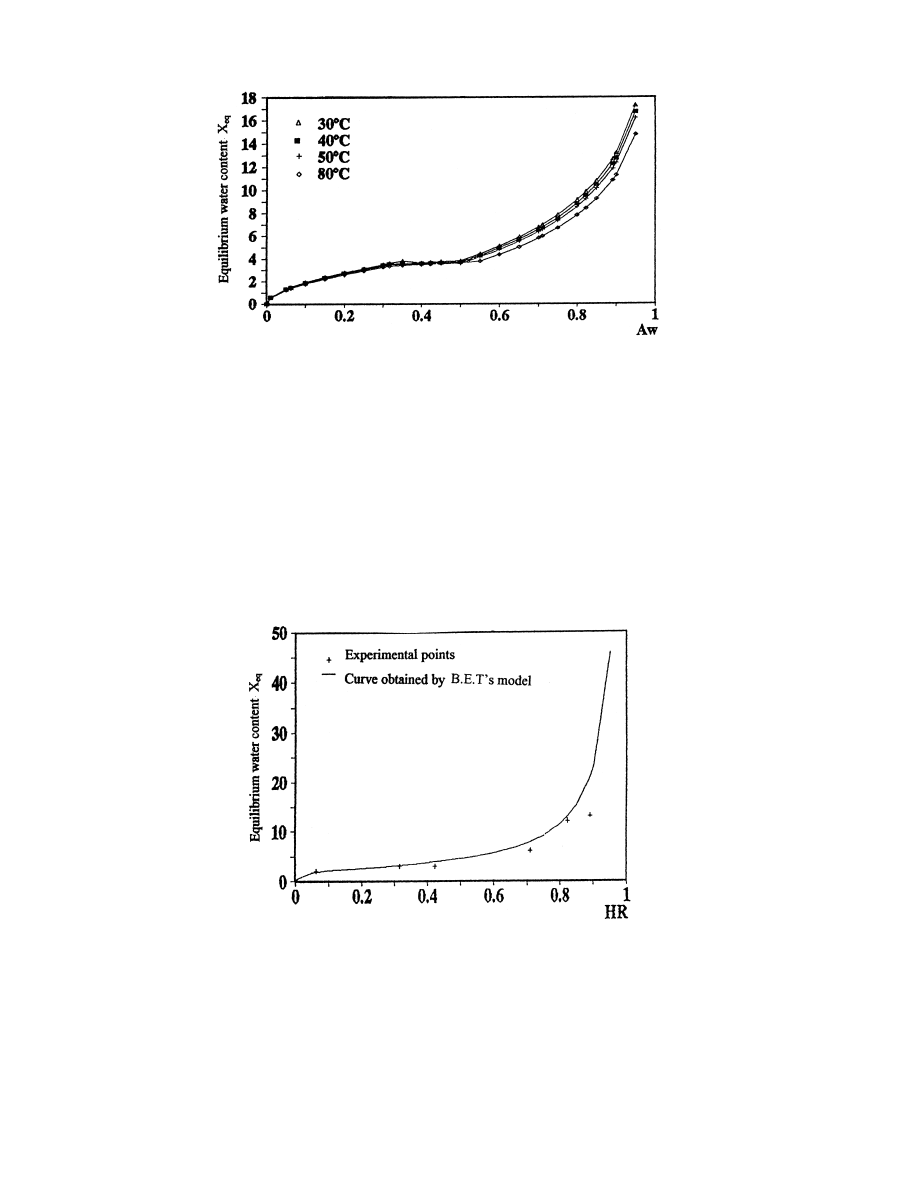
In Fig. 5, we plot the curve of sorption of verbena calculated by the B.E.T. model.

Unfortunately, this model is adapted only at low air moisture content …0RHRR50%). This

corresponds to ®xation of the monolayer of water molecules.

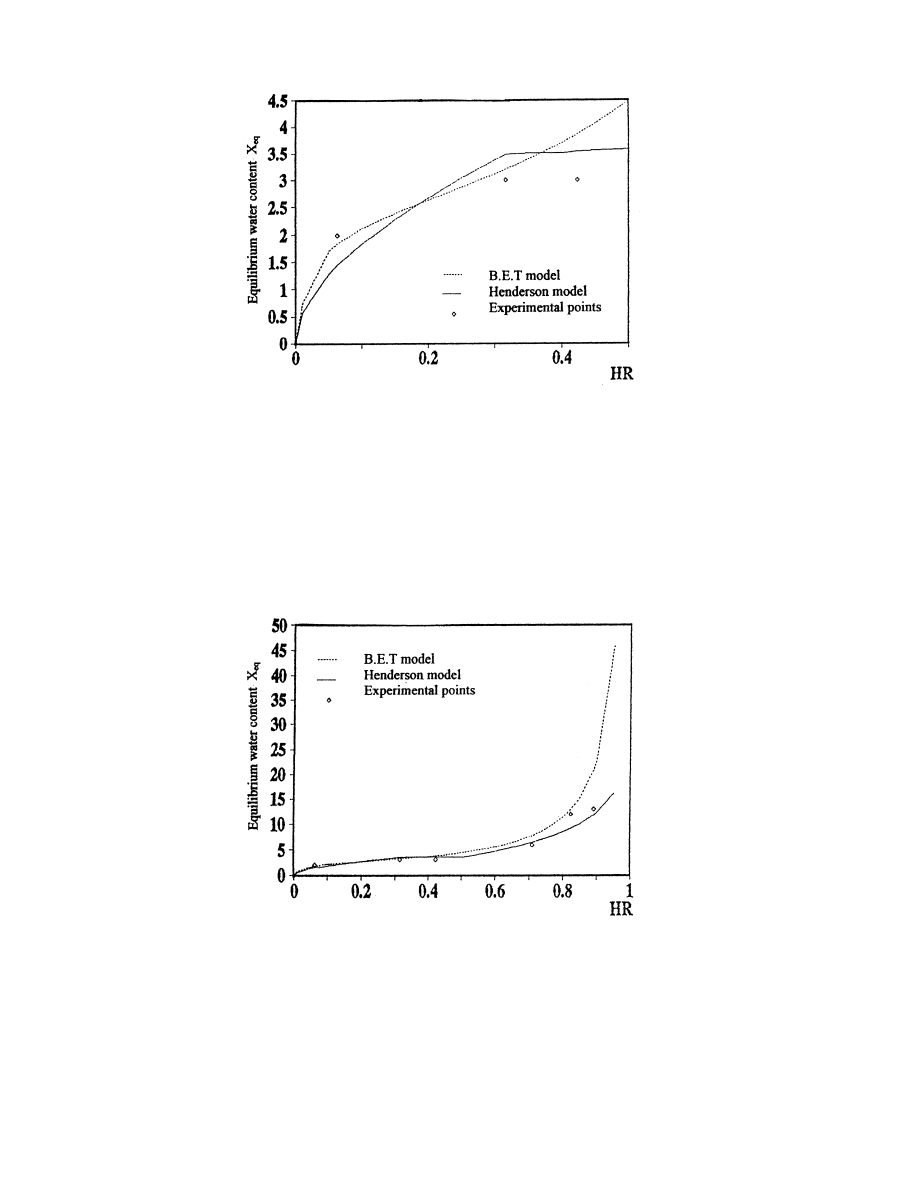
To compare the performances of the two models, we plot in Figs. 6 and 7 the experimental

points and the curves obtained by Henderson's and the B.E.T. model for activities of water

varying between 0 and 100%. We can conclude that the B.E.T. model describes better the

isotherm of sorption of verbena than Henderson's. However, this model is valid only in the

interval 0RHRR50%: For high air moisture contents, the results obtained by this model are

quite far from the experimental points.

Fig. 4. Isotherm of sorption calculated with Henderson's model for di€erent temperatures.

Fig. 5. Isotherm of sorption calculated with the B.E.T. model for T ˆ 408C.

A. Belghit et al. / Energy Conversion & Management 41 (2000) 1303±1321

1309

3. Kinetics of drying of verbena

3.1. Introduction

In the previous section, we studied the hygroscopic equilibrium of verbena. This allowed us

to have an idea on the equilibrium water content relative to a given air moisture content. The

results of this study allowed us also to have the curves of sorption. This kind of curve is

Fig. 6. Comparison between the isotherms of sorption of verbena calculated with the B.E.T. and Henderson's

models for 0RHRR50%:

Fig. 7. Isotherms of sorption of verbena calculated with the B.E.T. and Henderson's models for 0RHRR100%:

A. Belghit et al. / Energy Conversion & Management 41 (2000) 1303±1321

1310

necessary for determination of the drying kinetics of the product and the conditions permitting

its storage

In the drying literature, di€erent models and theories are used in order to study drying

kinetics and apprehend the physical laws governing heat and mass transfer during the drying

process [3,7]. However, since the transfer mechanisms are complex and the biological products

are abundant, a unique model could not represent all the situations.

3.2. Material and method

3.2.1. Description of experimental apparatus

The di€erent experiments undertaken consist of studying the drying kinetics of verbena in a

drying tunnel working by forced convection in a controlled atmosphere.

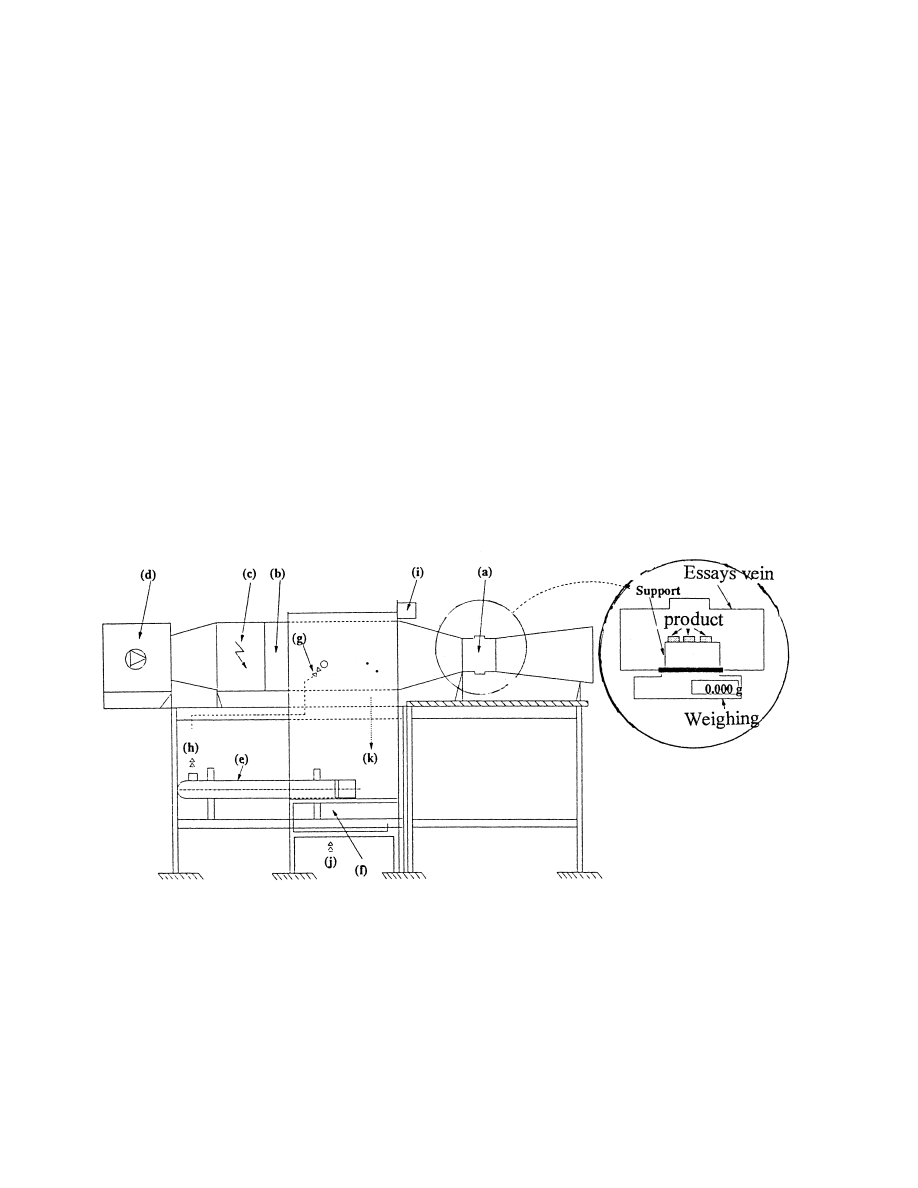
The experimental apparatus (Fig. 8) is a laboratory-drying tunnel which allows us to have an

air¯ow with controlled characteristics. The whole apparatus includes:
. A treatment air unit (d) with a variable fan velocity allowing us to have an average air

velocity in the essays vein (a) varying between 4 and 12 m s

ÿ1

. In order to have low air

velocities, which are necessary for drying processes, we have adopted the inlet air system.

The air¯ow is, therefore, made uniform with a nest of screens placed upstream of the last

system.

. A heating battery (c) of 24 kW installed power, regulated by a temperature probe.

. A water humidi®er (b) supplied by water at variable temperature by the intermediary of a

vaporizer (e) regulated by a humidity probe. It is characterized by:

Fig. 8. Schematic representation of the laboratory drying tunnel: (a) essays vein, (b) humidi®er, (c) heating system,

(d) fan, (e) heating system, (f) electrovan, (g) control van, (h) hot water, (i) humidity and temperature probes, (j)

cold water, (k) throwing out.

A. Belghit et al. / Energy Conversion & Management 41 (2000) 1303±1321

1311

*

an installed power: 12 kW;

*

a water ¯ow rate: 1.4 10

ÿ4

m

3

s

ÿ1

;

*

a maximum air moisture content: 80%.

. An essays vein (a) of square shape of dimension (25 cm 25 cm) supplied upstream by a

convergence for a good velocity distribution and down stream by a weak angle (78) of

divergence so as to avoid the removement in the essays vein. This vein contains a site for

®xing the samples of product and entrances to place thermocouples and a Pitot tube for the

air velocity measurement.

. A command cupboard controlling:

*

a heating battery regulator;

*

an air moisture regulator;

*

a control of the ventilation velocity;

*

a control of the electrovane of the humidi®er circuit.

3.2.2. Parameters measured

The parameters measured during every experiment are:

. Temperature

Temperature measurement is made by Chromel/Alumel thermocouples of diameter d ˆ 1

mm and measurement accuracy of about 0.5 K. The temperature is measured in various

places of the essays vein:

*

at the surface of the product;

*

in the drying air;

*

in the inlet and outlet of the essays vein.

The verbena leaf on which the temperature measurement is done remains isolated in the

same drainage of hot air ¯ow (within the essays vein) with the others in order to avoid all

in¯uence on the weight product measurement.

. Air moisture content

It is done by a thermohygrometer with an accuracy of 0.1%, recalibrated by some

ambiences with reduced air moisture. This allows us measuring directly the average air

moisture content.

. Drying air velocity

It is done by means of a digital velocimeter linked to a Pitot tube placed in the essays vein

near the surface of the product. The measurement accuracy is about 0.1 ms

ÿ1

.

. Loss mass of product

It is done by a display digital weighing apparatus with an accuracy of 0.001 g. This

weighing apparatus allows us to follow continuously the loss mass of product during the

drying process.

3.3. Experimental set-up

Since the verbena leaves are considerably light and their dimensions are very small, the

A. Belghit et al. / Energy Conversion & Management 41 (2000) 1303±1321

1312

experiment could not be undertaken on isolated leaves. So, we were led to dry our aromatic herb

in a thick layer. A digital weighing apparatus allows us to follow the product mass loss during the

drying process. Placed right beneath the essays vein, the weighing apparatus must play the role of

a stand for the drying product. Nevertheless, for the same reasons evoked above, a weak air¯ow

rate might throw the product outside the vein. In order to rectify this problem, we used a grilled

cage as a support for the product. This grilled cage is placed upon the weighing apparatus.

The measurement method consists of ®xing values of drying air velocity and temperature of

drying for every test. The system is left in order to stabilize during an hour until attaining the

equilibrium temperature. Then, the product is introduced in the essays vein. From this

moment, we began to follow the variation of weight of the product as a function of time. The

time separating two successive measurements is about a few seconds in the beginning of the

drying process. As and when the mass product decreases during drying, we increase the time

interval until becoming an hour in the drying end.

This way of proceeding, called continuous drying, involves considerable ¯uctuations of mass

due to the e€ect of the air thrust. Some researchers adopted, as a solution, taking measurements

after the ventilation was stopped [8]. The drying is then not continuous, and the perturbations

brought by these stops involve other errors in measurement.

The drying curves are based on the variation of the product water content as a function of time.

Knowing the wet mass, the dry mass is obtained by putting the product, at the end of every

experiment, in an oven regulated at 1058C until dewatering completely the product. Thus, we

obtain an experimental curve representing the variation of product water content as a function of

time.

3.4. Results and discussion

We study in this section the variation of product water content as a function of time and the

in¯uence of drying air velocity and drying air temperature on the rate of drying in order to

determine the characteristic curve of drying. Our experimental tests are undertaken in the

experimental conditions given in Table 2.

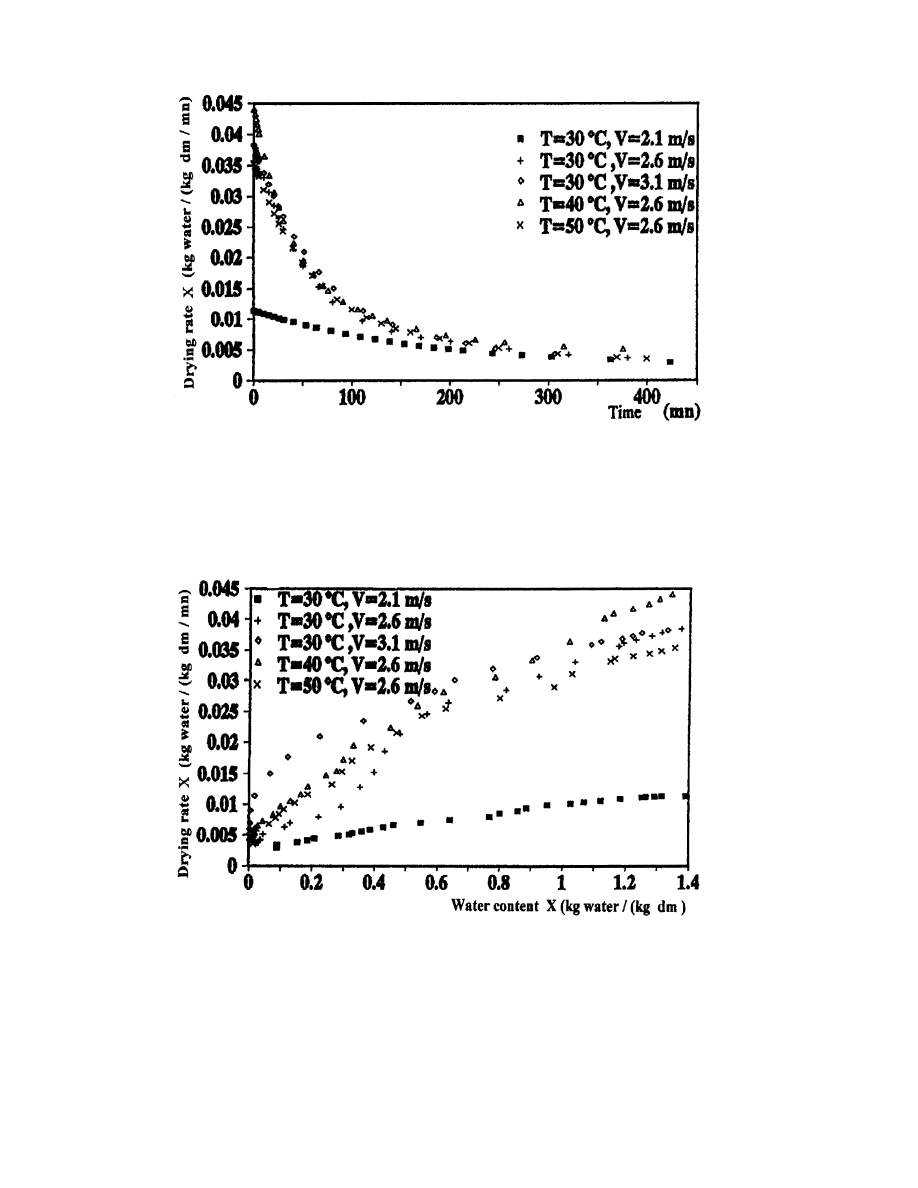
According to Figs. 9±11, representing the drying curves, we note that the drying air conditions

have an important in¯uence on the rate of these curves. Thus, we can conclude two main results:
. There is an absence of phase 0, where the temperature of the product is increased without

Table 2

Conditions of drying air for di€erent experiment essays

Test number Drying air velocity V

(m s

ÿ1

)

Dry-bulb temperature T

1

(8C)

Wet-bulb temperature T

h

(8C)

Air moisture content HR

(%)

1

2.1

30

18.5

26

2

2.6

30

20.2

40

3

3.1

30

19.4

38

4

2.6

40

23.5

28

5

2.6

50

25.4

15

A. Belghit et al. / Energy Conversion & Management 41 (2000) 1303±1321

1313

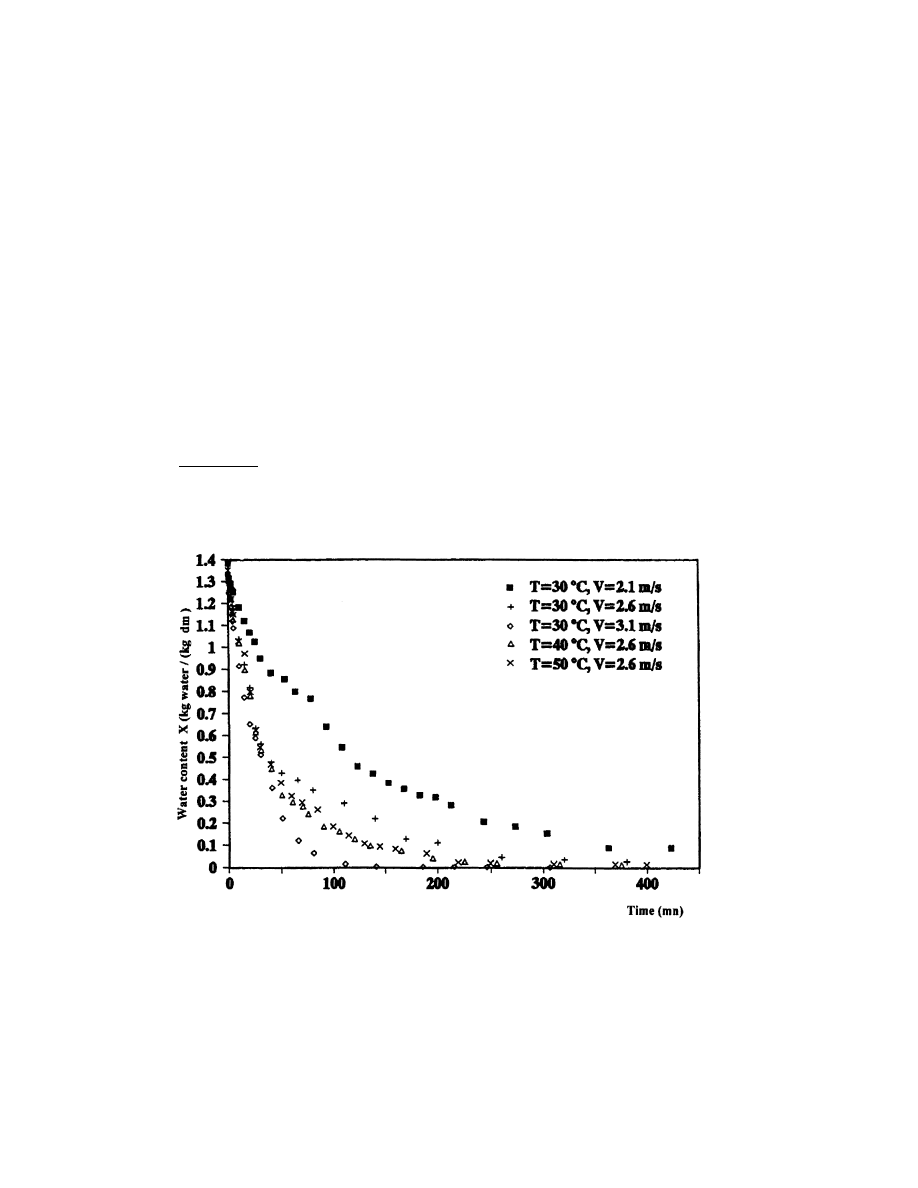
any substantial loss of water and phase 1, the constant rate period. There is only the

presence of the falling rate period (phase 2). This result is compatible with the drying

literature. Bimbenet et al. [9] noted that the phase 0 disappears when the product is compact

or in leaves and that the constant rate period (phase 1) is not observed in several biological

products. This appears clearly in Figs. 10 and 11 which represent a falling rate period since

the beginning of the drying process.

. There is a perfect agreement between the experimental results and theoretical predictions [3].

The variation of air conditions seems to have no e€ect on the drying kinetics at the end of the

drying process, at which we note that the drying curves have a tendency to coincide. At the

falling rate period (phase 2 is the unique period observed in the drying of verbena), the external

air conditions have an in¯uence which decreases until disappearing at the end of drying.

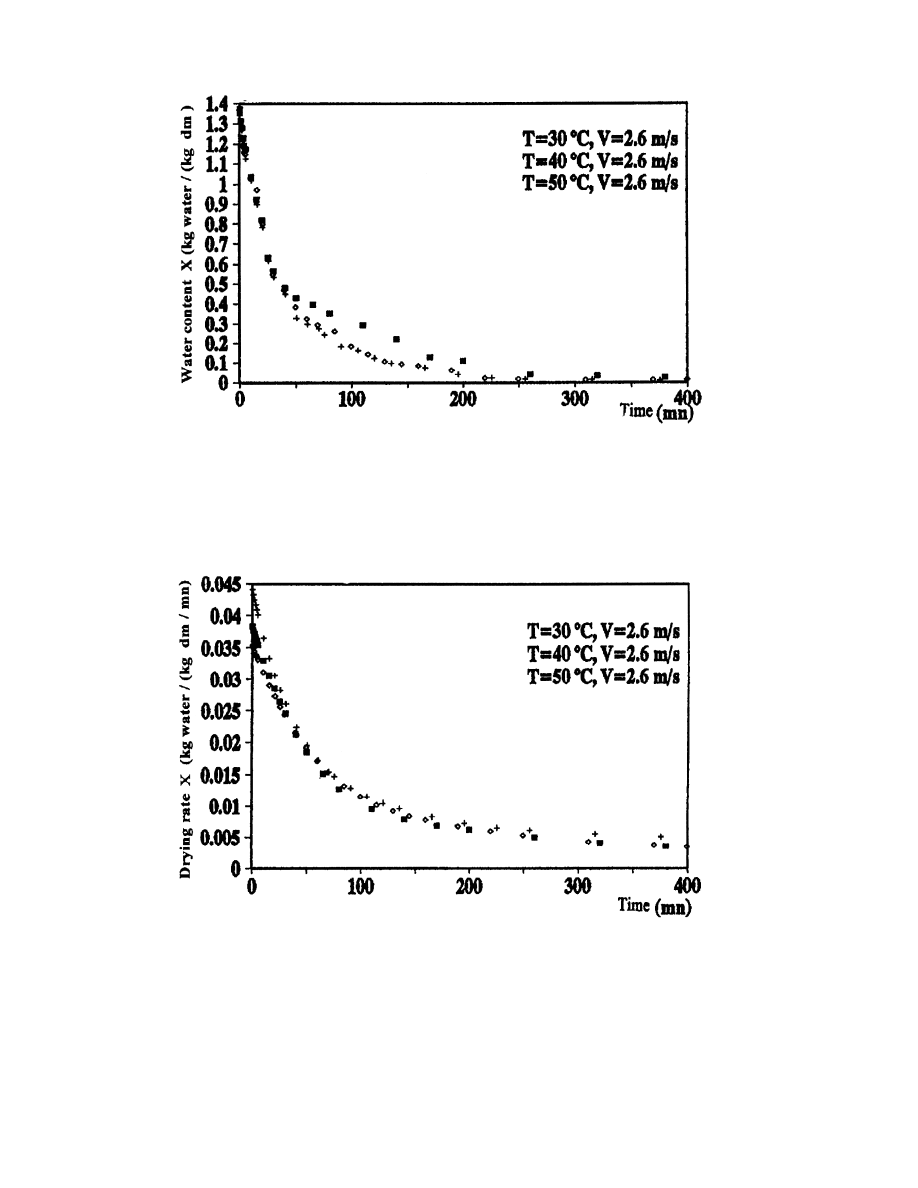
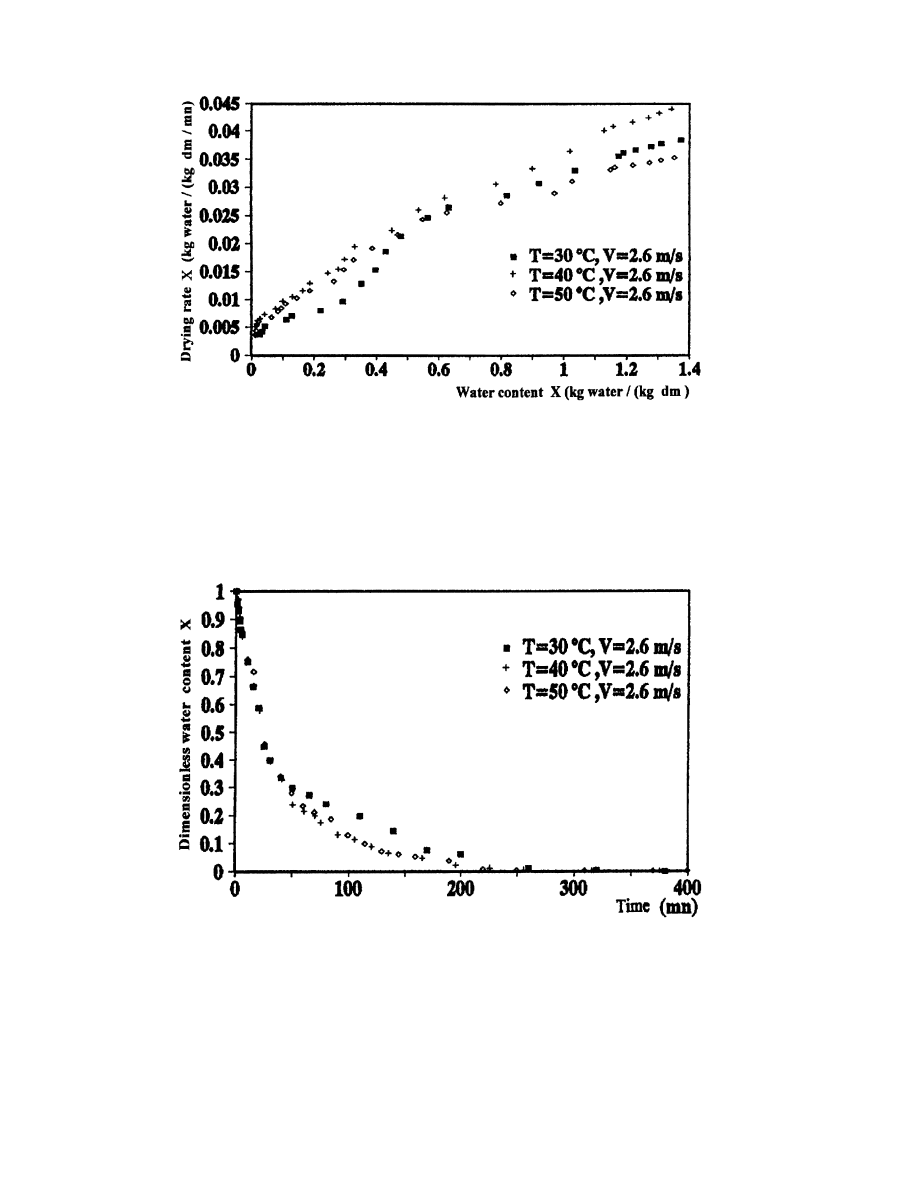
3.4.1. In¯uence of temperature

In this study, we are going to use the results of tests 2, 4 and 5 which are conducted at the

same drying air velocity for di€erent temperatures. Figs. 12±14 represent the drying curves in

the speci®ed conditions. Fig. 15 represents the variation of dimensionless water content X

as a

function of time:

X

ˆ

ÿ

X ÿ X

eq

ÿ

X

in

ÿ X

eq

…5†

The dimensionless water content is lower as the dry bulb temperature of air is bigger, but the

Fig. 9. Variation of verbena water content as a function of time for di€erent drying air conditions.

A. Belghit et al. / Energy Conversion & Management 41 (2000) 1303±1321

1314

drying rate increases with temperature. However, for the ®fth experiment, an anomaly appears

because the drying rate is less than the cases of experiments 2 and 4, even though the

temperature has increased. This could be explained by the fact that the drying is not controlled

alone by the temperature (desorption), but rather by an appreciable di€usional resistance

Fig. 10. Variation of verbena drying rate as a function of time for di€erent drying air conditions.

Fig. 11. Variation of drying rate as a function of water content for di€erent drying air conditions.

A. Belghit et al. / Energy Conversion & Management 41 (2000) 1303±1321

1315

which is sensible to the drying air velocity [10]. Moreover, we note clearly, according to the

curves of Figs. 12±14, that the temperature does not have a great in¯uence. So, the resistance

due to the super®cial evaporation is not negligible.

Fig. 12. In¯uence of drying air temperature on the evolution of water content as a function of time.

Fig. 13. In¯uence of drying air temperature on the evolution of drying rate as a function of time.

A. Belghit et al. / Energy Conversion & Management 41 (2000) 1303±1321

1316

3.4.2. In¯uence of drying air velocity

In order to make evident the in¯uence of the drying air velocity on the kinetics of

drying, we conducted some experimental tests by varying the air velocity and keeping the

temperature stationary …T

1

ˆ 308C). The results of tests 1, 2 and 3 are shown in Figs.

16±19.

Fig. 14. In¯uence of drying air temperature on the evolution of drying rate as a function of water content.

Fig. 15. In¯uence of drying air temperature on the evolution of dimensionless water content as a function of time.

A. Belghit et al. / Energy Conversion & Management 41 (2000) 1303±1321

1317

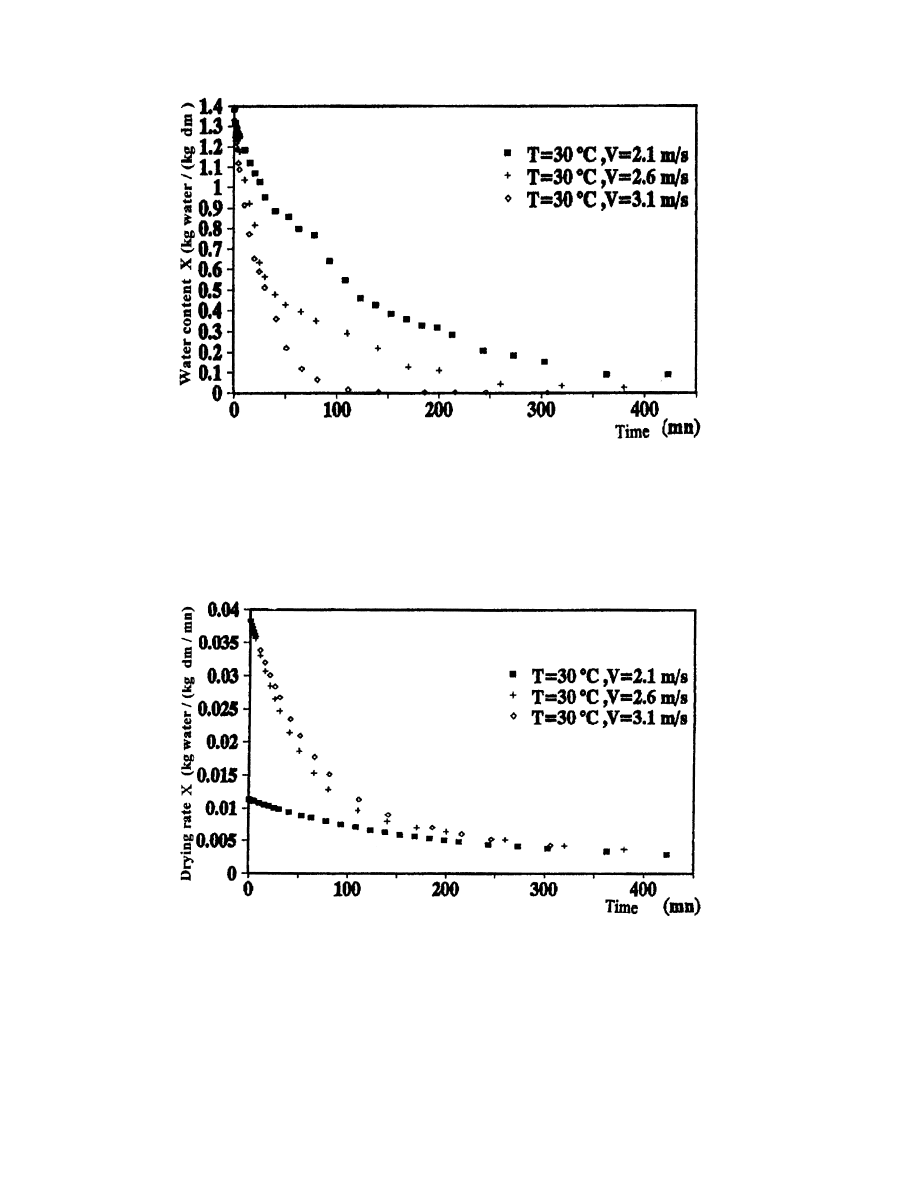
The obtained results are in perfect agreement with the theory [3]. Indeed, the water content has

a decreasing rate when the drying air velocity increases. However, the drying rate increases when

the drying air velocity increases. Daguenet [3] explains this phenomenon by giving the drying rate

as a function of a transfer coecient of the water vapor which increases with the air velocity. This

Fig. 16. In¯uence of drying air velocity on the evolution of water content as a function of time.

Fig. 17. In¯uence of drying air velocity on the evolution of drying rate as a function of time.

A. Belghit et al. / Energy Conversion & Management 41 (2000) 1303±1321

1318

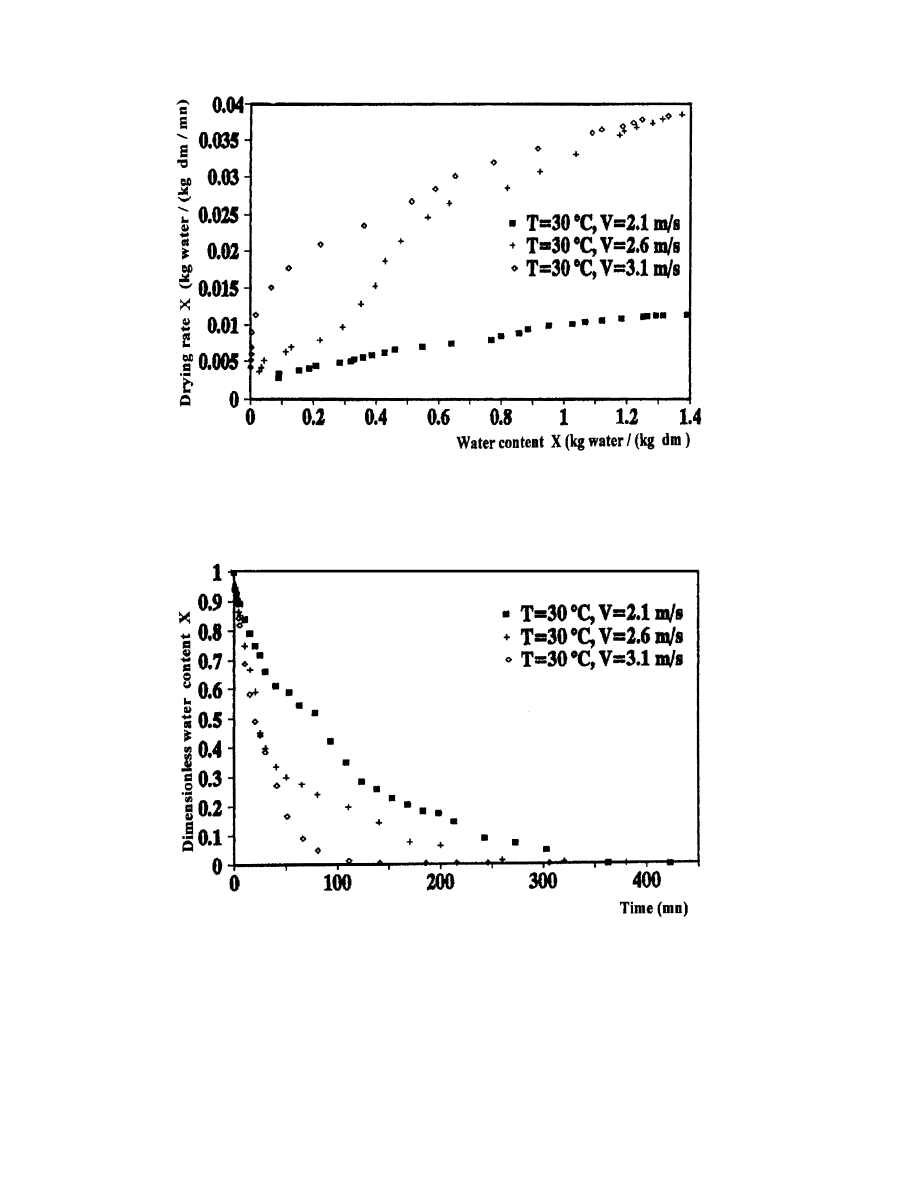
Fig. 18. In¯uence of drying air velocity on the evolution of drying rate as a function of water content.

Fig. 19. In¯uence of drying air velocity on the evolution of dimensionless water content as a function of time.

A. Belghit et al. / Energy Conversion & Management 41 (2000) 1303±1321

1319

parameter exerts, therefore, an important in¯uence on the rate of drying. In the case of verbena,

the drying air velocity seems to have a more important e€ect than the temperature.

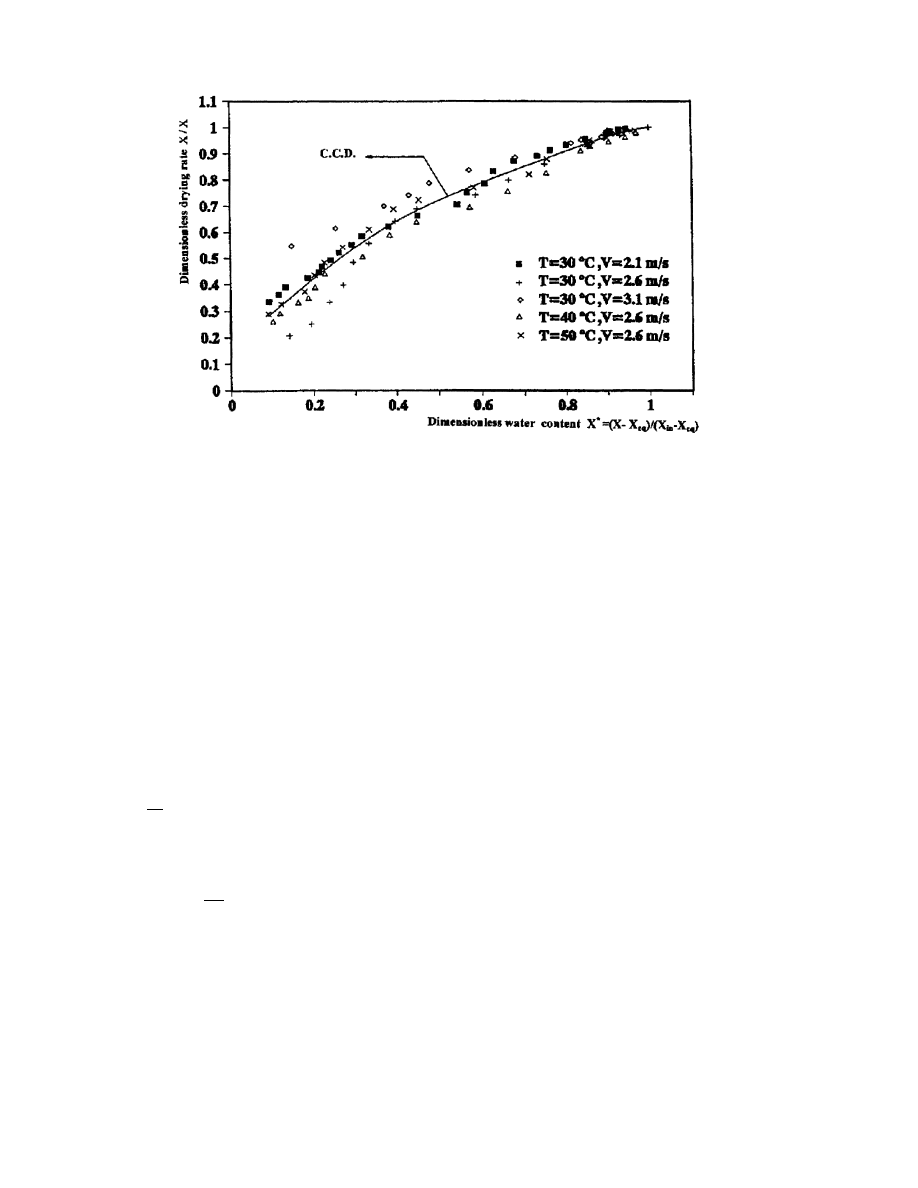
3.4.3. Determination of the characteristic curve of drying (C.C.D)

The goal of this section is to synthesize the obtained results by determining from the

di€erent experiments a basic curve called the characteristic curve of drying (C.C.D). The

pursued method [11] consists of plotting the dimensionless drying rate _X= _X

i

as a function of

the dimensionless water content X

. This lead to a narrowing of the di€erent values obtained

around an average curve called the C.C.D.

The equilibrium water content X

eq

can be determined from the isotherm of sorption. Fig. 20

represents the C.C.D. This kind of curve is interesting because it describes the drying kinetics

of a product by knowing its initial and equilibrium water contents for every drying air condition

A ®tting of the C.C.D allowed us to determine its equation. It is a ®fth degree polynomial

equation whose coecients are the following:

_X

_X

i

!

ˆ 0:1880 ‡ 0:8315X

‡ 3:2493X

2

ÿ 9:7577X

3

‡ 10:3257X

4

ÿ 3:8368X

5

…6†

For the determination of _X

i

, we used the relation suggested by Fornell [10]:

_X

i

ˆ

ÿ

dX

dt

i

ˆ aV

b

…T

1

ÿ T

h

†

…7†

The exploitation of the results permitted the identi®cation of the coecients a and b:

Fig. 20. Drying characteristic curve of verbena obtained for di€erent air conditions.

A. Belghit et al. / Energy Conversion & Management 41 (2000) 1303±1321

1320

a ˆ 9:01 10

ÿ5

and b ˆ 3:25

4. Conclusions

The experiments described in the ®rst section consist of determining the isotherm of sorption

that led to other results. Thus, by smoothing six experimental points, we obtained a third degree

polynomial equation which describes the isotherm of sorption and whose coecients are the

following:

X

eq

…408C† ˆ 0:0037 ‡ 0:00215 HR ÿ 0:00006 HR

2

‡ 5:8156 10

ÿ7

HR

3

…8†

The calculation of Henderson's constants (k and n ) allowed us to determine the isotherms of

sorption of verbena for di€erent temperatures. By using the B.E.T. model, we have compared the

experimental points and the curves of sorption calculated by the two models.

From these results, we could conclude, on the one hand, that the sorption isotherm of

verbena follows the general rate of the sorption curve given by Multon [12]. On the other

hand, the model of Henderson describes very well the isotherm obtained at 408C. So, we could

exploit the obtained results at 408C with a satisfactory precision for the analysis of other

drying experiments conducted at temperatures neighboring to 408C.

In Section 2, we plotted the characteristic curve of drying of verbena that we have exploited

to determine the kinetic properties of verbena. We noted, in particular, the absence of phases 0

and 1 [9] and the in¯uence of air temperature and drying air velocity on the rate of drying.

Finally, we have determined the characteristic curve of drying of the verbena.

References

[1] Boutaleb CB. Etude expeÂrimentale du seÂchage convectif de plantes meÂdicinales: application aÁ la sauge et aÁ la

verveine. TheÁse de 3eÁme cycle, Universite Cadi Ayyad, Marrakesh, Morocco, 1997.

[2] Daudin JD. Calcul des cineÂtiques de seÂchage par l'air chaud des produits biologiques solides. Sciences des

Aliments 1983;3(1):1±36.

[3] Daguenet M. Les seÂchoirs solaires: theÂorie et pratique. Publication de l'UNESCO, Paris, France, 1985.

[4] Belahmidi M, Belghit A, Mrani A, Mir A, Kaoua M. Approche expeÂrimentale de la cineÂtique de seÂchage des

produits agro-alimentaires. Revue GeÂneÂrale de Thermique 1993;380/381:444±53.

[5] Henderson SM. A basic concept of equilibrium moisture. Agric Eng 1952;33(1):29±32.

[6] Brunauer S, Emmet PH, Teller E. Adsorption of gases in multimolecular layers. J Am Chem Soc 1983;60:309.

[7] Belghit A, Belahmidi M, Bennis A, Boutaleb BC, Benet S. Etude numeÂrique d'un seÂchoir solaire fonctionnant

en convection forceÂe. Revue GeÂneÂrale de Thermique 1997;36:837±50.

[8] Ferrao P, Figueiredo A, Freire F. Experimental analysis of the drying kinetics of a food product. Drying

Technology 1998;16(8):1687±702.

[9] Bimbenet JJ, Daudin JD, Wol€ E. Air drying kinetics of biological particles. In: Proceedings of the Fourth

International Drying Symposium, Kyoto. 1984.

[10] Fornell A. SeÂchage de produits biologiques par l'air chaud. Calcul de seÂchoirs. TheÁse de docteur ingeÂnieur,

ENSIA-Massy France, 1979.

[11] Van Arsdel WB, et al. Food dehydration. Westport: AVI Publishing Company, 1973.

[12] Multon JL. Etat de liaison de l'eau dans les aliments. ProbleÁmes fondamentaux de seÂchage. ATP-PIRDES, 1980.

A. Belghit et al. / Energy Conversion & Management 41 (2000) 1303±1321

1321