Tomasz Zarębski

Politechnika Szczecińska

Instytut Elektrotechniki

ul. Sikorskiego 37

70-313 Szczecin

SPOSÓB REGULACJI GŁĘBINOWYCH SILNIKÓW INDUKCYJNYCH

ZASILANYCH Z ALTERNATYWNYCH ŹRÓDEŁ ENERGII

1. Wprowadzenie

Silniki głębinowe mają szerokie zastosowanie w układach napędowych pomp

odśrodkowych. Układy takie są stosowane przede wszystkim w przemyśle wydobywczym

zarówno do osuszania wyrobisk górniczych z wód gruntowych (szyby w kopalniach węgla

kamiennego, odkrywki węgla brunatnego) jak i do wydobywania ropy naftowej [3]. Spotyka

się je również w studniach głębinowych oraz w miejskich zakładach wodociągowych.

Zdarzają się również bardzo specyficzne zastosowania tych silników, jak na przykład

wydobycie płynnej siarki, przepompownie różnego rodzaju zanieczyszczeń itp.

Wynika stąd, że silniki głębinowe są stosowane przede wszystkim do wydobycia

wody oraz ropy naftowej. Ze względu na specyfikę występowania złóż obu tych surowców

ich konstrukcja jest różna.

Silniki pomp ropy naftowej pracują w ekstremalnych warunkach. Tak np. przy

wydobywaniu ropy naftowej spod dna morskiego na głębokości 2000 m poddawane są one

ciśnieniu cieczy w odwiercie dochodzącemu do 20 MPa. Pompowana ropa naftowa często ma

właściwości ścierne wywołane zawartością piasku z dna wokół pokładu. Ponadto, w

pompowanej cieczy mogą się znajdować wtrącenia stałe, które mogą spowodować nagły

wzrost obciążenia silnika. Natomiast wtrącenia gazowe mogą być przyczyną nagłego

zmniejszenia obciążenia.

Silniki napędowe pomp wodnych pracują w nieco lepszych warunkach, a ponadto na

mniejszych głębokościach. W przypadku zastosowania takich napędów w studniach

głębinowych wymagana jest regulacja ich wydatku. W pompowanej wodzie, zwłaszcza w

przypadku osuszania wyrobisk górniczych, również mogą znajdować się różne zawiesiny,

części stałe, wtrącenia gazowe oraz substancje chemicznie aktywne.

Silniki tego typu, ze względu na możliwe zastosowania, mogą pracować w miejscach

odległych od energetyki zawodowej. Takie sytuacje mają najczęściej miejsce w przypadku

indywidualnych użytkowników posiadających własne niekonwencjonalne elektrownie,

baterie słoneczne lub elektrownie wiatrowe, o niewielkich mocach. Jak powszechnie

wiadomo, najcięższym stanem pracy silnika indukcyjnego jest jego rozruch. Dlatego w takich

przypadkach należy tak dobrać układ sterujący jego pracą, aby przy ograniczonej mocy źródła

zasilania możliwy był jego rozruch.

Silniki głębinowe pracują z reguły w pionowych odwiertach. Ze względu na pracę na

dużych głębokościach w szybach o średnicy niewiele większej od średnicy silnika. Dla

uzyskania odpowiedniej mocy silnika należy zwiększyć jego długość. Zasilanie odbywa się

poprzez odwiert. Również poprzez odwiert doprowadza się przewody stanowiące kanały

informacyjne o stanie pracy silnika.

Silniki z długim wałem są podatne na powstawanie drgań skrętnych oraz ugięcia. Co

może być przyczyną występowania zjawiska tarcia wału o stojan [1].

Warunki pracy silników głębinowych napędzających pompy oraz specyficzna ich

konstrukcja stwarzają szereg ograniczeń, które należy uwzględnić przy rozpatrywaniu

zagadnień rozruchu. Z ograniczeń tych należy wymienić:

• niekontrolowane pulsacje momentu obciążenia, które deformują teoretyczną

charakterystykę mechaniczną pompy,

• czas rozruchu jest uwarunkowany momentem bezwładności układu, tłumieniem

wibracji oraz obciążeniem; tłumienie wibracji w pompie zależy od cech pompowanej

cieczy,

• trwania rozruchu powinien być możliwie krótki, by zapewnić szybkie przechodzenie

przez prędkość odpowiadającą rezonansowi mechanicznemu układu silnik - pompa,

• w skrajnym przypadku przy bardzo trudnym rozruchu powinna istnieć możliwość

forsowania napięcia w celu zwiększenia momentu rozruchowego,

Ostatnie ograniczenie dotyczy rozruchu silników po dłuższych postojach. Podczas

rozruchu może pojawić się dodatkowy moment oporowy wynikający z działania cieczy, w

której jest zanurzony układ silnik – pompa. W tym przypadku dla dokonania rozruchu

niezbędne jest forsowanie napięcia.

2. Regulacja rozruchu silników pomp głębinowych

Najtrudniejszą sprawą podczas rozruchu jest przejście przez prędkość rezonansu

mechanicznego. Z tego względu należy tak projektować układ rozruchowy, aby przejście

przez tę prędkość odbywało się możliwie najkrócej. Ponadto znaczny prąd rozruchowy jest

przyczyną dużych obciążeń cieplnych, które mogą w dużym stopniu obniżyć trwałość silnika.

W celu zminimalizowania tych obciążeń celowe jest przeprowadzanie rozruchu przy

stałym przyspieszeniu. Ponieważ w czasie trwania rozruchu zawsze występują pulsacje

momentu obciążenia, co powoduje, że wartość chwilowa przyspieszenia zmienia się, można

mówić tylko o zachowaniu warunku średniej wartości przyspieszenia.

Jakość rozruchu w dużej mierze zależy od przyjętego algorytmu sterowania układem

rozruchowym. Biorąc jednak pod uwagę aktualne możliwości sterowania należy szukać

rozwiązań kompromisowych. Muszą one z jednej strony spełnić sprzeczne wymagania

dotyczące odpowiedniej regulacji momentu silnika, a z drugiej – ograniczenia prądu

rozruchowego. Powstaje więc zagadnienie dotyczące wyboru kryteriów przy opracowaniu

algorytmu sterowania rozruchem, przy równoczesnym uwzględnieniu ograniczonej z natury

ilości kanałów informacyjnych.

Z powyższego wynika, że dla uwzględnienia wymienionych warunków rozruchu

należy:

• utrzymywać stałą średnią wartość przyśpieszenia poprzez odpowiednią regulację

momentu maksymalnego,

• ograniczyć nagrzewanie silnika.

3. Równoczesna regulacja napięcia i częstotliwości

Przy rozpatrywaniu rozruchu spełniającego wyżej wymienione warunki zakładamy, że

istnieje możliwość regulacji częstotliwości oraz napięcia zasilającego silnik. Przez zmianę

częstotliwości możemy wpływać na wartość poślizgu krytycznego.

Jako czas rozruchu

τ

r

przyjmujemy czas liczony od początku rozruchu (s = 1) do

chwili osiągnięcia przez silnik poślizgu krytycznego (s = s

k

). Przedział ten (0

< τ < τ

r

)

stanowi 90

÷ 95 % całkowitego czasu do osiągnięcia przez układ silnik-pompa prędkości

ustalonej. W czasie 0 -

τ

r

występują największe przeciążenia prądowe.

W związku z określonym wyżej czasem rozruchu τ

r

możemy opracować taki algorytm

zmiany częstotliwości f(τ) w przedziale 0 -

τ

r

, aby silnik rozwijał moment maksymalny.

Wartość tego momentu wynika z założonego przyspieszenia. Zależy ono od rodzaju silnika,

głębokości na której ma pracować i innych czynników decydujących p warunkach jego pracy.

Wymaganą wartość momentu uzyskuje się poprzez regulacje napięcia zasilającego.

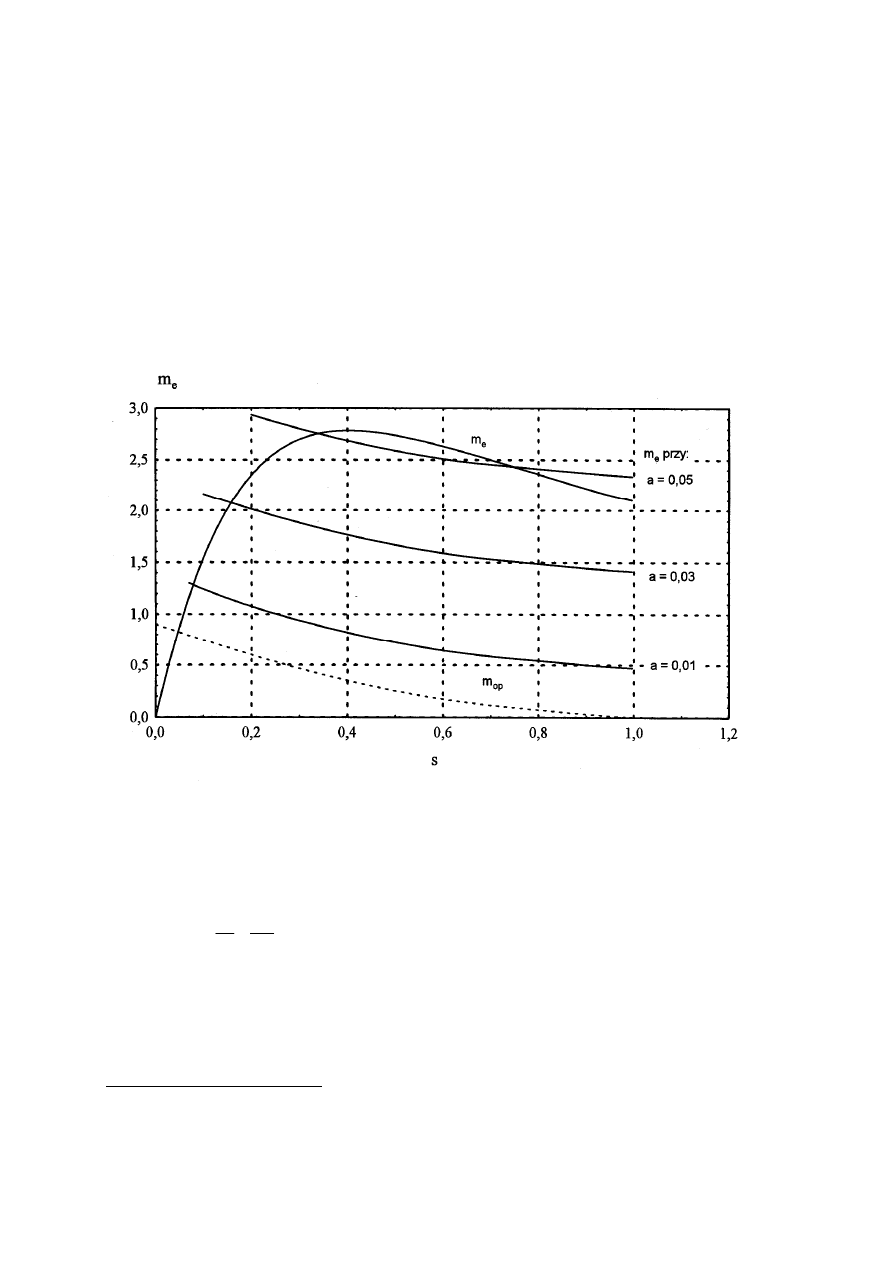
Na rysunku 1 przedstawiono obliczone charakterystyki m = f(s) silnika

1

uwzględniające powyższe warunki. W tym przypadku przyspieszenie 0,05 odpowiada

praktycznie rozruchowi bezpośredniemu.

Rys. 1. Przykładowy przebieg teoretycznych (1) charakterystyk momentu silnika i momentu oporow-

ego przy różnych wartościach założonego względnego przyspieszenia (a = 0,01; 0,03 i 0,05)

Ruch układu silnik-pompa w wartościach względnych opisuje zależność (1):

)

m

m

(

H

1

d

ds

e

op

j

−

=

τ

(1)

1

Obliczenia przeprowadzono dla typowego silnika głębinowego o następujących danych

znamionowych: typ SG-Me 18/33; P

n

=33 kW; U

n

=380V; I

n

=75,5 A; n

n

=2860 obr/min;

cosφ

n

=0,81; η

n

=0,82; I

r

/I

n

= 5,8; M

r

/M

n

= 2,2.

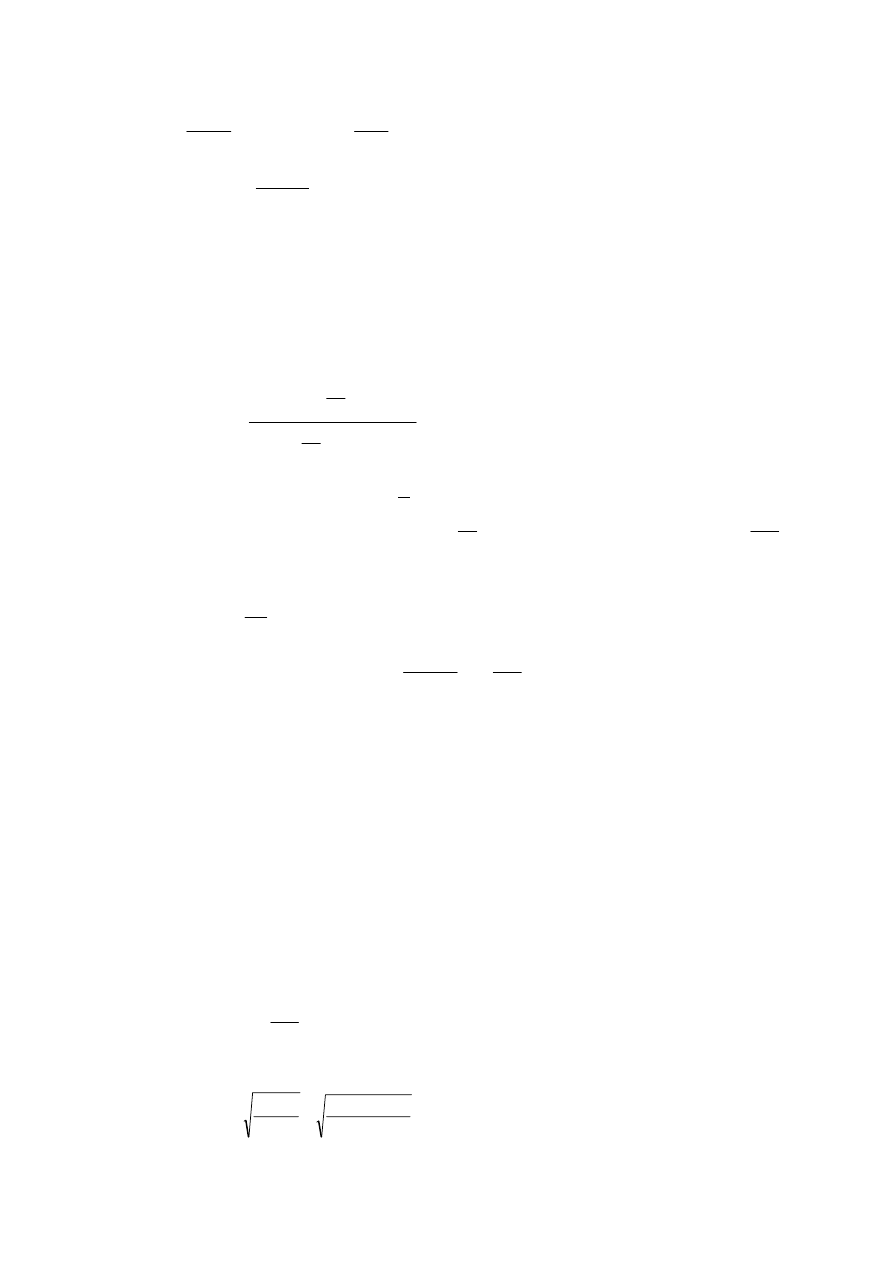
gdzie:

0

0

s

ω

ω

ω

−

=

- poślizg ;

pM

J

H

2

0

j

ω

=

- stała bezwładności mas wirujących, ω

0

– prędkość

synchroniczna,

0

n

n

p

I

U

3

M

ω

=

– moment odniesienia, p – liczba par biegunów, m

e

- moment

elektromagnetyczny, m

op

- moment oporowy.

Moment oporowy m

op

jest w przybliżeniu proporcjonalny do kwadratu prędkości wału

ω. Zastępując prędkość przez poślizg otrzymujemy m

op

=k(1-s)

2

, (gdzie k - współczynnik

zależny od charakterystyki pompy).

Moment elektromagnetyczny w jednostkach względnych jest równy:

]

x

)

C

s

r

r

[(

C

s

r

u

m

2

2

k

2

f

2

'

1

f

2

2

e

α

α

+

⋅

+

⋅

⋅

=

(2)

gdzie: u – wartość względna napięcia, C = C

a

+j C

r

- współczynnik zespolony korygujący

uproszczenie schematu zastępczego [2],

n

f

f

=

α

- częstotliwość względna

C

C

x

r

r

r

1

1

'

1

α

−

=

.

Występujące we wzorze (2) rezystancje i reaktancje są odniesione do impedancji

znamionowej

n

n

n

I

U

Z

=

.

Poślizg s

f

określa zależność

α

αω

ω

αω

s

1

1

s

0

0

f

−

−

=

−

=

.

Jako drugi z warunków, który powinien być spełniony, jest ograniczenie ilości wydzielanego

ciepła. Wielkość strat cieplnych charakteryzuje tzw. całka cieplna

∫

=

r

0

2

1

d

i

Q

τ

τ

,

(3)

gdzie: i

1

– wartość chwilowa prądu stojana, τ

r

– czas trwania rozruchu.

Przy rozruchu o stałym przyspieszeniu moment silnika jest równy:

2

j

e

)

s

1

(

k

aH

m

−

+

=

.

(4)

Niezbędną dla spełnienia równości (2) wartość momentu m

e

otrzymamy przez

odpowiednią regulację napięcia. Wyrażenie (2) możemy przedstawić w postaci

α

f

2

2

2

e

s

r

i

m

⋅

=

.

(5)

Po przekształceniu zależności (5) możemy obliczyć prąd wirnika

2

e

2

f

e

2

r

)

s

1

(

m

r

s

m

i

+

−

=

=

α

α

.

(6)

Przy założeniu i

1

≈

i

2

= i, całka cieplna może być zastąpiona sumą iloczynów

,

określonych po podziale rozpatrywanego przedziału czasu 0

< τ < τ

τ

Δ

⋅

2

j

2

i

r

na dostatecznie małe

odcinki Δτ. Otrzymamy wtedy:

τ

Δ

Σ

⋅

=

2

j

2

i

Q

(7)

gdzie:

2

j

j

ej

2

j

2

r

)

s

1

(

m

i

+

−

=

α

;

co odpowiada momentowi w j-tym odcinku przedziału czasu 0

< τ < τ

r

m

ej

= aH + k(1-s

j

)

2

.

gdzie: s

j

= 1 – a τ

j

; τ

j

= j Δτ; j = 1, 2, 3, ...

Teoretyczny koniec rozruchu nastąpi, gdy poślizg s

j

= s

k

przy częstotliwości

znamionowej.

Jak wyżej wspomniano, przy jednoczesnej regulacji napięcia i częstotliwości silnik w

czasie rozruchu powinien rozwijać moment maksymalny przy poślizgu krytycznym

określonym zależnością (8)

2

2

k

2

1

2

fk

x

'

r

C

r

s

α

+

=

.

(8)

Wyrażając poślizg krytyczny przez prędkość kątową wirnika otrzymamy

)

x

'

r

C

r

1

(

2

2

k

2

1

2

α

α

ω

+

−

=

.

(9)

Określenie względnej częstotliwości α dla każdej chwilowej wartości prędkości ω w

wygodnej dla analitycznego badania postaci jest bardzo uciążliwe. Dlatego założono, że r

1

<<

x

k

. Otrzymamy wtedy:

)

s

1

(

x

C

r

x

C

r

k

2

k

2

−

+

=

+

=

ω

α

.

(10)

Korzystając z (6) i (10) otrzymamy wyrażenie na prąd wirnika

k

e

2

x

C

m

i

=

.

(11)

W tym przypadku prąd wirnika wynika z założonego przyspieszenia i jest regulowany

w czasie rozruchu przez zmianę napięcia.

Na rysunku 2 przedstawiono obliczone na podstawie (7) przebiegi całki cieplnej w

zależności od przyspieszenia. Krzywa 1 stanowi przebieg rozruchu przy regulacji napięcia i

stałej częstotliwości, a krzywa 2 przy regulacji napięcia i częstotliwości według przyjętego

algorytmu.

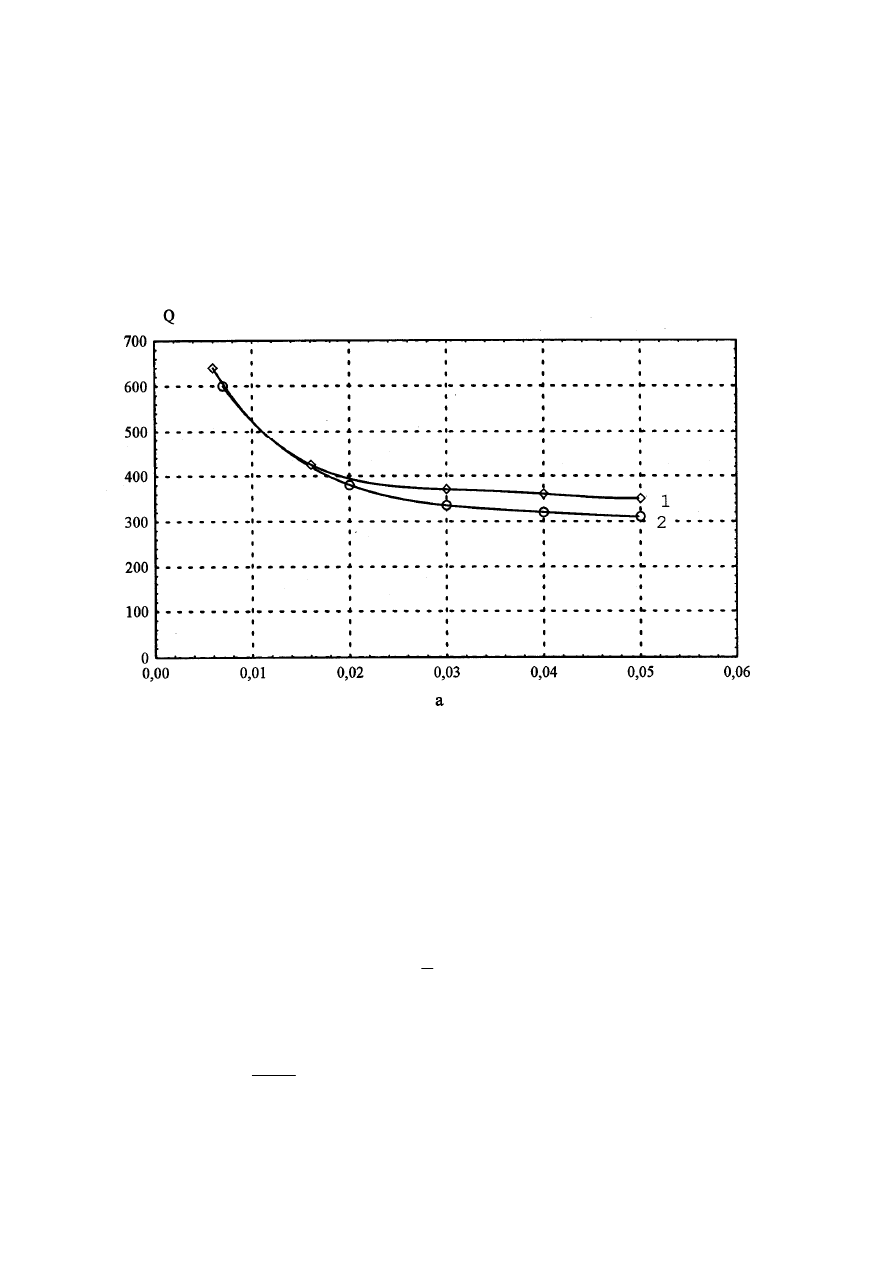
Z przebiegów tych wynika, ze funkcja cieplna osiąga mniejszą wartość przy

jednoczesnej regulacji napięcia i częstotliwości. Należy podkreślić, że dla przyspieszeń a >

0,3. funkcja Q(a) pozostaje praktycznie stała.

Wynika stąd, że bardziej korzystny jest rozruch przy jednoczesnej regulacji napięcia i

częstotliwości.

Rys. 2. Przebieg całki cieplnej: 1- regulacja napięcia przy f = const, 2 – jednoczesna regulacja napięcia

i częstotliwości.

Przy załączeniu do sieci silnika na założoną wartość napięcia oprócz prądów

okresowych, odpowiadających stanowi ustalonemu, pojawiają się wymuszone składowe

aperiodyczne, zanikające wykładniczo w czasie. Przybliżonej ich oceny można dokonać

poprzez sumowanie funkcji Q obliczonej w wyżej podany sposób i całkowej wielkości

∫

∞

τ

=

0

2

1

'

d

I

Q

, gdzie

a

T

t

1

s

1

e

I

I

−

=

=

(12)

gdzie: I

s=1

– wartość skuteczna okresowej składowej prądu I

1

przy s = 1

2

1

k

a

r

r

x

T

+

≅

– stała czasowa zanikania prądu I

1

.

Po określeniu całki w (12) mamy

2

T

I

'

Q

a

2

1

s

=

=

.

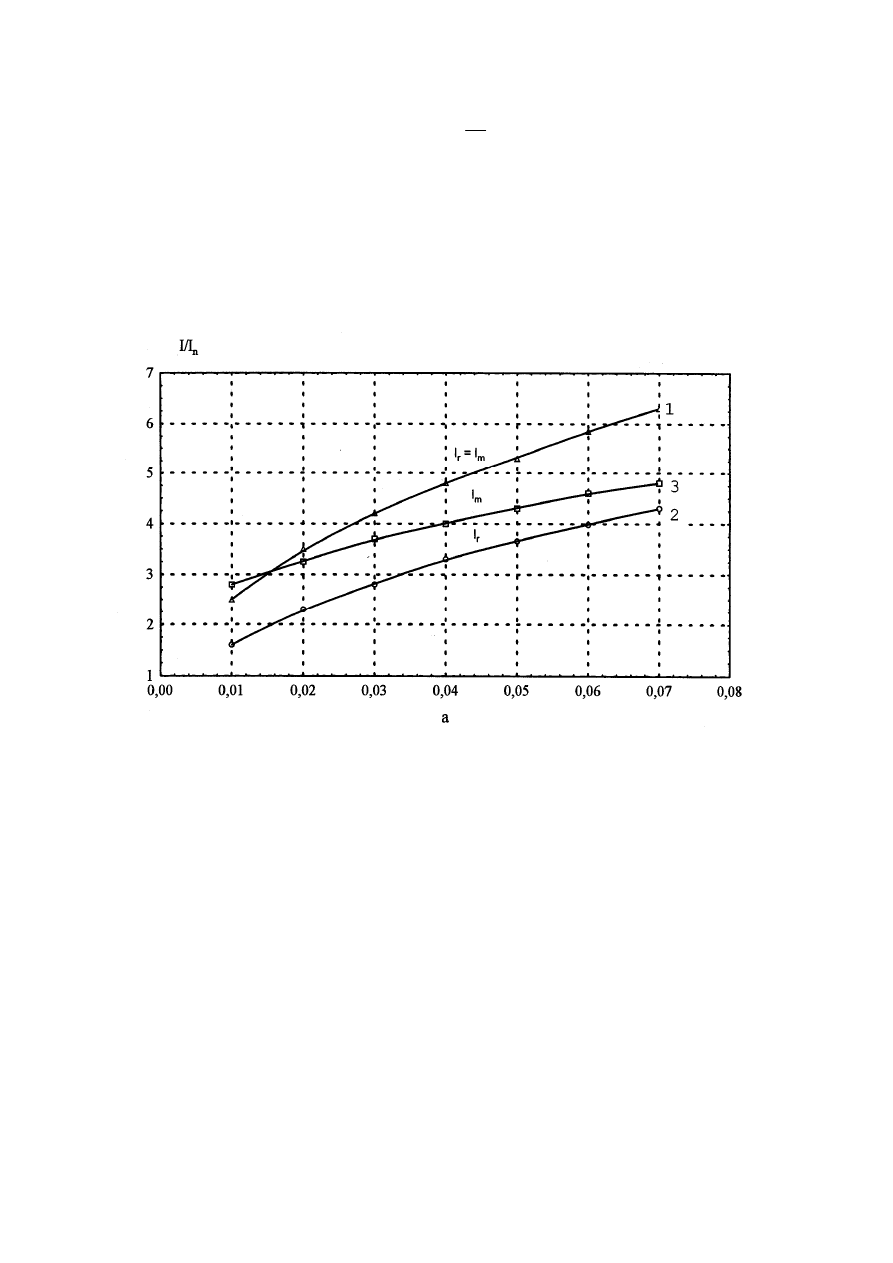
Należy zwrócić uwagę, że wraz ze zmniejszeniem zadanego przyspieszenia zmniejsza

się maksymalny prąd I

m

, odpowiadający w danym przypadku chwili (

τ = 0) po włączeniu

silnika do sieci zasilającej. Ilustruje to rys.3, na którym krzywa 1 przedstawia zmianę

wartości skutecznej składowej periodycznej prądu sieci I

p

przy

τ = 0 i różnych wartościach

przyspieszenia a = - ds/d

τ.

Rys. 3. Zmiana prądów rozruchowego i maksymalnego przy zadanym przyspieszeniu: 1- regulacja

napięcia przy f = const, 2,3 – jednoczesna regulacja napięcia i częstotliwości.

Podsumowując, z punktu widzenia minimalizacji funkcji cieplnej Q, najkorzystniejszy

jest rozruch bezpośredni, w przybliżeniu odpowiadający dla rozpatrywanych napędów

warunkowi a = 0,06

÷ 0,07. W związku z tym, zmniejszenie przyspieszenia wirnika do

wartości 0,02

÷ 0,04 mało wpływa na wielkość Q (rys.2), chociaż prądy rozruchowe i

momenty udarowe w tej sytuacji zmniejszają się 1,5

÷ 2 razy (rys.3). Dalsze zmniejszenie

parametru a powoduje szybki wzrost funkcji cieplnej Q, dlatego przy realizacji płynnego

rozruchu pomp głębinowych rozpatrywanego typu, wartość przyspieszenia należy ograniczyć

od dołu a

≥ 0.02 ÷ 0.03.

Wyniki obliczeń wartości skutecznej prądu stojana z pominięciem wpływu

składowych aperiodycznych przy równoczesnej regulacji napięcia i częstotliwości pokazują

krzywe 2 i 3 na rys. 3. Przy obliczeniach tak dobrano wartości chwilowe napięcia

zasilającego, aby silnik pracował przez cały czas trwania rozruchu przy poślizgu krytycznym.

Właściwości otrzymanych funkcji niewiele się różnią od wcześniej otrzymanych, gdy

zmieniało się napięcie przy stałej znamionowej częstotliwości.

Zmiana częstotliwości wg opisanego algorytmu pozwala dodatkowo obniżyć wartość

udarowej składowej okresowej prądu przy s = 1 w przybliżeniu 1.5 raza. W tym czasie można

zaobserwować zmniejszenie maksymalnego prądu w zakresie mniejszych poślizgów, przy

czym ze zmniejszeniem parametru a różnica między prądem udarowym I

p

i maksymalnym I

m

zgodnie z rys. 24 (krzywe 2 i 3) rośnie tak, że dla a = 0,017 prąd maksymalny I

m

przy

równoczesnej regulacji napięcia i częstotliwości jest taki sam, jak w przypadku zmiany tylko

napięcia.

4. Wnioski

Z przeprowadzonych rozważań wynikają następujące wnioski:

1. Zaproponowany sposób sterowania rozruchem silnika głębinowego, przy założeniu

utrzymywania stałej wartości przyspieszenia i ograniczenia funkcji cieplnej Q, pozwala na

poprawienie jego jakości.

2. Wraz ze zmniejszeniem napięcia i przyspieszenia rośnie czas trwania rozruchu oraz

wartość funkcji cieplnej. W zakresie przyspieszeń a > 0,03 funkcja Q(a) prawie się nie

zmienia.

3. Przy wyborze przyspieszenia poniżej wartości 0,03 obserwuje się szybki wzrost wartości

funkcji cieplnej, co ogranicza możliwość rozruchu silnika z przyspieszeniem mniejszym

niż a < 0,02.

4. Ze względu na trudne warunki pracy silnika falownik realizujący rozruch według

omówionego sposobu regulacji powinien mieć możliwie prostą budowę.

5. Przy obniżeniu przyspieszenia 2 – 2,5 raza (w porównaniu z rozruchem bezpośrednim)

wartość funkcji cieplnej rośnie o 6 – 10 %, natomiast udarowe prąd i moment są mniejsze

1,5 – 1,6 raza. Z tego punktu widzenia wydaje się celowe, by podczas rozruchu silnika

zasialnego ze źródła o ograniczonej mocy poprzez regulację napięcia ograniczyć wartość

przyspieszenia do wartości a = 0,02 – 0,03.

6. Literatura

1. Brinner T.R., Traylor F.T, Stewart R.H.: Cauves and preventium of vibration

injuced failures in submersible oil well pumping equipment. AIMH-SPE New Gricam, LA,

Sept (1982)..

2. Kowalowski H.: Maszyny i napęd elektryczny. Warszawa, PWN, (1983).

3. Зюзев А. М.: Технологический электропривод системы ТПН-АД для агрегатов

нефтегазового комплекса. Электротехника, № 8, 1998.

Streszczenie: Obserwowany w ostatnich latach wzrost zainteresowania alternatywnymi

źródłami energii spowodował, że indywidualni użytkownicy instalują tego typu urządzenia na

własnych posiadłościach. W wielu przypadkach niekonwencjonalne „domowe elektrownie”

mają stosunkowo niedużą moc. Ogranicza to w dość znaczny sposób możliwość zasilania z

nich układów napędowych z silnikami indukcyjnymi, które mają znaczny prąd rozruchowy.

W referacie zaproponowano sposób regulacji silników głębinowych indukcyjnych

wykorzystanych do napędu pomp odśrodkowych. Przedstawiony sposób regulacji tego typu

napędów pozwala na forsowanie napięcia podczas rozruchu oraz w znaczny sposób obniża

wartość początkową prądu rozruchowego. Przeprowadzono również analizę napędu pod

kątem wydzielanego przez napęd ciepła w czasie rozruchu. Wykazano, że przyjęty sposób

regulacji poprawia właściwości napędu również w tym zakresie. Omówiony sposób regulacji

może być wykorzystany do wszystkich napędów z silnikami indukcyjnymi.