WYTRZYMAŁOŚĆ MATERIAŁÓW

Wykład 2.

1. Liczba Poissona

2. Uogólnione prawo Hooke’a

3. Zagadnienia statycznie

niewyznaczalne

4. Naprężenia własne

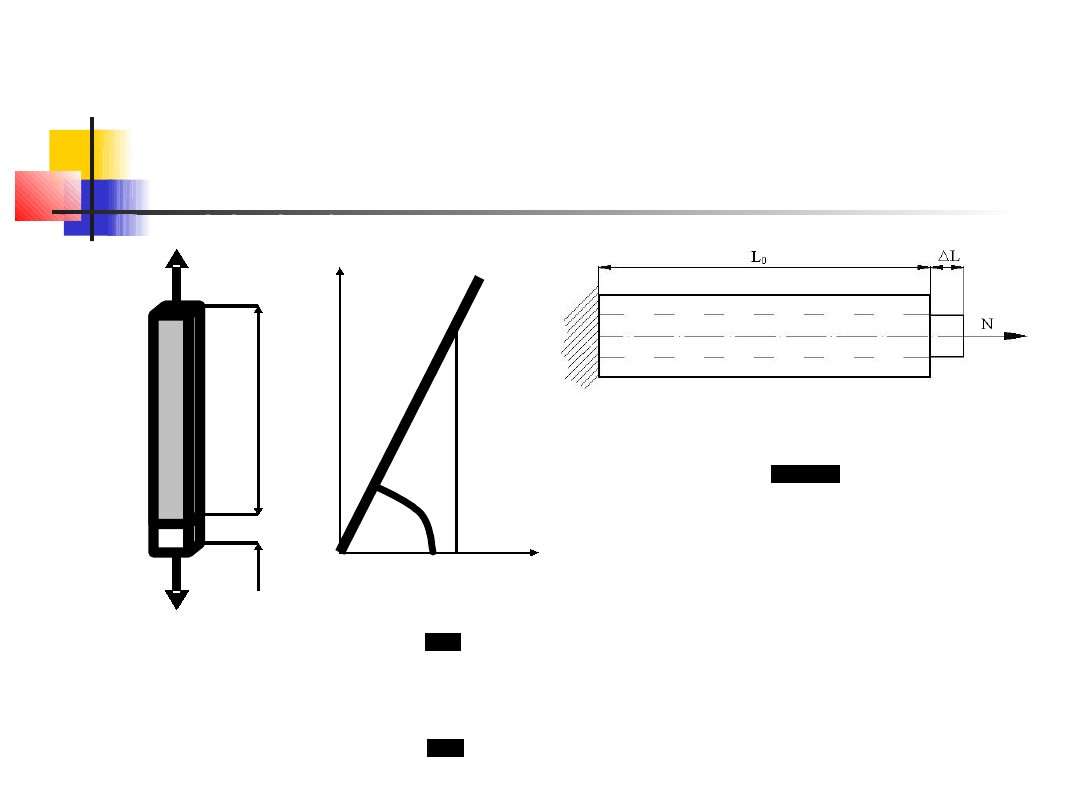
Prawo Hooke’a

dla równomiernego jednokierunkowego
rozciągania

N

L

0

(

σ

)

N

∆

l

(

ε

)

α

σ

b)

EF

NL

l

0

=

∆

∆

l –wydłużenie pręta, L

0

– długość

początkowa pręta

E

σ

ε

=

ε

=

l

l

∆

- wydłużenie względne

(odkształcenie liniowe)

E – moduł sprężystości Younga
(stała materiałowa)

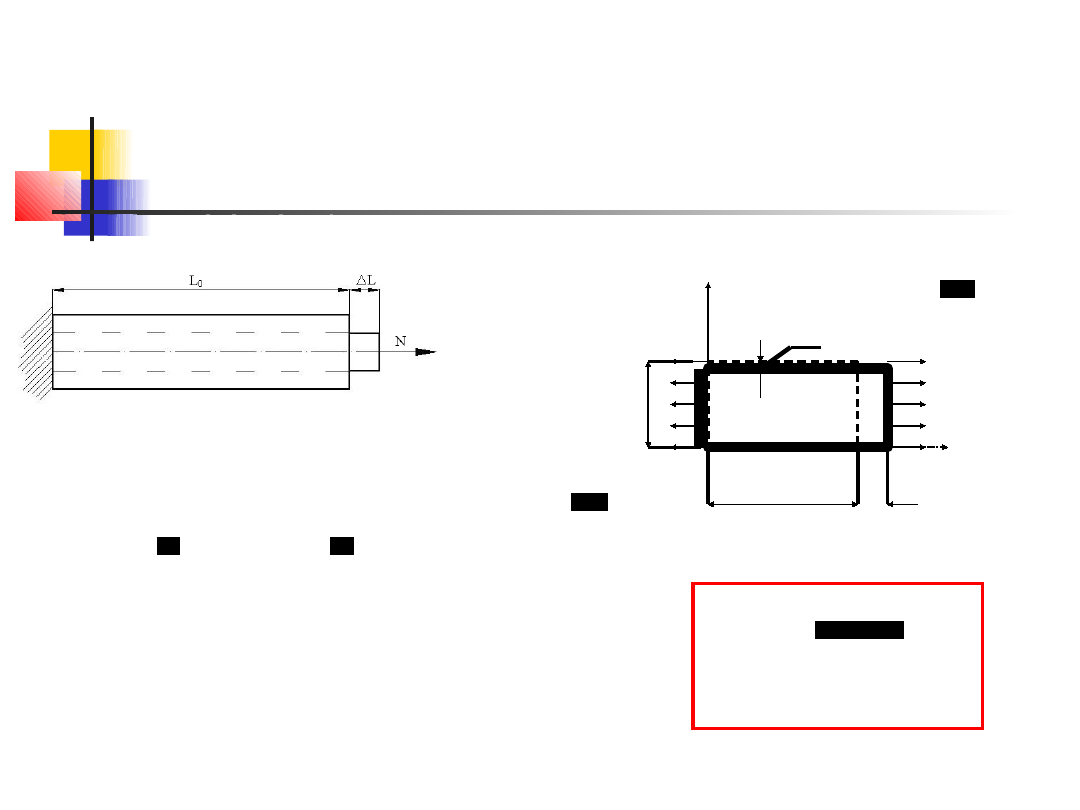
Liczba Poissona

(współczynnik odkształcalności poprzecznej)

y

x

σ

x

a)

l

σ

x

∆

l

b

∆

b

wzd

poprz

ε

ε

ν

−

=

W pręcie rozciąganym

:

E

E

poprz

wzd

σ

ν

ε

σ

ε

−

=

=

,

.

Przedział zmienności liczby Poissona: 0

≤

ν

≤

0.5.

b

b

poprz

∆

=

ε

Ogólnie:

ε

wzd

=

l

l

∆

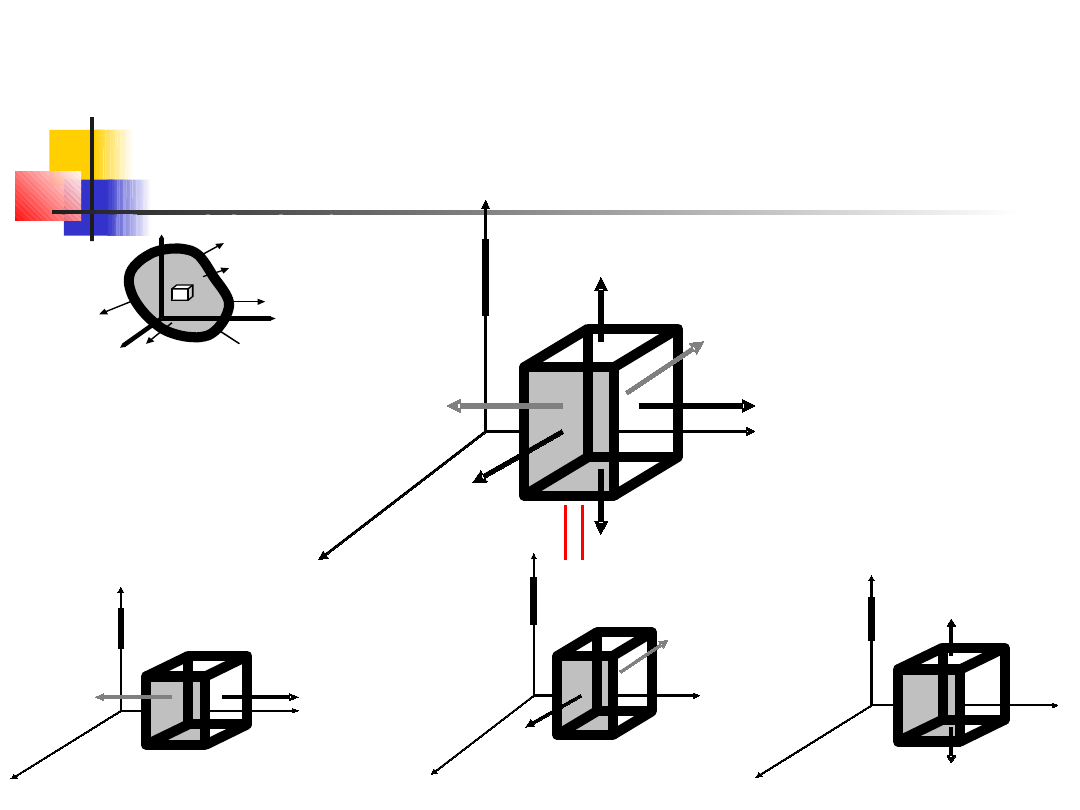
Uogólnione prawo Hooke’a

z

x

y

σ

y

σ

y

z

x

y

σ

z

z

x

y

σ

z

z

x

y

σ

x

σ

x

+

σ

z

z

x

y

σ

z

σ

x

σ

x

σ

y

σ

y

+

Uogólnione prawo Hooke’a

Prawo Hooke’a obowiązujące dla stanu jednokierunkowego

ściskania lub rozciągania możemy rozszerzyć na
trójkierunkowy stan naprężeń, gdzie

σ

x

,

σ

y

,

σ

z

są naprężeniami

normalnymi odpowiednio w kierunkach x,y, z.

)]

(

[

1

z

y

x

x

E

σ

σ

ν

σ

ε

+

−

=

)]

(

[

1

x

E

z

y

y

σ

σ

ν

σ

ε

+

−

=

)]

(

[

1

y

x

z

z

E

σ

σ

ν

σ

ε

+

−

=

Uogólnione prawo Hooke,a –
płaski stan naprężenia – σ

z

= 0

]

[

1

y

x

x

E

νσ

σ

ε

−

=

]

[

1

x

y

y

E

νσ

σ

ε

−

=

]

[

y

x

z

E

σ

σ

ν

ε

+

−

=

Odkształcenie w kierunku osi z:

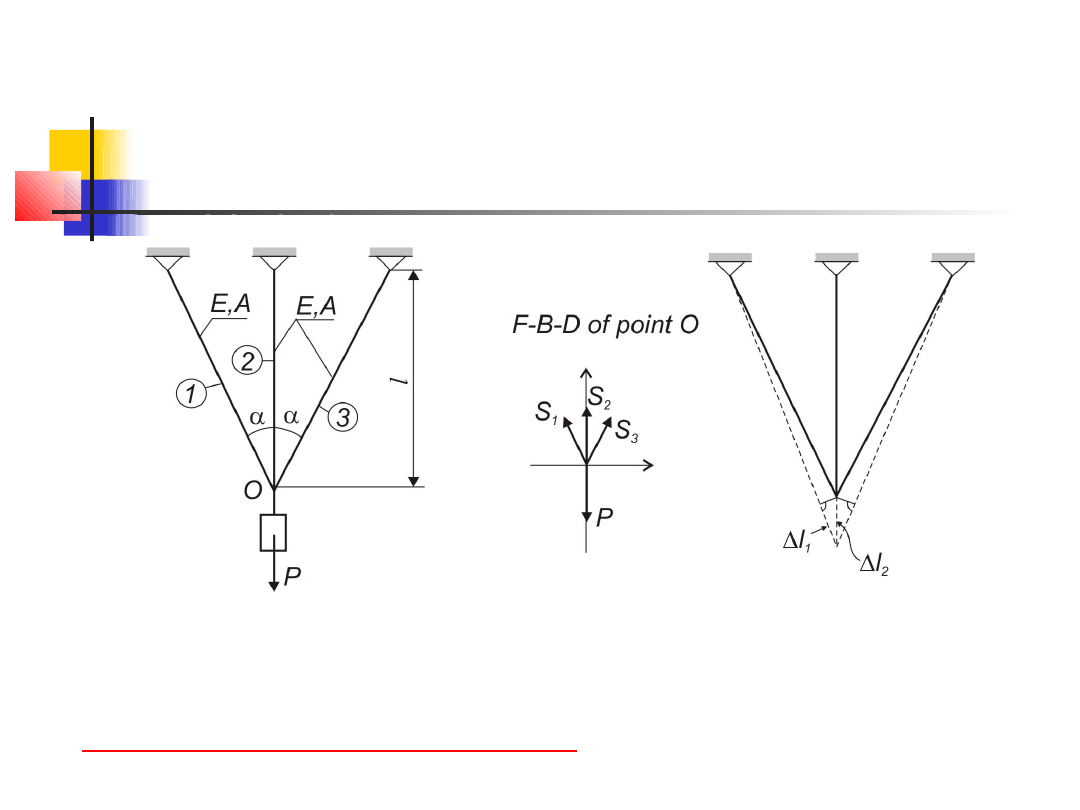
Zagadnienia statycznie
niewyznaczalne

S

1

= S

3

S

2

+ 2S

1

cos

α

= P

Równania równowagi:

∆

l

1

=

∆

l

2

cos

α

Równanie ciągłości odkształceń:

Trzy niewiadome - dwa równania –

zagadnienie statycznie niewyznaczalne

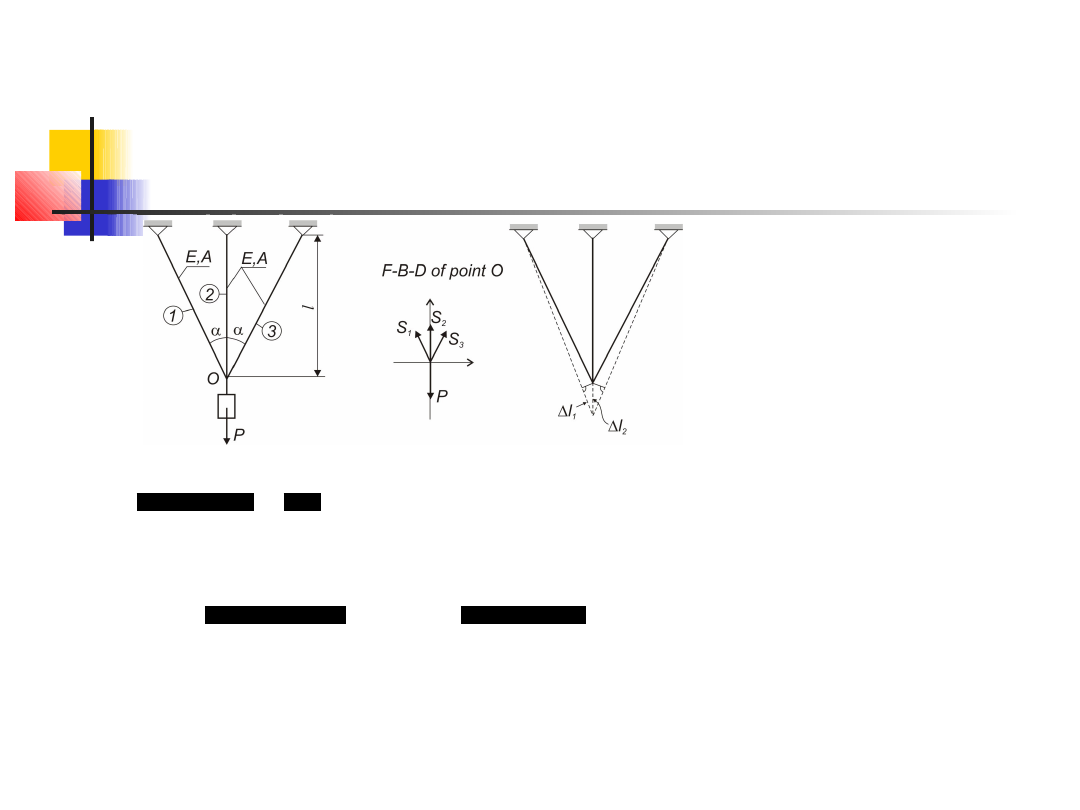
Zagadnienia statycznie
niewyznaczalne

)

(

cos

)

cos(

)

cos(

2

2

1

2

1

α

α

α

S

S

EA

l

S

EA

l

S

=

⇒

=

)

(

cos

1

)]

(

cos

1

[

)

(

cos

3

2

3

2

1

α

α

α

+

=

+

=

P

S

P

S

Naprężenia własne

Naprężenia własne

naprężenia
montażowe

naprężenia cieplne

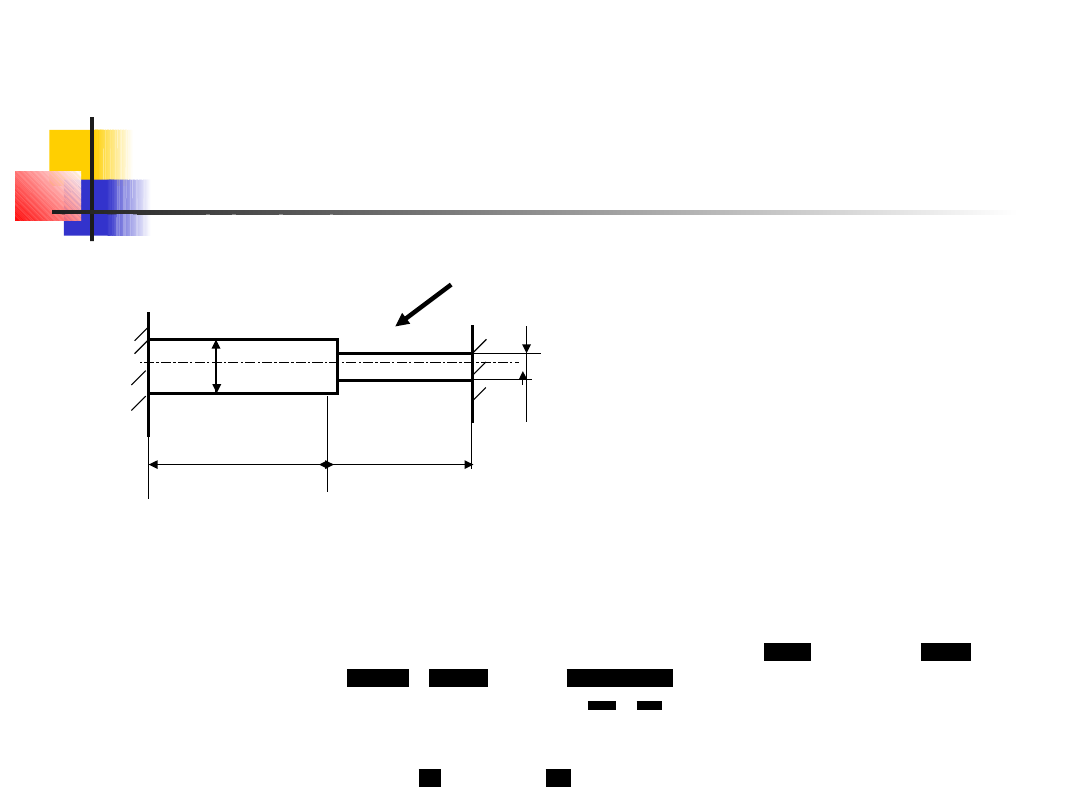
Naprężenia cieplne -

Obliczyć siłę

wewnętrzną w pręcie i naprężenia po
podgrzaniu.

Dane: E,

α

,

∆

t, l, D, d

∆

t

l/2

l/2

φ

D

φ

d

t

l

l

t

∆

⋅

⋅

=

∆

α

m

t

m

t

ca

l

l

l

l

l

∆

=

∆

⇒

=

∆

−

∆

=

∆

0

2

2

1

1

2

1

2

2

EF

Nl

l

EF

NL

l

l

l

l

m

=

∆

=

∆

∆

+

∆

=

∆













+

∆

=

⇒

⋅

+

⋅

=

∆

2

2

2

2

1

1

2

2

4

2

4

d

D

t

E

N

d

E

Nl

D

E

Nl

t

l

α

π

π

π

α

2

2

1

1

F

N

F

N

=

=

σ

σ

Wydłużenie cieplne (o tyle wydłużyłby się pręt,, gdyby był

swobodny):

Pręt

nie

może

zmienić

długości: