Zadanie III- 18. Marchewka Robert IZM 51
Cząstki argonu o średnicy
[ ]
m
d
10
10
*
96
,
3
−
=
znajdują się w zbiorniku o zasobie objętości
[ ]
3
1 m
V
=
w temperaturze
[ ]
C
t
°
= 0
oraz przy ciśnieniu
[
]
Atm
p
1
=
. Wiedząc, uniwersalna
stała gazowa
⎥⎦
⎤
⎢⎣
⎡
=
kmolK
J
B
8314
, masa cząsteczkowa argonu
⎥⎦
⎤
⎢⎣
⎡
=
mol
g
M
95
,
39
, liczba
Avogadra
⎥⎦
⎤
⎢⎣
⎡
=
mol
N
A
1
10
*
023
,
6
23
. Objętość zasobu masy rtęci
⎥⎦
⎤
⎢⎣
⎡
=
3
13546
m
kg
r
ς
, oblicz
średnią drogę swobodną
τ
cząstki argonu, średnią liczbę zderzeń cząstek
n
z
między sobą w
jednostce objętości w przedziale czasu
[ ]
s
t
1
=
Δ
.
Dane: Obliczyć:
?
?
?
=
=
=
n
z
z
τ
[ ]
[ ]
[ ]
[ ]
[ ]
s
t
m
kg
mol
N
mol
g
M
kmolK
J
B
Atm
p
C
t
m
V
m
d
V
A
1
13546
1
10
*
023
,
6
95
,
39
8314
1
0
1
10
*
96
,
3
3
23
3
10
=
Δ
⎥⎦
⎤
⎢⎣
⎡
=
⎥⎦
⎤
⎢⎣
⎡
=
⎥⎦
⎤
⎢⎣
⎡
=
⎥⎦
⎤
⎢⎣
⎡
=
=
=
=
=
°
−
ς
1. wyznaczenie masy cząsteczki argonu
A
AV
CZAV
N
M
m
=
2. wyznaczenie stałej Bolcmana
A
N
B
k
=
3. wyznaczenie prędkości średniej cząsteczki argonu
2
1
2
1
2
1
_
8
8
8
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
AV
AV
A
A
CZAV
M
BT
M
N
BTN
m
kT
π
π
π
υ
4. wyznaczenie drogi L przebytej przez cząsteczkę argonu w czasie
t
Δ
t
M
BT
t
L
AV
Δ
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
Δ
=
*
8
2
1
_
π
ϑ
5. wyznaczenie ilości cząsteczek argonu w objętości V przy ciśnieniu p i temperaturze T
kT
pV
V
V
N
n
kT
n
p
AV
A
AV
AV
=
=
=
=
0
0
6. wyznaczenie ciśnienia w jednostkach IS
[ ]
[ ]
[
]
mmHg
Tr
Atm
p
g
k
p
r
760
760
1
*
*
=
=
=
=
ς
7. wyznaczam objętościową ilość cząstek argonu w temperaturze T i ciśnieniu p
⎥⎦
⎤
⎢⎣
⎡
=
=
=
=
=
3
25
26
1
10
*
67842
,
2
16
,
273
*
8314
81
,
9
*
76
,
0
*
13546
10
*
023
,
6
m
BT
hg
N
BT
P
N
V
N
n
r
A
A
AV
OA
ς
8. wyznaczenie masy zredukowanej cząstek przy zderzeniu binarnym
2
2
1
2
1
2
1
m
m
m
m
m
m
m
m
=
=
=
+
=
μ
μ
9. wyznaczenie średniej prędkości względnej cząstek „bombardujących” cząstkę nieruchomą
_
2
1
2
1
2
8
2
8
V
m
kT
kT
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
π
πμ
ϖ
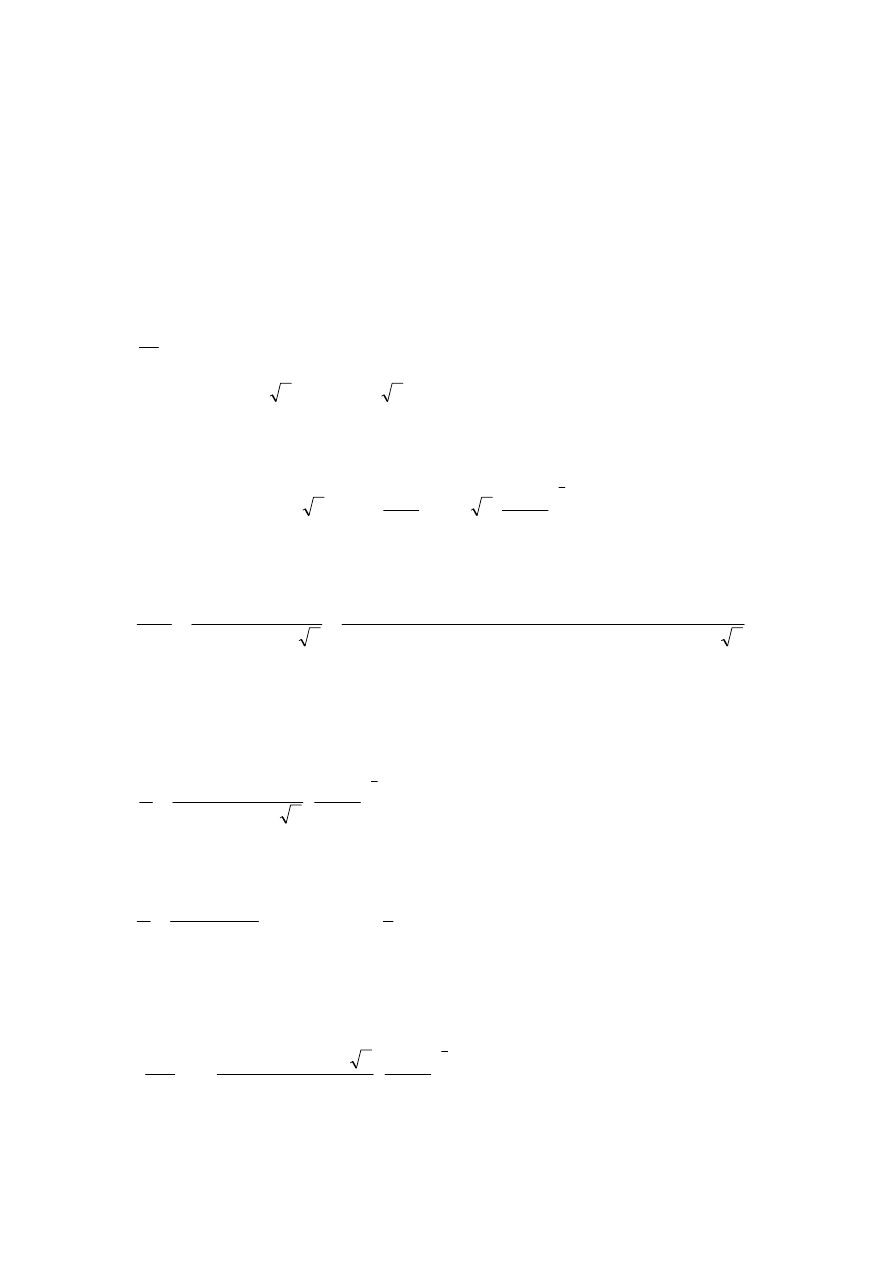
10. wyznaczenie wysokości walca o podstawie całkowitego przekroju czynnego na zderzenie
cząstka cząstka równego polu koła o promieniu równym średnicy cząstki w którym zawarte są
środki ciężkości cząsteczek argonu „bombardujących” nieruchomą cząstkę argonu w czasie
t
Δ
Ze średnią prędkością względną
ϖ .
t
H
Δ
= *
ϖ
11. wyznaczenie objętości walca
l
d
t
d
t
d
V
t
l
H
d
V
AV
AV
AV
H
AV
H
2
2
*
2
_
2
2
_
2
π
ϑ
π
ϖ
π
ϑ
π
=
Δ
=
Δ
=
Δ
=
=
12. wyznaczenie ilości cząstek argonu zawartych w walcu
t
M
BT
d
BT
hg
N
l
d
n
V
n
N
AV
AV
i
AV
AV
AV
H
AV
AV
Δ
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
=
*
8
2
*
2
2
1
2
2
0
0
π
π
ς
π
13.wyznaczenie średniej drogi cząsteczki między zderzeniami
[ ]
m
d
hg
N
BT
N
l
AV
V
AV
AV
20
20
26
2
10
*
3775
,
5
2
*
10
*
96
,
3
*
76
,
0
*
14
,
3
*
81
,
9
*
13546
*
10
*
023
,
6
16
,
273
*
8314
2
−
−
=
=
=
=
τ
π
ς
τ
14. obliczam średni czas między zderzeniami
[ ]
s
BT
M
d
hg
N
BT
T
AV
AV
V
AV
10
2
1
2
_
10
*
413
,
1
8
2
−
=
⎟
⎠
⎞
⎜
⎝
⎛
=
=
π
π
ς
ϑ
τ
15. wyznaczenie ilości zderzeń jakich cząstka doznała w jednostce czasu
⎥⎦
⎤
⎢⎣
⎡
=
=
=
−
s
T
z
1
10
*
07714
,
7
10
*
413
,
1
1
1
9
10
16. obliczam ilość zderzeń zachodzących między cząsteczkami w jednostce objętości i czasu
2
1
2
2
2
2
2
2
2
8
2
*
2
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
AV
AV
V
AV
AV
n
M
BT
T
B
d
g
h
N
z
n
z
π
π
ς
Zad. III 19 Marchewka Robert JZM 51
Prędkość dźwięku w powietrzu w funkcji temperatury określają następujące wartości
( ) (
)
⎥⎦
⎤
⎢⎣
⎡
=
=
s
m
a
T
a
344
16
,
293
1
( ) (
)
⎥⎦
⎤
⎢⎣
⎡
=
=
s
m
a
T
a
700
16
,
1273
2
. Oblicz średnie kwadratów
prędkości
Śr
V
cząstek azotu w podanych temperaturach wiedząc, że uniwersalna stała
gazowa
⎥⎦
⎤
⎢⎣
⎡
=
kmolK
J
B 8314
, liczba Avogadra
⎥⎦
⎤
⎢⎣
⎡
=
mol
N
A
1
10
*
023
,
6
23
zaś masa
cząsteczkowa azotu
⎥⎦
⎤
⎢⎣
⎡
=
mol
J
M
N
013
,
28
2
i porównaj z prędkościami dzwięku w
powietrzu dla tych temperatur.
1. wyznaczenie średniej E
K
cząsteczki azotu w funkcji średniej kwadratów jej cząsteczek
2
2
1
V
m
E
N
=
oraz temperatury
kT
E
2
3
=
1.1 wyznaczenie masy cząsteczki azotu
A
N
N
N
M
m
2
2
=
1.2 wyznaczenie stałej Bolcmana
A
N
B
k
=
2. wyznaczenie średniej kwadratów prędkości
2
1
2
2
2
2
2
2
2
2
3
3
3
3
2
3
2
1
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
=
=
=
=
N
Śr
N
A
N
A
N
N
M
BT
V
V
M
BT
N
M
BTN
m
kT
V
kT
V
m
3. wyznaczenie wartości średnich kwadratów prędkości
[ ]
( )
[ ]
( )
[ ]
s
m
kg
kg
s
m
kg
J
kmol
kg
K
K
kmol
J
V
s
m
T
V
K
T
s
m
M
BT
T
V
K
T
Śr
Śr
N
Śr
=
=
=
=
⎥⎦
⎤
⎢⎣
⎡
=
⎟
⎠
⎞
⎜
⎝
⎛
=
=
⎥⎦
⎤
⎢⎣
⎡
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
=
*
*
*
7
,
1064
013
,
28
16
,
1273
*
8314
*
3
16
,
1273
903
,
510
013
,
28
16
,
293
*
8314
*
3
3
16
,
293
2
2
2
1
2
2
2
1
2
1
1
1
Janczewska Dorota P-51
Zad. III 28
Dla jakiej długości fali
λ
max
przypada maksimum funkcji rozkładu widmowego objętości
gęstości zasobu energii promieniowania
ρ
T
(
λ) = ε
λ
(
λ) dla ciała ludzkiego i jaka jest wartość
funkcji rozkładu widmowego gęstości strumienia emisji energii promieniowania i strumienia
emisji promieniowania dla tej długości fali wiedząc, że stała Plancka h= 6, 6262 * 10
-34
[ J*
s], stała Wiena
σ
w
= 2,898* 10
-3
[mK], stała Boltzmana k= 1,3806* 10
-23
[
K
J ], prędkość
światła w próżni c= 3* 10
8
[
s
m ]
Dane:
Obliczyć:
σ = 5,76*10
-8
[
4
2
sk
m
J
]
λ
m
=?
σ
r
= 2,898*10
-3
[mK]
R
T
(
λ
m
)=?
k= 1,3806* 10
-23
[
K
J ],
R
T
=?
h= 6, 6262 * 10
-34
[ J*s]
c= 3* 10
8
[
s
m ]
1. Funkcja rozkładu widmowego objętościowej gęstości zasobu energii promieniowania.
ρ
T
(
λ) = ε
λ
(
λ)=
)
1
)
(exp(
*
8
5
−
∏
KT
hc
hc
λ
λ
[
3
m
J
m
1
]
Wykres tej funkcji
ε
λ
(
λ)
λ
m
λ
λ
λ
ε
λ
d
d
)
(
= 0
5(exp(
KT
hc
λ
) - 1) -
KT
hc
λ
* exp(
KT
hc
λ
)=0
Gdzie:
h- stała Planca
k- stała Boltzmana
c- prędkość światła
x=
KT
hc
λ
Metodą numeryczną (Newtona) otrzymujemy:
5 =
x
e
x
−
−
1
⇒ x = 4,965
Prawo Wiena
λ
m
*T=
σ
w
λ
m
*T=
965
,
4
*
k
hc
=2,898*10
-3
[mK]=
σ
w
2. Wyznaczenie długości fali
λ
m
odpowiadającej maximum wartości funkcji rozkładu
Widmowego objętościowej gęstości zasobu energii promieniowania
λ
m
=
T
w
σ
=
76
,
309
10
*
898
,
2
3
−
= 9,35563*10
-6
[m]
gdzie:
T
ciała
= 36,6
0
C
T=309,76
[K]
3. Obliczamy wartość funkcji rozkładu widmowego gęstości strumienia emisji energii
promieniowania
R
T
(
λ)=
4
)
( c
T
λ
ρ
=
4
)
( c
λ
ε
λ
=
)
1
)
(exp(
2
5
2
−
∏
KT
hc
hc
λ
λ
[
2
* m
s
J
m
1
]
R
T
(
λ)=
=
−
∏
−
−
−
−
−
)
1
)
76
,
309
*
10
*
3806
,
1
*
10
*
35563
,
9
10
*
3
*
10
*
6262
,
6
(exp(
*
)
10
*
35563
,
9
(
)
10
*
3
(
*
10
*
6262
,
6
*
2
23
6
8
34
5
6
2
8
34
=3,645* 10
7
4. Obliczam gęstość strumienia emisji energii promieniowania
R
T
(
λ)
λ
m
λ
R
T=
4
0
)
(
T
dh
R
T
σ
λ
=
∫
∞
[
s
m
J
2
]
2
3
4
5
15
2
c
h
k
∏
=
σ
[
4
2
sk
m
J
]
R
T
=
2
3
4
5
15
2
c
h
k
∏
* T
4
R
T=
2
8
3
34
4
23
5
)
10
*
3
(
*
)
10
*
6262
,
6
(
*
15
)
10
*
3806
,
1
*(
*
2
−
−
∏
=
530,303
[
s
m
J
2
]
Zadanie III. 29.
Michał Kozieł WP 53
Obliczyć przyrost ilości energii cieplnej wyemitowany w przedziale czasu
[ ]
h
t
2
=
Δ
przez
ciało doskonale czarne o temperaturze
[ ]
K
T 1000
=
i o powierzchni emisji
[ ]
2
1
,
0 m
A
=
w
paśmie długości fal od
[ ]
nm
650
1
=
λ
do
[ ]
nm
700
2
=
λ
wiedząc, że stała Planca
[
]
s
J
h
×
×
=
− 34
10
6262
,
6
, stała Boltzmana
⎥⎦
⎤
⎢⎣
⎡
×
=
−
K
J
k
23
10
3806
,
1
, prędkość
światła w próżni
⎥⎦
⎤
⎢⎣
⎡
×
≈
s
m
c
8
10
3
. Całkowanie funkcji rozkładu widmowego gęstości
strumienia emisji energii promieniowania przeprowadzić mnożąc jej wartość średnią w
rozpatrywanym przedziale całkowania przez przyrost długości fal w przedziale całkowania.
Dane: Obliczyć:
?
=
Δ Q
[ ]
[ ]
[ ]
[ ]
[ ]
[
]
⎥⎦
⎤
⎢⎣
⎡
×
≈
⎥⎦
⎤
⎢⎣
⎡
×
=
×
×
=
=
=
=
=
=
Δ
−
−
s
m
c
K
J
k
s
J
h
m
m
m
A
K
T
h
t
8
23
34
2
1
2
10
3
10
3806
,
1
10
6262
,
6
7
,
0
65
,
0
1
,
0
1000
2
μ
λ
μ
λ
1. Funkcja rozkładu widmowego gęstości strumienia emisji energii promieniowania
( )
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
×
=
1
exp
2
5
2
kT
hc
hc
R
T
λ
λ
π
λ
⎥⎦
⎤
⎢⎣
⎡
×
m
s
m
J
1
2
2. Elementarny przyrost gęstości strumienia emisji energii promieniowania w zakresie
przyrostu długości fal od
1
λ do
1
1
λ
λ
d
+
( )
λ
λ
d
R
dR
T
T
=
⎥⎦
⎤
⎢⎣
⎡
s
m
J
2
3. Gęstość strumienia emisji energii promieniowania w zakresie długości fal od
1
λ do
λ
λ
Δ
+
1
2
1
λ
λ
λ
=
Δ
+
( )
∫
=
2
1
λ
λ
λ
λ
d
R
R
T
T
⎥⎦
⎤
⎢⎣
⎡
s
m
J
2
4. Elementarny przyrost strumienia emisji energii promieniowania w zakresie długości fal
λ
λ
λ
Δ
=
−
1
2
z elementarnego przyrostu powierzchni emisji energii promieniowania
dA
dA
R
Q
d
T
×
=
•
⎥⎦
⎤
⎢⎣
⎡
s
J
5. Strumień emisji energii promieniowania w zakresie długości fal
λ
λ
λ
Δ
=
−
1
2
z
powierzchni emisji energii promieniowania A
A
R
dA
R
Q
T
A
T
∫
=
=
•
0
⎥⎦
⎤
⎢⎣
⎡
s
J
6. Elementarny przyrost ilości energii wyemitowanej w zakresie długości fal od
1
λ do
2
λ z
powierzchni A w elementarnym przedziale czasu
t
Δ
dt
Q
Q
•
=
δ
[ ]
J
7. Ilość energii wypromieniowanej w zakresie długości fal od
1
λ do
2
λ z powierzchni A w
elementarnym przedziale czasu
t
Δ
t
Q
dt
Q
Q
t
t
Δ
=
=
Δ
•
•
∫
2
1
[ ]
J
8. Średnia długość fali dla rozpatrywanego przedziału długości fal
[ ]
m
śr
μ
λ
λ
λ
675
,
0
2
2
1
=
+
=
9. Obliczam wartość funkcji rozkładu widmowego gęstości strumienia emisji promieniowania
dla wartości średniej długości fali.
( )
⎥⎦
⎤
⎢⎣
⎡
×
×
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
×
×
×
×
×
×
×
×
×
×
×
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
×
=
−
−
−
m
s
m
J
kT
hc
hc
R
śr
śr
śr
T
1
10
45529
,
1
1
1000
10
3806
,
1
675
10
3
10
6262
,
6
exp
675
10
3
10
6262
,
6
14
,
3
2
1
exp
2
2
6
23
8
34
5
16
34
5
2
λ
λ
π
λ
10. Obliczam wartość gęstości strumienia emisji energii promieniowania dla zakresu długości
fal od
1
λ do
2
λ
[ ]
m
μ
λ
λ
λ
05
,
0
1
2
=
Δ
=
−
( )
4
10
7,27645
×
=
Δ
×
=
λ
λ
śr
T
T
R
R
⎥⎦
⎤
⎢⎣
⎡
s
m
J
2
11. Obliczam wartość strumienia emisji energii promieniowania
3
10
7,27645
−
•
×
=
=
A
R
Q
T
⎥⎦
⎤
⎢⎣
⎡
s
J
12. Obliczam przyrost ilości energii cieplnej
3904
,
52
=
Δ
=
Δ
t
A
R
Q
T
[ ]
J
Zadanie III 30
Wykorzystując równanie stanu dla gazu fotonowego oblicz objętościową gęstość zasobu energii ε i ciśnienie
promieniowania p dla temperatury T
s
=6000 [K] oraz dla temperatury T=10
7
[K]. Wiedząc ,że stała Plancka
h=6,6262*10
-34
[J*s], stała Boltzmana k=1,3806*10
-23
[J/K], prędkość światła w próżni c=3*10
8
[m/s].
Dane: Szukane
T
s
=6000 [K]
=
IV
ε
?
T=10
7
[K] p=?
h=6,6262*10
-34
[J*s]
k=1,3806*10
-23
[J/K]
c=3*10
8
[m/s]
Prawo Stefana Boltzmana
R
T
=σT
4
⎥⎦
⎤
⎢⎣
⎡
=
=
−
4
3
8
2
3
4
5
10
*
67
,
5
14
2
sK
m
J
c
h
k
π
σ
Funkcja rozkładu widmowego
( )
( )
⎥⎦
⎤
⎢⎣
⎡
−
⎟
⎠
⎞
⎜
⎝
⎛
=
=
m
s
m
J
kT
hc
hc
c
R
T
T
1
*
1
exp
2
4
*
2
5
2
λ
λ
π
λ
ρ
λ
( )
( )
⎥⎦
⎤
⎢⎣
⎡
−
⎟
⎠
⎞
⎜
⎝
⎛
=
=
Hz
s
m
J
kT
h
c
h
c
R
T
T
1
*
1
exp
2
4
*
2
2
2
ν
ν
ν
ρ
ν
Funkcja rozkładu widmowego
( )
( )
( )
⎥⎦
⎤
⎢⎣
⎡
−
⎟
⎠
⎞
⎜
⎝
⎛
=
=
=
m
m
J
kT
hc
hc
E
n
T
1
*
1
exp
2
2
5
λ
λ
π
λ
λ
ε
λ
ρ
λ
λ
λ
Średni zasób energii promieniowania
( )
[ ]
J
kT
h
h
E
1
exp
−
⎟
⎠
⎞
⎜
⎝
⎛
=
ν
ν
ν
( )
[ ]
J
kT
hc
hc
E
⎥
⎦
⎤
⎢
⎣
⎡
−
⎟
⎠
⎞
⎜
⎝
⎛
=
1
exp
4
λ
λ
Objętościowa gęstość zasobu emitowania
( )
⎥⎦
⎤
⎢⎣
⎡
=
=
∫
3
4
m
J
T
d
IV
β
λ
λ
ε
ε
λ
3
3
4
5
15
8
c
h
k
π
β
=
Uwzględniając ,że ciśnienie gazu w teorii kinetycznej określona jest wzorem :
2
3
1
ϑ
mn
p
=
m – masa cząsteczki gazu w kilogramach [kg]
n – objętość gęstości zasobu masy [1/m^3]
f
m
- uśredniona masa spoczynkowa fotonu
2
3
1
nc
m
p
f
=
ν
nh
E
h
=
h=0,1,2,3,……
Średni zasób energii fotonu może być oznaczany:
( )
( )
λ
ϑ
E
E
=
( )
( )
( )
⎥
⎦
⎤
⎢
⎣
⎡
−
⎟
⎠
⎞
⎜
⎝
⎛
=
−
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛ −
=
=
=
=
∑
∑
∑
∞
=
∞
=
∞
=
1
exp
1
exp
*
*
0
0
0
kT
hc
c
h
kT
h
h
kT
En
Bf
E
E
f
E
E
E
E
n
n
n
n
n
n
n
λ
λ
ν
ν
λ
ϑ
Funkcja rozkładu widmowego średniego zasobu energii
( ) ( )
( ) ( )
( )
λ
ε
λ
λ
λ
λ
λ
λ
λ
=
=
n
m
c
n
E
f
2
( )
( ) ( )
λ
λ
λ
λ
λ
ε
λ
λ
d
n
m
c
d
f
2
=
( )
( ) ( )
∫
∫
∞
∞
=
0
0
2
λ
λ
λ
λ
λ
ε
λ
λ
d
n
m
c
d
f
n
m
c
f
IV
2
=
ε
4
T
IV
β
ε
=
⎥⎦
⎤
⎢⎣
⎡
=
=
−
4
3
16
10
*
56
,
7
4
K
m
J
c
σ
β
T
s
=6000 [K]
⎥⎦
⎤
⎢⎣
⎡
=
3
98
,
0
m
J
ε
p = 3*10
-6
[atm]
⎥⎦
⎤
⎢⎣
⎡
=
3
12
10
*
56
,
7
m
J
ε
[ ]
atm
p
IV
7
10
*
5
,
2
3
1
=
=
ε
Paweł Padée
Przyjmując, iż temperatura powierzchni Słońca równa jest T
s
=5750 [K], określ gęstość
strumienia emisji energii promieniowania słonecznego na powierzchni Ziemi R
Tsz.
Ponieważ
całkowita energia powierzchni Ziemi jest prawie stała, zatem promieniowanie absorbowane
przez Ziemię równoważne jest emitowanemu. Oblicz średnią dobową temperaturę
powierzchni Ziemi T
z
i oszacuj gęstość strumienia emisji promieniowania Ziemi R
Tz
i oceń
całkowitą produkcję entropii na powierzchni Ziemi wiedząc, że stała Boltzamnna
⎥⎦
⎤
⎢⎣
⎡
×
=
−
4
2
8
10
67
,
5
K
sm
J
σ
, promień Słońca r
s
=7
×10
8
[m], odległość Ziemi od Słońca
r
sz
=1,496× 10
11
[m], promień Ziemi r
z=
6,37 ×10
6
[m].
Dane: Obliczyć:
T
s
=5750
[K]
R
Tz
=?
⎥⎦
⎤
⎢⎣
⎡
×
=
−
4
2
8
10
67
,
5
K
sm
J
σ
T
z
=?
r
s
=7
×10
8
[m]
R
Tsz
=?
r
sz
=1,496
× 10
11
[m]
r
z=
6,37
×10
6
[m]
1.Obliczam gęstość strumienia emisji energii na powierzchni Słońca:
R
Ts
= σ T
s
4
= 61,203
×10
6
⎥⎦
⎤
⎢⎣
⎡
s
m
J
2
2.Obliczam gęstość strumienia energii promieniowania Słońca na powierzchnię sfery na
której znajduje się orbita Ziemi (założenie: strumień emitowany z powierzchni Słońca jest
stały)
Strumień energii =const= Q
s
(S
s-
powierzchnia Słońca S
oz-
powierzchnia sfery na której jest
orbita Ziemi)
Q
s =
R
Ts
×S
s
= R
Tsz
×S
oz
⎥⎦
⎤
⎢⎣
⎡
=
=
Π
Π
=
×
=
s
m
J
T
r
r
T
r
r
R
S
S
R
s
sz
s
s
sz
s
Ts
oz
s
Tsz
2
4
2
2
4
2
2
1340
4
4
σ
σ
3.Obliczam strumień energii promieniowania słonecznego padającego na Ziemię:
3.1.Obliczam pole przekroju obwodu Ziemi:
S
obz
=Πr
2
= 127,41
×10
12
m
2
3.2 Obliczam strumień emisji energii promieniowania słonecznego padającego na Ziemię:
Q
sz
= R
Ts
× S
obz
=
[ ]
W
r
T
r
r
z
s
sz
s
15
2
4
2
2
10
73
,
170
×
=
Π
×
σ
3.3 Szacuję strumień emisji energii promieniowania Ziemi:
Q
z
= Q
sz
= 170,73 × 10
15
[W]
4.Obliczam gęstość strumienia emisji energii promieniowania Ziemi:
R
Tz
=
z
sz
S
Q S
z
=4Π
2
z
r
R
Tz
=
⎥⎦
⎤
⎢⎣
⎡
=
=
s
m
J
R
T
r
r
Tsz
s
sz
s
2
4
2
2
335
4
1
4
1
σ
5.Obliczam średnią dobową temperaturę powierzchni Ziemi :
R
Tz
=
4
z
T
σ
T
z
=
4
σ
Tz
R
= 278,1 [K]
Produkcja entropii na powierzchni Ziemi:
Jeżeli T= const na powierzchni Ziemi wówczas:
A
dS
z
=
T
dQ
z
⎥⎦
⎤
⎢⎣
⎡
×
=
=
=
K
W
T
Q
T
dt
dQ
dt
dS
z
z
z
15
10
61392
,
0
Tomasz Gawkowski gr. M31
1
Zadanie III – 27 Tomasz Gawkowska gr. M31
Dla wnęki reprezentujące ciało doskonale czarne o określonej temperaturze, długość fali
równa jest
λmax
1
=6500[Å].
Jaka będzie długość fali jeżeli wartość temperatury ścianki wnęki wzrośnie tak, że wartość
funkcji rozkładu widmowego gęstości strumienia emisji energii promieniowania zwiększy się
dwukrotnie?
DANE: SZUKANE:
[ ]
(
)
(
)
[ ]
mK
R
R
T
T
3
1
2
1
10
*
898
,
2
max
2
max
Å
6500
max
−
=
=
=
δω
λ
λ
λ
?
?
?
max
2
1
2
=
=
=
T
T
λ
1. Z równania Viena mamy
2
2
1
1
*
max
*
max
T
T
T
λ
λ
δω
λ
=
=
=
czyli,
2
2
1
1
max
max
λ
δω
λ
δω
=
=
T
T
2. Funkcja rozkładu widmowego gęstości strumienia emisji energii promieniowania
(
)
(
)
(
)
(
)
(
)
(
)
(
)
5
1
2
1
5
2
5
1
1
2
1
2
2
5
1
2
2
1
5
1
2
5
2
5
2
max
max
max
max
max
2
max
max
max
1
exp
*
max
2
max
2
max
1
exp
*
max
2
max
1
exp
*
2
1
exp
*
2
λ
λ
λ
λ
λ
λ
λ
λ
δω
λ
λ
λ
δω
λ
λ
δω
λ
λ
λ
=
=
=
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
∏
=
=
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
∏
=
=
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
∏
=
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
∏
=
RT
R
R
R
k
hc
hc
RT
R
k
hc
hc
R
k
h
hc
kT
hc
hc
R
T
T
T
T
T
T
Tomasz Gawkowski gr. M31
2
3. Obliczam długość fali
λmax
2
oraz jednostkę
[ ]
[ ]
nm
3
,
567
Å
5673
1486
,
1
6500
max
max
2
1
max
2
1
5
2
=
=
=
=
λ
λ
λ
4. Obliczam wartość temperatury oraz jednostkę
[ ]
[ ]
K
m
K
m
K
m
T
T
K
m
K
m
K
m
T
T
3
9
3
3
2
2
2
3
9
3
3
1
1
1
10
*
11
,
5
*
10
*
3
,
567
10
*
898
,
2
nm
*
5673
10
*
898
,
2
max
10
*
46
,
4
*
10
*
650
10
*
2898
nm
*
650
10
*
898
,
2
max
=
⎥⎦
⎤
⎢⎣
⎡
=
⎥⎦
⎤
⎢⎣
⎡
=
=
=
⎥⎦
⎤
⎢⎣
⎡
=
⎥⎦
⎤
⎢⎣
⎡
=
=
−
−
−
−
−
−
λ
δω
λ
δω