Podstawy techniki cyfrowej i

mikroprocesorowej

Algebra Boole'a

Tomasz Piasecki

P

o

d

st

aw

y

T

ec

h

n

ik

i

C

yf

ro

w

ej

i

M

ik

ro

p

ro

ce

so

ro

w

ej

P

o

d

st

aw

y

T

ec

h

n

ik

i

C

yf

ro

w

ej

i

M

ik

ro

p

ro

ce

so

ro

w

ej

A

lg

eb

ra

B

o

o

le

'a

A

lg

eb

ra

B

o

o

le

'a

Algebra Boole'a

Algebra Boole'a

• Algebra Boole'a została nazwana dla uhonorowania wkładu

angielskiego uczonego George'a Boole'a w formalizację i
algebraizację logiki

• Algebra Boole'a operuje na dwuwartościowych argumentach,

przyjmujących wartości 0 i 1

• Elementarne operacje:

– suma logiczna: „

∨

”, „+”

– iloczyn logiczny: „

∧

”, „•”

– negacja: „

¬

”, „ ”

P

o

d

st

aw

y

T

ec

h

n

ik

i

C

yf

ro

w

ej

i

M

ik

ro

p

ro

ce

so

ro

w

ej

P

o

d

st

aw

y

T

ec

h

n

ik

i

C

yf

ro

w

ej

i

M

ik

ro

p

ro

ce

so

ro

w

ej

A

lg

eb

ra

B

o

o

le

'a

A

lg

eb

ra

B

o

o

le

'a

Algebra Boole'a - własności

Algebra Boole'a - własności

• Przemienność:

A•B = B•A,

A+B = B+A

• Łączność:

(A+B)+C = A+(B+C)

(A•B)•C = A•(B•C)

• Rozdzielność:

A•(B+C) = A•B+A•C

A+(B•C) = (A+B)•(A+C)

• tożsamość:

A+0 = A

A•0 = 0

•

A+1 = 1

A•1 = A

•

A+A = A

A•A = A

• komplementarność

A A=1

A⋅A=0

P

o

d

st

aw

y

T

ec

h

n

ik

i

C

yf

ro

w

ej

i

M

ik

ro

p

ro

ce

so

ro

w

ej

P

o

d

st

aw

y

T

ec

h

n

ik

i

C

yf

ro

w

ej

i

M

ik

ro

p

ro

ce

so

ro

w

ej

A

lg

eb

ra

B

o

o

le

'a

A

lg

eb

ra

B

o

o

le

'a

Algebra Boole'a - prawa

Algebra Boole'a - prawa

• Prawo de Morgana

• Prawo sklejania

• Prawo pochłaniania

AB=A⋅B

A⋅B= A B

A⋅B A⋅B= A



AB⋅ AB= A

A⋅B B= AB

P

o

d

st

aw

y

T

ec

h

n

ik

i

C

yf

ro

w

ej

i

M

ik

ro

p

ro

ce

so

ro

w

ej

P

o

d

st

aw

y

T

ec

h

n

ik

i

C

yf

ro

w

ej

i

M

ik

ro

p

ro

ce

so

ro

w

ej

A

lg

eb

ra

B

o

o

le

'a

A

lg

eb

ra

B

o

o

le

'a

Funkcje boolowskie

Funkcje boolowskie

• Funkcja boolowska to dowolne odwzorowanie f:X

→

Y,

gdzie B={0,1}, X jest podzbiorem B

n

, Y jest

podzbiorem B

m

.

• Jeżeli funkcja jest określona dla całego zbioru B

n

nazywamy ją funkcją zupełną. W przeciwnym
wypadku jest to funkcja niezupełna, nie w pełni
określona

• Liczba wszystkich n-argumentowych boolowskich

funkcji zupełnych jest równa

2

2

n

P

o

d

st

aw

y

T

ec

h

n

ik

i

C

yf

ro

w

ej

i

M

ik

ro

p

ro

ce

so

ro

w

ej

P

o

d

st

aw

y

T

ec

h

n

ik

i

C

yf

ro

w

ej

i

M

ik

ro

p

ro

ce

so

ro

w

ej

A

lg

eb

ra

B

o

o

le

'a

A

lg

eb

ra

B

o

o

le

'a

Funkcje boolowskie

Funkcje boolowskie

• Funkcje boolowskie są podstawowym sposobem na formalny

zapis tzw kombinacyjnych układów logicznych.

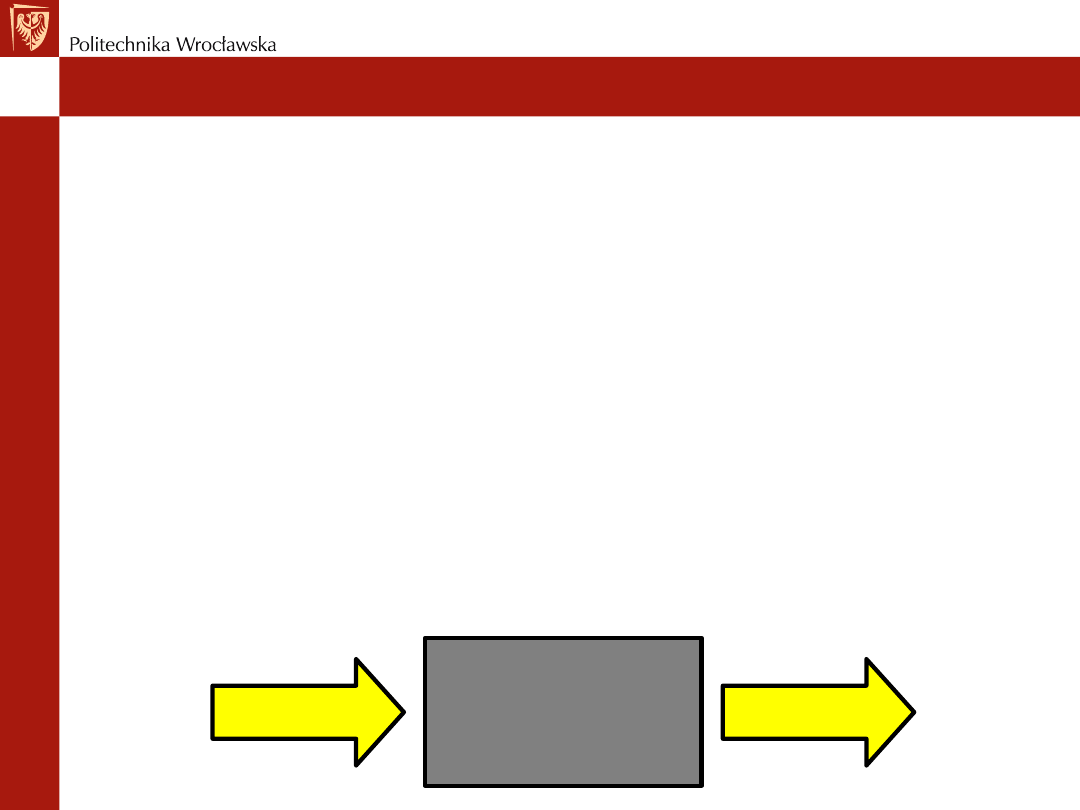
• Kombinacyjne układy logiczne to układy posiadające wejścia i

wyjścia. Stan logiczny każdego z wyjść układu kombinacyjnego
zależy wyłącznie od stanu logicznego wejść układu.

• Przyjęło się stosować następującą nomenklaturę:

– X – słowo wejściowe układu, może być wielobitowe
– x

n

– bit słowa wejściowego, bit najmłodszy oznaczany x

0

– Y – słowo wyjściowe, analogicznie oznacza się w nim bity

układ kombinacyjny

x

0

,...,x

n

y

0

,...,y

n

P

o

d

st

aw

y

T

ec

h

n

ik

i

C

yf

ro

w

ej

i

M

ik

ro

p

ro

ce

so

ro

w

ej

P

o

d

st

aw

y

T

ec

h

n

ik

i

C

yf

ro

w

ej

i

M

ik

ro

p

ro

ce

so

ro

w

ej

A

lg

eb

ra

B

o

o

le

'a

A

lg

eb

ra

B

o

o

le

'a

Funkcje dwu zmiennych

Funkcje dwu zmiennych

A. Skorupski, Podstawy

Techniki Cyfrowej

P

o

d

st

aw

y

T

ec

h

n

ik

i

C

yf

ro

w

ej

i

M

ik

ro

p

ro

ce

so

ro

w

ej

P

o

d

st

aw

y

T

ec

h

n

ik

i

C

yf

ro

w

ej

i

M

ik

ro

p

ro

ce

so

ro

w

ej

A

lg

eb

ra

B

o

o

le

'a

A

lg

eb

ra

B

o

o

le

'a

Sposoby zapisu funkcji boolowskich

Sposoby zapisu funkcji boolowskich

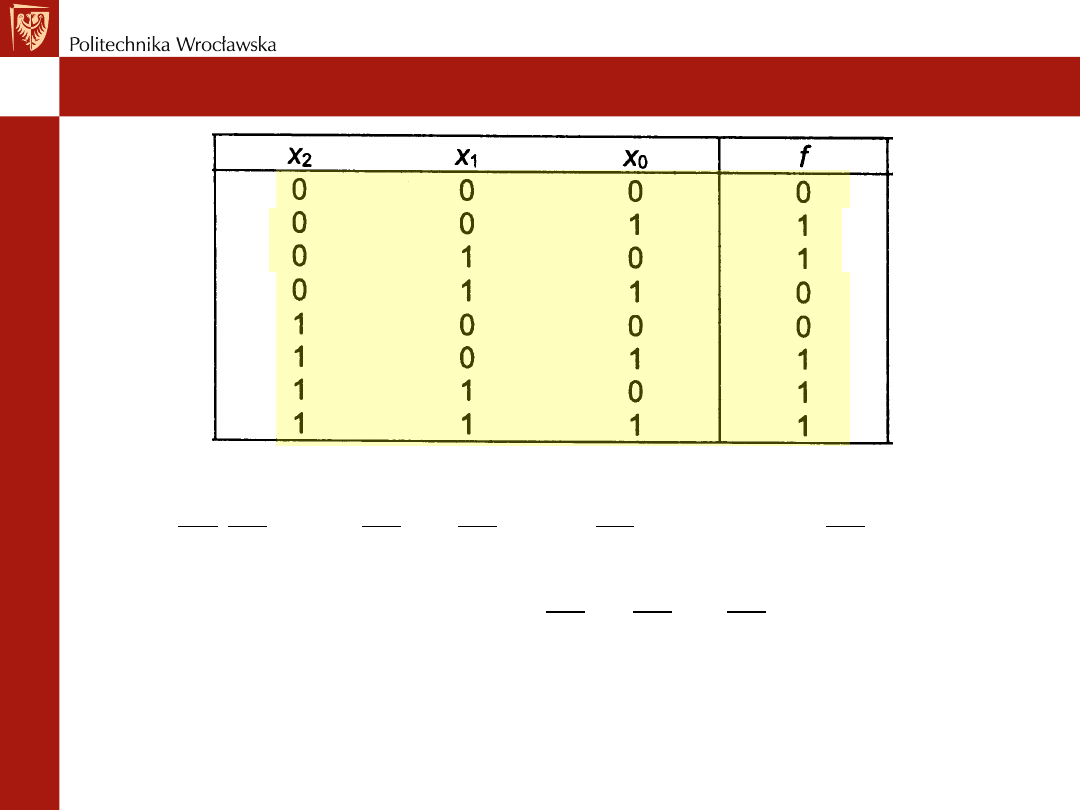
• tabela prawdy
• zapis algebraiczny

– termy iloczynowe i sumowe
– postać kanoniczna sumy
– postać kanoniczna iloczynu

• zapis dziesiętny
• mapa Karnaugha

P

o

d

st

aw

y

T

ec

h

n

ik

i

C

yf

ro

w

ej

i

M

ik

ro

p

ro

ce

so

ro

w

ej

P

o

d

st

aw

y

T

ec

h

n

ik

i

C

yf

ro

w

ej

i

M

ik

ro

p

ro

ce

so

ro

w

ej

A

lg

eb

ra

B

o

o

le

'a

A

lg

eb

ra

B

o

o

le

'a

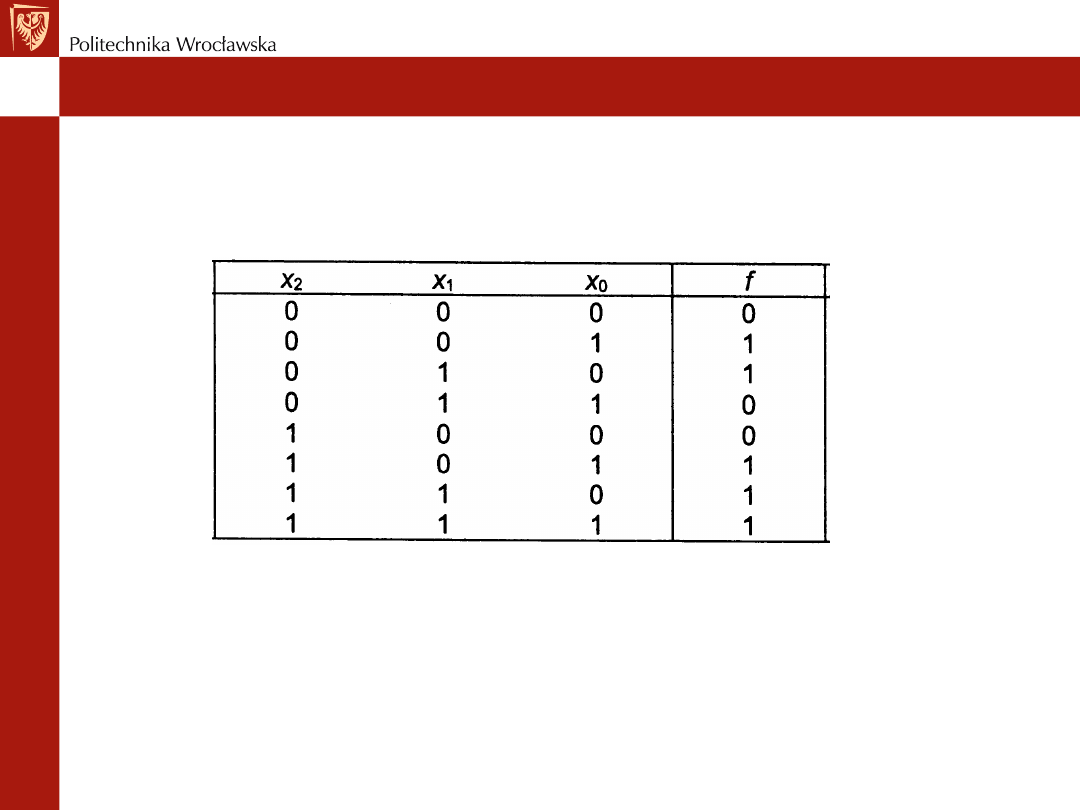
Tabela prawdy, postaci kanoniczne

Tabela prawdy, postaci kanoniczne

f = x

2

x

1

x

0



x

2

x

1

x

0



x

2

x

1

x

0



x

2

x

1

x

0



x

2

x

1

x

0

f = x

2



x

1



x

0

⋅

x

2



x

1



x

0

⋅

x

2



x

1



x

0



A. Skorupski, Podstawy

Techniki Cyfrowej

P

o

d

st

aw

y

T

ec

h

n

ik

i

C

yf

ro

w

ej

i

M

ik

ro

p

ro

ce

so

ro

w

ej

P

o

d

st

aw

y

T

ec

h

n

ik

i

C

yf

ro

w

ej

i

M

ik

ro

p

ro

ce

so

ro

w

ej

A

lg

eb

ra

B

o

o

le

'a

A

lg

eb

ra

B

o

o

le

'a

Zapis dziesiętny

Zapis dziesiętny

• Skrótowy zapis kanoniczny sum lub iloczynów. Termy zupełne

koduje się liczbami dziesiętnymi odpowiadającymi liczbom NKB
będącymi argumentami funkcji

0
1
2
3
4
5
6
7

f =

∑

3



1, 2, 5, 6, 7



f =

∏

3



0,3, 4



A. Skorupski, Podstawy

Techniki Cyfrowej

P

o

d

st

aw

y

T

ec

h

n

ik

i

C

yf

ro

w

ej

i

M

ik

ro

p

ro

ce

so

ro

w

ej

P

o

d

st

aw

y

T

ec

h

n

ik

i

C

yf

ro

w

ej

i

M

ik

ro

p

ro

ce

so

ro

w

ej

A

lg

eb

ra

B

o

o

le

'a

A

lg

eb

ra

B

o

o

le

'a

Kod Gray'a

Kod Gray'a

• Specjalny sposób kodowania liczb słowami binarnymi. Sąsiadujące

wartości różnią się stanem tylko jednego bitu

• Pełny kod Gray'a:

NKB

Gray

000

000

001

001

010

011

011

010

100

110

101

111

110

101

111

100

Pełny kod Gray'a nie jest jedynym kodem spełniającym w.w. założenia

P

o

d

st

aw

y

T

ec

h

n

ik

i

C

yf

ro

w

ej

i

M

ik

ro

p

ro

ce

so

ro

w

ej

P

o

d

st

aw

y

T

ec

h

n

ik

i

C

yf

ro

w

ej

i

M

ik

ro

p

ro

ce

so

ro

w

ej

A

lg

eb

ra

B

o

o

le

'a

A

lg

eb

ra

B

o

o

le

'a

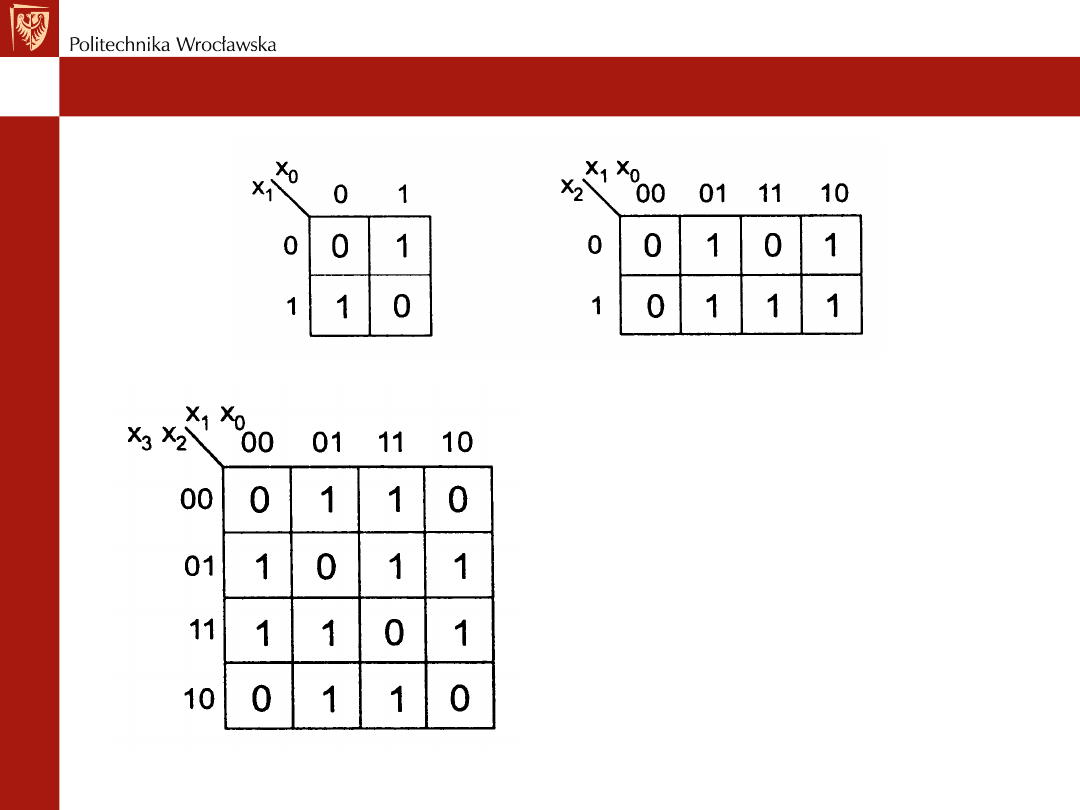
Mapa Karnaugh'a

Mapa Karnaugh'a

• Zapisana jest w niej wartość funkcji
• Sąsiadujące ze sobą pola różnią się

stanem tylko jednego bitu – dzięki
kodowaniu stanów wg kodów Gray'a

A. Skorupski, Podstawy

Techniki Cyfrowej