ZAKŁAD OCHRONY I KSZTAŁTOWANIA
ŚRODOWISKA
WYDZIAŁ INŻYNIERII ŚRODOWISKA
PRZEDMIOT:
HYDROLOGIA
PROWADZĄCY:
dr inż. Bogdan Ozga-Zieliński
Dla:
Inżynieria Środowiska sem. III
ZAKŁAD OCHRONY I KSZTAŁTOWANIA
ŚRODOWISKA
WYDZIAŁ INŻYNIERII ŚRODOWISKA
PRZEDMIOT:
HYDROLOGIA
PROWADZĄCY:
dr inż. Bogdan Ozga-Zieliński
Dla:
Inżynieria Środowiska sem. III
ĆWICZENIA AUDYTORYJNE:
7
TEMAT :
Przepływy maksymalne roczne o określonym
prawdopodobieństwie przewyższenia.
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Najprostsze charakterystyki przepływów maksymalnych rocznych
Przepływy główne II rzędu
WWQ
SWQ
ZWQ
NWQ
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Najprostsze charakterystyki przepływów maksymalnych rocznych
Przepływy główne II rzędu
WWQ
SWQ
ZWQ
NWQ
Największy przepływ maksymalny roczny zaobserwowany
w ciągu N lat obserwacji.
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Najprostsze charakterystyki przepływów maksymalnych rocznych
Przepływy główne II rzędu
WWQ
SWQ
ZWQ
NWQ
Największy przepływ maksymalny roczny zaobserwowany
w ciągu N lat obserwacji.
Średnia wartość przepływów maksymalnych rocznych
w ciągu N lat obserwacji.
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Najprostsze charakterystyki przepływów maksymalnych rocznych
Przepływy główne II rzędu
WWQ
SWQ
ZWQ
NWQ
Największy przepływ maksymalny roczny zaobserwowany
w ciągu N lat obserwacji.
Średnia wartość przepływów maksymalnych rocznych
w ciągu N lat obserwacji.
Mediana - wartość przekroczona z prawdopodobieństwem
p = 0.5 i nie przekroczona z prawdopodobieństwem q =0.5
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Najprostsze charakterystyki przepływów maksymalnych rocznych
Przepływy główne II rzędu
WWQ
SWQ
ZWQ
NWQ
Największy przepływ maksymalny roczny zaobserwowany
w ciągu N lat obserwacji.
Średnia wartość przepływów maksymalnych rocznych
w ciągu N lat obserwacji.
Mediana - wartość przekroczona z prawdopodobieństwem
p = 0.5 i nie przekroczona z prawdopodobieństwem q =0.5
Najmniejszy zaobserwowany przepływ maksymalny roczny
w ciągu N lat obserwacji.
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Najprostsze charakterystyki przepływów maksymalnych rocznych
Przepływy główne II rzędu
WWQ
SWQ
ZWQ
NWQ
Największy przepływ maksymalny roczny zaobserwowany
w ciągu N lat obserwacji.
Średnia wartość przepływów maksymalnych rocznych
w ciągu N lat obserwacji.
Mediana - wartość przekroczona z prawdopodobieństwem
p = 0.5 i nie przekroczona z prawdopodobieństwem q =0.5
Najmniejszy zaobserwowany przepływ maksymalny roczny
w ciągu N lat obserwacji.
Informacja ta jest niewystarczająca – szczególnie w odniesieniu do WWQ
Nie ma żadnej pewności co do możliwości wystąpienia takiego (lub bardziej
katastrofalnego) zdarzenia w przyszłości.
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Najprostsze charakterystyki przepływów maksymalnych rocznych
Przepływy główne II rzędu
WWQ
SWQ
ZWQ
NWQ
Największy przepływ maksymalny roczny zaobserwowany
w ciągu N lat obserwacji.
Średnia wartość przepływów maksymalnych rocznych
w ciągu N lat obserwacji.
Mediana - wartość przekroczona z prawdopodobieństwem
p = 0.5 i nie przekroczona z prawdopodobieństwem q =0.5
Najmniejszy zaobserwowany przepływ maksymalny roczny
w ciągu N lat obserwacji.
Najprostsze oszacowanie: Pr(WQ
N+1
>
=
WWQ) = 1/(N+1)
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Najprostsze charakterystyki przepływów maksymalnych rocznych
Przepływy główne II rzędu
WWQ
SWQ
ZWQ
NWQ
Największy przepływ maksymalny roczny zaobserwowany
w ciągu N lat obserwacji.
Średnia wartość przepływów maksymalnych rocznych
w ciągu N lat obserwacji.
Mediana - wartość przekroczona z prawdopodobieństwem
p = 0.5 i nie przekroczona z prawdopodobieństwem q =0.5
Najmniejszy zaobserwowany przepływ maksymalny roczny
w ciągu N lat obserwacji.
Najprostsze oszacowanie: Pr(WQ
N+1
>
=
WWQ) = 1/(N+1)
Wniosek: Trzeba zastosować metody statystyczne do analizy własności losowych
przepływów maksymalnych rocznych WQ
i
(i =1, 2, …, N)
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
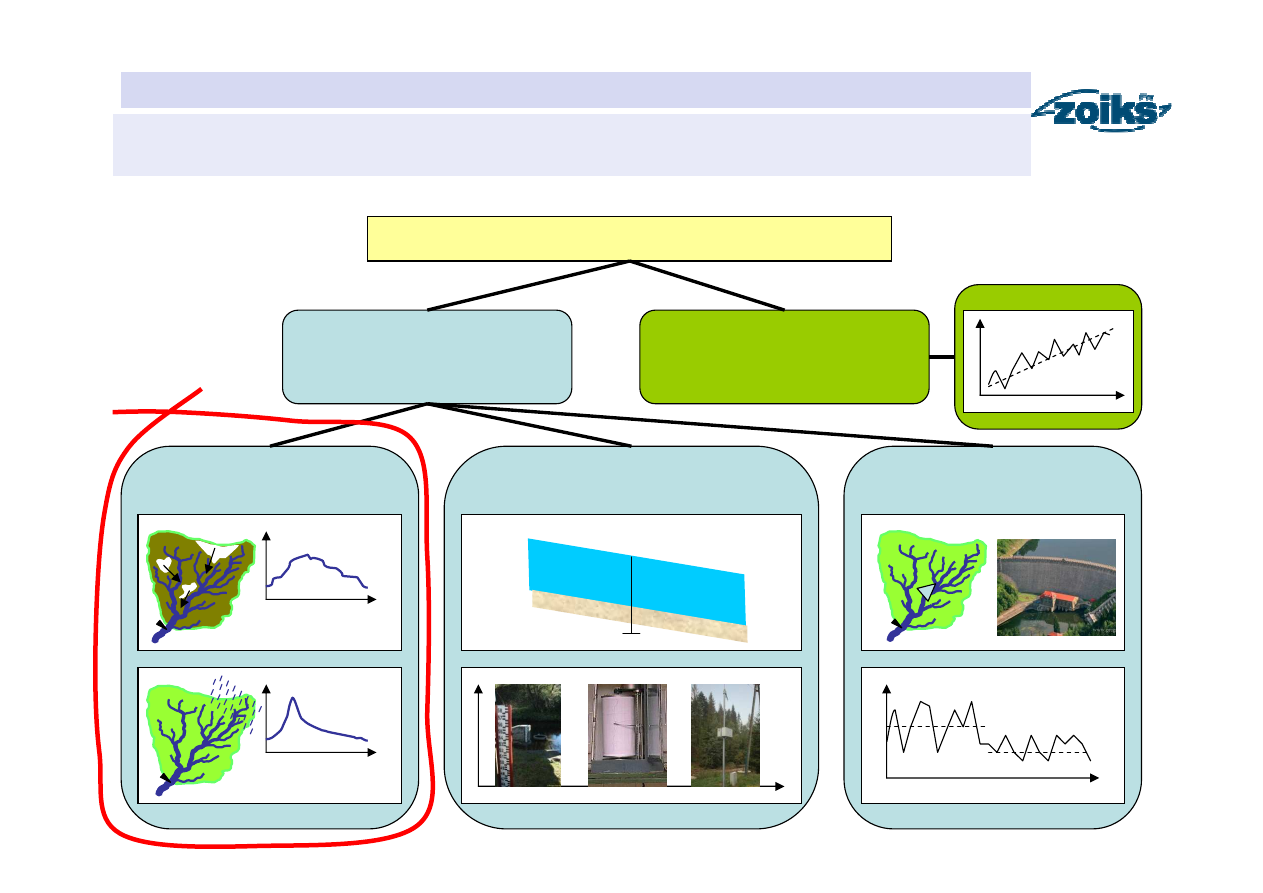
Niejednorodno
ść
ci
ą
gów pomiarowych
Wykrywana metodami
genetycznymi
Wykrywana metodami
statystycznymi
Aprioryczna
Pomiarowa
(eksperymentu)
Czasowa
P
s
P
Wezbranie roztopowe
Wezbranie deszczowe
Q
Q
t
t
Zima
Lato
t
0
H
Zbudowanie zapory
t
Q
max
Q
max
t
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
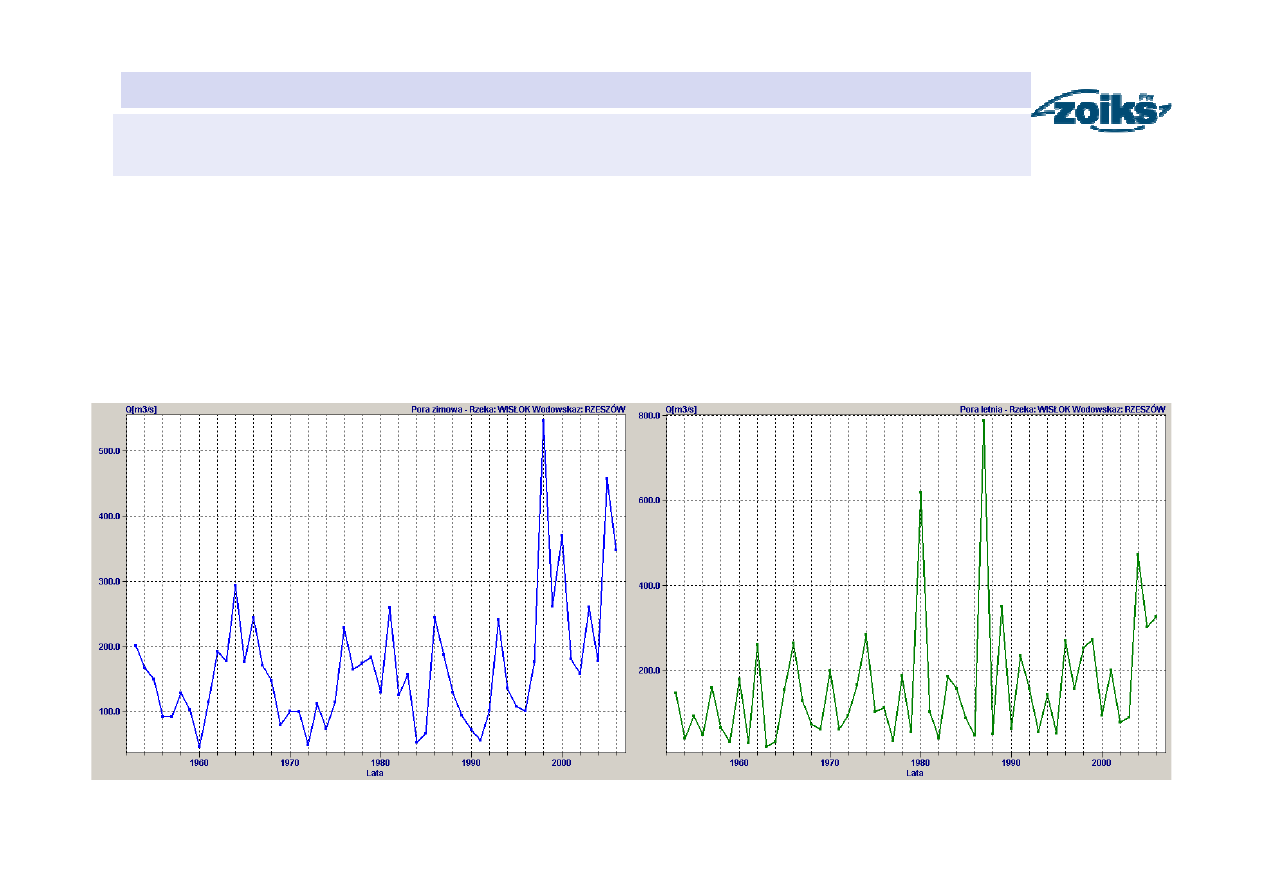
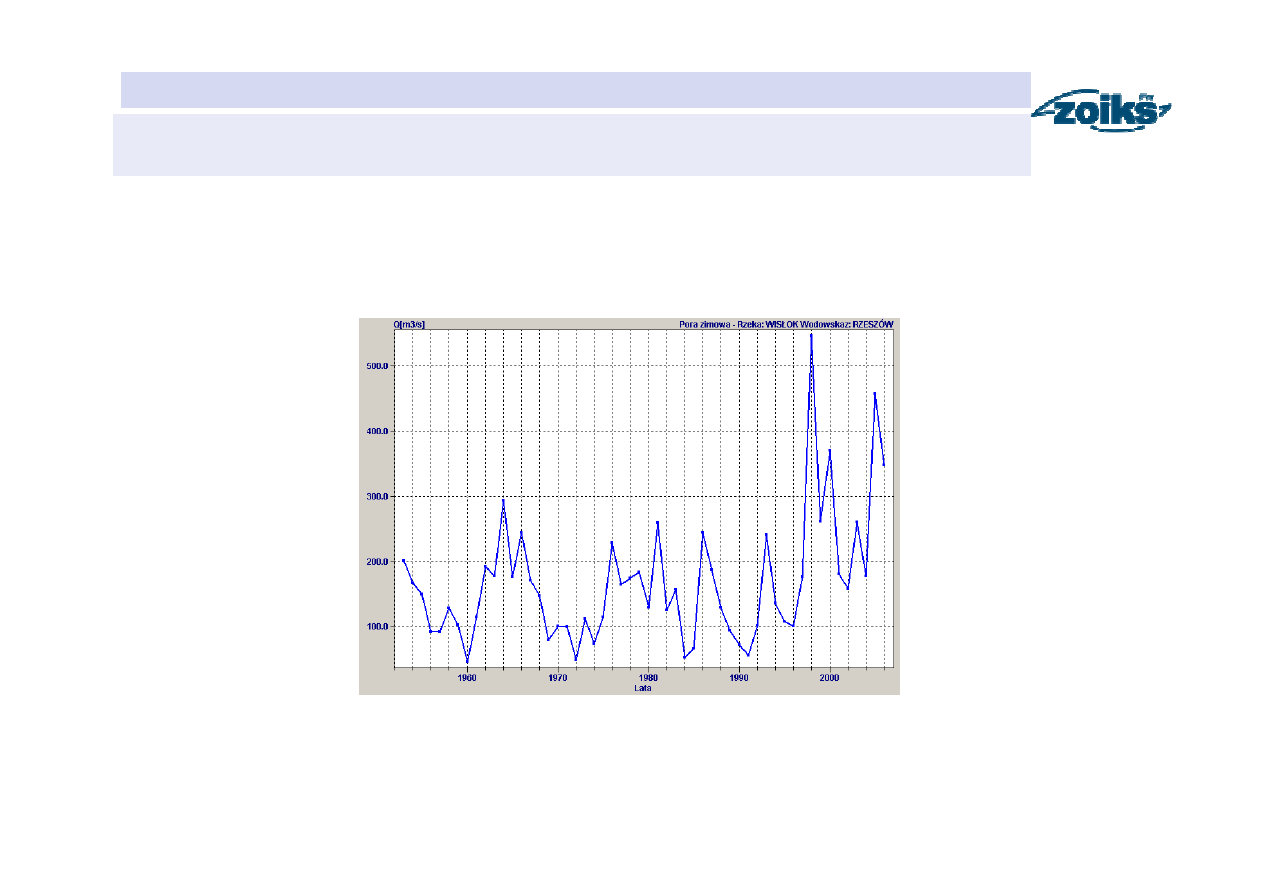
Ciągi przepływów maksymalnych rocznych pory zimowej i pory letniej
Rzeka: WIS
Ł
OK Wodowskaz: RZESZÓW
1953-2006 (54 lata obserwacji)
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
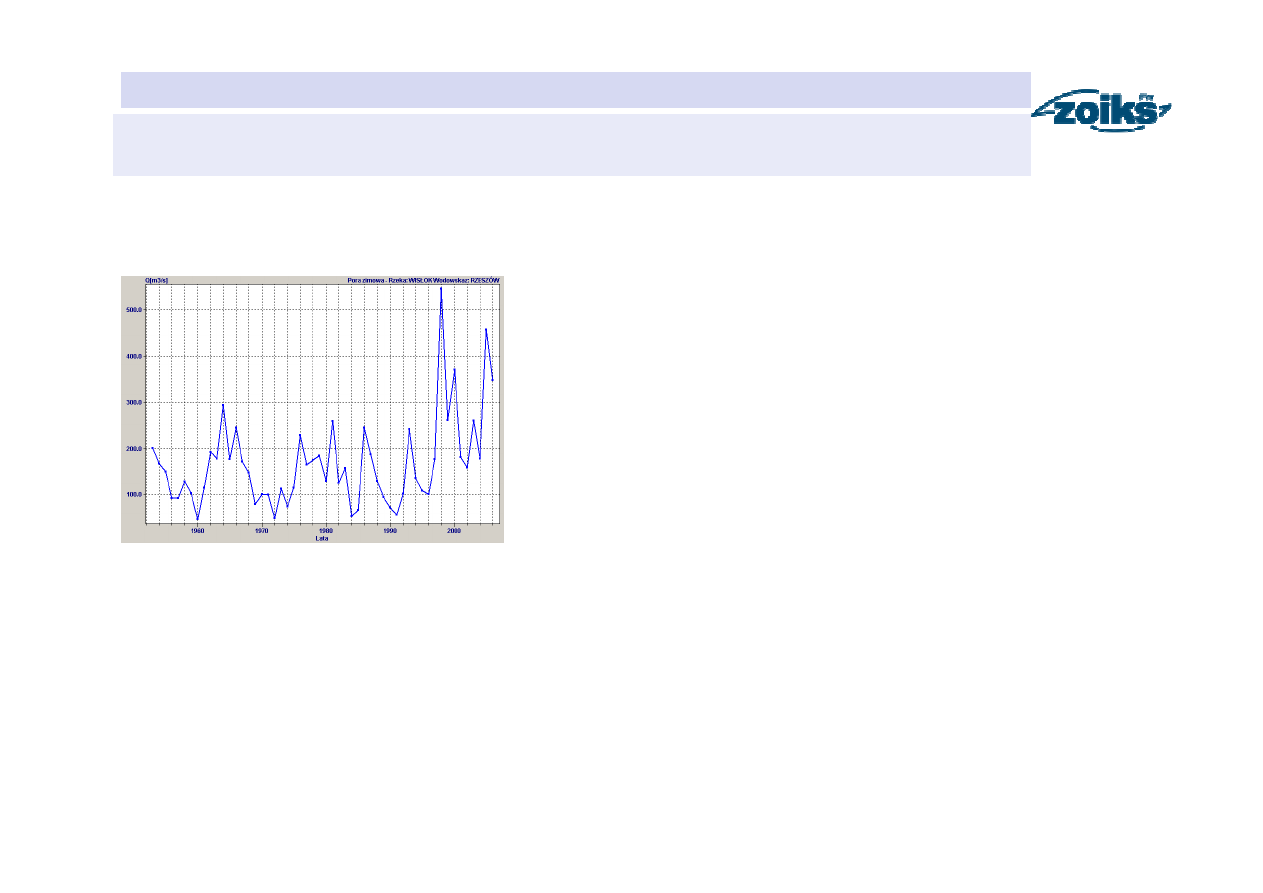
Analiza własności losowych przepływów maksymalnych rocznych
pory zimowej
Dla przepływów maksymalnych rocznych pory letniej analiza przeprowadzona będzie
w ten sam sposób.
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Analiza własności losowych przepływów maksymalnych rocznych
pory zimowej (zmienna losowa X)
Konwencja oznaczeń
-
Przepływ maksymalny roczny pory zimowej zaobserwowany w roku i
(i = 1, 2, …, N)
i
x
m
x
-
Przepływ maksymalny roczny pory zimowej jako element o numerze
m (m = 1, 2, …, N) w uporządkowanym nierosnąco ciągu
N
m
x
x
x
x
≥
≥
≥
≥
≥
...
...
2
1
Dla przepływów maksymalnych rocznych pory letniej będą to odpowiednio
symbole oraz
i
y
m
y
Dla przepływów maksymalnych rocznych bez względu na genezę będą to
odpowiednio symbole oraz
m
z
i
z
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
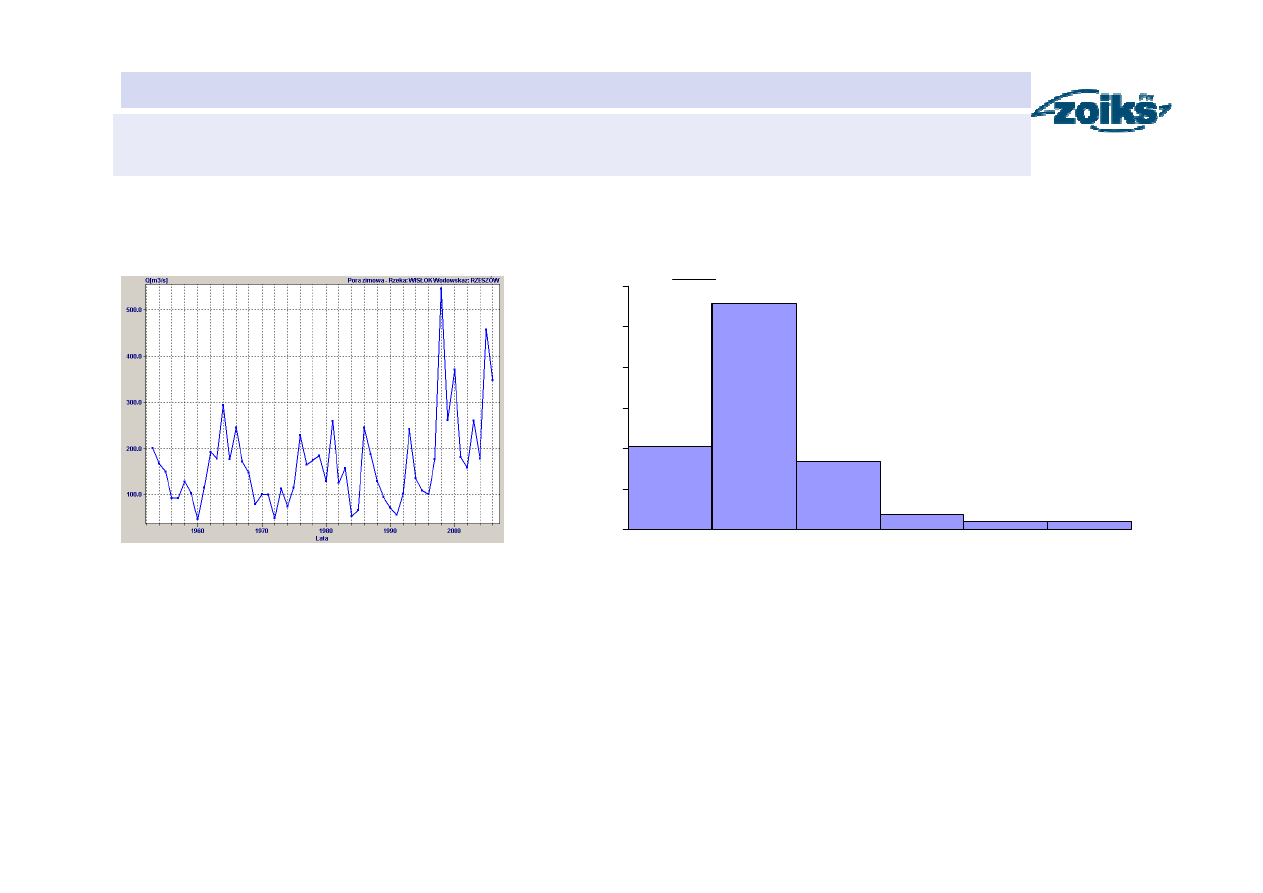
Analiza własności losowych przepływy maksymalnych rocznych
pory zimowej (zmienna losowa X)
54
=
N
0
0.001
0.002
0.003
0.004
0.005
0.006
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
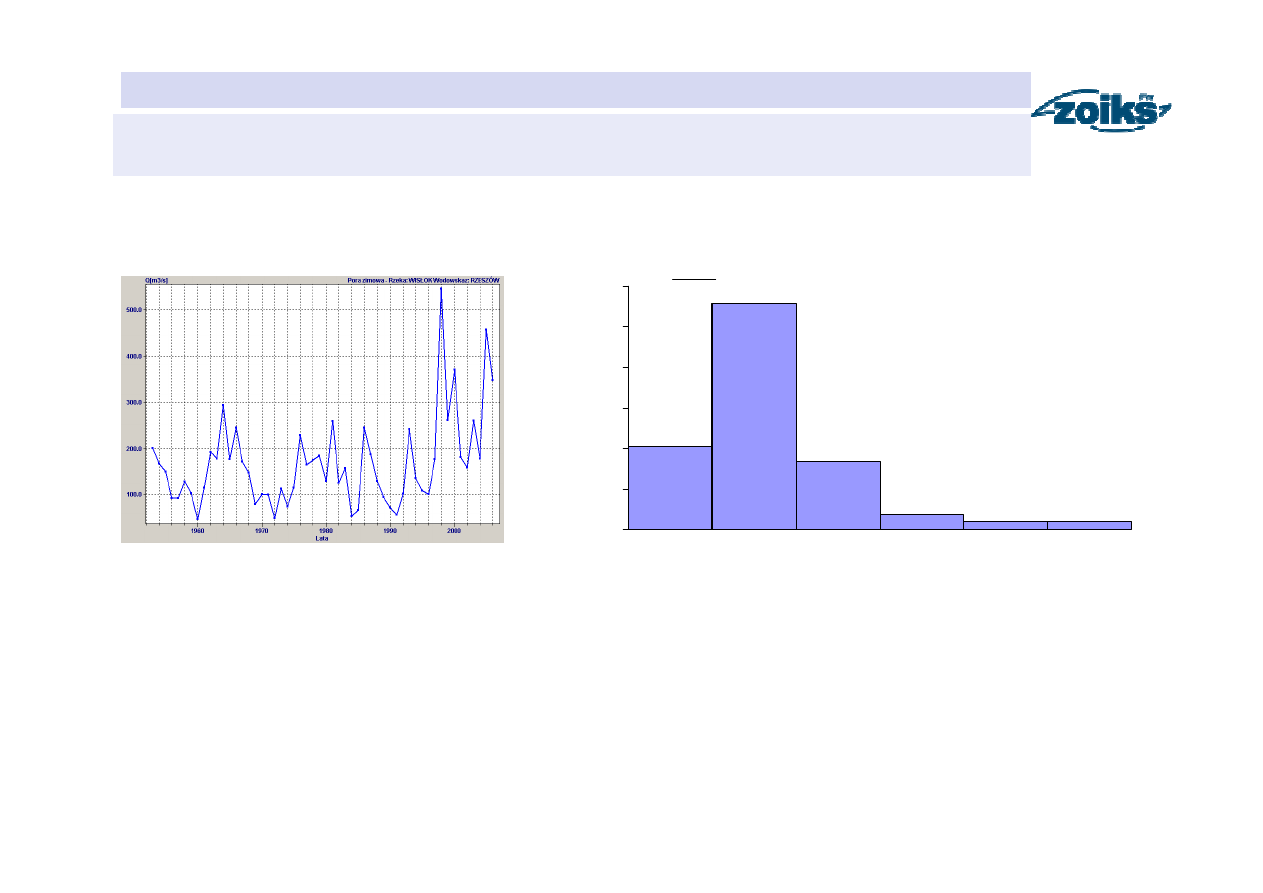
HYDROLOGIA
Histogram gęstości przepływów maksymalnych rocznych
xN
n
g
∆
=
x
0 100 200 300 400 500
54
=
N
0
0.001
0.002
0.003
0.004
0.005
0.006
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
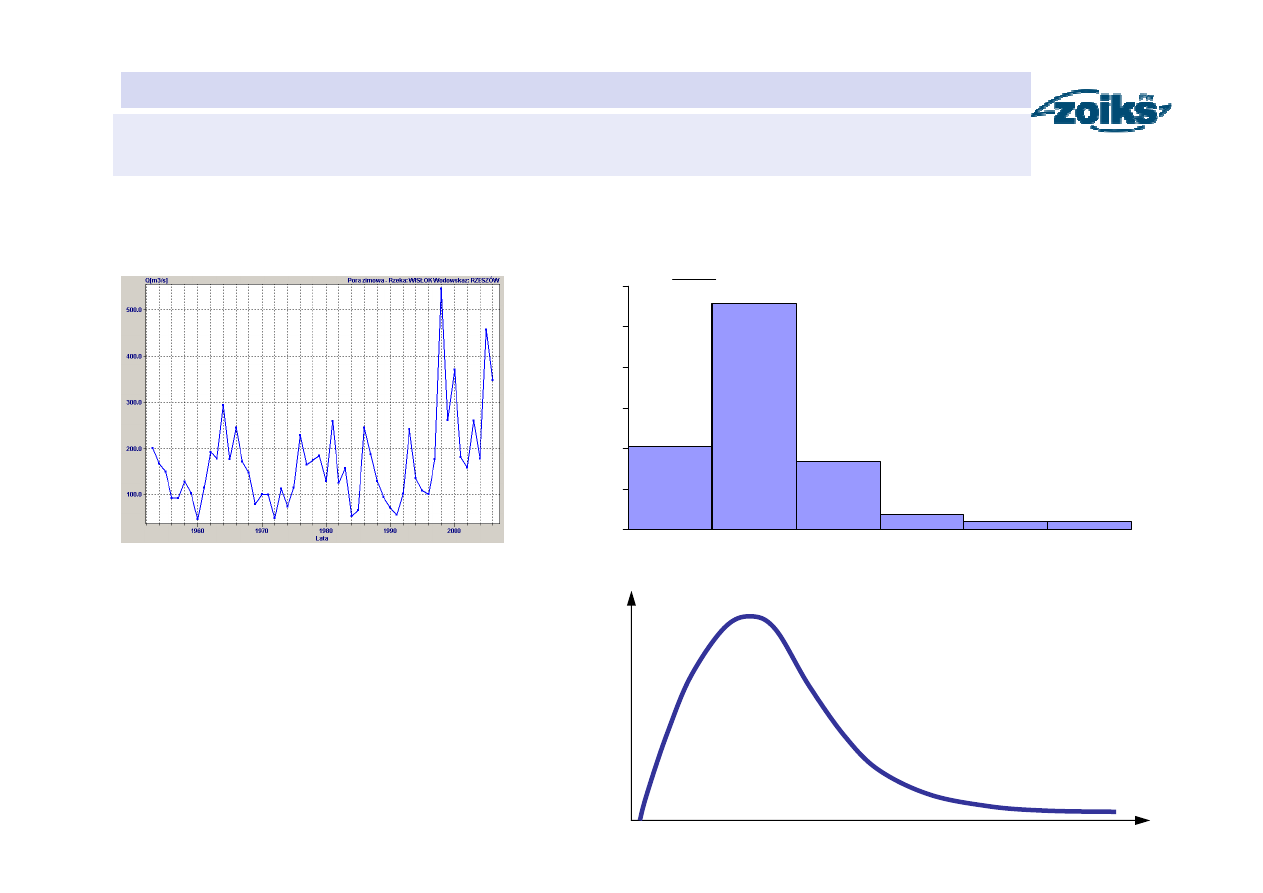
HYDROLOGIA
Histogram gęstości przepływów maksymalnych rocznych
xN
n
g
∆
=
x
0 100 200 300 400 500
54
=
N
)
(
0
x
f
g
x
N
→
→
∆
∞
→
0
0.001
0.002
0.003
0.004
0.005
0.006
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
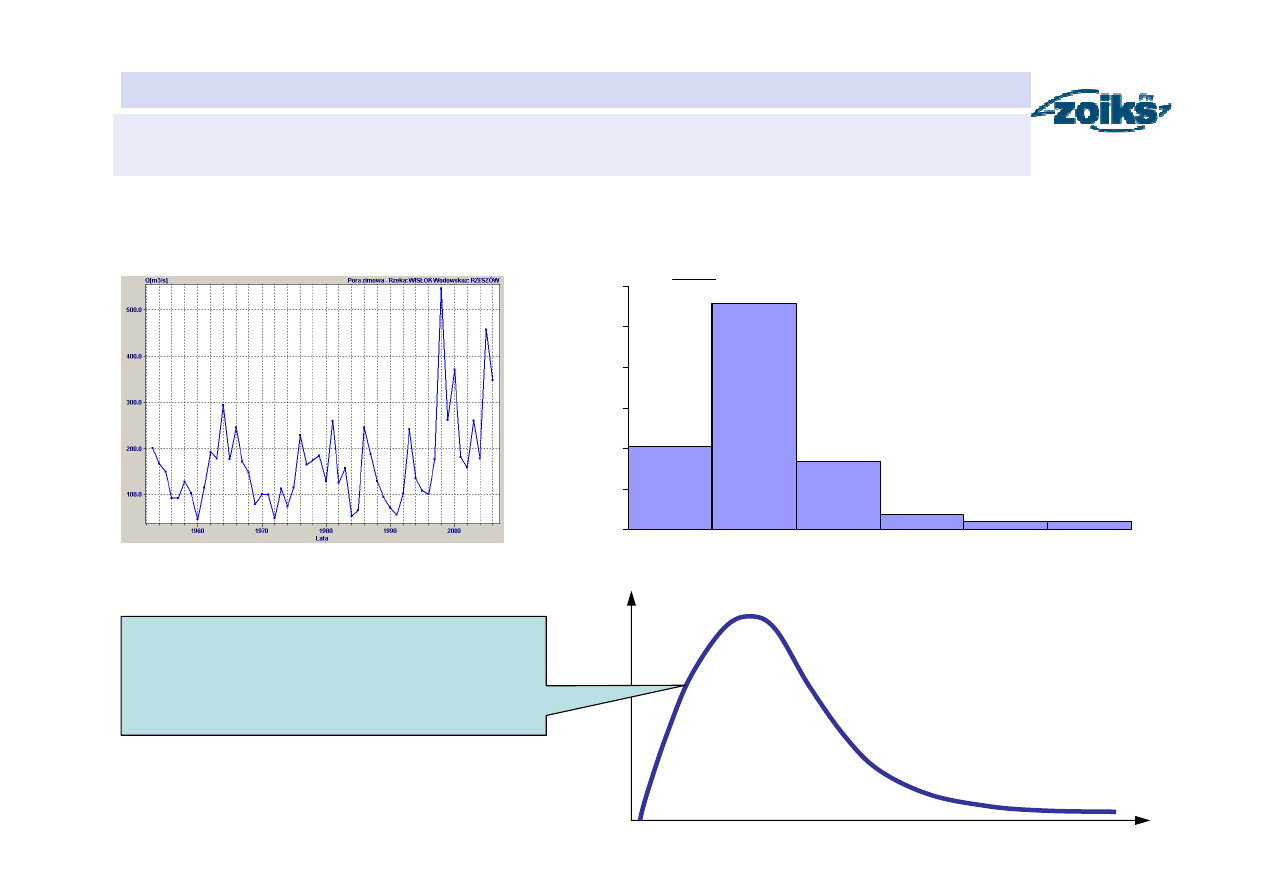
HYDROLOGIA
Histogram i funkcja gęstości przepływów maksymalnych rocznych
xN
n
g
∆
=
x
0 100 200 300 400 500
54
=
N
)
(
0
x
f
g
x
N
→
→
∆
∞
→
x
)
(x
f
0 100 200 300 400 500
Funkcja gęstości
prawdopodobieństwa
zmiennej losowej X
0
0.001
0.002
0.003
0.004
0.005
0.006
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
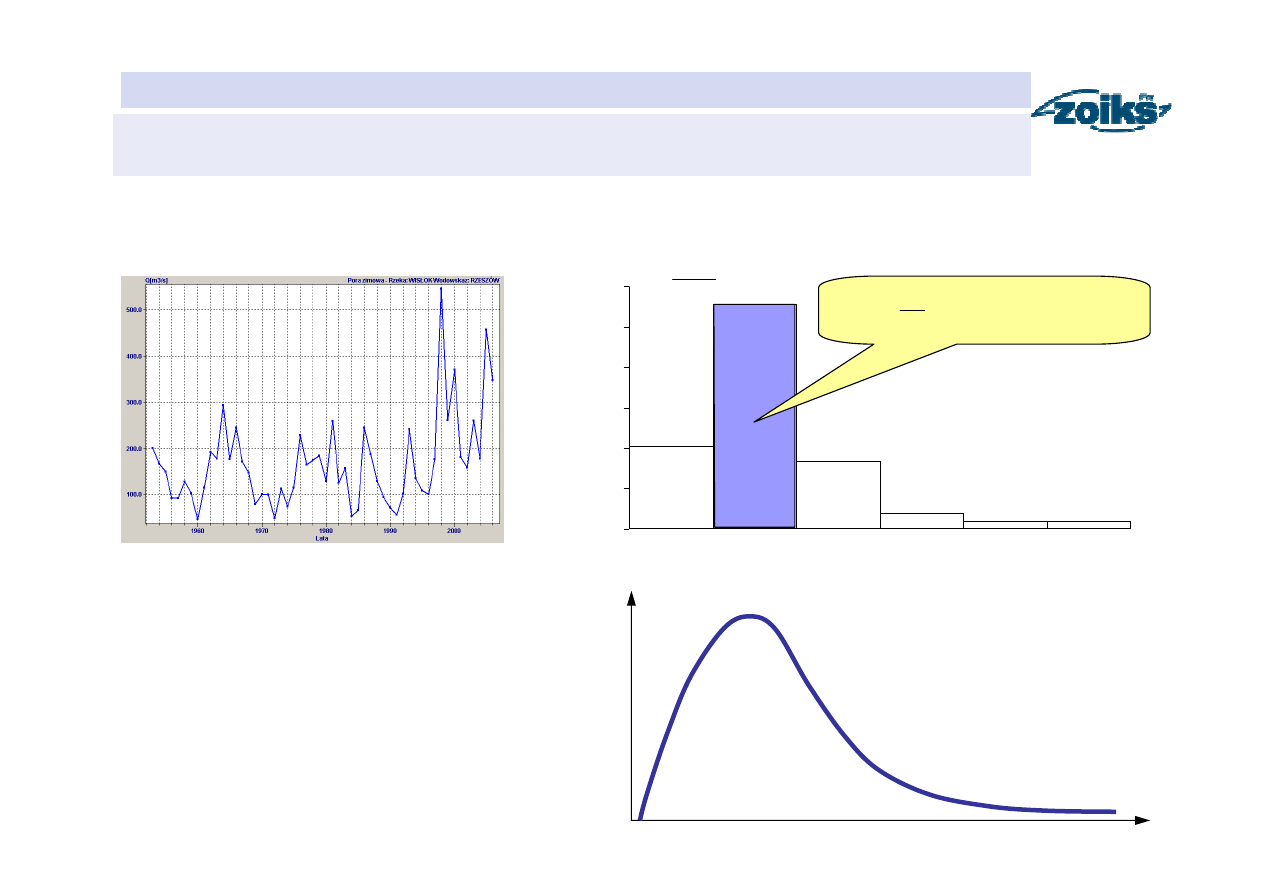
Histogram i funkcja gęstości przepływów maksymalnych rocznych
xN
n
g
∆
=
x
0 100 200 300 400 500
54
=
N
x
)
(x
f
0 100 200 300 400 500
Funkcja gęstości
prawdopodobieństwa
zmiennej losowej X
Model teoretyczny dla wszystkich
możliwych wartości przepływów
maksymalnych rocznych
(populacji generalnej)
0
0.001
0.002
0.003
0.004
0.005
0.006
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
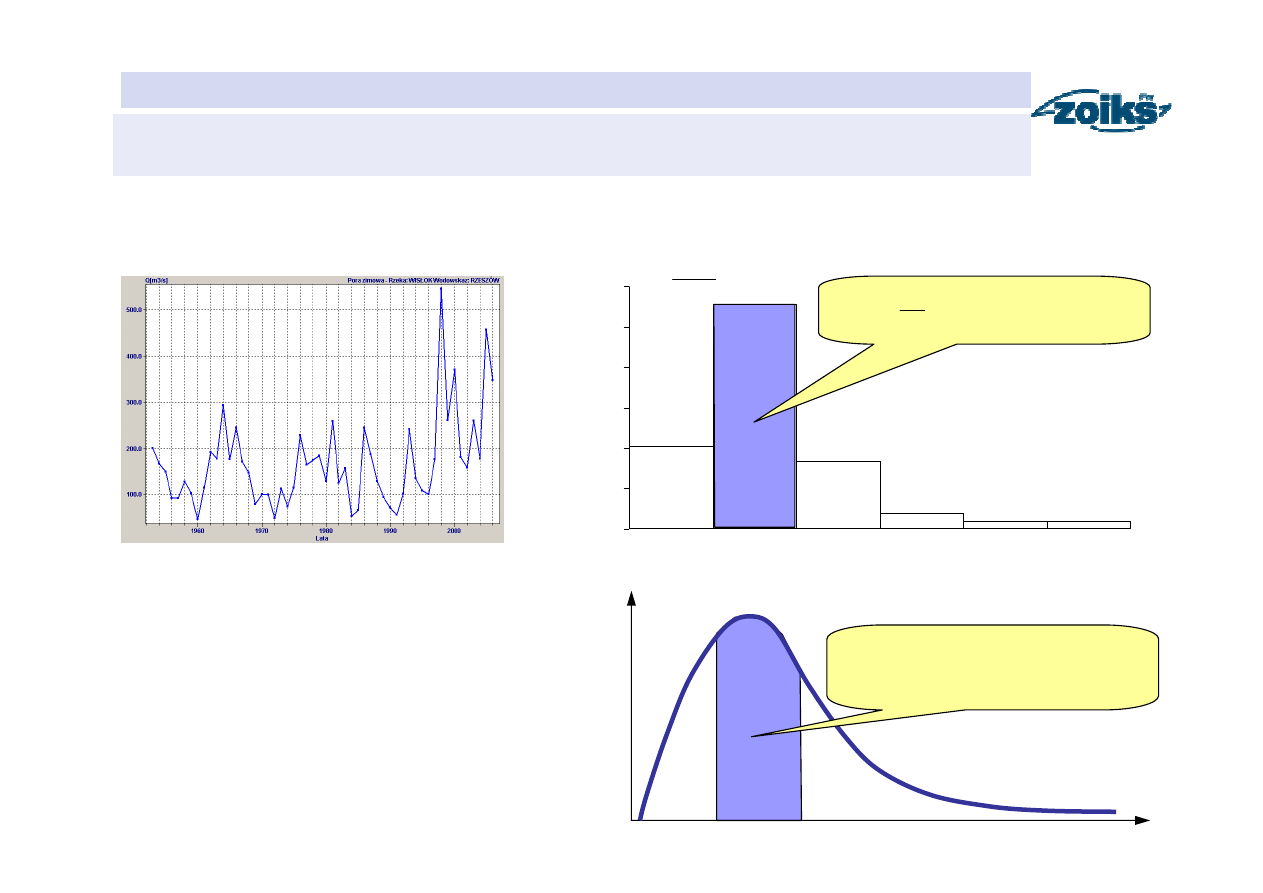
Histogram i funkcja gęstości przepływów maksymalnych rocznych
xN
n
g
∆
=
x
0 100 200 300 400 500
54
=
N
x
)
(x
f
0 100 200 300 400 500
)
200
100
Pr(
<
≤
=
=
∆
X
N
n
x
g
0
0.001
0.002
0.003
0.004
0.005
0.006
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
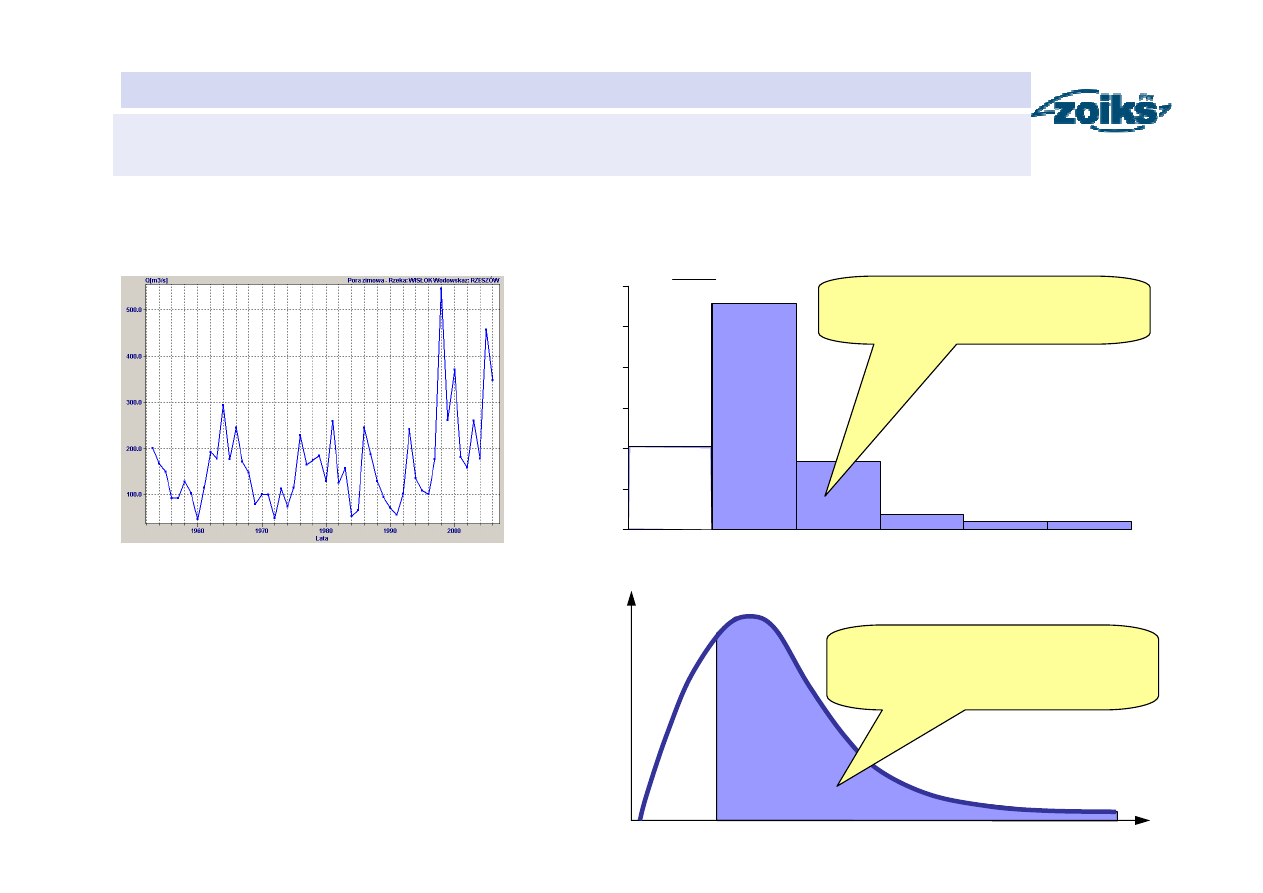
Histogram i funkcja gęstości przepływów maksymalnych rocznych
xN
n
g
∆
=
x
0 100 200 300 400 500
54
=
N
x
)
(x
f
0 100 200 300 400 500
)
200
100
Pr(
<
≤
=
=
∆
X
N
n
x
g
∫
=
=
=
<
≤
200
100
)
(
)
200
100
Pr(
x
x
dx
x
f
X
0
0.001
0.002
0.003
0.004
0.005
0.006
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
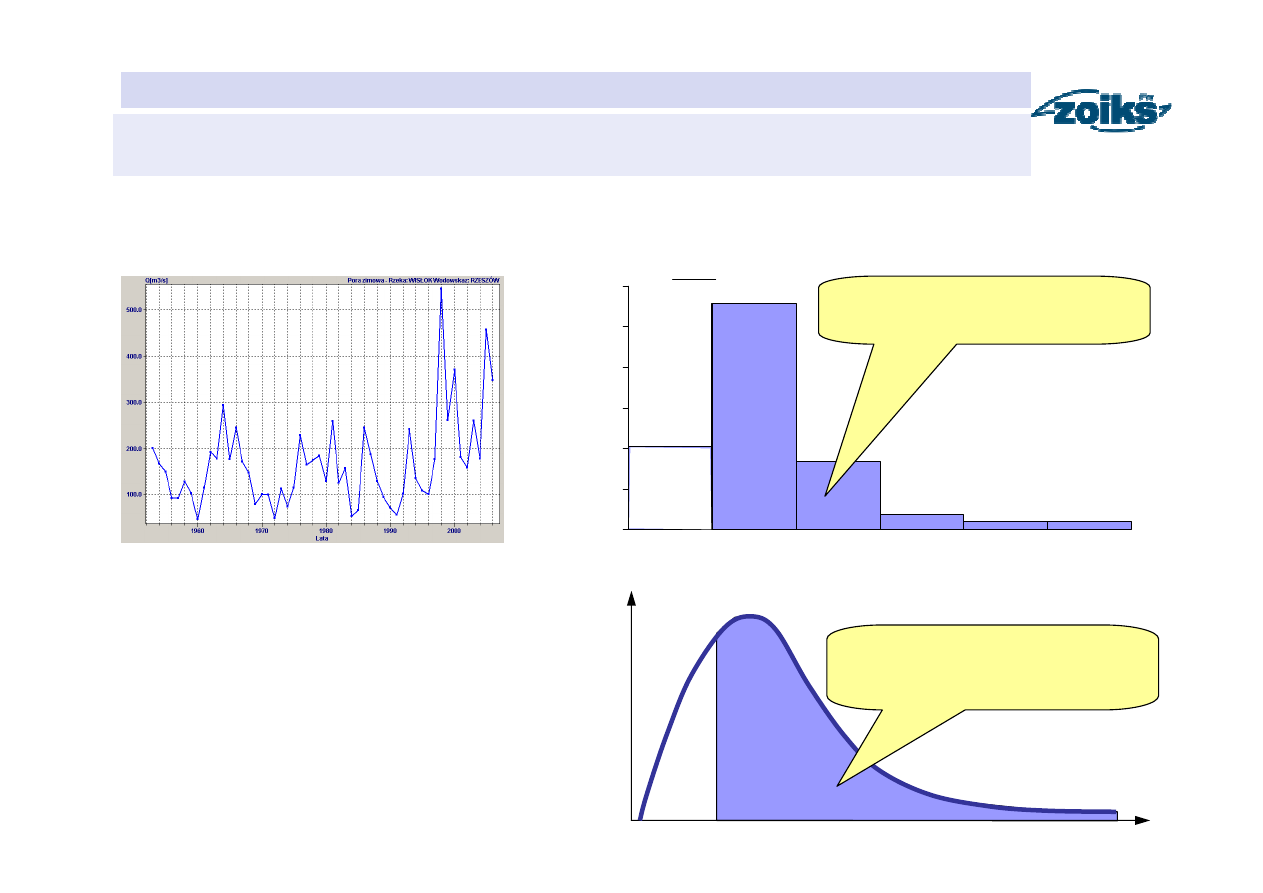
HYDROLOGIA
Funkcja prawdopodobieństwa przewyższenia
xN
n
g
∆
=
x
0 100 200 300 400 500
54
=
N
x
)
(x
f
0 100 200 300 400 500
)
100
Pr(
≥
=
∆
∑
X
x
g
∫
+∞
=
=
≥
100
)
(
)
100
Pr(
x
dx
x
f
X
∫
+∞
=
=
≥
x
dx
x
f
x
p
x
X
)
(
)
(
)
Pr(
Funkcja prawdopodobieństwa przewyższenia
zmiennej losowej X
0
0.001
0.002
0.003
0.004
0.005
0.006
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Funkcja prawdopodobieństwa przewyższenia
xN
n
g
∆
=
x
0 100 200 300 400 500
54
=
N
x
)
(x
f
0 100 200 300 400 500
)
100
Pr(
≥
=
∆
∑
X
x
g
∫
+∞
=
=
≥
100
)
(
)
100
Pr(
x
dx
x
f
X
UWAGA!
Dla zmiennej losowej typu ciągłego
ale zdarzenie to nie jest niemożliwe!
0
)
Pr(
=
=
x
X
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
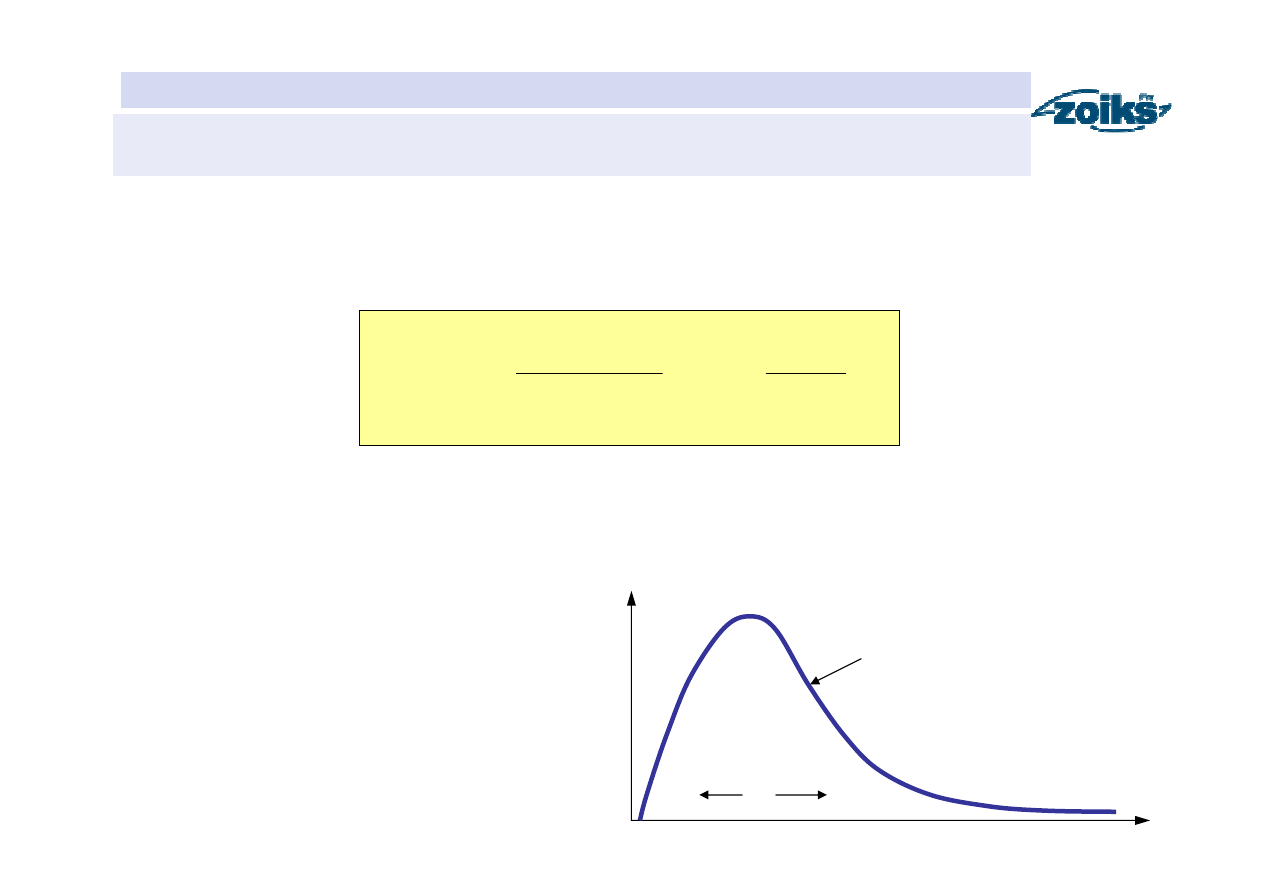
Przykłady teoretycznych funkcji gęstości prawdopodobieństwa
x
)
(x
f
Rozkład gamma
GA
(Pearsona III typ)
−
−
Γ
−
=
−
α
λ
α
λ
λ
d
x
d
x
x
f
exp
)
(
)
(
)
(
1
Parametry:
Zakres zmienności:
d
X
≥
0
>
λ
0
>
α
)
(
λ
Γ
- funkcja gamma Eulera
d
α
λ
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
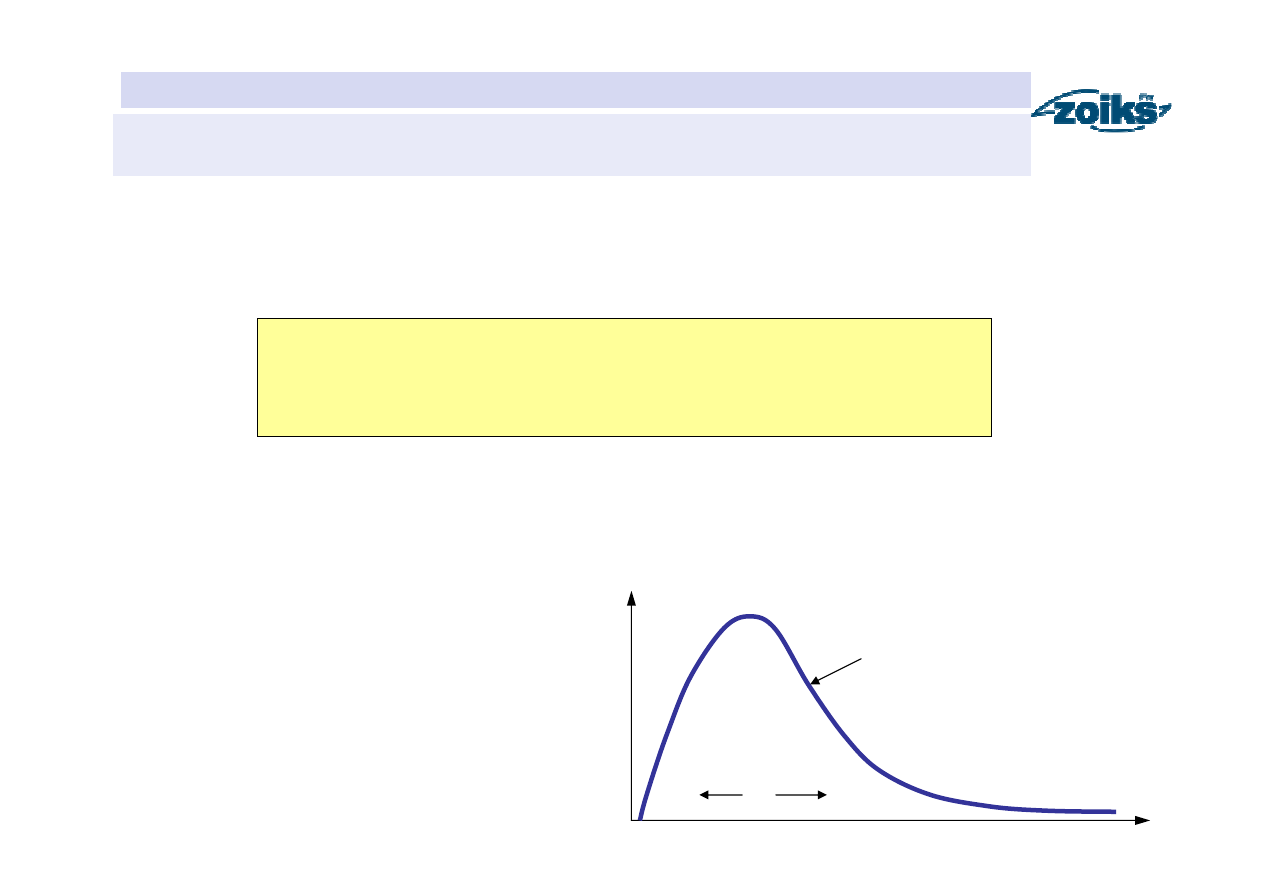
Przykłady teoretycznych funkcji gęstości prawdopodobieństwa
x
)
(x
f
Rozkład Weibulla
WE
(Fishera-Tippetta III typ min.)
d
α
β
]
)
(
exp[
)
(
)
(
1
β
β
β
β
α
βα
d
x
d
x
x
f
−
−
−
=
−
−
−
Parametry: ,
Zakres zmienności:
d
X
≥
0
>
α
0
>
β
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
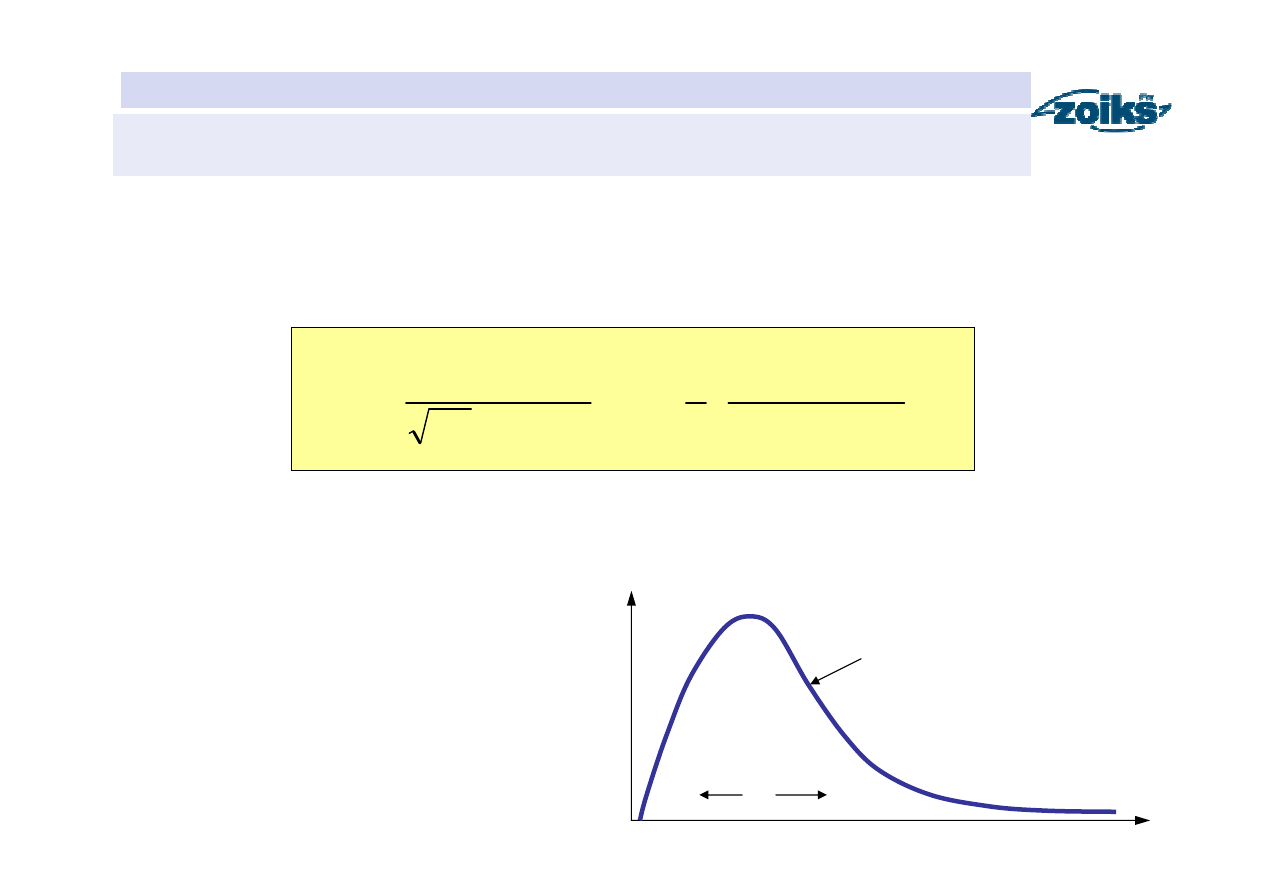
Przykłady teoretycznych funkcji gęstości prawdopodobieństwa
x
)
(x
f
Rozkład log-normalny
LN
d
µ
σ
−
−
−
−
=
2
)
ln(
2
1
exp
)
(
2
1
)
(
σ
µ
σ
π
d
x
d
x
x
f
Parametry: ,
Zakres zmienności:
d
X
≥
0
>
µ
0
>
σ
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
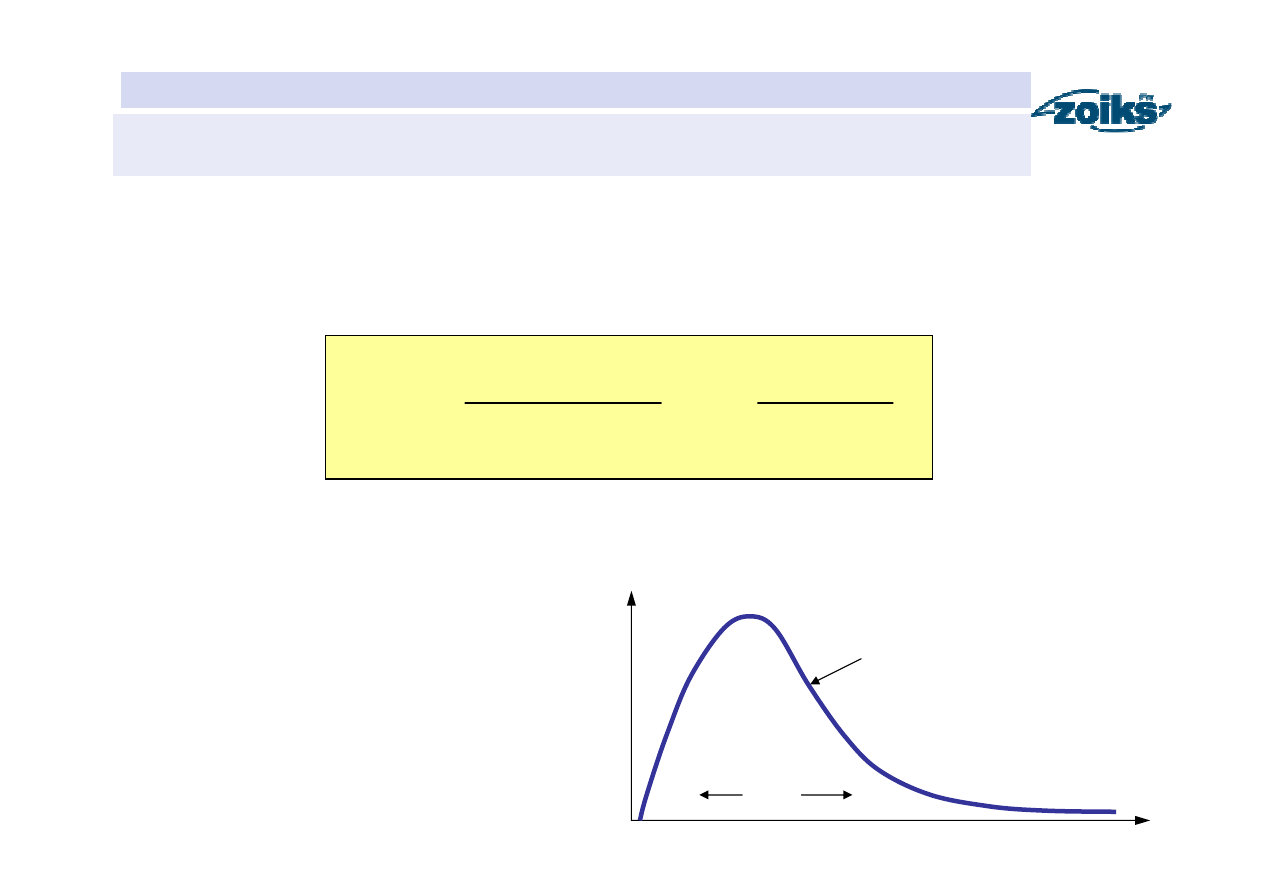
Przykłady teoretycznych funkcji gęstości prawdopodobieństwa
x
)
(x
f
Rozkład log-gamma
LG
(log-Pearsona III typ)
d
d, α
λ,
α
−
−
Γ
−
=
−
α
λ
α
λ
λ
d
x
x
d
x
x
f
ln
ln
exp
)
(
)
ln
(ln
)
(
1
Parametry:
Zakres zmienności:
d
X
≥
0
>
λ
0
>
α
- funkcja gamma Eulera
)
(
λ
Γ
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
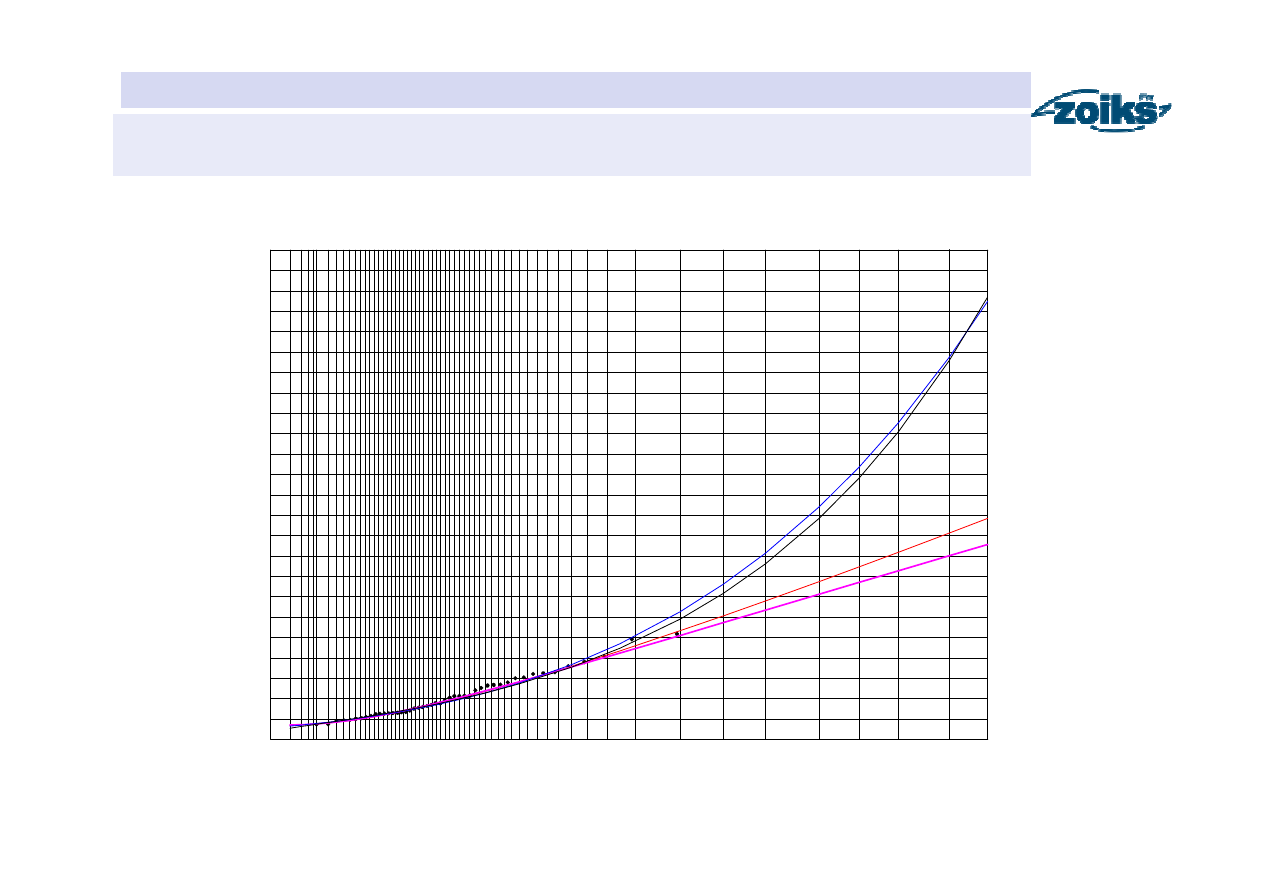
Podziałka prawdopodobieństwa
0
100
200
300
400
500
600
100 99.9
98
90
80
70
60
50
40
30
20
10 8
6
4
2
1
0.5
0.2
0.1
0.05
0.01
0.02
p [%]
WE
GA
LN
LG
]
/
[m
3
max,
s
Q
p
Funkcje prawdopodobieństwa przewyższenia przep
ł
ywów maksymalnych
rocznych pory zimowej w przekroju Sucha na Skawie
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Podziałka prawdopodobieństwa
0
100
200
300
400
500
600
100 99.9
98
90
80
70
60
50
40
30
20
10 8
6
4
2
1
0.5
0.2
0.1
0.05
0.01
0.02
p [%]
WE
GA
LN
LG
]
/
[m
3
max,
s
Q
p
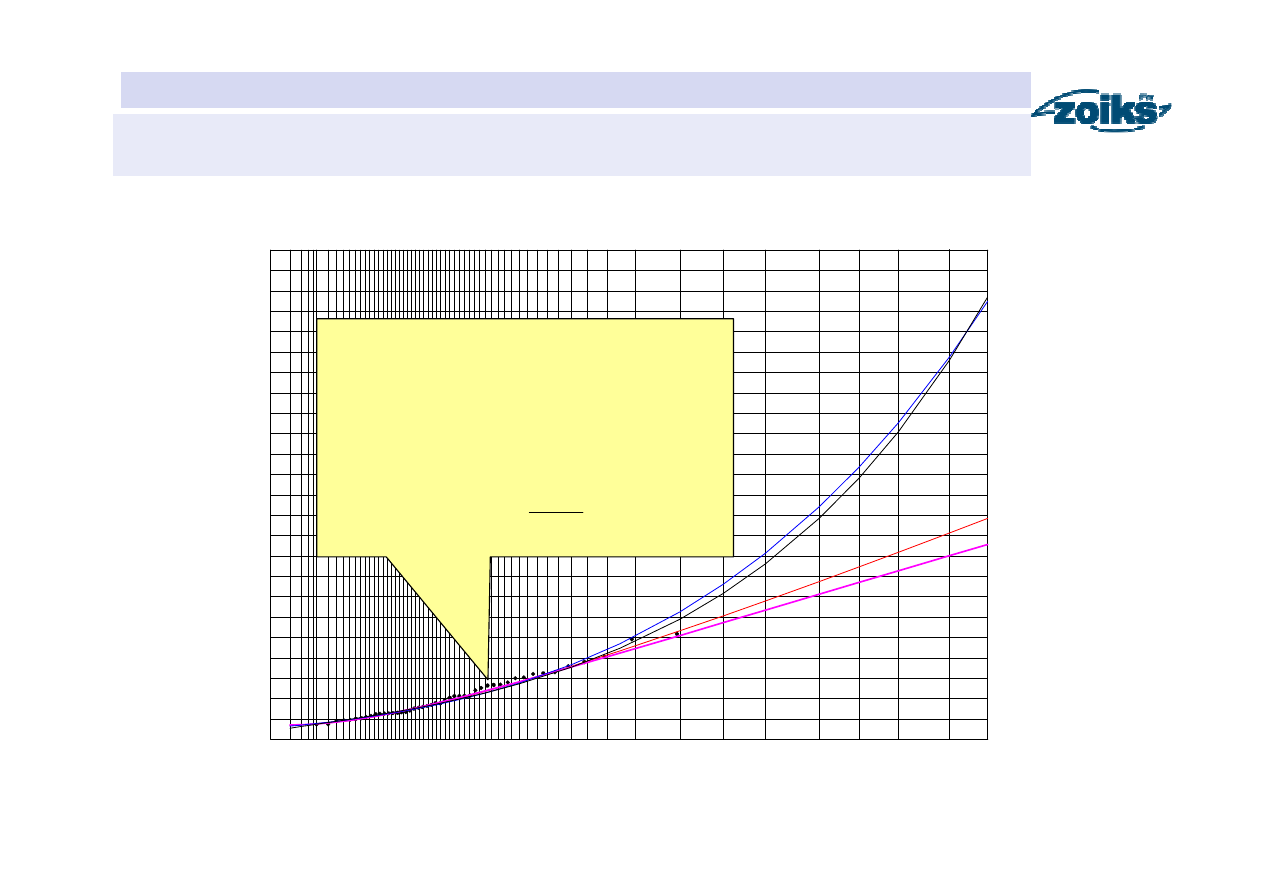
Funkcje prawdopodobieństwa przewyższenia przep
ł
ywów maksymalnych
rocznych pory zimowej w przekroju Sucha na Skawie
Punkty empirycznego rozkładu
prawdopodobieństwa przewyższenia.
Uporządkowanym w ciąg nierosnący
przepływom maksymalnym rocznym
przyporządkowuje się empiryczne
prawdopodobieństwo przewyższenia
1
ˆ
,
+
=
N
m
p
N
m
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Podziałka prawdopodobieństwa
0
100
200
300
400
500
600
100 99.9
98
90
80
70
60
50
40
30
20
10 8
6
4
2
1
0.5
0.2
0.1
0.05
0.01
0.02
p [%]
WE
GA
LN
LG
]
/
[m
3
max,
s
Q
p
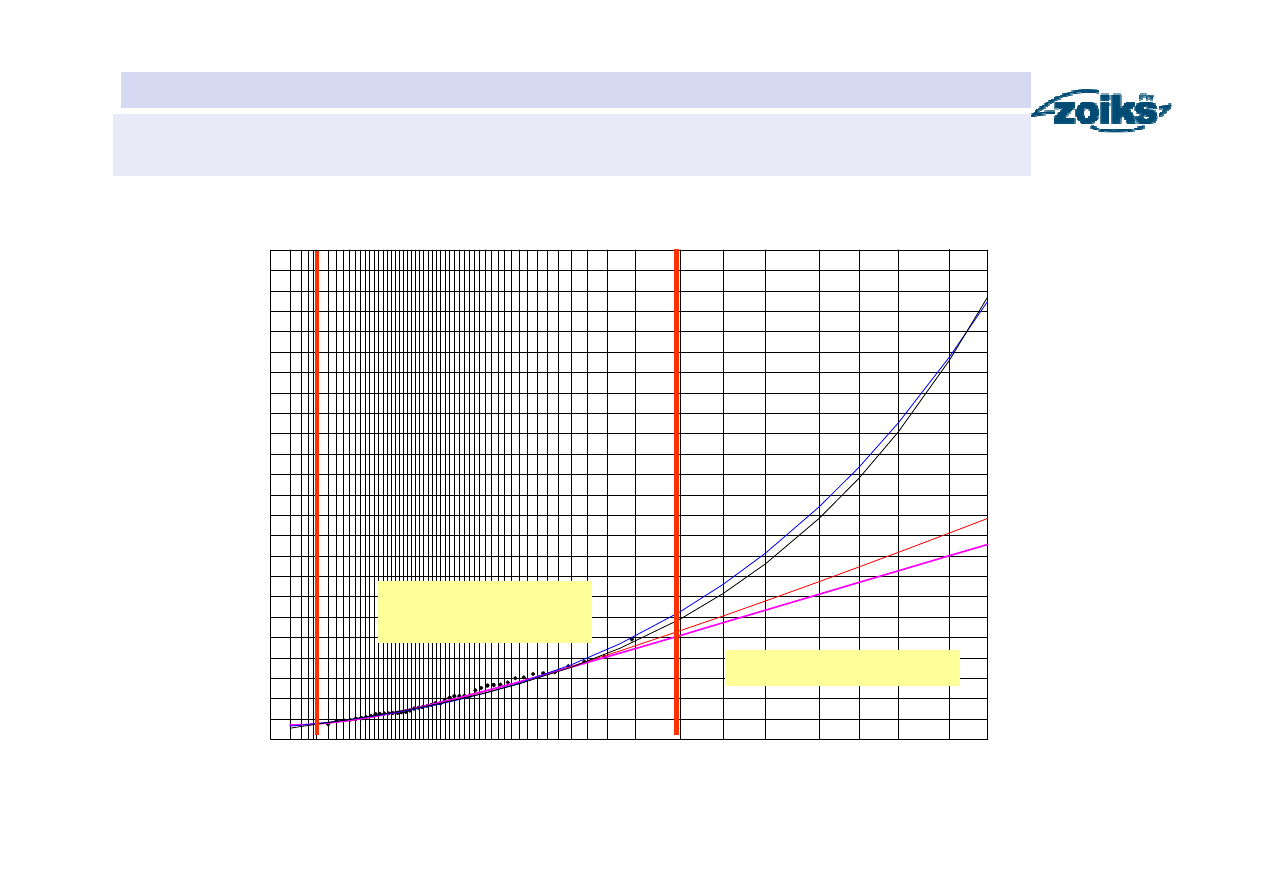
Funkcje prawdopodobieństwa przewyższenia przep
ł
ywów maksymalnych
rocznych pory zimowej w przekroju Sucha na Skawie
Zakres obserwacji
i interpolacji
Zakres ekstrapolacji
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Podziałka prawdopodobieństwa
0
100
200
300
400
500
600
100 99.9
98
90
80
70
60
50
40
30
20
10 8
6
4
2
1
0.5
0.2
0.1
0.05
0.01
0.02
p [%]
WE
GA
LN
LG
]
/
[m
3
max,
s
Q
p
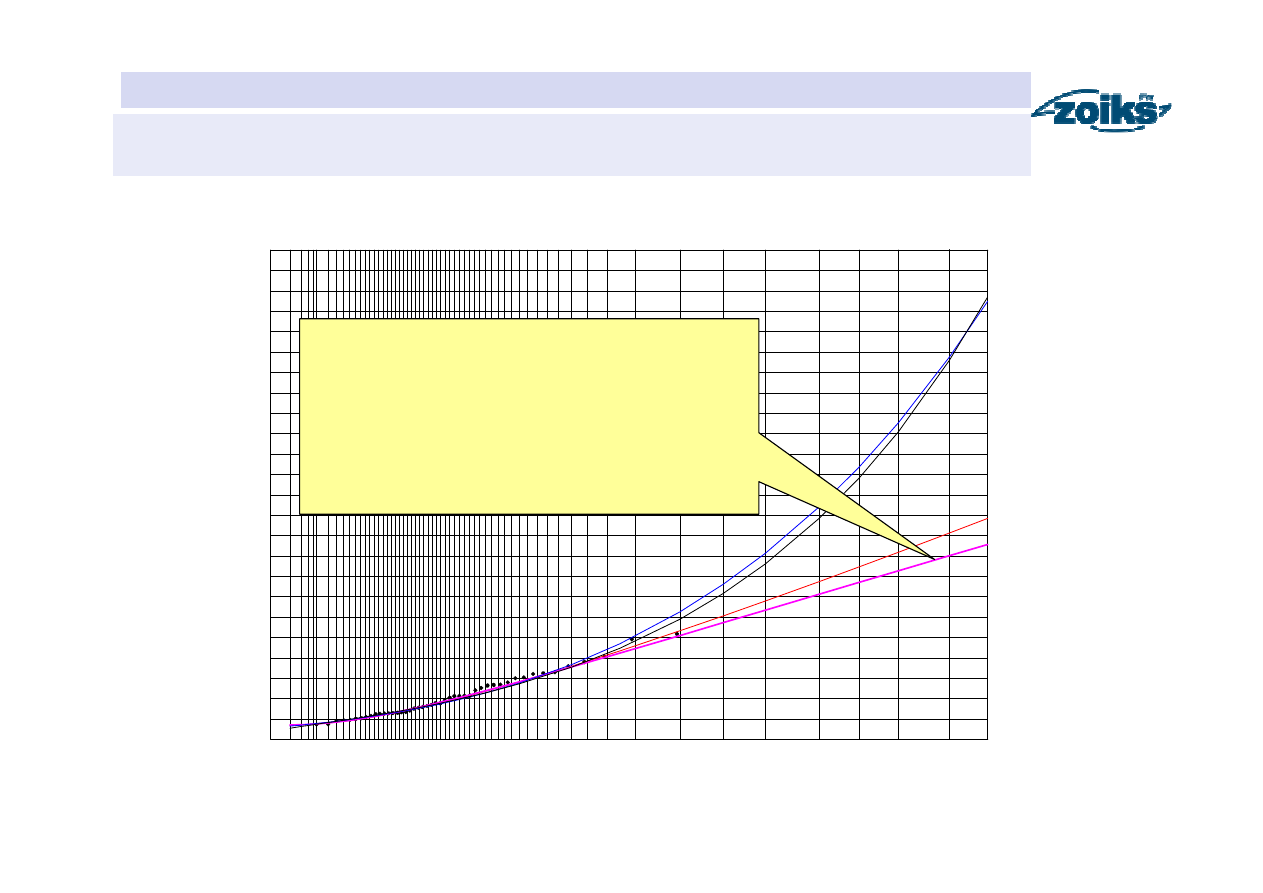
Funkcje prawdopodobieństwa przewyższenia przep
ł
ywów maksymalnych
rocznych pory zimowej w przekroju Sucha na Skawie
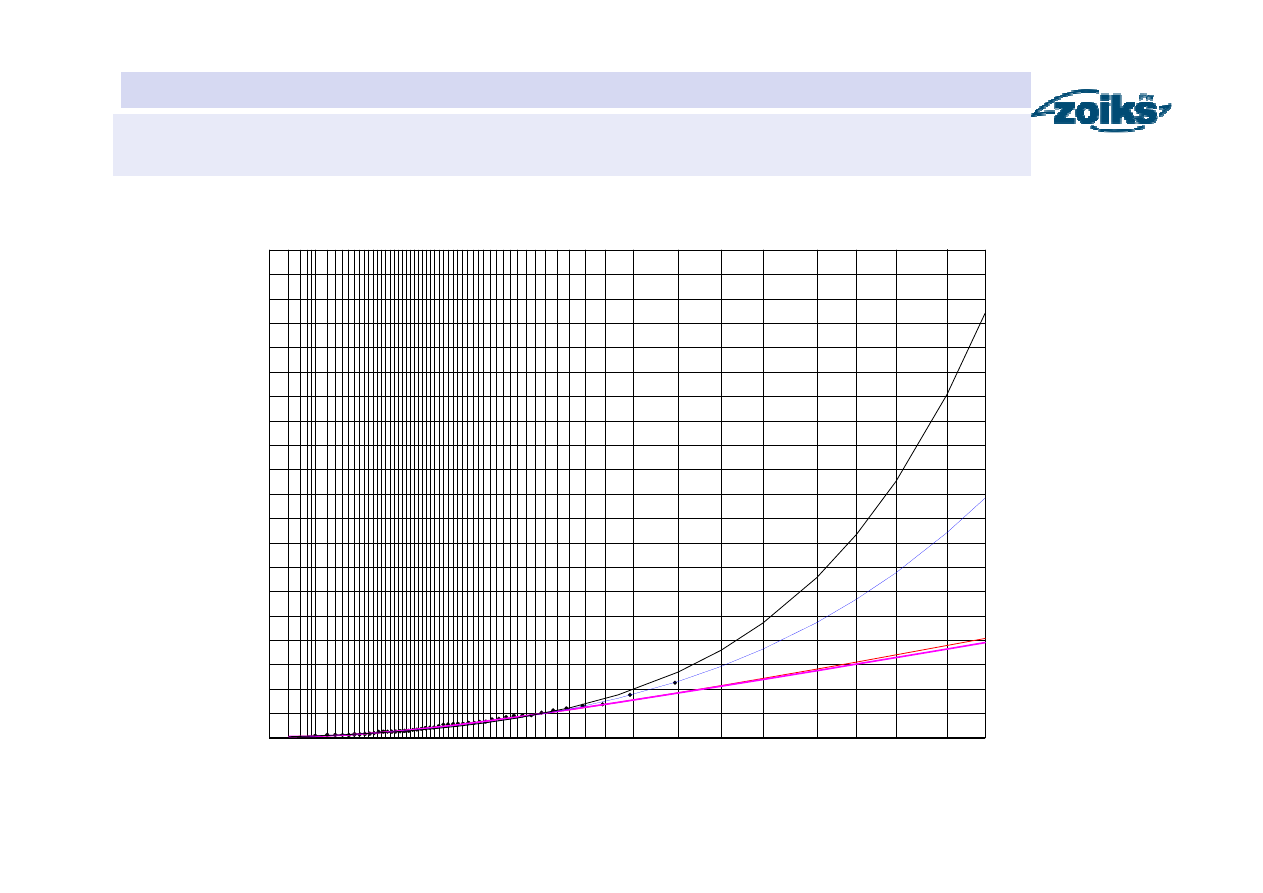
Najbardziej wiarygodna funkcja
prawdopodobieństwa przewyższenia
wybrana na podstawie trzech kryteriów:
1. Test zgodności χ
2
Pearsona
2. Minimalna odległość Kołmogorowa
3. Kryterium informacyjne Akaike
0
1000
2000
3000
4000
100 99.9
98
90
80
70
60
50
40
30
20
10 8
6
4
2
1
0.5
0.2
0.1
0.05
0.01
0.02
p [%]
WE
GA
LN
LG
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Podziałka prawdopodobieństwa
]
/
[m
3
max,
s
Q
p
Funkcje prawdopodobieństwa przewyższenia przep
ł
ywów maksymalnych
rocznych pory letniej w przekroju Sucha na Skawie
0
1000
2000
3000
4000
100 99.9
98
90
80
70
60
50
40
30
20
10 8
6
4
2
1
0.5
0.2
0.1
0.05
0.01
0.02
p [%]
WE
GA
LN
LG
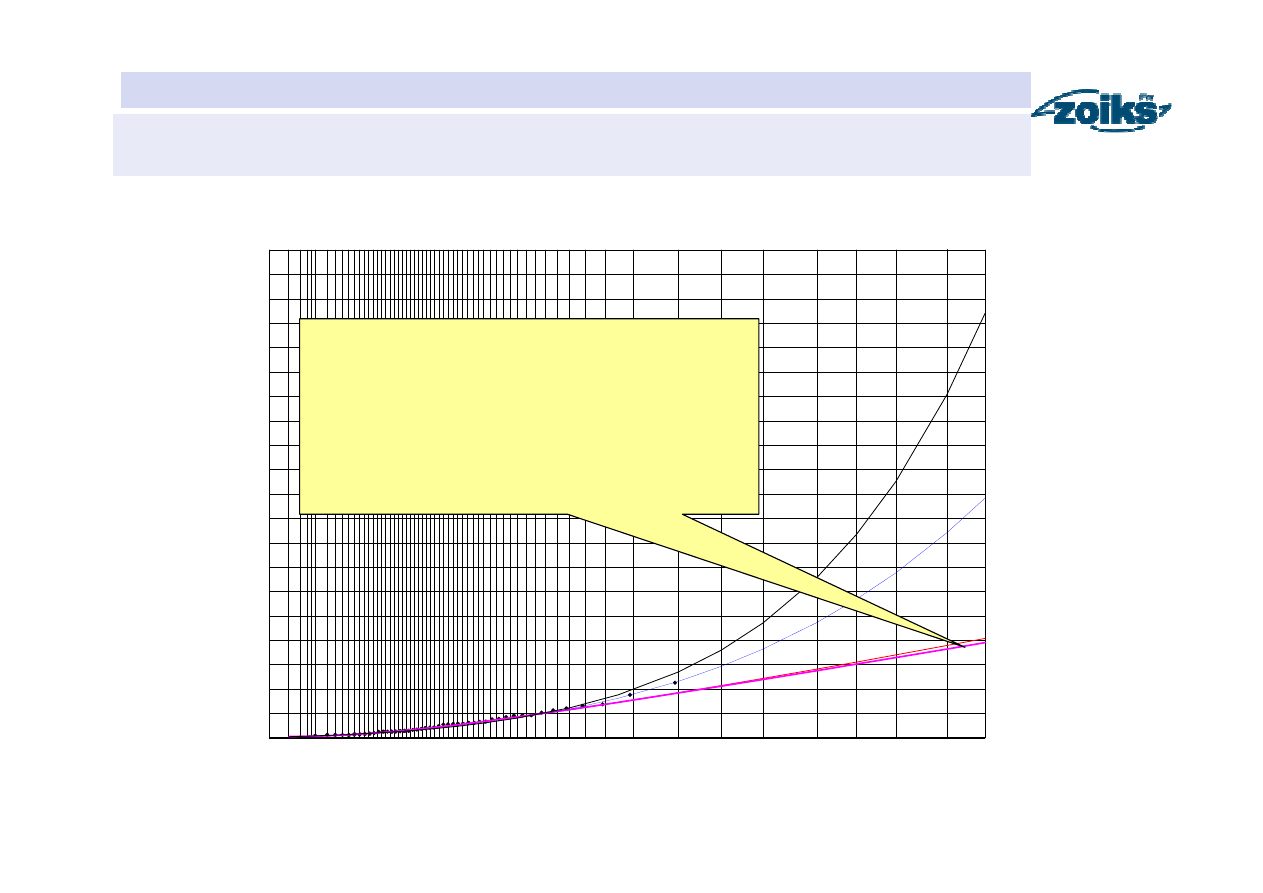
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Podziałka prawdopodobieństwa
]
/
[m
3
max,
s
Q
p
Funkcje prawdopodobieństwa przewyższenia przep
ł
ywów maksymalnych
rocznych pory letniej w przekroju Sucha na Skawie
Najbardziej wiarygodna funkcja
prawdopodobieństwa przewyższenia
wybrana na podstawie trzech kryteriów:
1. Test zgodności χ
2
Pearsona
2. Minimalna odległość Kołmogorowa
3. Kryterium informacyjne Akaike
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Przepływy miarodajne
Zasady projektowania i eksploatacji urządzeń wodnych w randze
Rozporządzeń Ministra zalecają stosowanie przep
ł
ywów miarodajnych Q
m
jako przep
ł
ywów maksymalnych rocznych Q
max,p
o określonym
prawdopodobieństwie przewyższenia p bez względu na ich genezę.
Rozporządzenie Ministra Środowiska
z dn. 20 kwietna 2007 r.
w sprawie warunków technicznych, jakim powinny odpowiadać budowle
hydrotechniczne i ich usytuowanie.
Dz.U. Nr 86 poz. 579, z 2007 r.
http://www.abc.com.pl/serwis/du/2007/0579.htm
Rozporządzenie Ministra Transportu i Gospodarki Morskiej
z dn. 30 maja 2000 r.
w sprawie warunków technicznych, jakim powinny odpowiadać drogowe obiekty
inżynierskie i ich usytuowanie.
Dz.U. Nr 63 poz. 735, z 2000 r.
http://www.abc.com.pl/serwis/du/2000/0735.htm
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Metoda obliczeń (wprowadzenie)
PROBLEM
Jak obliczyć funkcję prawdopodobieństwa przewyższenia przep
ł
ywów
maksymalnych rocznych p
R
(z) (bez względu na ich genezę) mając
określoną funkcję prawdopodobieństwa przewyższenia przep
ł
ywów
maksymalnych rocznych pory zimowej p
Z
(x) i funkcję
prawdopodobieństwa przewyższenia przep
ł
ywów maksymalnych
rocznych pory letniej p
L
(y)?
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Metoda obliczeń (wprowadzenie)
PROBLEM
Jak obliczyć funkcję prawdopodobieństwa przewyższenia przep
ł
ywów
maksymalnych rocznych p
R
(z) (bez względu na ich genezę) mając
określoną funkcję prawdopodobieństwa przewyższenia przep
ł
ywów
maksymalnych rocznych pory zimowej p
Z
(x) i funkcję
prawdopodobieństwa przewyższenia przep
ł
ywów maksymalnych
rocznych pory letniej p
L
(y)?
Aby to wyjaśnić skorzystamy z prostego przyk
ł
adu w odniesieniu do
zmiennej losowej typu dyskretnego.
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
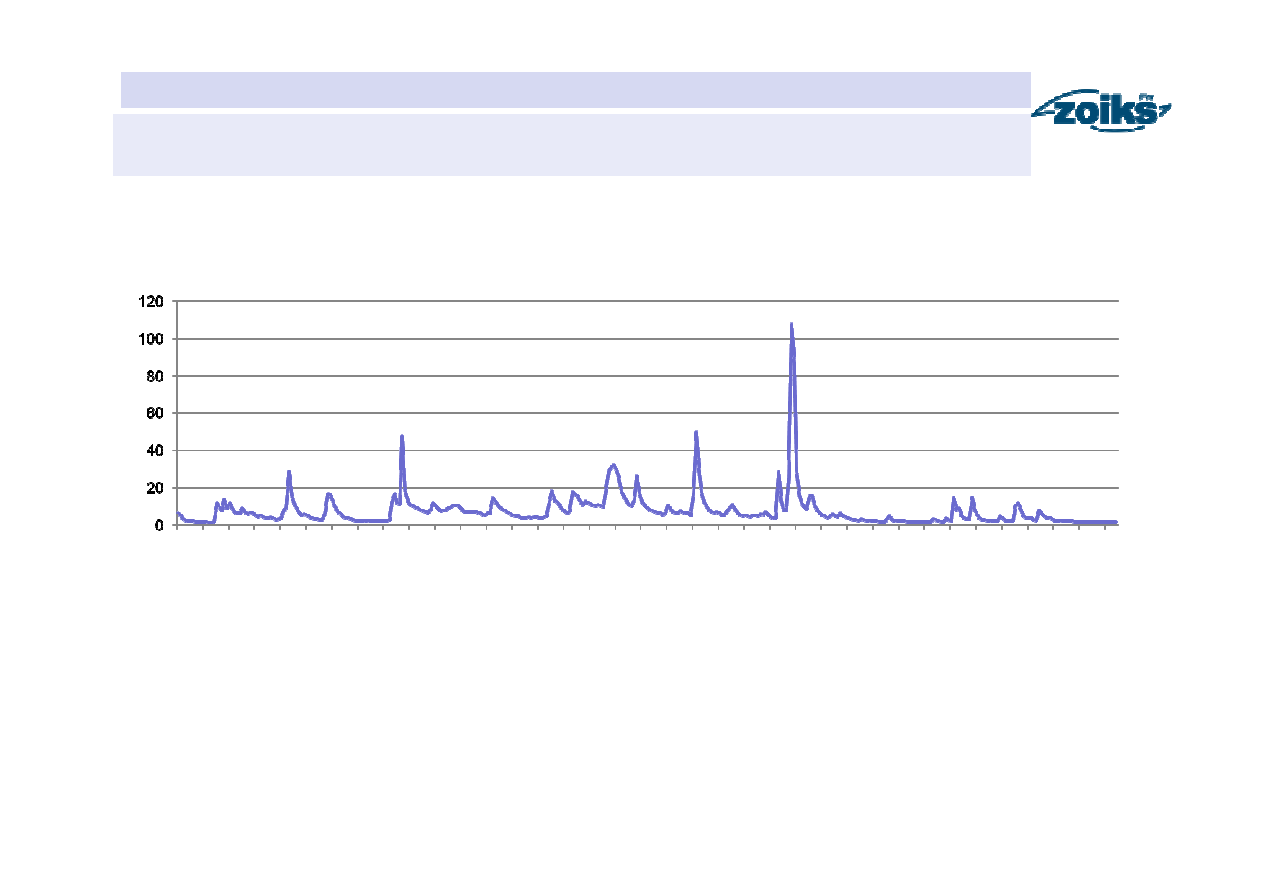
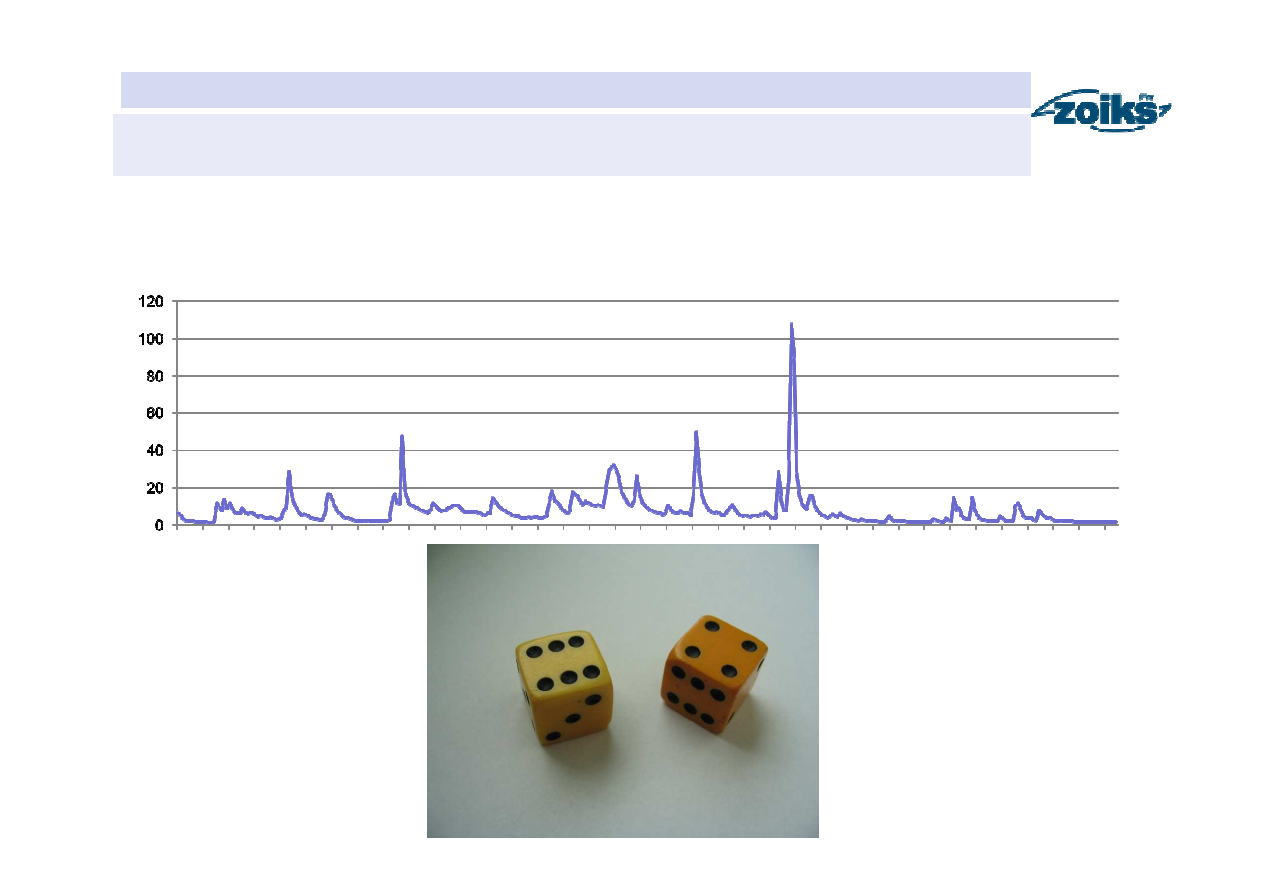
Metoda obliczeń (wprowadzenie)
Rzeka: Skawa Wodowskaz: Sucha Rok: 1995
Q [m
3
/s]
Q
max,Z
Q
max,L
Z
Q
x
max,
=
L
Q
y
max,
=
R
Q
z
max,
=
)
,
max(
y
x
z
=
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Metoda obliczeń (wprowadzenie)
Rzeka: Skawa Wodowskaz: Sucha Rok: 1995
Q [m
3
/s]
Q
max,Z
Q
max,L
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Rzut jedną kostką
Zbiór zdarze
ń
elementarnych
(1) (2) (3) (4) (5) (6)
6 1/6 1/6
5 1/6 2/6
4 1/6 3/6
3 1/6 4/6
2 1/6 5/6
1 1/6 6/6
)
(
P
k
X
=
)
(
P
k
X
≥
k
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Rzut dwiema kostkami
(1, 1) (2, 1) (3, 1) (4, 1) (5, 1) (6, 1)
(1, 2) (2, 2) (3, 2) (4, 2) (5, 2) (6, 2)
(1, 3) (2, 3) (3, 3) (4, 3) (5, 3) (6, 3)
(1, 4) (2, 4) (3, 4) (4, 4) (5, 4) (6, 4)
(1, 5) (2, 5) (3, 5) (4, 5) (5, 5) (6, 5)
(1, 6) (2, 6) (3, 6) (4, 6) (5, 6) (6, 6)
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Rzut dwiema kostkami (metoda alternatywy zdarzeń)
)
(
P
k
Z
=
)
(
P
k
Z
≥
k
(1, 1) (2, 1) (3, 1) (4, 1) (5, 1) (6, 1)
(1, 2) (2, 2) (3, 2) (4, 2) (5, 2) (6, 2)
(1, 3) (2, 3) (3, 3) (4, 3) (5, 3) (6, 3)
(1, 4) (2, 4) (3, 4) (4, 4) (5, 4) (6, 4)
(1, 5) (2, 5) (3, 5) (4, 5) (5, 5) (6, 5)
(1, 6) (2, 6) (3, 6) (4, 6) (5, 6) (6, 6)
6
5
4
3
2
1
)
,
max(
2
1
k
k
z
=
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Rzut dwiema kostkami (metoda alternatywy zdarzeń)
)
(
P
k
Z
=
)
(
P
k
Z
≥
k
(1, 1) (2, 1) (3, 1) (4, 1) (5, 1)
(6, 1)
(1, 2) (2, 2) (3, 2) (4, 2) (5, 2)
(6, 2)
(1, 3) (2, 3) (3, 3) (4, 3) (5, 3)
(6, 3)
(1, 4) (2, 4) (3, 4) (4, 4) (5, 4)
(6, 4)
(1, 5) (2, 5) (3, 5) (4, 5) (5, 5)
(6, 5)
(1, 6) (2, 6) (3, 6) (4, 6) (5, 6) (6, 6)
6 11/36 11/36
5
4
3
2
1
)
,
max(
2
1
k
k
z
=
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Rzut dwiema kostkami (metoda alternatywy zdarzeń)
)
(
P
k
X
=
)
(
P
k
X
≥
k
(1, 1) (2, 1) (3, 1) (4, 1)
(5, 1)
(6, 1)
(1, 2) (2, 2) (3, 2) (4, 2)
(5, 2)
(6, 2)
(1, 3) (2, 3) (3, 3) (4, 3)
(5, 3)
(6, 3)
(1, 4) (2, 4) (3, 4) (4, 4)
(5, 4)
(6, 4)
(1, 5) (2, 5) (3, 5) (4, 5) (5, 5)
(6, 5)
(1, 6) (2, 6) (3, 6) (4, 6) (5, 6) (6, 6)
6 11/36 11/36
5 9/36 20/36
4
3
2
1
)
,
max(
2
1
k
k
z
=
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Rzut dwiema kostkami (metoda alternatywy zdarzeń)
)
(
P
k
X
=
)
(
P
k
X
≥
k
(1, 1) (2, 1) (3, 1)
(4, 1)
(5, 1) (6, 1)
(1, 2) (2, 2) (3, 2)
(4, 2)
(5, 2) (6, 2)
(1, 3) (2, 3) (3, 3)
(4, 3)
(5, 3) (6, 3)
(1, 4) (2, 4) (3, 4) (4, 4)
(5, 4) (6, 4)
(1, 5) (2, 5) (3, 5) (4, 5) (5, 5) (6, 5)
(1, 6) (2, 6) (3, 6) (4, 6) (5, 6) (6, 6)
6 11/36 11/36
5 9/36 20/36
4 7/36 27/36
3
2
1
)
,
max(
2
1
k
k
z
=
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Rzut dwiema kostkami (metoda alternatywy zdarzeń)
)
(
P
k
X
=
)
(
P
k
X
≥
k
(1, 1) (2, 1)
(3, 1)
(4, 1) (5, 1) (6, 1)
(1, 2) (2, 2)
(3, 2)
(4, 2) (5, 2) (6, 2)
(1, 3) (2, 3) (3, 3)
(4, 3) (5, 3) (6, 3)
(1, 4) (2, 4) (3, 4) (4, 4) (5, 4) (6, 4)
(1, 5) (2, 5) (3, 5) (4, 5) (5, 5) (6, 5)
(1, 6) (2, 6) (3, 6) (4, 6) (5, 6) (6, 6)
6 11/36 11/36
5 9/36 20/36
4 7/36 27/36
3 5/36 32/36
2
1
)
,
max(
2
1
k
k
z
=
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Rzut dwiema kostkami (metoda alternatywy zdarzeń)
)
(
P
k
X
=
)
(
P
k
X
≥
k
(1, 1)
(2, 1)
(3, 1) (4, 1) (5, 1) (6, 1)
(1, 2) (2, 2)
(3, 2) (4, 2) (5, 2) (6, 2)
(1, 3) (2, 3) (3, 3) (4, 3) (5, 3) (6, 3)
(1, 4) (2, 4) (3, 4) (4, 4) (5, 4) (6, 4)
(1, 5) (2, 5) (3, 5) (4, 5) (5, 5) (6, 5)
(1, 6) (2, 6) (3, 6) (4, 6) (5, 6) (6, 6)
6 11/36 11/36
5 9/36 20/36
4 7/36 27/36
3 5/36 32/36
2 3/36 35/36
1
)
,
max(
2
1
k
k
z
=
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Rzut dwiema kostkami (metoda alternatywy zdarzeń)
)
(
P
k
X
=
)
(
P
k
X
≥
k
(1, 1)
(2, 1) (3, 1) (4, 1) (5, 1) (6, 1)
(1, 2) (2, 2) (3, 2) (4, 2) (5, 2) (6, 2)
(1, 3) (2, 3) (3, 3) (4, 3) (5, 3) (6, 3)
(1, 4) (2, 4) (3, 4) (4, 4) (5, 4) (6, 4)
(1, 5) (2, 5) (3, 5) (4, 5) (5, 5) (6, 5)
(1, 6) (2, 6) (3, 6) (4, 6) (5, 6) (6, 6)
6 11/36 11/36
5 9/36 20/36
4 7/36 27/36
3 5/36 32/36
2 3/36 35/36
1 1/36 36/36
)
,
max(
2
1
k
k
z
=
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Rzut dwiema kostkami (przykład dla k = 4)
(1, 1)
(2, 1)
(3, 1)
(4, 1)
(5, 1)
(6, 1)
(1, 2)
(2, 2)
(3, 2)
(4, 2)
(5, 2)
(6, 2)
(1, 3)
(2, 3)
(3, 3)
(4, 3)
(5, 3)
(6, 3)
(1, 4)
(2, 4)
(3, 4)
(4, 4)
(5, 4)
(6, 4)
(1, 5)
(2, 5)
(3, 5)
(4, 5)
(5, 5)
(6, 6)
(1, 6)
(2, 6)
(3, 6)
(4, 6)
(5, 6)
(6, 6)
36
/
18
)
4
(
1
=
p
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Rzut dwiema kostkami (przykład dla k = 4)
(1, 1)
(2, 1)
(3, 1)
(4, 1)
(5, 1)
(6, 1)
(1, 2)
(2, 2)
(3, 2)
(4, 2)
(5, 2)
(6, 2)
(1, 3)
(2, 3)
(3, 3)
(4, 3)
(5, 3)
(6, 3)
(1, 4)
(2, 4)
(3, 4)
(4, 4)
(5, 4)
(6, 4)
(1, 5)
(2, 5)
(3, 5)
(4, 5)
(5, 5)
(6, 6)
(1, 6)
(2, 6)
(3, 6)
(4, 6)
(5, 6)
(6, 6)
36
/
18
)
4
(
2
=
p
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Rzut dwiema kostkami (przykład dla k = 4)
(1, 1)
(2, 1)
(3, 1)
(4, 1)
(5, 1)
(6, 1)
(1, 2)
(2, 2)
(3, 2)
(4, 2)
(5, 2)
(6, 2)
(1, 3)
(2, 3)
(3, 3)
(4, 3)
(5, 3)
(6, 3)
(1, 4)
(2, 4)
(3, 4)
(4, 4)
(5, 4)
(6, 4)
(1, 5)
(2, 5)
(3, 5)
(4, 5)
(5, 5)
(6, 6)
(1, 6)
(2, 6)
(3, 6)
(4, 6)
(5, 6)
(6, 6)
1
36
/
18
36
/
18
)
4
(
)
4
(
2
1
=
+
=
+
p
p
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Rzut dwiema kostkami (przykład dla k = 4)
(1, 1)
(2, 1)
(3, 1)
(4, 1)
(5, 1)
(6, 1)
(1, 2)
(2, 2)
(3, 2)
(4, 2)
(5, 2)
(6, 2)
(1, 3)
(2, 3)
(3, 3)
(4, 3)
(5, 3)
(6, 3)
(1, 4)
(2, 4)
(3, 4)
(4, 4)
(5, 4)
(6, 4)
(1, 5)
(2, 5)
(3, 5)
(4, 5)
(5, 5)
(6, 6)
(1, 6)
(2, 6)
(3, 6)
(4, 6)
(5, 6)
(6, 6)
1
)
4
(
)
4
(
2
1
=
+
p
p
Obszar podwojonego
prawdopodobieństwa
koniunkcji zdarzeń
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Rzut dwiema kostkami (przykład dla k = 4)
(1, 1)
(2, 1)
(3, 1)
(4, 1)
(5, 1)
(6, 1)
(1, 2)
(2, 2)
(3, 2)
(4, 2)
(5, 2)
(6, 2)
(1, 3)
(2, 3)
(3, 3)
(4, 3)
(5, 3)
(6, 3)
(1, 4)
(2, 4)
(3, 4)
(4, 4)
(5, 4)
(6, 4)
(1, 5)
(2, 5)
(3, 5)
(4, 5)
(5, 5)
(6, 6)
(1, 6)
(2, 6)
(3, 6)
(4, 6)
(5, 6)
(6, 6)
36
/
27
36
/
9
36
/
18
36
/
18
)
4
Pr(
=
−
+
=
≥
k
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Rzut dwiema kostkami (metoda alternatywy zdarzeń)
)
(
P
k
X
=
)
(
P
k
Z
≥
k
(1, 1) (2, 1) (3, 1) (4, 1) (5, 1) (6, 1)
(1, 2) (2, 2) (3, 2) (4, 2) (5, 2) (6, 2)
(1, 3) (2, 3) (3, 3) (4, 3) (5, 3) (6, 3)
(1, 4) (2, 4) (3, 4) (4, 4) (5, 4) (6, 4)
(1, 5) (2, 5) (3, 5) (4, 5) (5, 5) (6, 5)
(1, 6) (2, 6) (3, 6) (4, 6) (5, 6) (6, 6)
6 11/36 11/36
5 9/36 20/36
4 7/36 27/36
3 5/36 32/36
2 3/36 35/36
1 1/36 36/36
)
,
max(
2
1
k
k
z
=
Sprawdź wynik!
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Rzut dwiema kostkami (uogólnienie)
(1, 1)
(2, 1)
(3, 1)
(4, 1)
(5, 1)
(6, 1)
(1, 2)
(2, 2)
(3, 2)
(4, 2)
(5, 2)
(6, 2)
(1, 3)
(2, 3)
(3, 3)
(4, 3)
(5, 3)
(6, 3)
(1, 4)
(2, 4)
(3, 4)
(4, 4)
(5, 4)
(6, 4)
(1, 5)
(2, 5)
(3, 5)
(4, 5)
(5, 5)
(6, 6)
(1, 6)
(2, 6)
(3, 6)
(4, 6)
(5, 6)
(6, 6)
)
4
(
)
4
(
)
4
(
)
4
(
)
4
(
2
1
2
1
p
p
p
p
p
−
+
=
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
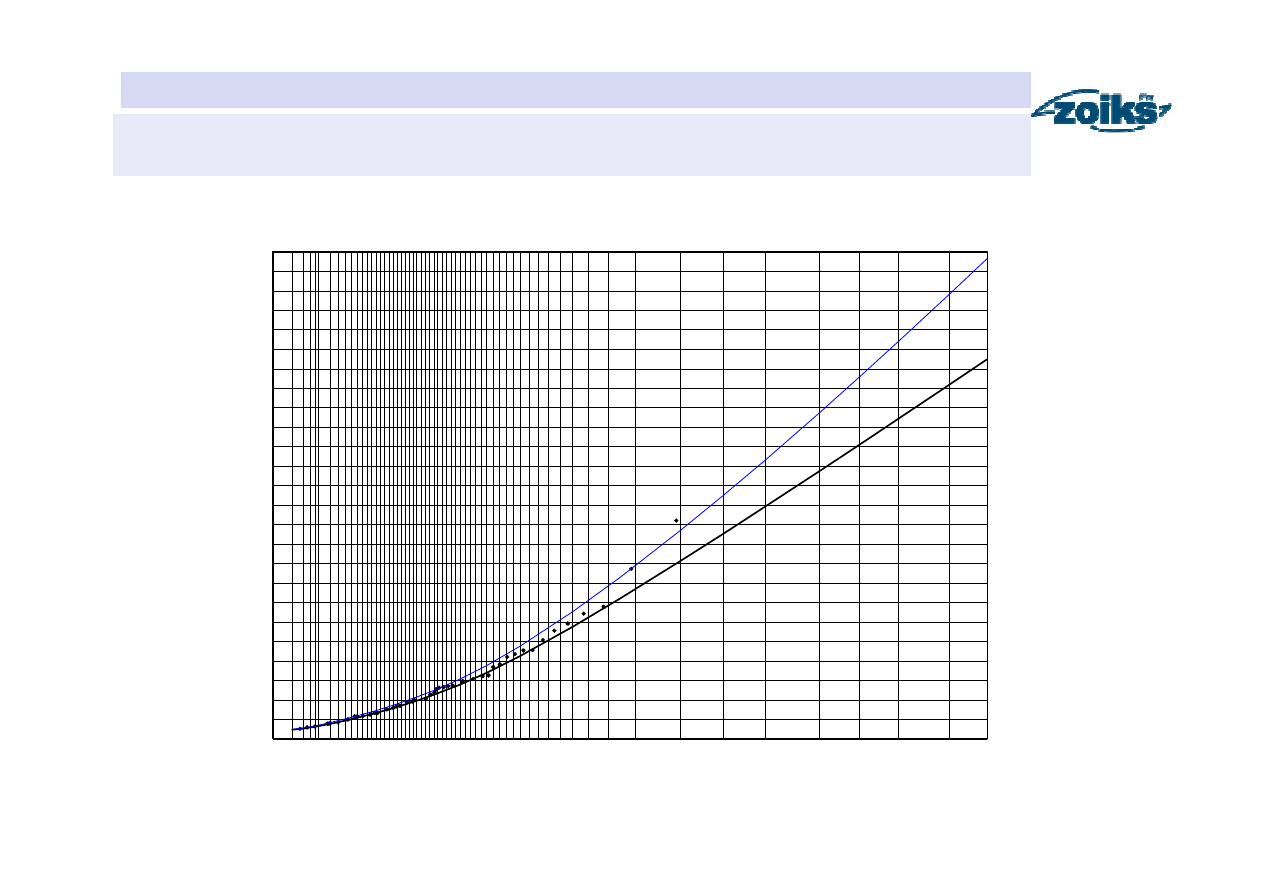
Prawdopodobieństwo przewyższenia przepływów maksymalnych rocznych
bez względu na ich genezę (metoda alternatywy zdarzeń)
Wniosek:
p
R
(z) = p
Z
(z)+p
L
(z)-p
Z
(z)p
L
(z)
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
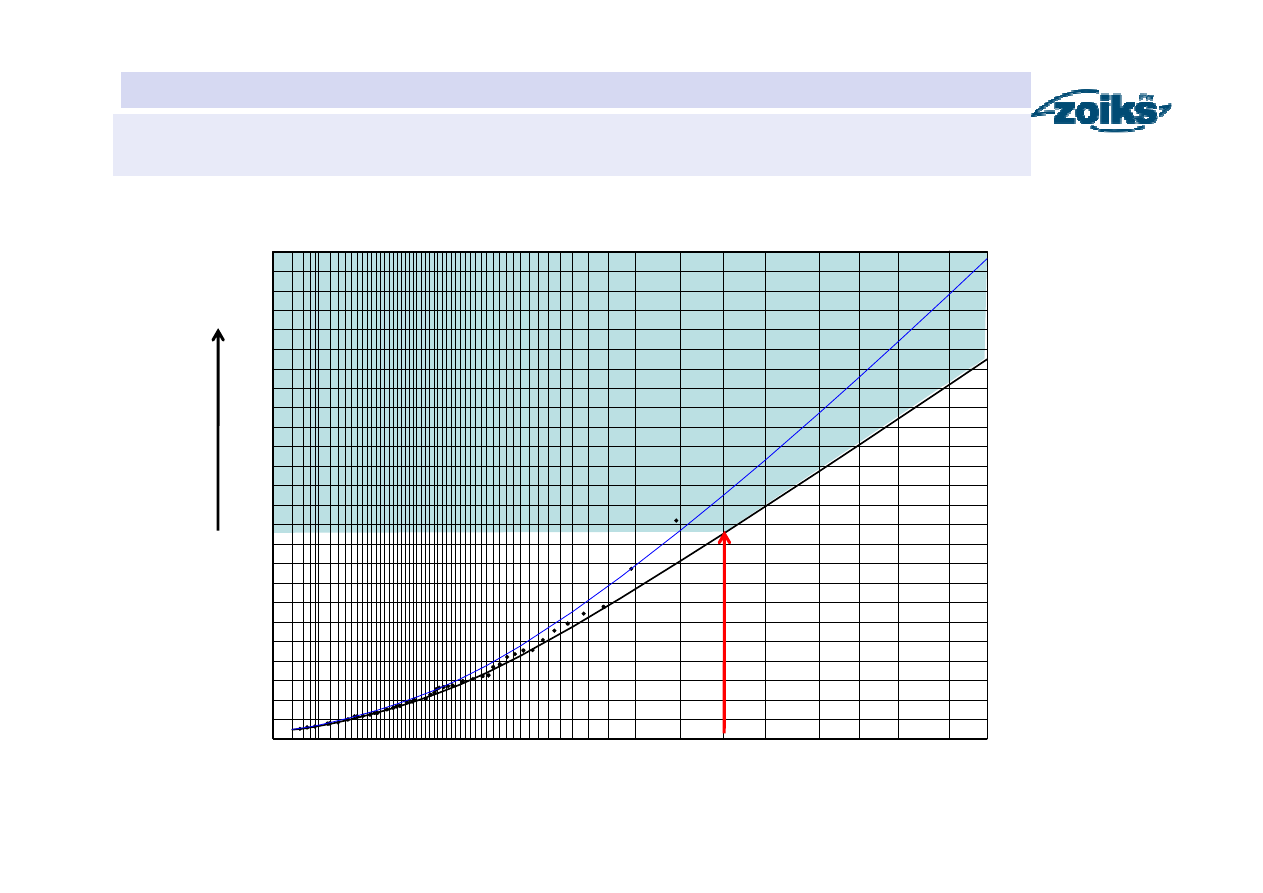
Wyniki obliczeń
0
200
400
600
800
1000
100 99.9
98
90
80
70 60
50
40
30
20
10 8
6
4
2
1
0.5
0.2
0.1
0.05
0.01
0.02
p [%]
WE-WE
P
α
= 84%
Metoda alternatywy zdarzeń. Przekrój Sucha na Skawie.
]
/
[m
3
max,
s
Q
p
0
200
400
600
800
1000
100 99.9
98
90
80
70 60
50
40
30
20
10 8
6
4
2
1
0.5
0.2
0.1
0.05
0.01
0.02
p [%]
WE-WE
P
α
= 84%
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Interpretacja wyników obliczeń
Metoda alternatywy zdarzeń. Przekrój Sucha na Skawie.
]
/
[m
3
max,
s
Q
p
%
1
max,
Q
∞
+
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Średni okres powtarzalności zdarzenia
- potocznie „woda stuletnia”
%
1
max,
Q
Prawdopodobieństwo zdarzenia polegającego na osiągnięciu lub przekroczeniu
wartości wynosi p = 0.01
Zgodnie z częstotliwościową interpretacją prawdopodobieństwa, zdarzenie to
zachodzi jeden raz na sto zaobserwowanych zdarzeń przepływów maksymalnych
rocznych, a więc jeden raz na sto lat obserwacji
Średni okres powtarzalności zdarzenia wynosi więc
%
1
max,
Q
[lata]
1
p
T
=
Jest to średni (przeciętny), a nie dokładny okres powtarzalności zdarzenia
Przepływy maksymalne roczne o określonym prawdopodobieństwie
przewyższenia
HYDROLOGIA
Średni okres powtarzalności zdarzenia – niektóre możliwe przypadki
%
1
max,
Q
100 lat
100 lat
100 lat
%
1
max,
Q
100 lat
100 lat
100 lat
%
1
max,
Q
100 lat
100 lat
100 lat
ĆWICZENIA AUDYTORYJNE:
8
TEMAT :
Przepływy konwencjonalne – wybrane przykłady.
Przepływy konwencjonalne – wybrane przykłady
HYDROLOGIA
Przepływy konwencjonalne
Przepływy konwencjonalne są ustalane na różne potrzeby związane
z wykorzystaniem i ochroną zasobów wodnych bądź ograniczeniem
szkodliwego działania wód.
Nazwa, definicja, symbol oznaczenia oraz metoda wyznaczania
każdego z tych przepływów są przedmiotem konwencji (umowy).
Lista przepływów konwencjonalnych jest całkowicie otwarta.
Przepływy konwencjonalne – wybrane przykłady
HYDROLOGIA
Przepływ dozwolony
Przykład nazwy, definicji i przyjętego symbolu oznaczenia:
Rozporządzenie Ministra Środowiska
z dn. 17 sierpnia 2006 r.
w sprawie zakresu instrukcji gospodarowania wodą.
Dz.U. Nr 150 poz. 1087, z 2006 r.
http://www.abc.com.pl/serwis/du/2006/1087.htm
§ 1. Ilekroć w rozporządzeniu jest mowa o:
17) przepływie dozwolonym - rozumie się przez to przepływ poniżej
budowli piętrzącej, który nie powoduje szkód powodziowych na
terenach poniżej tej budowli;
§ 2. W instrukcji należy posługiwać się następującymi oznaczeniami:
9)
dla przepływu dozwolonego - Q
doz
;
Przepływy konwencjonalne – wybrane przykłady
HYDROLOGIA
Przepływ dozwolony
Wartość przepływu dozwolonego - w przypadku terenów
zagospodarowanych o bogatej infrastrukturze - ustala się w
zależności od warunków lokalnych za pomocą modelowania
matematycznego obszarów zalewu przy różnych wartościach
natężenia przepływu poniżej urządzenia wodnego.
Wartość przepływu dozwolonego - w przypadku terenów
niezagospodarowanych, pozbawionych infrastruktury - ustala się w
przybliżony sposób jako:
lub
Obszar zatapiany przy takiej wartości natężenia przepływu określa
się jako strefę stałego zagrożenia powodziowego.
SWQ
Q
=
doz
%
50
max,
doz
Q
Q
=
Przepływy konwencjonalne – wybrane przykłady
HYDROLOGIA
Przepływ nienaruszalny
Przykład rozszerzonej definicji:
Encyklopedia Ramowej Dyrektywy Wodnej.
http://www.rdw.org.pl/
Przepływ nienaruszalny - jest to umowny (w danym przekroju cieku i dla
danego okresu roku) właściwy dla założonego ekologicznego stanu cieku,
przepływ, którego wielkość i jakość, ze względu na zachowanie tego
stanu, nie mogą być, a ze względu na instytucję powszechnego
korzystania z wód, nie powinny być, z wyjątkiem okresów zagrożeń
nadzwyczajnych, obniżane poprzez działalność człowieka. Dla części
przepływu nienaruszalnego związanej z koniecznością zachowania
założonego ekologicznego stanu cieku przyjęto nazwę przepływ
nienaruszalny hydrobiologiczny (przepływ hydrobiologiczny).
Przepływy konwencjonalne – wybrane przykłady
HYDROLOGIA
Przepływ nienaruszalny
Przykład unormowania sposobu wyznaczania wartości:
Rozporządzenie Ministra Środowiska
z dnia 28 kwietnia 2004 r.
w sprawie zakresu i trybu opracowania planów gospodarowania wodami na obszarach
dorzeczy oraz warunków korzystania z wód regionu wodnego.
Dz. U. Nr 126 poz. 1318
2.5. Hydrograficzne charakterystyki obszaru dorzecza
9. Wielkością przepływu wód zabezpieczającą założony stan ekologiczny
cieku regionu wodnego jest przepływ nienaruszalny. Wielkość tego
przepływu jest wyznaczana wg metody Kostrzewy, z uwzględnieniem
kryterium hydrobiologicznego i rybacko-wędkarskiego (przeżywalności
ryb), lub wg metody małopolskiej. Wielkości przepływów
nienaruszalnych są określane na podstawie wielkości przepływów wody.
Przepływy konwencjonalne – wybrane przykłady
HYDROLOGIA
Przepływ nienaruszalny metoda Kostrzewy
Kostrzewa H., 1977. Weryfikacja kryteriów i wielkości przepływu nienaruszalnego dla
rzek Polski. Materiały Badawcze IMGW, Warszawa
Podstawowymi kryteriami określania przepływu nienaruszalnego, któremu
jakościowo odpowiadają wody pierwszej i drugiej klasy czystości są:
• przesłanki hydrobiologiczne warunkujące zachowanie
podstawowych form flory i fauny, charakterystycznych dla
środowiska wodnego rzek Q
nh
,
• wymagania rybacko wędkarskie (kryterium przeżywalności ryb) Q
nr
,
• ochrona obiektów przyrodniczych o charakterze parków
narodowych i rezerwatów oraz zachowanie piękna krajobrazu Q
nop
,
• wymagania rzecznej turystyki wodnej Q
nt
.
Najistotniejsze znaczenie dla większości rzek w Polsce mają dwa pierwsze
kryteria.
Przepływy konwencjonalne – wybrane przykłady
HYDROLOGIA
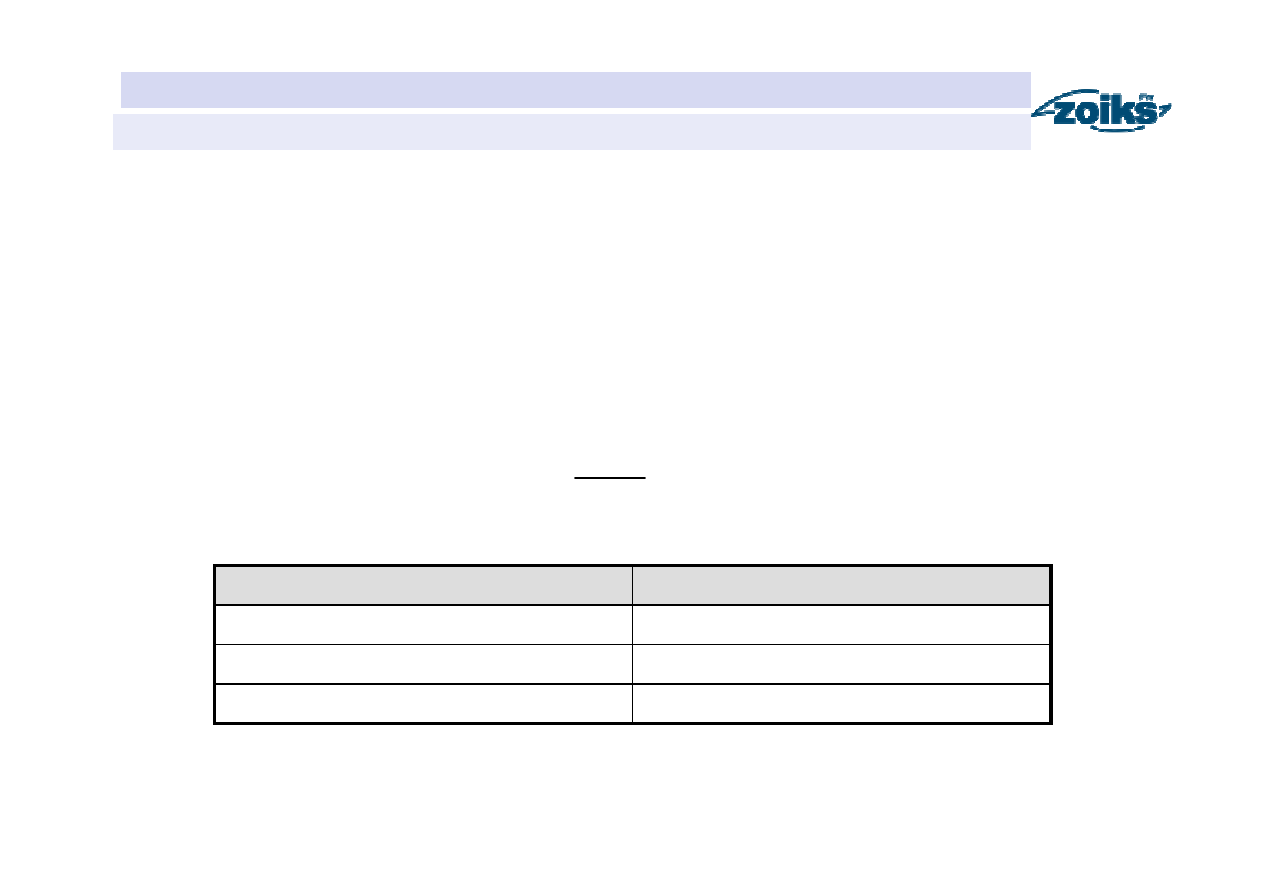
Przepływ nienaruszalny hydrobiologiczny
(uproszczona metoda Kostrzewy – parametryczna)
Ustalenie typu hydrologicznego rzeki na podstawie wartości średniego
spływu jednostkowego
]
km
[ls
1000
2
-
1
-
A
SSQ
q
SSQ
=
G - górski
q
SSQ
≥ 13.15
Pr,Pg – przejściowy i podgórski
4.15 ≤ q
SSQ
< 13.15
N - nizinny
q
SSQ
< 4.15
Typ hydrologiczny rzeki
Średni spływ jednostkowy
Przepływy konwencjonalne – wybrane przykłady
HYDROLOGIA
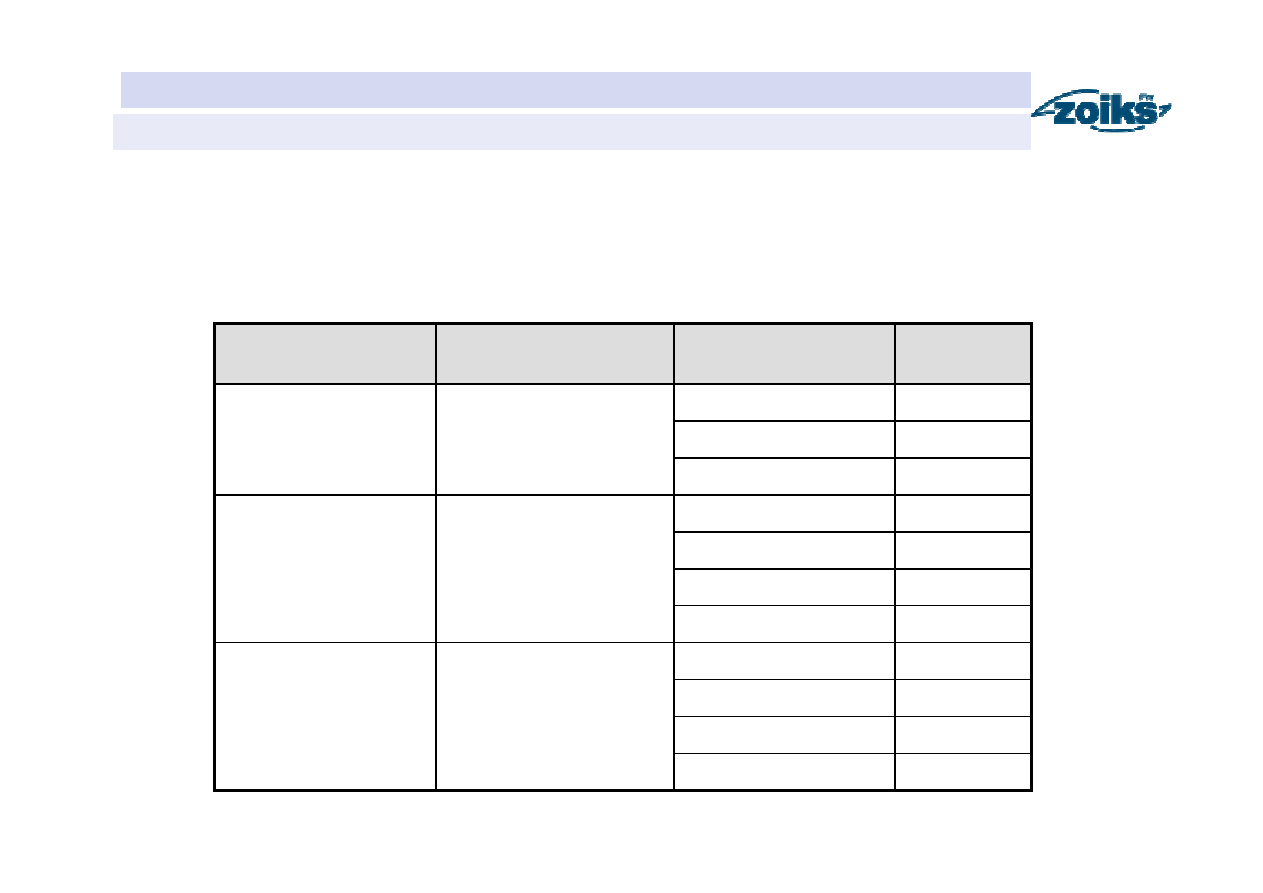
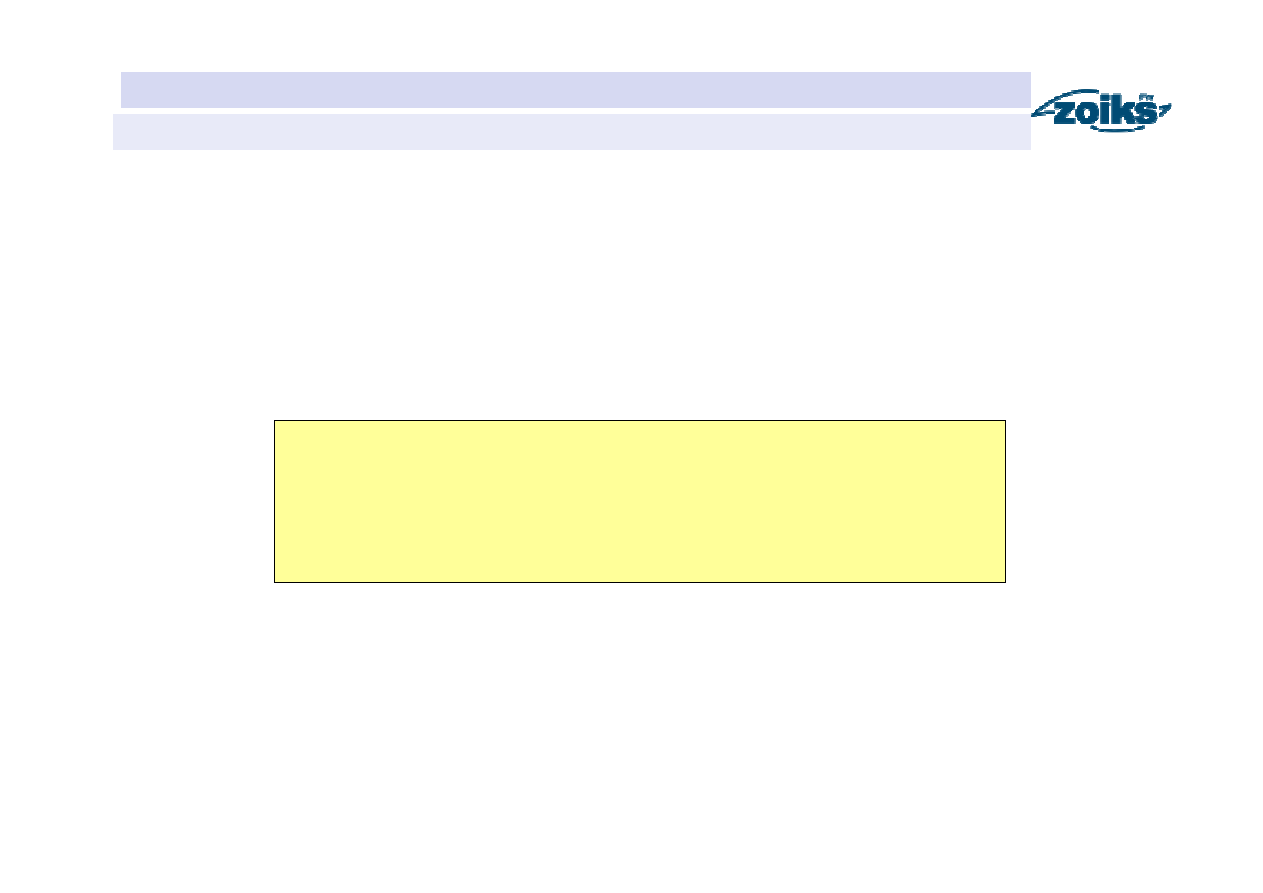
Przepływ nienaruszalny hydrobiologiczny
(uproszczona metoda Kostrzewy – parametryczna)
Wyznaczanie wartości parametru k
0.5
A ≥ 2500
0.55
1500 ≤ A < 2500
0.76
750 ≤ A < 1500
1.17
300 ≤ A < 750
0.30
G
0.50
A ≥ 2500
0.52
1500 ≤ A < 2500
0.77
500 ≤ A < 1500
1.27
A < 500
0.25
Pr,Pg
0.50
A ≥ 2500
0.58
1000 ≤ A < 2500
1.00
A < 1000
0.2
N
Parametr
k
Powierzchnia
zlewni A [km
2
]
Prędkość
miarodajna [ms
-1
]
Typ hydrologiczny
rzeki
Przepływy konwencjonalne – wybrane przykłady
HYDROLOGIA
Przepływ nienaruszalny hydrobiologiczny
(uproszczona metoda Kostrzewy – parametryczna)
≤
>
=
NNQ
kSNQ
NNQ
NNQ
kSNQ
kSNQ
Q
nh
gdy
gdy
Przepływy konwencjonalne – wybrane przykłady
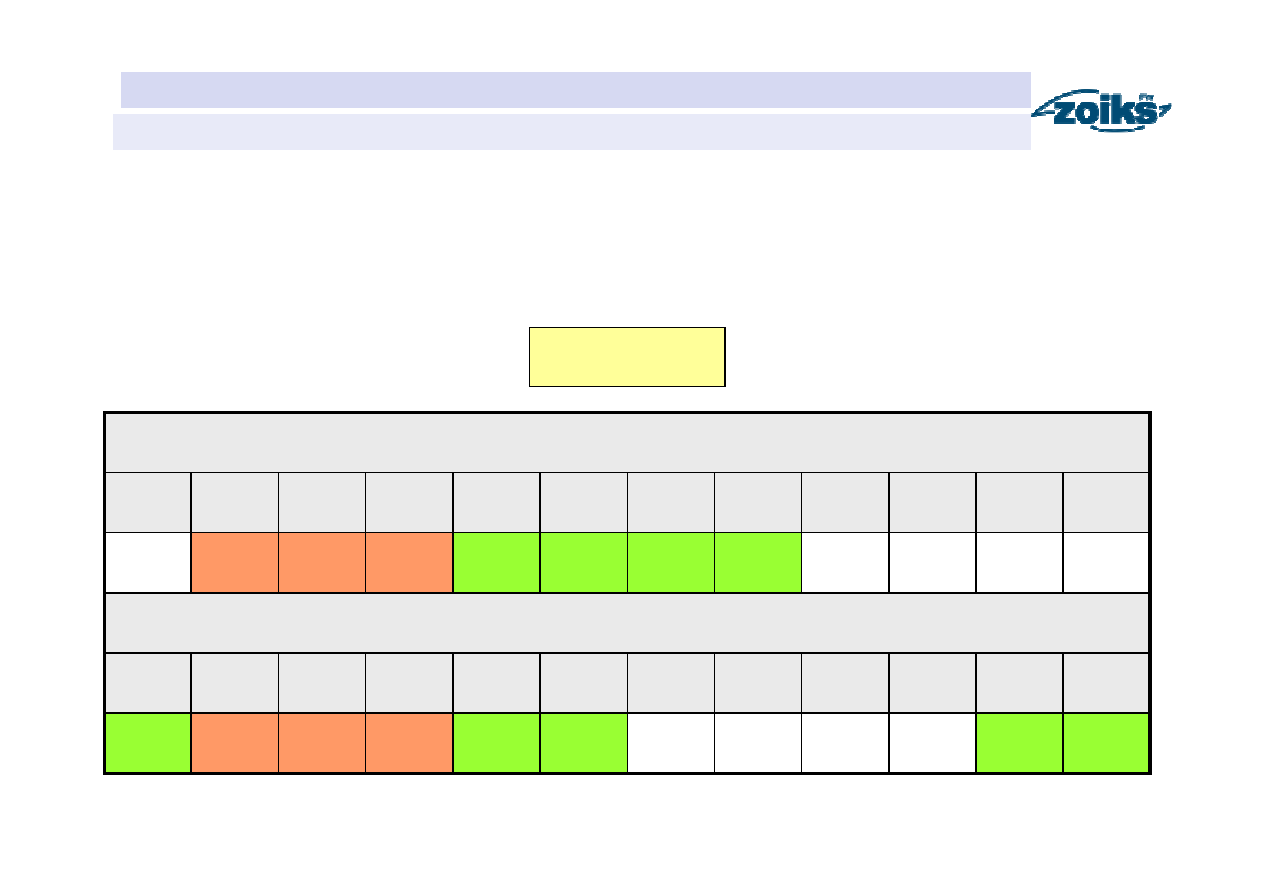
HYDROLOGIA
Przepływ nienaruszalny Q
nr
(kryterium rybacko-wędkarskie w metodzie Kostrzewy)
Rzeki ryb łososiowatych
• Faza wędrówek tarłowych i rozrodu Q
nr
= SNQ
III-IV
, Q
nr
= SNQ
IX-XI
• Faza wzrostu Q
nr
= SNQ
V-VIII
• Faza przezimowania Q
nr
= SNQ
XII-II
Rzeki ryb nizinnych
• Faza wędrówek tarłowych i rozrodu Q
nr
= SNQ
III-VI
• Faza wzrostu Q
nr
= SNQ
VII-XI
• Faza przezimowania Q
nr
= SNQ
XII-II
Przepływy konwencjonalne – wybrane przykłady
HYDROLOGIA
Przepływ nienaruszalny
(metoda Kostrzewy)
Przykład dla wodowskazu Sól na Sole (typ hydrologiczny górski, A = 54.2 km
2
)
0.123
0.123
0.122
0.122
0.122
0.122
0.359
0.359
0.040
0.040
0.040
0.123
X
IX
VIII
VII
VI
V
IV
III
II
I
XII
XI
Q
nr
dla ryb łososiowatych
0.122
0.122
0.122
0.122
0.148
0.148
0.148
0.148
0.040
0.040
0.040
0.122
X
IX
VIII
VII
VI
V
IV
III
II
I
XII
XI
Q
nr
dla ryb nizinnych
Q
nh
= 0.122
SSQ
1974-93
= 1.02 m
3
/s SNQ
1974-93
= 0.076 m
3
/s NNQ
1974-93
= 0.030 m
3
/s
DZIĘKUJĘ ZA UWAGĘ