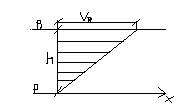
15 płyny ruchome
∂ V
∂ V
v=c≠e
=
y
x
= 0 ruch ustalony
∂ t
∂ t
x – składowa pozioma jedn. sił masowych y = -y - składowa pionowa sił masowych
∂ P = 0 z zało
∂
żenia ruchu
x
2
2
V
∂
V
∂
V
∂
∂
µ ∂
∂
y
1 p
Vy
V
1.
x
x
+
V +
V = x
x
−
+
+
x
y
2
2
t
∂
x
∂
y
∂
ρ t
∂
ρ
x
∂
y
∂
2
2
V
∂
V
∂
V
∂
∂
µ ∂
∂
y
y
y
1 p
Vy
V
2.
+
V +
V = − y
x
−
+
+
x
y
2
2
t
∂
y
∂
∂
ρ t
∂
ρ
x
∂
y
∂
2
µ ∂ V
3.
a
x
=
2
ρ y
∂
2
2
Całkujemy wobec tego
∂
µ/ ρ≠0 oraz V
d V
x
x
=
dla y=0→Vx=0 ; y=h→Vx=VB
2
2
y
∂
dy
x − y V
µ VB
∂
0 =
p
lub
= υ
−
− ρ 1 ∂ p
∂
−
x
ρ ∂ y
p=xy+c dla y=h p0=-υh+c → c=p0+υh, ostatecznie : p=υ(h-y+p0) dla y=0 ; pB=υh+p0