Temat

a 2

Gen

e e

n ra

r l

a iza

z cj

c a

Hanna Ligarska

Gr 3 nr 17

SP

S R

P A

R WO

W Z

O D

Z A

D NI

N E

E TE

T C

E H

C N

H I

N CZ

C N

Z E

N

1. Dane formalno-prawne:

1.1 Zleceniodawca: Wydział Geodezji Górniczej i Inżynieri Środowiska Akademi Górniczo-Hutniczej w Krakowie.

1.2 Wykonawca: Hanna Ligarska

1.3 Okres wykonywania zlecenia:

- termin rozpoczęcia prac: 15.11.2013r.

-termin zakończenia prac: 7.12.2013r.

1.4 Przedmiot zlecenia: Generalizacja

2. Opracowanie wyników:

2.1 Generalizacja, która była celem tego tematu w programie MicroStation jest możliwa za pomocą nakładki „genm”, która działa na podstawie „Metody Chrobaka”. Metoda ta polega na upraszczaniu lini w zależności od skali mapy. Program zachowuję umiejscowienie wierzchołków figury, lecz na postawie tzw. ekstremów lokalnych za pomocą sąsiednich wierzchołków, pierwszymi dwoma stają się najważniejsze wierzchołki w danej łamanej.

Następnie na ich podstawie tworzone są trójkąty, mające za podstawę odcinek między wierzchołkami, a trzecim wierzchołkiem staje się punkt, który spełnia następujące warunki: 1) Długości boków są co najmniej równe długości podstawy 2) Posiada największą wysokość z możliwych długości w badanym przedziale W ten sposób budujemy pary odcinków dla generalizowanego obiektu. Najkrótszą długość boku możemy obliczyć ze wzoru ε=sM gdzie s-miara progowa rozpoznawalności a M –

j

j

j

mianownik skali mapy opracowywanej. Dzięki ε wiadome jest jak uprościć obiekt. Gdy suma j

boków jest mniejsza od dwukrotnej wartości ε to po uproszczeniu łańcuch punktów j

zastępuje cięciwa, w innym przypadku można utworzyć nowy punkt. Położenie nowego punktu jest zależne od przyrostów współrzędnych (zbieżny lub rozbieżny). Ostatecznie można wykonać ocenę dokładności generalizacji, którą wykonujemy dzięki jednoznacznemu wyborowi i usuwaniu wierzchołków a także jeśli kształt lini przed generalizacją nie jest zbyt daleki od rzeczywistości, każde uproszczenie zostało opisane, są określone najkrótsze odległości pomiędzy odrzucanymi punktami a pozostającymi wierzchołkami lini pierwotnej, które są jednocześnie pozornymi błędami. Do wykonania analizy dokładności wykorzystuje się prawo przenoszenia się błędów i jeden stopień swobody dla odrzucanych wierzchołków.

2.2 W temacie 2 zadanie polegało na wykonaniu kilkukrotnej generalizacji w programie Microstation. W tym celu w wymienionym programie zostało utworzonych 8 obiektów smartline zamieszczonych poniżej. Obiekty te posiadają wspólne wierzchołki i w ogólnym kształcie przypominają „latawiec”. Każdy z odcinków zawiera ok. 50 punktów załamań, dzięki którym możliwa była generalizacja. Skalą wyjściową jest skala 1:500. Prawie wszystkie wydruki kolejnych etapów zostały wykonane w odpowiadającej im skali, poza dwoma

ostatnimi. Ponieważ skala była na tyle mała, że nie był możliwy wydruk w odpowiadającej jej skali. W związku z tym zamieszczono wyniki tej generalizacji w skali wyjściowej, czyli 1:500. Generalizacja była wykonywana w kolejnych, co raz mniejszych skalach, dążąc do otrzymania 8 odcinków prostych o wspólnych wierzchołkach oraz 16 punktów (każdy odcinek posiada 2 punkty końcowe). Następnie na podstawie wyników opracowano wykres w programie AutoCad, który przedstawia procent pozostałych punktów po generalizacji.

2.3 Wnioski:

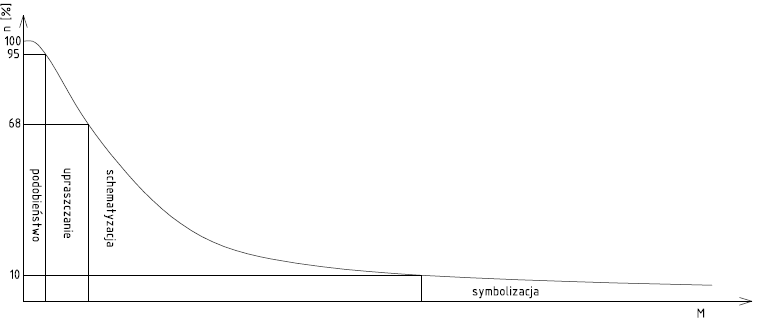
Skalą początkową była skala 1: 500, skalą dla której udało się otrzymać 8 odcinków prostych była skala 1: 80 000. Dzięki skalom pośrednim udało się uzyskać efekt wygładzania konturów obiektu, co jest pokazane w zestawieniu wszystkich map, każdej w odpowiadającej jej skali. Można również w łatwy sposób zauważyć, że obiekt staje się co raz mniej czytelny, aż w ostatnim etapie nawet trudno zauważalny. Uważam, że w tym temacie w sposób jasny i poprawny przedstawiłam generalizację obiektu i odpowiednio dobrałam kolejne skale. Na załączonym wykresie można również zauważyć, że generalizacja polega na symbolizacji już w skali mniejszej od 25 000 ze względu na wielkość rysunku. W

związku z tym w przypadku tworzenia mapy obiekt można zastąpić symbolem.

Generalizowany obiekt został wydrukowany we wszystkich skalach i po ocenie wzrokowej bez przeszkód można go zobaczyć do skali 1: 50 000 przy skali 1: 75 000 oraz 1: 80 000

trzeba zbliżyć do siebie arkusz na ok. 15cm aby zauważyć kształt i linie łączące środek

„latawca”. Na podstawie załączonej tabeli można zauważyć, że procent punktów pozostałych po generalizacji maleje proporcjonalnie, np. Dla skali 1: 500 wynosił 100%, dla skali 1: 5 000 ok. 50%, dla skali 1: 50 000 5%. W całym procesie oprócz usuwania punktów, nowe były dodawane do obiektu od skali 1: 1000 aż do 1: 10 000, w każdej kolejnej program już tylko usuwał następne punkty.

Ze

Z st

s aw

a ie

i n

e i

n e

e ot

o r

t zy

z m

y an

a yc

y h

h war

a t

r oś

o c

ś i

i po

p

o ge

g n

e er

e a

r l

a iz

i a

z c

a jij:

ilość punktów

ilość

ilość

ilość

% punktów

Nr

Wartość

przed

punktów

punktów

punktów po

pozostałych

genera-

Skala

ef

generalizacją

odrzuconych

dodanych

generalizacji

w

lizacj

[m]

n0

n1

n2

n3

generalizacji

1

500

437

0

0

437

100,00

0,25

2

1000

437

13

3

427

97,05

0,5

3

2000

437

61

7

383

86,26

1

4

3000

437

117

15

335

74,12

1,5

5

5000

437

201

8

244

54,83

2,5

6

10000

437

333

2

106

24,15

5

7

15000

437

373

0

64

14,65

7,5

8

25000

437

398

0

39

8,92

12,5

9

50000

437

415

0

22

5,03

25

10

75000

437

420

0

17

3,89

37,5

11

80000

437

421

0

16

3,66

40

12

100000

437

421

0

16

3,66

50

Wyk

y r

k es

e

s za

z l

a e

l żn

ż o

n śc

ś i

i %

% po

p z

o o

z s

o t

s ał

a yc

y h

h pu

p n

u k

n t

k ów

ó po

p

o ge

g ne

n r

e al

a i

l zac

a jij

i o

d

d sk

s a

k l

a i

l