Kraków, dn 02.11.2010r.

Rychcik Paulina

Semestr V

WIL gr 311/2010

St. niestacjonarne

P R O J E K T

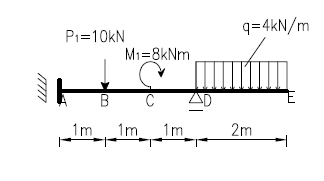
Projekt belki zginanej poprzecznie Zaprojektować wymiary przekroju poprzecznego zginanej belki ze względu na stan graniczny nośności i użytkowania.

Po zaprojektowaniu wyznaczyć rozkład naprężeń normalnych i stycznych w przekroju α-α oraz obliczyć naprężenia główne i ich kierunki w punkcie K przekroju.

Zadaniem jest zaprojektowanie belki stalowej o podanym profilu i schemacie statycznym oraz określenie stanu naprężeń w zadanym punkcie K.

R = 175 MPa

Rt = 0.6⋅R

α

α

1

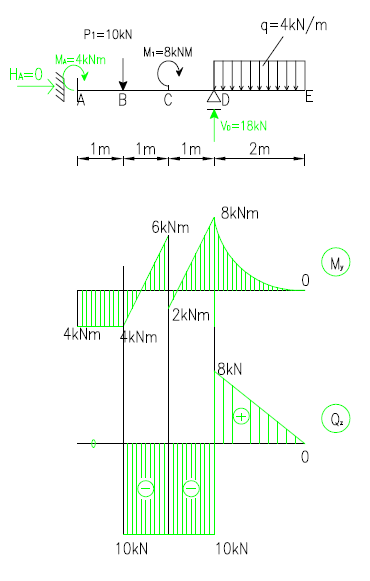
1. Statyka - wykresy sił przekrojowych Obliczenia statyki

ΣX =0

HA = 0

ΣY=0

-10+VD-4·2=0

VD= 18kN

ΣM(A)=0

-10-8+18·3-8·4+MA=0

MA= -4kNm

Spr.

ΣM(C)=0

2

-8+10-4+18-16=0 0=0

M(A) = 4 kNm

F(A) = 0

M(B) = 4 kNm

F(B) = -10 kN

M(C) = - 6 kNm

F(C) = -10 kN

M(D) = - 8 kNm

F(D) = 8 kN

M(E) = 0

F(E) = 0

2.

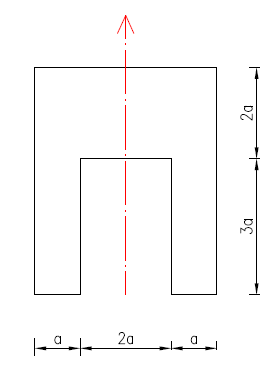
GEOMETRIA PRZEKROJU

A = 4a·5a-3a·2a=14a2

Sy = 4a·5a·2,5a-2a·3a·1,5a= 41a3

zc = Sy / A =41a3/14a2 = 2,93a 3.

MOMENT BEZWŁADNOŚCI

4a ⋅ (5a)³

2a ⋅ (3a)³

Jyo = [

+ 4a⋅5a⋅(2,5a-2,93a)² ] - [

+ 2a⋅3a⋅(2,93a-1,5a)²] =

12

12

= [ 41,67 + 3,698] a4 - [ 4,5+12,269 ] a4 = 45,368a4 - 16,769a4 = 28,599a4

Jyo = 28,6a4

4. WSKAŹNIK WYTRZYMAŁOŚCI J

28,6a 4

W

yo

y =

=

= 9,76 a3

z max

9

,

2

a

3

c

5. MAKSYMALNE NAPRĘŻENIA NORMALNE

M

σ

=

max

max

≤ R

Wy

M

M

max ≤ R → W

max

≥

W

y

W

y

y

8

3

kNm

,

9 76 a

⇒

≥

a

−2

≥ ,

1 67 ⋅10 m

3

175 ⋅10 kPa

3

6. MAKSYMALNE NAPRĘŻENIA STYCZNE

ma Q

x

⋅ S )

0

(

z

≤ Rt

I ⋅ b )

0

(

y

Sy(z=0) = 2a·4a·a+2(a·0,07a·0,07/2a)=8 a3+0,0049a3= 8,0049a3

B(0) = 2a

1 k

0 N ⋅ 0

,

8 04 a 3

9

3

≤ 6

,

0

1

⋅ 75 1

⋅ 0 kPa

28 a 4

6

,

⋅ a

2

a

2

≥ 3

,

0 65 1

⋅ 0− m→ a

2

= 3

,

0 65 1

⋅ 0− m

Przyjęto do wykonania a=1,7 ·10-2 m

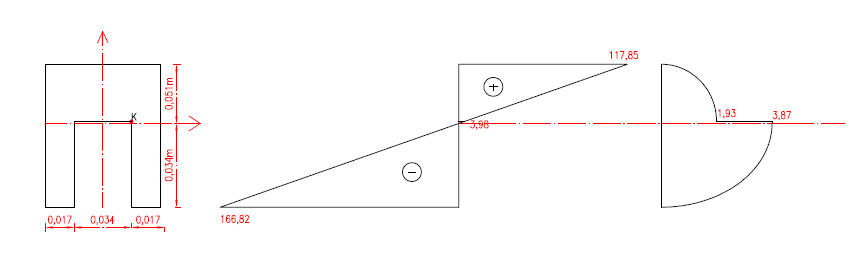
7. Wyznaczenie wykresów naprężeń normalnych I stycznych w przekroju α-α

M α-α

y

= 8kNm

Q α-α

z

= 8kN

Moment bezwładności

Jy = 28,6a4 =28,6·(1,7·10-2)4 = 238,87·10-8 m α−α

M

k

8 Nm

max

σ =

z =

z

x

I

8

23 8

,

8 7⋅10−

y

g

k

8 Nm

σ =

⋅ 0

,

0 3519=11 8

,

7 M

5 Pa

x

23 8

,

8 7 1

⋅ 0 8−

d

k

8 Nm

σ =

⋅ 0

,

0

(

498 )

1 = 1

− 6 8

,

6

M

2 Pa

x

23 8

,

8 7⋅10 8

−

K

k

8 Nm

σ =

⋅ 0

,

0 0119= 9

,

3

M

8 Pa

x

2388

, 7⋅10 8

−

Wartość naprężeń stycznych: Włókna na osi obojętnej z=0

Sy(z=0) = 8,0049a3=8,0049·(1,7·10-2)3 = 39,328·10-6 m3

α−α

Q

⋅ S

6

−

3

⋅

⋅

z

y(0)

k

8 N 39 3

, 28 10 m

τ =

=

= 8

,

3

M

7 Pa

xz

I ⋅ b

)

0

(

2388

, 7⋅10 8

− ⋅ 4

,

3 ⋅10 2

−

y

( z)

4

z=0,07a = 0,119·10-2 m

S

-2

y(z=0,119·10 ) = 2·4·(1,7·10-2)3 = 39,304·10-6 m3

α−α

Q

⋅ S

6

−

3

⋅

⋅

z

y

k

8 N 39 3

, 04 10 m

τ =

=

= 9

,

1

M

3 Pa

xz

I ⋅ b

2388

, 7⋅10 8

− ⋅ 8

,

6 ⋅10 2

−

y

( z)

α−α

Q

⋅ S

6

−

3

⋅

⋅

z

y

k

8 N 39 3

, 04 10 m

τ =

=

= 8

,

3

M

7 Pa

xz

I ⋅ b

2388

, 7⋅10 8

− ⋅ 4

,

3 ⋅10 2

−

y

( z)

5