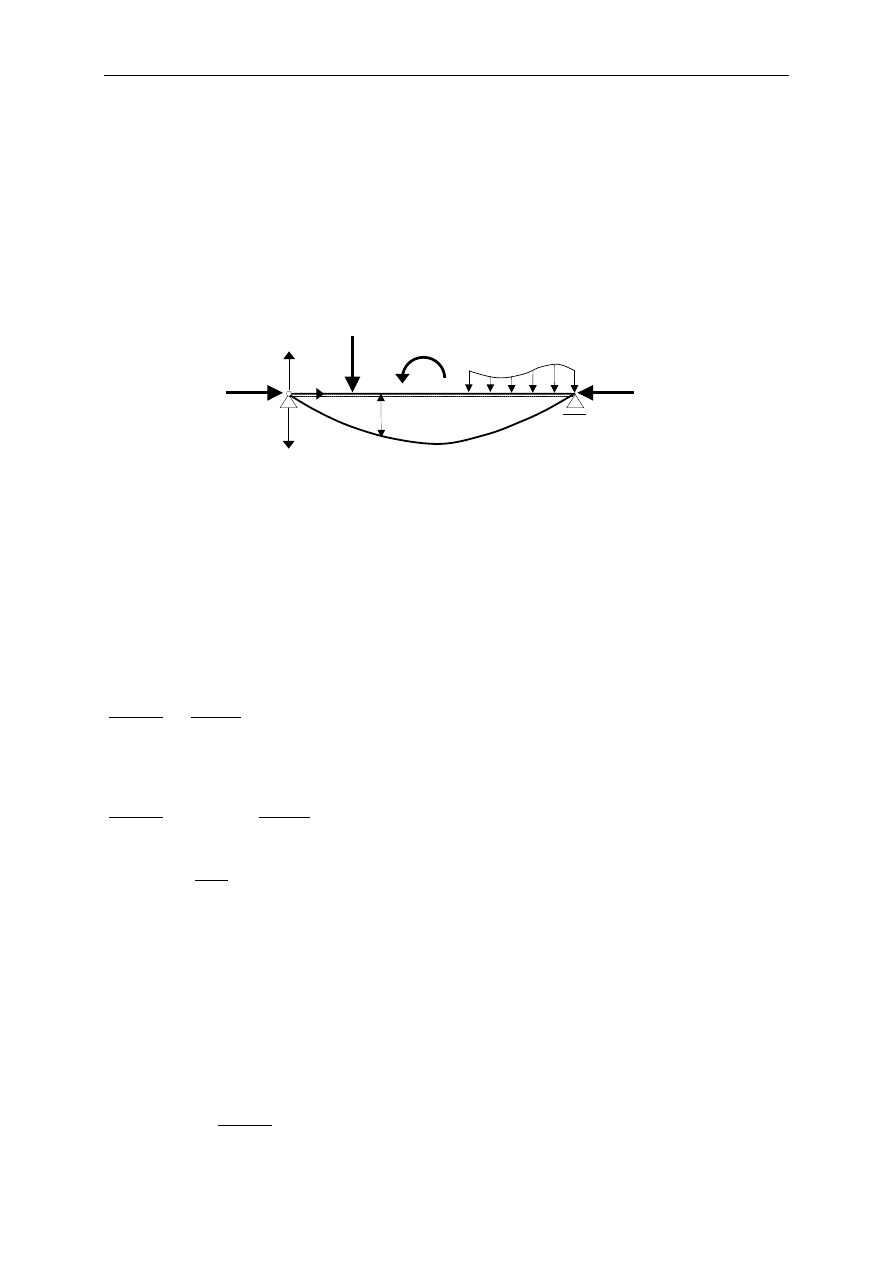
Adam Bodnar: Wytrzymałość Materiałów. Zginanie poprzeczne ze ściskaniem

206

18. ZGINANIE POPRZECZNE ZE ŚCISKANIEM

18.1. Postawienie zagadnienia

Przy omawianiu zagadnienia mimośrodowego ściskania bardzo mocno zostało podkreślone,
ż

e otrzymane wzory mogą być stosowane tylko wówczas, gdy konstrukcja spełnia warunki

pozwalające na przyjęcie zasady zesztywnienia. Teraz zajmiemy się przypadkiem, który
pokazuje jak istotne są konsekwencje rezygnacji z przyjęcia zasady zesztywnienia i jak
wysoce błędne byłyby wyniki obliczeń przy jej przyjęciu. Przypadek ten występuje, gdy do
ś

ciskanego osiowo pręta pryzmatycznego przyłożone jest jeszcze obciążenie powodujące jego

poprzeczne zginanie (rys. 18.1). W pokazanej na poniższym rysunku belce, układ sił

Rys. 18.1

obciążających jest przyczyną jej ugięcia i łatwo zauważyć, że w konfiguracji aktualnej (po
przyłożeniu obciążeń) równanie momentów zginających można zapisać, uwzględniając
wpływ przemieszczeń osi belki na ich wartości, w postaci:

( )

( )

( )

x

w

P

x

M

x

M

y

y

+

=

0

(18.1)

gdzie:

( )

x

M

y

0

- moment zginający w belce nieodkształcalnej.

W przyjętym układzie odniesienia równanie różniczkowe ugiętej osi belki ma postać:

( )

( )

y

y

EJ

x

M

dx

x

w

d

−

=

2

2

.

Podstawienie do niego funkcji momentów (18.1) daje równanie:

( )

( )

( )

y

y

EJ

x

M

x

w

k

dx

x

w

d

0

2

2

2

−

=

+

(18.2)

gdzie:

y

EJ

P

k =

2

.

(18.3)

Rozwiązaniem niejednorodnego równania różniczkowego zwyczajnego (18.2) jest funkcja

( )

( )

kx

B

kx

A

x

w

x

w

s

cos

sin

+

+

=

(18.4)

gdzie:

( )

x

w

s

- całka szczególna tego równania,

A

oraz

B

- stałe całkowania zależne od

kinematycznych warunków brzegowych belki.

Znając funkcję

( )

x

w

, momenty zginające i siły poprzeczne w belce wyznaczamy z

zależności:

( )

( )

2

2

x

d

x

w

d

EJ

x

M

y

y

−

=

X

w

w(x)

P

P

Z

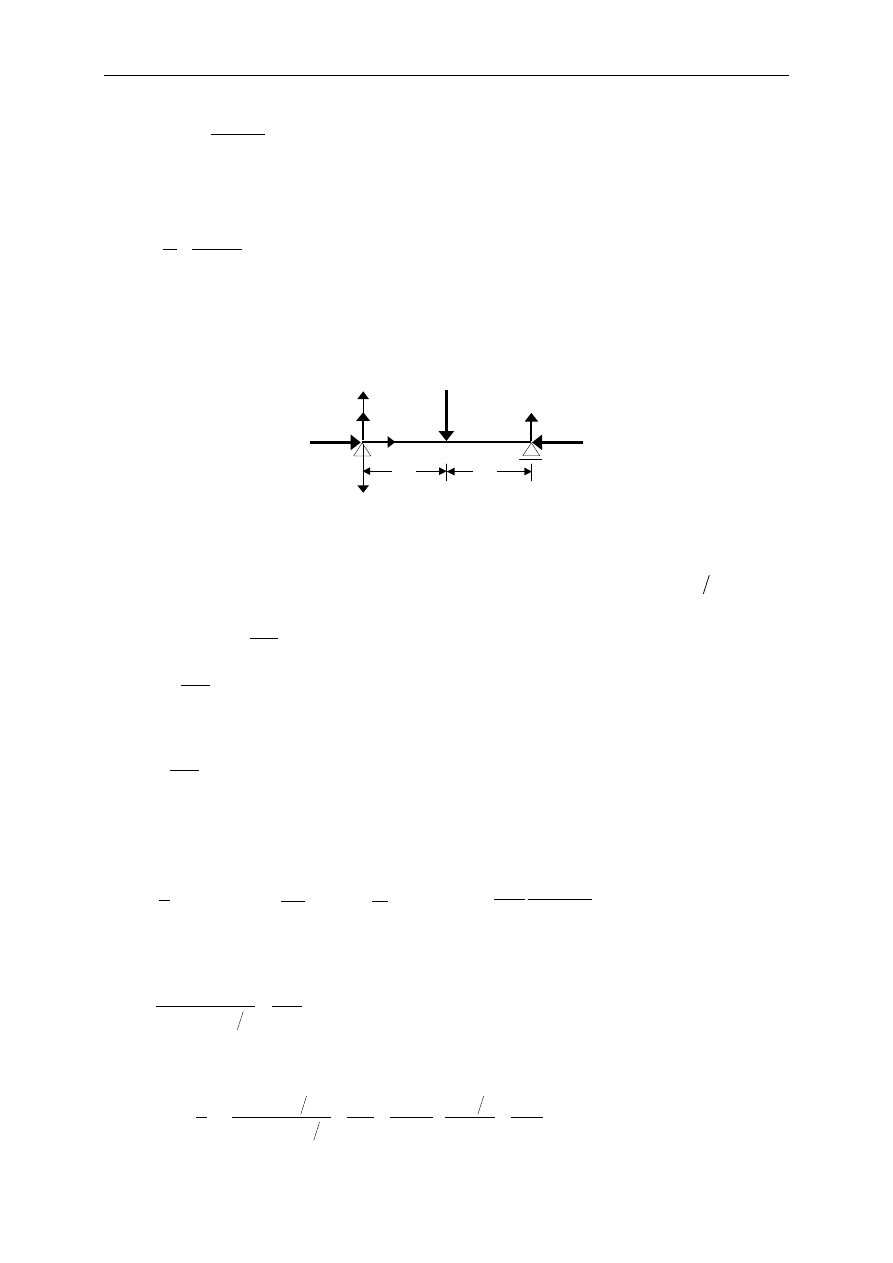
Adam Bodnar: Wytrzymałość Materiałów. Zginanie poprzeczne ze ściskaniem

207

( )

( )

3

3

x

d

x

w

d

EJ

x

Q

y

z

−

=

.

Wartości naprężeń normalnych dla tego przypadku w przyjętych układach odniesienia
wynoszą:

( )

z

J

x

M

A

P

y

y

x

−

−

=

σ

.

(18.5)

18.2. Belka wolnopodparta obciążona siłą w środku rozpiętości

Rozważmy, pokazaną na rys.18.2 belkę wolnopodpartą obciążoną w środku siłą

Q

,

prostopadłą do jej osi i ściskającą osiowo siłą

P.

Rys. 18.2

Ze względu na symetrię belki rozpatrywać będziemy tylko jeden przedział

2

0

l

x ≤

≤

Poniewa

ż

( )

2

0

x

Q

x

M

y

=

wi

ę

c łatwo zgadn

ąć

i sprawdzi

ć

przez podstawienie,

ż

e:

( )

P

x

Q

x

w

s

2

−

=

jest całk

ą

szczególn

ą

równania niejednorodnego (18.2), w zwi

ą

zku z czym

jego całka ogólna ma posta

ć

:

( )

kx

B

kx

A

P

x

Q

x

w

cos

sin

2

+

+

−

=

.

(18.6)

Z kinematycznych warunków brzegowych wyznaczymy stałe całkowania:

( )

2

1

2

0

0

2

2

0

0

2

2

0

0

1

/

kl

cos

kP

Q

A

B

kl

cos

A

k

P

Q

B

l

w

/

w

/

'

=

=

→









=

+

−

=

→

=













=

,

a po ich wstawieniu do (18.6) otrzymamy funkcj

ę

ugi

ęć

belki:

( )

P

x

Q

kl

P

k

kx

Q

x

w

2

2

cos

2

sin

−

=

.

(18.7)

Maksymalne ugi

ę

cie belki wyst

ą

pi w jej

ś

rodku rozpi

ę

to

ś

ci i ma warto

ść

:













−

=

−

=













=

2

3

2

2

tg

2

4

2

cos

2

2

sin

2

max

k

l

k

kl

EJ

Q

P

l

Q

kl

P

k

kl

Q

l

w

w

y

.

w(x)

Q

l/

2

l/

2

P

P

Q/

2

Q

/2

Z

X

Adam Bodnar: Wytrzymało

ść

Materiałów. Zginanie poprzeczne ze

ś

ciskaniem

208

Poprzez szereg przekształce

ń

mo

ż

emy ostatecznie zapisa

ć

:

( )

u

EJ

l

Q

w

y

1

3

48

max

κ

=

,

(18.8)

gdzie:

2

kl

u =

,

( )













−

=

3

1

tg

3

u

u

u

u

κ

.

Zwi

ą

zek mi

ę

dzy momentem zginaj

ą

cym i drug

ą

pochodn

ą

ugi

ę

cia daje:

( )

2

cos

2

sin

kl

k

kx

Q

x

M

=

(18.9)

Maksymalny moment zginaj

ą

cy wyst

ę

puje w

ś

rodku rozpi

ę

to

ś

ci belki i ma warto

ść

:

( )

u

l

Q

l

M

M

2

4

2

max

κ

=













=

,

(18.10)

gdzie:

( )

u

u

u

tg

2

=

κ

Dokonajmy krótkiej analizy wzoru (18.8) podaj

ą

cego warto

ś

ci maksymalnego ugi

ę

cia w

postaci iloczynu maksymalnego ugi

ę

cia w belce przy przyj

ę

ciu zasady zesztywnienia i funkcji

( )

u

1

κ

. Je

ś

li zauwa

ż

ymy,

ż

e argument tej funkcji mo

ż

na wyrazi

ć

w zale

ż

no

ś

ci od warto

ś

ci

przyło

ż

onej siły

ś

ciskaj

ą

cej P i siły krytycznej Eulera

E

kr

P

, gdy

ż

E

kr

y

P

P

EJ

P

l

u

kl

u

2

2

2

π

=

=

→

=

,

to dla

,

0

=

P

( )

1

1

=

u

κ

i

y

EJ

l

Q

w

48

max

3

=

,

a dla

,

E

kr

P

P →

( )

∞

=

u

1

κ

i

∞

→

w

max

.

Otrzymany wynik pokazuje,

ż

e w przypadku przyło

ż

enia siły krytycznej przemieszczenia

belki b

ę

d

ą

wzrasta

ć

do niesko

ń

czono

ś

ci przy dowolnie małym obci

ąż

eniu poprzecznym.

Analogiczne wnioski daje analiza wzoru na maksymalny moment zginaj

ą

cy. Ni

ż

ej pokazane

s

ą

warto

ś

ci funkcji

( )

u

1

κ

i

( )

u

2

κ

w zale

ż

no

ś

ci od stosunku

E

kr

P

P

.

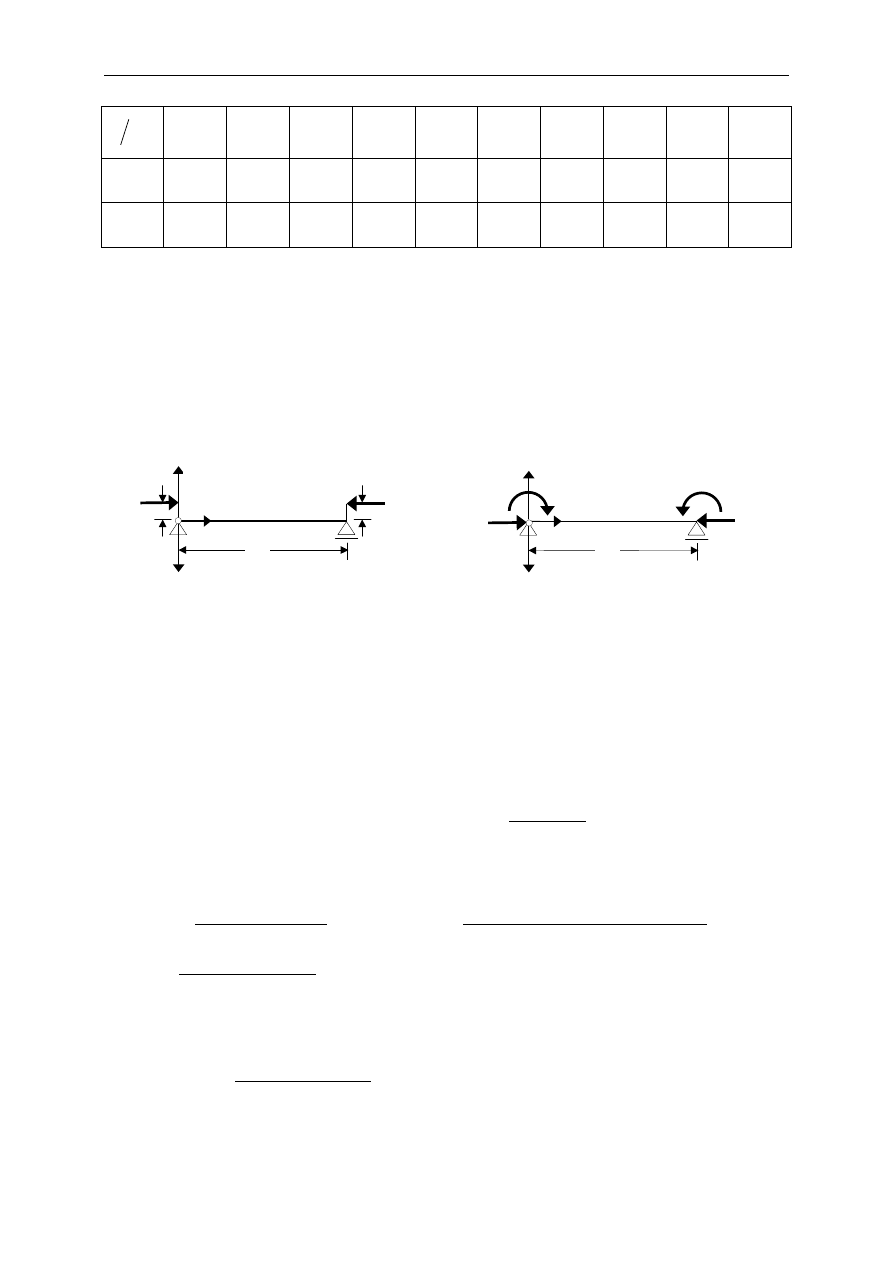
Adam Bodnar: Wytrzymało

ść

Materiałów. Zginanie poprzeczne ze

ś

ciskaniem

209

E

kr

P

P

0.1

0.2

0.3

0.4

0.5

0.5

0.7

0.8

0.9

1.0

( )

u

1

κ

1.110

1.248

1.423

1.658

1.983

2.479

3.301

4.943

9.871

∞

( )

u

2

κ

1.091

1.205

1.351

1.545

1.817

2.223

2.900

4.253

8.307

∞

Wyniki pokazane w tabelce mog

ą

dowodzi

ć

,

ż

e przy sile

ś

ciskaj

ą

cej o warto

ś

ci

E

kr

P

.

1

0

uwzgl

ę

dnienie zasady zesztywnienia mo

ż

e dawa

ć

10% ró

ż

nice w warto

ś

ciach momentów

zginaj

ą

cych.

18.3. Belka wolnopodparta mimośrodowo ściskana

Teraz przedmiotem rozwa

ż

a

ń

b

ę

dzie belka wolnopodparta pokazana na rys. 18.3 obci

ąż

ona

siłami

ś

ciskaj

ą

cymi P równoległymi do jej osi zaczepionymi na mimo

ś

rodzie e. Zasada de

Saint Venanta pozwala na zast

ą

pienie tej belki równowa

ż

n

ą

jej belk

ą

obci

ąż

on

ą

momentami

zginaj

ą

cymi M = Pe na podporach i

ś

ciskaj

ą

c

ą

osiowo sił

ą

P.

Rys. 18.3

W tym przypadku

( )

e

P

x

M

y

=

0

, a całka szczególna równania niejednorodnego (18.2), równa

si

ę

:

( )

e

x

w

s

−

=

, wi

ę

c jego całka ogólna przyjmuje posta

ć

:

( )

kx

B

kx

A

e

x

w

cos

sin

+

+

−

=

.

(18.11)

Stałe całkowania wyznaczone z kinematycznych warunków brzegowych s

ą

równe:

( )

( )

kl

sin

kl

cos

e

e

A

e

B

kl

cos

e

kl

sin

A

e

e

B

l

w

/

w

/

−

=

=

→







=

+

+

−

=

→

=

=

0

0

2

0

0

1

.

St

ą

d funkcja ugi

ęć

osi belki przyjmuje posta

ć

:

( )

(

)

(

)









−

−

+

=

=

+

−

+

−

=

+

−

+

−

=

1

sin

sin

sin

sin

cos

sin

sin

cos

sin

cos

sin

sin

cos

kl

x

l

k

kx

e

kl

kx

kl

kxl

k

kx

e

e

kx

e

kl

kx

kl

e

e

e

x

w

,

a równanie momentów zginaj

ą

cych przedstawia zale

ż

no

ść

:

( )

(

)









−

−

+

+

=

1

sin

sin

sin

kl

x

l

k

kx

Pe

Pe

x

M

y

.

(18.12)

Maksymalne ugi

ę

cie belki wyst

ą

pi w

ś

rodku jej rozpi

ę

to

ś

ci i ma warto

ść

:

≡

e

e

w(x)

l

P

P

Z

X

M = Pe

w(x)

l

P

P

Z

X

M = Pe

Adam Bodnar: Wytrzymało

ść

Materiałów. Zginanie poprzeczne ze

ś

ciskaniem

210

(

)

1

2

/

sec

1

2

cos

1

2

max

−

=













−

=













=

kl

e

kl

e

l

w

w

,

(18.13)

st

ą

d maksymalny moment zginaj

ą

cy, który te

ż

wyst

ą

pi w

ś

rodku rozpi

ę

to

ś

ci, wynosi:

2

/

sec

2

max

kl

Pe

l

M

M

y

y

=













=

.

(18.14)

Poniewa

ż

:

E

kr

P

P

kl

2

2

π

=

,

to przy

,

E

kr

P

P →

zarówno maksymalne ugi

ę

cie jak i maksymalny moment zginaj

ą

cy w belce

zmierzaj

ą

do niesko

ń

czono

ś

ci przy dowolnie małym mimo

ś

rodzie e.

Inaczej mówi

ą

c przyło

ż

enie do belki siły krytycznej powoduje jej zniszczenie, gdy

ż

praktycznie nie jest mo

ż

liwe idealnie osiowe obci

ąż

enie pr

ę

ta.