12 FALE (8 stron)
Falami nazywamy rozprzestrzeniające się w ośrodku materialnym lub polu zaburzenia pewnej wielkości fizycznej charakteryzującej stan tego ośrodka lub pola, na przykład fale biegnące wzdłuż gumowego węża, fale wzbudzone na powierzchni wody, fale dźwiękowe lub fale
elektromagnetyczne.
Na razie będziemy zajmowali się głównie falami sprężystymi, które polegają na
rozprzestrzenianiu się zaburzeń mechanicznych, czyli odkształceń, w ośrodkach materialnych o
własnościach sprężystych.
Właściwościami ośrodka decydującymi o prędkości rozchodzenia się fal są jego bezwładność i sprężystość. Wszystkie ośrodki materialne, zarówno ciała stałe jak ciecze i gazy, które mają te własności – mogą przewodzić fale.
Fale powstają przy wytrącaniu pewnego elementu ośrodka sprężystego z jego normalnego położenia, co powoduje jego drgania wokół położenia równowagi. Dzięki sprężystym
własnościom ośrodka zaburzenie to przekazywane jest elementom sąsiednim. Rozchodzenie się
fal sprężystych polega na wzbudzaniu drgań cząstek ośrodka coraz bardziej odległych od źródła.
Najważniejszą cechą odróżniającą fale sprężyste od innych uporządkowanych ruchów cząstek ośrodka jest to, że rozchodzenie się fal sprężystych nie jest związane z przenoszeniem substancji.
Elementy środka drgają w ograniczonym obszarze wokół swoich stałych położeń równowagi.
Natomiast energia może być przenoszona przez ruch falowy nawet na duże odległości. Energia
fali sprężystej jest to energia potencjalna i kinetyczna materii. Jej przenoszenie polega na przekazywaniu energii sąsiednim elementom ośrodka bez przemieszczania się tych elementów.
Rodzaje fal
Ze względu na kierunek ruchu cząstek ośrodka fale dzielimy na podłużne i poprzeczne. Jeżeli ruchy cząstek materii są prostopadłe do kierunku rozchodzenia się fali to mamy do czynienia z
falą poprzeczną. Na przykład gdy naciągnięty poziomo sznur wprowadzimy z jednej strony w ruch drgający poprzeczny to wzdłuż sznura pobiegnie fala poprzeczna. Poprzeczne są też fale elektromagnetyczne. Fale poprzeczne mogą powstawać tylko w ośrodkach mających sprężystość
postaci, czyli kształtu. Własność taką mają ciała stałe oraz powierzchnie cieczy.
Jeżeli ruch cząstek materii odbywa się wzdłuż kierunku rozchodzenia się fali to mamy do czynienia z falą podłużną. Na przykład, jeżeli jeden koniec pionowo rozciągniętej sprężyny wprowadzimy w pionowy ruch drgający, to wzdłuż sprężyny pobiegnie fala podłużna. Falami podłużnymi są też fale dźwiękowe rozchodzące się w gazach i cieczach. Fale podłużne związane
są ze sprężystością objętościową, polegają na rozprzestrzenianiu się zagęszczeń ośrodka. Mogą
one występować zarówno w ciałach stałych jak i w cieczach lub gazach.
Niektóre fale nie są ani ściśle podłużne ani poprzeczne (fale “mieszane“). Na przykład fale powstające na swobodnej powierzchni cieczy polegają na ruchu cząsteczek zarówno wzdłuż
kierunku propagacji fali jak i w kierunku poprzecznym.
Własności fal zależą również od ilości wymiarów przestrzeni, w której się rozchodzą. Fale poruszające się wzdłuż struny lub sprężyny są jednowymiarowe. Fale na powierzchni są dwuwymiarowe a w przestrzeni rozchodzą się fale trójwymiarowe.
Dla fal rozchodzących się w przestrzeni dwu- i trójwymiarowej amplituda drgań jest tym mniejsza im bardziej dany element ośrodka oddalony jest od źródła fali. Związane jest to z tym, że energia wysyłana ze źródła musi być rozdzielona na coraz większą ilość cząstek.
W przypadku ośrodka jednowymiarowego amplituda (i energia) pozostaje stała. Podobnie jest w
przypadku fal rozchodzących się w jednym kierunku w ośrodkach wielowymiarowych. (fale płaskie)
12/ 1
Ze względu na zachowanie się cząstek materii w czasie kiedy fala rozchodzi się w ośrodku wyróżniamy:
pojedynczą falę – impuls przebiegający przez ośrodek. W tym przypadku każda cząstka pozostaje w spoczynku dopóki nie dobiegnie do niej impuls, następnie porusza się przez krótki
czas i znowu osiąga stan bezruchu. Pojedyncze fale wytwarzane są przez pojedyncze zaburzenie
w miejscu nazywanym źródłem fali.
ciąg fal - Jeżeli zamiast jednego zaburzenia spowodujemy ciąg zaburzeń to w ośrodku powstanie
ciąg fal. Jeżeli zaburzenia są periodyczne – otrzymujemy periodyczny ciąg falowy w którym każda cząsteczka porusza się okresowo.
Fale jednowymiarowe
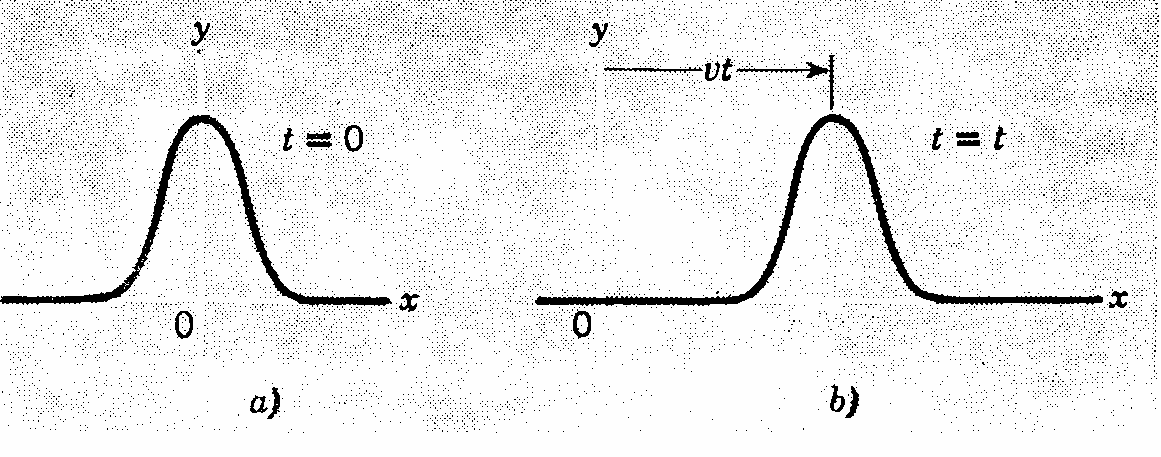
Niech będzie dana jednorodna ciągła struna (lub sznur) rozciągająca się wzdłuż osi x. Struna taka stanowi układ jednowymiarowy. W chwili t = 0 kształt struny można przedstawić w postaci:
y(x,0) = f(x)
gdzie y jest przemieszczeniem elementu struny znajdującego się w położeniu x. Z doświadczenia wiadomo, że odkształcenie przesuwa się wzdłuż struny lub sznura nie zmieniając swego kształtu.
W czasie t przebywa ono odległość s = v⋅ t gdzie v jest prędkością rozchodzenia się fal w tej strunie (prędkość ta zależy od własności ośrodka w którym rozchodzi się fala). Po czasie t struna będzie miała kształt opisany równaniem:
y(x,t) = f(x-vt)
Daje ono taki sam kształt fali w punkcie x = vt w chwili t jaki mieliśmy w punkcie x = 0 we wcześniejszej chwili t = 0.
Wyrażenie y = f(x-vt) opisuje falę dowolnego kształtu biegnącą w dodatnim kierunku wzdłuż
osi OX a wyrażenie y = f(x+vt) – w kierunku ujemnym. Dla ustalonego t = t0 funkcja f opisuje kształt struny w wybranej chwili (jak fotografia). Dla ustalonego x opisuje zmiany położenia wybranego elementu struny w czasie.
Funkcja f(x-vt) jest ogólnym wyrażeniem opisującym rozchodzenie się fali o prędkości v. Jest ona rozwiązaniem jednowymiarowego równania falowego:
2
2
∂ f
1 ∂ f
=
2
2
2
∂ x
v
∂ t
Równanie falowe jest odpowiednikiem równania ruchu, opisuje ono zależność przyspieszenia elementów ośrodka od jego odkształcenia. Każda dwukrotnie różniczkowalna funkcja argumentu
(x-vt) jest rozwiązaniem tego równania.
12/ 2

Sprawdzenie:
∂ 2 f = v 2 f ′
∂ t 2
∂ 2
f = f ′
∂ x 2
Funkcja f(x ± vt) jest funkcją jednej zmiennej, φ = x ± vt , opisującej fazę drgań punktu, położonego w odległości x od źródła. Faza ta mierzona jest w chwili t.
Fale harmoniczne
Rozważmy teraz strunę, której punkt x = 0 podłączony jest do generatora drgań harmonicznych.
Wówczas przemieszczenie elementu struny znajdującego się w punkcie x=0 opisane będzie równaniem: y(0, t) = A cosω t
Ruch elementu znajdującego się w odległości x od źródła w chwili t jest identyczny jak ruch elementu znajdującego się w punkcie x = 0 we wcześniejszym czasie t`, gdzie t` różni się od t o czas, który fala zużywa na przebycie odległości x, czyli o ∆ t = x/v
t` = t – x/v
zatem:
y(x, t) = y(0, t`) = A cosω (t –x/v)
y(x, t) = A cos(ω t – ω x / v)
Dla ustalonej chwili czasu zmiana fazy na jednostkę długości wynosi k = ω /v
y = A cos(ω t - k x) k = ω /v - nazywamy liczbą falową [ k] =1/m y(x, t) = A cos(ω t – kx )
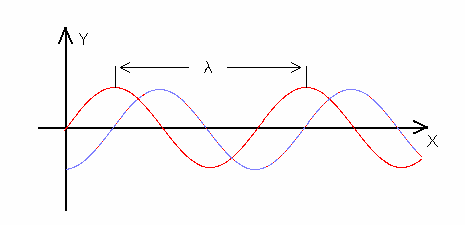
Odległość między dwoma najbliższymi punktami będącymi w danej chwili w tej samej fazie (np.
dwoma maksimami) nazywamy długością fali λ
ϕ 1(x) - ϕ 2(x + λ ) = 2π
(ω t - k x) - (ω t - k (x + λ )) = 2π t = const π
2
kλ = 2π λ =
k
12/ 3
Okresem fali, T, nazywamy najkrótszy czas, po którym dany punkt ośrodka znajdzie się znowu w tej samej fazie drgań . x = const
ϕ (t + T) − ϕ (t) = 2π
[ω (t + T) − k x] - [ω t – k x] = 2π
ω
π
2
T = 2π T = ω
λ
π
2
π
2 v
=
=
= vT λ = vT
k
ω
Okres fali T jest równy czasowi potrzebnemu na przebycie przez falę długości λ .
Zasada superpozycji
W tym samym obszarze w przestrzeni może rozchodzić się jednocześnie bardzo wiele różnych fal. Każda z nich pobudza cząsteczki ośrodka do drgań. Doświadczenie pokazuje, że fale te rozchodzą się niezależnie od siebie. Wychylenie badanego elementu ośrodka w danej chwili jest
sumą wychyleń jakich doznawałby ten element pod działaniem każdej fali z osobna. Ta własność wektorowej addytywności wychyleń elementu ośrodka nosi nazwę zasady
superpozycji. Zasada ta obowiązuje wówczas, gdy siła sprężysta jest proporcjonalna do odkształcenia ośrodka. Zawodzi przy bardzo dużych odkształceniach. Na przykład powyżej granicy sprężystości przestaje obowiązywać prawo Hookeà i nie można posługiwać się
związkiem F = − ksx , powstają wówczas fale nieliniowe.
Superpozycja dwu fal biegnących
Rozważmy generator wysyłający fale ψ (0, t)=A cosω 1t + A cosω 2t
Ponieważ fale spełniają zasadę superpozycji więc fala biegnąca
ψ (x, t) = ψ 1(x, t) + ψ 2(x, t) = Acos(ω 1 t - k1 x)+Acos(ω 2 t – k2 x)
ω ω
ω ω
ψ ( x, t) = 2 A cos( 1 −
k
2
1 − k
k
k
t −
2 x )
1 + 2
1 +
cos
t −
2 x
2
2
2
2
ψ (x, t) = Amod(x, t)cos(ωś r t - kś r x)
gdzie: Amod(x, t) = 2Acos(ω mod t - kmod x)
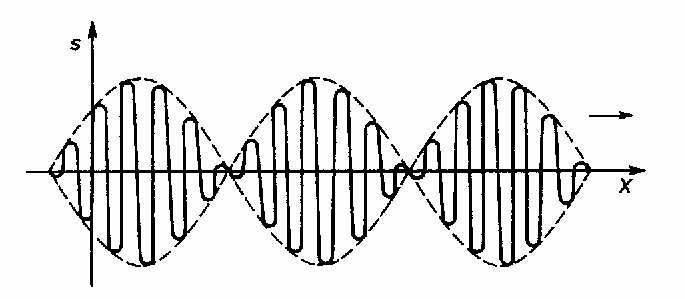
Otrzymaliśmy prawie sinusoidalną falę biegnącą o częstotliwości kątowej ωśr i liczbie falowej kśr i modulowaną amplitudą
12/ 4
Prędkość grupowa
Załóżmy, że częstotliwości ω1 i ω2 różnią się nieznacznie, wówczas ω mod jest małe w porównaniu z ωśr. Aby podążyć za daną stałą wartością amplitudy Amod(x, t) musimy utrzymać stałą wartość jej argumentu.
ϕ m = (ω mod t – kmod x) = const
dx
ω
ω −
mod
1
2
=
ω
v
=
=
ω = v
mod
f k
dt
k
k − k
mod
1
2
Prędkość rozchodzenia się modulacji vmod oraz paczek falowych nazwana jest prędkością grupową , vg =∆ω/∆ k . Prędkość grupowa jest prędkością, z jaką rozchodzi się energia fali.
Jeżeli rozważane fale nie podlegają dyspersji to znaczy ich prędkość fazowa vf jest stała, niezależna od częstotliwości ani liczby falowej (na przykład dla fal dźwiękowych, dla fal poprzecznych na strunie a także dla fal świetlnych w próżni lub powietrzu) to prędkość grupowa równa jest prędkości fazowej fali, vg = vf..
Interferencja fal
Szczególnym przypadkiem superpozycji fal jest ich interferencja. Rozważmy dwie fale o tej samej częstości ω 1 = ω 2 = ω i równych amplitudach rozchodzące się z tą samą prędkością, w tym samym kierunku, lecz różniące się fazami o φ. Ważne jest, aby różnica faz była stała w czasie.
y
y
ω t kx ϕ
1 =
cos(
m
− − )
B + C
B − C
cos B + cos C = 2 cos
cos
y
y
ω t kx
2 =
cos(
m
− )
2
2
y = y + y = ym
ω t − kx −ϕ +
ω t − kx
1
2
[cos(
)
cos(
)]
1
1
y = 2 y cos(
m
ω t − kx − ϕ)cos ϕ
2
2
1
1
y = 2 y cos
m
ϕ cos(ω t − kx − ϕ)
2
2
otrzymujemy falę o tej samej częstości i liczbie falowej co fale y1 i y2 oraz
1
A = 2 y cos
m
ϕ
amplitudzie zależnej od różnicy faz między nimi, amplituda ta jest stała,
2
nie zależna od x lub t i zawarta w granicach od 0 do 2ym
A∈ ( 0 , 2ym)
Fale stojące
Fale rozchodzące się w ciałach o skończonych wymiarach odbijają się od powierzchni tych ciał i dają początek falom poruszającym się w przeciwnym kierunku. Fale te nakładają się z falami
pierwotnymi zgodnie z zasadą superpozycji . Rozważmy to na przykładzie struny:
y
y
kx
ω t
1 =
cos(
m
− )
y
y
kx
ω t
2 =
cos(
m
+ )
y = y1+y2 = ym cos(kx-ω t) + ym cos(kx+ω t)
y = (2ym coskx) cosω t
Równanie to jest równaniem tzw. fali stojącej. Elementy struny w dowolnym punkcie wykonują
drgania harmoniczne o częstości ω i amplitudzie zależnej od położenia A=2ymcoskx, przy czym w danej chwili wszystkie są w tej samej fazie.
12/ 5
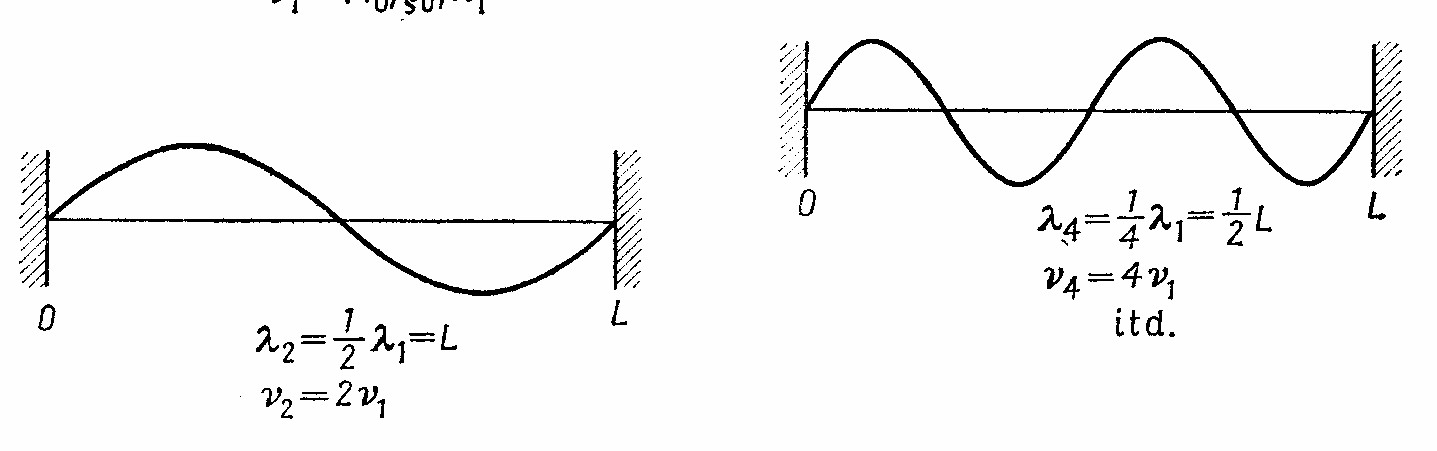

W punktach w których
1
3
5
kx = π , π , π ,...
2
2
2
amplituda przyjmuje wartość zerową, są to
tzw. węzły.
W punktach kx = π, 2π ,..... zwanych
strzałkami, amplituda jest maksymalna.
Energia nie jest przenoszona wzdłuż struny
ani w jedną ,ani w drugą stronę ponieważ nie
może ona przepływać przez węzły, które
pozostają stale w spoczynku. Energia jest
zmagazynowana w strunie, którą można
traktować
jako
zbiór
oscylatorów
harmonicznych o różnych amplitudach.
Odbicie.
• Jeżeli jeden z końców struny jest sztywno zamocowany to zgodnie z III zasadą dynamiki Newtona zamocowanie to działa na strunę siłą taką samą jak struna na zamocowanie ale przeciwnie skierowaną. Ta siła reakcji wytwarza falę odbitą biegnącą w przeciwnym kierunku, której wychylenie ma przeciwny znak niż znak fali padającej. Dzięki temu możliwe jest zerowe wychylenie punktu zamocowania. Fala odbita ma w punkcie zamocowania fazę różną o π od fali
padającej. W punkcie zamocowania powstaje węzeł.
• Jeżeli zachodzi odbicie impulsu od swobodnego końca struny to nie ma żadnego zamocowania,
które mogłoby działać siłą reakcji przeciwnie skierowaną do siły która działa na element końcowy struny. Wychylenie fali odbitej jest więc takie samo jak wychylenie fali padającej. Przy odbiciu od wolnego końca faza nie ulega zmianie. Powstaje tam strzałka.
Rezonans
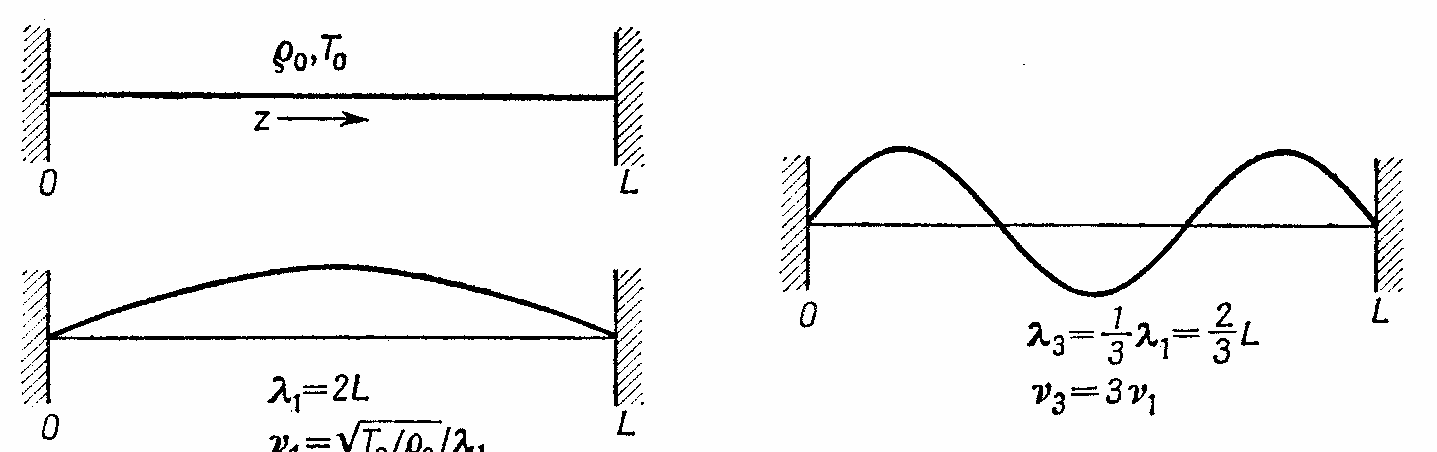
Warunki odbicia fal od końców struny narzucają ograniczenia na tworzące się w strunie fale stojące. Są to tak zwane warunki brzegowe. Np. dla struny zamocowanej na obu końcach mogą powstawać fale, które mają punkty węzłowe na końcach oraz dowolną ilość węzłów między nimi.
Na strunie mogą powstawać fale, spełniające warunek, że na całej długości struny mieści się całkowita ilość połówek fali:
L = n λ n/2.
2 L
stąd λ =
n
n
oraz częstość
v
v
f =
= n
n
λ
2 L
n
12/ 6
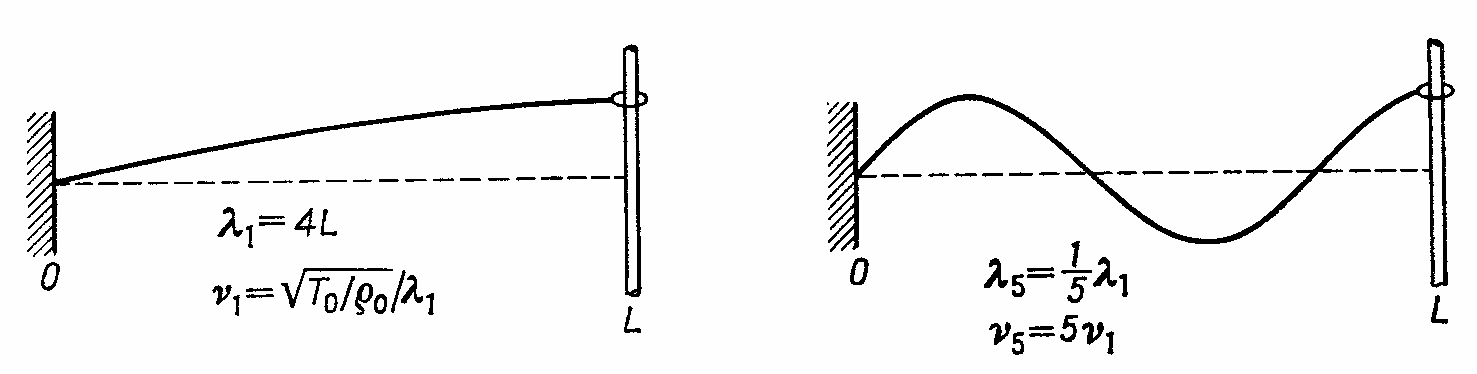
Jeżeli wprawioną w drgania strunę pozostawimy w spokoju drgania jej stopniowo zanikną wskutek strat energii w punktach zamocowania lub z powodu oporu powietrza. Możemy jednak dostarczać energię takiej strunie przez zastosowanie zewnętrznej siły wymuszającej. Jeżeli siła wymuszająca F = F0 cos(ω t) będzie miała częstość bliską częstości rezonansowej struny, amplituda drgań będzie duża, podobnie jak w przypadku drgań wymuszonych. Różnica między pojedynczym oscylatorem a struną, w której powstają fale stojące, polega na tym, że rezonans może mieć miejsce przy wielu różnych częstościach siły wymuszającej ω n, dla których 1
1
1
4 L
L =
n
λ
λ
, L = (2 n + )
1
λ a stąd λ
n =
n +
n
2
4
n
4
2 n + 1
2 v
π
v
π
ω =
= (2 n + )
1
n
λ
2 L
n
Dowolny ruch struny przy określonych warunkach brzegowych, np. zamocowanie obu końców zawsze można opisać przyjmując, że w strunie wywołano jednocześnie więcej niż jedną falę stojącą . W ogólnym przypadku trzeba wzbudzić nieskończenie wiele drgań.
Rozkład spektralny
Dowolny ruch o okresie T można przedstawić jako sumę składowych harmonicznych dodanych z odpowiednimi amplitudami i fazami.
1
f t
( ) =
a 0 + a cos
1
ω t + b sin
1
ω t + ...... + a cos n t
ω .....
n
+
π
2
gdzie ω
2
=
= ∑ a cos nω t
b sin nω t
T
n
+ ∑ n
n
n
Szereg taki nazywa się szeregiem Fouriera.
Jeżeli ruch jest nieperiodyczny to szereg Fouriera zastępuje się przez całkę Fouriera.
∞
a(ω) = 2
ω
∞
∞
∫ F( t)cos tdt
π
f ( t) = ∫ a(ω) cosω t ω
d
+ ∫ b(ω)sinω t ω
d
gdzie
0
∞
2
0
0
b(ω) =
ω
∫ F( t)sin tdt
π 0
Każdy ruch źródła fali można przedstawić w postaci złożenia prostych ruchów harmonicznych.
Ponieważ w wyniku ruchu harmonicznego źródła, powstają w ośrodku fale harmoniczne, więc dowolne rozchodzące się w ośrodku fale można rozpatrywać jako kombinacje fal harmonicznych.
∞
∞
f ( x, t) = ∫ a(ω) sin(ω t − kx) ω
d
+ ∫ b(ω)cos(ω t − kx) ω
d gdzie k=ω/v
0
0
Wykres zależności współczynników Fouriera a i b od częstości a(ω ) i b(ω ) nazywamy rozkładem spektralnym.
12/ 7
Energia w ośrodku trójwymiarowym.
Jeżeli w ośrodku izotropowym znajduje się niewielkie źródło fal to rozchodzą się w nim fale
kuliste. Natężenie fali przestrzennej jest to moc przechodząca przez jednostkową powierzchnię
prostopadłą do kierunku jej rozchodzenia.
1) Przy założeniu, że nie ma absorpcji całkowita energia przenoszona przez fale w ciągu
sekundy pozostaje stała i równa mocy wysyłanej ze źródła.
E
= P = I ⋅ S = const
t
Dla punktu odległego o r od źródła S = 4π r2 więc aby P mogło pozostać stałe musi zmieniać się natężenie fali I(r)
P
z
2
=
P = I ( r) ⋅ 4π ⋅ r
I ( r)
2
4π ⋅ r
Ponieważ natężenie fali jest proporcjonalne do kwadratu amplitudy więc amplituda A∼1/r
- maleje proporcjonalnie do r -1
2
I ~ A
2
2
P ~ A ω
2) Rozchodzeniu się fal w ośrodku jednorodnym towarzyszy strata energii w przypadku fal
dźwiękowych spowodowana lepkością i przewodnictwem cieplnym. Zjawisko to nazywa się
pochłanianiem fal. Amplituda i natężenie fali płaskiej rozchodzącej się w dodatnim kierunku osi x zależą w sposób wykładniczy od współrzędnej x :
− x
A( x) = A e γ
2
− x
I ( x) = I e γ
0
0
gdzie A0 - amplituda a I0 - natężenie w punkcie x = 0, γ - współczynnik pochłaniania W przypadku fal kulistych nakładają się dwa efekty: pochłanianie i zwiększanie powierzchni.
2
e − r
γ
I ( r) = I 0
2
4π r
3)
Dodatkową utratę energii fali powoduje zjawisko zwane rozpraszaniem fal. Polega ono
na przemianie fali dźwiękowej w zbiór fal rozchodzących się we wszystkich możliwych kierunkach. Rozpraszanie zachodzi w wyniku oddziaływania fali z napotykanymi po drodze przeszkodami.
12/ 8
Wyszukiwarka
Podobne podstrony:
Fizyka 1 15 fale sprężyste
06 Fale sprezyste[1]
F 14 fale sprezyste 2006 id 166 Nieznany
F10 Fale sprezyste
MF11 fale spr Ö+ yste
42Główne parametry ośrodka przenoszącego fale sprężyste
a22 fale sprezyste (01 16) CP2AXYOFF3KG6MIKC2CGIVHPQEOS62SPZFRM5XA
Fizyka 1 15 fale sprężyste
06 Fale sprezyste[1]
sprawdzian drgania i fale sprężyste
F10 Fale sprezyste
15 Fale w ośrodkach sprężystych
więcej podobnych podstron