ag÷
ość funkcji
1
Zadania z rozwi ¾
azaniami
1. Wyznaczyć na podstawie de…nicji granic ¾
e funkcji f (x) = x2 9 w punkcie
x 3
x0 = 3:
Rozwiazanie: Niech (xn)1 b ¾
edzie dowolnym ci ¾
agiem o wyrazach róznych
n=1
od 3 i takim, ·
ze lim xn = 3: Obliczmy postać wyrazu ogólnego ci ¾
agu
n!1
(f (xn))1
n=1
x2
(x
f (x
n
9
n
3)(xn + 3)
n) =
=
= xn + 3:
xn
3
xn
3
Zatem, z uwagi na fakt, i·
z lim xn = 3 oraz lim 3 = 3, mamy
n!1
n!1
lim f (xn) = lim (xn + 3) = lim xn + lim 3 = 3 + 3 = 6: n!1
n!1
n!1
n!1
St ¾
ad, na mocy de…nicji granicy funkcji w punkcie, mamy lim f (x) = 6:
x!3
2. Wyznaczyć , na podstawie de…nicji , granice funkcji f (x) = x2 9x 2 gdy 2x 3
(a) x ! +1;
(b) x ! 1.
Rozwi ¾
azanie:
a Niech (xn)1
b ¾
edzie dowolnym ci ¾
agiem takim,
x
n=1
·
ze lim n = +1:
n!1
Przekszta÷
caj ¾
ac ogólny wyraz ci ¾
agu (f (xn))1
mamy
n=1
x2
xn
9
2
f (x
n
9xn
2
xn
n) =
=
:
(1)
2xn
3
2
3
xn
Zauwa·
zmy, ·
ze
2
3
lim
= lim
= 0:
(2)
n!1 xn
n!1 xn
Zatem
xn
9
2
lim f (x
xn
n) = lim
= +1:
n!1
n!1
2
3
xn
1
Na mocy de…nicji granicy funkcji otrzymujemy lim f (x) = +1
x!+1
b Niech teraz (xn)1
b ¾
edzie dowolnym ci ¾
agiem takim,
x
n=1
·
ze lim n =
n!1
1: Korzystaj ¾
ac z (1) oraz (2) mamy
xn
9
2
lim f (x
xn
n) = lim
=
1:
n!1
n!1
2
3
xn
St ¾
ad, na mocy de…nicji granicy funkcji, mamy lim f (x) =
1:
x! 1
3. Wyznaczyć granic ¾
e funkcji f (x) =
x3
27
w punkcie x = 3:
x2
5x+6
Rozwi ¾
azanie: Przekszta÷
caj ¾
ac wzór funkcji mamy
x3
27
(x
3) x2 + x + 9
x2 + x + 9
f (x) =
=
=
:
x2
5x + 6
(x
3)(x
2)
x
2
Zatem
x2 + x + 9
lim f (x) = lim
= 21:
x!3
x!3
x
2
4. Wyznaczyć granice jednostronne funkcji f (x) = x+6 w miejscu zerowym x 3
mianownika.
Rozwi ¾
azanie: Zauwa·
zmy, ·
ze
x
3 < 0 dla x 2 ( 1; 3) oraz x
3 > 0 dla x 2 (3; +1)
oraz
lim (x
3) = 0 i lim (x + 6) = 9
x!3
x!3
Obliczamy granic ¾
e lewostronn ¾
a:
x + 6
lim f (x) = lim
=
1:
x!3
x!3 x
3
Obliczamy granic ¾
e prawostronn ¾
a:
x + 6
lim f (x) = lim
= +1:
x!3+
x!3+ x
3
5. Zbadać ci ¾
ag÷
ość nastepuj ¾
acych funkcji
(a)
8
< x + 2
dla
x > 2
f (x) =
4
dla
x = 2
:
x2 + 2
dla
x < 2;
2
x + 1
dla
x < 0
f (x) =
2x
dla
x
0:
Rozwi ¾
azania:
a Zauwa·
zmy, ·
ze funkcja f jest ci ¾
ag÷
a w przedziale (2; +1) jako funkcja
liniowa. Podobnie, funkcja f jest ci ¾
ag÷
a w przedziale ( 1; 2) jako funkcja
kwadratowa. Sprawdzamy zatem ci ¾
ag÷
ość funkcji f w punkcie x0 = 2: W
tym celu obliczamy granice jednostrone funkcji w punkcie x0 : lim f (x) = lim (x + 2) = 4;
x!2+
x!2+
lim f (x) = lim
x2 + 2 =
2:
x!2
x!2
Poniewa·
z granice jednostronne funkcji w punkcie x0 = 2 s ¾
a ró·
zne, zatem
nie istenieje granica funkcji f w punkcie x0 = 2; a st ¾
ad funckja nie jest
ci ¾
ag÷
a w punkcie x0 = 2:
b Zauwa·
zmy, ·
ze funkcja f jest ci ¾
ag÷
a w przedziale (0; +1) jako funkcja
wyk÷
adnicza. Podobnie, funkcja f jest ci ¾
ag÷
a w przedziale ( 1; 0) jako
funkcja liniowa.
Badamy ci ¾
ag÷
ość funkcji f w punkcie x0 = 0: Wyz-
naczamy granice jednostrone funkcji w punkcie x0 : lim f (x) = lim 2x = 1;
x!0+
x!0+
lim f (x) = lim (x + 1) = 1:
x!0
x!0
Zatem istnieje granica funkcji f w punkcie x0
lim f (x) = lim f (x) = lim f (x) = 1: x!0
x!0+
x!0
Jednocześnie f (x0) = f (0) = 1;w konsekwencji lim f (x) = f (0):
x!0
Stwierdzamy zatem, ·
ze f jest ci ¾
ag÷
a równie·
z w punkcie x0 = 0:
2
Zadania do samodzielnego rozwi ¾
azania
1. Oblicz ( o ile istniej ¾
a) granice funkcji w podanym punkcie
(a) f (x) = 5x2
3x + 4 w punkcie x0 =
2;
(b) f (x) = x2 2x+1 w punkcie x
x2
1
0 = 1;
(c) f (x) = x2 4x+4 w punkcie x
x 2
0 = 2;
3
p
(d) f (x) =
x+1
1 x w punkcie x
x
0 = 0;
p
(e) f (x) =
1+x2
1
p
w punkcie x
25+x2
5
0 = 0;
(f) f (x) = sin 5x w punkcie x
sin 2x
0 = 0;
1
(g) f (x) = e 1 x w punkcie x0 =
1;
(h) f (x) =
x 1
p
w punkcie x
3 x+26 3
0 = 1;
1
(i) f (x) = 3 x2 +5 w punkcie x
1
0 = 0;
5 x2 +3
(j) f (x) = 2x 2 w punkcie x0 = 2;
(k) f (x) = x+5 w punkcie x
x+4
0 =
4;
(l) f (x) = x 3 w punkcie x
x2
9
0 = 3;
2 x
÷
. f (x) = 2
w punkcie x
5
0 = 5
2
x
m. f (x) = 5 x+1 w punkcie x0 =
1
p
n. f (x) = (x 1) 2 x w punkcie x
(x2
1)
0 = 1:
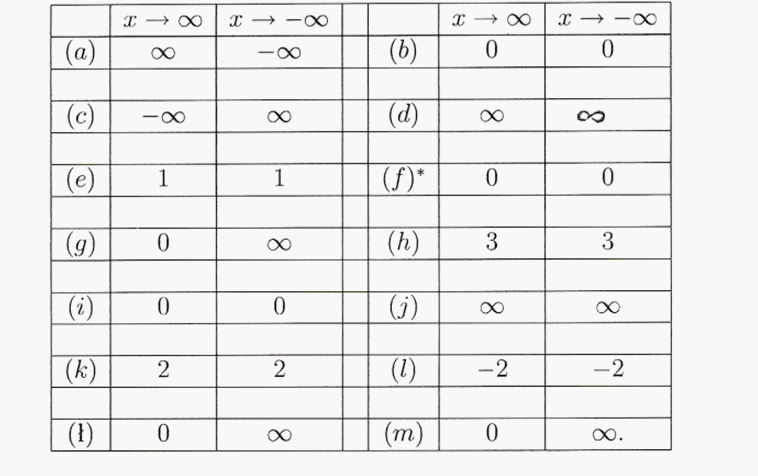
2. Wyzanczyć graniece funkcji f gdy x ! +1 oraz x ! 1: (a) f (x) = 3x2+4 ;
x 1
(b) f (x) = x2+x+1 ;
x3
4
(c) f (x) =
7x5
4x3
x;
(d) f (x) = 3x4
3x3 + 5;
1
(e) f (x) = e 1 x2 ;
(f) f (x) = 2+cos x ;
x2
(g) f (x) = 2 x;
1
(h) f (x) = 3
+1
x2
;
(i) f (x) = 3 4x2 x+1;
(j) f (x) = 32x2 x 3;
(k) f (x) = log 4x3+1
2
;
x3
(l) f (x) = log 9x4 x2+3
2
;
x4+2
3x3
x+5
÷
. f (x) = 1
;
2
x2 +4x+7
m. f (x) = 4
x
1
:
3. Obliczyć granice jednostronne funkcji w podanym punkcie x0 i stwiedzić, czy funkcja posiada w granic ¾
e w punkcie x0
(a) f (x) = x2
x + 5 w punkcie x0 = 1;
4
1
w punkcie x
x2
4
0 =
2;
(c) f (x) = x2+6x+9 w punkcie x
x+3
0 =
3;
p
p
(d) f (x) =
2+x+
2 x w punkcie x
x+1
0 =
1;
1
(e) f (x) = 1 x w punkcie x
4
0 = 0:
4. Zbadać ci ¾
ag÷
ość nast ¾
epuj ¾
acych funkcji
(a)
x
dla
x > 0
f (x) =
x2
dla
x
0;
(b)
8
< x3 + 1 dla x > 1
f (x) =
1
dla
x =
1
: x + 1 dla x < 1;
(c)
x 1
dla
x 6= 1
f (x) =
x3
1
1
dla
x = 1;
3
(d)
3x 3
dla
x 6= 2
f (x) =
x 2
4
dla
x = 2;
(e)
(
log
1
dla
x 6= 2
f (x) =
2
x2+4
0
dla
x =
2;
(f)
2x
dla
x
2
f (x) =
2x
dla
x > 2;
(g)
x
1
dla
x < 0
f (x) =
1
dla
x
0;
(h)
8
x
<
1
dla
x < 0
3
f (x) =
0
dla
x = 0
: x2 1 dla x > 0:
5. Zbadać ciag÷
ość funkcji w zale·
zności od parametru p
x2 + 3x + p
dla
x
1
f (x) =
5x2 + 3p + 1
dla
x > 1:
5
2.1
Odpowiedzi
1
1. (a) 30; (b) 0; (c) 0; (d) 1; (e) 5; (f ) 5=2; (g) e 2 ; (h) 27; (i) 0; (j) 1; (k) nie istnieje; (l) 1 ; (÷
) 125 ; (m) nie istnieje; (n) 1 .
6
8
2
3. (a) granica istnieje i jest równa 5; (b) granica nie istnieje; (c) granica istnieje i jest równa 0; (d) granica nie istnieje; (e) granica nie istnieje.
4. (a) funkcja ciag÷
a; (b) funkcja nie jest ci ¾
ag÷
a; (c) funkcja ci ¾
ag÷
a; (d) funkcja
nie jest ci ¾
ag÷
a; (e) funkcja nie jest ci ¾
ag÷
a; (f) funkcja ci ¾
ag÷
a; (g) funkcja
ci ¾
ag÷
a; (h) funkcja nie jest ci ¾
ag÷
a.
5. Funkcja jest ciag÷
a dla p =
1.
6