(dynamika)
Rozwi¹
(dynamika)
22
a trampolina
b Ziemia
c proca
d œciana
e druga ³ódka
f poduszka powietrzna
g S³oñce
h powietrze
i œcianka rurki
j pod³o¿e
23 Stoj¹cy samochód, bo bezw³adnoœæ cia³a wi¹¿e siê tylko z jego mas¹ (cia³o o wiêkszej masie ma wiêksz¹ bezw³adnoœæ).
24 Wszystkie pytania dotycz¹ zjawiska bezw³adnoœci.
a Zag³ówek chroni przed skutkami zderzenia z samochodem jad¹cym z ty³u.
b Sprinter nie zatrzymuje siê natychmiast, bo ma pewn¹ bezw³adnoœæ i dopie-ro na skutek oddzia³ywania pod³o¿a mo¿e zmniejszyæ swoj¹ szybkoœæ.
c Posiadaj¹ca pewn¹ bezw³adnoœæ skóra przy szybkim ruchu „nie zd¹¿y” siê rozci¹gn¹æ, co w³aœnie jest bolesne.
d Kierowca gwa³townie zahamowa³.
25 Wartoœæ pêdu Ziemi
m
m
kg
24
24
4
28
×m
p = m u= ×
6 10 kg×30000
= ×
6 10 × ×
3 10 kg
= ×
18 10
.
s
s
s
Tak. Kierunek prêdkoœci Ziemi ulega zmianie, wiêc zmienia siê tak¿e kierunek jej pêdu.
26 W tym przypadku spe³nione jest prawo zachowania pêdu dla uk³adu obu ch³opców. W chwili pocz¹tkowej pêd ch³opców by³ równy zeru. Jeœli Krzysiek uzyska³ pêd o wartoœci
m
kg× m
p = 55kg×2
=110
,
K
s
s
to Wojtek uzyska³ pêd o tej samej wartoœci i przeciwnym zwrocie: kg × m
11 m
3 m
m
p =110
= kg
40
×u , st¹d u =
=2
= ,75
2
.
W
s
W
W
4 s
4 s
s
164
2
Wojtek zacz¹³ siê poruszaæ z prêdkoœci¹ o wartoœci 2,75 m/s i o przeciwnym zwrocie ni¿ Krzysiek.
27 W chwili pocz¹tkowej uk³ad cia³: tacka i naczynie z wod¹ – spoczywa. Je-
œli woda uzyska pewn¹ prêdkoœæ w lewo i trafia przed tackê, tacka wraz z naczy-niem uzyskuje pêd o takiej samej wartoœci i przeciwnym zwrocie, tzn. zacznie poruszaæ siê w prawo.
28
a Szybkoœci kul by³y odwrotnie proporcjonalne do ich mas: u : =1 0
: 25
,
= 4 , tzn. v = 4 v .
2 u1
2
1
Wynika to z zasady zachowania pêdu. Pêd uk³adu jest równy zeru przed i po przepaleniu nitki, wiêc wektory pêdów obu kul maj¹ przeciwne zwroty, ale równe wartoœci:
m u = m u .
1
1
2
2
b i c Szybkoœci kul by³yby mniejsze, ale ich iloraz by³by taki sam, jak po-przednio, bo zale¿y on tylko od stosunku mas kul. Gdyby u¿yto innej sprê¿y-ny, to u i u by³yby inne, ale ich iloraz pozosta³by taki sam.
1
2
d Pêdy obu kul uleg³y zmianie na skutek si³ wzajemnego oddzia³ywania. Pêd uk³adu kul nie uleg³ zmianie, bo si³y wewnêtrzne nie mog¹ zmieniæ pêdu uk³adu cia³. Pêd ten zarówno przed jak i po rozprê¿eniu sprê¿yny by³ równy zeru. Wektory pêdów koñcowych kul s¹ wektorami przeciwnymi.
e Pêd kuli o masie m zmieni³ siê na skutek dzia³ania kuli o masie m . Pêd kuli 1
2
o masie m zmieni³ siê na skutek dzia³ania kuli o masie m . Obie te kule od-2
1
dzia³ywa³y na siebie za poœrednictwem sprê¿yny.
29
a Kajak podczas mojego skoku zostaje odrzucony do ty³u z prêdkoœci¹ o wartoœci 2 m/s – tak wynika³oby z zasady zachowania pêdu, zastosowanej do uk³adu: moje cia³o i kajak.
b W rzeczywistoœci kajak ruszy do ty³u z mniejsz¹ szybkoœci¹, bo dzia³a nañ doœæ du¿a si³a zewnêtrzna (opór wody), która powoduje, ¿e pêd uk³adu nie jest zachowany.
c Si³y wewnêtrzne miêdzy mn¹ a kajakiem to si³y tarcia miêdzy moimi stopa-mi a pod³og¹. Powinny to byæ si³y tarcia spoczynkowego, jeœli nie chcê siê po-165
(dynamika)
œlizgn¹æ. Wiadomo, ¿e si³a tarcia spoczynkowego nie mo¿e byæ zbyt du¿a, dla-tego nie mo¿e ona nadaæ mi zbyt du¿ej szybkoœci, tzn. bardzo zmieniæ mojego pêdu.
30
a Pêd uk³adu dzia³o-pocisk przed wystrza³em by³ równy zeru. Jeœli pocisk uzyska³ pêd w jak¹œ strojnê, dzia³o musia³o uzyskaæ pêd o takiej samej warto-
œci zwrócony w przeciwn¹ stronê.
km
1000 m
m
b p =0,36 kg×400
=0,36 kg×400
= 40 kg
.
p
h
3600 s
s
m
m
c 1000 kg×u
,
sk¹d
u =0,04 .
dz = 40 kg s
dz
s
m
m
d p =1000 kg×0,04 = 40 kg
.
dz
s
s
e Pêdy pocisku i dzia³a maj¹ jednakowe wartoœci, ten sam kierunek i przeciwne zwroty.
31 W rozwa¿anym przypadku jest spe³niona zasada zachowania pêdu. Wartoœæ pêdu uk³adu ch³opiec – wózek przed wskoczeniem ch³opca na wózek jest równy wartoœci pêdu ch³opca:
1000 m
1000
m
p = 40 kg×10
=
kg
.
ch
3600 s
9
s
Po wskoczeniu ch³opiec i wózek poruszaj¹ siê z t¹ sam¹ szybkoœci¹ u : x
1000
m
5 m
kg
=(40 kg+160 kg)×u , st¹d u =
.
9
s
x
x
9 s
Wynika to z zasady zachowania pêdu uk³adu ch³opiec-wózek.
32
a Si³a mojego ciê¿aru i si³a nacisku na pod³ogê to nie jest ta sama si³a.
b Chocia¿ maj¹ one te same 1) wartoœci, 2) kierunki i 3) zwroty, to s¹ to ró¿ne si³y.
c Ró¿ni¹ siê: punktami przy³o¿enia (si³a ciê¿aru dzia³a na mnie, a si³a nacisku na pod³ogê), Ÿród³ami dzia³ania (si³a ciê¿aru pochodzi od Ziemi, a Ÿród³em si³y nacisku jestem ja); si³y te maj¹ tak¿e inne natury: si³a ciê¿aru ma naturê grawitacyjn¹, a si³a nacisku – sprê¿yst¹.
166
2
33
a Si³a przyci¹gania ziemskiego pionowo w dó³, si³a pochodz¹ca od nitki (si³a sprê¿ystoœci) pionowo w górê.
b Si³a przyci¹gania ziemskiego – pionowo w dó³, si³a sprê¿ystoœci od pod³o¿a – pionowo w górê, si³a od nitki – poziomo w prawo, jeœli powierzch-nia nie jest g³adka, to si³a tarcia (od pod³o¿a) – poziomo w lewo.
c Si³a przyci¹gania ziemskiego – pionowo w dó³, si³a oporu powietrza – kierunek zgodny z kierunkiem prêdkoœci, zwrot przeciwny.
d Si³a od naszej rêki – pionowo w górê, si³a ciê¿koœci – pionowo w dó³.
e Si³a ciê¿koœci – pionowo w dó³, si³a od lin, na których wisi skoczek – pionowo w dó³, si³a oporu powietrza – pionowo w górê.
f Si³a przyci¹gania ziemskiego – pionowo w dó³, si³a oporu powietrza – kierunek zgodny z kierunkiem prêdkoœci, zwrot przeciwny.
g Si³a ciê¿koœci – pionowo w dó³, si³a (sprê¿ystoœci) od ksi¹¿ki – pionowo w górê, si³a tarcia (od ksi¹¿ki) nadaj¹ca prêdkoœæ – w prawo.
34
a Ch³opiec dzia³a na skrzyniê si³¹ zwrócon¹ w prawo, która jest równowa-
¿ona przez si³ê tarcia, której Ÿród³em jest pod³oga i która jest zwrócona w lewo. Si³a przyci¹gania ziemskiego jest równowa¿ona przez si³ê sprê¿ysto-
œci pod³ogi.
b Si³a przyci¹gania ziemskiego jest równowa¿ona przez zwrócon¹ w górê si³ê sprê¿ystoœci sprê¿yny.
c Na skoczka dzia³a si³a przyci¹gania ziemskiego, która jest równowa¿ona przez dzia³aj¹ce w górê dwie si³y: opór powietrza i si³ê od lin spadochronu.
d Na szalkê dzia³a w dó³ si³a przyci¹gania ziemskiego i si³a nacisku owoców oraz w górê – si³a od sprê¿yny, która równowa¿y si³y zwrócone w dó³.
35
a Racjê mia³a tylko Karolina.
b Jeœli si³y dzia³aj¹ce na cia³o równowa¿¹ siê, a cia³o porusza siê (oczywiœcie ruchem jednostajnym po linii prostej, bo tylko takim ruchem mog³oby siê wówczas poruszaæ), to kierunek i zwrot prêdkoœci cia³a nie musi byæ zgodny z kierunkiem i zwrotem ¿adnej z si³ sk³adowych. O tym, po jakiej prostej cia³o 167
(dynamika)
siê wówczas porusza, decyduje wy³¹cznie jego prêdkoœæ, któr¹ cia³o ma w chwili, gdy si³y zaczê³y siê równowa¿yæ.
36
a Skrzynia i winda spadaj¹ z przyspieszeniem o takiej samej wartoœci, wiêc skrzynia w ogóle nie naciska na pod³ogê windy.
b Si³ê, któr¹ sznurek dzia³a na skrzyniê
F 2
mo¿na roz³o¿yæ na sk³adowe: poziom¹ i
pionow¹, która powoduje zmniejszenie na-
r
F
cisku na pod³o¿e. Nacisk na pod³o¿e F
1
N
jest teraz mniejszy od ciê¿aru.
F = F
F
F
N
c
2
N
Fc
c Ciê¿ar skrzyni mo¿na roz³o¿yæ na dwie
si³y: przyciskaj¹c¹ skrzyniê do deski i œci¹-
gaj¹c¹ skrzyniê z deski. Si³a nacisku ma
F = F
N
p
wartoœæ równ¹ sk³adowej przyciskaj¹cej
skrzyniê do deski, jest wiêc mniejsza od
FN
Fc
F
ciê¿aru skrzyni.
p
d W tym przypadku si³a nacisku ma tak¹
sam¹ wartoœæ jak ciê¿ar.
F = F
N
c
Fc
FN
e Sprê¿yna dzia³a na skrzyniê si³¹ zwrócon¹ w górê, wiêc wartoœæ si³y nacisku jest mniejsza od wartoœci ciê¿aru skrzyni.
37
a 9 N, w prawo,
b 0 N,
c 4 N, w prawo,
d 6 N, w lewo,
e 5 N, w prawo,
f 10 2 N » 14,1 N, w prawo w dó³.
g 5 N, w prawo w dó³.
168
2
38
F
9 N
m
a a =
=
= 45
.
b a = 0 .
m
0,2 kg
s2
4 N
m
m
c a =
=20
.
d a = 30
.
0,2 kg
s2
s2
m
m
e a = 25
.
f a » 70,5
.
s2
s2
m
g a = 25
.
s2
39
a 9 N, w lewo,
b 0 N,
c 4 N, w lewo,
d 6 N, w prawo,
e 5 N, w lewo,
f 14,1 N, w lewo w górê,
g 5 N, w lewo w górê.
40
m
a F + F =1 kg×0,7
,
F + F = 0,7 N ,
1
2
s2
1
2
m
F - F =1 kg×0,1
,
F - F = 0,1 N ,
1
2
s2
1
2
2 F = 0,8 N ,
F = 0,4 N ,
1
1
2 F = 0,6 N ,
F = 0,3 N .
2
2
b F = F 2
2
0,5 N ,
F 1
1 + F 2
=
w
Fw
0,5 N
m
a =
=0,5
.
1 kg
s2
F 2
c W trzecim (przypadek b).
Kierunek przyspieszenia jest zgodny (jak zawsze) z kierunkiem si³y wypad-r
kowej, która le¿y na przek¹tnej prostok¹ta zbudowanego na wektorach si³ F
r
1
i F .
2
169
(dynamika)
41
a I: jednostajnie przyspieszonym, II: jednostajnym, III: jednostajnie opóŸ-
nionym.
m
b I: wartoœæ przyspieszenia: a=1 , II – a=0 , III: wartoœæ opóŸnienia: s2
5 m
a =
.
3 s2
c I: F = 30 N , II: F = 0 , III: F = 50 N.
d I: zgodnie ze zwrotem prêdkoœci, III: przeciwnie do zwrotu prêdkoœci.
42
a
x (m)
100
90
80
70
60
50
40
30
20
10
1
2
3
4
5
6
7
8
9
10
t (s)
170
2
b 1 m, 3 m, 5 m, 7 m, 9 m, 11 m; 12 m, 12 m, 12 m, 12 m, 12 m.
c Przez pierwsze 6 sekund samochód porusza³ siê ruchem jednostajnie przyspieszonym. Wynika to st¹d, ¿e drogi przebyte w kolejnych sekundach maj¹
siê do siebie jak kolejne liczby nieparzyste. W ostatnich czterech sekundach ruch by³ jednostajny, bo w ka¿dej sekundzie samochód przebywa³ takie same drogi.
d Najpierw si³a wypadkowa by³a sta³a i mia³a zwrot zgodny ze zwrotem prêd-koœci samochodu (a wiêc tak¿e zgodny ze zwrotem osi x).
W ostatnich czterech sekundach si³a wypadkowa by³a równa zeru.
2 x
×
2 36 m
m
F = ma ,
a =
2
,
2 =
2
=
1
t
36 s
s2
m
F =1000 kg×2
,
2 = 2000 N = 2 kN
1
s
F = 0 .
2
e
m
2
2
2 2 ×100 s
a t
s
s=
=
=100 m .
2
2
W samej dziesi¹tej sekundzie samochód przeby³by drogê
s = s 19
× =1 m×19=19 m .
10
1
43
a Potrzebna jest wartoœæ prêdkoœci pocz¹tkowej, przy której samochód roz-pocz¹³ hamowanie. Wartoœæ ta wynosi 12 m/s, bo samochód przy koñcu ruchu w ka¿dej sekundzie przebywa³ 12 m.
Jeœli samochód maj¹c szybkoœæ 12 m/s wyhamowa³ po 8 s, to w ka¿dej sekundzie szybkoœæ musia³a maleæ o 1,5 m/s.
m
12 s
m
wartoœæ opóŸnienia
a =
=1,5
.
8 s
s2
171
(dynamika)
m
b F = ma=1000 kg×1,5
.
2 = 1500 N = 1,5 kN
s
Zwrot si³y by³ przeciwny do zwrotu prêdkoœci.
c
m
0+ u
12 s
s=
0 × t =
×8 s= 48 m .
2
2
d Czas hamowania wyd³u¿y³by siê dwukrotnie, bo opóŸnienie zmala³oby 2 razy (tzn. w ci¹gu ka¿dej sekundy szybkoœæ mala³aby tylko o 0,75 m/s). Zatem droga hamowania by³aby tak¿e 2 razy wiêksza.
44
m
1 N =1 kg 1
×
, wiêc
s2
m
kg
N
s2
m
a =10
=10
=10
.
kg
kg
s2
45
m
m
a F =3 kg×10
,
F
=1 kg×10
.
2 = 10 N
2 = 30 N
c 1
s
c 2
s
30 N
m
10 N
m
b a =
=10
,
a =
=10
.
1
3 kg
s2
2
1 kg
s2
Pogl¹d, ¿e jeœli pominiemy opór powietrza, to wszystkie cia³a spadaj¹ z tym samym przyspieszeniem po raz pierwszy wyg³osi³ Galileusz. Przyspieszenie r
to nazywamy przyspieszeniem ziemskim i oznaczamy liter¹ g.
g t 2
c Drogê przebyt¹ podczas spadania wyra¿amy wzorem s=
. Skoro do-
2
niczki spad³y z tej samej wysokoœci, to czas spadania by³ jednakowy.
d Szybkoœæ uzyskana przez cia³o spadaj¹ce swobodnie w czasie t wyra¿a siê wzorem u= g t , wiêc obydwie doniczki uzyska³y jednakowe szybkoœci.
46 Dzia³aj¹ca na wiewiórkê podczas „lotu” si³a przyci¹gania ziemskiego powoduje jej ruch w dó³. Jeœli wiewiórka ma siê znaleŸæ na tej samej wysokoœci po wykonaniu skoku, musi posiadaæ prêdkoœæ pocz¹tkow¹ zwrócon¹ skoœnie w górê.
172
2
47
a Koñce rozci¹gniêtej sprê¿yny dzia³aj¹ w ka¿dej chwili na obie kulki si³ami o takiej samej wartoœci. Poniewa¿ masy kulek s¹ ró¿ne, ró¿ne bêd¹ tak¿e wartoœci ich przyspieszeñ wzglêdem sto³u.
m
0,05 kg×0,6 s2
m
F = m a
,
sk¹d
a =
=0,2
.
1
1 = m a
2
2
2
0,15 kg
s2
m
b F = m a
0,05 kg 0,6
0,03 N ,
1
1 =
×
2 =
s
m
F = m a
0,15 kg 0,2
0,03 N .
2
2 =
×
2 =
s
c W miarê jak naprê¿ona sprê¿yna wraca do swojej luŸnej postaci, wartoœci si³ dzia³aj¹cych na kulki malej¹. Skoro malej¹ wartoœci si³, malej¹ tak¿e warto-
œci przyspieszeñ.
d Ka¿da kulka porusza siê ruchem przyspieszonym z malej¹cym przyspieszeniem. S¹ to ruchy niejednostajnie przyspieszone.
48
r
a ród³em si³y ciê¿aru F jest Ziemia, a przedmiotem dzia³ania flakon.
c
r
ród³em si³y nacisku F jest flakon, a si³a ta dzia³a na stó³. ród³em si³y sprê-
n
r
¿ystoœci F jest stó³, a przedmiotem dzia³ania flakon.
s
r
r
b Do zastosowania I zasady dynamiki potrzebne s¹ si³y F i F ; dzia³aj¹ one c
s
na to samo cia³o, maj¹ tak¹ sam¹ wartoœæ, ten sam kierunek, przeciwne zwroty, wiêc równowa¿¹ siê wzajemnie.
r r
c Do zastosowania III zasady dynamiki potrzebne s¹ si³y F i F , w tym przy-n
s
padku zasadê tê mo¿na zastosowaæ do flakonu i sto³u, które dzia³aj¹ na siebie wzajemnie; si³y te nie mog¹ siê równowa¿yæ, bo dzia³aj¹ na dwa ró¿ne cia³a.
173
(dynamika)
49
a
Przedmiot
WartoϾ
Nr
Nazwa si³y
Zwrot si³y
ród³o si³y
dzia³ania
si³y
si³y
1
Ciê¿ar d¿okeja
500 N
w dó³
Ziemia
d¿okej
2
Ciê¿ar konia
5000 N
w dó³
Ziemia
koñ
Nacisk konia z d¿okejem
3
5500 N
w dó³
koñ
pod³o¿e
na pod³o¿e
Nacisk d¿okeja na grzbiet
4
500 N
w dó³
d¿okej
koñ
konia
Si³a sprê¿ystoœci grzbietu
5
500 N
w górê
koñ
d¿okej
konia
6
Si³a sprê¿ystoœci pod³o¿a
5500 N
w górê
pod³o¿e
koñ
b O spoczynku d¿okeja decyduje równowaga si³ 1 i 5. O spoczynku konia decyduje równowaga si³ 2, 4, 6.
c 4 i 5; 3 i 6.
d Nie.
50
a Si³omierz wska¿e 50 N.
b Lina ci¹gnie hak w lewo si³¹ o wartoœci 50 N, wiêc hak dzia³a na linê w prawo si³¹ o takiej samej wartoœci.
c W obu przypadkach na koñce liny dzia³aj¹ si³y o takich samych wartoœ-
ciach.
d Nie, zawsze mo¿emy przeprowadziæ rozumowanie podobne do przeprowa-dzonego wy¿ej i utwierdziæ siê w tym przekonaniu.
e Nie, by³oby to sprzeczne z III zasad¹ dynamiki.
174
2
51
a Pogl¹d A nie jest s³uszny. Gdyby miêdzy klockiem le¿¹cym na stole a sto³em nie by³o tarcia, to zawieszenie na lince nawet klocka o bardzo ma³ej masie spowodowa³oby ruch przyspieszony ca³ego uk³adu. Jeœli uk³ad spoczywa, to widocznie na klocek le¿¹cy na stole dzia³a si³a tarcia o wystarczaj¹co du¿ej wartoœci, aby zrównowa¿yæ si³ê pochodz¹c¹ od linki.
WypowiedŸ B jest niepoprawna, bo gdyby si³a tarcia mia³a wiêksz¹ wartoœæ ni¿ si³a ciê¿aru klocka o masie m , to ca³y uk³ad porusza³by siê z przyspiesze-1
niem „do ty³u”, bowiem tak by³aby zwrócona si³a wypadkowa, dzia³aj¹ca na ca³y uk³ad.
WypowiedŸ C: Z faktu, ¿e klocek spoczywa nie mo¿na wyci¹gaæ wnioski,
¿e na klocek nie dzia³a si³a tarcia. W tym przypadku na klocek o masie m 2
dzia³a si³a tarcia spoczynkowego, bo klocek ten ci¹gnie linka (tarcie spoczynkowe pojawia siê zawsze wtedy, gdy podczas spoczynku wystêpuje si³a rów-noleg³a do powierzchni styku dwóch cia³).
Autor wypowiedzi D pope³ni³ podobny b³¹d jak ta osoba, która wypowie-dzia³a zdanie B. Gdyby tak by³o, to klocek o masie m porusza³by siê z przy-2
spieszeniem w lewo, bo tak by³aby zwrócona dzia³aj¹ca nañ si³a wypadkowa.
Skoro spoczywa, to si³y te równowa¿¹ siê, zatem musz¹ one mieæ jednakowe wartoœci.
b Poprawne wyjaœnienie:
Spoczynek klocka o masie m 2
t³umaczymy tak: si³a od linki
(zwrócona w prawo) i si³a tar-
m 2
T
N
cia spoczynkowego, zwana tak-
¿e si³¹ tarcia statycznego (zwró-
cona w lewo) równowa¿¹ siê:
N
N = T .
m
Klocek o masie m spoczywa,
1
1
bo si³a jego ciê¿aru (w dó³) i
m g
1
si³a od linki (w górê) równo-
wa¿¹ siê:
m g = N .
1
Wynika z tego, ¿e T = m g . Si³a tarcia spoczynkowego ma wiêc tak¹ sam¹
1
wartoœæ, jak si³a ciê¿aru klocka wisz¹cego. Si³a ta jest mniejsza od wartoœci maksymalnej tarcia statycznego, przy której klocek móg³by ruszyæ.
175
(dynamika)
Uwaga: Na rysunku zaczepiliœmy wektor si³y tarcia w œrodku klocka (tak jak siê to czêsto robi), mimo ¿e dzia³a ona na doln¹ powierzchniê klocka, sty-kaj¹c¹ siê z pod³o¿em.
52
a i b Szybkoœæ kropli deszczu jest znacznie mniejsza od obliczonej z powodu oporu powietrza. Kropla spada najpierw ruchem przyspieszonym, ale przy wzrastaj¹cej szybkoœci wzrasta wartoœæ si³y oporu powietrza. Gdy wzroœnie ona tak, ¿e zrównowa¿y ciê¿ar kropli, to od tej chwili kropla spada ruchem ruchem jednostajnym.
c Nazwa pochodzi st¹d, ¿e prêdkoœæ kropli wzrasta tylko do pewnej granicy, przy której nastêpuje równowaga si³ ciê¿aru i oporu powietrza.
u
Fop
u gran
mg
t
53 Na samochód dzia³a tak¿e si³a oporu powietrza. Jej wartoœæ wzrasta wraz ze wzrostem szybkoœci samochodu, wiêc wartoœæ si³y wypadkowej maleje.
Samochód porusza siê ruchem niejednostajnie przyspieszonym, jego szybkoœæ wzrasta, ale wartoœæ przyspieszenia maleje. Po osi¹gniêciu pewnej szybkoœci wartoœæ si³y oporu powietrza wzroœnie tak, ¿e zrównowa¿y si³ê ci¹gu i od tej chwili samochód porusza siê ruchem jednostajnym.
176
Rozwi¹zania
2
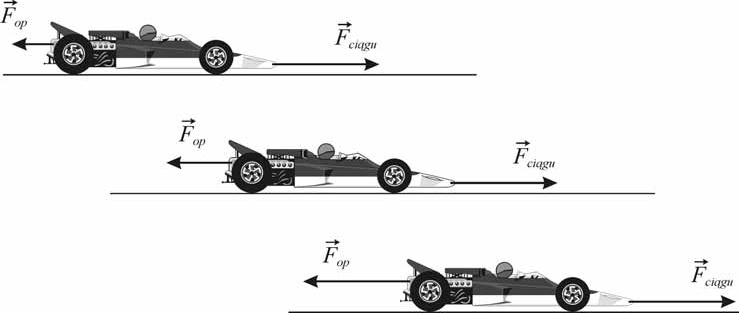
54
a Samochód nie zacznie siê poruszaæ, bo nie oddzia³uje poziomo z ¿adnym innym cia³em.
r
r
b Si³a F dzia³a w kierunku poziomym, ku ty³owi samochodu, wiêc si³a F
1
2
dzia³a w przód. Si³y te maj¹ takie same wartoœci (III zasada dynamiki).
r
c S¹ to si³y tarcia. Si³ê F nazywamy w praktyce si³¹ ci¹gu.
2
d Si³y te nie równowa¿¹ siê wzajemnie, bo ka¿da dzia³a na inne cia³o.
r
e Samochód rusza pod dzia³aniam si³y F .
2
55
a
1. Skoro na skrzynki nie dzia³a poziomo ¿adna si³a, si³y tarcia nie ma.
2. Skrzynki spoczywaj¹, wiêc jest spe³niona I zasada dynamiki. Wartoœæ r
si³y tarcia jest równa wartoœci si³y F , a jej zwrot jest przeciwny.
1
r
r
3. Wartoœæ si³y tarcia jest równa sumie wartoœci si³ F i F , a jej zwrot 1
2
jest przeciwny.
4. Wartoœæ si³y tarcia (kinetycznego) jest na pewno mniejsza od sumy r
r
wartoœci si³ F i F , bo skrzynki poruszaj¹ siê z przyspieszeniem.
1
3
b Wartoœæ si³y tarcia zale¿y od wartoœci si³y, która przyciska cia³o do pod³o¿a. Piotrek powinien wiêc przesuwaæ ka¿d¹ skrzynkê oddzielnie.
177
(dynamika)
56
a Szafa pozostanie w spoczynku. Z I zasady dynamiki wiemy, ¿e si³y musz¹
siê wtedy równowa¿yæ. Wynika z tego, ¿e si³a o wartoœci 80 N musi byæ wówczas zrównowa¿ona przez si³ê o przeciwnym zwrocie i o wartoœci równej 80 N. Jest to tzw. si³a tarcia spoczynkowego (zwanej tak¿e si³¹ tarcia statycznego).
b Skrzynia nadal pozostanie w spoczynku. Si³y znowu równowa¿¹ siê, wiêc si³a tarcia spoczynkowego bêdzie mia³a wówczas wartoœæ 180 N.
c Maksymalna wartoœæ tarcia spoczynkowego (zwanego tak¿e maksymal-nym tarciem statycznym) wynosi 200 N. Gdy dzia³amy si³¹ wiêksz¹, skrzynia zostanie wprawiona w ruch. Podczas ruchu wystêpuje tarcie kinetyczne, które-go wartoœæ jest mniejsza od 200 N, zatem si³a wypadkowa bêdzie mia³a wartoœæ wiêksz¹ od 40 N, ale bêdzie ona sta³a (tarcie kinetyczne ma sta³¹ wartoœæ podczas ruchu), wiêc ruch szafy bêdzie jednostajnie przyspieszony.
57
a Skoro podczas dzia³ania si³y o wartoœci 180 N szafa posiada przyspieszenie, to widocznie si³a wypadkowa dzia³aj¹ca na ni¹ jest ró¿na od zera. Wynika z tego, ¿e wartoœæ si³y tarcia kinetycznego, dzia³aj¹cego na szafê jest mniejsza od 180 N.
b Mo¿na obliczyæ wartoœæ si³y tarcia kinetycznego na podstawie II zasady dynamiki:
m
180 N - T = ma ,
180 N - T
,
k = 50 kg×0,2
k
s2
T =180 N-10 N ,
T =170 N .
k
k
c Si³a tarcia kinetycznego nie zale¿y od tego, jakim ruchem porusza siê cia³o, nie zale¿y te¿ od jego szybkoœci, ani od wartoœci przyspieszenia, zatem wartoœæ tarcia kinetycznego w dalszym ci¹gu bêdzie wynosi³a 170 N. Si³a wypadkowa ma³aby wartoœæ 200 N -170 N= 30 N. Wartoœæ przyspieszenia szafy wynosi³aby
178
2
30 N
m
a =
=0,6
.
50 kg
s2
Tak wiêc zmieni³aby siê si³a wypadkowa i przyspieszenie szafy.
179