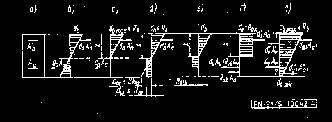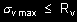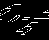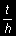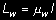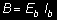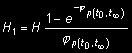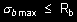
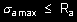
PN-91/S-10042 Obiekty mostowe Konstrukcje betonowe, żelbetowe i sprężone Projektowanie Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

Powrót do spisu treści

Poprzednia strona

6. ZASADY PROJEKTOWANIA

6.1. Dobór materiałów. Zalecane do stosowania klasy betonu w różnych elementach mostowych podano w 3.1 i 3.2.

Zestaw asortymentów stali stosowanych w budowie mostów betonowych podano w 4.1 i 4.2. Zaleca się:

- stosowanie wyższych klas stali do wyższych klas betonu,

- stosowanie do betonu zbrojonego prętów żebrowanych,

- stosowanie lin do strunobetonu,

- stosowanie odmiany I cięgien sprężających,

- preferowanie kabli n ⋅ 15,5 lub innych podobnych zamiast lin wielozwitych.

6.2. Schematy zastępcze. Obliczeniowe schematy zastępcze powinny możliwie dokładnie odpowiadać rzeczywistej pracy mostu.

6.3. Rozpiętości obliczeniowe

6.3.1. Dźwigary główne. Rozpiętości obliczeniowe l t przęseł dźwigarów głównych należy przyjmować:

- jako rozpiętość przęsła w osi łożysk,

- dla małych rozpiętości przy podparciu bez łożysk dla l t ≤ 10 m, l t = 1,05 l 0, gdzie l 0 - rozpiętość w świetle krawędzi podparcia, z tym że l t ≤ l 0 + h, gdzie h - wysokość dźwigara na podporze,

- jako rozstaw osiowy rygli i słupów w ustrojach ramowych,

- w dźwigarach ze wspornikami dla wspornika jego długość od osi podpory do końca wspornika.

6.3.2. Elementy drugorzędne. Rozpiętości obliczeniowe elementów drugorzędnych należy przyjmować:

- jako rozstaw osiowy elementów połączonych monolitycznie z dźwigarami, jeśli szerokość tych elementów nie jest większa od 1/6 ich rozstawu,

- w innych przypadkach l t = 1,05 l 0 z tym, że l t ≤ l 0 + h, (wg 6.3.1), gdzie h - wysokość dźwigara drugorzędnego na podporze, lub wysięg od krawędzi utwierdzenia dla wsporników.

6.3.3. Inne przypadki. Można przyjmować inne rozpiętości elementów lub rozpatrywać inne przypadki konstrukcji i ich modelu geometrycznego pod warunkiem właściwego uzasadnienia.

6.4. Zasady obliczeń wytrzymałościowych i wymiarowanie. Konstrukcje mostowe z betonu niezbrojonego, żelbetowe i z betonu sprężonego należy wymiarować przy założeniu liniowego rozkładu odkształceń i naprężeń w betonie z pominięciem strefy rozciąganej z wyjątkiem przypadków w których założono inaczej.

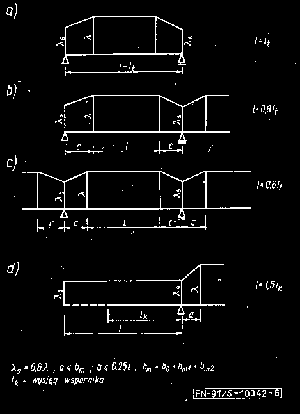
Schematy różnych przypadków rozkładu naprężeń podano na rys. 4.

Rys. 4. Schematy rozkładów naprężeń w różnych przypadkach:

a) przekrój, b) przypadek fazy I (zginanie), c) przypadek fazy II (zginanie); wykres trójkątny naprężeń w strefie ściskania, d) zginanie elementu betonowego bez zarysowania, e) przypadek przekroju z rysą, f) przypadek fazy III; wykres prostokątny w strefie ściskania przy sprawdzaniu nośności granicznej, g) przypadek ściskania mimośrodowego elementów żelbetowych lub sprężonych

Wymiarowanie polega na spełnieniu warunków (27), (28), (29) lub (30), czyli na porównaniu naprężeń obliczeniowych z wytrzymałościami obliczeniowymi

(27)

(28)

INTEGRAM BUDOWNICTWO

Część 7 Strona 1

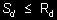
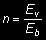
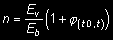
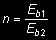
PN-91/S-10042 Obiekty mostowe Konstrukcje betonowe, żelbetowe i sprężone Projektowanie Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

(29)

lub porównaniu obliczeniowych sił przekrojowych S d z odpowiednią nośnością obliczeniową R d (30)

Przykłady zastosowania metody NL podano w załączniku 1.

Fazę I (z uwzględnieniem rozciągania betonu) należy przyjmować w obliczeniach elementów z betonu niezbrojonego, betonu zbrojonego przy ściskaniu z małym mimośrodem, sprężonego przy sprężeniu pełnym oraz ograniczonym i przy określaniu sztywności na zginanie elementów żelbetowych i sprężonych (rys. 4b), d) i g).

Fazę II (bez uwzględniania rozciągania betonu) stosuje się do wymiarowania elementów żelbetowych i częściowo sprężonych oraz do obliczania ugięć elementów zarysowanych wg rys. 4c).

Faza III. Sprawdzenie nośności granicznej w założeniu uplastycznienia fazy ściskanej wg rys. 4f).

6.5. Przekroje

6.5.1. Przekrój brutto i netto. Przekrój brutto jest to całkowity przekrój elementu bez potrącania otworów na pręty zbrojeniowe i cięgna sprężające oraz osłony lub kanały kablowe, uważany jako jednolity przekrój betonowy.

Przekrój netto jest to pole przekroju elementu z potrąceniem wszystkich otworów na pręty zbrojeniowe i zbrojenie sprężające.

6.5.2. Przekrój sprowadzony, używany do wyznaczania naprężeń i sztywności, jest to przekrój zastępczy równy całkowitemu polu przekroju brutto powiększonemu o pole przekroju stali zbrojeniowej lub sprężającej pomnożonemu przez liczbę n stanowiącą stosunek współczynnika sprężystości liniowej stali do analogicznego współczynnika betonu uwzględniającego wpływ czasu obciążenia.

Obciążenia krótkotrwałe są to obciążenia doraźne, w tym ruchome i inne zmienne, w tym stałe których okres nie przekracza jednego miesiąca. Obciążenia długotrwałe są to obciążenia stałe lub prawie stałe, w tym wywołane siłami sprężającymi. Rzeczywiste obciążenia są obciążeniami długotrwałymi z nakładającymi się na nie obciążeniami krótkotrwałymi. Jeśli siły wewnętrzne lub naprężenia wywołane obciążeniami zmiennymi w miarodajnych przekrojach (punktach) nie przekraczają 25% obciążeń długotrwałych umownie uznaje się obciążenia długotrwałe jako dominujące.

Jeśli obciążenia długotrwałe wynoszą nie więcej niż 25% obciążeń krótkotrwałych obciążenia krótkotrwałe uznaje się za dominujące.

Przy obciążeniach krótkotrwałych przyjąć należy wartość n jako stosunek wartości współczynnika E = 200 000 MPa do współczynnika sprężystości betonu wg rozdz. 3 tabl. 3 lub innych udokumentowanych wartości

(31)

Dla betonów stosowanych w mostach żelbetowych można przyjąć n = 7. Jeśli nie uwzględnia się wpływów reologicznych i skurczu przy obciążeniach długotrwałych należy przyjąć 3 n lub n = 20. Przy obciążeniach pośrednich można przyjąć 2 n lub n = 15 w odniesieniu do wszystkich obciążeń.

Przy obliczeniach konstrukcji mostów z betonu sprężonego można stosować te same zasady przyjmując n = 6 dla obciążeń krótkotrwałych i n = 18 dla obciążeń długotrwałych lub przyjmować E b podzielone przez wartość 1 + ϕ(t0, t) (32)

gdzie ϕ(t0, t) współczynnik pełzania wg tabl. 5.

Dla przekrojów złożonych z betonów o różnych właściwościach należy uwzględnić cechy sprężyste tych betonów łącznie z ich odkształceniami skurczu i pełzania, wprowadzając

- dla obciążeń krótkotrwałych

(33)

gdzie E b1 i E b2 - współczynniki sprężystości betonu w części 1 i 2 przekroju zespolonego zgodnie z tabl. 3

- dla obciążeń długotrwałych

INTEGRAM BUDOWNICTWO

Część 7 Strona 2

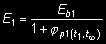
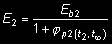
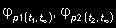
PN-91/S-10042 Obiekty mostowe Konstrukcje betonowe, żelbetowe i sprężone Projektowanie Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

(34)

gdzie E 1 i E 2 - współczynniki sprężystości betonu uwzględniające czas obciążenia t 1 i t 2 każdej części przekroju zgodnie z tabl. 3 i punktem 3.6.2.

(35)

(36)

gdzie

- współczynniki pełzania w części 1 lub 2 wg tabl. 5 i punktu 3.6.2 dla czasów obciążeń t 1 i

t 2 na okres t = ∞.

Do obciążeń długotrwałych zalicza się tu ciężary własne i siły sprężające.

Przekrój sprowadzony należy stosować w obliczeniach naprężeń w elementach z betonu zbrojonego lub sprężonego przy zapewnieniu zespolenia cięgien z betonem.

6.5.3. Szerokość współpracująca płyty z żebrem

6.5.3.1. Warunki współpracy płyty z żebrem. Współpracę płyty z żebrem w belce teowej należy uwzględniać, jeśli są spełnione następujące warunki:

a) grubość płyty t jest nie mniejsza niż 0,05 całkowitej wysokości belki h (żebra wraz z płytą), b) płyta jest monolityczna lub zespolona z żebrem,

c) zbrojenie połączenia płyty monolitycznej z żebrem jest wykonane zgodnie z 8.4.

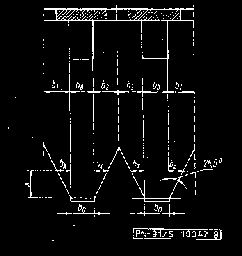
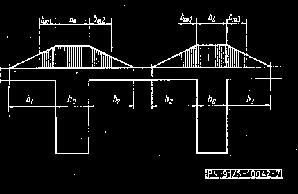
6.5.3.2. Szerokość współpracująca przy zginaniu. Jeśli nie wykonuje się dokładnych obliczeń dźwigarów płytowych, belkowo-płytowych i rusztów można wprowadzić zastępczy model szerokości współpracującej zapewniający w przybliżeniu równoważne wyniki przy obliczaniu wymiarów lub sprawdzaniu bezpieczeństwa wg rys. 5.

Rys. 5. Schemat płyt współpracujących

Do obliczeń statycznych należy przyjmować przekrój brutto.

Przy określaniu wymiarów przekrojów, ustalaniu zbrojenia, wyznaczaniu naprężeń porównywalnych z wytrzymałościami obliczeniowymi zgodnie z zasadami wg 6.4 w przekrojach układów belkowo-płytowych należy przyjmować szerokość współpracującą płyty po jednej lub obydwu stronach żebra.

Szerokość współpracującą płyty z jednej strony żebra należy wyznaczać korzystając ze współczynnika λ

oznaczającego stosunek tej szerokości do połowy rozpiętości płyty w świetle lub do wysięgu wspornika płyty wg wzorów (37)

w których:

b 1 - całkowity wysięg wspornika,

b 2 - połowa rozpiętości w świetle płyty pola skrajnego,

b 3 - połowa rozpiętości w świetle płyty pola wewnętrznego,

b m1 - szerokość współpracująca płyty na wsporniku,

b m2 - szerokość współpracująca płyty z jednej strony żebra w polu skrajnym,

INTEGRAM BUDOWNICTWO

Część 7 Strona 3

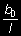
PN-91/S-10042 Obiekty mostowe Konstrukcje betonowe, żelbetowe i sprężone Projektowanie Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

b m3 - szerokość współpracująca płyty z jednej strony żebra w polu pośrednim.

Wartości λ podane w tabl. 10 obliczono w zależności od:

t/ h, b 0/ l oraz b 1/ l przy określaniu b m1/ b 1

t/ h, b 0/ l oraz b 2/ l przy określaniu b m2/ b 2

t/ h, b 0/ l oraz b 3/ l przy określaniu b m3/ b 3

gdzie:

b 0 - szerokość żebra,

t - grubość płyty,

h - całkowita wysokość żebra łącznie z płytą,

l - rozpiętość podporowa l t przęsła swobodnie podpartego,

- odległość miejsc zerowych momentów zginających w układach ciągłych, którą w przybliżeniu można przyjąć: dla przęsła skrajnego l = 0,8 l t

dla przęseł wewnętrznych l = 0,6 l t.

Dla wsporników o wysięgu b 1 miarodajną do wyznaczenia szerokości współpracującej wartość l należy przyjąć równą 1,5 b 1.

Nad podporami żeber (dźwigarów) współczynnik λ zmniejsza się do wielkości λs = 0,6 λ, a szerokość współpracującą płyty do wielkości 0,6 λ b mi.

Na długości przypodporowej c ≤ 0,25 l t wartości λ oraz b mi należy obliczać wg interpolacji liniowej (rys. 6).

Szerokości współpracujące płyt ściskanych należy uwzględniać przy wymiarowaniu dźwigarów teowych, dwuteowych, skrzynkowych na działanie momentów zginających i sił poprzecznych, jeśli nie wykonuje się dokładnych obliczeń rozkładu naprężeń w przekroju poprzecznym. W odniesieniu do płyt rozciąganych można wykorzystywać szerokości współpracujące przy założeniu, że maksymalne naprężenie rozciągające w betonie nie przekroczy wartości wytrzymałości obliczeniowej na rozciąganie.

Gdy jednostronny wysięg płyty b 1 ≤ 0,3 h, należy przyjmować λ = 1.

Tablica 10. Wartości współczynnika λ do wyznaczania szerokości współpracującej płyty b 1/ l lub b 2/ l lub b 3/ l

1,0

0,9

0,8

0,7

0,6

0,5

0,4

0,3

0,2

0,1

0,10

0,18

0,20

0,22

0,26

0,31

0,38

0,48

0,62

0,82

1,00

0,10

0,05

0,18

0,20

0,22

0,26

0,31

0,38

0,48

0,62

0,82

1,00

0,02

0,19

0,22

0,25

0,28

0,33

0,39

0,48

0,62

0,82

1,00

0,10

0,19

0,21

0,24

0,28

0,32

0,39

0,49

0,63

0,82

1,00

0,15

0,05

0,20

0,22

0,25

0,28

0,33

0,40

0,50

0,64

0,83

1,00

0,02

0,23

0,26

0,28

0,32

0,37

0,44

0,53

0,67

0,84

1,00

0,10

0,21

0,23

0,26

0,30

0,35

0,42

0,52

0,66

0,84

1,00

0,20

0,05

0,23

0,26

0,30

0,34

0,38

0,45

0,55

0,68

0,85

1,00

0,02

0,30

0,33

0,36

0,41

0,47

0,54

0,63

0,75

0,88

1,00

0,10

0,28

0,31

0,35

0,39

0,44

0,50

0,58

0,70

0,86

1,00

0,30

0,05

0,32

0,36

0,40

0,44

0,50

0,56

0,63

0,74

0,87

1,00

0,02

0,42

0,46

0,50

0,55

0,62

0,69

0,78

0,85

0,91

1,00

INTEGRAM BUDOWNICTWO

Część 7 Strona 4

PN-91/S-10042 Obiekty mostowe Konstrukcje betonowe, żelbetowe i sprężone Projektowanie Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

Rys. 6. Schemat rozkładu λ wzdłuż długości przęseł

Poza szerokością współpracującą płyta również podlega działaniu sił wewnętrznych i naprężeń o wartości wynikającej z obliczeń. Jeśli nie wykonuje się dokładnych obliczeń można założyć rozkład naprężeń według rys. 7. Przyjęto w nim założenie, że na szerokości żebra naprężenia odpowiadają poziomowi wyznaczonemu przy założeniu szerokości współpracującej, na odległości b mi wynoszą połowę tej wartości, zaś w odległości 2 b mi wynoszą zero. Siły wewnętrzne wywołane lokalnymi naciskami kół poza szerokością współpracującą mogą się nakładać z siłami wewnętrznymi stanowiącymi normową podstawę wymiarowania żebra z płytą współpracującą.

Rys. 7. Uproszczony rozkład naprężeń rzeczywistych

6.5.3.3. Szerokość współpracująca płyty w przenoszeniu sił sprężających. Szerokość współpracującej płyty w przenoszeniu siły podłużnej zaczepionej w przekroju końcowym zmienia się liniowo w zależności od odległości x. W

miejscu przyłożenia, przy x = 0 odpowiada szerokości żebra, czyli b = b 0. W odległości x szerokość ta wynosi b = b 0 + x, co wynika z zależności b = b 0 + 2×tgα. Kąt rozkładu siły z miejsca obciążenia przyjęto α = 26,5° (rys. 8).

6.5.3.4. Szerokość współpracująca pasm płytowych przy obciążeniu skoncentrowanym. Obciążenie skoncentrowane na pasmie płytowym rozumianym zgodnie z 6.6.3 może być traktowane jako przenoszone przez wycinek pasma o szerokości b m w sposób równomierny. Szerokość b m zależy od położenia obciążenia, szerokości INTEGRAM BUDOWNICTWO

Część 7 Strona 5

PN-91/S-10042 Obiekty mostowe Konstrukcje betonowe, żelbetowe i sprężone Projektowanie Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

pasma i jego grubości oraz sposobu podparcia pasma. W tabl. 11 przytoczono wartości b m dla czterech wariantów podparcia przy wyznaczaniu zastępczych wartości momentów zginających m w przekroju podporowym utwierdzenia oraz w przęśle i sił poprzecznych q w przekrojach podporowych.

Rys. 8. Szerokość współpracująca b m płyty obciążonej siłą podłużną na końcu żebra

6.6. Rodzaje elementów ze względu na modele mechaniczne

6.6.1. Dobór modelu. Do określania sił przekrojowych należy dobrać odpowiedni model mechaniczny elementu.

W budownictwie mostowym mogą to być:

- elementy prętowe (belki o różnych przekrojach - w tym skrzynkowych, słupy, łuki, pale).

- płyty, dźwigary belkowo-płytowe,

- tarcze, układy tarczowe,

- powłoki, sklepienia,

- bryły.

Tablica 11. Szerokości zastępcze pasm płytowych obciążonych na polu prostokąta INTEGRAM BUDOWNICTWO

Część 7 Strona 6

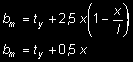
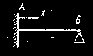
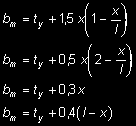
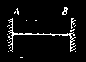
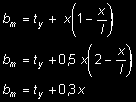
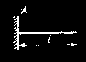
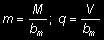
PN-91/S-10042 Obiekty mostowe Konstrukcje betonowe, żelbetowe i sprężone Projektowanie Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

Schemat

Wielkość

b m

m L

V A

m L

m A

V A

V B

m L

m A

V A

m L

b m = t y + 1,5 x

V A

b m = t y + 0,3 x

M - maksymalny moment,

V - maksymalna siła poprzeczna na podporze z indeksem A (lub B),

x - współrzędna osi obciążenia.

6.6.2. Elementy prętowe. Jaku pręty należy traktować elementy o dowolnym przekroju poprzecznym, w których jeden wymiar jest co najmniej czterokrotnie większy od każdego z pozostałych. Elementy zginane, w których odległość sąsiednich miejsc zerowych wartości momentów zginających równa się co najmniej dwukrotnej wysokości całkowitej przekroju można obliczać korzystając z modelu mechaniki prętów lub układów prętowych.

Obciążenie przyłożone do powierzchni elementu należy sprowadzić do osi środków ciężkości w przekrojach poprzecznych rozkładając je pod kątem 45° przez warstwy niekonstrukcyjne (np. nawierz chnię i warstwy nadbetonu) oraz samą belkę. Taki rozkład obciążenia należy przewidzieć od strony podparć i łożysk. Obciążenie rozłożone wzdłuż

osi musi być równoważne obciążeniu przyłożonemu do elementu.

Warunkiem, aby elementy o przekrojach cienkościennych, otwartych lub zamkniętych mogły być traktowane jako pręty jest warunek nieodkształcalności przekroju poprzecznego.

W odniesieniu do prętów obowiązują wytrzymałościowe kryteria bezpieczeństwa wg 6.4 oraz warunki bezpieczeństwa ze względu na groźbę utraty stateczności.

Łuki są to pręty krzywoliniowe obciążone w płaszczyźnie od strony wypukłej. Metoda obliczania łuku zależy od wyniosłości łuku f/ l oraz jego szerokości b, gdzie: f - strzałka łuku, l - rozpiętość teoretyczna łuku.

Dla łuków bezprzegubowych l należy przyjmować jako odległość między środkami przekrojów zamocowania, dla łuków przegubowych jako odległość między środkami przegubów.

Łuki z betonu niezbrojonego powinny być obliczane ze względu na warunek nie wystąpienia rozciągań, przy stałych obciążeniach według metody linii ciśnień. Jeśli f/ l ≥ 1/3 można nie uwzględniać w obliczeniach części poniżej wezgłowi.

Obliczenia za pomocą metody linii ciśnień mogą być zastosowane, jeśli; b/ l ≥ 1/4, f/ l ≥ 1/3, 1 ≤ 20 m dla mostów drogowych i l ≤ 10 m dla mostów kolejowych, zaś odległości między górnym poziomem zwornika i nawierzchni 0,50 m dla mostów drogowych oraz 1,50 m dla mostów kolejowych.

Do bardziej płaskich łuków należy stosować beton zbrojony i uwzględniać wpływ części budowli poniżej wezgłowi, a szczególnie fundamentów na działanie sił rozporowych wywołanych obciążeniami i wpływem temperatury.

INTEGRAM BUDOWNICTWO

Część 7 Strona 7

PN-91/S-10042 Obiekty mostowe Konstrukcje betonowe, żelbetowe i sprężone Projektowanie Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

Długość wyboczeniową L w dla łuków bezprzegubowych należy obliczać wg wzoru

w którym współczynnik µw w zależności od wyniosłości łuku f/ l należy przyjmować wg tabl. 12.

Tablica 12. Współczynnik µw do obliczania długości wyboczeniowej Lw mostów łukowych f/ l

0,10

0,15

0,20

0,25

0,30

0,35

0,40

0,45

0,50

µw

0,36

0,37

0,38

0,40

0,42

0,45

0,48

0,51

0,54

Dla łuków dwuprzegubowych należy przyjąć współczynniki µw1 = 1,55 µw, dla łuków trójprzegubowych µw2 1,60 µw.

6.6.3. Płyty. Jako płytę należy traktować płaski element obciążony prostopadle do płaszczyzny środkowej, w której wymiar grubości płyty t jest co najmniej czterokrotnie mniejszy od mniejszego z pozostałych lub od odległości między punktami zerowymi krzywizny w układach ciągłych.

Obciążenie skoncentrowane, działające na płytę należy sprowadzić do płaszczyzny środkowej płyty zakładając jego rozkład pod kątem 45° przez warstwy niekonstrukcyjne i połow ę grubości płyty w kierunkach prostopadłych względem obwodu zarysu obciążenia. Dla obciążenia na polu prostokąta a× b przy grubości warstw niekonstrukcyjnych s oraz grubości płyty t pole rozkładu obciążenia wyniesie

Płaszczyzną środkową płyty jest płaszczyzna przechodząca przez środek grubości płyty, niezależnie od występującego w niej zbrojenia.

Minimalną grubość płyt żelbetowych pomostu mostów drogowych i kolejowych należy projektować zgodnie z rozdz. 12, nawet gdyby obliczenie statyczne wykazywało możliwość zastosowania płyty o mniejszej grubości.

Płyty o kącie naroża w planie różniącym się od kąta prostego nie więcej niż 15° mo żna obliczać jak prostokątne.

Płyty o skosach większych należy obliczać jako płyty ukośne.

Pasmem płytowym nazywa się płytę prostokątną, której naprzemianległe boki są znacznie dłuższe od pozostałych.

Pasmem płytowym jest płyta oparta na dwóch równoległych podporach lub utwierdzona jednostronnie i swobodnie nadwieszona na pozostałych lub przynajmniej na przeciwległym boku.

6.6.4. Tarcze. Płaski element, którego długość jest mniejsza od czterokrotnej wysokości, obciążony w płaszczyźnie środkowej, należy traktować jako tarczę i obliczać według zasad mechaniki budowli.

Efekt tarczy należy uwzględniać w strefie przekrojów podporowych jako lokalny wpływ obciążenia skupionego w strefie podparcia oraz w strefie zakotwień, jeśli nie stosuje się przestrzennego modelu. Efekt tarczowy występuje w węzłach rusztów, np. w połączeniu elementów poprzecznych z podłużnymi.

Elementy tarczowe mogą podlegać jednoczesnemu zginaniu. Wtedy należy stosować nakładanie się wyników obliczeń elementu jako tarczy i jako płyty zgodnie z wymaganiami mechaniki dźwigarów powierzchniowych.

Przyczółki są kombinacjami elementów tarczowych i płytowych. Studnie o przekroju prostokątnym, dźwigary skrzynkowe i inne są również kombinacjami elementów tarczowych i innych.

6.6.5. Powłoki. Element przestrzenny o krzywoliniowej powierzchni środkowej i grubości nie większej niż 1/4

najmniejszego wymiaru poprzecznego, należy traktować jako powłokę i obliczać według zasad mechaniki budowli.

Sklepienia są to powłoki o zmiennej w jednej płaszczyźnie krzywiźnie projektowane i wymiarowane na zasadzie linii ciśnień jako powłoki minimalnie zbrojone, nawet zbrojone wyłącznie tylko ze względu na skurcz.

W projektowaniu ich obowiązują zasady i warunki jak przy łukach. Ich cechą jest stała grubość w przekroju poprzecznym.

Rurociągi i przepusty o przekroju kołowym lub innym są również powłokami o przekroju zamkniętym o stałej lub zmiennej krzywiźnie w płaszczyźnie prostopadłej do osi. To samo można odnieść do studni o przekroju kołowym.

6.6.6. Bryły. Elementy zwarte o wymiarach nie odpowiadających warunkowi pręta, płyty lub tarczy należy traktować jako bryły i obliczać według specjalnych zasad mechaniki budowli lub stosować metody uproszczone.

Jako bryły sztywne należy traktować fundamenty przy obliczaniu nacisków na grunt i na grupy pali, masywne przyczółki i ściany oporowe niezbrojone lub minimalnie zbrojone przy sprawdzaniu ich na stateczność. Jako bryły należy INTEGRAM BUDOWNICTWO

Część 7 Strona 8

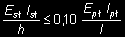
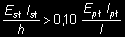
PN-91/S-10042 Obiekty mostowe Konstrukcje betonowe, żelbetowe i sprężone Projektowanie Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

traktować wszystkie elementy prefabrykowane w czasie transportu i montażu przy sprawdzaniu ich stateczności w czasie montażu.

6.7. Rozkład obciążeń z miejsc ich przyłożenia

6.7.1. Obciążenie płyty pomostu. Obciążenie prostopadłe do płyt pomostów i innych elementów poddanych zginaniu należy przyjmować jako siły rozkładające się z miejsca przyłożenia obciążenia pod kątem 45° a ż do płaszczyzny środkowej płyty oraz 30° przez warstwy gruntowe lub 15° przez tłucze ń, jeśli nie ma innych udokumentowanych danych.

Jeśli przy rozkładzie nacisków kilku kół w szeregu poprzez warstwy nawierzchni i płytę pomostu występują odcinki nakładania się nacisków należy przyjąć długość łączącą skrajne punkty nacisków skrajnych kół jako odcinek równomiernego rozłożenia sumy nacisków.

6.7.2. Obciążenie pod zakotwieniami wywołane siłami sprężania dźwigarów kablobetonowych elementów płaskich można przyjmować w obliczeniach jako rozkładające się względem osi kabli pod kątem 30° w płaszczy źnie elementu.

Założenie takie należy przyjąć przy określaniu zasięgu sprężania w strefie przylegającej do zakotwienia przy braku bardziej dokładnych podstaw.

6.8. Wpływ różnic i zmian sztywności

6.8.1. Różnice sztywności w układach ciągłych i ramowych. Przy obliczaniu belek ciągłych i ram należy uwzględnić różnice sztywności, jeśli stosunek największego momentu bezwładności do najmniejszego przekracza wartość 2,00 i jeśli ta różnica dotyczy długości nie mniejszej niż 10% długości przęsła lub elementu ramy.

Sztywność elementów B przy obliczaniu konstrukcji statycznie niewyznaczalnych należy przyjmować dla przekrojów brutto i niezarysowanych wg wzoru

(38)

w którym:

E b - współczynnik sprężystości wg rozdz. 3,

I b - sprowadzony moment bezwładności.

6.8.2. Wpływ sztywności połączenia słupów z płytą na dobór schematu. W układach słupowo-płytowych ze słupami zamocowanymi w płycie, w których spełniony jest warunek

(39)

w którym:

E sł I sł - sztywność giętna wszystkich słupów podpory równa sumie sztywności pojedynczych, h - wysokość podpory od spodu przęsła do wierzchu fundamentu, dla podpór palowych wysokość od spodu przęsła do rzeczywistego utwierdzenia w fundamencie lub umownego utwierdzenia w gruncie,

E pł I pł - sztywność giętna całego przęsła,

l - rozpiętość krótszego przęsła sąsiadującego z podporą,

płytę przęsła lub przęseł należy traktować w przybliżonych obliczeniach jako swobodnie podpartą na słupach, zaś obrót słupów w utwierdzeniu w płycie przyjmować równy obrotowi płyty w przekroju podparcia.

Jeśli spełniona jest nierówność

(40)

układ ten należy traktować jako ramowy lub płytowo-prętowy.

6.8.3. Wpływ zmian sztywności w czasie i na skutek uszkodzeń. W określonych przypadkach wpływy reologiczne powodują w konsekwencji obniżenie sztywności na skutek wzrostu odkształceń betonu w wyniku pełzania. Wpływ ten należy uwzględniać w elementach z betonu sprężonego i częściowo sprężonych. Należy uwzględnić zmiany sztywności przy wyznaczaniu sił wewnętrznych oraz w rozkładzie naprężeń w przekrojach.

Wpływ redukcji sił w elementach z betonu zbrojonego na skutek wpływów reologicznych z ewentualnym zarysowaniem należy uwzględniać w ustrojach ramowych przy rozpiętości przęseł powyżej 30 m jako wpływ na rozpór skrajnej podpory od obciążenia działającego długotrwale zgodnie ze wzorem

INTEGRAM BUDOWNICTWO

Część 7 Strona 9

PN-91/S-10042 Obiekty mostowe Konstrukcje betonowe, żelbetowe i sprężone Projektowanie Powielanie dokumentu zabronione. Wszelkie prawa zastrzeżone.

(41)

w którym:

H - wartość rozporu bez uwzględniania redukcji,

H 1 - wartość rozporu po uwzględnieniu redukcji,

- współczynnik pełzania zgodnie z rozdz. 3,

e - liczba Eulera.

Następna strona

Powrót do spisu treści

INTEGRAM BUDOWNICTWO

Część 7 Strona 10