Pytania na egzamin dyplomowy
Grupa A. MECHANIKA, WYTRZYMAŁOŚĆ MATARIAŁÓW, MATERIAŁOZNAWSTWO
1. Co to jest moment siły F względem punktu O?
Momentem siły F (rys.1.1) względem punktu O nazywamy wektor Mo równy iloczynowi siły F
i odległości h (promienia wodzącego)
Mo=Fh
(1.1)
Rys. 1.1 Moment siły F względem punktu O
Wektor ten jest prostopadły do płaszczyzny trójkąta OAB. Wartość liczbowa momentu Mo=Fh jest więc równa podwojonemu polu trójkąta OAB
2. Z jakich warunków równowagi wyznacza się reakcje w podporach dla układów statycznie wyznaczalnych?
Reakcje w podporach dla płaskich układów statycznie wyznaczalnych określa się z warunków równowagi płaskiego układu sił. Wychodzi się z założeń, że wypadkowa sił jest równa 0, zatem sumy składowych sił działających na układ są równe 0, a także suma momentów względem dowolnego punktu jest równa 0
∑ P
P
M
(1.2)
ix =
,
0
∑ iy = ,0 ∑ iO = .0
Powyższe równanie można zastąpić sumą momentów dowolnego punktu A położonego w da-
nej płaszczyźnie
∑ P
M
M
(1.3)
ix =
,
0
∑ A = ,0 ∑ O = .0
oraz za pomocą trzech równań momentów względem trzech punktów położonych w płaszczyźnie, ale nie leżących na jednej prostej
∑ M
M
M
(1.4)
B =
,
0
∑ A = ,0 ∑ O = .0
W przypadku przestrzennych układów statycznie wyznaczalnych reakcje w podporach określa się z warunków równowagi przestrzennego układu sił
∑ F
M
ix =
,
0
∑ ix = ,0
∑ F
M
(1.5)
iy =
,
0
∑ iy = ,0
∑ F
M
iz =
,
0
∑ iz = .0
3. Co to jest wektor główny i moment główny?
Wektor główny jest równy geometrycznej sumie wszystkich sił układu i przyłożony w środku redukcji O. Moment główny jest geometryczną sumą momentów tych sił względem środka redukcji.
4. Co to jest moment gnący i siła tnąca, jak się te wielkości wyznacza?
Moment gnący w danym przekroju belki jest równy sumie momentów, względem środka ciężkości tego przekroju, wszystkich sił zewnętrznych działających na część belki odciętą tym przekrojem. Momenty gnące wyznacza się poprzez podzielenie belki na odcinki, dla których definiuje się równania momentów gnących. Na podstawie równań określa się rodzaj funkcji, opisującej dany przedział, wyznaczając dodatkowo skrajne wartości przedziałów. Na podstawie otrzymanych wyników buduje się wykres momentów gnących.
Siła tnąca w danym przekroju belki to rzut wypadkowej wszystkich sił zewnętrznych działających na część belki odciętą tym przekrojem, na płaszczyznę tego przekroju. Siły tnące wyznacza się dla odcinków określonych wcześniej przy momentach gnących danej belki. Siły tnące można obliczyć również, korzystając z twierdzenia Schwedlera-śurawskiego, gdzie siła tnąca w danym przekroju jest pierwszą pochodną momentu gnącego w tym przekroju.
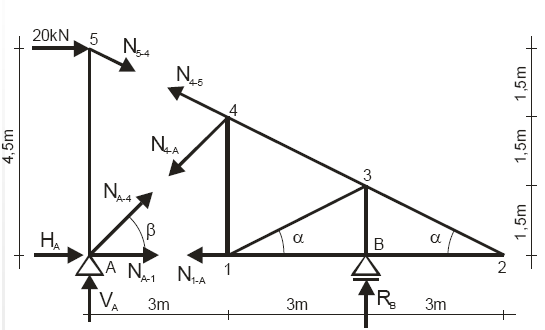
5. Na czym polega metoda Rittera, przykład zastosowania.
Metoda Rittera polega na przecięciu kratownicy przez trzy pręty, z których przynajmniej jeden nie może być równoległy do pozostałych. Do obliczeń wybiera się lewą lub prawą część kratownicy, a przecięte pręty zastępuje się siłami. Dla wybranej części określa się warunki równowagi, z których wyznacza się siły w prętach. Metodę Rittera stosuje się wtedy, gdy chcemy określić siły w wybranych prętach kratownicy. Często metoda ta ma zastosowanie w kratownicach symetrycznych.
Rys. 1.2. Kratownica trójkątna podzielona metodą Rittera
6. Co to jest środek masy w układach wielorasowych i co to są momenty statyczne?
Momentem statycznym układu punktów materialnych względem dowolnego punktu O nazywa
się sumę iloczynu mas mi przez ich promienie wodzące ri
r
r
S = ∑ m r .
(1.6)
i i
Środek masy lub inaczej środek bezwładności, jest to punkt, który charakteryzuje rozmieszcze-nie mas w ciele lub układzie ciał. Środek masy ma taką właściwość, że w czasie ruchu ciała porusza się tak, jakby masa całego ciała była skupiona w tym jednym punkcie, i poruszała się pod wpływem wszystkich sił działających na to ciało. Położenie środka masy danego układu określone jest iloczynem momentu statycznego układu i jego całkowitej masy
r
r
∑ m r
(1.7)
i i
r =
,
C
mc
w którym masa całego układu
m
m .
(1.8)
c = ∑
i
Rys. 1.3. Środek masy układu
Po zrzutowaniu równania wektorowego (1.7) na osie prostokątnego układu współrzędnych (rys.
1.3) otrzymuje się
∑ m x
∑ m y
∑ m z
i
i
i
i
i
i
x =
,
y =
,
z =
(1.9)
C
C
C
m
m
m
C
C
C
W polu grawitacyjnym ziemskim środek masy jest utożsamiony ze środkiem ciężkości ciał
sztywnych.
7. Co to są geometryczne momenty bezwładności
Geometryczny moment bezwładności charakteryzuje kształt ciała i rozkład odległości jego poszczególnych punktów od osi obrotu. Jest to moment bezwładności jednorodnego (o stałej gęstości) ciała podzielony przez jego gęstość.
Geometryczny moment bezwładności określa się z zależności
I
y 2 dV .
(1.10)
G = ∫
V
gdzie:
V – całkowita objętość ciała
I
y 2 dA .
(1.11)
G = ∫
A
gdzie:
A – pole powierzchni figury
Mając dany geometryczny moment bezwładności można wyznaczyć moment bezwładności ciała z zależności
I = I
(1.12)
G ⋅ ρ
8. Co to są momenty bezwładności i po co się je wyznacza.
Moment bezwładności to miara bezwładności ciała w ruchu obrotowym względem określonej osi obrotu. Moment bezwładności względem osi wyznacza się z zależności
I = ∫ z 2 dm .
(1.13)
m
gdzie:
z – odległość elementu dm od danej osi
Moment bezwładności określa bezwładność ciała w ruchu obrotowym. Im większy moment bezwładności, tym trudniej zmienić jest ruch obrotowy ciała np. zmieniając jego prędkość kątową. Za pomocą momentu bezwładności bryły sztywnej, obracającej się względem danej osi z prędkością kątową względem tej osi, można wyrazić energię kinetyczną tej bryły z zależności 1
(1.14)
2
E =
.
k
ω
I
2
9. Co to są momenty dewiacji?
Moment dewiacji, inaczej moment bezwładności odśrodkowy, względem osi x,y jest równy sumie iloczynów mas przez współrzędne x oraz y każdego elementu.
I
xy dm .
(1.15)
xy = ∫
m
Moment dewiacji może przyjmować wartości dodatnie, ujemne oraz równe zeru.
10. Jakie wielkości opisują ruch punktu materialnego i jak się je definiuje.
Głównymi wielkościami są prędkość, przyspieszenie oraz tor punku. Prędkość punktu materialnego to pochodna przemieszczenia po czasie. Z kolei przyspieszenie to pochodna prędkości po czasie, a zatem, druga pochodna przemieszczenia. Tor punktu to zbiór punktów w przestrzeni, w których znajdował się rozpatrywany punkt ruchomy. Tor określa rodzaj ruchu.
Kiedy tor jest linią prostą, punkt porusza się ruchem prostoliniowym. W przypadku ruchu krzywoliniowego, prędkość i przyspieszenie można rozbić na dwie składowe, rzutując wektory prędkości i przyspieszenia na osie układu współrzędnych. Wtedy imienne rzuty prędkości i przyspieszenia są kolejno pierwszą i drugą pochodną rzutu przemieszczenia punktu po czasie, v = x&
v = y&
(1.16)
x
y
a = v& = x&
&
a = v& = y&
&
.
x
x
y
y
2
2
2
2
v = v + v
a = a + a
x
y
x
y

Przyspieszenie można dodatkowo rozłożyć na składową styczną i normalną (nas. Pytanie).
W przypadku ruchu po okręgu prędkość kątowa punktu jest pochodną po drodze kątowej, a przyspieszenie kątowe, drugą pochodną.
W przypadku ruchu harmonicznego, np. wahadła, używa się dodatkowo dwóch wielkości fizycznych opisujących ruch punktu: okres ruchu
π
2
(1.17)
T = ω
oraz częstość (częstotliwość) ruchu
1
(1.18)
f =
T
11. Co to jest przyspieszenie styczne i normalne
W przypadku ruchu krzywoliniowego całkowite przyspieszenie ciała można rozłożyć na dwie składowe : styczną at i normalną an
Rys. 1.4. Przyspieszenie normalne i styczne
Składowa styczna (przyspieszenie styczne) jest równoległa do prędkości (styczna do toru), a zatem do kierunku ruchu. Składowa normalna (przyspieszenie normalne) jest prostopadła do prędkości, a zatem do kierunku ruchu. Poszczególne składowe wyznacza się z zależności dv
(1.19)
a =
.
t
dt
v 2
(1.20)
a =
.
n
R
gdzie:
R – promień krzywizny toru
12. Zasada zachowania energii mechanicznej
W dowolnym ruchu przebiegającym bez tarcia (i innych strat energii) energia mechaniczna układu izolowanego jest stała. Nie może być utworzona, zniszczona, a jedynie może zmieniać swoją formę. Układ izolowany to taki układ, na który nie działają siły zewnętrzne lub siły te się równoważą.
E
= E + E = const
M
k
p
mv 2
.
(1.16)
+ mgh = const
2
Do czynienia z zasadą zachowania energii mamy np. podczas skoku wzwyż. Sportowiec, gdy odbija się od podłoża jego energia potencjalna rośnie o tyle, o ile maleje energia kinetyczna, gdy zaś jest w najwyższym punkcie (tuż nad poprzeczką), to jego energia potencjalna jest maksymalna, a kinetyczna zerowa, następnie, gdy zaczyna spadać jego energia kinetyczna rośnie o tyle, o ile maleje energia potencjalna, a gdy spadając uderzy o ziemię jego energia potencjalna jest równa zeru, a kinetyczna maksymalna. W każdy z etapów, skoku wzwyż suma energii kinetycznej i potencjalnej jest taka sama.
Wyszukiwarka
Podobne podstrony:
grupa A 1 12
Projekt infr grupa 12
grupa 12, Jednostka ludzka podczas całego swego życia należy do różnych grup społecznych
kolokw 3 grupa 12
MDwAK TABELE GRUPA 12
grupa 12
zajecia.12.grupa.023
nefrologia 11 na 12 grupa 2 test na zaliczenie
12 osobowosc narcystyczna (grupa B)
12 Grupa społecznaid 13244
Kolo 2 grupa 1 poniedzialkowa 8.12.08, III rok, Patomorfologia, 1 koło, Giełdy
11 12-domena,grupa robocza
Ko-o 2 grupa 1 poniedzialkowa 8.12.08, IV rok, IV rok CM UMK, Patomorfologia
więcej podobnych podstron