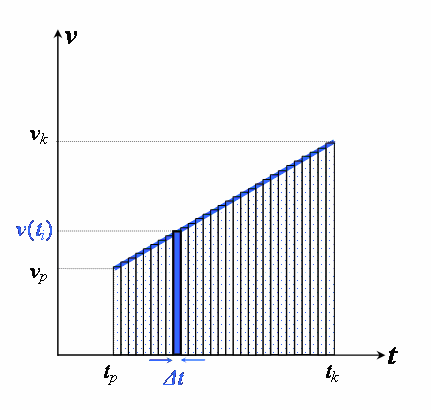
Wyprowadzenie wzoru na przemieszczenie w ruchu jednostajnie zmiennym metodą całkowania
υ
υk
tk
υ( ti)
x
x
lim
υ t ∆t
υ t dt
(1)
k −
p =
∑ ( i ) = ∫ ( )
∆
t → 0 i
ti
υp
prędkość końcowa w ruchu jednostajnie zmiennym: υ = υ( t ) = υ + a( t − t ) k
k
p
k
p
tzn. dla dowolnego t ∈< t p ,tk > : υ( t) = υ + a( t − t ) p
p
z (1):
t
t
k
k
x
x
υ t() dt
( υ
a t
(
t ) dt
k −
p =
=
p +
− p
=
∫
∫
t
t
p
p
rozłożenie na sumę całek: t
t
t
k
k
k
= υ dt
a t dt
a t dt
p
+
−
p
=
∫
∫
∫
t
t
t
p
p
p
wyłączenie przed znak całki czynników niezależnych od t: t
t
t
k
k
k
= υ
dt
a t dt
a t
dt
p
+
− p
=
∫
∫
∫
t
t
t
p
p
p
obliczenie całek:
2
=
t
t
t
t
1
k
υ [ t]
a[
]
a t
t
[ ]
υ ( t
t
a t
t
a t t
t
p
k −
)
p
+
( 2 k − 2 )
p
− ( p k − 2)
p
=
p
+
k
−
k
t
t
p
=
t
p
p
p
2
2
= υ ( t
t
a t
t
t t
t
p
k −
p
+ 1
)
( 2 k − 2 p − 2 p k + 2 2 ) p
=
2
2
= + t p
1
= υ ( t − t ) + a ( 2
t − 2
2
t t + t ) p
k
p
2
k
p k
p
2
= ( t − )
k
t p
1
2
x − x = υ ( t − t ) +
a ( t − t ) k
p
p
k
p
k
p
2
Wyszukiwarka
Podobne podstrony:
materialy 1a
L1-1a, Ratownictwo Medyczne, Materiały ze studiów, Medycyna Ratunkowa
1a, Skrypty, UR - materiały ze studiów, studia, studia, Błażej, Semestr I
EiE materiały wykładowe 1A serw decrypted
Dynamika punktu materialnego w jednym wymiarze 1A
MateriaL,oznawstwo i Techniki W Skrypt 1A id 284244
Test-1A, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
Materiały Infrastruktura 1a, Technika Rolnicza, Rok 4, semestr 8, Infrastruktura
EiE materiały wykładowe 1A serw
Sprawozdanie 1A - Statyczna Próba Rozciągania, PG, Materiałoznawstwo, Laborki
1a zest. obrotow i sald, Materiały - technik administracji Żak
LISTA STRZELANIA 1A, WAT-materiały
EAiC materiały wykładowe 1A serw(full permission)
Materiałoznawstwo i Techniki Wytwarzania Sprawozdanie 1A
L1-1a, Ratownictwo Medyczne, Materiały ze studiów, Medycyna Ratunkowa
Dynamika punktu materialnego w jednym wymiarze 1A
więcej podobnych podstron