Rzeszów, dn. 27.11.2012r.

Wyznaczanie stosunku C /C

p

v

metodą Clement-Desormes

Ćwiczenie nr 52

Fizyka – laboratorium

Arkadiusz Bednarz

79326

1imd L1 (Grupa: 1)

Spis treści:

1. Zarys teoretyczny

2. Cel

e i

l p

i rze

rz b

e ie

b g

ie ć

w

ć icz

ic e

z n

e ia

3. Oblic

l z

ic e

z n

e ia

i

a i

z

i e

z s

e ta

s w

ta ien

ie ie

ie wyników

4. Wnioski

1. Zarys teoretyczny

Ciepło właściwe – cie

i pł

p o

ł

o po

p t

o rze

r bn

b e

n

e do

d

o zwiększe

s ni

n a temperatury cia

i ła o

o j

e

j dn

d o

n s

o t

s kow

o ej

e masie o jedną

jednostkę

gdzie

∆Q – dostarczone ciepło;

m – masa ciała;

∆T – przyrost temperatury.

To

T

o s

a

s mo

o ciepł

p o

o wła

ł śc

ś i

c we możn

o

a

żn zdefiniować również dla chłodzenia. W uk u ładzi

d e S

I jednostką ciepła

właściwego jest dżul przez kilog o ra

r m i przez kelwin:

Ci

C epł

p o

ł

o właś

a c

ś iwe

w j

es

e t

s wi

w el

e koś

o c

ś ią

i cha

h ra

r kter

e y

r st

s yczną

zn dl

d a

l

a da

d ne

n j

e

j su

s b

u s

b t

s an

a c

n j

c i

j w da

d n

a e

n j

e

j tem

e pe

p ra

r tur

u ze

r

(jest st

s ał

a ą mater

e i

r ał

a ow

o ą)

ą .

) Mo

M że

o zależeć od

o

d tempe

p ra

r tur

u y

r , dl

d at

a ego

o pr

p e

r c

e yzyjni

n e

i j

e s

j zy

s

jest

s wzór

zó

r zapi

p sa

s n

a y

n w

postaci różniczkowej

Przemiana izobaryczna − pr

p o

r c

o es

e

s te

t rm

r od

o y

d na

n miczny

zn , podczas którego ciśnienie uk u ładu

d

u ni

n e ul

u ega

zmiani

n e, na

n t

a om

o iast

s po

p zo

o

s

zo t

s a

t łe

ł pa

p ra

r metry

r term

r od

o y

d na

n miczne czynnika mogą si

s ę zmieni

n ać

a . Procesy

izob

zo a

b ry

r czne

zn mogą zacho

h d

o zi

d ć zaró

r w

ó no

n

o w sp

s o

p s

o ó

s b

ó

b od

o w

d r

w a

r c

a alny

n , j

ak i n

i

n eo

e d

o w

d ra

r c

a aln

l y

n . Odw

d ra

r cal

a ny

n pr

p o

r c

o e

c s

s

izob

zo a

b ry

r czny

zn pr

p ze

r ds

d t

s awia n

a

n

a wykre

r si

s e krzy

r

wa zwana

n izobarą. Praca wykon

o a

n na

n pr

p ze

r z uk

u ład

d (l

( ub

u

b na

n d

d

uk

u łade

d m)

) w od

o w

d ra

r cal

a ny

n m pr

p o

r c

o es

e i

s e

i izob

zo a

b r

a y

r czny

zn m jest

s r

ó

r w

ó na

n ubytkowi (lub

przyrostowi) entalpii uk

u ładu

d .

u W

W szc

s zegól

ó no

n ś

o c

ś i

c , gdy

d jed

e y

d ny

n wkład

d do

d

o pr

p a

r cy st

s ano

n w

o i pr

p a

r c

a a

ob

o j

b ęt

ę oś

o c

ś i

c ow

o a (

p

( o

p l

o egaj

a ąc

ą a na

n zmiani

n e ob

o j

b ęt

ę oś

o c

ś i u

k

u ładu)

u ,

) j

est

s on

o a

n wyra

r żon

żo a

n wzor

zo e

r m:

gdzie

W – praca wykon

o a

n na

n pr

p ze

r z uk

u ład,

d

p – ciśnienie,

∆V – wzrost objętości uk

u ład

a u

d .

u

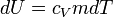
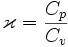
Dla gazu

zu do

d s

o k

s on

o a

n łego przemiana izobaryczna spełnia zależność: V – objętość,

T – temperatura.

Przemiana izochoryczna – pr

p o

r c

o e

c s

s t

erm

r od

o y

d na

n miczny zacho

h d

o zą

d cy pr

p zy

r

st

s ałej

e o

b

o j

b ę

j t

ę oś

o c

ś i

c (V

( =

con

o s

n t

s )

t .

)

Opr

p ó

r c

ó z ob

o j

b ęt

ę oś

o c

ś i ws

w zy

s

st

s kie po

p zo

o

s

zo t

s ał

a e pa

p r

a a

r metry

r ter

e m

r od

o y

d na

n miczne

zn mogą si

s ę zmieni

n ać.

Pod

Po c

d zas

s pr

p ze

r miany

n izoc

zo ho

h r

o y

r czne

zn j ni

n e j

e

j st

s wykon

o ywana

n praca, uk

u ład

d może

o wymieni

n ać e

ne

n r

e g

r ię z

ot

o oc

o zeni

n e

i m tylko

o w wyni

n ku ciepl

p ne

n go

o pr

p ze

r pł

p ywu

u ene

n rg

r ii. Z pi

p er

e w

r sze

s j

ze zasa

s d

a y

d term

r od

o y

d na

n miki wynika,

że całe ciepło do

d p

o r

p o

r w

o a

w dzo

d

n

zo e

n lub

u

b od

o p

d ro

r w

o a

w dzo

d

n

zo e

n z gazu w pr

p o

r c

o es

e i

s e

i izoc

zo ho

h r

o y

r czny

zn m j

est

s zuży

zu

wane

n na

n

po

p w

o iększe

s ni

n e l

ub

u

b po

p m

o ni

n ej

e s

j ze

s ni

n e j

e

j go energii wewnętrznej: δQ = dU.

Przekształcając wzór na cie

i p

e ł

p o

o wła

ł śc

ś i

c we otrzymujemy:

gdzie m jest masą gazu.

W

W izoc

zo ho

h r

o y

r czne

zn j

j pr

p ze

r miani

n e

i st

s a

t łej

e masy gazu, ciśn

ś i

n eni

n e

i wywiera

r ne

n na

n śc

ś ian

a k

n i na

n cz

c yni

n a j

es

e t

s wpr

p o

r s

o t

s

proporcjonalne do temperatury.

gdzie:

p – ciśnienie

T – temperatura

Wykładnik adiabaty w ter

e m

r od

o yna

n mice – bezwymiarowa wielkość równa st s os

o u

s n

u k

n ow

o i ciepła

właściwego w pr

p ze

r miani

n e i

zo

i

b

zo a

b ry

r czne

zn j do ciepła właściwego w pr

p ze

r miani

n e i

zoc

zo ho

h r

o y

r czne

zn j. Występuje

jako parametr w pr

p a

r wi

w e Poi

Po s

i s

s o

s n

o a

n opisującym przemianę adiabatyczną gazu zu do

d s

o k

s ona

n łego.

Wy

W kładn

d i

n k adi

d aba

b ty na

n zywany

n je

j st

s r

ó

r w

ó ni

n eż wsp

s ó

p ł

ó c

ł zynni

n kiem w ró

r w

ó na

n ni

n u

u Poi

Po ss

s o

s n

o a

n lub

u kappą, od

na

n zwy gre

r ckiej

e li

l te

t ry

r , któr

ó ą

r

ą j

est

s na

n j

a c

j zęśc

ś i

c ej

e

j ozn

o

a

zn czany

n .

Zgodnie z definicją

gdzie:

– wykładn

d i

n k adi

d a

i ba

b t

a y,

– ciep

e ł

p o

o wł

w aśc

ś iwe w przemianie izobarycznej,

– ciep

e ł

p o

o wł

w aśc

ś iwe w przemianie izochorycznej.

Zamiast

s ci

c epł

p a wła

ł śc

ś i

c wego

o może tu

u by

b ć uży

u

te ciepł

p o

ł

o mol

o o

l w

o e, po

p n

o i

n ewa

w ż dl

d a da

d ne

n j

e

j

su

s b

u s

b t

s anc

n j

c i

j r

ó

r żn

ó

i

żn ą s

i

s ę

i on

o e

n o

o s

t

s ał

a y czynn

n i

n k.

Równanie Clapeyrona, rów

ó na

w

n

na i

n e st

s a

t nu

a

ga

g zu

a

dos

do ko

s

na

ko

ł

na ego

g to równanie stanu op

o i

p su

s j

u ą

j ce

c związek

po

p m

o iędz

d y tempe

p ra

r tur

u ą

r , ci

c śn

ś i

n eni

n em i ob

o j

b ęt

ę oś

o c

ś ią

i gazu doskonałego, a w sp

s o

p s

o ó

s b

ó

b pr

p zy

r

bl

b iżon

żo y

n

opisujący gazy rzeczywiste. Sfo

Sf r

o m

r uł

u ow

o ane

n zos

zo t

s ał

a o

o w 1

8

1 3

8 4

3

4 ro

r k

o u

u pr

p ze

r z Be

B no

n î

o t

î a Cl

C a

l pe

p yro

r n

o a

n . Prawo to

można wyrazić wzorem

gdzie:

p – ciśnienie

V – objętość

n – liczba moli gazu

zu (b

( ę

b dą

d ca

c miarą

r li

l czby

zb cząst

s eczek (i

( l

i oś

o c

ś i

c )

) r

o

r zw

o

ażane

n go gazu)

zu

T – temperatura (b

( e

b zwzględn

d a

n ),

) T [K] = t [°C] + 273,15

R – uniwersalna st

s a

t ła

a gazow

zo a: R = NAkB, gdzie: NA – stała Avogadra (l ( i

l czba

zb Avog

o adr

d a

r )

a ,

) kB –

stała Boltzmanna, R = 8,

8 31

3 4

1 J/(mol·K)

Ró

R w

ó na

n ni

n e t

o

o j

e

j st

s wypr

p o

r w

o ad

a za

d ne

n na

n po

p d

o s

d t

s a

t wie zało

ł że

o ń:

ń

1. gaz składa

d si

s ę z po

p r

o u

r s

u za

s j

za ący

c ch

h si

s ę cząst

s eczek;

2. cząst

s eczki zde

zd rza

r j

za ą s

i

s ę

ę ze so

s b

o ą

b or

o a

r z ze śc

ś iank

n ami na

n czyni

n a w

któr

ó y

r m si

s ę zna

zn j

a du

d j

u ą

j ;

ą

3. br

b a

r k od

o d

d zi

d aływań

ń między

d

cząst

s eczkow

o ych

h w gazie, z wyjątkiem od

o p

d y

p cha

h ni

n a

i w mom

o enc

n ie

zde

zd rze

r ń

ń cząst

s ec

e zek;

4. ob

o j

b ęt

ę oś

o ć

ś

ć (r

( o

r zm

o

iary

r )

) cząst

s ecze

c k jest

s po

p m

o ij

i ana

n ;

5. zde

zd rze

r ni

n a cząst

s eczek są

s doskonale sprężyste;

Ró

R w

ó na

n ni

n e t

o,

o mimo

o że wypro

r w

o adzo

d

n

zo e

n w ra

r mach

h wyide

d ali

l zow

zo ane

n go

o mod

o e

d lu,

u do

d b

o r

b ze

r op

o i

p su

s j

u e

j

większość substancji gazow

zo ych w obszarze ciśnień do ok. 100 atmosfer i t empe

p ra

r tur

u y

r do

d

o 30

3 0

0 –

400 °C

° ,

C or

o a

r z w tempe

p ra

r tu

t r

u ze

r tro

r c

o hę

h wi

w ększe

s j

ze od

o

d t

empe

p ra

r tur

u y

r sk

s ra

r pl

p an

a i

n a

a gazu.

zu

2. Cel

e i

l p

i rze

rz b

e ie

b g

ie ć

w

ć icz

ic e

z n

e ia

Cel ćwiczenia:

•

Pra

Pr ktyczne

zn zapo

p zn

o

a

zn ni

n e si

s ę z

pr

p ze

r bi

b egiem pr

p ze

r mian

n gazow

zo ych.

h

•

Zapoznanie się z metod

o ą

d wyzna

zn czani

n a st

s os

o u

s n

u k

n u

u C /C .

p

v

•

Wy

W zna

zn czeni

n e st

s os

o u

s n

u k

n u

u κ=

κ C

/C dla powierza.

p

v

Przebieg ćwiczenia:

•

Zamkną

n ć kra

r n

n wylot

o ow

o y. Przy

Pr

po

p moc

o y po

p mpki rę

r czne

zn j

e

j wtło

ł c

o zyć do

d

o zbi

zb or

o n

r i

n ka po

p w

o ietr

t ze

r

ut

u rzy

r

muj

u ąc

ą na

n dc

d iś

i n

ś i

n e

i ni

n e

i dwu

d

d

wu zi

d est

s u

u kil

i ku

u milimetró

r w

ó sł

s up

u a

p c

ie

i czy w mano

n metrze

r .

•

Prze

Pr z od

o p

d o

p w

o iedn

d i

n ob

o r

b ó

r t

ó kur

u k

r a zawor

o u

r

u od

o ł

d ączyć po

p m

o pk

p ę od

o

d zbior

o n

r i

n ka, po

p zo

o

s

zo t

s a

t wiaj

a ą

j c

je

j dn

d o

n c

o ześn

ś i

n e

i zamkni

n ęty kra

r n

n wylot

o ow

o y. Odc

d zekać kilka minu

n t

u na

n us

u t

s al

a eni

n e s

i

s ę

i tempe

p ra

r t

a ur

u y

r w

zbi

zb or

o n

r i

n ku

u i n

o

n t

o ow

o ać

a ró

r żn

ó

i

żn cę

c po

p zi

o om

o ów

ó cieczy w mano

n m

o etrze

r .

•

Otwor

o zy

r

ć kra

r n

n wylot

o ow

o y na pr

p ze

r cią

i g kilku

u se

s kun

u d

n

d i po

p

o wyró

r w

ó na

n ni

n u

u si

s ę c

iśn

ś i

n en

e i

n a

a g

azu

zu w

zbi

zb or

o n

r i

n ku

u z ciśn

ś i

n eni

n em zewnę

n trzn

r

y

zn m zamkną

n ć go

o po

p n

o o

n wn

o

i

wn e.

•

Po pewnym czasie (5-8

8 minu

n t

u )

) od

o c

d zytać ró

r żn

ó

i

żn c

i e po

p zi

o om

o ów

ó cieczy w mano

n metrze

r .

•

Cy

C kl po

p m

o iaró

r w

ó po

p w

o tór

ó zy

r

ć 10

1

0 –krotnie.

•

Na podstawie uzyskanych

h da

d ny

n ch

h wyzna

zn czyć wart

r oś

o ć

ś

ć κ dla każde

żd go

o cyklu

u po

p m

o iaró

r w

ó , a

na

n st

s ę

t pn

p i

n e

i ob

o l

b ic

i zyć wart

r oś

o ć

ś ś

r

ś e

r dn

d i

n ą t

ej

e

j wiel

e koś

o c

ś i.

i

•

Dla j

e

j dn

d e

n go

o cyklu

u po

p m

o iaró

r w

ó

wyzna

zn czyć bł

b ąd

d maksy

s malny

n . Pos

Po ł

s u

ł g

u uj

u ą

j c si

s ę metod

o ą

d

ą Stud

u e

d nt

n a

ok

o re

r śl

ś ić

i pr

p ze

r dzi

d ał na

n wart

r oś

o ć

ś rze

r czywist

s ą κ z poziomem ufności 0,95.

3. Obliczenia i zestawienie wyników Pomiar

h1 [mm] ±1 [mm]

h2 [mm] ±1 [mm]

h3 [mm] ±1 [mm]

К = ℎ1/ℎ3

1

132

39

93

1,4194

2

131

38

93

1,4086

3

129

38

91

1,4176

4

133

39

94

1,4149

5

130

38

92

1,4130

6

132

39

93

1,4194

7

134

39

95

1,4105

8

128

37

91

1,4066

9

130

38

92

1,4130

10

133

39

94

1,4149

Średnia

131,2

38,4

92,8

1,4138

Tabela 1: Pomiary i zestawienie wyników h3 = h1 – h2 – różnica wysokości (mianownik we wzorze na K w metodzie Clementa-Desormesa) Przykładowe obliczenia dla pomiaru nr 1.

ℎଷ = ℎଵ − ℎଶ = 132 − 39 = 93 [݉݉]

ℎ1

132

Кଵ =

=

= 1,4194

ℎ3

93

Wyznaczanie wartości średniej dla wielkości h1, h2 i h3, zostało dokonane metodą średniej arytmetycznej.

Przykład zastosowania ukażę na obliczaniu wartości średniej dla К.

Кଵ + Кଶ + Кଷ + Кସ + Кହ + К଺ + К଻ + К଼ + Кଽ + Кଵ଴

К =

݊

gdzie:

n = 10 liczba pomiarów

1,4194 + 1,4086 + 1,4176 + 1,4149 + 1,4130

К =

10

1,4194 + 1,4105 + 1,4066 + 1,4130 + 1,4149 + 1,4138

14,1379

+

=

= 1,4138

10

10

Obliczanie błędu pomiaru dla wyznaczania współczynnika adiabaty К rachunkiem pochodnej

,

logarytmicznej:

∆ℎ1 = ∆ℎ2 = 1 [݉݉] - błąd pomiaru wysokości słupka oleju

∆ℎ3 = ∆ℎ1 + ∆ℎ2 = 1 + 1 = 2[݉݉]

∆ℎ3

1

∆ К = ܭ ∗ ൬∆ℎ1 +

൰ = 1,4138 ∗ ൬ 1 +

൰ = 1,4138 ∗ ሺ0,00762 + 0,01077ሻ

ℎ1

ℎ3

131,2

92,8

= 1,4138 ∗ 0,01839 = 0,02599

К = 1,4138 ± 0,02599

Określanie przedziału na wartość rzeczywistą К

௡

ܵሺКሻ = ඨ

1

݊

∗ ෍ (К − К)ଶ

(݊ − 1)

ଵ

= ඨ 1 ∗ ሺሺ1,4138 − 1,4194ሻଶ + ሺ1,4138 − 1,4086ሻଶ + ⋯ + ሺ1,4138 − 1,4130ሻଶ + ሺ1,4138 − 1,4149ሻଶሻ

90

= ඨ0,0001692 = ඥ1,88028 ∗ 10ି଺ = 0,00137

90

Dla ߙ = 0,95; ݐ௡ఈ = 2,252 ሺݖ ݐܾ݈ܽ݅ܿ ݓݏ݌ółܿݖݕ݊݊݅݇óݓ ܵݐݑ݀݁݊ݐܽ − ܨ݅ݏℎ݁ݎܽሻ

∆ К = ݐ௡ఈ ∗ ܵሺКሻ = 2,252 ∗ 0,00137 = 0,0031

К = 1,4138 ± 0,0031

Zestawienie wyników

a) Współczynnik adiabaty wraz w błędem (metoda pochodnej logarytmicznej) К = 1,4138 ± 0,02599

∆ К = 1,84%

b) Współczynnik adiabaty wraz z błędem (metoda Studenta-Fishera) К = 1,4138 ± 0,0031

∆ К = 0,22%

4. Wnioski

Ćwiczenie zostało przeprowadzone poprawnie. Powodem początkowych nieudanych prób pomiarów była nieszczelność układu. Otrzymany współczynnik adiabaty jest zbliżonym do rzeczywistego dla powietrza suchego. Według otrzymanych wyników, dochodzę do wniosku, że przy założeniach błędu obliczonego metodą Studenta-Fishera, błąd nie przekracza 0,3%. Jako, że obliczaliśmy błąd maksymalny, za wielkość prawidłową przyjmuję błąd obliczony metodą pochodnej logarytmicznej, w której błąd nie przekracza 2 %.