Informatyka - Podstawy Programowania w Języku C++
prow. Sławomir Czarnecki
Zadania na laboratorium nr. 4
Uwaga ! Na laboratorium, zademonstrowany zostanie sposób wywoływania funkcji NEW(...) i DEL(...) dynamicznego alokowania i de-alokowania tablic jedno oraz dwuwymiarowych (tzn. wektorów oraz macierzy) z biblioteki bib.h. Zadanie drugie nawiązuje do tematyki wykładu z Mechaniki Teoretycznej – dział kinematyka – nauka o ruchu ciał sztywnych.
1. Dynamiczna alokacja i de-alokacja tablic.
• Wprowadź z klawiatury liczby całkowite dodatnie m i n .
• Zdefiniuj następnie dynamicznie tablice: wektor u[ m] typu int, wektor v[ m] typu long oraz wektor w[ m] i macierz t[ m][ n] typu double inicjalizując składowe definiowanych tablic dowolną, ale ustaloną liczbą (np. liczbą zero). Wykorzystaj w tym celu
odpowiednie wersje funkcji NEW(...) z biblioteki bib.h.
• Wyświetl na ekranie wszystkie składowe macierzy t[ m][ n] wywołując funkcję cout .
• Zmień składowe powyżej zdefiniowanych tablic wywołując funkcję random( …).
• Wyświetl na ekranie wszystkie składowe powyżej zdefiniowanych tablic wywołując odpowiednie wersje funkcji display(...) z biblioteki bib.h.
• Zwolnij zarezerwowaną dynamicznie na stercie pamięć wywołując funkcje DEL(...) z biblioteki bib.h.
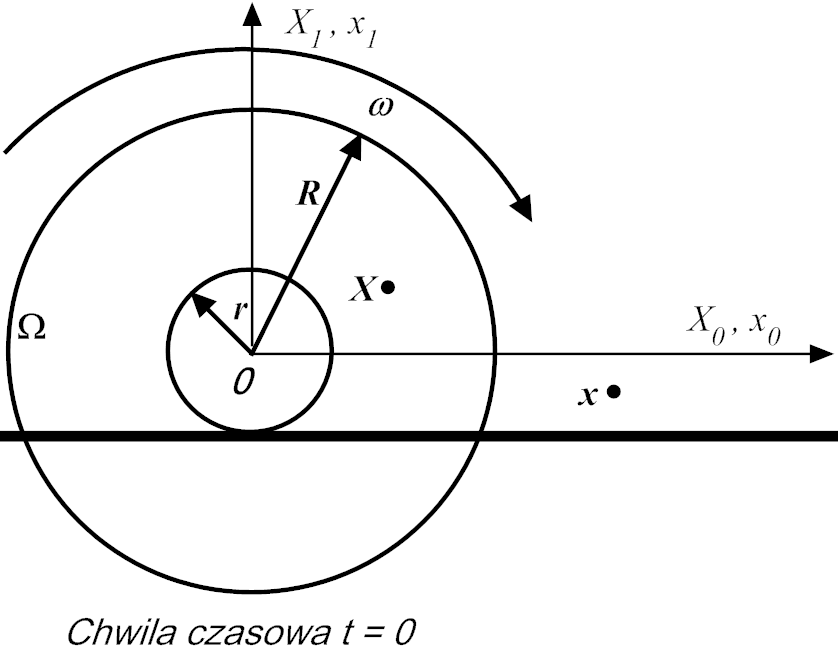
2. Wzdłuż poziomej linii prostej toczy się ze stałą prędkością kątową ω oraz bez poślizgu szpulka Ω o mniejszym promieniu r i o większym R – por. rys.1.
Rys.1. Szpulka w ruchu płaskim – toczenie się bez poślizgu ze stałą prędkością kątową.
Dla uproszczenia interpretacji formuł zakładamy, że R = ∞ . W chwili początkowej t = 0 , środek szpulki znajduje się w początku 0 globalnego układu współrzędnych kartezjańskich.
Ruch szpulki Ω w globalnym układzie współrzędnych kartezjańskich i w przedziale czasu T = [0, ∞) opisuje odwzorowanie
x X cos ω t + X sin ω t + ω r t
2
0
0
( )
1
( )
F : Ω × T → ℝ , x = F ( ,
X t ),
=
,
(1)
x
− X sin ω t + X cos ω t
1
0
( )
1
( )
x
gdzie:
0
2
x =
∈
ℝ oznacza punkt przestrzenny definiujący położenie punktu
x
1
X
materialnego
0
X =
∈ Ω
identyfikującego punkt szpulki Ω w chwili czasowej t ∈ T .
X
1
Definiując trajektorię jako zbiór
ℑ = (
{ x, t)∈ F ( ,
Ω t)× T}
odwzorowanie odwrotne
1
G
F −
=
: ℑ → Ω
do odwzorowania
2
F : Ω × T → ℝ
możemy zdefiniować następująco:
X x cos ω t − x sin ω t − ω r t cos ω t
0
0
( ) 1 ( )
( )
G : ℑ → Ω, X = G (x, t ),
=
.
(2)
X
x sin ω t + x cos ω t − ω r t sin ω t
1 0
( ) 1
( )
( )
Nietrudno jest sprawdzić, że dla dowolnych X, x, t :
F G
( ,
x t ), t =
x oraz G F
( ,
X t ), t =
X .
Wektor prędkości v definiujemy jako pole materialne
F
∂
v − X ω sin ω t + X ω cos ω t + ω r
2
0
0
( )
1
( )
v : Ω × T → ℝ , v =
(X, t),
=
,
(3)
t
∂
v
− X ω cos ω t − X ω sin ω t
1
0
( )
1
( )
natomiast opis przestrzenny V wektora prędkości v definiujemy jako pole przestrzenne V
x ω + ω r
V : ℑ →
,
Ω V ( ,
x t ) = v G
( ,
x t )
0
1
, t ,
=
.
(4)
2
V
− x ω + ω r t
1 0
Zdefiniuj i zainicjalizuj trzy zmienne typu double: r = 1[ m], ω = 3 [1/ s] , T = 5 [ s].
Zdefiniuj i zainicjalizuj zmienną n = 100 typu int, oznaczającą liczbę chwil czasowych, w przedziale czasu T.
Zdefiniuj dynamicznie dwa wektory: X[2], x[2] typu double. Składowe wektora X
zainicjalizuj dowolnymi liczbami wskazującymi wybrany punkt materialny szpulki
Ω , a składowe wektora x zainicjalizuj dowolnymi liczbami wskazującymi wybrane miejsce w przestrzeni
2
ℝ .
Zdefiniuj dynamicznie cztery macierze: FX[ n][2], Gx[ n][2], v[ n][2], V[ n][2]. W
każdym z n wierszy oblicz następnie według formuł odpowiednio: (1), (2), (3) i (4) położenia punktu materialnego X, punkty materialne przechodzące przez miejsce x, wektor prędkości v punktu materialnego X oraz wektor prędkości V w miejscu x w n,
T
równo odległych od siebie chwilach czasowych t = i × T
△
i = 0,1,..., n −1, T
△ =
.
i
n −1
Zapisz do czterech plików tekstowych: trajektoria.txt, X.txt, predkosc.txt, V.txt składowe macierzy odpowiednio: FX, Gx, v, V w taki sposób, aby na podstawie zapisanych danych, możliwe było sporządzenie wykresów w Excelu wizualizujących
(w sposób dyskretny) odpowiednio: trajektorię wybranego punktu materialnego X, zbiór punktów materialnych przechodzących przez wybrane miejsce x, wektor
prędkości v wybranego punktu materialnego X, wektory prędkości V punktów materialnych przechodzących przez wybrane miejsce x w kolejnych chwilach
czasowych t ( i = 0,1,..., n − )
1 .
i
Uwaga ! Znacznie „lepszą” wizualizację wektora prędkości v można uzyskać, sporządzając jego prezentację w postaci odcinków o początkach w n zmieniających się punktach x reprezentujących – zmieniające się – położenie punktu X w kolejnych chwilach t i o końcach w punktach x + v . Taka wizualizacja umożliwia bowiem i
potwierdzenie znanego faktu styczności (w każdej chwili czasowej t) wektora prędkości do toru ruchu punktu. Analogiczna uwaga dotyczy wizualizacji wektora
prędkości v w ustalonym miejscu x przestrzeni, czyli wizualizacji tzw. opisu przestrzennego V materialnego pola wektorowego v. Początki odcinków
reprezentujących wektor V w kolejnych chwilach czasowych t powinny być zawsze i
w ustalonym punkcie x, natomiast ich końce w punktach x + V . Zamieszczone w uwadze wskazówki powinny być uwzględnione w zmienionym nieco sposobie zapisu
danych do plików tekstowych predkosc.txt, V.txt , umożliwiającym sporządzenie w Excelu rysunków zgodnych z przedstawioną wyżej interpretacją.
Wyszukiwarka
Podobne podstrony:
infa, Inf Lab08
infa, Inf Lab08
infa, Inf Lab10 11
infa, Inf Lab03
infa Inf Lab10 11
Inf Lab08
infa Inf Lab07
infa Inf Lab04
infa, Inf krata
infa Inf Lab03
infa Inf Lab06
infa, Inf Lab06
Inf Lab08
infa, Inf Lab10 11
inf wstep NET, Inżynieria Środowiska [PW], sem 4, Infa, woiągi, Płyta;Inf i Prog
INF dec5
BEZPIECZE STWO SYSTEM W INF
Sys Inf 03 Manning w 06
więcej podobnych podstron