Informatyka - Podstawy Programowania w Języku C++

prow. Sławomir Czarnecki

Zadania na laboratorium nr. 8

1. Zdefiniuj dwie wersje funkcji „silnia”

!

n

dla dowolnego

0

n ≥

. Pierwszą wersja

rekurencyjną:

unsigned

long

long

silnia(

unsigned

long

long

n)

i drugą wersję iteracyjną

unsigned

long

long

SILNIA(

unsigned

long

long

n)

Przetestuj działanie obu tych funkcji (

dla

n

nie większego od

20).

2. Zdefiniuj dwie wersje funkcji „największy wspólny dzielnik liczb naturalnych m i n”.
Pierwszą wersja rekurencyjną:

unsigned

long

long

nwd(

unsigned

long

long

m,

unsigned

long

long

n)

i drugą wersję iteracyjną

unsigned

long

long

NWD(

unsigned

long

long

m,

unsigned

long

long

n)

w oparciu o algorytm I z Lab 3:

• Krok 1. Dopóty dopóki m n

≠ wykonaj następujące podstawienie

jeśli

m > n, to m = m – n

w przeciwnym przypadku:

n = n – m

• Krok 2. NWD(m , n) = m

Przetestuj działanie obu tych funkcji.

3. Zdefiniuj (bardzo niewydajną) rekurencyjną wersję

unsigned

long

long

binomial(

unsigned

long

long

n,

unsigned

long

long

k)

funkcji na współczynnik dwumianowy

(

)

!

!

!

n

n

k

k n k

 

=

 

−

 

dla 0

k

n

≤ ≤

korzystając z następującej prostej do udowodnienia indukcyjnie zależności rekurencyjnej

1

1

0

1

1

0

lub

n

n

k

n

n

k

k

k

k

k

n



−

−



 



+

< <

  

 



=

−



 



 

  

=

=



która pozwala wyeliminować konieczność obliczania wyrażenia typu !

n lub !

k .

Algorytm rekurencyjny oblicza aż 2

1

n

k

 

−

 

 

wyrazów w celu obliczenia wartości

n

k

 

 

 

.

Wykorzystując tablicę

(

) (

)

1

1

n

k

+ ×

+

=

B

B

, gdzie składowa

[ ][ ]

(

)

0,1,..., ,

0,1,...,

B i

j

i

n

j

k

=

=

będzie zawierała wartość

i

j

 

 

 

możliwe jest „skonstruowanie” znacznie wydajniejszej

iteracyjnej wersji algorytmu

unsigned

long

long

BINOMIAL(

unsigned

long

long

n,

unsigned

long

long

k)

Definiowanie składowych macierzy B oparte jest rekurencyjną zależność

[ ][ ]

[ ][

]

[

][ ]

1

1

1

0

1

0

lub

B i

j

B i

j

j

i

B i

j

j

j

i



−

− +

−

< <

= 

=

=



oraz o realizację w porządku wstępującym, rozpoczynającym się od pierwszego wiersza i
wyliczającym po kolei wartości w wierszach tablicy B. Każda kolejna składowa wiersza (od
lewej do prawej) jest wyliczana na podstawie wartości składowych w wierszu
poprzedzającym przy wykorzystaniu powyższej zależności rekurencyjnej. Ostatnia obliczana

wartość, to

[ ][ ]

n

B n k

k

 

=  

 

. Np. przy obliczaniu

4

2

n

k

=









=





mamy

B[0][0] = 1

(wartość B[0][0] nie jest potrzebna w dalszych obliczeniach)

B[1][0]

=

1

B[1][1]

=

1

B[2][0]

=

1

B[2][1]

=

B[1][0] + B[1][1] = 1 + 1 = 2

B[2][k=2]

=

1

B[3][0]

=

1

B[3][1]

=

B[2][0] + B[2][1] = 1 + 2 = 3

B[3][k=2]

=

B[2][1] + B[2][2] = 2 + 1 = 3

B[n=4][0]

=

1

B[n=4][1]

=

B[3][0] + B[3][1] = 1 + 3 = 4

B[n=4][k=2] =

B[3][1] + B[3][2] = 3 + 3 = 6

(

Uwaga ! możliwych jest jeszcze szereg wielu dodatkowych ulepszeń

). Przetestuj działanie

obu tych funkcji.

4. Zdefiniuj dwie, odpowiednio rekurencyjną i iteracyjną wersję

double

bisection(

double

( *f )(

double

),

double

a,

double

b,

double

eps)

double

BISECTION(

double

( *f )(

double

),

double

a,

double

b,

double

eps)

funkcji poszukiwania pierwiastka ciągłej funkcji jednej zmiennej rzczywistej

:

f

→

ℝ

ℝ w

przedziale domkniętym

[ ]

,

I

a b

=

⊂ ℝ

z dokładnością eps > 0, w oparciu o algorytm metody

bisekcji. Zakładamy, że wartości funkcji f na końcach przedziału I są różne od zera i mają
różne znaki.
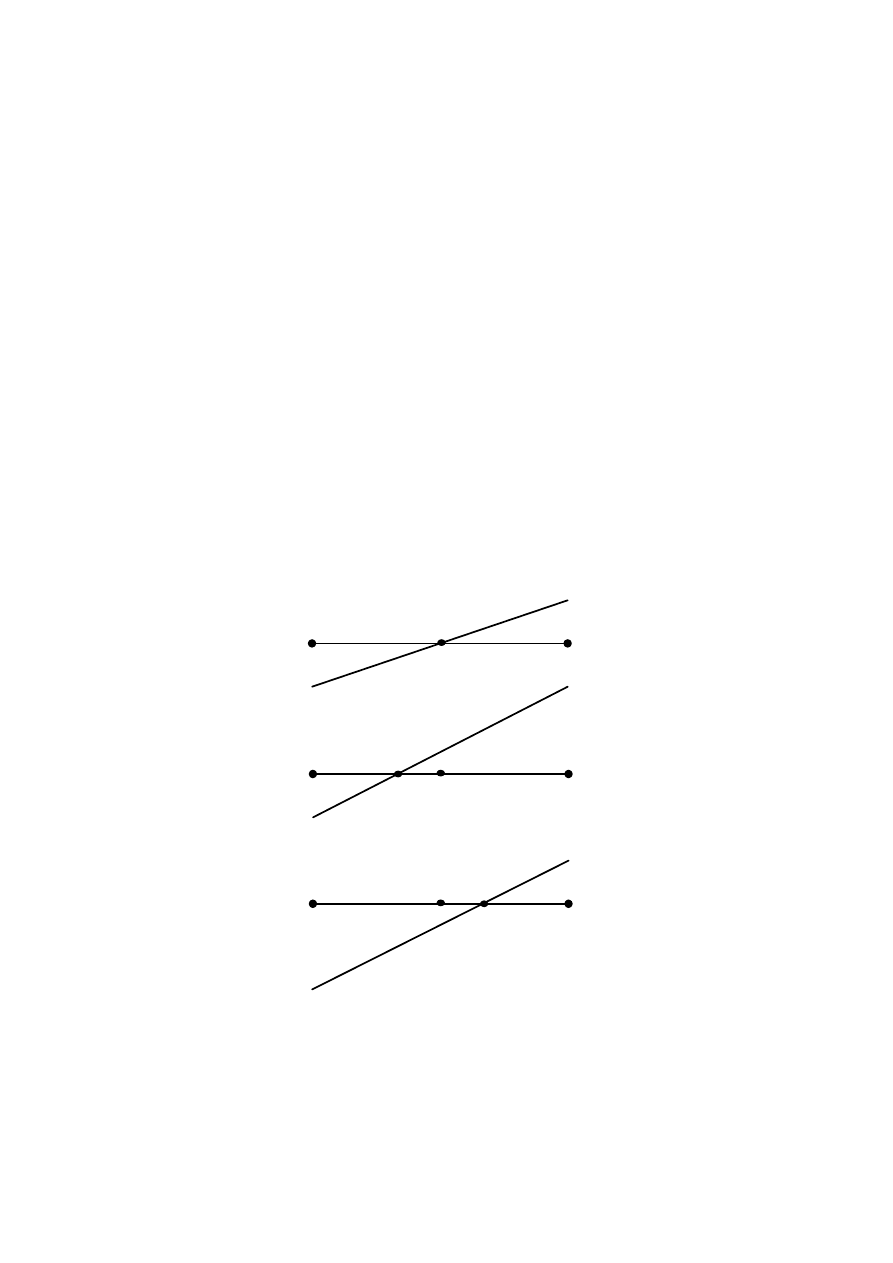
W wersji rekurencyjnej mamy:

• Pre: x

lewy

< x

prawy

, eps > 0. Znaki f(x) w punktach x

lewy

i x

prawy

muszą być różne, co

wystarcza do stwierdzenia, że w przedziale [x

lewy

, x

prawy

] znajduje się co najmniej

jeden pierwiastek.

• Rozpoczynamy od wyznaczenia punktu środkowego x

srodek

= (x

lewy

+ x

prawy

) / 2.

• Należy wyróżnić dwa przypadki elementarne: x

prawy

– x

lewy

< eps lub f(x

srodek

) = 0 dla

których pierwiastek = x

srodek

.

• Nie spełnienie żadnego z przypadków elementarnych prowadzi do rekurencyjnego

wywołania funkcji:

bisection(f, x

lewy

, x

srodek

, eps) jeśli f(x

lewy

) f(x

srodek

) < 0

lub
bisection(f, x

srodek

, x

prawy

, eps) jeśli f(x

lewy

) f(x

srodek

) > 0.

x

lewy

x

lewy

x

lewy

x

prawy

x

prawy

x

prawy

x

srodek

x

srodek

x

srodek

f(x

prawy

)

f(x

lewy

)

f(x

lewy

)

f(x

lewy

)

f(x

prawy

)

f(x

prawy

)

pierwiastek

pierwiastek

pierwiastek

W wersji iteracyjnej strategia polega poszukiwaniu pierwiastka od skrajnego lewego punktu
przedziału I w kierunku prawym lub od skrajnego prawego punktu przedziału I w kierunku
lewym, w zależności od tego, w którym z tych punktów wartość funkcji jest ujemna. Każdy
kolejny przyrost (dodatni lub ujemny) jest połową wartości ostatniego przyrostu, przy czym
nie dopuszczamy do sytuacji, w której wartość funkcji w nowo sprawdzanym punkcie byłaby

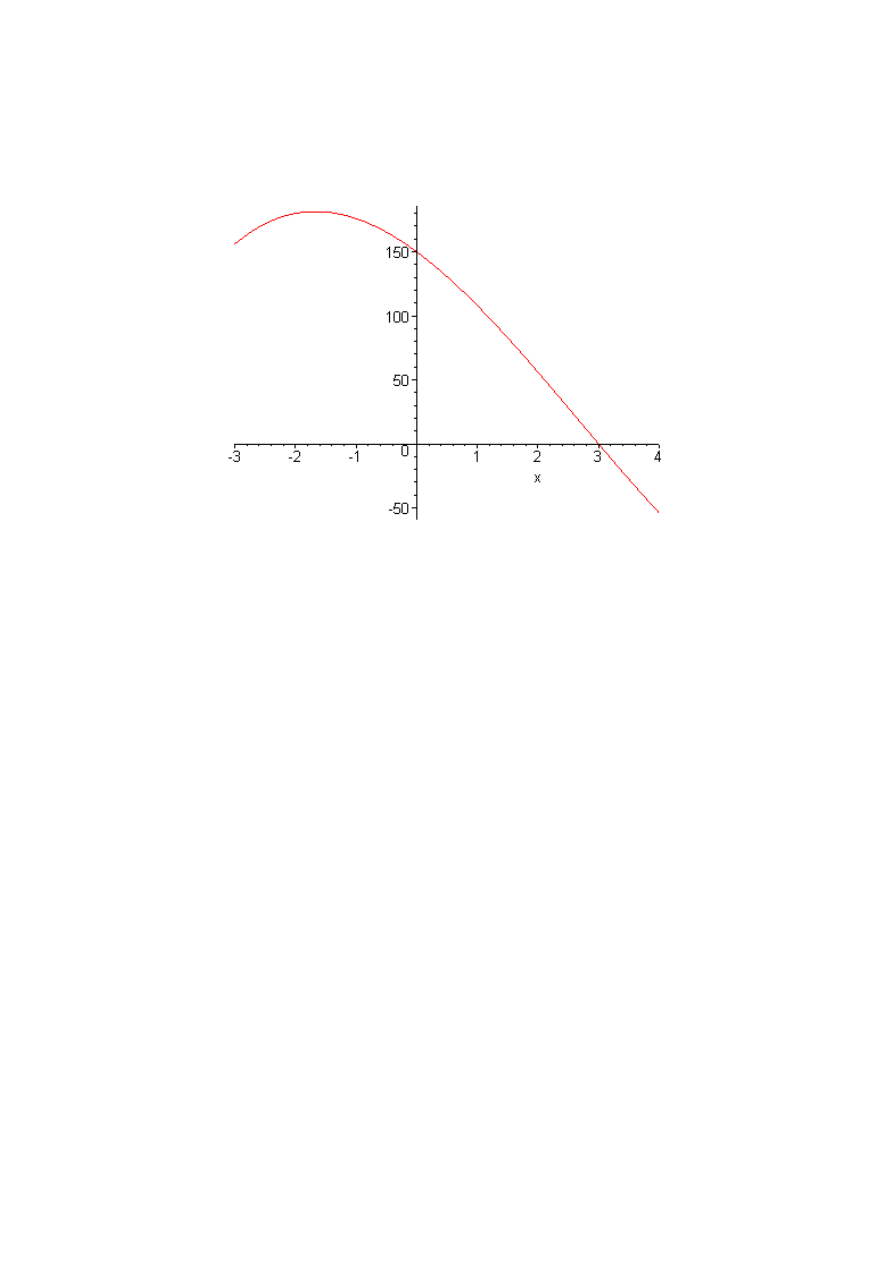
dodatnia (zawsze jesteśmy po ujemnej stronie). Szczegóły będą omówione na laboratorium.
Przetestuj działanie obu tych funkcji dla funkcji

( )

3

2

8

35

150

f x

x

x

x

=

−

−

+

w przedziale

[-3 , 4], której wykres przedstawiono na poniższym rysunku.