Modele ze zmiennymi zlogarytmowanymi

Rozważmy funkcję produkcji typu Cobba-Douglasa, postaci:

β2

β3

Y

C K

L

eε

=

⋅

⋅

⋅

gdzie Y to produkcja, K – kapitał, L – praca, C jest pewną stałą, zaś e – podstawa logarytmu naturalnego. β

2

i β są parametrami tego modelu.

3

Ponieważ nie zachodzi jedno z założeń KMRL, mówiące o tym , że model powinien być liniowy względem swoich parametrów, nie powinno się go szacować MNK.

Istnieje jednak nieskomplikowany sposób przekształcenia powyższej postaci modelu do takiej, w której będzie on względem parametrów liniowy. Przekształcenie to polega na zlogarytmowaniu modelu stronami.

Pamiętając o własnościach logarytmów, dostajemy:

ln Y = ln C + β ln K + β ln L + ε

2

3

Wiadomo również, że logarytm ze stałej również jest stałą, podstawiając więc: β = ln C , mamy: 1

ln Y = β + β ln K + β ln L + ε

1

2

3

a więc model, który spełnia założenie KMRL o liniowości względem parametrów.

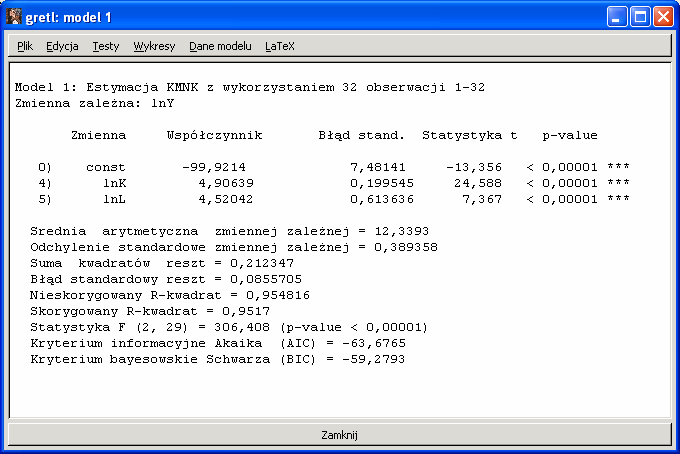
Korzystając z danych dotyczących produkcji, kapitału i pracy, po zlogarytmowaniu ich i oszacowaniu modelu, otrzymujemy:

Otrzymaliśmy oszacowania parametrów, powinniśmy teraz je zinterpretować. Jednakże zmienne poddaliśmy przekształceniu logarytmicznemu, co może nastręczać problemy interpretacyjne. Okazuje się jednak (patrz skrypt prof. Góreckiego, rozdział 5), że logarytmowanie zmiennych jest dość powszechną praktyką ekonomiczną, gdyż parametry mają wtedy interpretację w kategoriach elastyczności, a więc często bardziej pożądaną z punktu widzenia zastosowań ekonomicznych.

Powiemy więc, że jednoprocentowy wzrost kapitału ( K) powoduje średnio 4,9-cio procentowy wzrost produkcji ( Y). Analogicznie interpretujemy parametr przy zmiennej lnL.

Ćwiczenie.

a. Proszę zweryfikować istotność kapitału i pracy w modelu, oraz istotność równania regresji (łączną istotność zmiennych objaśniających).

b. Proszę zweryfikować hipotezę mówiącą, że produkcja względem kapitału charakteryzuje się stałymi przychodami skali.

c. Proszę zweryfikować hipotezę mówiącą, że wraz ze wzrostem pracy o 1%, produkcja rośnie średnio o 5,5%.

Zapisanie postaci teoretycznej modelu na logarytmach nie powinno stanowić żadnej trudności. Jak jednak zapisać postać teoretyczną funkcji Cobba-Douglasa, od której wyszliśmy? Należy zwrócić uwagę, że parametry β i β są dokładnie takie same w modelu na logarytmach oraz w wyjściowym. Nie wiemy 2

3

jedynie ile wynosi C z wyjściowego modelu, wiemy natomiast, że dane jest równaniem: β = ln C , a 1

oszacowaniem dla β jest 9

− 9,92. Z prostego przekształcenia otrzymujemy:

1

4

− 4

C = eβ ≈ 4,03 ⋅10

.

1

Teoretyczną postać funkcji Cobba-Douglasa zapiszemy więc jako:

−44

4,91

4,52

Y = 4,03 ⋅10

⋅ K

⋅ L

Zadanie:

Znany już Państwu model konsumpcji benzyny oszacowano w innej postaci:

ln G = β + β ln Y + β ln Pg + β ln Puc + ε

t

1

2

t

3

t

4

t

t

gdzie G jest konsumpcją benzyny w mld litrów, Y to dochód per capita ($), Pg jest ceną benzyny ($), zaś Puc – ceną używanych samochodów ($).

Oto oszacowanie modelu metoda najmniejszych kwadratów:

a. Oceń istotność zmiennych objaśniających w modelu.

b. Czemu służy zlogarytmowanie zmiennej zależnej i zmiennych niezależnych?

c. Jaka jest interpretacja oszacowań parametrów modelu? Zinterpretuj je.

d. Czy regresja jest istotna na poziomie istotności 0,05?

e. Zakładając, że inne wielkości się nie zmieniły, zaś cena benzyny wzrosła o 3%, o ile procent zmieniła się konsumpcja benzyny? O ile litrów się ona zmieniła, jeśli przed wzrostem cen G

kształtowała się na poziomie 320?