Wykład 10.
Temat: Estymacja
estyma – poważanie/szacunek;
- estymacja może być punktowa lub przedziałowa: estymacja przedziałowa – polega na skonstruowaniu przedziału liczbowego, który z określonym z góry (przyjętym) prawdopodobieństwem (bliskim 1) będzie zawierał nieznaną wartość szacowanego parametru; przedział ten nazywamy przedziałem ufności.
P{g1(zn) < Q < g2(zn)} = 1 – α
P – prawdopodobieństwo
Q – parametr szukany
1 – α – współczynnik ufności
- to badacz określa współczynnik ufności, jednak zwyczajowo przyjmuje się go jako: 0,90 (α
= 0,10), 0,95 (α = 0,05) lub 0,99 (α = 0,01); dla
1 – α = 0,90 (α = 0,10), z0,10 = 1,64
1 – α = 0,95 (α = 0,05), z0,05 = 1,96
1 – α = 0,99 (α = 0,01), z0,01 = 2,56
Jak to działa? W miarę wykonywania kolejnych pomiarów, obliczając średnią z każdego pomiaru oraz odchylenie przeciętne uzyskujemy kolejne średnie dla całego rozkładu: x1 – δ1 = µ1
x2 – δ2 = µ2
x3 – δ3 = µ3
…
xn – δn = µn
───────
=
x = δ (gdy równe 0) = µn
=
x – średnia ze wszystkich średnich
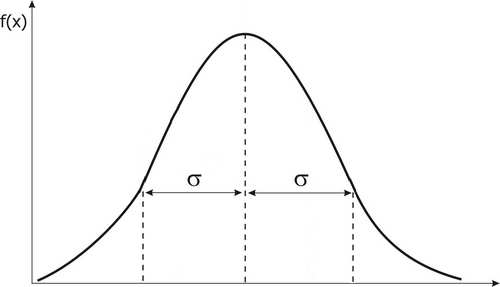
BŁĘDY MAJĄ ROZKŁAD NORMALNY!
obszar
zakreskowany to
przedział ufności
90,00%
-1
0, µ 1
Z
Z0,10
Z0,10
1,64
1,64
Jak wyznaczyć przedział ufności dla średniej µ w populacji o znanej liczebności, o rozkładzie normalnym ze znanym odchyleniem standardowym?
Korzystamy ze wzoru:
_ σ _ σ
P{(x - zα──) < Q < (x + zα──)} = 1 – α
√N √N
g1
g2
oraz:
x1 - µ
z = ──── - błąd standardowy statystyki z próby σ
─
√N
Przykład 1.
Populacja pracowników pewnej firmy:
N = 196 osób
x = 6,9 lat
σ = 2,8 lat
1 – α = 0,95 (95,00% szans na to, że parametr znajdzie się w przedziale) czyli zα = 1,96
2,8
g1 = 6,9 – 1,96 * ──── = 6,508
√196
2,8
g2 = 6,9 + 1,96 * ──── = 7,292
√196
czyli dla współczynnika ufności równego 0,95 średni staż pracy znajduje się w przedziale: 6,508 < µ < 7,292
Są dwa sposoby zwiększenia precyzji obliczeń:
- zmniejszamy współczynnik ufności;
- zwiększamy liczebność próby.
A jak obliczyć przedział ufności dla zmiennych jakościowych?
Korzystamy ze wzoru:
n n
─(1 - ─)
P
{( n ─ - zα √ N N ) < p < N
─────
N
n n
( n
─(1 - ─)
─ + zα
√ N N )} = 1 – α
N
─────
N
Przykład 2.
Dla 1 – α = 0,95 oblicz, jaka część uczniów pali papierosy, jeżeli w próbie N = 1000 uczniów, papierosy paliło 360.
n = 360
n 360
pi = ── = ─── = 0,36 (36%)
N 1000
0,36*0,64
g1 = 0,36 – 1,96 * √────── = 33,03%
1000
0,36*0,64
g1 = 0,36 – 1,96 * √────── = 38,98%
1000
Wyszukiwarka
Podobne podstrony:
WstĂŞp do Filozofii wykÂł.V - 10.11.2010, Wstęp do filozofii
PŁwSL I 2013 zima wykł 10
Podstawy metrologii wykł 10 2010 statystyka
a Mat inf. dz.wykl 10 , 1 „Równowaga przeżywania"(EB=Experience Balance)
2009 IV wykl 10 kalandrowanie
Kinezjologia wykł $ 10 08r
wykł 10 fizj roślin, biologia, fizjologia roślin
WstĂŞp do Filozofii. wykÂł I.6.10.2010, Wstęp do filozofii
KAiGN wykl 10
Klinika wykl T 10 SIDS
Wykl 10 Nowy
MD wykl 10 id 290163 Nieznany
Język jako narzedzie komunikacji wykł 10 11.12.07
archi wykl 10
Język jako narzedzie komunikacji wykł 4# 10 07
Wykł 10 Kult 2010 Hodowle kom w produkcji szczepionek
Podstawy metrologii wykł 10 2010 statystyka
więcej podobnych podstron