1

WYKŁAD Nr 10

PODSTAWY

PROJEKTOWANIA

KONSTRUKCJI

ŻELBETOWYCH

Semestr V , r .ak. 2009/2010

Opracowanie - prof. dr hab. inż. Andrzej Łapko

Obliczeniowa kontrola stanu

granicznego ugięć elementów

żelbetowych

2

Wprowadzenie – potrzeba

kontroli ugięć

 Kontrola ugięć ma istotne znaczenie z uwagi na:

- zapewnienie wymaganej użytkowalności konstrukcji,

- możliwość uszkodzeń przylegających elementów niekonstrukcyjnych,

- np. lekkie ściany działowe ,
- odczucia estetyczne użytkowników.

Ugięcia elementów żelbetowych zależą od wielu czynników, trudnych do obliczenia
w sposób ścisły. Są funkcją czasu, co wynika ze zjawiska skurczu i pełzania betonu
oraz relaksacji stali zbrojeniowej.

W większości norm projektowania postuluje się obliczanie ugięć elementów
wywołanych kombinacją obciążeń długotrwałych.

3

Wprowadzenie, wymagania PN-EN 1992-1-

1:2008

Sprawdzanie ugięć jest konieczne w konstrukcjach żelbetowych dachowych i stropowych
budownictwa mieszkaniowego, przemysłowego, rolniczego i użyteczności publicznej.

W innych przypadkach należy kontrolować ugięcia jedynie tych elementów,
które mają specjalne wymaganie w warunkach eksploatacji.

Stan graniczny ugięć należy kontrolować przyjmując obciążenia obliczeniowe
równe charakterystycznym (bez współczynników bezpieczeństwa). Można stosować:

-sposób uproszczony, polegający na kontroli wskaźnika sztywności elementu,

- metodę analityczną, polegającą na obliczeniu ugięcia zgodnie z warunkiem

lim

a

a 

Ugięcie graniczne a

lim

przyjmuje się w zwykłych przypadkach jako równe 1/250 rozpiętości

(odległość względem podpór). Gdy istnieje możliwość uszkodzenia przyległych części konstrukcji
- przyjmuje się 1/500 rozpiętości.

4

Graniczną wartość ilorazu rozpiętości do wysokości można
oszacować według wyrażeń podanych niżej i pomnożenie
przez współczynniki korekcyjne zależne od rodzaju zbrojenia i
innych zmiennych.





















































2

3

0

0

lim

1

2

,

3

5

,

1

11









ck

ck

f

f

K

d

l



































0

*

*

0

lim

12

1

5

,

1

11











ck

ck

f

f

K

d

l

Uproszczony sposób kontroli

stanu granicznego ugięcia wg PN-EN

gdzie (l/d)

lim

– dopuszczalna wartość ilorazu rozpiętości do wysokości

przekroju
K – współczynnik uwzględniający różne systemy konstrukcyjne,
patrz tablica niżej

-

umowny stopień zbrojenia

- wymagany stopień zbrojenia rozciąganego (w przęśle) lub na

podporze wspornika
- wymagany stopień zbrojenia ściskanego (w przęśle) lub na
podporze wspornika

0



3

0

10







ck

f





*



Jeżeli ρ  ρ

0

Jeżeli ρ > ρ

0

5

Uproszczony sposób kontroli stanu granicznego ugięcia wg
Eurokodu 2

(stosuje się, gdy klasa betonu jest zbliżona do B30)

Graniczne stosunki l /d rozpiętość/wysokość użyteczna dla elementów żelbetowych bez ściskania

osiowego

 

System konstrukcyjny

K

Znaczne

naprężenia

w betonie

 = 1,5 %

Małe

naprężenia

w betonie

 = 0,5 %

Belki swobodnie podparte jedno lub
dwukierunkowo płyty swobodnie podparte
 
Skrajne przęsła belek lub jednokierunkowo
pły ciągłych lub dwukierunkowo zbrojonych
płyt ciągłych na dłuższej krawędzi
 
Środkowe przęsła belek oraz
jednokierunkowo lub dwukierunkowo
zbrojonych płyt
 
Stropy bezbelkowe oparte na słupach (przy
sprawdzaniu ugięć należy przyjmować
większą rozpiętość)
 
Wsporniki

1,0

 
 

1,3

 
 
 

1,5

 
 
 

1,2

 

0,4

14

 
 

18

 
 
 

20

 
 
 

17

 

6

20

 
 

26

 
 
 

30

 
 
 

24

 

8

Uwaga 1:

Podane wartości zostały dobrane w sposób bezpieczny i obliczenia

mogą często wykazać, że możliwe jest zaprojektowanie cieńszych elementów.
Uwaga 2:

W płytach pracujących dwukierunkowo, sprawdzanie zaleca się

przeprowadzać przy założeniu krótszej rozpiętości. W płytach pełnych powinno się
przyjmować dłuższą rozpiętość.
Uwaga 3:

Wartości dopuszczalne podane dla płyt pełnych odpowiadają mniej

ostrym ograniczeniom niż ugięcia w środku rozpiętości l/250 dla słupów.
Doświadczenia wykazały, że jest to uzasadnione.
 

6

Uproszczony sposób kontroli stanu granicznego ugięcia

wg PN-EN 1992-1-1:2008

Uproszczona kontrola stanu granicznego ugięć płyt stropowych i stropodachowych
polega na kontroli

wskaźnika sztywności elementu

- parametru decydującego pośrednio

o podatności ustroju na deformacje.

Należy wykazać, że wskaźnik sztywności l

/d ustroju nie przekracza wartości granicznych,

obliczonych ze wzorów, lub ujętych w tablicy (gdy klasa betonu jest inna niż C25/30)

gdzie: (l

eff

/d)

lim

- wartość graniczna wskaźnika sztywności,



1





3

- współczynniki korekcyjne wartości podstawowej wskaźnika sztywności.,

d - wysokość użyteczna przekroju.

lim

3

2

1















d

l

d

l

eff







7

Jeśli l > 8,5 m, to dla płyt stosuje się mnożnik

Należy wykazać, że wskaźnik sztywności l

eff

/d ustroju nie przekracza wartości granicznych,

podanych w tablicy

Współczynniki korekcyjne wartości granicznej wskaźnika sztywności

Współczynnik



1

zależy od rodzaju elementu i jego rozpiętości

efektywnej:

Jeśli l > 7,,0 m, to dla płyt i belek stosuje się mnożnik

eff

l

0

,

7

1





eff

l

5

,

8

1





•gdzie: l

eff

- rozpiętość efektywna elementu

8

gdzie

Współczynniki korekcyjne wartości podstawowej wskaźnika sztywności

Współczynnik



2

oblicza się, gdy naprężenia



s

w zbrojeniu są inne

niż 310 MPa

gdzie



s

- naprężenie w przekroju prętów zbrojenia dla założonych

obciążeń.
M

Sd

- moment zginający określony dla obciążeń długotrwałych

przy



f

= 1,0,

z - ramię sił wewnętrznych, wyznaczone w przekroju
zarysowanym (II faza)
Można w uproszczeniu przyjąć:

req

s

prov

s

yk

s

A

A

f

,

,

2

500

310











1

s

Ed

s

zA

M





przy



1

 0,5 %, z = 0,90d,

przy 0,5 %<



1

 1,0 %, z = 0,85d,

przy



1

> 1,0 %,

z = 0,80d.

9

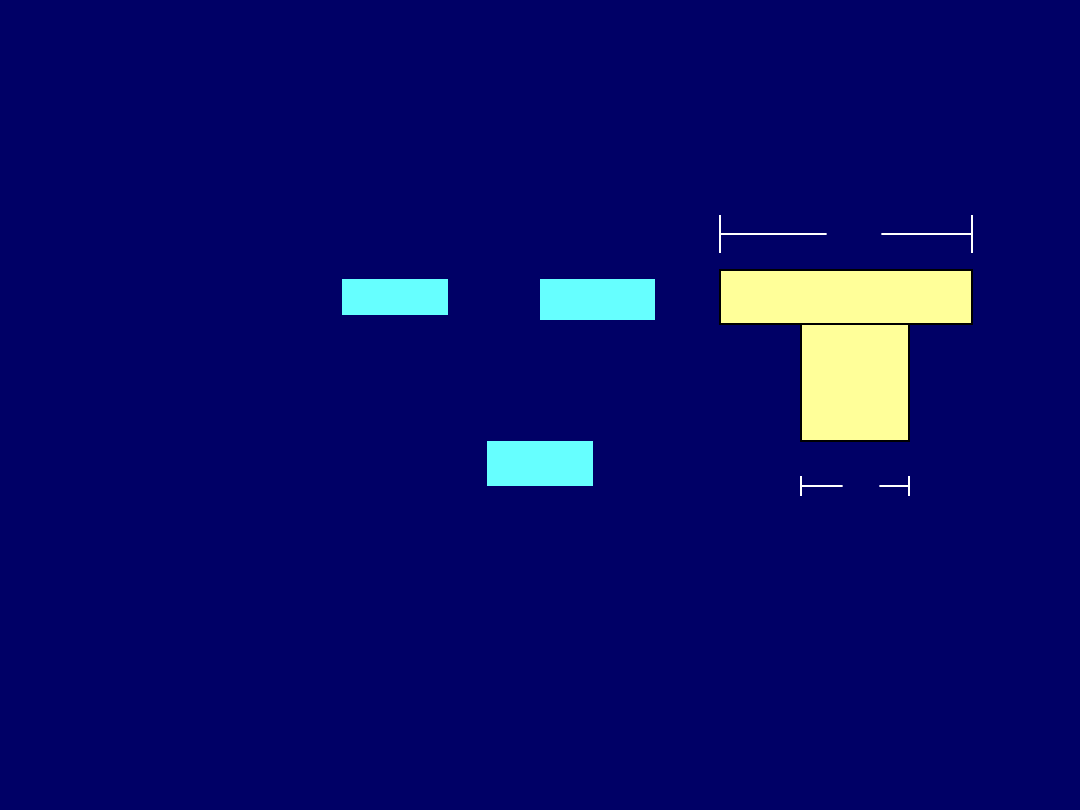
Współczynniki korekcyjne wartości podstawowej wskaźnika sztywności

Współczynnik



3

oblicza się, gdy przekrój ma półkę o szerokości

większej niż 3 x b

W przeciwnym
przypadku

8

,

0

3





0

,

1

3





b

b

ef

gdy

b

b

eff

3



10

Jeżeli stosunek rozpiętości do wysokości belki (smukłość belki) spełnia warunki
podane niżej,
Ugięcia mogą być uważane jako nie przekraczające granic podanych w Eurokodzie
2.

Graniczną wartość ilorazu rozpiętości do wysokości można oszacować według
wyrażeń podanych niżej i pomnożenie przez współczynniki korekcyjne zależne
od rodzaju zbrojenia i innych zmiennych.





















































2

3

0

0

lim

1

2

,

3

5

,

1

11









ck

ck

f

f

K

d

l



































0

*

*

0

lim

12

1

5

,

1

11











ck

ck

f

f

K

d

l

Uproszczony sposób kontroli stanu granicznego ugięcia wg
Eurokodu 2

gdzie (l/d)

lim

– dopuszczalna wartość ilorazu rozpiętości do wysokości

przekroju
K – współczynnik uwzględniający różne systemy konstrukcyjne,
patrz tablica niżej

-

umowny stopień zbrojenia

- wymagany stopień zbrojenia rozciąganego (w przęśle) lub na

podporze wspornika
- wymagany stopień zbrojenia ściskanego (w przęśle) lub na
podporze wspornika

0



3

0

10







ck

f





*



Jeżeli ρ  ρ

0

Jeżeli ρ > ρ

0

11

Podstawy obliczania ugięć

zginanych elementów żelbetowych

12

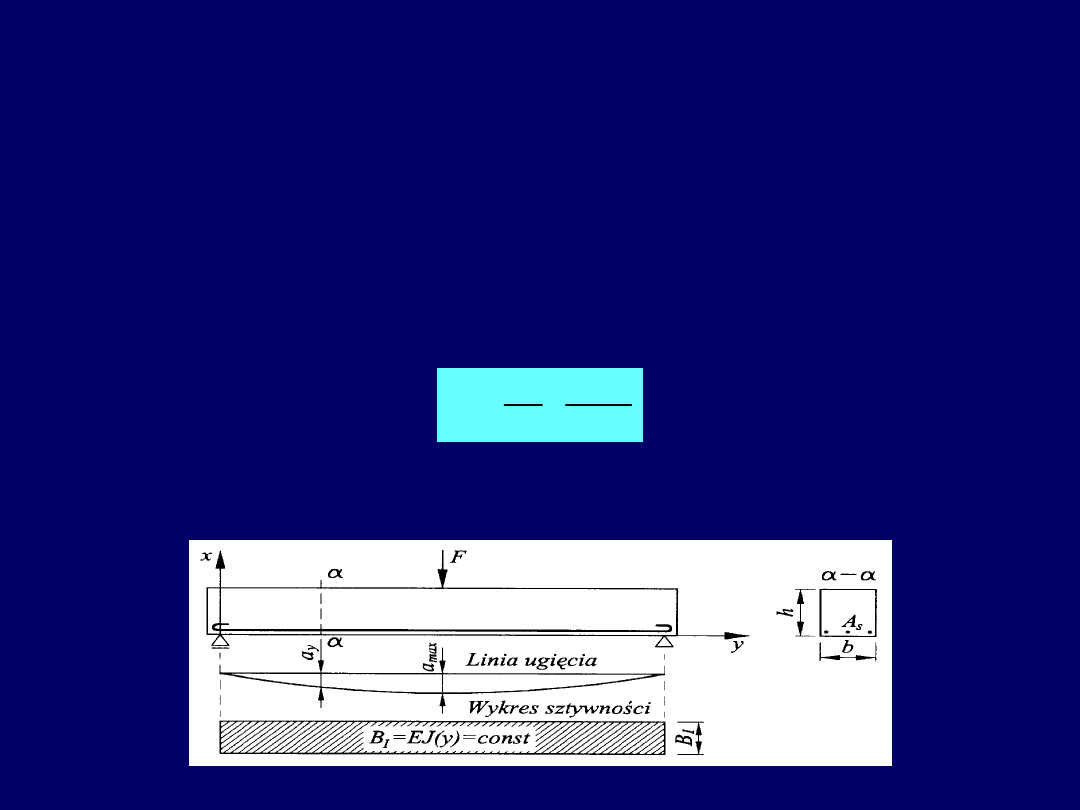
Ugięcie elementu żelbetowego jest funkcją wielu parametrów wpływających na
odkształcenia i naprężenia w betonie i stali zbrojeniowej zależnych od poziomu
obciążenia i właściwości materiałowych betonu i zbrojenia, a także od czasu

W modelu liniowo-sprężystym (FAZA I) przemieszczenie pionowe a (ugięcie) elementu
niezarysowanego wyznacza się na podstawie krzywizny

. W przypadku zginania

krzywizna może być obliczona z uproszczonego równania osi odkształconej elementu

 

 

,

2

2

y

J

E

y

M

dy

a

d

y











gdzie: E J(y) = B

I

- sztywność przekroju elementu, którego położenie opisano współrzędną y.

13

gdzie: M

Ed

– obliczeniowy moment zginający (przy współczynniku obciążenia



f

= 1,0)

r - promień krzywizny elementu odkształconego,
B – sztywność elementu na zginanie

B

M

r

Ed





1



W elemencie zginanym niezarysowanym

krzywizny obliczamy ze wzoru

Wskutek zarysowania w ustroju żelbetowym następuje redystrybucja naprężeń w zbrojeniu
rozciąganym, co powoduje przyrost krzywizny i spadek sztywności elementu na odcinku
między rysami. Zarysowanie wyraźnie zmniejsza sztywność elementu i zwiększa ugięcia

14

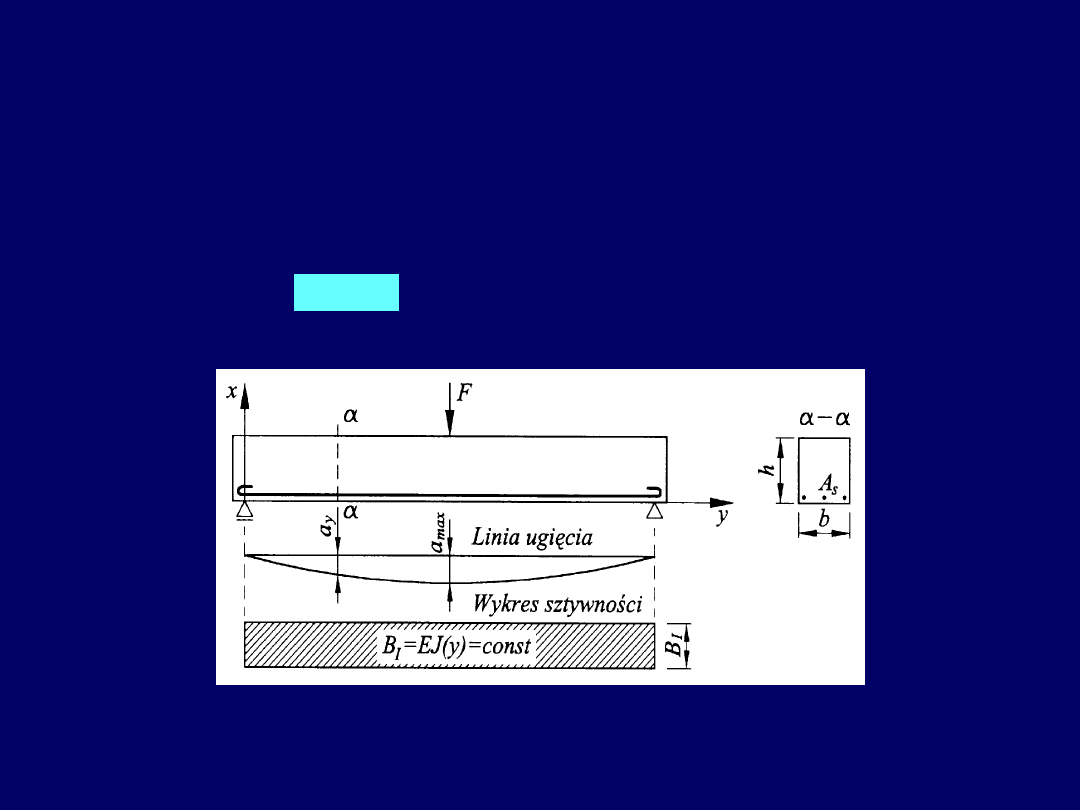
Ugięcia elementów niezarysowanych

-

Faza I

Element zginany nie wykazuje zarysowania (I faza), gdy spełniony jest warunek

cr

Ed

M

M 

gdzie M

cr

– moment rysujący

Krzywizna i ugięcie elementu zginanego w fazie I (bez rys)

15

Ugięcia elementów niezarysowanych

-

Faza I

W modelu liniowo-sprężystym ugięcie a elementu w fazie I (bez rys) wyznacza się
na podstawie krzywizny

, która w przypadku zginania może być obliczona

z uproszczonego równania osi odkształconej elementu

 

 

,

2

2

y

J

E

y

M

dy

a

d

y









gdzie: E J(y) - sztywność przekroju (B), którego położenie opisane jest współrzędną y.

Jeżeli moment bezwładności
przekroju J(y) = const. na długości
elementu to sztywność elementu B
jest również stała

16

Ugięcia elementów niezarysowanych

-

Faza I

Z równania

 

 

,

2

2

y

J

E

y

M

dy

a

d

y









gdzie: C , D - stałe całkowania zależne od warunków brzegowych i rodzaju obciążenia.

Obliczenia ugięcia elementu zginanego w fazie I można
dokonać ze wzoru

ugięcie można obliczyć poprzez całkowanie krzywizny na długości l
elementu zginanego

 

 

D

Cy

y

y

y

EJ

y

M

a





















d

d

B

l

M

a

eff

Ed

k

2







gdzie: B - sztywność elementu na zginanie,

l

eff

- rozpiętość efektywna elementu,



k

- współczynnik wyrażający stałe całkowania

17

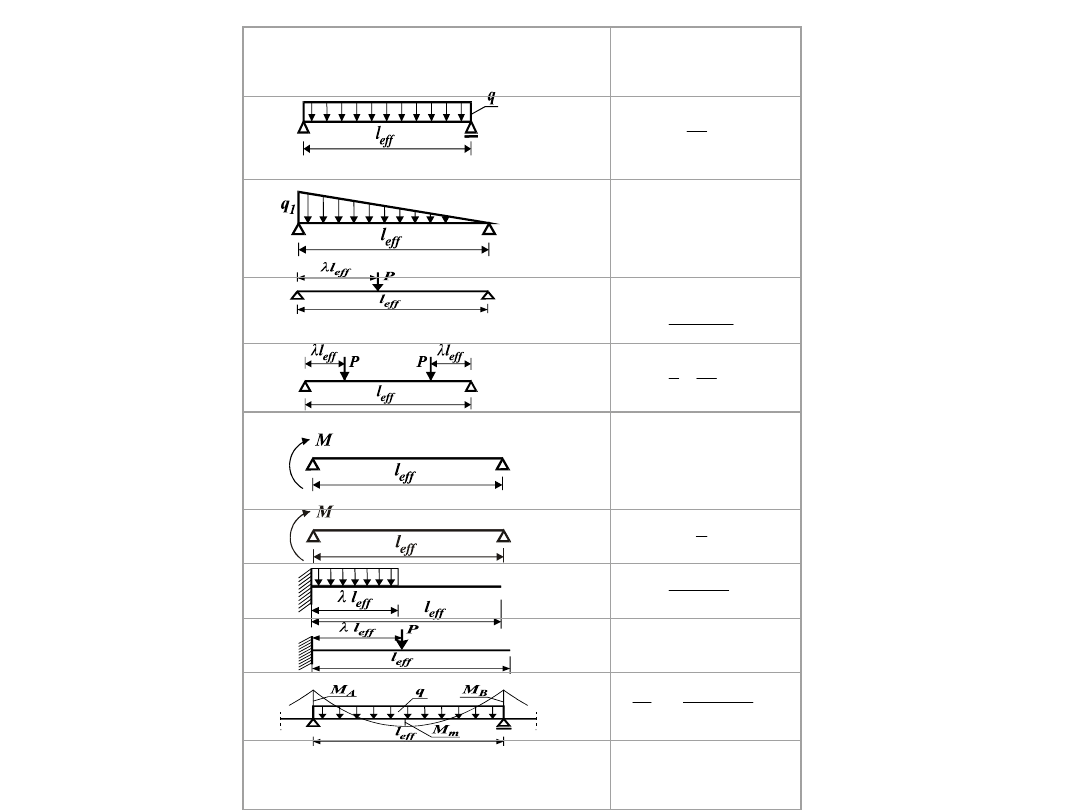
48

5













1

48

4

3

2

6

8

1

2





8

1





6

4























m

B

A

M

M

M

10

1

48

5

Układ obciążenia i schemat statyczny

elementu

Współczynnik



k

 

 

 

0,102

 
 

dla

 = 0,5 

k

= 1/12

 

 
 

 

 

0,0625

 

 

 

dla



= 1



k

=

1/3.

 
 

 
 

6

/

)

3

(



 

18

Sztywność przekroju B w zginanych

elementach niezarysowanych

- przy obciążeniach długotrwałych

-

dla

obciążeń

krótkotrwałych

I

cm

J

E

B 

0

I

eff

c

J

E

B

,





gdzie: E

cm

- średni moduł sprężystości betonu,

E

c,eff

- efektywny moduł sprężystości (z uwzględnieniem pełzania betonu).

J

I

– moment bezwładności przekroju w fazie I

Efektywny moduł sprężystości betonu, w zależności od czasu t działania obciążenia

 

0

,

,

1

t

t

E

E

cm

eff

c







- gdzie φ(t, t

o

) współczynnik pełzania przy obciążeniach

długotrwałych

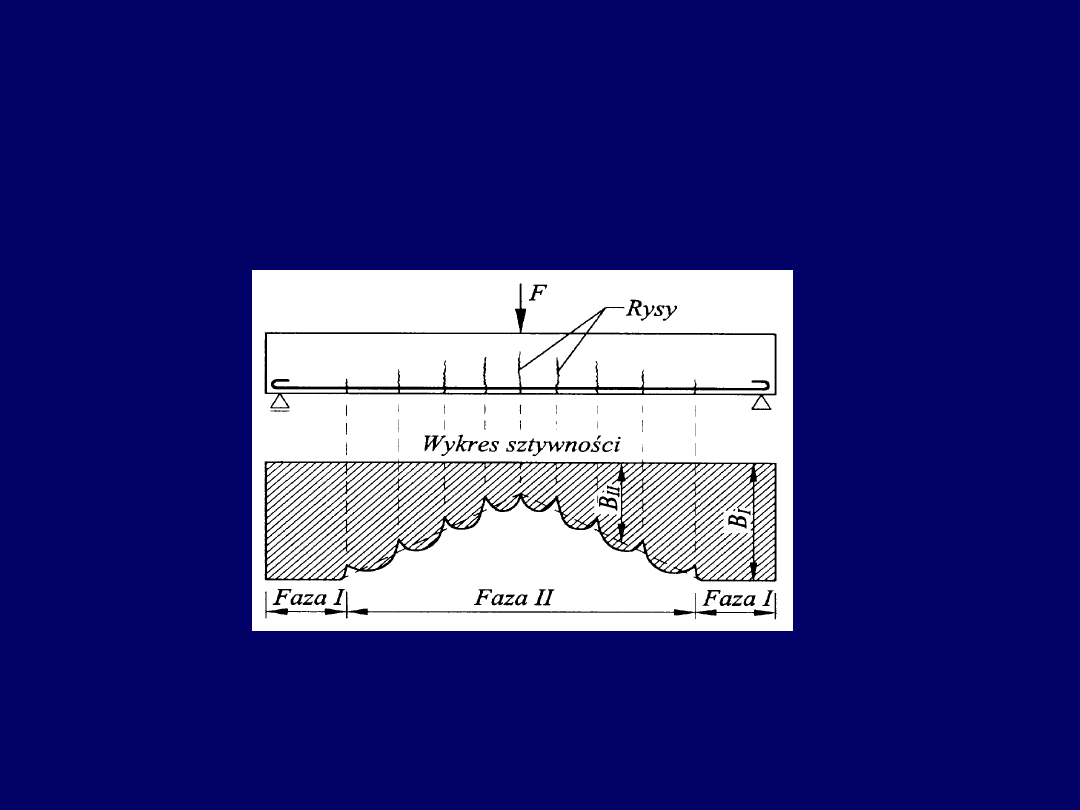
19

Ugięcia elementów zarysowanych

W elemencie żelbetowym zarysowanym (w fazie II) sztywność
zmienia się na długości ustroju, z uwagi na rozkłady naprężeń w
zbrojeniu - sztywność B

II

Wpływ zarysowania na spadek sztywności zginania elementu

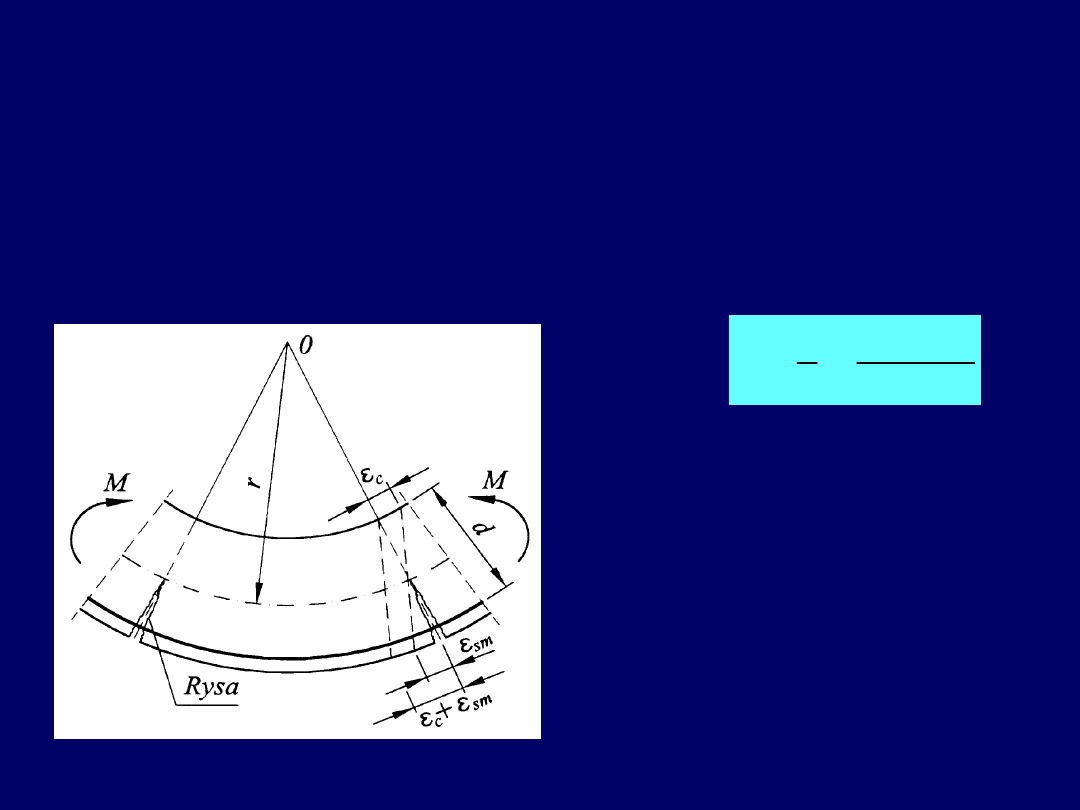
20

Określenie sztywności na zginanie,

związanej

z krzywizną elementu

Uśrednioną krzywiznę



na długości elementu zarysowanego wyznaczamy na

podstawie odkształceń



sm

zbrojenia rozciąganego i odkształceń



c

w skrajnym

włóknie ściskanym na odcinku między rysami.

gdzie d – wysokość użyteczna przekroju
w obliczanym elemencie zginanym.

d

r

c

sm













1

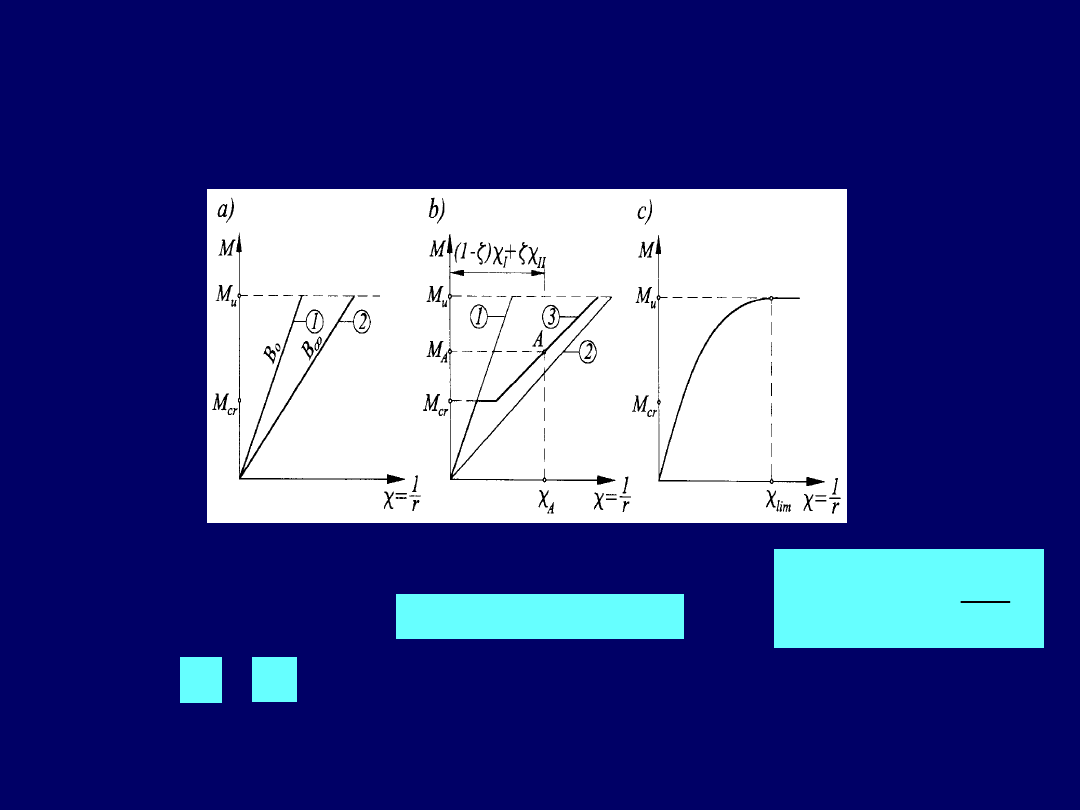
21

Średnie odkształcenia w zbrojeniu rozciąganym i

betonie ściskanym wyznacza się z

uwzględnieniem współpracy

betonu i zbrojenia na odcinku między rysami

W formie skróconej zapisujemy





I

s

II

s

sm















1

gdzie: i - odpowiednio odkształcenia w fazie I i czystej
fazie II,

- współczynnik uwzględniający efekt współpracy zbrojenia i
betonu
na odcinku między rysami (tension stiffening effect)

I

s



II

s



2

2

1

1

















II

s

II

sr











gdzie

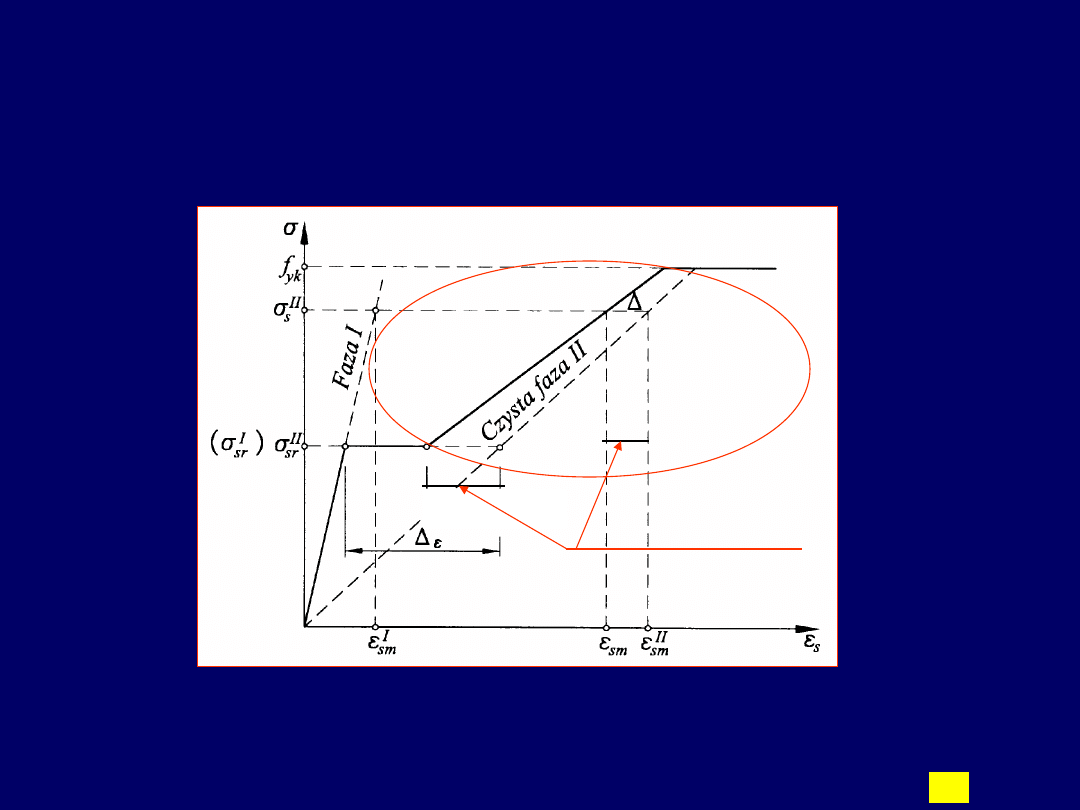
22

Interpretacja graficzna do wyznaczenia

średnich odkształceń zbrojenia – z

uwzględnieniem efektu „tension stiffening”

Δε

sm

Do chwili zarysowania przekroju naprężenia i odkształcenia w zbrojeniu opisane są linią prostą
(faza I). Po osiągnięciu obciążenia rysującego (momentu lub siły), dochodzi do powstania rysy,
a odkształcenia w zbrojeniu (w przekroju przez rysę) wzrastają skokowo o wartość





Obszar
wystąpien
ia
efektu
„tension
stifening
”

efekt „tension stifening”



23

Współczynnik uwzględniający efekt

współpracy zbrojenia i betonu na

odcinku między rysami

Przyjmując liniową zależność między naprężeniem i momentem zapisujemy

2

2

1

1

















II

s

II

sr











Współczynnik



1

określa się następująco:

- dla prętów żebrowanych



1

= 1,0,

-dla prętów gładkich



1

= 0,5.

Współczynnik



2

zależy od czasu działania i powtarzalności

obciążenia:
- dla jednokrotnego obciążenia krótkotrwałego



2

=

1,0,
- dla obciążeń długotrwałych lub wielokrotnie powtarzalnych



2

=

0,5.

2

2

1

1

















Ed

cr

M

M







24

Sztywność zginania pod obciążeniem

długotrwałym

-w fazie II

- w fazie I

Wykorzystujemy wzór ogólny na krzywiznę z uwzględnieniem efektu
„Tension stifening”

Współczynnik

 wyraża wpływ współpracy betonu i zbrojenia na odcinku między rysami

I

eff

c

I

J

E

B

,



II

eff

c

II

J

E

B

,







I

eff

c

Ed

II

eff

c

Ed

m

J

E

M

J

E

M

,

,

1













i obliczymy średnią krzywiznę elementu na odcinku między rysami





I

II

m















1

25

Sztywność zginania pod obciążeniem

długotrwałym.

Podstawiając
wyrażenie

otrzymujemy

Średnia krzywizna elementu na odcinku między rysami





I

eff

c

Ed

II

eff

c

Ed

m

J

E

M

J

E

M

,

,

1













2

2

1

1

















II

s

II

sr























































I

II

s

sr

II

eff

c

Ed

m

J

J

J

E

M

1

1

2

2

1

,











26

Sztywność zginania pod obciążeniem

długotrwałym

Podstawiając
wyrażenie

Otrzymujemy
po
przekształcen
iach

Sztywność B



zarysowanego przekroju zginanego można wyznaczyć z

przekształcenia wzoru













































I

II

s

sr

II

eff

c

Ed

m

J

J

J

E

M

1

1

2

2

1

,











B

M

r

Sd





1



































I

II

s

sr

II

eff

c

J

J

J

E

B

1

1

2

2

1

,











Sd

M

B 

27

Sztywność zginania pod obciążeniem

krótkotrwałym

Sztywność B

0

zarysowanego przekroju zginanego

wyznacza się ze wzoru































I

II

s

sr

II

cm

J

J

J

E

B

1

1

2

2

1

0









gdzie M

Ed

- moment zginający wywołany obciążeniem krótkotrwałym

Ugięcie oblicza się ze wzoru ogólnego

B

l

M

a

eff

Ed

k

2







28

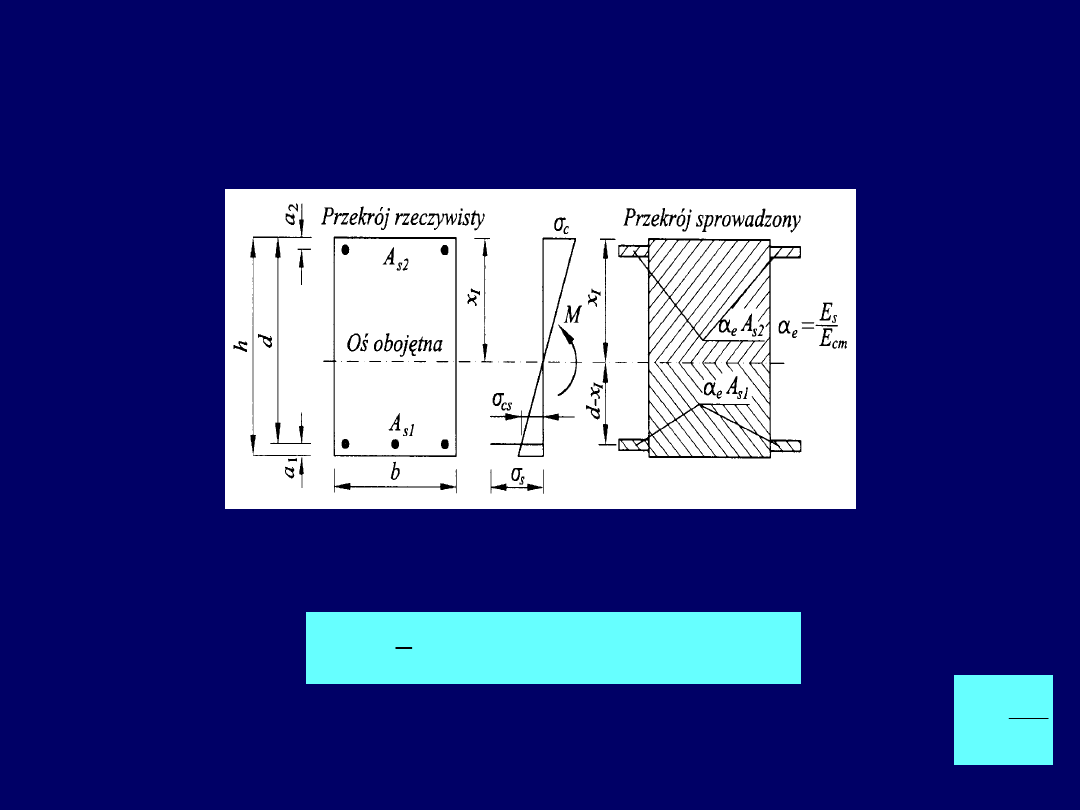
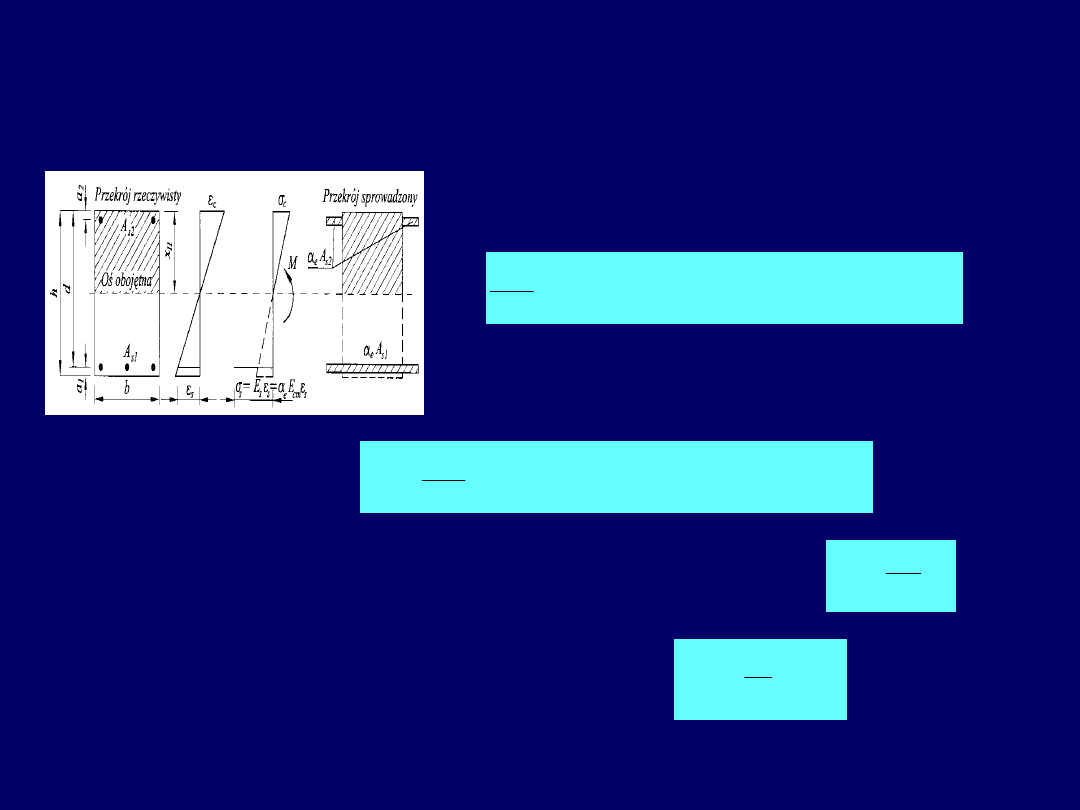
Algorytm obliczania ugięć elementów

żelbetowych

Przekroje niezarysowane - I faza

Położenie osi obojętnej x

I

w przekroju określa się na podstawie równania sumy

momentów statycznych względem poszukiwanego zasięgu strefy ściskanej









0

2

1

2

2

























I

s

e

I

s

e

I

x

d

A

a

x

A

h

x

bh





gdzie



e

- współczynnik dla obciążeń krótkotrwałych.

cm

s

e

E

E





29

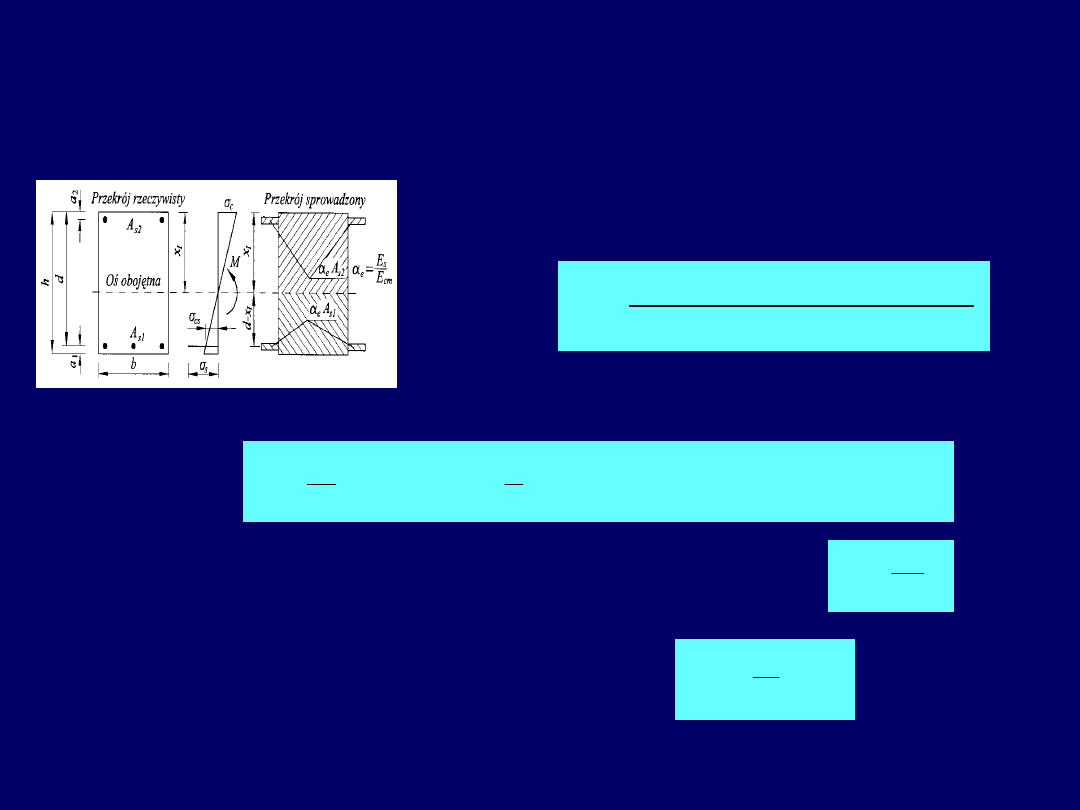
Algorytm obliczania ugięć elementów

żelbetowych

Przekroje niezarysowane – I faza

Położenie osi obojętnej x

I

- naprężenia w skrajnym ściskanym włóknie betonu









.

5

,

0

2

1

2

2

1

2

s

s

e

s

s

e

I

A

A

bh

a

A

d

A

bh

x















Moment bezwładności przekroju w fazie I









2

1

2

2

2

2

3

2

12

1

I

s

e

I

s

e

I

I

x

d

A

a

x

A

h

x

bh

bh

J































I

I

c

x

J

M





- naprężenia w zbrojeniu rozciąganym





I

I

e

s

x

d

J

M









30

Algorytm obliczania ugięć elementów

żelbetowych

Przekroje zarysowane – II faza

Położenie osi obojętnej x

II

- naprężenia w skrajnym ściskanym włóknie betonu

Moment bezwładności przekroju w fazie II

II

II

c

x

J

M





- naprężenia w zbrojeniu rozciąganym





II

II

e

s

x

d

J

M

















0

2

1

2

2

2











II

e

II

e

II

x

d

bd

a

x

bd

bx

















2

2

2

2

1

3

3

a

x

bd

x

d

bd

bx

J

II

e

II

e

II

II



















31

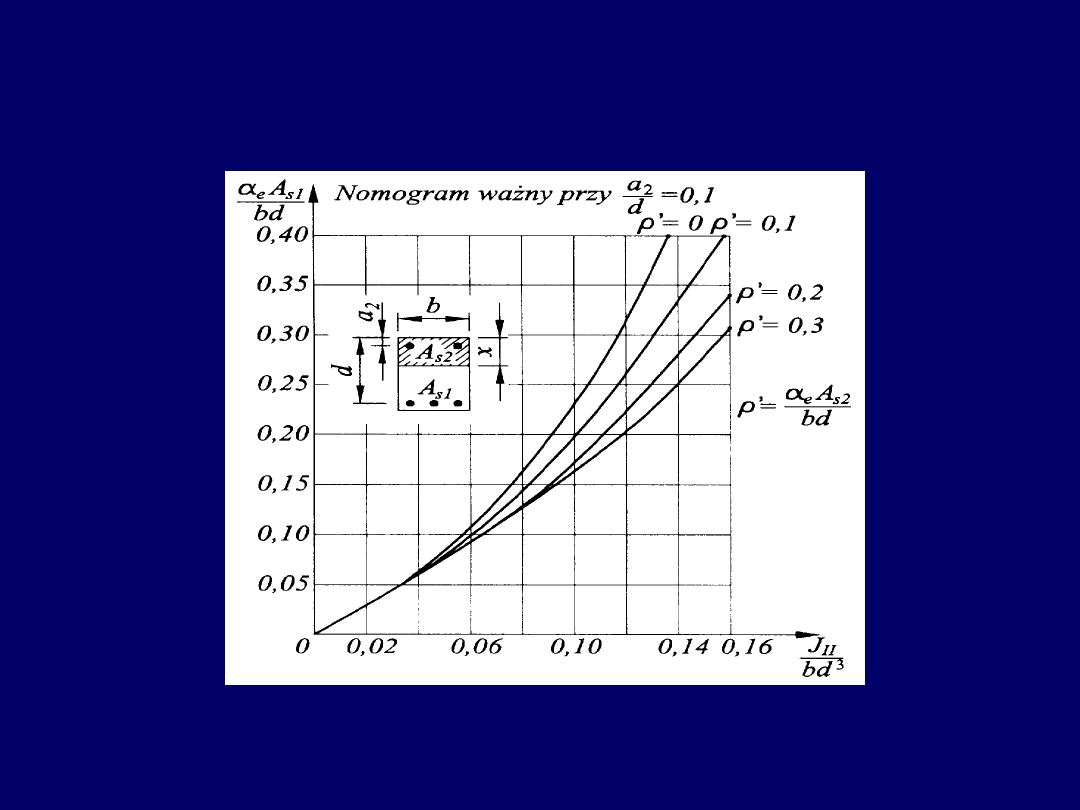
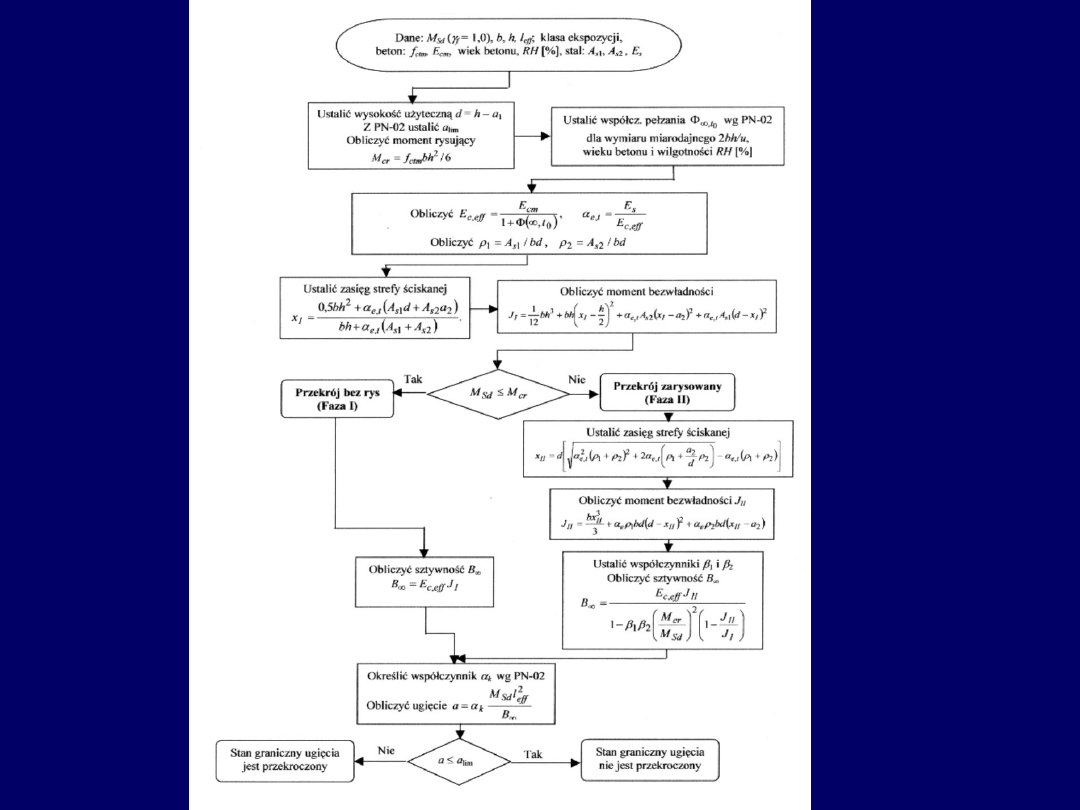
Moment bezwładności przekroju w

fazie II

- nomogram

32

Algorytm obliczania ugięć

elementów zginanych

33

KONIEC