1

PODSTAWY

PROJEKTOWANIA

KONSTRUKCJI

BETONOWYCH

Semestr V , r .ak. 2011/2012

Koncepcje konstrukcji

zbrojonych

Właściwości betonu

konstrukcyjnego

WYKŁAD NR 1-część A

Opracowanie - prof. dr hab. inż.. Andrzej Łapko

2

Koncepcje wzmocnienia konstrukcji z betonu

poprzez stosowanie wkładek zbrojeniowych

– osiągnięcie myśli inżynierskiej XIX i XX w.

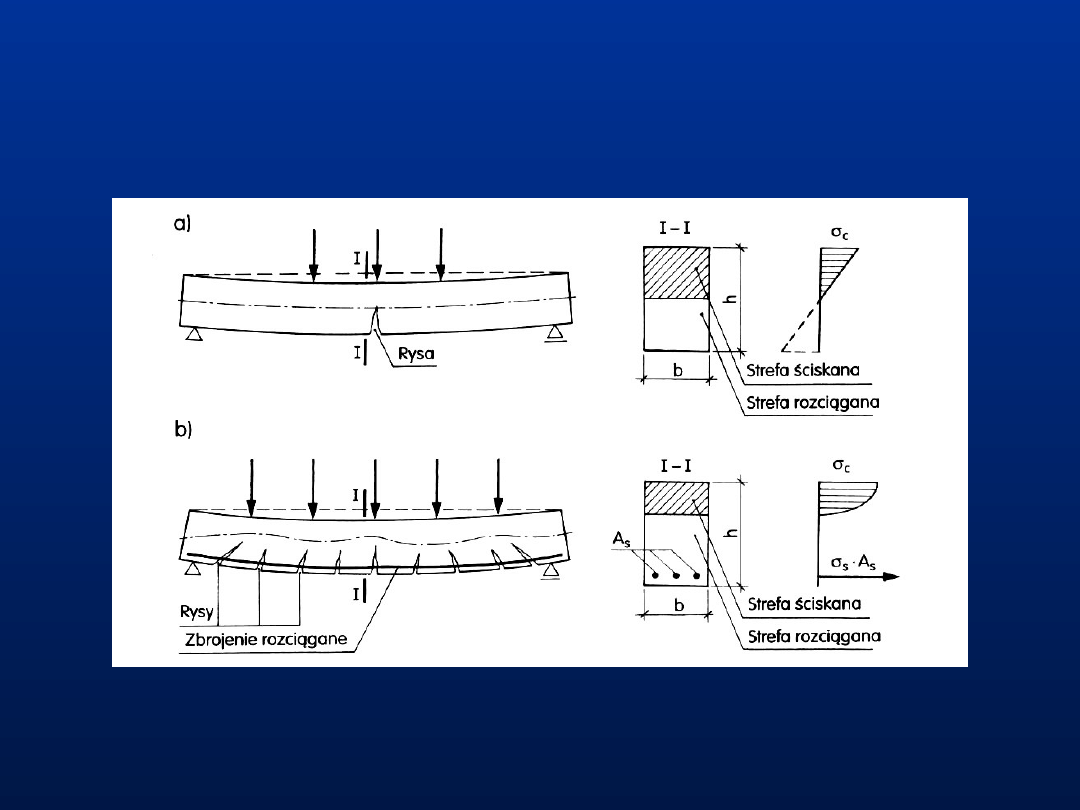
Schemat pracy belki z czystego betonu (a) i belki zbrojonej wkładkami ze stali (b)

3

Koncepcje wzmocnienia konstrukcji z

betonu

poprzez stosowanie wkładek

zbrojeniowych

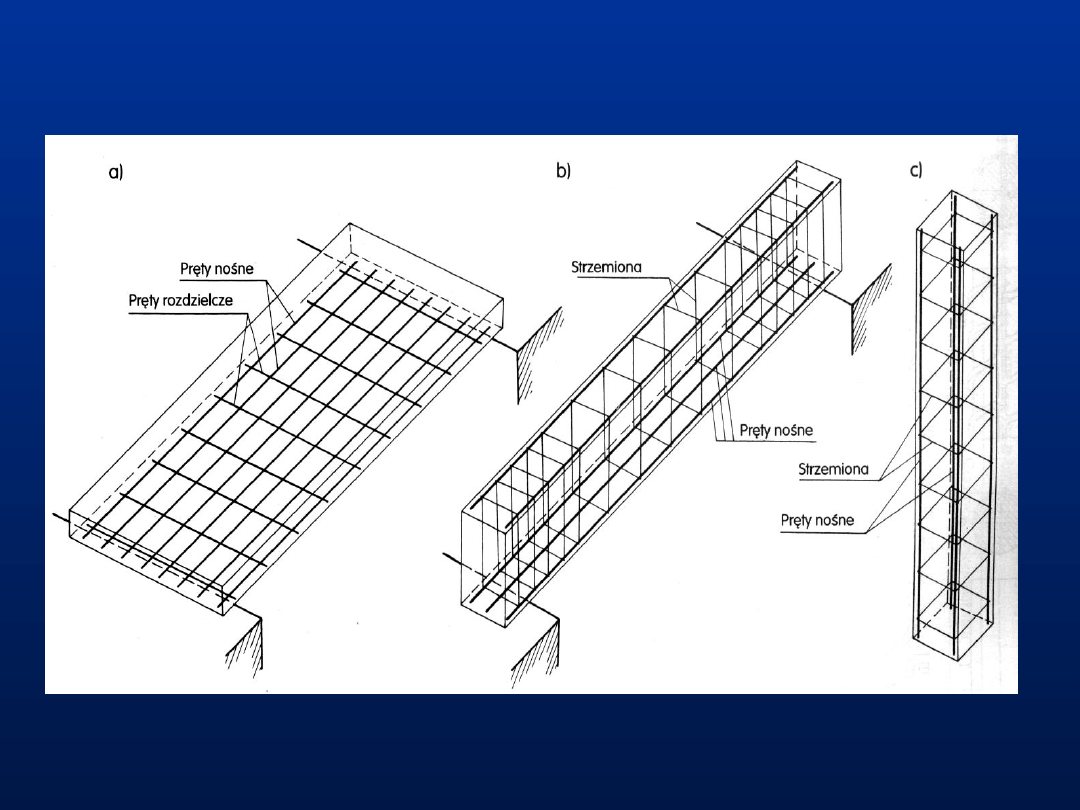
Schematy rozmieszczenia wkładek zbrojenia w elementach nośnych z betonu

(a) w płycie żelbetowej, b) w belce żelbetowej, c) w słupie żelbetowym

4

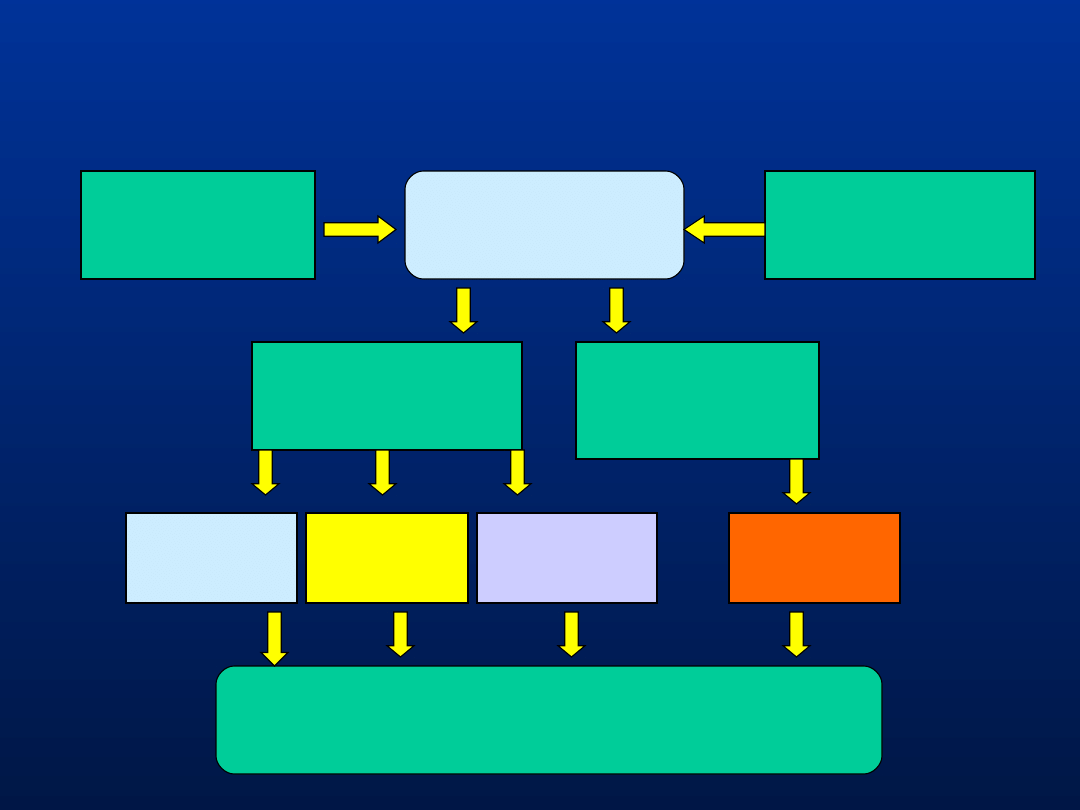
Rodzaje konstrukcji z betonu zbrojonego

Konstrukcje z betonu

zbrojonego

Matryca cementowa

- beton

Zbrojenie

Pręty, druty, cięgna,

siatki, włókna

Zbrojenie ciągłe

Zbrojenie nieciągłe

Żelbet

Beton

sprężony

Siatkobeton

Włóknobeton

kompozyt

Elementy i konstrukcje wykonywane

monolitycznie lub jako prefabrykaty

5

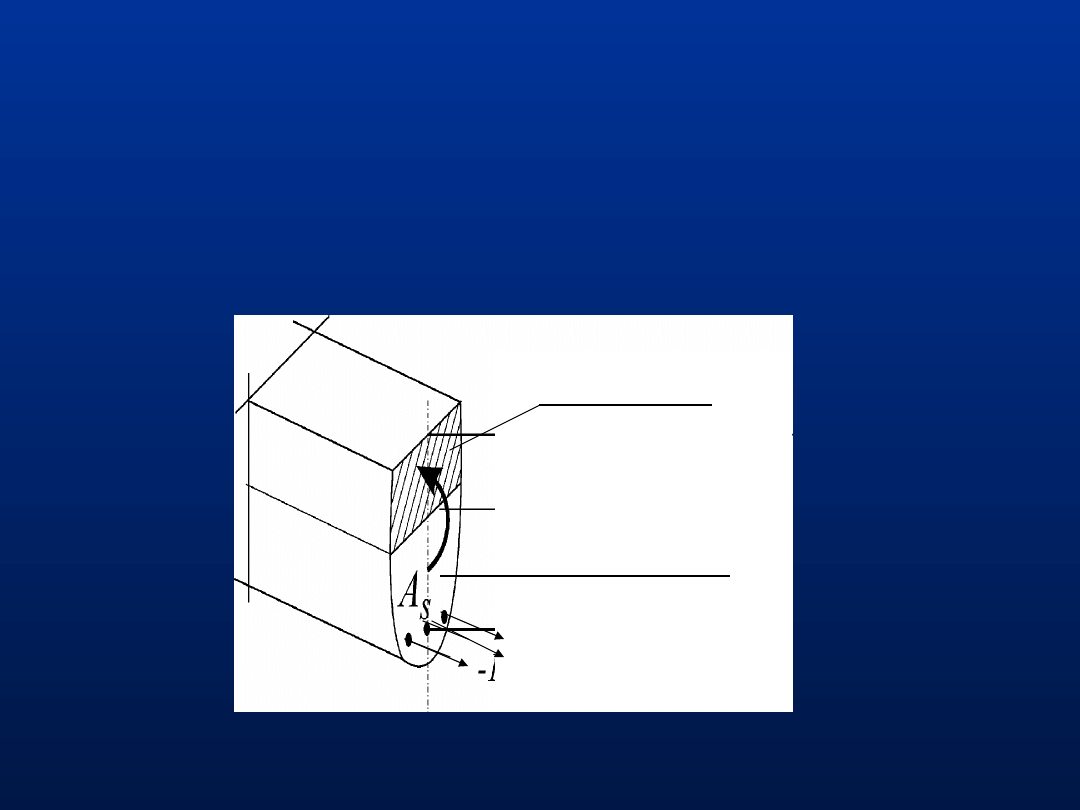
Konstrukcje żelbetowe – konstrukcje z betonu

wzmocnionego w sposób celowy wkładkami ze

stali zbrojeniowej

Strefa ściskana

Strefa rozciągana

M

Ed

6

Podstawą projektowania konstrukcji betonowych jest

norma europejska (Eurokod 2) o symbolu PN-EN 1992-1-

1:2008

7

Właściwości betonu do

konstrukcji

8

Wytrzymałość betonu na ściskanie

Jest to maksymalne obciążenie ściskające, jakie

jest w stanie przenieść próbka betonu na

jednostkę powierzchni

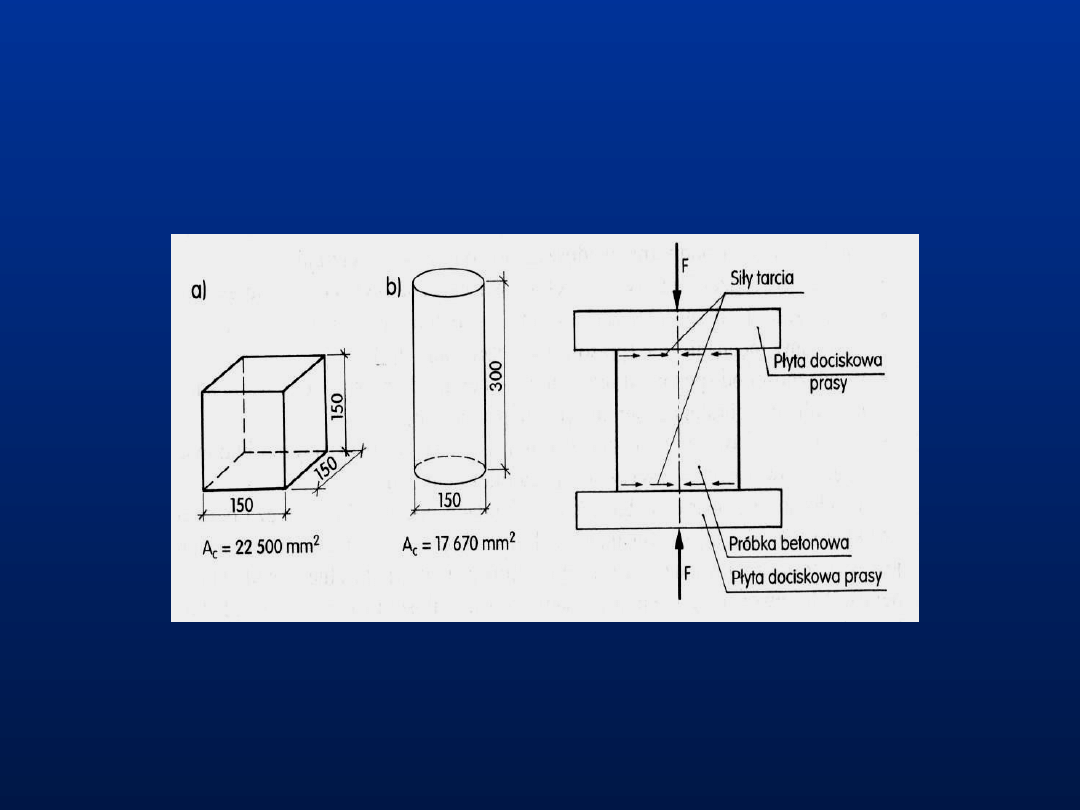
Normowe próbki do badań wytrzymałości betonu na ściskanie

Badania wytrzymałości betonu na ściskanie przeprowadza się w Polsce

na próbkach kostkowych (standardowa próbka o boku 15 cm)

Warunki badań - Instrukcja ITB nr 194 (1998) i PN-EN –206 –1:2003

9

Normowe próbki po badaniach wytrzymałości betonu na ściskanie

a) próbka walcowa, b) próbka kostkowa

10

Wytrzymałość na ściskanie betonu –
zależy od wielu parametrów:

 

       Składu betonu wynikającego z rodzaju,

uziarnienia
i wytrzymałości kruszywa,
       Rodzaju i ilości cementu,

       Wskaźnika c/w,

       Warunków środowiska (warunki termiczno

–
wilgotnościowe podczas pielęgnacji),
       Sposobu obciążenia,

       Geometrii badanych elementów próbnych,

       Czasu obciążenia oraz wieku betonu.

11

Ocena statystyczna wytrzymałości betonu

Wytrzymałość średnia i gwarantowana

Dla potrzeb statystycznej kontroli jakości partii

betonu wymagane

jest zbadanie serii n próbek (pożądana liczba próbek

wynosi 15).

Na tej podstawie dokonuje się estymacji

(oszacowania)

wartości średniej wytrzymałości f

cm

betonu, wg wzoru

 

(1)







n

i

ci

cm

f

n

f

1

1

12

         

Ocena statystyczna wytrzymałości betonu















n

i

cm

ci

f

f

n

s

1

2

1

1

Średnie odchylenie standardowe s wyników badań w
danej serii wynosi:

Odchylenie standardowe charakteryzuje otrzymane wyniki.

Im wyższa jest wartość odchylenia s,

tym wytrzymałość gwarantowana betonu jest niższa.

(2)

13

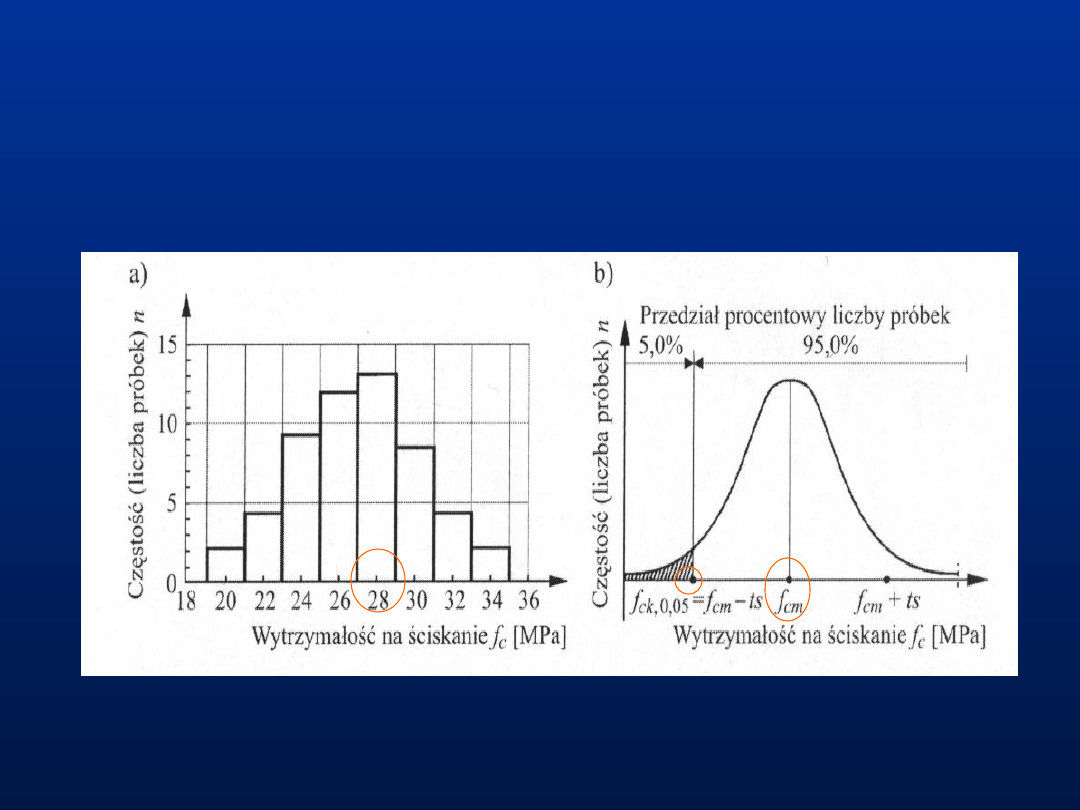
Funkcje rozkładu wytrzymałości betonu – w rozkładzie normalnym

Funkcja Gaussa definiuje na osi odciętych wytrzymałość średnią - f

cm

oraz gwarantowaną wytrzymałość betonu określaną z założonym

prawdopodobieństwem p(t) = 95% (t - parametr rozkładu).

Funkcje rozkładu normalnego używane w ocenie statystycznej jakości betonu:

a) –histogram wytrzymałości betonu na ściskanie,

b) – wykres prawdopodobieństwa w rozkładzie normalnym

14

         

Ocena statystyczna wytrzymałości betonu

Z wykresu prawdopodobieństwa w rozkładzie normalnym można
wyznaczyć wartość parametru t, który dla p = 95% wynosi 1,64.
Dla założonego prawdopodobieństwa p = 95% i znanej wartości
t można określić wytrzymałość gwarantowaną na podstawie wartości
średniej i odchylenia standardowego s

s

f

f

cm

ck







64

,

1

05

.

0

,















n

i

cm

ci

f

f

n

s

1

2

1

1

gdzie:

Wartość f

ck,005

jest to pięcioprocentowy kwantyl wytrzymałości

betonu na ściskanie.

(3)

15

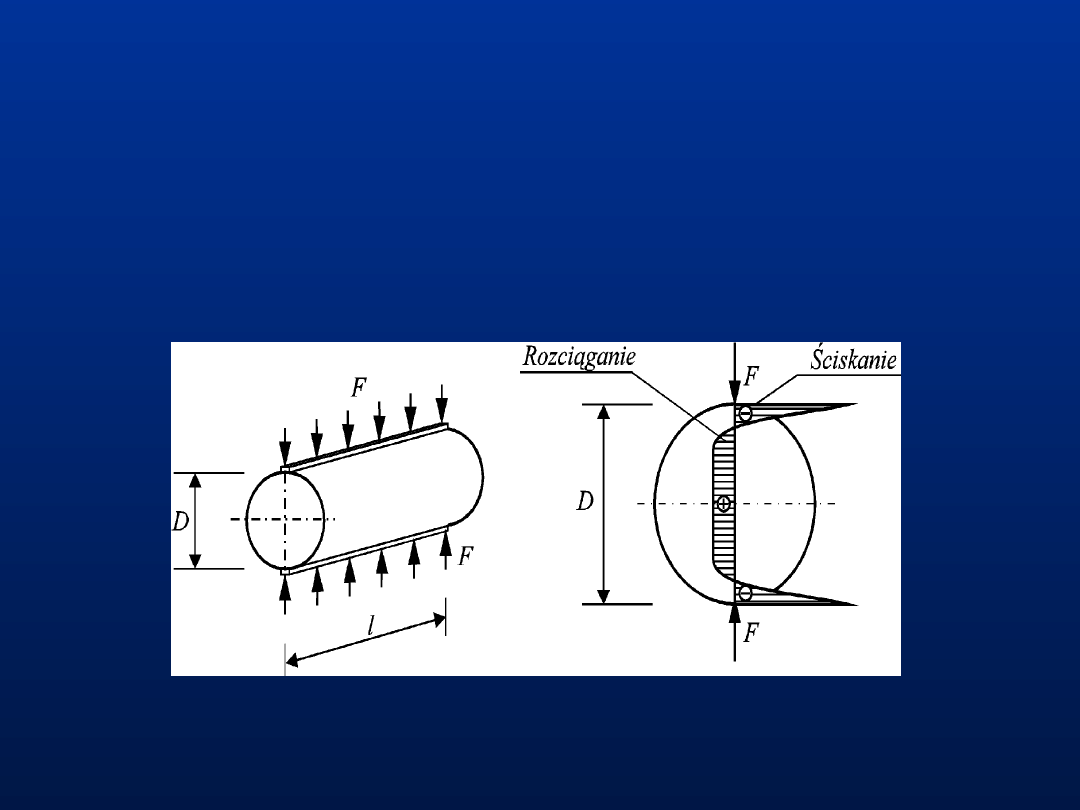
Wytrzymałość betonu na rozciąganie

 

Wytrzymałość betonu na rozciąganie utożsamiać należy

z maksymalnym naprężeniem rozciągającym, jakie jest w stanie

przenieść beton podlegający jednoosiowemu rozciąganiu.

Pośredni sposób pomiaru wytrzymałości betonu metodą „brazylijską”

16

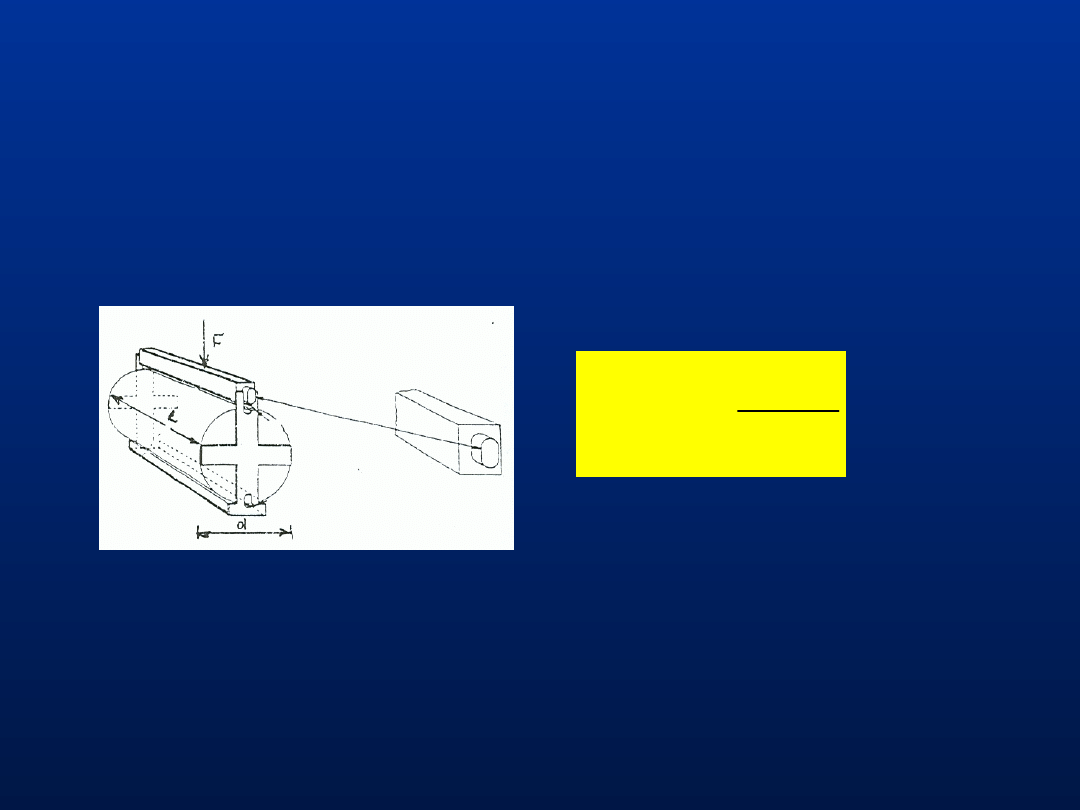
Metoda brazylijska badania wytrzymałości betonu na rozciąganie

Wytrzymałość betonu na rozciąganie f

ct,sp

wyraża się wzorem

D

l

F

c

f

sp

ct



2

,



gdzie F - maksymalne obciążenie przyłożone wzdłuż
tworzącej walca, D – średnica, l - długość walca, c -
współczynnik korekcyjny

.

17

Wytrzymałość na rozciąganie przy zginaniu

Metoda pośrednia

- zginania betonowych

pryzmatycznych beleczek próbnych o przekroju 150
x 150 mm.
Badanie

to

wykonuje

się

w

maszynie

wytrzymałościowej przez obciążenie elementów
próbnych

wolno

podpartych

dwoma

siłami

skupionymi

przyłożonymi

w

jednej

trzeciej

rozpiętości beleczki.
 

l

F/2

F/2

2

,

bh

l

F

f

n

f

ct



gdzie F

n

jest siłą niszczącym próbkę, l jest rozpiętością beleczki,

b oraz h oznaczają wymiary jej przekroju.

18

Rodzaje wytrzymałości betonu

określone

w Eurokodzie 2 (PN-EN 1992-1-

1:2008)

Wytrzymałość

charakterystyczna

walcowa

betonu
na ściskanie

–

(5 % kwantyl rozkładu wytrzymałości) pomierzonej na walcach
o średnicy 15 cm i wysokości 30 cm - odpowiednik
wytrzymałości gwarantowanej
w konstrukcji (w jednoosiowym stanie naprężenia).

Wytrzymałość charakterystyczna kostkowa na
ściskanie

mierzona na kostkach 15 x 15 x 15cm -

gwarantowana przez producenta jako 5 % kwantyl rozkładu
statystycznego

Średnia wytrzymałość betonu na ściskanie

 

cube

ck

f

,

f

ck

,

cm

f

19

  

Wytrzymałość charakterystyczna betonu na

rozciąganie

ustalana jako 5 % kwantyl rozkładu statystycznego

wytrzymałości

 
  

Wytrzymałość średnia betonu na rozciąganie

–

w stanie rozciągania osiowego

.

Wytrzymałość betonu na rozciąganie wg
Eurokodu 2

f

ctk

,

f

ctm

,

20

Pojęcie klasy betonu

 

Podstawą określenia

klasy betonu

- jest wytrzymałość

gwarantowana betonu na ściskanie:

W Normie Europejskiej (Eurokod 2) PN-EN-1992-1:2008 –

symbolem klasy betonu jest litera C i dwie liczby (pierwsza określa

wielkość f

ck

– walcową, druga f

ck,cube

– kostkową). Przykład:

C16/20

-

w tej klasie f

ck

= 16 MPa oraz f

ck,cube

= 20 MPa.

W normie polskiej PN-B-03264:2002 - symbolem klasy betonu

jest litera B wraz z liczbą określającą wytrzymałość . Przykład

klasy - symbol

B20

– oznacza, że beton ma wytrzymałość

gwarantowaną (określaną na kostkach) 20 MPa.

21

Wytrzymałości obliczeniowe betonu –

do projektowania konstrukcji z betonu na

nośność

   

Wytrzymałość

obliczeniowa

betonu

na

ściskanie

–

f

cd

c

ck

cc

cd

f

f







•

Wytrzymałość obliczeniowa betonu na

rozciąganie

-

f

ctd

c

ctk

ct

ctd

f

f







gdzie



c

- częściowy współczynnik bezpieczeństwa dla betonu,

wg Eurokodzie 2 w załączniku polskim -



c

= 1,4

,

w Polskiej normie



c

= 1,5

α

cc

, α

ct

–

współczynniki korekcyjne (w Eurokodzie 2 zalecono przyjąć 1.0)

22

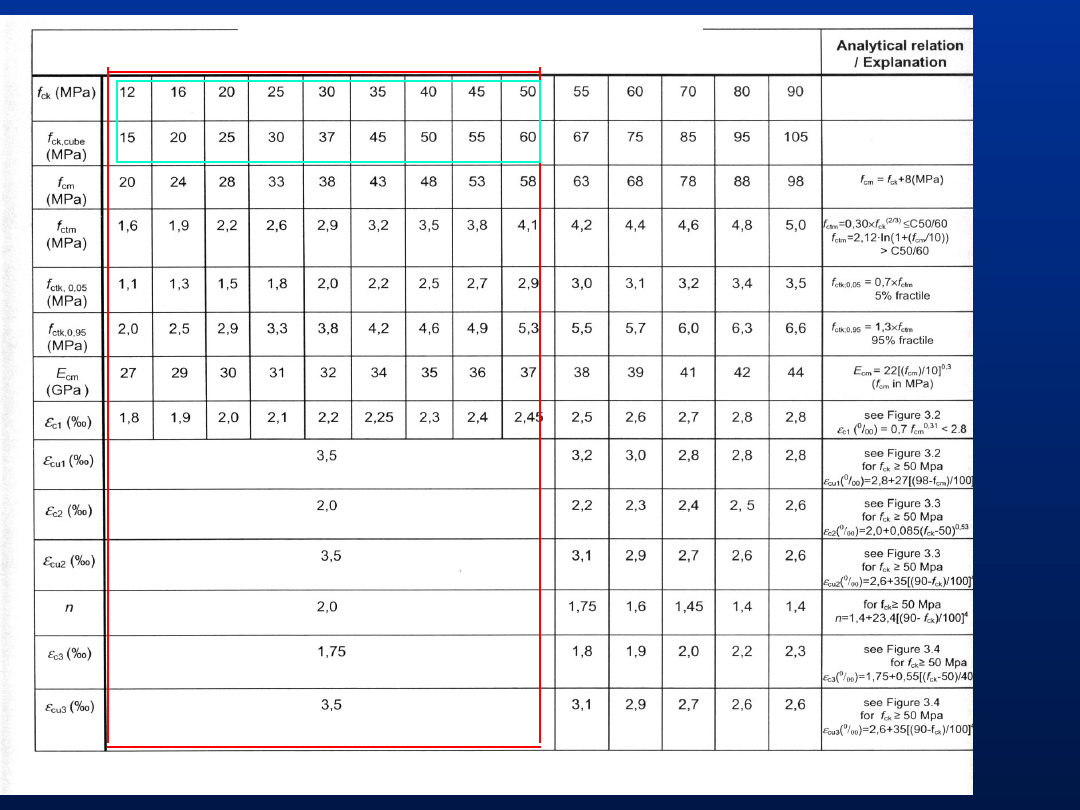
22

Klasy betonu według Eurokodu 2

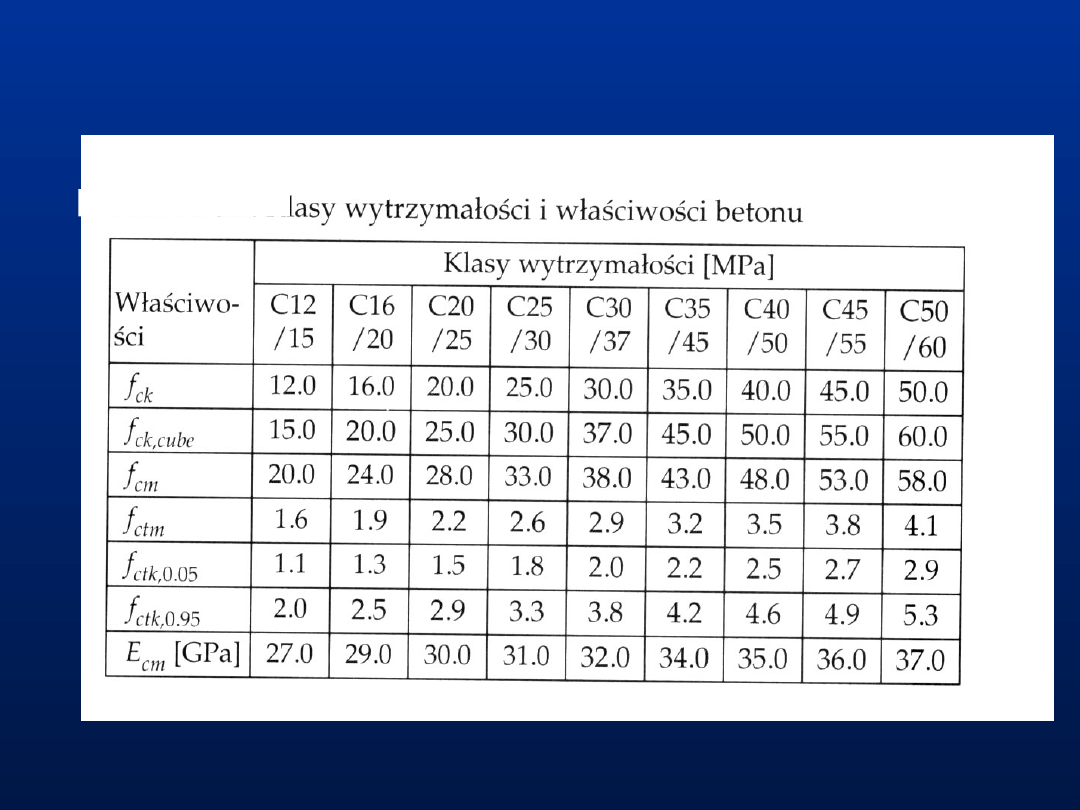
23

Charakterystyka klas betonów zwykłych wg normy

Europejskiej - Eurokod 2 (PN-EN 1992-1-1:2008)

24

Odkształcalność doraźna betonu

– moduł sprężystości

Odkształcenia betonu

ε

c

- efekt działania

obciążeń:
       Mechanicznych
       Termicznych.
Rozróżnia się:
       Odkształcenia sprężyste (liniowe lub

nieliniowe)
       Odkształcenia plastyczne (trwałe)

W przypadku betonu efekty sprężystych odkształceń mogą
być rozpatrywane
jedynie na krótkim odcinku krzywej naprężenie -
odkształcenie.
Przy wyższych naprężeniach zależności



-



są już wyraźnie

nieliniowe.

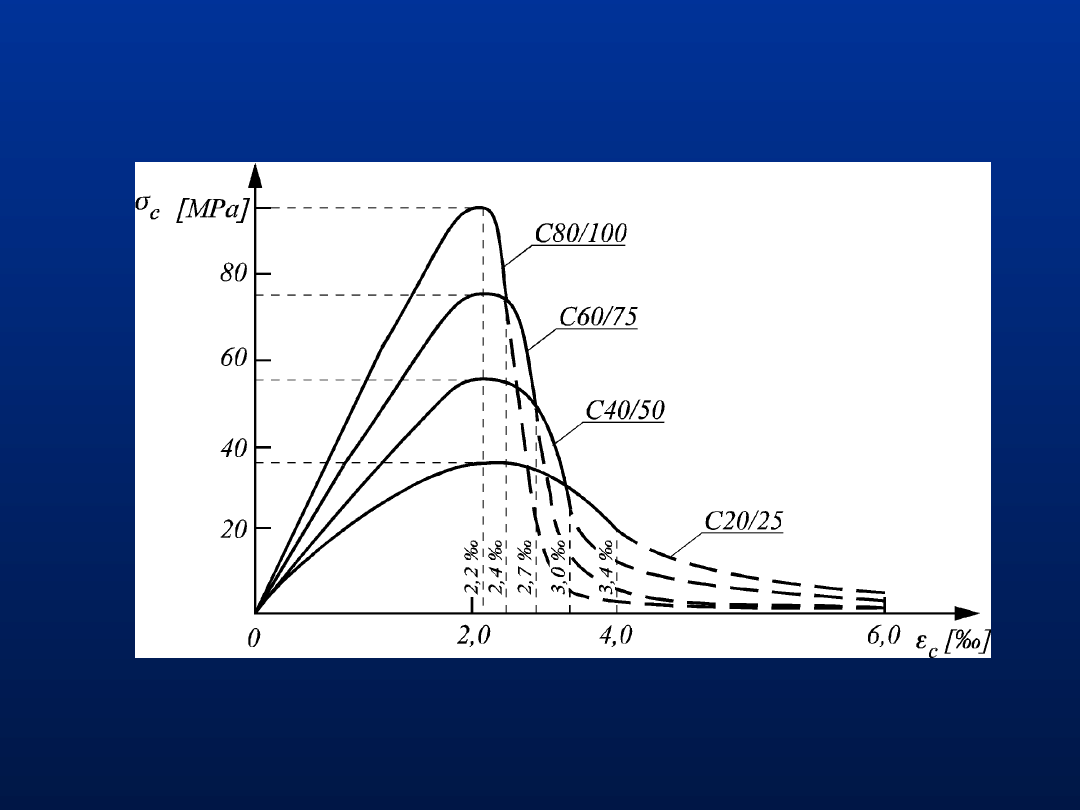
25

Nieliniowość funkcji



-



dla betonów różnych klas

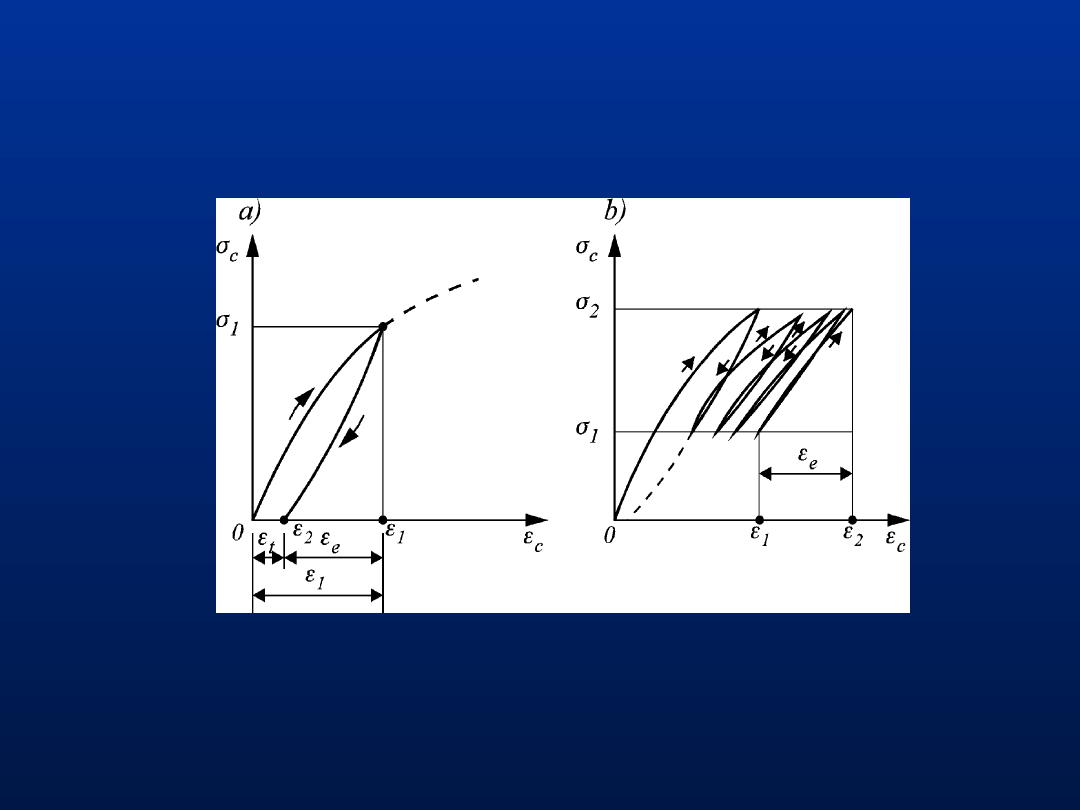
26

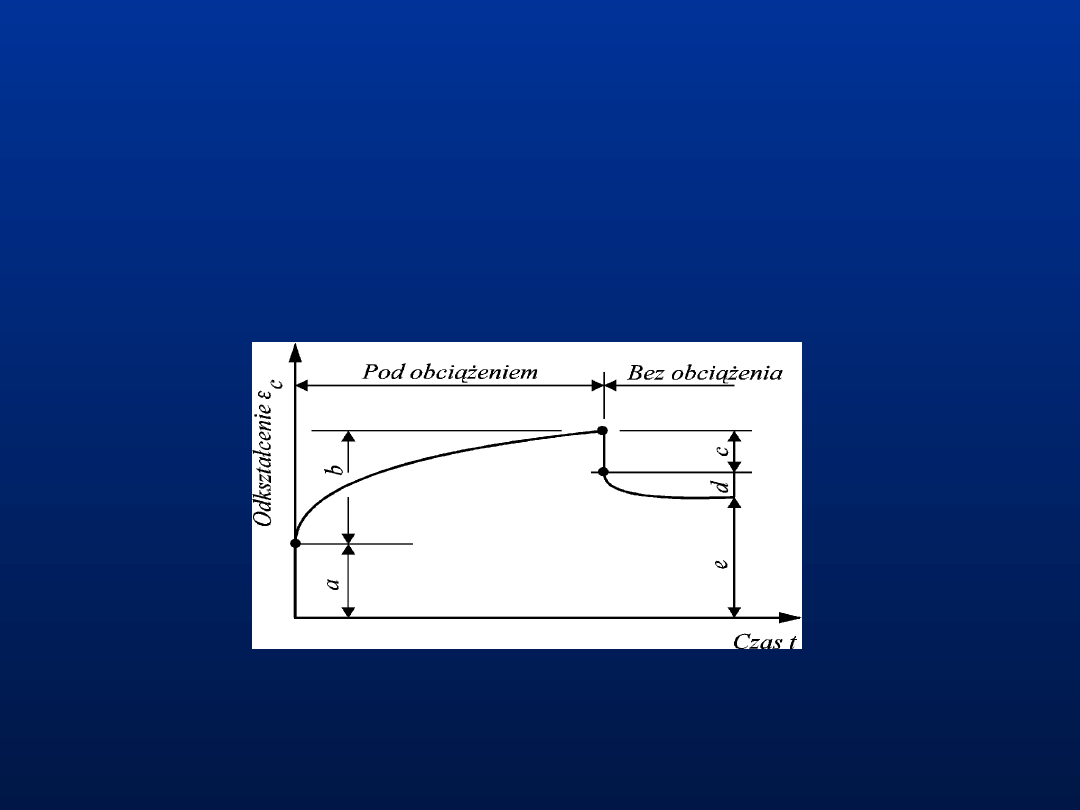
Pętle histerezy: a)- przy jednokrotnym obciążeniu i
odciążeniu

b)- przy wielokrotnym obciążaniu i odciążaniu

Cykl obciążania i odciążania konstrukcji z betonu

Po odciążeniu występują odkształcenia trwałe



t

(stanowią około 15 % odkształceń całkowitych)

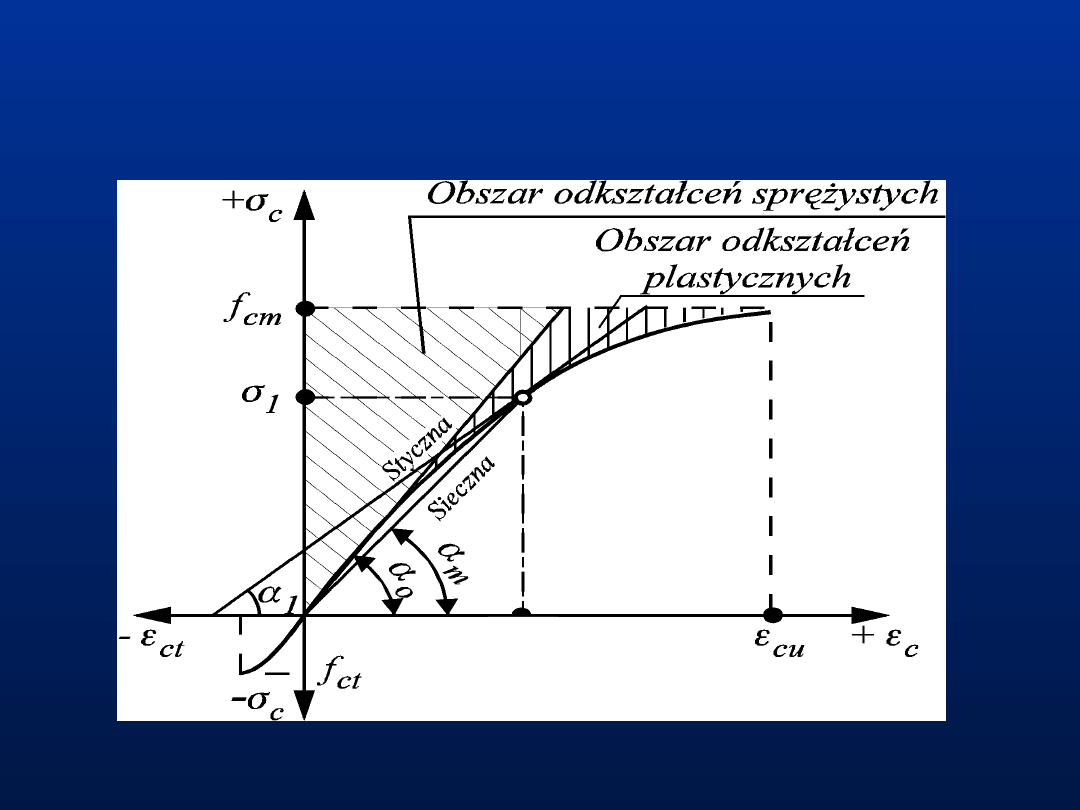
27

Funkcja



-



opisująca zmienność modułu

sprężystości betonu

ε

c2

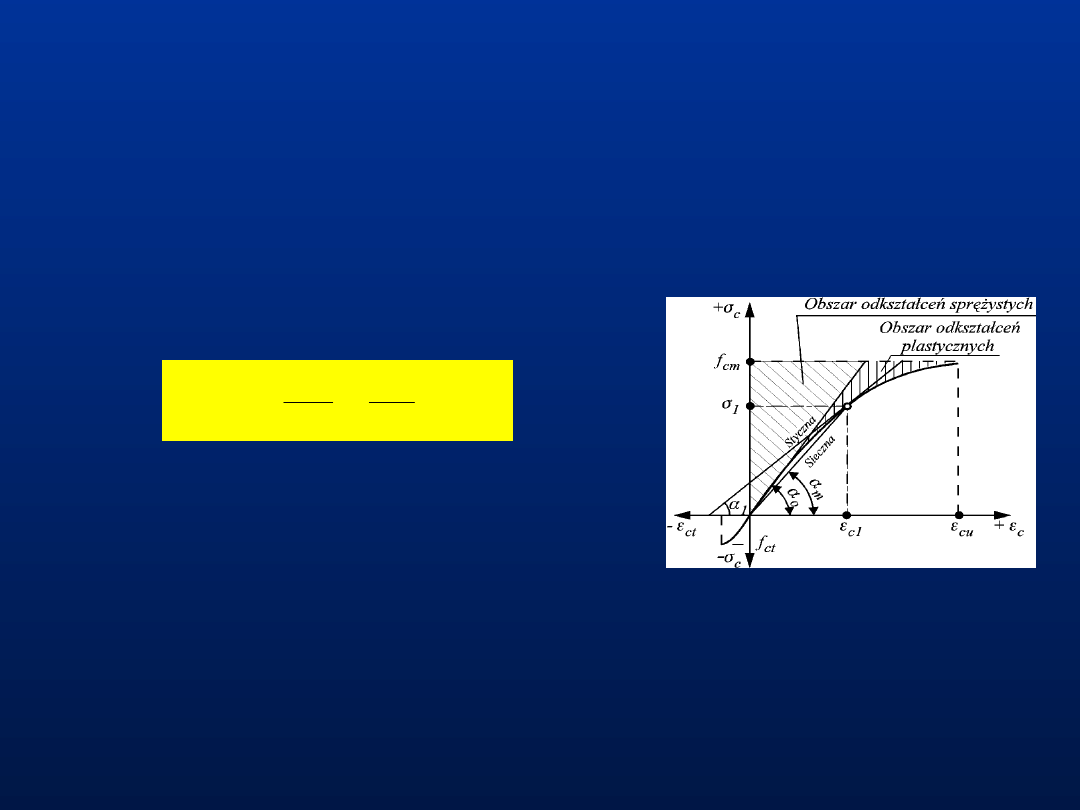
28

 Moduł sprężystości betonu

Funkcję stanu odkształcenia próbki betonowej
można określić poprzez iloraz



/



, który w

ujęciu

granicznym

jest

definiowany

jako

chwilowy

współczynnik

odkształcalności

podłużnej betonu.

1

0

tg

lim



























d

d

E

c

gdzie



1

- kąt nachylenia stycznej do krzywej



-



.

29

Definicje współczynnika

odkształcalności podłużnej

betonu:

Współczynnik chwilowy E

c

,

będący styczną do

krzywej odkształceń w dowolnym punkcie
krzywej



-



,

 

Współczynnik średni E

cm

,

będący sieczną

poprowadzoną

przez

początek

układu

współrzędnych (



= 0) oraz punkt na krzywej o

współrzędnych (



=0,4f

ck

). Wartości podano w

tablicy klas betonów Eurokodu 2 (dla betonów
na kruszywach kwarcytowych).

30

Odkształcenia reologiczne

betonu –

Skurcz i pęcznienie

Efekt odparowania i wiązania wody w masie
betonu
i zmniejszenia jego objętości – to zjawisko

skurczu betonu.

W warunkach stałej i podwyższonej wilgotności
zachodzi proces odwrotny - zwiększenie
objętości elementu, czyli zjawisko

pęcznienia

betonu.

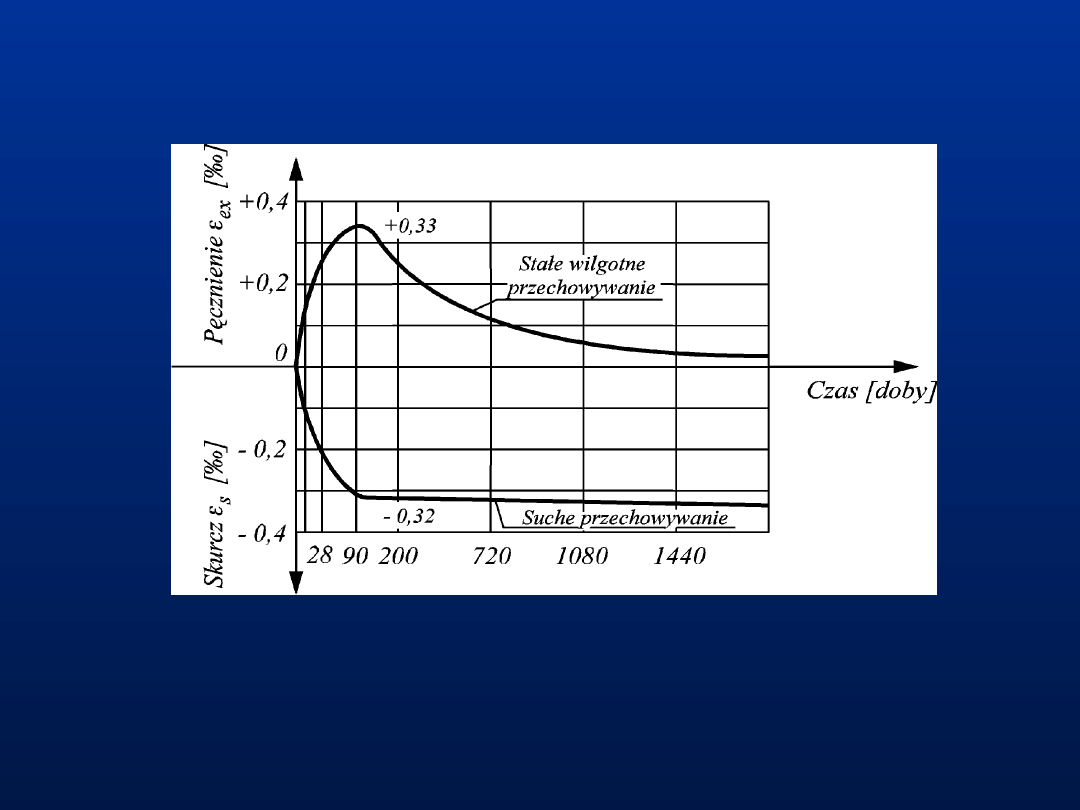
31

Funkcje doświadczalne odkształceń skurczu i pęcznienia betonu wg Graffa

32

Skurcz betonu

Odkształcenia skurczu zależą od składu betonu
(zawartość cementu w 1 m

3

masy), wskaźnika w/c,

klasy betonu, wilgotności środowiska, a także
wymiarów zewnętrznych elementu.

Odkształcenia skurczowe



cs

składają się z:

odkształcenia skurczu początkowego (zwanego
skurczem autogenicznym) oraz skurczu właściwego
(spowodowanego wysychaniem), który to proces ma
charakter reologiczny. Oblicza się zatem sumę dwu
składników

cd

ca

cs











gdzie



ca

– odkształcenie spowodowane skurczem autogenicznym, narastające w

stosunkowo krótkim czasie po ułożeniu betonu,



cd

– odkształcenie spowodowane wysychaniem betonu, narastające w czasie,

w wyniku migracji cząsteczek wody przez masę stwardniałego betonu.

33

Pełzanie betonu

Pełzanie – zachodzi w warunkach swobody
odkształcenia elementu, gdy powiększają się
plastyczne deformacje betonu od długotrwale
działających naprężeń (mechanicznych bądź
termicznych).

Schematyczny wykres odkształceń opóźnionych betonu

34

Pełzanie betonu

gdzie φ – współczynnik pełzania określany w zależności od poziomu naprężeń
ściskających



c

działających na element z betonu.

• Skład betonu i klasy wytrzymałości,
• Poziom obciążenia,
•

Warunki

środowiska

(wilgotność,

temperatura)
• Wiek betonu w chwili przyłożenia
obciążenia.

Odkształcenia wywołane pełzaniem betonu pod wpływem
naprężeń ściskających



c

działających na element w przedziale

czasu od t

0

do t zapisujemy









c

c

cc

E

t

t







0

0

,

,







35

Koniec części 1-A