Przedmiot i
metodologia fizyki
Wykład 1A
Dr hab. inż. Jerzy ZIELIŃSKI prof.
WAT
Zakład Fizyki i Technologii
Kryształów bud 5, pok. 218
Tel. 6837545; sekretariat
6839731
Email: jzielinski@wat.edu.pl
Przedmiot i
metodologia fizyki
Wykład 1A
Dr hab. inż. Jerzy ZIELIŃSKI prof.
WAT
Zakład Fizyki i Technologii
Kryształów bud 5, pok. 218
Tel. 6837545; sekretariat
6839731
Email: jzielinski@wat.edu.pl
PROGRAM
Wykład – 16 godz. semestr I + 20 semestr II
Ćwiczenia – 14 godz. semestr I + 22 semestr II
Laboratoria -
18 godz. semestr II
Kurs
Wykład – 10 godzin
Ćwiczenia – 20 godzin
Zasady zaliczania w semestrze
I
• Przedmiot jest zaliczany na ostatnich zajęciach
• Zaliczanie w formie pracy pisemnej polega na
od-powiedzi na 6 pytań definicyjnych i jedno
opisowe.
• Podstawą dla zaliczenia przedmiotu jest
wcześniej-sze zaliczenie ćwiczeń
rachunkowych i kursu.
Literatura
1975
1997
1997
1994
2003
1994
2002
1991
2001
Fizyka dla inżynierów cz. I i cz.. II, WNT
Fizyka, WNT
Fizyka cz. I i cz. .II, WNT
Podstawy fizyki dla elektroników Skrypt WAT
Krótki kurs fizyki dla inżynierów, Skrypt
Fizyka ogólna. Przykłady i zadania z fizyki cz. I.
Rozwiązania i odpowiedzi do zadań z fizyki cz. .II.
Skrypt WAT
Wybrane przykłady zadań do wykładu z fizyki dla
inżynierów,
Fizyka ogólna – ćwiczenia laboratoryjne cz. I i II.
Skrypt WAT
Wybrane zagadnienia z fizyki skrypt WAT
J. Massalski
M. Massalska
Cz. Bobrowski
J. Orear,
A. Rogalski
M. Demianiuk
Z. Raszewski i
inni
M Demianiuk
S. Bartnicki i
inni
Z. Raszewski,
J. Zieliński, T.
Kostrzyński
Rok
wydania
Literatura
autor
Istota fizyki
poszukiwanie i poznawanie
podstawowych praw przyrody
ścisły związek fizyki z techniką
fizyka jest nauką ścisłą –
matematyczny opis praw fizycznych
fizyka opiera się na pomiarach
WEKTORY
Opracowanie
M. Demianiuk
na
podstawie prezentacji
Ewa Popko-Płaczek IFPWr
www.if.pwr.wroc.pl/~popko
Mieczysław Demianiuk IFT WAT
Krótki kurs fizyki dla inżynierów WAT 2003
John Millis Physics 152
Summer 2004 millis@purdue edu
M.Kozlowski
Wprowadzene do fizyki , Uw, 2002/2003
Paweł Trautman Jan Gaj
Fizyka w doświadczeniach UW. semestr letni 2002/2003
Układy odniesienia
z
P(x,y,z)
z
O y
x
y
x
Kartezjański układ
odniesienia
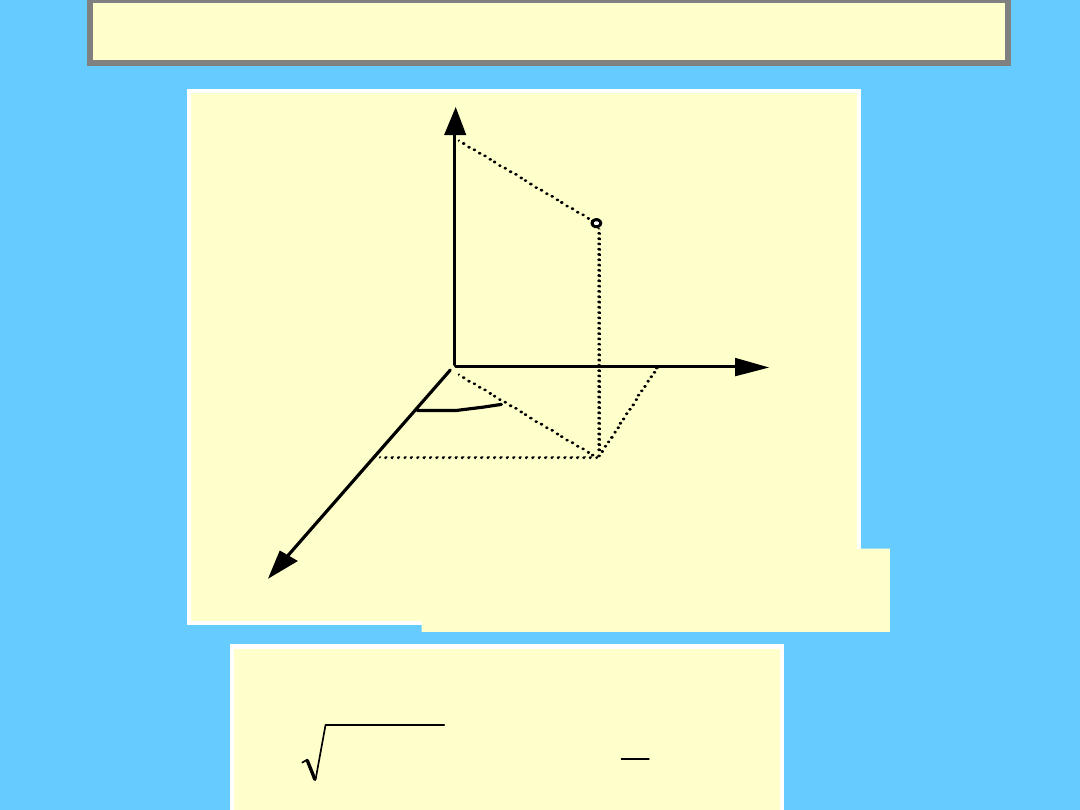
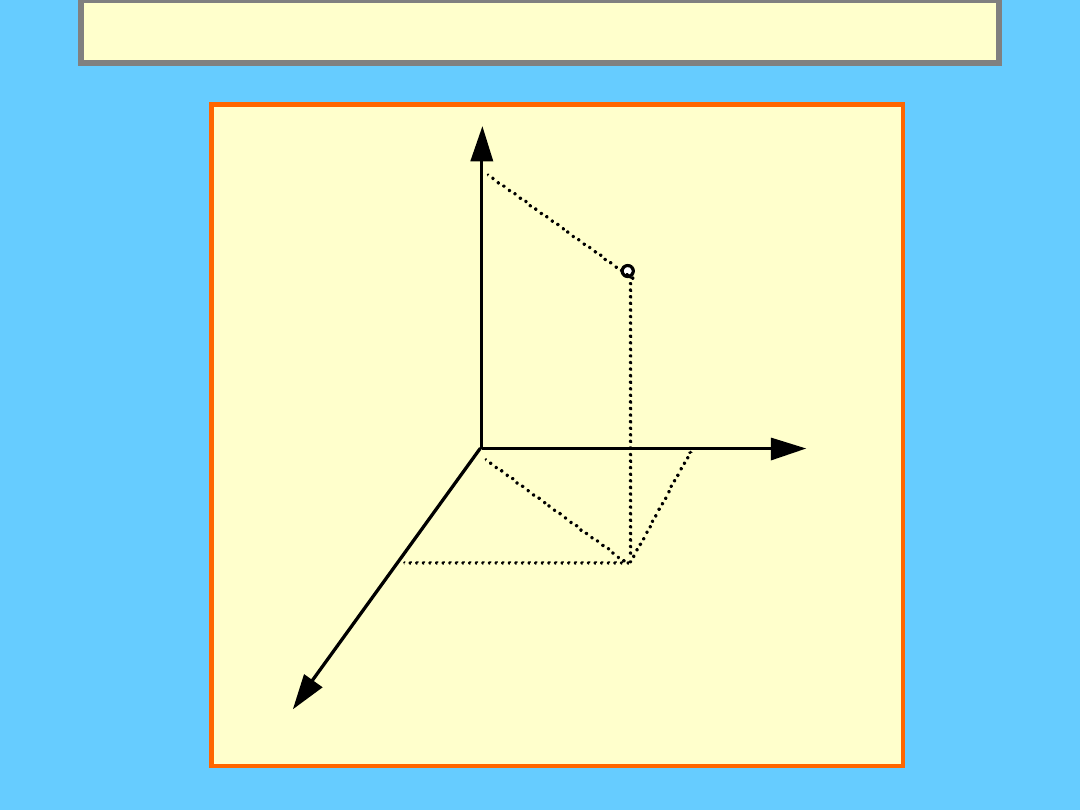
Układy odniesienia c.d.
z
P(r,
,z)
z
O y
r x
y
x
z
z
x
y
arctg
y
x
r
z
z
r
y
r
x
;
;
;
sin
;
cos
2
2
Cylindryczny układ
odniesienia
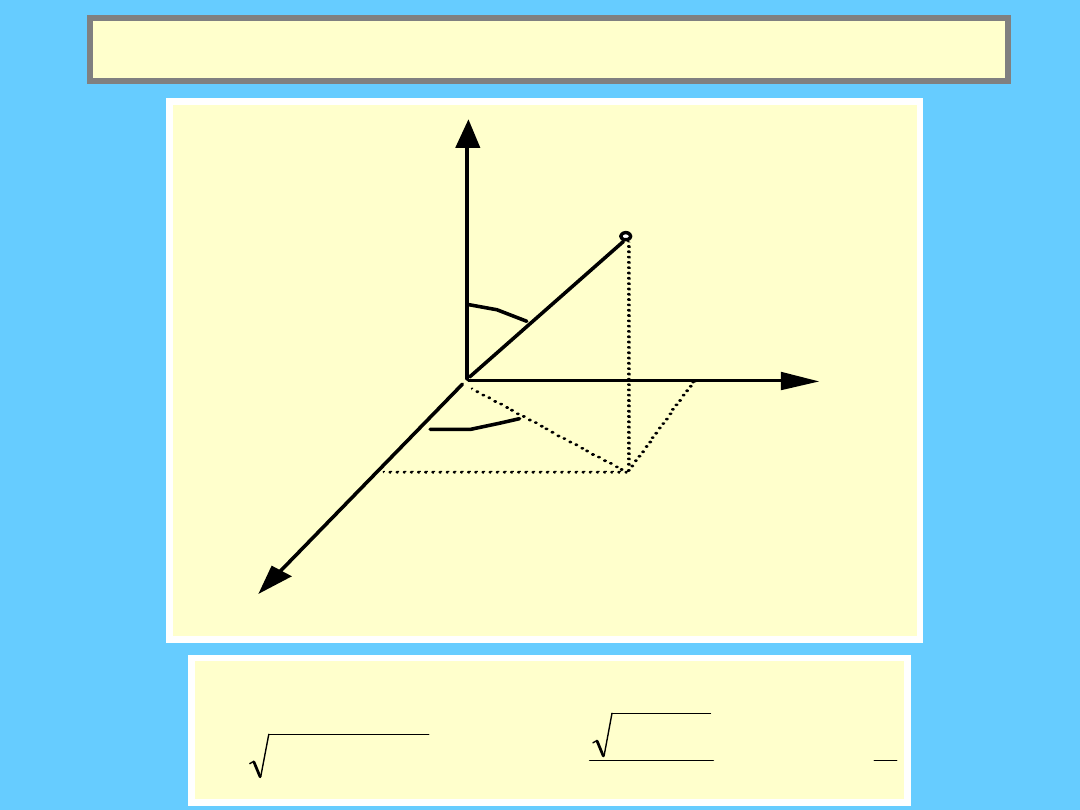
Układy odniesienia c.d.
x
y
arctg
z
y
x
arctg
z
y
x
r
r
z
r
y
r
x
;
;
cos
;
sin
sin
;
cos
sin
2
2
2
2
2
z
P(r,
,
)
r
z
O y
x
y
x
Sferyczny układ
odniesienia
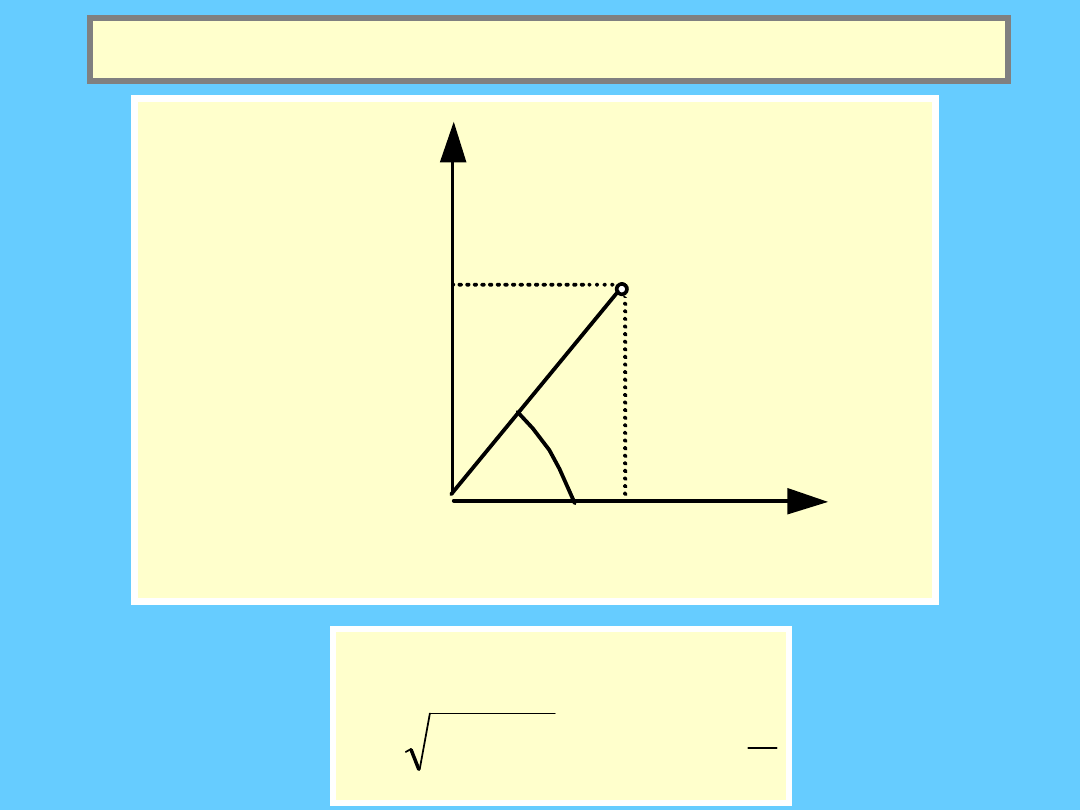
Układy odniesienia c.d.
z
P(r,
)
y
O x x
x
y
arctg
y
x
r
r
y
r
x
;
;
sin
;
cos
2
2
Biegunowy układ odniesienia
Pomiar wielkości fizycznej
Jest to procedura
umożliwiająca
przypisanie wartości
liczbowej wielkości
fizycznej.
Polega on na
porównaniu wielkości
mierzonej z wielkością
standardową.
Jednostki
układu
SI
Jednostki podstawowe i uzupełniające układu SI
L.p.
Wielkość
Symbol
wielkości
Jednostka Symbol
jednostki
Wymiar Wzór
określajacy
Jednostki podstawowe
1
Długość
l,b,h,r,d,s metr
m
m
2
Masa
m, M
kilogram
kg
kg
3
Czas
t, T
sekunda
s
s
4
Natężenie prądu elektrycznego
I
amper
A
A
5
Temperatura
w
skali
termodynamicznej
T,
kelwin
K
K
6
Liczność (ilość) materii
n,
mol
mol
mol
7
Światłość
I, J
kandela
cd
cd
Jednostki uzupełniające
8
Kąt płaski
radian
rad
=l/r
9
Kąt bryłowy
steradian
sr
S/r
2
l-długość, b-szerokość ,h-wysokość ,r-promień , d-średnica , s-droga .
Definicje jednostek podstawowych i
uzupełniających układu SI
Metr
jest to długość równa 1
650 763, 73 długości fali w
próżni
promieniowania
odpowiadającego
przejściu
między po-ziomami 2p
10
i 5d
5
,
atomu
86
Kr (kry-ptonu 86).
Definicje jednostek podstawowych i
uzupełniających układu SI
Kilogram
jest
to
masa
międzynarodowe-go wzorca tej
jednostki przechowywa-nego w
Międzynarodowym Biurze Miar
w Sevres.
Definicje jednostek podstawowych i
uzupełniających układu SI
Sekunda
jest to czas równy
9 192 631 770 okresów
promieniowania
odpowiadającego
przejściu
między dwo-ma nadsubtelnymi
poziomami stanu pod-stawowego
133
Cs (cezu 133) .
Definicja ta pozwala określić
sekundę z dokładnością 10
-12
czyli 100 razy dokła-dniej niż w
przypadku
posługiwania
się
ruchem obrotowym Ziemi
Definicje jednostek podstawowych i
uzupełniających układu SI
Amper
jest to prąd elektryczny
nie
zmieniający
się,
który
płynąc w dwóch równoległych
prostoliniowych, nieskoń-czenie
długich przewodach o przekroju
znikomo małym, umieszczonych
w próżni w odległości jednego
metra od siebie, wywołałby
między tymi prze-wodami siłę
2
.
10
-7
N (niutona) na każdy metr
długości.
Definicje jednostek podstawowych i
uzupełniających układu SI
Kelwin
jest to 1/273,16
temperatury termodynamicznej
punktu potrójnego wody.
Definicje jednostek podstawowych i
uzupełniających układu SI
Mol
jest to liczność (ilość)
materii występująca, gdy liczba
cząstek jest równa liczbie
atomów zawartych w masie 12
g (gramów) czystego węgla
12
C .
Definicje jednostek podstawowych i
uzupełniających układu SI
Kandela
jest to światłość, jaką
ma w kierunku prostopadłym
powierzchnia
1/60
cm
2
(centymetra
kwadratowego)
powierzchni ciała doskonale
czarnego
w
temperaturze
krzepnięcia
platyny
pod
ciśnieniem 101 325 Pa (paskali).
Definicje jednostek podstawowych i
uzupełniających układu SI
Steradian
jest kątem bryłowym
o wierzchołku w środku kuli,
wycinającym z powierzchni tej
kuli pole równe kwadratowi jej
promienia.
Radian
jest kątem płaskim o
wierzchołku w środku koła,
wycina-jącym z obwodu tego
koła łuk o długości równej jego
promieniowi.
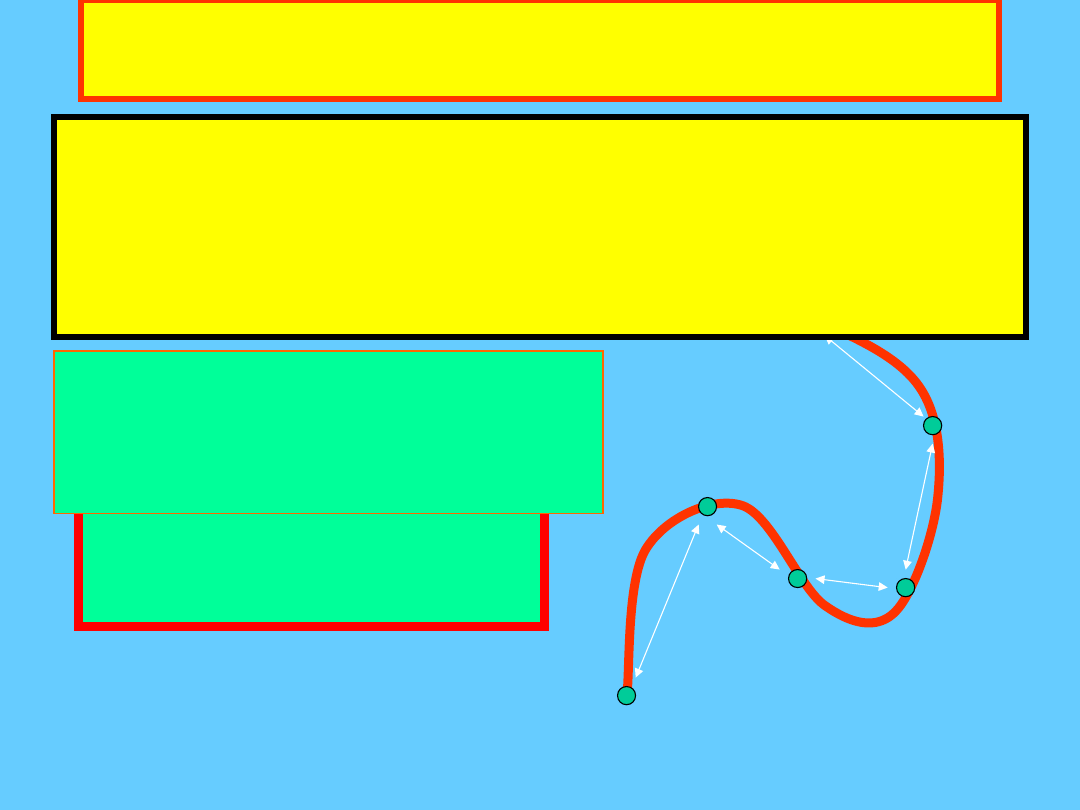
Skalary
i
i
krzywa
0
s
s
ds
l
lim
i
Przykład na podst. www.if.pwr.wroc.pl/~popko
•Skalar
wielkość fizyczna całkowicie
określona przez podanie jedynie jej
wartości (wymiaru) (temperatura,
długość, masa,…)
Przykład: skalar
związany z
rozmiarami obiektów
Wektory
•Wektor
wielkość zorientowana w
przestrze-ni
wymagająca
dla
jej
określenia
zarówno
wartości
(wymiaru) oraz kierunku i zwrotu(siła,
przemieszczenie, prędkość,…)
– Wektory przedstawiany za
pomocą strzał-ki, której długość jest
proporcjonalna
do
war-tości
wektora, strzałka leży na kierunku
dzia-łania
wielkości
fizycznej
reprezentowanej przez wektor, zaś
ostrze strzałki wskazuje zwrot
wektora
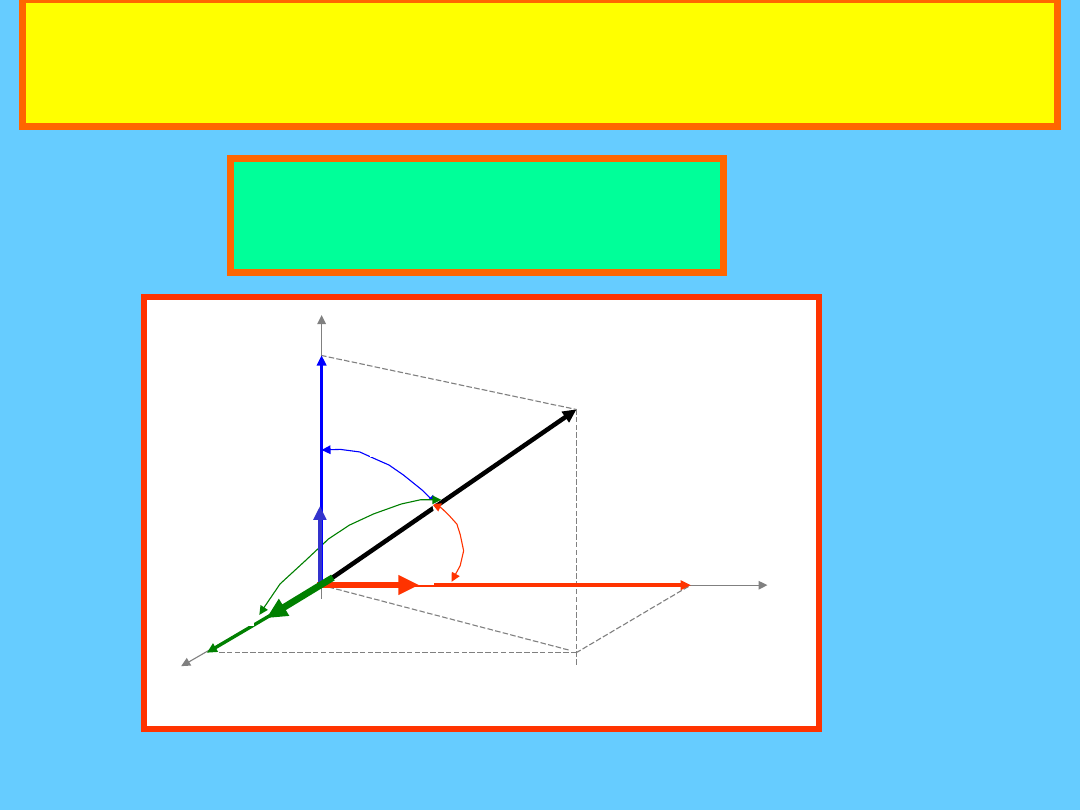
Wektor w układzie Kartezjańskim jako
element zorientowany
k
a
j
a
i
a
a
z
y
x
j
k
a
z
i
a
x
j
a
y
i
k
x
y
z
a
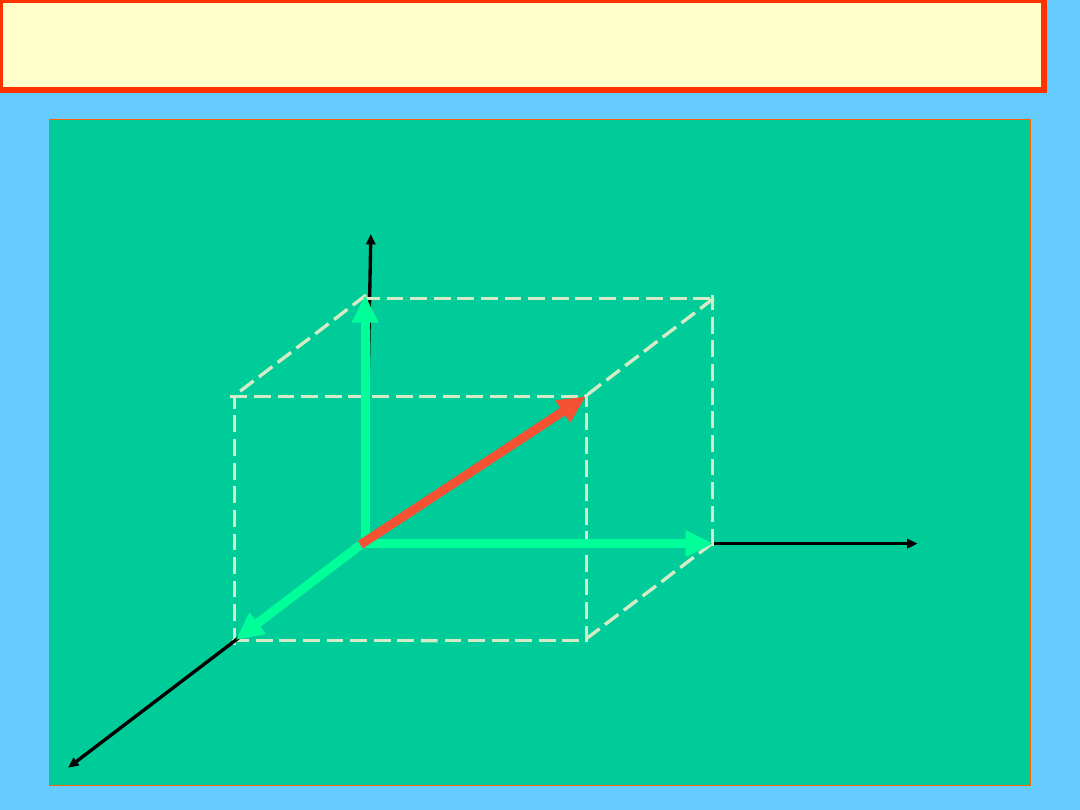
Wektor w przestrzeni R
3
- przykład 1
Trzy liczby (1, 2, 3)
y
x
z
2
1
3
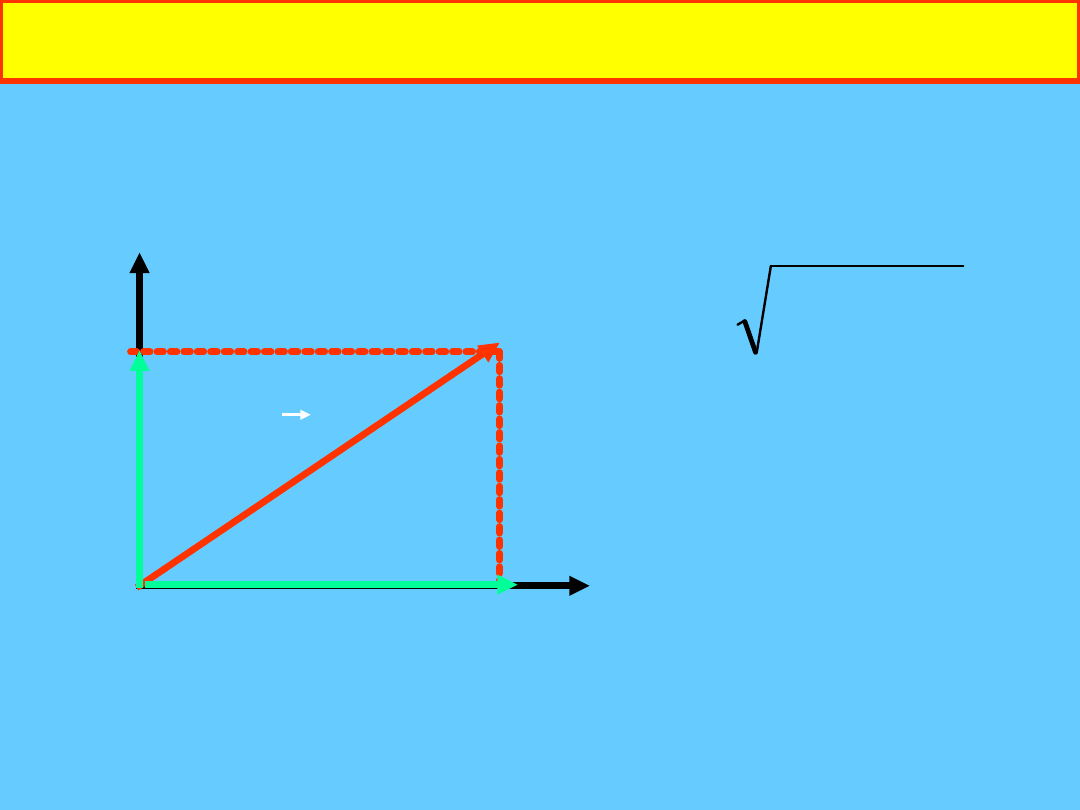
Wektory w przestrzeni R
2
: przykład 2
A
A
A
2
y
2
x
cosΘ
A
A
x
Θ
sin
A
A
y
)
/A
(A
tan
x
y
-1
y
x
Prędkość
A
A
y
A
x
Siła
Na podst. Glynn Bricker Office: Phys 07 Phone: (49)4-7794 E-mail:
bricker@physics.purdue.edu
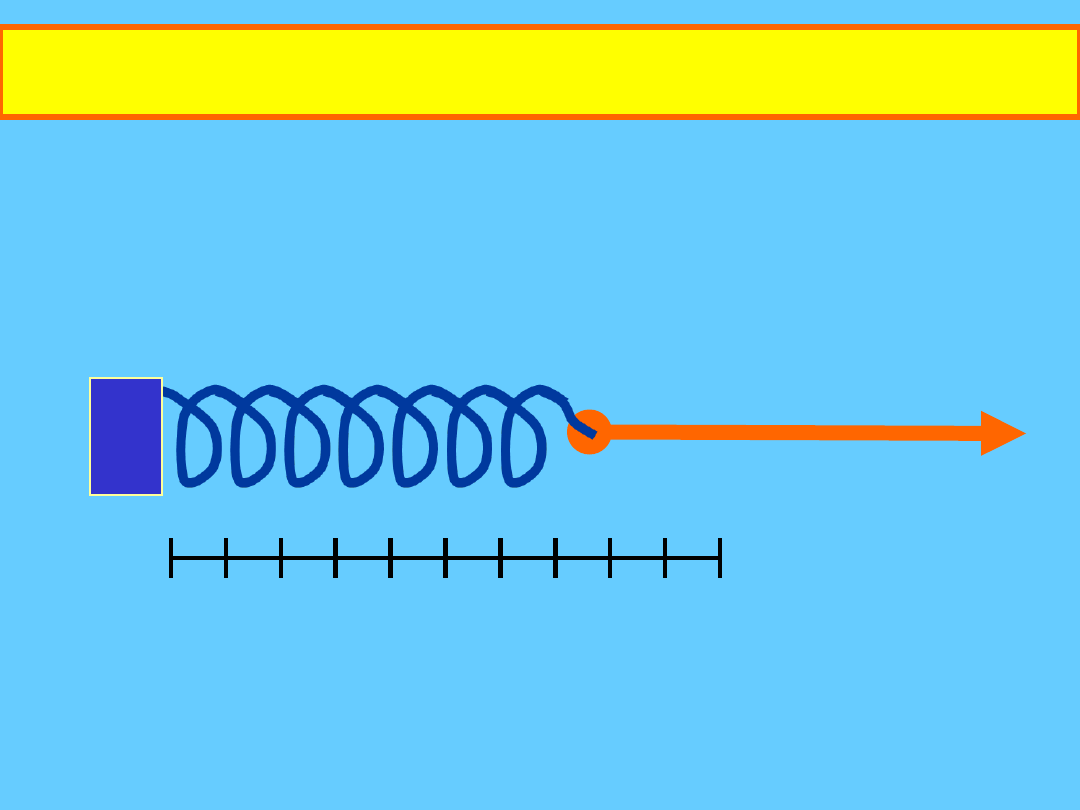
Wektory w przestrzeni R
1
: przykład 3
0
2
4
6
8
10 N
F
Graficzne dodawanie wektorów
(metodą trójkąta lub wielokąta)
> Wybrać skalę
> Narysować pierwszy wektor
o właściwej
dla skali długości w kierunku jego
działania w danym układzie współrzędnych
i z właściwym zwrotem
> Narysować kolejny wektor
o właściwej
dla skali długości w kierunku jego
działania w danym układzie współrzędnych
i z właściwym zwrotem, którego
po-czątek
będzie znajdował się na końcu strzałki
wektora pierwszego
Dodawanie wektorów
•Podczas dodawania wektorów
,
bierzemy pod uwagę ich wielkości
(moduły), kierunki i zwroty.
Jednostki
muszą być identyczne
•Dwie metody dodawania
wektorów
•Metoda graficzna
•Metoda algebraiczna
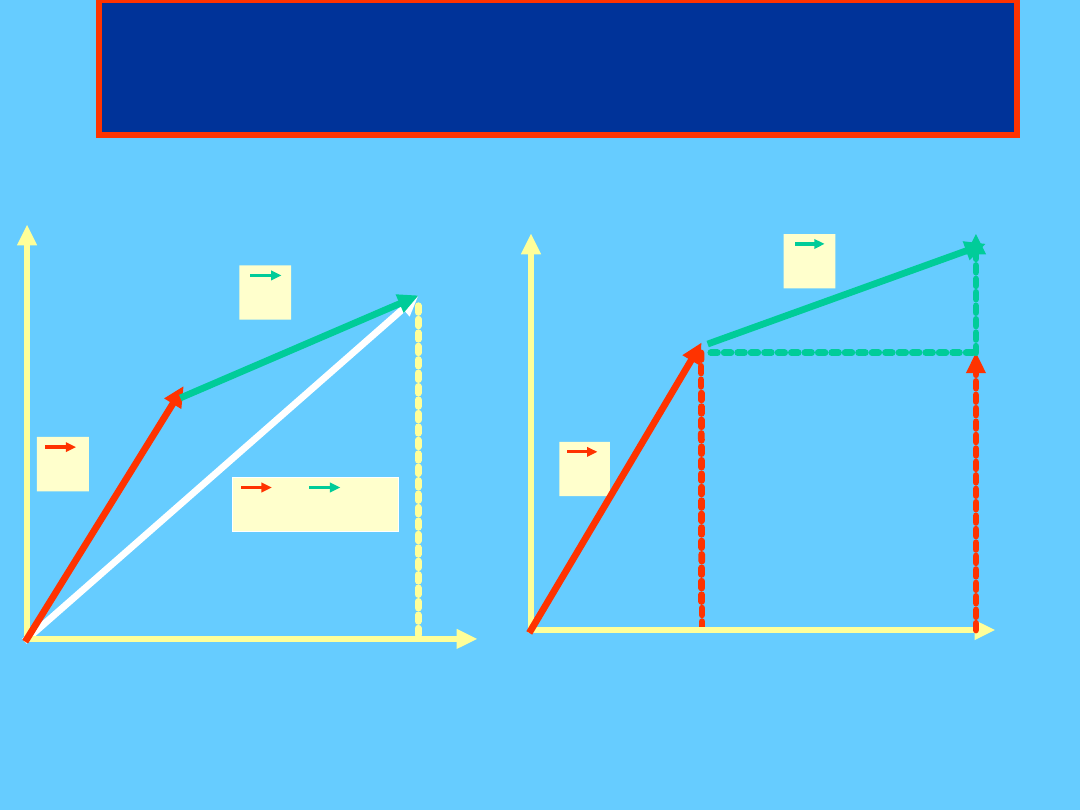
Dodawanie wektorów
A
B
A
x
A
y
B
x
B
y
A + B
B
A
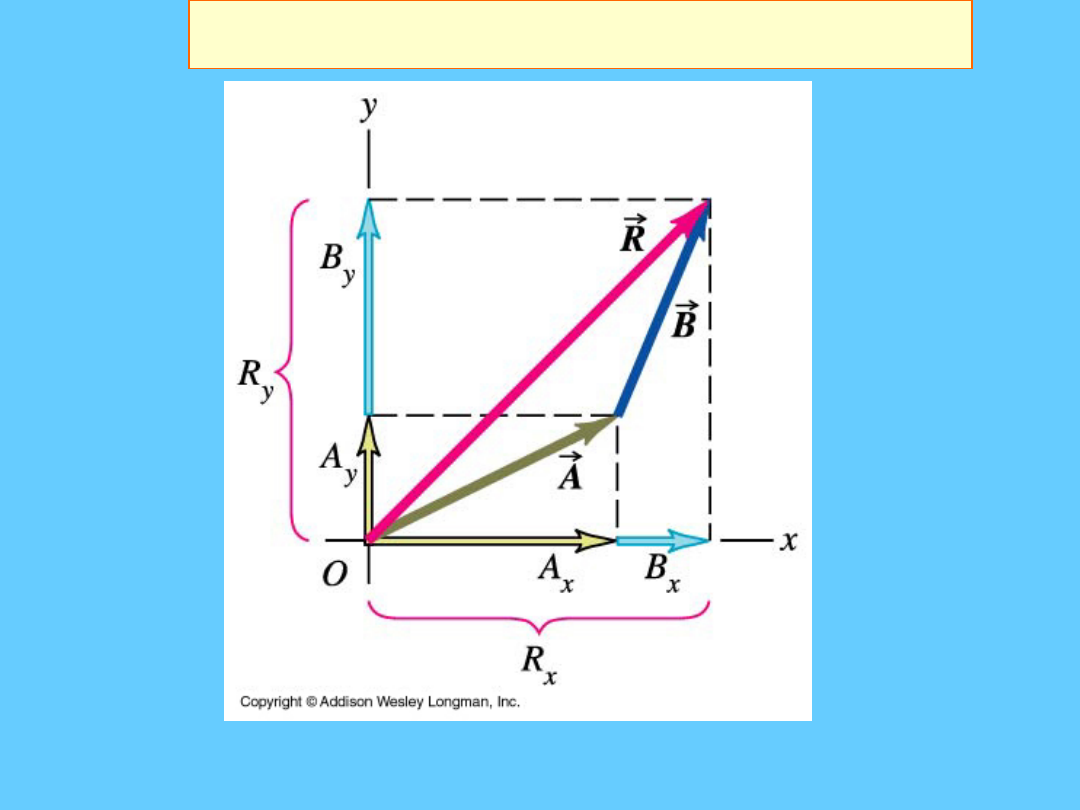
Dodawanie wektorów
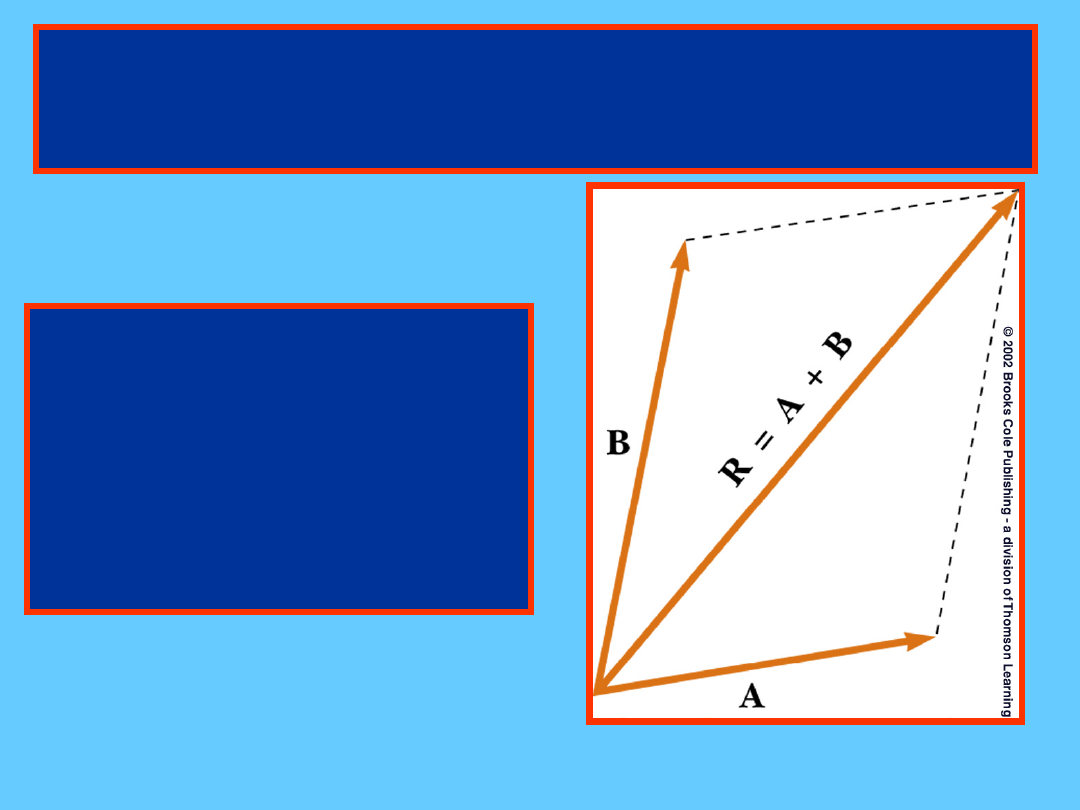
Metoda równoległoboku
graficznego dodawania
wektorów
•
W metodzie tej
dodajemy kolejno po
dwa wektory
•
Wszystkie wektory
łącznie z wypadkowym
kreślimy od wspólnego
początku
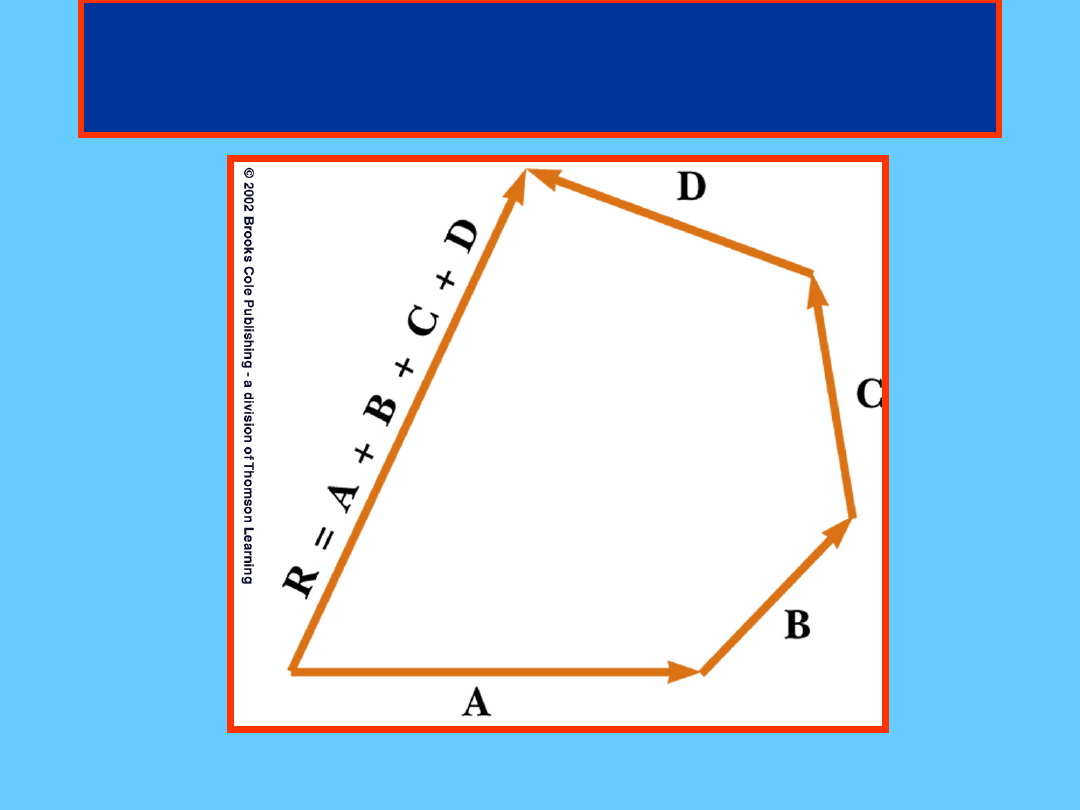
Graficzne dodawanie
wektorów
Algebraiczne dodawanie
wektorów
k
c
j
c
i
c
k
b
a
j
b
a
i
b
a
b
a
z
y
x
z
z
y
y
x
x
x
x
s
W
y
y
s
W
z
z
s
W
2
2
2
z
y
x
W
W
W
W
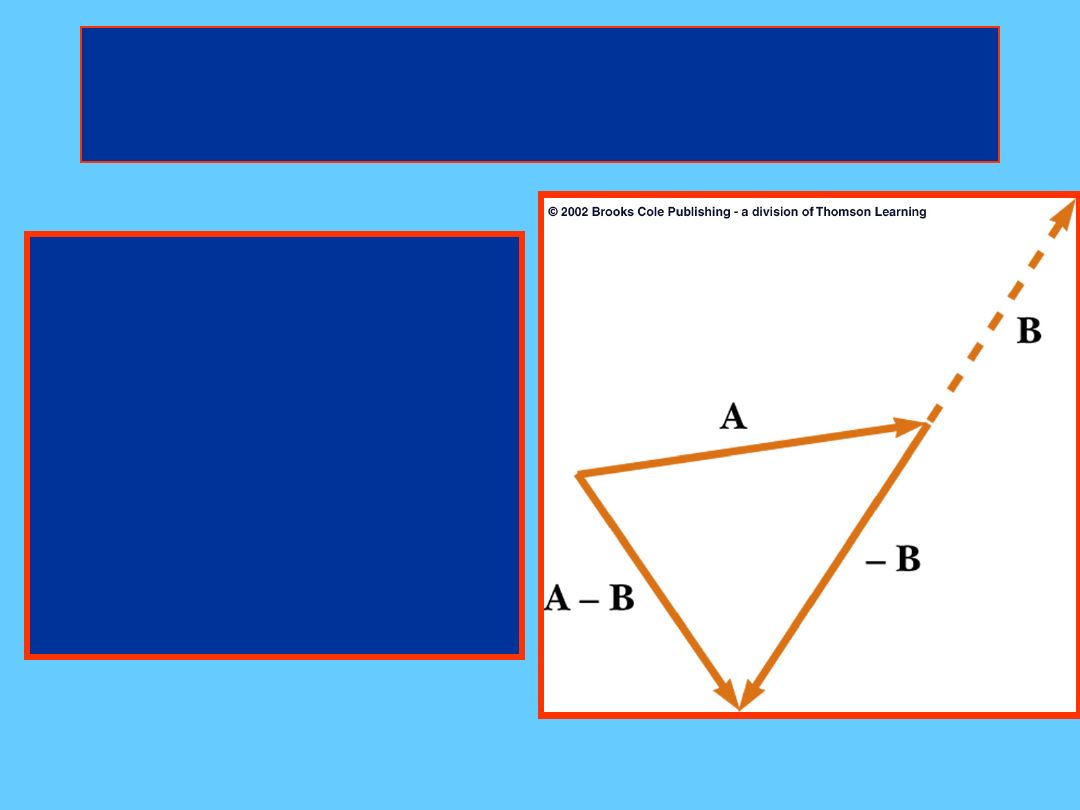
Odejmowanie wektorów
• Odejmowanie
jest
szczególnym
przypadkiem
dodawania
• Jeśli szukamy
A – B
,
wówczas stosujemy
sumowanie
A+(-B)
stosując procedurę
dodawania
Iloczyn skalarny wektorów
0
0
0
1
1
1
k
j
k
i
j
i
k
k
j
j
i
i
b
a
b
a
b
a
b
a
ab
b
a
z
z
y
y
x
x
,
,
;
,
,
,
cos
0
ab
ab
b
a
b
a
b
a
b
a
z
z
y
y
x
x
;
=
)
,
(
cos
c
b
b
a
b
a
+
=
c
)
+
(
liczba).
(
,
cos
B
A
B
A
Iloczyn skalarny dwóch wektorów jest
przemienny.
A
A
B
B
=
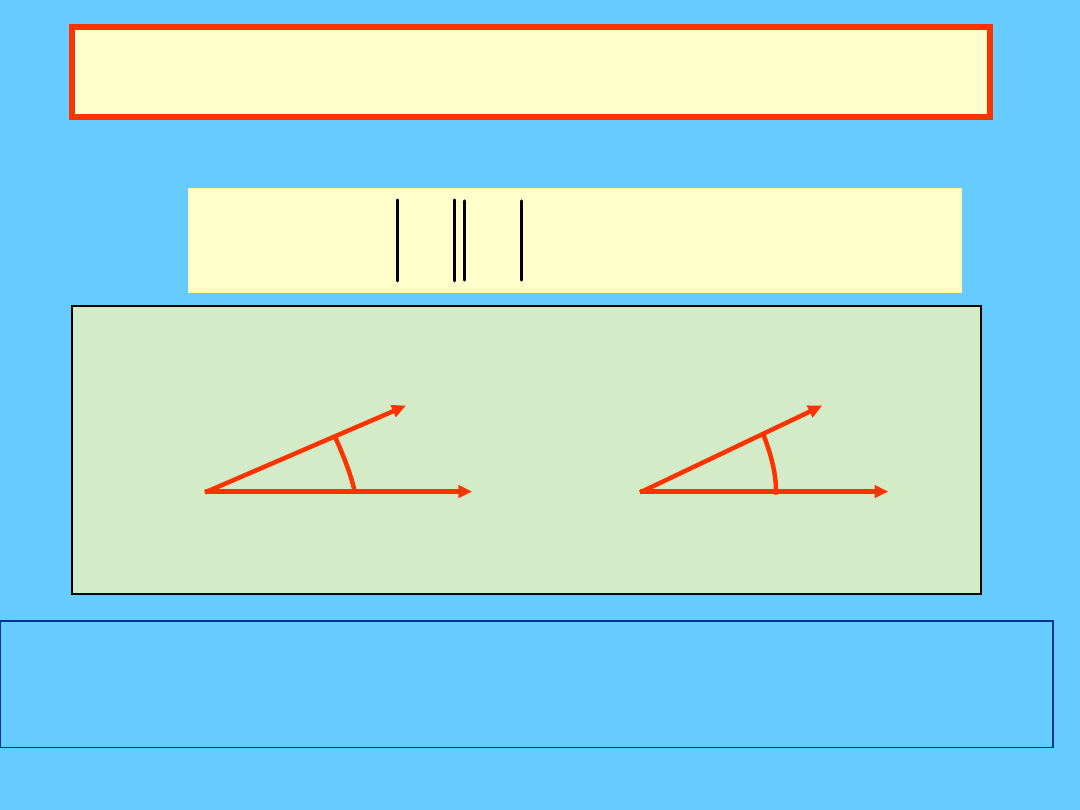
Iloczyn skalarny c.d.
Kąt między wektorami
b
a
b
a
cos
1
Kąt miedzy dwoma wektorami jest
zdefiniowany przez iloczyn skalarny
A
B
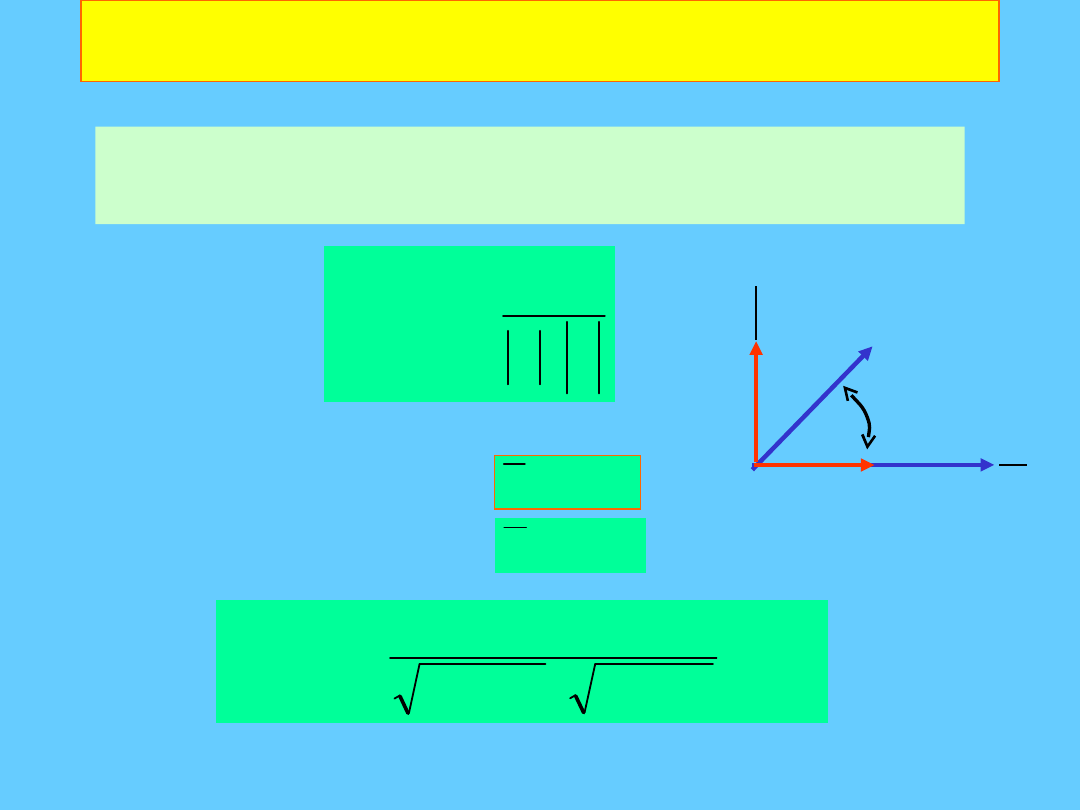
Kąt między wektorami[2,0] and
[1,1].
45
1
1
0
2
1
0
1
2
cos
2
2
2
2
1
i
j
[2,0]
A
[1,1]
B
x
y
= 45
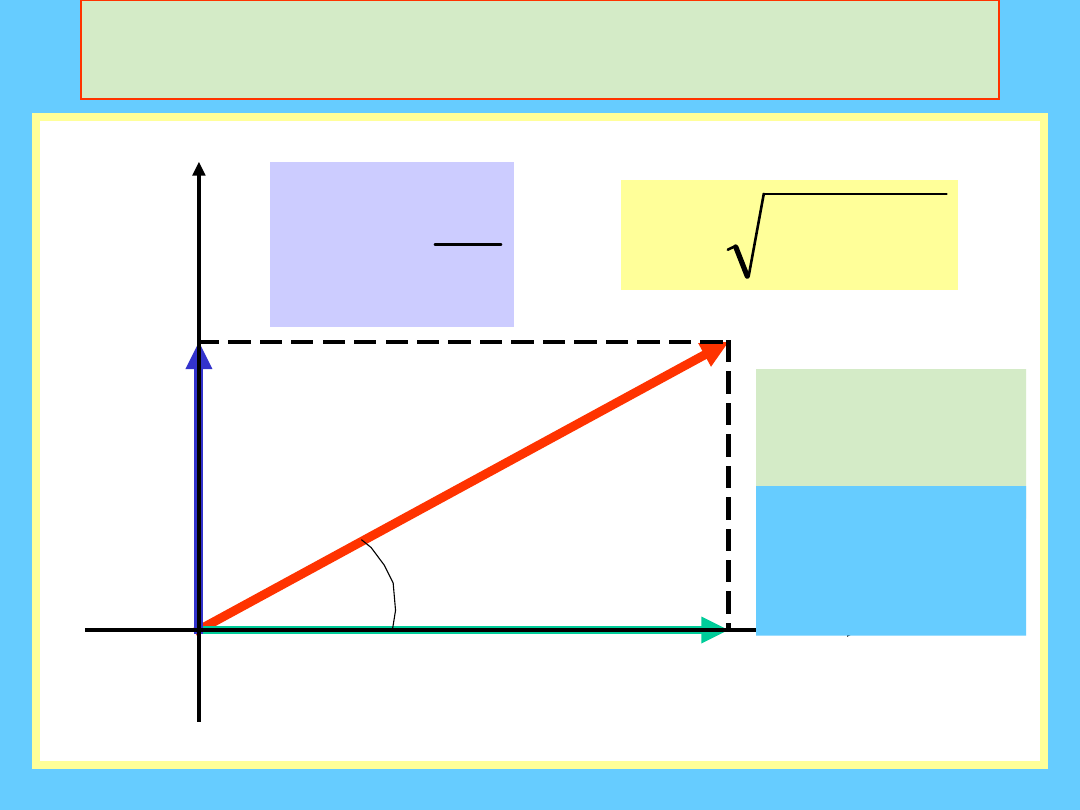
Składowe wektora
y
x
O
a
y
a
x
a
a
a
x
=acos
a
y
=asin
2
2
y
x
a
a
a
x
y
a
a
tg
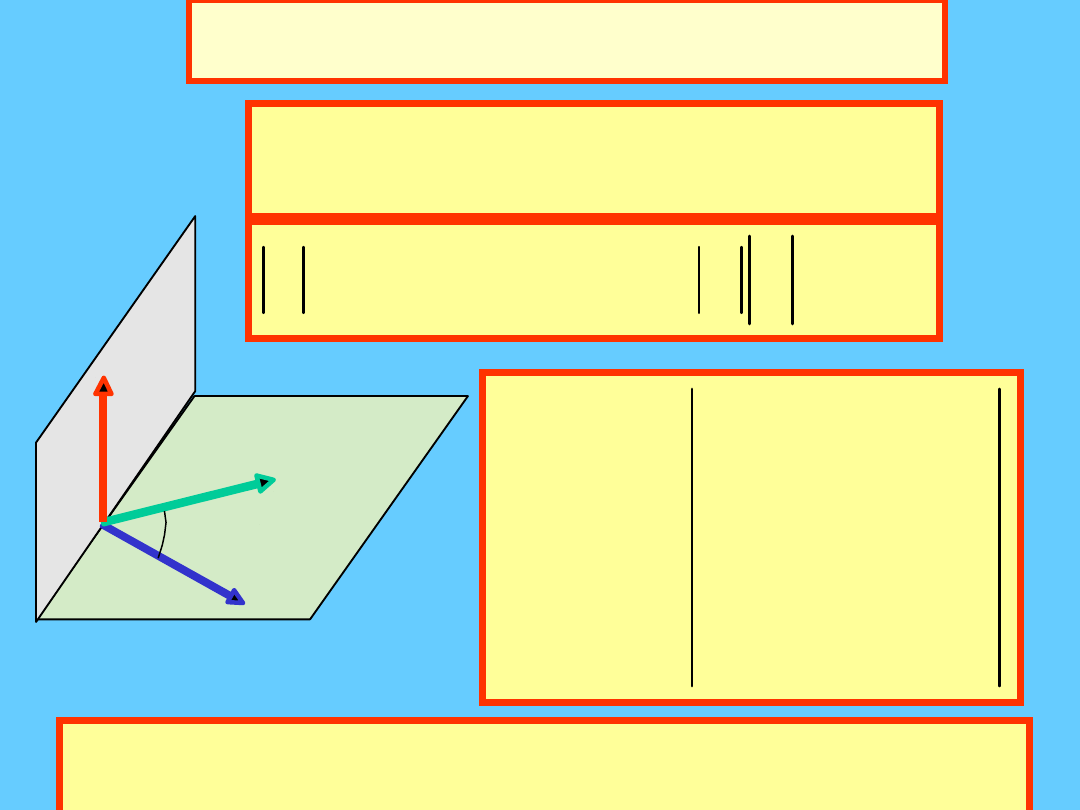
Iloczyn wektorowy wektorów
c
b
a
c
b
a
c
b
a
]
,
[
lub
sin
=
)
b
,
a
(
sin
b
a
ab
c
z
y
x
z
y
x
b
b
b
a
a
a
b
a
k
j
i
k
)
(
+
j
)
(
+
i)
(
x
y
y
x
z
x
x
z
y
z
z
y
b
a
b
a
b
a
b
a
b
a
b
a
b
a
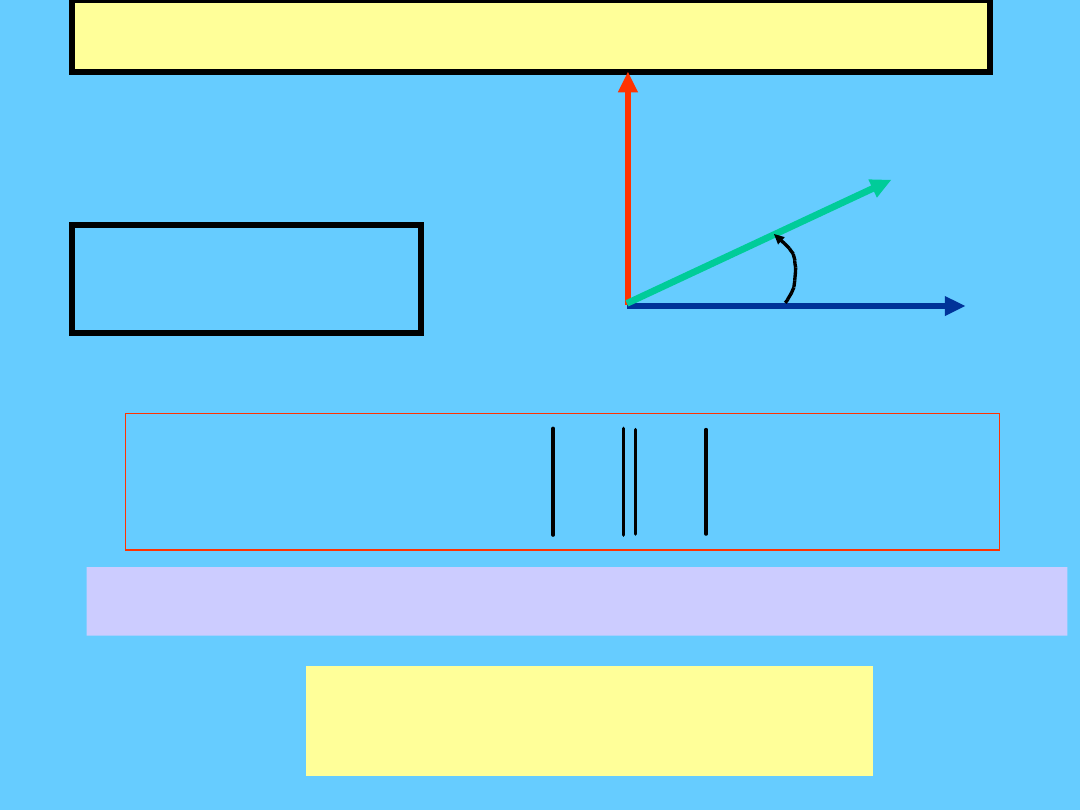
Iloczyn wektorowy c.d.
B
A
C
.
ˆ
sin
e
B
A
B
A
C
Iloczyn wektorowy nie jest przemienny.
.
A
B
B
A
A
B
C
Składowe iloczynu
wektorowego
]
b
a
b
[a
k
]
b
a
b
[a
j
]
b
a
b
[a
i
b
a
1
2
2
1
3
1
1
3
2
3
3
2
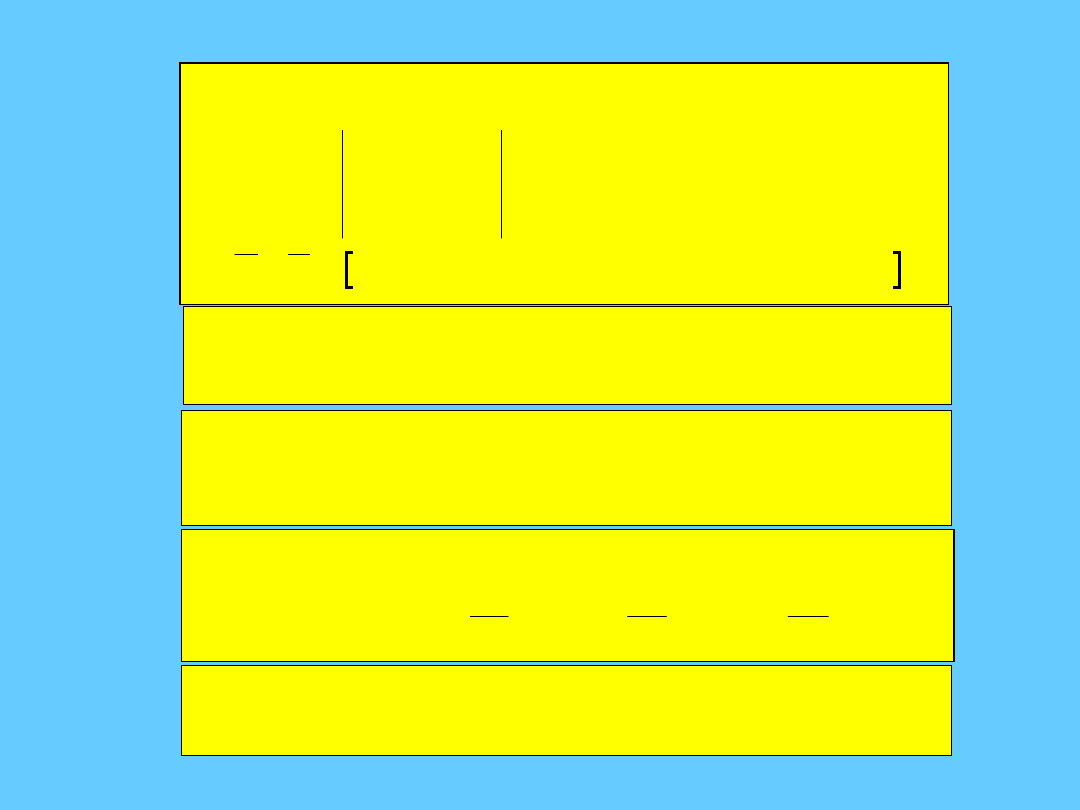
Iloczyn wektorowy -twierdzenia
A B
i
j
k
A A A
B B B
x
y
z
x
y
z
A B
A B
A B A B
A B A B
A B
y z
z y
z x
x z
x y
y x
,
,
A
B
B
A
C
A
B
A
C
B
A
d
d
d
d
d
d
B
A
B
A
B
A
C
B
A
B
C
A
C
B
A
nieprzemienny
Rozdzielność ze względu na dodawanie
różniczkowanie
Użyteczna tożsamość
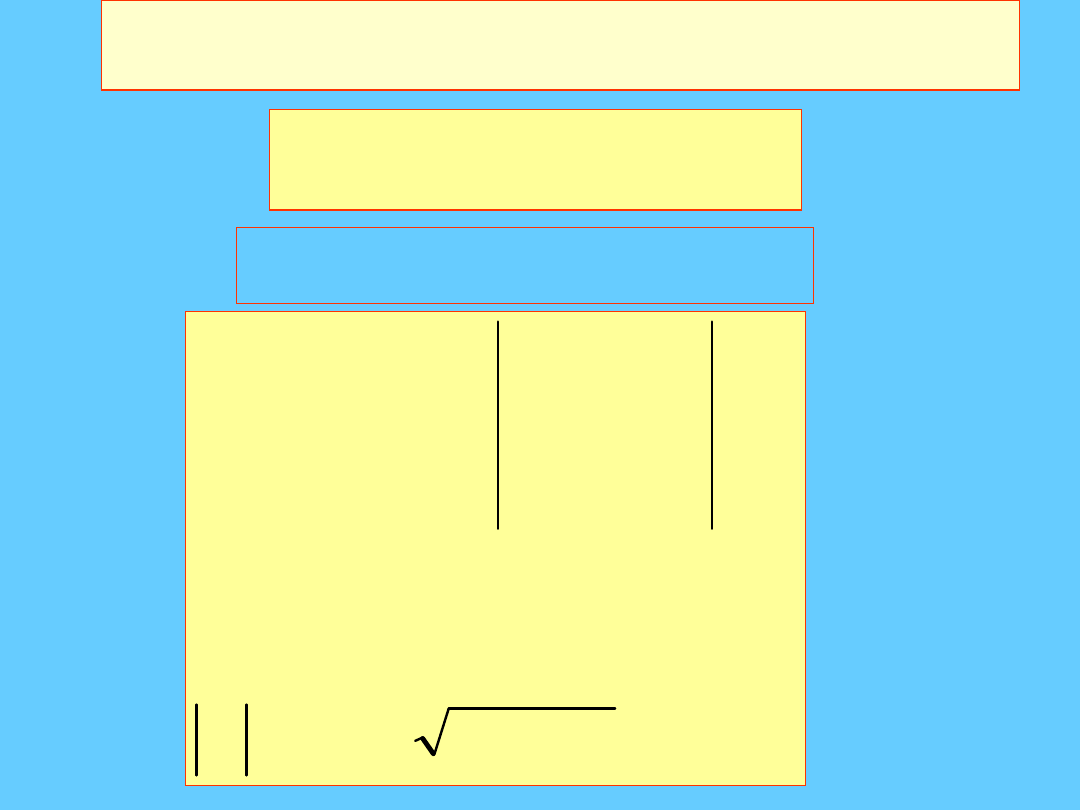
Przykład
Na podst. M.Kozlowski ,Wprowadzene do fizyki , Uw, 2002/2003
.
0
,
0
,
1
4
,
5
,
2
B
A
i
Iloczyn
wektorowy
,
25
16
,
5
4
,
5
4
0
0
0
1
4
5
2
C
C
k
j
C
k
j
i
k
j
i
B
A
C
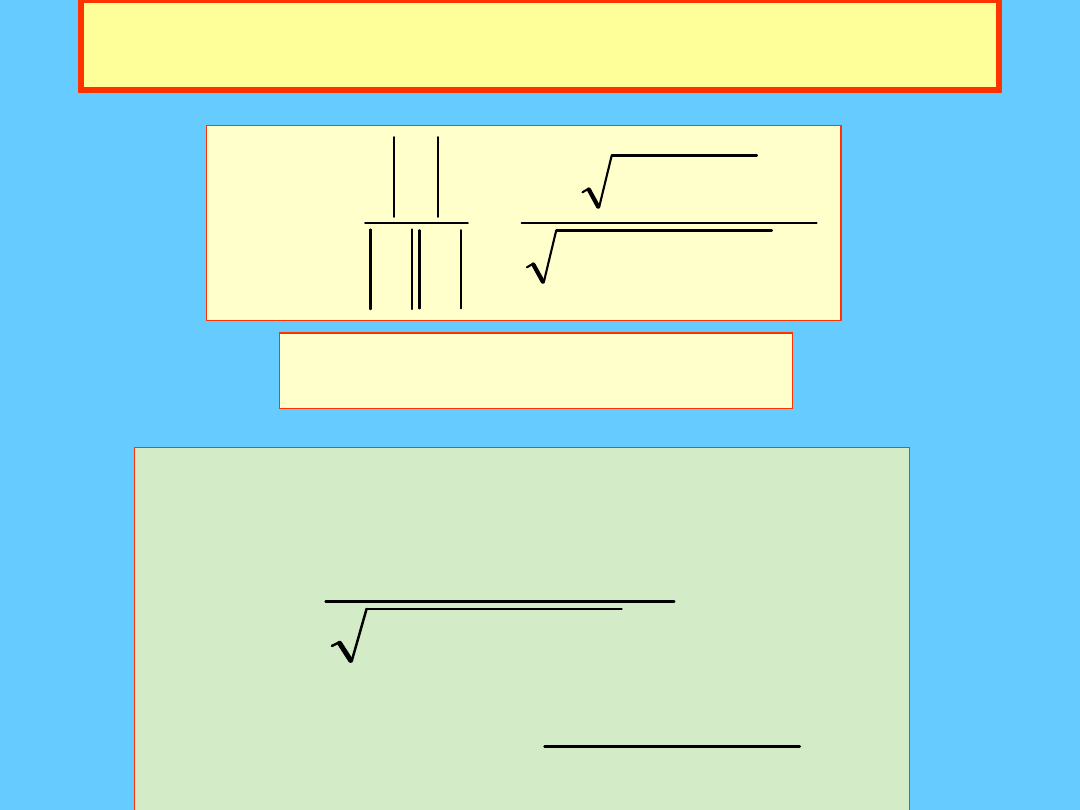
Przykład c.d.
Na podst. M.Kozlowski ,Wprowadzene do fizyki , Uw, 2002/2003
Iloczyn skalarny
.
1
16
25
4
4
25
16
cos
sin
,
1
16
25
4
2
cos
,
2
2
2
B
A
.
1
16
25
4
25
16
sin
B
A
C
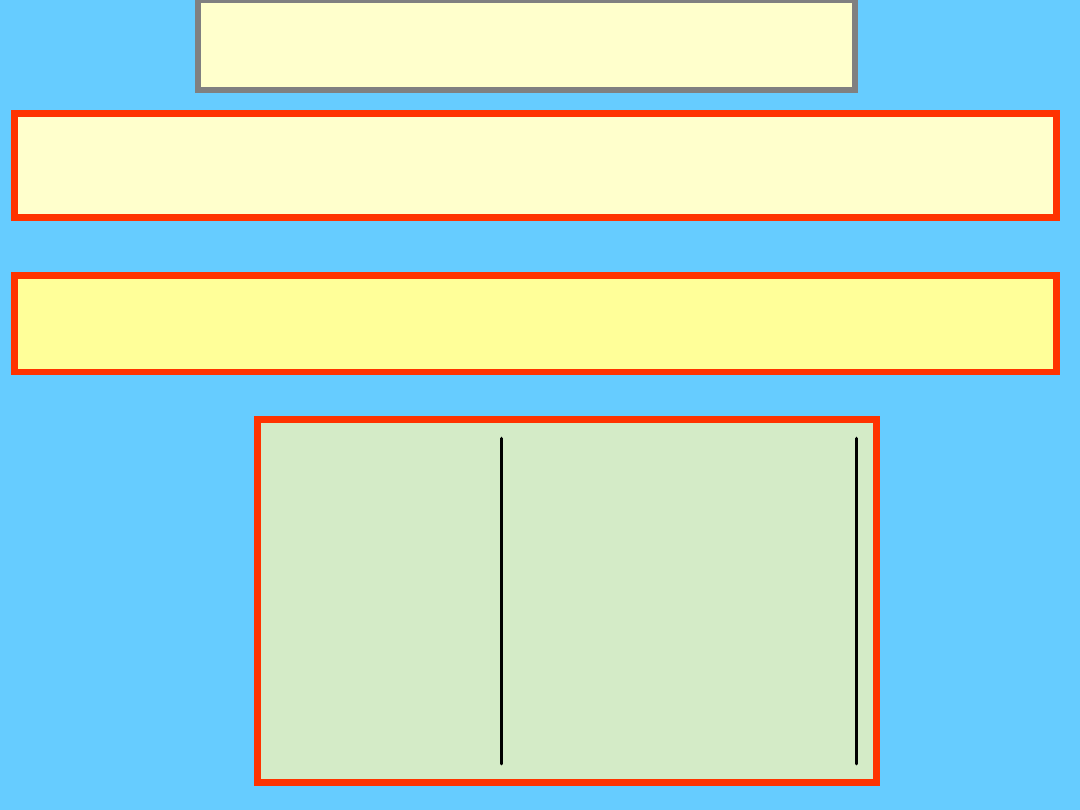
Iloczyn mieszany
wektorów
b
a
c
a
c
b
c
b
a
c
b
a
]
[
lub
]
[
]
[
]
[
]
[
]
[
]
[
a
b
c
c
a
b
b
c
a
b
a
c
a
c
b
c
b
a
z
y
x
z
y
x
z
y
x
c
c
c
b
b
b
a
a
a
c
b
a
Podwójny iloczyn wektorowy
b
c
a
b
a
c
c
a
b
c
b
a
)
(
)
(
Pola skalarne i
wektorowe
Pochodna wektora względem argumentu
skalarnego
k
)
(
j
)
(
i)
(
)
(
=
t
a
t
a
t
a
t
a
a
z
y
x
k
j
i
)
(
)
(
lim
dt
da
dt
da
dt
da
t
t
a
t
t
a
t
dt
a
d
z
y
x
0
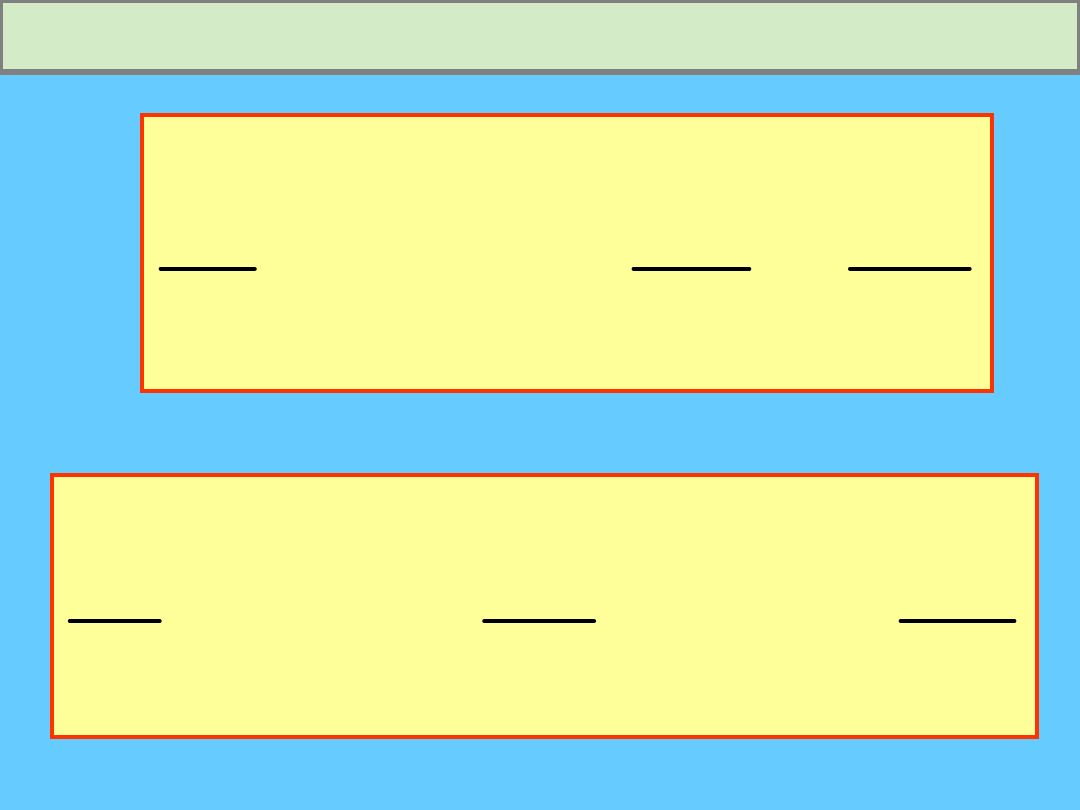
Pochodna wektora względem argumentu
skalarnego
dt
d
dt
d
dt
d
b
a
=
)
b
+
a
(
dt
d
a
b
dt
d
dt
d
b
a
=
)
b
a
(
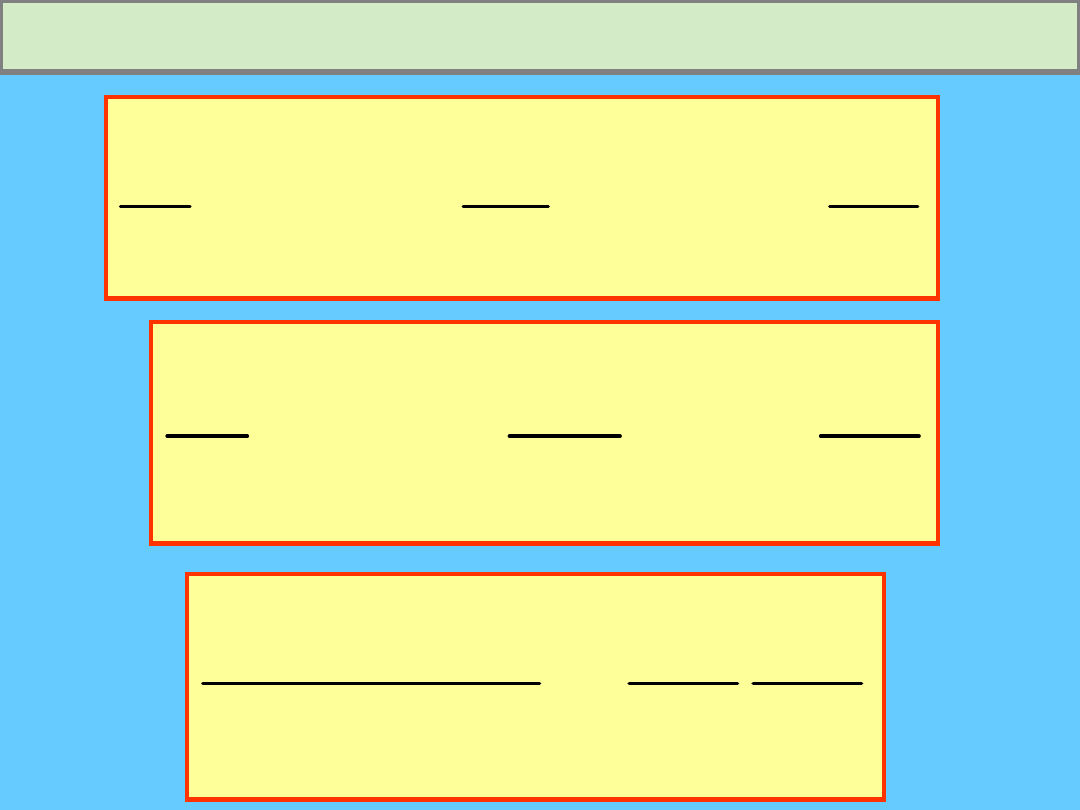
Pochodna wektora względem argumentu
skalarnego
dt
d
a
b
dt
d
dt
d
b
a
=
)
b
a
(
dt
d
a
dt
d
dt
d
a
=
)
b
(
dt
d
d
a
d
dt
t
a
d
=
)]
(
[